A Numerical Study for Reducing Cavitation in a Butterfly Valve with a Perforated Plate

2.1. 수치해석 모델

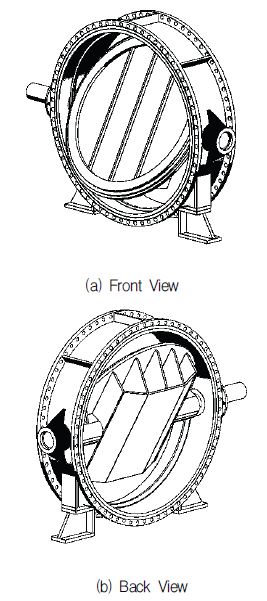
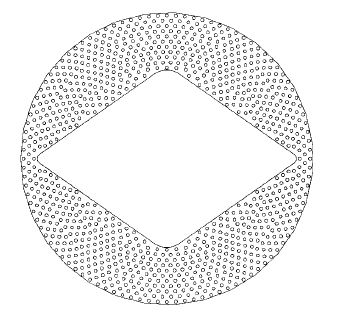
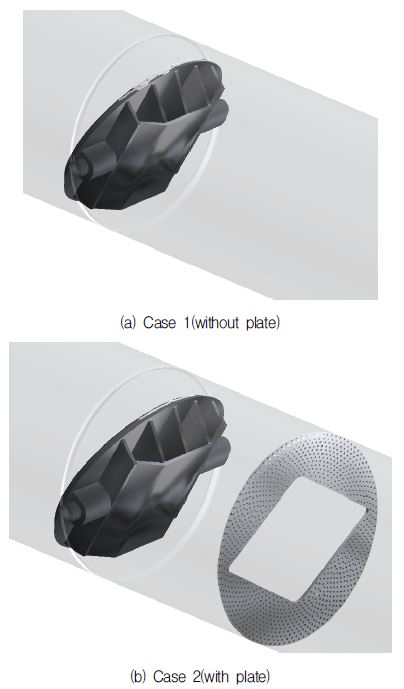
본 연구에서 적용된 버터플라이밸브는 ㈜삼진정밀에서 제공한 BFV 2800A 모델로, Fig. 1와 같이 유로의 직경은 D = 2800mm이다. 전체적인 경향을 파악하기 위하여 개도 θ = 10∼60°에 대해서 입구 유속 V 1∼5m/s로 해석을 진행하였고, 특히 개도 θ = 30° 이하의 빠른 유속 조건에서 공동현상이 심각하게 발생하는 것을 확인하였다. 그리하여 본 연구의 해석대상을 개도 θ = 30°에 대해 입구 유속을 V = 3 ∼5m/s까지 변경하였고, 다공판을 설치한 후에도 같은 조건으로 해석을 진행하였다. 밸브 상류측 길이는 5D로 설정하여 유동이 충분히 발달할 수 있도록 하고, 밸브 하류측 길이는 10D로 설정하여 밸브와 다공판을 지나며 교란된 유동이 충분히 안정화되도록 설정하였다.(6) Fig. 2는 공동현상 발생 저감을 위해 설치한 다공판의 모습으로, 직경은 밸브와 같고 두께는 t = 40 mm, ø = 3mm인 구멍이 약 800개 뚫려있다. 실제 다공판의 위치는 확정된 것이 아니므로, 개연성 확인을 위하여 밸브의 개폐에 간섭하지 않는 유동 후류방향으로 1D의 위치에 설치되었다고 가정하였다.

Fig. 1

Geometry of butterfly valve

Fig. 2

Geometry of a perforated plate

2.2. 수치해석 방법

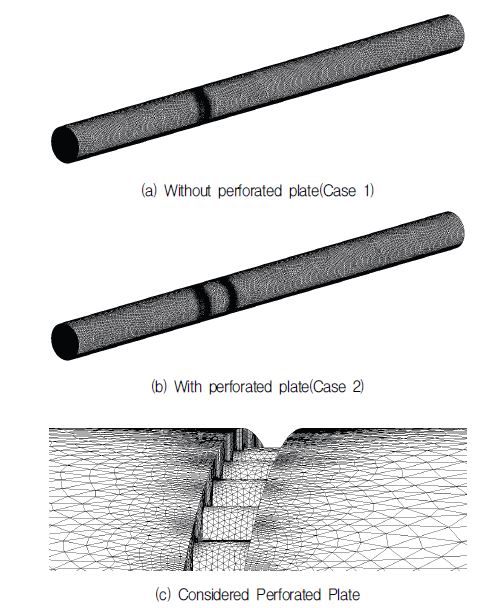
본 연구에서는 터보기계를 포함한 유체기계 해석에 최적화된 CFD 상용코드인 CFX를 사용하였다.(7) 수치해석에서 사용된 계산격자는 CFX Mesh와 ICEM CFD의 기법을 종합하여 만들어진 Workbench-based Meshing Application을 사용하였으며 Fig. 3에 나타나 있다. 밸브와 다공판의 복잡한 형상 때문에 전체적으로 tetrahedral 격자를 사용했으며, 점성저층(viscous sublayer)영역의 정확한 해석을 위하여 경계조건이 벽면으로 적용되는 부분에 대해서는 prism 격자를 사용하였다. 다공판이 없는 경우(Case 1)에는 생성된 격자수가 154만개, 다공판이 있는 경우(Case 2)에는 1124만개로 다공판에 의해 격자수가 약 7배 이상 증가하였다.

다공판의 경우, 유동 해석의 편의를 위하여 일정한 압력 강하를 발생시키는 다공성 매질(porous media)로 모사하여 해석할 수 있다.(8) 하지만 이런 방법을 채택할 경우, 다공판에서 걸리는 압력 강하량을 대상 매질의 porosity로 조절하는 시행착오법(trial-and-error)을 적용해야 하는 불편함이 있다. 더욱이 다공판 전후에서의 압력 강하량에 대한 실험적인 데이터가 없기 때문에 본 연구에서는 이러한 방법을 채택하지 않았다.

우선 유동 해석의 편의를 위한 개연성 있는 방안으로, 다공판을 간단한 형상으로 수정하여 경향성을 파악하였다. 많은 구멍들은 격자수를 급격하게 증가시켜 장시간의 해석이 필요하기 때문에 구멍들을 모두 생략하여 해석한 결과, 생략한 구멍만큼 유로의 단면적이 크게 줄어듦에 따라 공동현상을 과하게 예측하는 경향을 보였다. 그리하여 본 연구에서는 실제 다공판을 직접 고려하는 방법을 채택하기로 하였다.

Table 1은 해석영역의 경계조건을 정리한 것이다. 난류 모사를 위하여 SST(Shear Stress Transport)모델을 사용하였으며, 공동현상 해석을 위해서 multiphase 및 캐비테이션 모델로는 Rayleigh-Plesset equation을 사용하였다.(9) 작동유체는 20℃의 물(water)로, saturation pressure는 2.338kPa이다. 작동 유체인 물이 밀도가 크고 밸브의 직경이 매우 크기 때문에 자중을 무시할 수 없으므로 g = 9.81m/s²의 중력가속도를 적용하였다.

Table 1

Boundary Conditions

Fig. 3

Grid configuration

3.1. 유속에 따른 압력분포

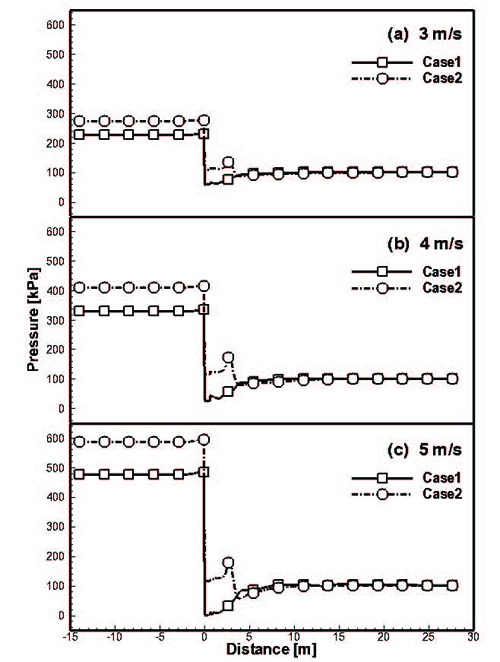
Fig. 4는 각 입구유속 조건에서의 배관 중심의 압력분포를 보여주며, 실선이 다공판이 설치되지 않은 경우(Case 1)이고 점선이 다공판이 설치된 경우(Case 2)이다. 거리가 0m(0D)인 지점이 밸브의 중심이고 –14m(5D)인 지점이 입구, 28m(10D)인 지점이 출구이다. 밸브를 지나며 압력이 급격하게 강하되는 모습을 보여주며, 압력 강하는 유속이 빠를수록 크게 일어난다. 표시된 압력은 모두 절대압력을 나타내며, 다공판이 없는 경우에는 밸브 근처에서 대기압(100kPa)이하로 낮아지는 모습을 볼 수 있다. 이로 인해 국부적으로 포화증기압(2.338kPa) 이하로 압력이 낮아져 밸브 근처에서 공동현상이 발생하리라는 예측이 가능하다. 반면에 다공판이 설치된 경우에는 밸브를 지난 후에 압력 강하가 발생하긴 하지만, 다공판이 없는 경우보다는 상대적으로 높은 압력을 유지한다. 즉 공동현상이 감소하리라는 예측이 가능하고, 최대 압력 강하 지점이 밸브(0D)가 아닌 다공판이 설치된 밸브 후단(1D)이기 때문에 상대적으로 밸브에 대한 직접적인 피해가 감소할 것이라는 예측이 가능하다. 그 이후로는 대기압으로 서서히 압력을 회복하며 출구까지 유지되는 경향을 보여준다.

Fig. 4

Pressure distribution along the centerline

3.2. 압력손실계수

압력 강하의 정도를 나타내는 압력손실계수, K는 밸브를 포함하여 유체기계의 설계에 매우 중요한 파라미터로 식 (1)과 같이 나타낼 수 있다. 이는 공동현상의 발생은 액체의 절대압력이 포화증기압까지 낮아지지 않더라도 급격한 압력 강하에 의해 국부적으로 발생할 수 있기 때문이다.

여기서, V는 평균 유입 속도, ρ는 물의 밀도이며, ∆P는 밸브의 상류측으로 밸브 직경의 2배(2D)인 지점과 하류측으로 밸브 직경의 6배(6D)인 지점의 사이의 압력 강하량으로 설정하였다.(10)

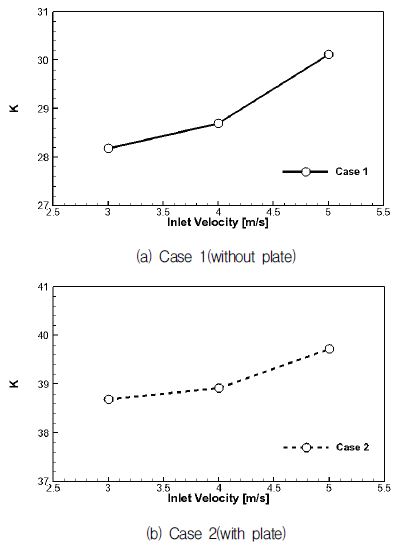
Fig. 5는 유속에 따른 압력손실계수의 변화를 보여주는데, 유속이 증가함에 따라 압력손실계수 또한 증가하는 모습을 보여준다. Fig. 5(b)에서 다공판을 설치했을 경우 Fig. 5(a)에 비해 압력손실계수가 더 높다. 이는 다공판에 의해 밸브에서의 속도증가량이 감소하여 그만큼 압력이 상승했고, 상대적으로 상승한 압력만큼 압력 강하량이 증가했기 때문이다. 한편 단면적이 일정한 배관에서 유속의 증가는 결국 유량이 증가하는 것과 같기 때문에, 유량이 증가함에 따라 압력손실계수가 증가하고 공동현상이 발생하기 쉬운 특징을 보여준다.

3.3. 공동현상 비교

수증기의 체적분율(vapor volume fraction)은 공동현상의 발생을 나타내는 지수라고 할 수 있다. 즉, 물이 좁은 개도의 밸브를 지나면서 유속이 급격히 빨라지게 되고, 포화증기압 이하로 낮아진 영역에서 수증기의 체적분율이 1이 되게 된다. 공동현상이 발생한 영역을 확인하기 위해 수증기의 체적분율에 대하여 10^-5에서 1까지의 범위를 체적으로 도시하였다.

Fig. 6은 V = 3 m/s의 유입 속도에서 다공판의 유무에 따른 공동현상의 발생을 고찰한 것이다. 단면적이 좁아지는 밸브 상단의 아주 좁은 영역에서 공동현상이 발생하는 것을Fig. 6(a)로부터 알 수 있다. Fig. 6(b)는 (a)와 동일한 입구 유속 조건에서의 유동이 다공판의 영향으로 인해 최대 압력 강하 지점이 밸브가 아닌 다공판이 설치된 위치로 이동하여, 밸브 상단에 보였던 공동현상이 약간 저감되었고 다공판에 소량 발생한 모습을 보여준다.

Fig. 7(a)는 V = 4 m/s의 유입 속도에서의 유동특성을 보여주는 그림이며, 단면적이 좁아지는 밸브 상단뿐만 아니라 밸브 중심의 회전축 부근에도 공동현상이 보인다. Fig. 7(b)는 (a)와 동일한 입구 유속 조건에서의 유동이 다공판의 영향으로 인해 최대 압력 강하 지점이 밸브가 아닌 다공판이 설치된 위치로 이동하여, 밸브 근처에 보였던 공동현상이 눈에 띄게 저감된 모습이다. 반면에 다공판 상단의 다수의 구멍에 국소적인 과도한 압력 강하로 인하여 공동현상이 발생함을 알 수 있으며, 이로 인해 유로 막힘 현상이 발생할 수 있을 것으로 예상된다.

Fig. 8(a)는 V = 5m/s의 유입 속도에서의 유동특성을 보여주는 그림이며, 밸브 후단의 전역에서 공동현상이 예측된다. 광범위한 공동현상으로 인해서 유로 막힘 현상이 매우 심하게 발생할 것으로 예상된다. Fig. 8(b)는 (a)와 동일한 입구 유속 조건에서의 유동이 다공판의 영향으로 인해, 최대 압력 강하 지점이 밸브가 아닌 다공판이 설치된 위치로 이동하여 밸브 후단의 전역에 보였던 공동현상이 확연하게 저감된 모습이다. 반면에 다공판 상단의 전역에 공동현상이 발생함을 알 수 있으며, 마찬가지로 유로 막힘 현상이 발생할 수 있을 것으로 예상된다. 따라서 개도 θ = 30°에 대해서는 유속 V = 5 m/s 이상에서 운용하면 다공판의 내구성이 크게 줄어들 것으로 판단된다.

Fig. 5

Coefficient of pressure loss

Fig. 6

Occurrence of cavitation at inlet velocity of V = 3 m/s

Fig. 7

Occurrence of cavitation at inlet velocity of V = 4 m/s

Fig. 8

Occurrence of cavitation at inlet velocity of V = 5 m/s

Table 2는 앞에 도시된 체적을 정량적으로 환산한 값들이다. 유속 V = 3m/s의 경우 다공판의 영향으로 공동현상이 발생하는 영역이 약 21.5%가 저감하였다. 유속 V = 4 m/s에 대해서는 85.3%, 유속 V = 5 m/s에 대해서는 94.0%의 저감 효과를 보여준다. 다공판의 설치로 인하여 충분히 공동현상을 저감할 수 있다고 판단된다.

Table 2

Volume of cavitation