저널 래버린스 실이 임펠러 추력 및 누설에 미치는 영향

1. 서 론

최근 소형 터보압축기는 단위 중량당 압축비를 증가시키기 위하여 소형화 및 고속화가 진행 중이다. 터보압축기는 회전부(rotor)와 비회전부(stator) 사이의 간극이 필연적으로 존재한다. 간극을 통해 발생하는 누설유량이 증가할 경우 토출 유량 및 압축 효율이 감소한다. 따라서 간극을 통해 발생하는 누설 유량이 압축기의 성능에 미치는 영향에 대한 많은 연구들이 수행되어 왔으며^[1-3], 압축기의 효율 증가를 위해 회전부와 비회전부 사이의 간극의 누설 최소화를 위한 누설 방지 시스템의 연구의 필요성이 증대되었다. 대표적인 누설 방지 시스템의 예로는 브러쉬 실(brush seal), 플로팅 링 실(floating ring seal), 래버린스 실(labyrinth seal) 등이 사용된다^[4]. 브러쉬 실은 접촉식 실로 래버린스 실에 비해 누설 유량이 크게 감소된다는 장점을 가지지만, 지속적으로 축과 브러쉬의 마찰로 높은 국소 열 발생으로 인한 열변형을 초래하고 브러쉬 팁의 마모가 발생하는 단점을 가진다^[5]. 플로팅 링 실과 래버린스 실은 비 접촉실로 회전부와 비회전부 사이의 마찰이 존재하지 않아 반영구적인 수명을 가지는 장점을 가진다. 하지만 플로팅 링 실은 래버린스 실에 비해 구동조건에 따른 복잡한 설계가 필요하다는 단점을 가진다^[6]. 래버린스 실은 회전부, 비회전부 혹은 양측 모두에 이(tooth)를 설치하여 공동(cavity)과 작은 간극의 반복에 의한 에너지 소산으로 유체의 누설 유량을 감소시킨다^[4]. 래버린스 실은 이와 같은 단순한 구조를 가져 제작과 설계가 간편하다는 장점으로 많은 연구가 수행되어 왔다. Iwatsubo^[7]는 터빈과 압축기에 적용되는 래버린스 실의 누설 유량 및 동적 계수 예측을 위한 bulk-flow model(BFM)을 개발하였으며, 저속 및 저압 조건의 실험결과와 BFM 해석 결과는 잘 일치하는 반면 고속 및 고압 조건의 실험결과와는 차이를 보임을 확인하였다. 이와 같은 문제점을 해결하고 더 정확한 예측을 위하여 현재까지 많은 해석적/실험적 연구가 수행되고 있다. Stoff^[8]는 래버린스 실 내부에서 발생하는 난류의 영향으로 인한 유동 흐름과 에너지 소산 특성을 확인하기 위하여 래버린스 실의 2차원 해석 모델을 개발하였다. 또한, LDA(laser-doppler anemometer)를 통해 측정된 실의 내부 유속을 이용하여 난류 소산 계수를 계산하였으며, 실험을 통해 계산된 난류 소산 계수와 2차원 해석 모델 결과의 비교를 통해 모델의 타당성을 검증하였다. Eser과 Kazakia^[9]는 BFM을 이용하여 래버린스 실의 누설 유량, 각각의 캐비티의 압력, 동적 계수에 대한 해석적 연구를 수행하였으며, 이를 기존 문헌의 실험결과와 비교하여 검증하였다. Yücel^[10]은 BFM을 이용하여 계단 형상의 래버린스 실의 압력 차이에 따른 누설 유량과 유입 속도에 따른 동적 계수에 대한 해석적 연구를 수행하였으며, 기존 문헌의 실험결과와 비교하여 검증하였다. San Andrés 등^[11]은 이(tooth)가 고정자와 회전자 사이에 엇갈려 위치하는 래버린스 실의 입, 출구의 압력차이와 축의 회전속도에 따른 래버린스 실의 누설 유량과 각 캐비티의 압력 분포를 측정하였으며, 시험을 통해 측정된 결과와 CFD(computational fluid dynamics), BFM의 해석 결과와의 비교를 통해 해석결과와 시험결과가 잘 일치함을 확인하였다.

터보압축기에서 발생하는 추력은 주로 임펠러(impeller)의 전면과 배면의 압력차이로 인해 발생하게 된다^[12]. 최근 고성능화로 인해 증대된 압축비에 의해 임펠러에 의해 발생하는 추력이 점차 증가하고 있다. 임펠러에 의해 발생하는 과도한 추력은 베어링의 수명 단축 및 파손, 더 나아가 회전체 동역학적 불안정성을 야기하여 추력 예측 및 감소를 위한 많은 연구가 수행되어 왔다^[13-16]. Kurokawa 등^[17]은 좁은 간격을 통해 누설이 발생하는 회전디스크의 유동 흐름에 대해 해석적 연구를 수행하였다. 회전디스크와 벽면 사이에 존재하는 간극의 크기에 따른 간섭 모델을 제시하였으며, 해석을 통해 간극의 크기가 감소함에 따라 유동의 압력이 크게 감소함을 보였다. 또한 누설 유량과 누설 방향에 따른 압력장 분포 해석을 통해 디스크의 외경에서 내경으로 흐르는 유량이 증가할 경우 후면의 압력이 급격히 강하되고 디스크의 내경에서 외경으로 흐르는 유량이 증가할 경우 압력이 완만히 감소함을 확인하였다. Poncet 등^[18]은 난류가 발생하는 회전디스크와 벽면 사이의 유동 흐름에 대한 실험적 연구를 수행하였다. 실험을 통해 다양한 속도 조건에서의 회전디스크 후면의 유동장 속도와 압력 분포를 측정하였으며, 회전디스크의 속도가 증가함에 따라 후면에서 압력이 급격히 감소함을 확인하였다. 또한 실험결과를 바탕으로 유동장의 코어층 속도 계수를 이용한 실험식을 개발하였다. Gantar 등^[19]은 1단 압축 펌프 임펠러의 후면의 누설 유량 변화에 따른 압력 분포와 유동장의 속도 분포를 측정하였다. 누설이 임펠러 내부의 방향으로 발생할 경우는 누설이 발생하지 않을 경우보다 후면의 압력은 외경에서 내경으로 이동함에 따라 급격히 감소하고 임펠러 후면과 벽면 사이의 간극의 중심에서의 유체의 회전속도가 증가함을 확인하였다. 누설이 외부의 방향으로 발생할 경우는 누설이 존재하지 않는 경우보다 후면의 압력은 증가하고, 유체의 회전속도가 감소함을 확인하였다. 또한 수치해석을 통한 유동해석결과를 실험결과와 비교하여 검증하였다. Kurokawa 등^[20]은 래버린스 실과 밸런싱 피스톤(balancing piston)이 적용된 로켓엔진의 산화제 펌프의 밸런싱 피스톤의 간극(clearance)에 따른 누설 유량 및 임펠러의 축방향 하중에 대한 해석을 수행하였으며, 이를 시험결과와의 비교를 통한 검증을 수행하였다. 노준구 등^[21], 최창호 등^[22], 그리고 김대진 등^[23]은 액체로켓엔진 원심터보펌프의 베인이 축추력에 미치는 영향에 대한 해석 및 실험적 연구를 수행하였다.

임펠러에 의해 발생하는 추력을 정확히 예측하기 위해서는 임펠러의 형상뿐만 아니라 누설 방지 시스템이 같이 고려되어야 한다. 하지만 임펠러에 의해 발생하는 추력과 누설 방지 시스템의 개별 연구는 많이 이루어지고 있는 반면, 상대적으로 누설 방지 시스템이 적용된 임펠러에 의해 발생하는 추력의 연구결과의 발표는 적은 실정이다. 이에 따라 본 논문에서는 래버린스 실이 적용된 임펠러에 의해 발생하는 추력에 대한 연구를 수행하고자 한다. 임펠러에 의해 발생하는 추력을 예측하기 위하여 임펠러 후면과 래버린스 실의 압력강하, 누설 유량에 대한 동시해 해석 모델을 개발하고 임펠러 각각의 요소에서 발생하는 압력 분포를 통해 추력을 계산하고자 한다. 또한, 개발된 동시해 해석 모델을 이용하여 임펠러의 회전속도, 래버린스 실의 클리어런스, 이의 개수, 임펠러 케이싱 사이의 간극의 변화가 임펠러에서 발생하는 추력과 누설 유량에 미치는 영향을 확인하고자 한다.

2. 래버린스 실이 조합된 임펠러의 추력 개요

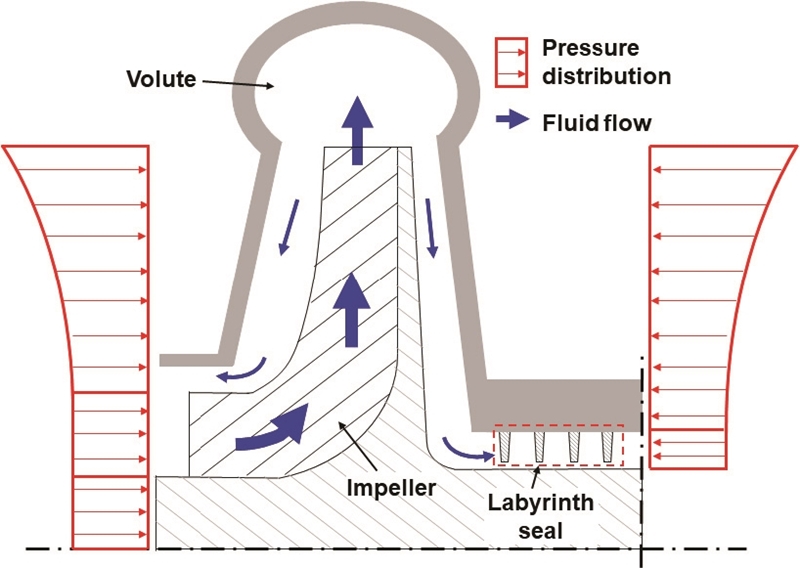
Fig. 1은 래버린스 실이 조합된 임펠러의 개략도를 보여준다. 작동 유체는 임펠러의 입구를 통해 유입되고 블레이드(blade)를 지나며 압축되어 볼루트(volute)를 통해 이동하게 된다. 또한, 임펠러 후면과 케이싱 사이 간극에서 채널 압력 차이에 의해 누설이 발생하며, 이를 감소시키기 위하여 임펠러 후면 이후 축방향 래버린스 실이 위치한다. 임펠러의 입구와 허브는 유체의 유입 압력과 동일한 압력이 가해지게 되며, 임펠러의 내경에서 외경으로 이동함에 따라 압축된 유체에 의해 점차적으로 압력이 증가한다. 또한, 임펠러 후면의 간극을 통해 발생하는 압축된 유체의 누설로 임펠러 후면의 초기 압력은 토출 압력과 동일한 값을 가지고, 임펠러 후면을 따라 흐르며 점차적으로 압력이 감소한다. 이와 같은 특성으로 임펠러의 전면과 후면의 압력 차이에 의해 발생하는 추력을 예측하기 위해서는 누설 유량이 고려된 임펠러에 의해 발생하는 압력 분포와 래버린스 실을 통과하는 누설 특성의 파악이 필수적이다. 래버린스 실을 통해 발생하는 누설은 실의 입구와 출구의 압력 차이에 의해 발생하게 되는데 래버린스 실이 조합된 임펠러의 경우 임펠러 후면의 압력이 래버린스 실의 입구의 압력이 된다. 이에 임펠러 후면의 압력 분포를 정확히 파악하기 위해서는 래버린스 실과 후면의 압력분포 동시해 해석이 필수적이다.

Fig. 1

Schematic view of flow direction and pressure distributions for impeller combined with labyrinth seals

3. 임펠러의 추력 및 압력 분포 해석 모델

3.1 임펠러의 추력 해석 모델

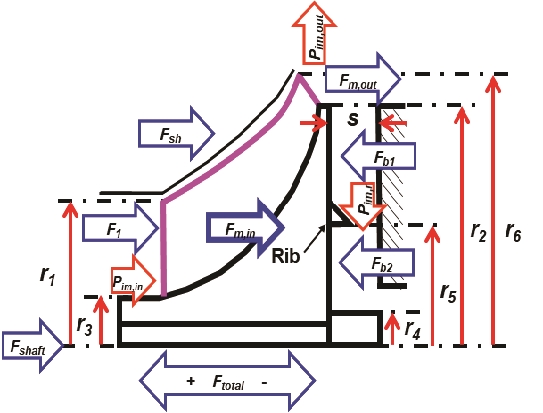
Fig. 2는 임펠러에 의해 발생하는 추력의 구성요소에 대한 개략도이다. 임펠러에서 발생하는 총 추력은 각각의 구성 요소들의 축방향 하중의합으로 나타나며, 식 (1)과 같이 표현된다^[12].

$\[ F_{total}=F_1+F_{sh}+F_{shaft}+F_m+F_{b1}+F_{b2} \]$

(1)

Fig. 2

Schematic view of impeller geometry and axial thrust force components

F₁은 임펠러 입구의 블레이드에서 발생하는 하중으로 식 (2)와 같이 계산된다.

$\[ F_1=\pi \left(r_1^2-r_3^2\right)\cdot P_{im,in} \]$

(2)

F_sh는 임펠러 슈라우드(shroud) 혹은 블레이드에서 발생하는 하중으로 2차 곡선의 압력강하^[24]로 가정하여 모델링을 수행하였으며, 식 (3)과 같이 계산된다.

$\[ F_{sh}=\begin{array}{l}{\int }_{r_1}^{r_6}2\pi rPdr,\\ \left(P=P_{im,in}+\left(P_{im,out}-P_{im,in}\right){\left\{\left(r-r_1\right)/\left(r_2-r_1\right)\right\}}^2\right)\end{array} \]$

(3)

F_shaft는 축에서 발생하는 하중으로 임펠러 허브(hub)에 가해지는 정압에 의해 발생하게 되며, 식 (4)와 같이 계산된다.

$\[ F_{shaft}=\pi r_3^2\cdot P_{im,in} \]$

(4)

F_m,in과 F_m,out는 임펠러의 유체의 유동에 의해 발생하는 하중으로 식 (5), (6)과 같이 계산된다.

$\[ F_{m,in}=\rho \cdot Q_{im,in}\cdot V_{im,in} \]$

(5)

$\[ F_{m,out}=\rho \cdot Q_{im,out}\cdot V_{im,out} \]$

(6)

일반적으로 원심 압축기(centrifugal compressor)의 임펠러에서 유체의 유동에 의해 발생하는 하중은 무시할 수 있을 정도로 매우 작을 값을 가진다^[20].

마지막으로 F_b1과 F_b2는 임펠러 후면의 압력 분포에 의한 하중으로 토출 압력(P_im,out)와 임펠러 후면의 압력(P_im,r)을 통해 계산이 가능하며, 식 (7), (8)과 같다. 이때 임펠러 후면의 압력(P_im,r)은 r에 관한 함수로 이루어지며, P_in,r5은는 립을 통과한 이후의 후면의 압력이다.

$\[ F_{b1}={\int }_{r_5}^{r_2}2\pi r{P}_{im,r}dr \]$

(7)

$\[ F_{b2}=\pi \left(r_5^2-r_4^2\right)\cdot P_{im,r_5} \]$

(8)

3.2 임펠러 후면의 압력 분포 해석 모델

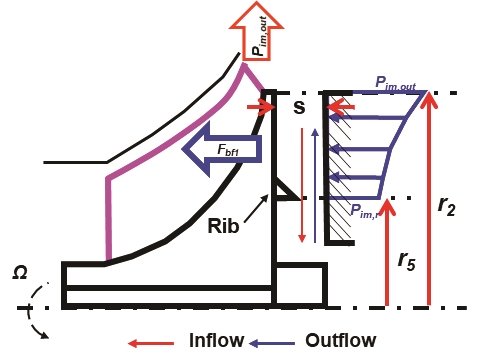
Fig. 3은 임펠러의 후면과 케이싱 벽면을 통해 발생하는 누설에 따른 후면의 압력 분포 변화와 추력에 대한 개략도를 보여준다. 임펠러의 후면 압력 분포 모델은 참고문헌^[24]의 모델을 사용하였으며, 식 (9)와 같이 표현된다.

Fig. 3

Schematic view of pressure distribution and axial thrust on rear of impeller considering leakage

임펠러 후면의 압력 분포 식에서 $$ \overline{P}, \overline{s},\overline{ r},\overline{Q}, {\overline{c}}_{2ul}$$는 각각 무차원화된 압력, 임펠러 후면과 케이싱 벽면 사이의 간극, 누설 유량, 임펠러 끝단에서의 유체의 속도이며, 식 (10), (11), (12), (13), (14)와 같이 표현된다.

$\[ P_{im,r}=\begin{array}{l}\overline{P}\cdot \left({\overline{P}}_{im,out}-\left\{\left[51.84\cdot \overline{Q}\cdot {\overline{c}}_{2ul}{\left(1-\overline{r}\right)}^2+0.25\cdot {\overline{c}}_{2ul}\cdot \left(1-\overline{r}\right)\right.\right.\right.\\ {\left.+56.3\cdot \overline{Q}\cdot \left(1-\overline{r}\right)+0.46\cdot \left(1-\overline{r}\right)-22.5\cdot \sqrt{\overline{Q}}\cdot \overline{s}\cdot \left(1-\overline{r}\right)\right]}^2\\ \left.\left.+0.028-0.7\cdot {\left(0.8-\overline{r}\right)}^2+{\left(1-\overline{r}\right)}^{7.28\cdot {\left(1-\overline{r}\right)}^2+2.345}\right\}\right)\end{array} \]$

(9)

$\[ \overline{P}=P_{im,out}/\left(\rho \cdot {\left(\mathrm{\Omega }\cdot r_2\right)}^2\right) \]$

(10)

$\[ \overline{s}=s/r_2 \]$

(11)

$\[ \overline{r}=r/r_2 \]$

(12)

$\[ \overline{Q}=\left({\dot{m}}_{lkg,r}/\rho \right)/\left(\mathrm{\Omega }\cdot r_2^3\right) \]$

(13)

$\[ {\overline{c}}_{2ul}=c_{2ul}/\left(\mathrm{\Omega }\cdot r_2\right) \]$

(14)

임펠러 끝단(impeller tip)에서 임펠러 후면으로 흐르는 유체의 원주방향 속도는 일반적으로 고정 벽면과 회전 벽면 사이의 유체의 유동으로 벽면의 회전 속도의 절반 값을 가지므로 $$ {\overline{c}}_{2ul}$$는 0.5를 적용하였다^[25].

4. 래버린스 실의 누설 유량 해석

4.1 래버린스 실의 누설 유량 해석 모델

Fig. 4는 비회전부에 이가 설치되어 있는 래버린스 실의 개략도를 보여준다. L, B, Tip, C_r, R_s는 각각 래버린스 실의 피치(pitch) 길이, 래버린스 실의 높이, 래버린스 실의 이(tooth)의 끝단 길이, 래버린스 실의 간극(clearance), 회전축의 반지름이다.

Fig. 4

Schematic view of straight journal labyrinth seal

래버린스 실의 누설 유량을 예측하기 위해서는 회전부와 비회전부 사이의 실의 틈새 유동의 특성을 파악하여야 한다. 하지만 일반적으로 실의 틈새는 매우 작고 난류 유동이 발생하며, 복잡한 형상으로 인해 정확한 해석이 어려운 문제점이 있다. 누설 유량을 예측하기 위해 현재까지 윤활이론을 기반으로 하는 bulk-flow 해석 모델이 널리 사용되고 있으며, 특히 1개의 공동(cavity)의 제어체적을 이용하는 one-control-volume model이 주로 사용되어 왔다^[9-11].

누설 유량은 Neumann^[26]의 실험식으로 계산이 가능하며 식 (15)로 표현된다. μ, C_i, AN, R, T, P_i는 각각 속도 분포 불균일성 보정계수, 오리피스 수축 계수, 래버린스 실 간극의 면적, 기제 상수, 실의 온도, 각 캐비티의 압력이다. 속도 분포 불균일성 보정계수(μ)와 오리피스 수축 계수(C_i)는 식(16), (17)로 표현되며 γ는 비열비이다. 또한 회전부, 비회전부에 실의 이가 존재하는 간극의 면적(AN)은 식 (18)과 같이 표현된다.

실 입구와 출구의 압력차이가 일정 수준 이상에 도달하면 래버린스 실의 마지막 공동에서 질식(choke) 현상이 발생하며, 압력의 차이가 증가하여도 누설 유량이 거의 증가하지 않게 된다. 질식 현상의 발생 판별 여부는 식 (19)의 임계조건을 통해 판별이 가능하며, 질식 현상이 발생할 경우 식 (20)의 Neumann-Chaplygin-Fliegner model^[27]을 통해 마지막 공동의 누설 유량을 계산할 수 있다.

$\[ \dot{m}=C_i\mu \frac{AN}{\sqrt{RT}}\sqrt{P_{i-1}^2-P_i^2} \]$

(15)

$\[ \begin{array}{cc}\mu =\sqrt{\frac{NT}{\left(1-J\right)NT+J}} ,& \left(J=1-{\left(1+16.6Cr/L\right)}^{-2} \right)\end{array} \]$

(16)

$\[ \begin{array}{cc}{C}_i=\frac{\pi }{\pi +2-5S_i+2S_i^2} ,& \left(S_i={\left(P_{i-1}/P_i\right)}^{\left(1-1/\gamma \right)}-1\right)\end{array} \]$

(17)

$\[ AN=\left\{\begin{array}{ll}\pi \cdot \left(2Rs+Cr\right)\cdot Cr& ,\mathrm{ }\mathrm{ }\mathrm{T}\mathrm{e}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{ }\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{r}\\ \pi \cdot \left(2\left(Rs+B\right)+C_r\right)\cdot Cr& ,\mathrm{ }\mathrm{ }\mathrm{T}\mathrm{e}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{ }\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{r}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{r}\end{array}\right. \]$

(18)

$\[ \begin{array}{cc}\frac{P_{NT-1}}{P_{NT}}\ge {\left(\frac{\gamma +1}{2}\right)}^{\left(\frac{\gamma }{\gamma -1}\right)}& , \left(P_{NT}=Ps,out\right)\end{array} \]$

(19)

$\[ {\dot{m}}_{NT}=C_{NT}\mu \frac{AN}{\sqrt{RT}}\sqrt{\gamma {\frac{2}{\gamma +1}}^{\left(\gamma +1\right)/\left(\gamma -1\right)}} \]$

(20)

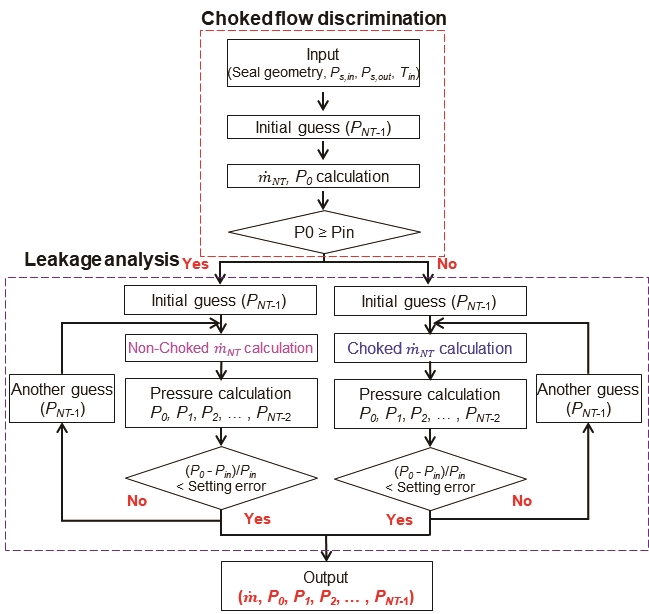
Fig. 5는 래버린스 실의 누설 유량과 각각의 공동의 압력계산을 위한 순서도이다. 초기 입력 조건으로 실의 유입압력(P_in), 실의 유출압력(P_out), 실의 온도(T_in)를 입력한 후 식 (19)의 질식 현상 임계조건을 통해 마지막 공동의 압력(P_NT-1)을 가정하여 계산된 유입압력(P₀)과 입력된 유입압력(P_in)을 통해 질식 현상 발생 여부를 판별한다. 이후 Newton-Raphson method를 이용하여 질식 현상이 일어나지 않을 경우 식 (15), 질식 현상이 발생할 경우 식 (20)을 통해 누설 유량과 각각의 공동의 압력을 계산하고 반복 계산을 통해 계산된 실의 유입압력(P₀)과 초기 입력 조건인 실의 유입압력(P_in)의 오차가 설정한 오차 이내의 범위에 도달하면 계산을 종료한다. 이를 통해 래버린스 실의 누설 유량과 각각의 공동의 압력을 산출한다.

Fig. 5

Flow chart showing the algorithm calculating cavities pressure and leakage flow rate of labyrinth seal

4.2 누설 유량 해석 결과 검증

검증은 참고문헌 [9]와 동일한 방식으로 참고문헌 [28]의 실험 결과와 해석 결과의 비교를 수행하였으며, Fig. 5의 순서도에 따라 해석을 수행하였다. 참고문헌 [28]은 입구온도(T_in) 298.2 K, 입구압력(P_s,in) 241.3 kPa, 출구압력(P_s,out) 206.8 kPa의 조건에서 클리어런스(C_r)는 0.16mm, 실의 이 개수(NT)가 2개인 래버린스 실의 누설 유량과 공동의 압력을 측정하였으며, Table 1은 본 논문에서 해석에 사용한 참고문헌 [28]의 래버린스 실의 형상과 구동 조건 정보를 보여준다. Table 2는 참고문헌 [28]의 측정 결과와 본 문헌에서 해석한 결과에 대한 비교를 보여준다. 입구압력(P_s,in)과 출구의압력(P_s,out)은 초기 조건으로 동일하며, 공동의 압력은 2.11 kPa로 약 1%, 누설 유량의 경우는 약 0.8 g/s로 약 4%의 오차로 잘 일치함을 확인하였다.

Table 1

Geometries and operating conditions of labyrinth seal Ref.[28]

Table 2

Predicted leakage flow rate and pressure distribution compared to experiment data in Ref.[28]

5. 래버린스 실을 갖는 임펠러 후면 압력 해석

5.1 래버린스 실을 갖는 임펠러 후면 압력 모델

Fig. 6은 래버린스 실을 가지는 임펠러 후면 압력분포의 개략도를 보여준다. 임펠러 입구의 압력과 래버린스 실의 출구의 압력은 주변의 압력으로 동일하며, 임펠러의 토출 압력과 임펠러 후면으로 초기 유입되는 압력은 동일하다 가정한다. 래버린스 실이 시작되는 지점(r₅)의 임펠러 후면의 압력(P_im,r)과 래버린스 실로 유입되는 압력(P_s,in) 그리고 임펠러의 후면을 따라 흐르는 누설 유량($$ {\dot{m}}_{lkg,r}$$)과 래버린스 실로 누설되는 유량($$ {\dot{m}}_{lkg,s}$$)이 동일하다 가정한다. 또한 임펠러 입구를 통해 유입되는 유량 ($$ {\dot{m}}_{\mathrm{i}\mathrm{n}}$$), 토출되는 유량($$ {\dot{m}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$$), 슈라우드를 통해 발생하는 누설 유량($$ {\dot{m}}_{lkg,f}$$), 임펠러의 후면을 따라 래버린스 실로 누설되는 유량($$ {\dot{m}}_{lkg,r}$$)의 합은 0이다.

Fig. 6

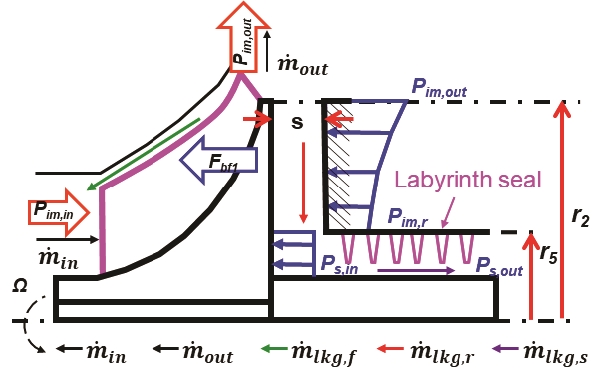
Schematic view of leakage flow direction and pressure distributions on rear of impeller with labyrinth seal

Fig. 7은 래버린스 실을 가지는 임펠러 후면의 압력강하와 누설 유량을 구하기 위한 순서도이다. 초기 임펠러, 실의 형상과 임펠러의 입구압력(P_im,in), 출구압력(P_im,out), 로터의 회전속도(Ω) 등의 구동조건을 입력한다. 초기 가정한 누설 유량을 이용하여 식 (9)를 통해 임펠러 후면의 누설 유량($$ {\dot{m}}_{lkg,r}$$)과 초기 실 위치(r₅)의 후면 압력(P_im,r5)을 계산한다. 이후 계산된 P_im,r5을 이용하여 Figure 5.의 순서도와 같이 래버린스 실의 누설 유량 및 공동의 압력이 계산된다. 임펠러 후면의 압력(P_im,r5)과 래버린스 실로 유입되는 압력(P_s,in) 그리고 임펠러의 후면의 누설 유량($$ {\dot{m}}_{lkg,r}$$)과 래버린스 실로 누설되는 유량($$ {\dot{m}}_{lkg,s}$$)이 일치할 경우 계산은 종료되고 일치하지 않을 경우는 P_im,r을 이용하여 계산된 래버린스 실의 누설 유량($$ {\dot{m}}_{lkg,s}$$)을 초기 가정 값으로 하여 반복계산을 통해 일치할 경우 계산이 종료한다. 이를 통해 임펠러 후면과 래버린스 실의 압력 분포와 래버린스 실을 통해 누설되는 누설 유량이 산출된다.

Fig. 7

Flow chart showing algorithm calculating pressure distribution and leakage flow rate at rear of impeller with labyrinth seal

5.2 래버린스 실을 갖는 임펠러 후면 압력 CFD 해석

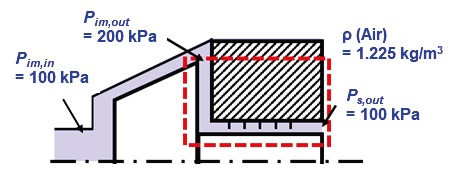
Fig. 8은 래버린스 실을 가지는 임펠러 후면의 압력 분포와 누설유량 그리고 래버린스 실의 누설 유량과 각각의 공동의 압력 해석을 위한 CFD 모델링의 개략도이다. 작동 유체로는 공기를 사용했으며, 임펠러 입구의 압력과 출구의 압력은 각각 100, 200 kPa이고 래버린스 실의 출구 압력은 100 kPa이다. Fig. 9는 CFD 모델이며 래버린스 실이 가지는 작은 간극에서의 유동의 특성을 정확히 해석하기 위하여 약 560만개의 다면체(polyhedral) 격자를 생성하였다.

Fig. 8

Schematic view and boundary conditions of impeller combined with labyrinth seal

Fig. 9

Photo of polyhedral mesh modeling for CFD analysis

Table 3은 CFD, BFM 해석에 사용된 임펠러와 실의 형상 그리고 구동 조건을 보여준다. 임펠러의 주요 치수인 외경(r₂), 실의 시작 높이(r5), 로터의 반지름(R_s)은 각각 35.5, 18.5, 12.5 mm 이며, 래버린스 실의 이의 수(NT)가 5개이고 실의 클리어런스(C_r)와 높이(B)는 각각 0.2 mm, 5.8 mm인 래버린스 실을 적용하였다.

Table 3

Geometries and operating conditions of the impeller and labyrinth seal for CFD and BFM analysis

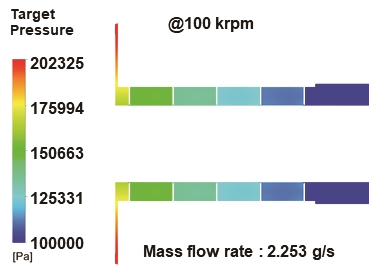
Fig. 10은 이상기체, 등온 조건에서의 k-ε 난류 모델을 사용한 CFD의 해석결과로 구동속도 100,000 rpm에서의 임펠러 후면과 래버린스 실의 압력 분포 및 누설 유량에 대한 해석결과를 보여준다. 임펠러 후면의 압력은 외경에서 내경으로 이동함에 따라 202 kPa에서 174 kPa까지 감소하는 경향을 보인다. 또한 래버린스 실은 초기 174 kPa의 압력이 유입되고 각각의 공동을 지남에 따라 압력이 감소하여 출구 압력인 100 kPa까지 감소하며, 2.253 g/s의 누설 유량이 발생한다.

Fig. 10

Contour plot of CFD analysis for pressure distribution and leakage flow rate at rear of impeller and labyrinth seal

5.3 BFM, CFD 해석 결과 비교 검증

Fig. 11은 CFD해석 결과를 BFM과 비교하기 위한 데이터 취득 구간을 보여준다. 임펠러 후면의 압력강하의 데이터를 취득하기 위하여 (a)와 같이 임펠러 후면과 케이싱 벽면 사이의 중앙의 데이터를 취득하였으며, 래버린스 실의 각각의 공동의 압력을 취득하기 위해 (b)와 같이 래버린스 실의 중앙의 데이터를 취득하였다. 또한 누설 유량 데이터를 취득하기 위하여 임펠러 후면의 후면을 통해 유입되는 유량과 래버린스 실을 통과하여 나오는 유량의 비교를 통해 동일한 값을 가짐을 확인하였다.

Fig. 11

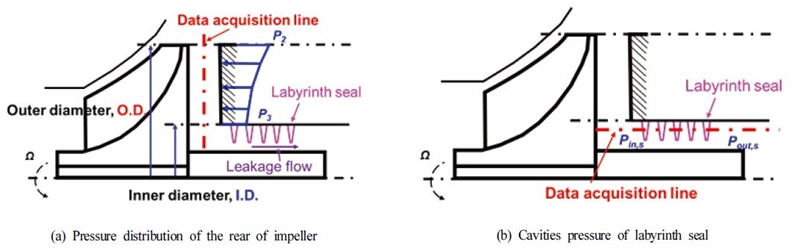
Data acquisition lines (a) pressure distribution of the rear of impeller and (b) cavities pressure of labyrinth seal

Fig. 12는 Fig. 11(a)와 같이 취득한 CFD의 해석 결과와 BFM을 통해 해석한 후면의 압력강하의 비교를 보여준다. BFM과 CFD 모두 임펠러의 외경에서 내경으로 이동함에 따라 압력강하가 감소하는 경향을 보이며, 최대 4 kPa 약 2% 이내의 오차를 보인다.

Fig. 12

Comparison of CFD and BFM analysis - predicted rear pressure of impeller versus radial location

Fig. 13은 Fig. 11(b)와 같이 취득한 CFD의 해석 결과와 BFM을 통해 해석한 래버린스 실의 각각의 공동 압력을 보여준다. CFD와 BFM의 실로 유입되는 초기 압력은 임펠러 후면의 압력에 의해서 결정되며, 각각 174 kPa, 166 kPa의 값을 가진다. 또한 CFD, BFM의 해석 결과 모두 유체 유동이 래버린스 실의 이와 회전축에 의해 형성된 오리피스(orifice)를 지남에 따라 압력이 감소하여 출구 압력인 100 kPa까지 감소한다. 해석 결과는 최대 8 kPa의 압력의 차이를 보이며, 약 5% 이내의 오차로 잘 일치한다.

Fig. 13

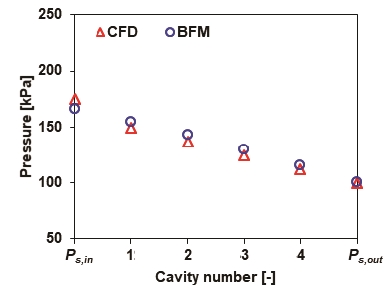
Comparison of CFD and BFM analysis - predicted cavities pressure of labyrinth seal versus cavity number

CFD와 BFM을 통해 계산된 임펠러의 후면을 따라 래버린스 실로 누설되는 유량은 Table 4를 통해 확인할 수 있으며, 각각 2.253 g/s, 2.583 g/s의 값을 가진다. 누설 유량의 해석 결과는 약 13%로 비교적 큰 오차를 가진다. 이는 Hirs^[29]의 윤활이론에 근거한 래버린스 실의 BFM 해석 모델의 경우 지배방정식이 CFD모델에 비해 단순하며, BFM 해석 모델의 경우 래버린스 실의 이 끝단의 길이(Tip)를 고려하지 않기 때문으로 사료된다.

Table 4

Comparison of leakage flow rate by BFM analysis to CFD analysis

6. 래버린스 실을 갖는 임펠러의 추력 예측

6.1 임펠러와 래버린스 실 형상에 따른 추력 예측

Table 5는 공기 조건에서의 래버린스 실이 적용된 임펠러의 추력을 예측하기 위해 사용한 임펠러와 래버린스 실의 형상치수 및 구동 조건을 보여준다. 형상 변화에 따른 특성 분석을 위하여 임펠러의 후면과 벽면사이의 간극(s), 래버린스 실의 클리어런스(C_r), 래버린스 실의 이의 개수(NT)를 변경하여 해석을 수행하였다.

Table 5

Geometries and operating conditions of impeller and labyrinth seal for predicted axial thrust and leakage flow

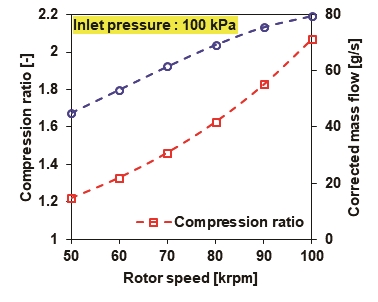
Fig. 14는 해석에 사용된 압축기의 속도에 따른 압축비 및 토출 유량을 보여준다. 압축비와 토출 유량은 속도가 증가함에 따라 증가하는 경향을 보인다. 압축비는 50,000 rpm에서 약 1.219, 100,000 rpm에서 약 2.069의 압축비를 가지며, 50,000 rpm 이하의 속도 구간에서의 압축비는 1에 가까워지므로 생략하였다. 이에 따라 초기 임펠러로 유입되는 압력은 100 kPa로 100,000 rpm에서 최대 206.9 kPa의 토출 압력을 가지는 압축기를 가정하여 해석을 수행하였다.

Fig. 14

Compression ratio and discharge flow rate versus rotor speed

Fig. 15는 Fig. 14의 속도에 따른 압축비를 이용하여 예측한 속도에 따른 임펠러의 추력과 후면을 통해 발생하는 누설 유량에 대한 해석 결과이다. 해석은 임펠러의 후면과 벽면 사이의 간극(s)과 래버린스 실의 클리어런스(C_r)이 각각 0.5 mm, 0.2 mm 이고 래버린스 실의 이의 수가 5개인 형상을 사용하였다. 로터의 회전속도가 증가함에 따라 추력은 약 119 N, 누설 유량은 약 1.9 g/s 증가한다. 이는 속도에 따른 압축비의 증가로 인하여 임펠러 후면의 압력이 증가하였고 이에 따라 임펠러에 의해 발생하는 추력이 증가하였음으로 사료된다. 또한 증가된 임펠러 후면의 압력에 의해 래버린스 실로 유입되는 입구와 출구의 압력의 차이가 증가하여 누설 유량이 증가하였음으로 사료된다.

Fig. 15

Predicted axial thrust force and leakage flow rate versus rotor speed. s = 0.5 mm, Cr = 0.2 mm, and NT = 5

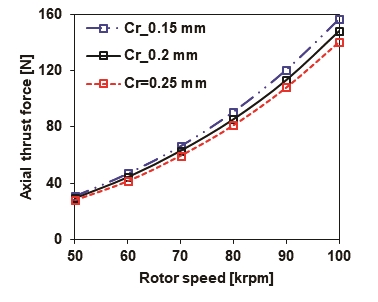
Fig. 16과 Fig. 17은 Fig. 14의 속도에 따른 압축비를 이용하여 래버린스 실의 클리어런스(C_r)에 따른 임펠러에 발생하는 추력과 누설 유량에 대한 예측 결과를 보여준다. 해석은 임펠러 후면의 간극(s)은 0.5 mm, 래버린스 실의 이의 수(NT)는 5개이며, 이외의 형상은 Table 5의 조건을 통해 해석을 수행하였다. 해석 결과는 Fig. 14의 결과와 동일하게 로터의 회전속도가 증가함에 따라 추력과 누설 유량은 증가하는 경향을 보인다. 또한 래버린스 실의 클리어런스가 0.15 mm 에서 0.25 mm로 증가함에 따라 추력은 최대 16 N의 감소하며, 누설 유량은 최대 1.24 g/s 증가한 결과를 보인다. 이는 실의 클리어런스 증가로 인하여 래버린스 실을 통해 누설되는 유량이 증가하여 임펠러 후면의 압력이 감소하였기 때문으로 사료되며, 참고문헌^[18]의 누설 유량 증가에 따른 임펠러 후면의 압력 감소와 유사한 경향을 보인다.

Fig. 16

Predicted axial thrust force versus rotor speed for increasing clearances. s = 0.5 mm and NT = 5

Fig. 17

Predicted leakage flow rate versus rotor speed for increasing clearances. s = 0.5 mm and NT = 5

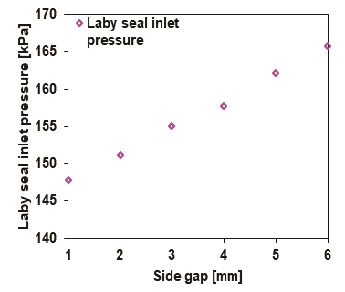
Fig. 18과 Fig. 19는 100,000 rpm의 구동속도에서 래버린스 실의 이의 개수(NT)의 증가에 따른 해석 결과를 보여준다. 해석에 사용된 임펠러 후면의 간극(s)와 실의 클리어런스(C_r)은 각각 0.5, 0.2 mm 이며, 이외의 형상은 Table 5를 이용하여 해석을 수행하였다. 해석 결과는 래버린스 실의 이의 개수(NT) 증가에 따라 추력은 143 N에서 153 N까지 증가하며, 누설 유량은 3.5 g/s에서 2.9 g/s까지 감소한 결과를 보여주는데, 이를 통해 이의 개수(NT) 증가가 누설량의 감소와 임펠러 후면의 추력 증가를 동시에 유발함을 알 수 있다. 또한, Fig. 18의 결과로부터 Fig. 19가 보여주는 래버린스 실의 이의 개수(NT) 증가에 따른 래버린스 실의 유입 압력(P_s,in) 증가의 결과도 유추가 가능하다. 일반적으로 래버린스 실의 입구와 출구의 압력의 차이가 증가할수록 누설 유량은 증가하는 경향을 보이지만, Fig. 18과 Fig. 19의 결과를 통해 래버린스 실의 형상 변화를 통해 실의 누설 특성을 크게 개선할 수 있음을 알 수 있다.

Fig. 18

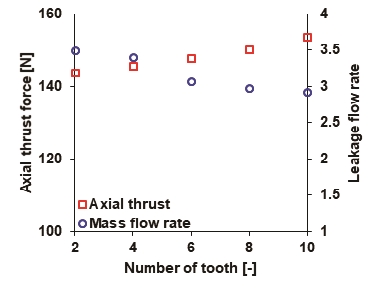
Predicted axial thrust force and leakage flow rate versus number of tooth. s = 0.5 mm, Cr = 0.2 mm and Ω = 100 krpm

Fig. 19

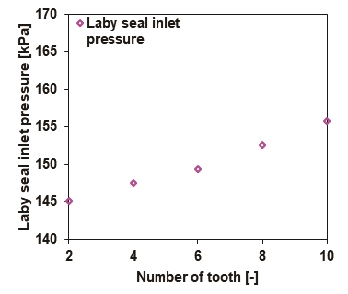
Predicted labyrinth seal inlet pressure versus number of tooth. s = 0.5 mm, Cr = 0.2 mm and Ω = 100 krpm

Fig. 20과 Fig. 21은 100,000 rpm의 구동속도에서 임펠러 후면과 케이싱 벽면 사이의 간극(s)의 변화에 따른 해석 결과로 각각 임펠러의 추력과 누설 유량, 래버린스 실의 유입압력에 대한 결과를 보여준다. 래버린스 실의 클리어런스(C_r)와 이의 개수(NT)는 각각 0.2 mm, 5개이며, 이외의 형상은 Table 5의 형상치수를 사용하여 해석을 수행하였다. 임펠러 후면과 케이싱 벽면 사이의 간극(s)이 증가할수록 임펠러에 의해 발생하는 추력은 138 N에서 156 N까지 증가하며, 누설 유량은 3.1 g/s에서 3.8 g/s까지 증가한 결과를 보인다. 임펠러에 의해 발생하는 추력의 증가는 후면의 간극(s)의 증가로 인하여 임펠러 후면과 케이싱 벽면의 간섭효과가 감소하여 후면의 압력이 증가하였기 때문으로 사료된다^[8]. 이는 Fig. 21의 후면 간극(s)의 증가에 따라 래버린스 실의 유입 압력(P_s,in)이 증가하는 경향을 통해 유추할 수 있다. 또한 누설 유량의 증가는 임펠러 후면 압력의 증가로 인하여 래버린스 실의 입구 압력(P_s,in)과 출구 압력(P_s,out)의 차이가 증가하였기 때문으로 사료된다.

Fig. 20

Predicted axial thrust force and leakage flow rate versus side gap. Cr = 0.2 mm, NT = 5, and Ω = 100 krpm

Fig. 21

Predicted labyrinth seal inlet pressure versus side gap. Cr = 0.2 mm, NT = 5, and Ω = 100 krpm

6.2 작동 유체 변화에 따른 추력 예측

Table 6은 공기와 냉매(R134a) 조건에서의 래버린스 실이 적용된 임펠러의 추력과 누설 유량을 예측하기 위해 사용된 임펠러와 래버린스 실의 형상치수와 구동 조건을 보여준다. 공기와 냉매 조건의 해석은 모두 동일한 구동 속도, 임펠러 입구와 출구의 압력으로 계산하였으며, 래버린스 실의 이의 개수(NT)를 2개부터 6개까지 변화시켜가며 해석을 수행하였다. Table 7은 해석에 사용된 공기와 냉매의 압력 200 kPa, 온도 298.2 K 에서의 유체 물성치를 보여준다. 냉매(R134a)는 공기에 비해 약 3.8배 높은 밀도를 가지며, 약 3.5배 작은 기체 상수를 보인다. 또한, 냉매는 공기에 비해 더 낮은 비열비(γ)와 동점도(v)를 가지고 있다.

Table 6

Geometries and operating conditions of the impeller and labyrinth seal for comparison of air and R134a conditions

Table 7

Properties of air and R134a at pressure of 200 kPa and temperature of 298.2 K for axial thrust and leakage flow analysis

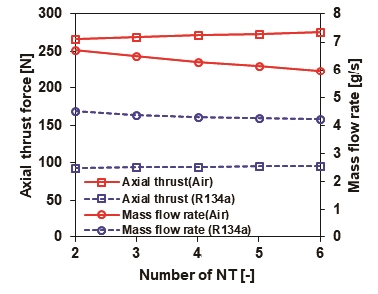
Fig. 22는 공기와 냉매 조건에서의 래버린스 실의 이의 개수(NT)변화에 따른 임펠러에 의해 발생하는 추력과 누설 유량의 해석결과를 보여준다. 작동 유체가 공기일 경우는 래버린스 실의 이의 개수(NT)가 증가함에 따라 임펠러의 추력은 266 N에서 275 N까지 증가하며, 누설 유량은 6.7 g/s에서 5.9 g/s까지 감소하는 경향을 보인다. 이에 반면 냉매의 경우의 추력은 93 N에서 95 N, 누설 유량은 4.51 g/s에서 4.2 g/s로 거의 일정하다. 또한 냉매 조건의 추력은 공기에 비해 최대 182 N 낮은 값을 보이며, 누설 유량은 2.2 g/s로 큰 차이를 보인다.

Fig. 22

Predicted axial thrust force and leakage flow rate versus number of tooth in air and R134a

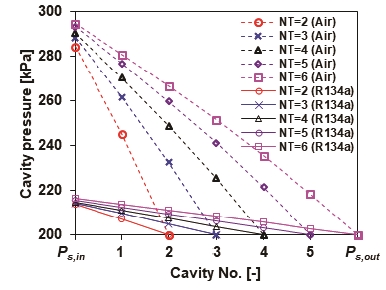
Fig. 23은 래버린스 실의 이의 개수 변화에 따른 래버린스 실 공동의 압력 분포를 보여준다. 공기와 냉매 조건 모두 유체 유동이 래버린스 실의 이와 회전축에 의해 형성된 오리피스(orifice)를 지남에 따라 압력이 감소하여 출구 압력(P_s,out)인 200 kPa까지 감소한다. 작동 유체가 공기일 경우 래버린스 실로 유입되는 초기 압력은 295 kPa인 반면 냉매의 경우는 215 kPa로 약 80 kPa의 차이를 보인다. 이는 공기에 비해 높은 유체 밀도를 가지는 냉매 조건에서 유체 관성력의 증가로 인하여 임펠러 후면의 압력이 급격히 감소하였기 때문으로 사료된다. 이로 인해 냉매 조건의 경우 급격히 감소된 후면의 압력의 영향으로 래버린스 실의 입출구의 압력차이가 매우 작아 래버린스 실의 이의 개수(NT)가 증가하였음에도 거의 일정한 임펠러의 추력과 누설 유량을 보인다.

Fig. 23

Predicted cavities pressure of labyrinth seal versus cavity number for variable number of tooth in air and R134a

7. 결 론

본 논문에서는 래버린스 실이 적용된 임펠러에서 발생하는 추력을 예측하기 위하여 임펠러 후면과 래버린스 실의 압력 분포 및 누설 유량의 동시해 해석 모델을 개발하고 이를 통해 추력과 래버린스 실의 누설 유량을 예측하였다.

1. Bulk-flow 모델을 이용한 래버린스 실의 해석 결과는 기존문헌의 실험 결과와 공동의 압력과 누설 유량이 각각 1%, 4% 이내로 잘 일치하였다.

2. 동시해 해석 모델을 통한 해석 결과는 CFD 해석 결과와 비교할 때 후면의 압력강하와 래버린스 실의 공동의 압력은 각각 2%, 5% 이내의 오차로 잘 일치하였다. 누설 유량은 13%로 상대적으로 큰 오차를 보이는데 이는 BFM 해석 모델이 래버린스 실의 이의 끝단 길이를 고려하지 않았기 때문으로 사료된다.

3. 압축비가 증가할수록 임펠러의 후면과 래버린스 실의 입출구 압력 차이가 증가하여 추력과 누설 유량이 증가한다.

4. 래버린스 실의 클리어런스가 증가함에 따라 누설유량은 증가하고 임펠러의 추력은 감소한다. 이는 증가된 누설 유량으로 인한 임펠러 후면의 압력 증가 때문으로 사료된다.

5. 래버린스 실 이의 개수가 증가할 경우 누설 유량은 감소하며 임펠러의 추력은 증가한다. 래버린스 실의 입출구의 압력차이가 증가하였음에도 누설 유량이 감소하는 경향을 통해 실의 형상이 누설 특성에 지배적인 영향을 미침을 알 수 있다.

6. 임펠러 후면과 케이싱 벽면 사이의 간극의 감소는 임펠러 후면의 유체 유동의 간섭효과를 증가시켜 추력과 누설 유량을 모두 감소시킨다.

7. 냉매 가스를 작동유체로 사용할 경우 임펠러의 추력과 누설 유량은 공기를 사용할 때보다 더 작은 값을 가지며, 이들의 값은 래버린스 실 이의 개수 변화에 상대적으로 둔감한 경향을 보인다. 이는 공기에 비해 높은 유체밀도로 인하여 임펠러 후면의 압력이 급격히 감소하고, 이에 따라 래버린스 실의 입출구의 압력의 차이가 감소하기 때문으로 사료된다.

8. 해석 결과를 통해 임펠러의 추력과 래버린스 실의 누설 성능은 상호 밀접히 연계되어 있음을 알 수 있으며, 설계 최적화를 통해 터보기계의 기계적 효율을 향상시킬 수 있을 것으로 사료된다.

Acknowledgments

본 연구는 2019년도 산업통상자원부의 재원으로 한국산업기술평가원(KEIT)의 지원을 받아 수행한 “1.6리 터급소형 디젤엔진의 저속성능 및 과도성능 개선을 위한 전동과급 기술개발” 연구과제의 일환으로 수행되었으며, 이에 관계자 여러분께 감사드립니다.

References

• Wellborn, S. R. and Okiishi, T. H., 1999, “The Influence of Shrouded Stator Cavity Flows on Multistage Compressor Performance,” ASME J. Turbomach., Vol. 212, pp. 496∼498. [https://doi.org/10.1115/98-GT-012]
• Misho, B. and Ribi, B., 2009, “Influence of Labyrinth Seal Leakage on Centrifugal Compressor Performance,” ASME Turbo expo, No.GT2009-59524, pp.1283∼1293.
• Choi, C. H., Noh, J. G., Kim D. J., Hong, S. S. and Kim, J., 2009, “Effects of Floating-Ring Seal Clearance on the Pump Performance for Turbopumps,” J. Propul. Power, Vol. 25, No. 1. [https://doi.org/10.2514/1.36806]
• Muller, H. K., 2019, Fluid Sealing Technology: Principles and Applications, 1st Edition, Talor & Francis. (ISBN: 978-0-203-75571-6)
• San Andrés, L. and Anderson, A., 2015, “An All-Metal Compliant Seal Versus a Labyrinth Seal: A Comparison of Gas Leakage at High Temperatures,” J. ENG. Gas Turbines Power, Vol. 137, No. 5, pp. 052504. [https://doi.org/10.1115/1.4028665]
• Mayor, E., “Mechanical Seals,”, 1997, 3rd Edition, Newnes-Butterworth. (ISBN: 978-0-408-00307-0)
• Iwatsubo, T., 1980, “Evaluation of Instability Forces of Labyrinth Seals in Turbines or Compressors,” NASA Tech. Rep., No. 80N29715.
• Stuff, H., 1980, “Incompressible Flow in a Labyrinth seal,” J. Fluid Mech., Vol. 100, No. 4, pp.817∼829. [https://doi.org/10.1017/S0022112080001437]
• Eser, D. and Kazakia, J. Y., 1995, “Air Flow in Cavities of labyrinth Seals,” INT. J. Eng. Sci., Vol. 33, No. 15, pp. 2309∼2326. [https://doi.org/10.1016/0020-7225(95)00072-6]
• Yücel, U., 2004, “Calculation of Leakage and Dynamic Coefficients of Stepped Labyrinth Gas Seals,” Applied Mathematics and Computation, Vol. 152, No. 2, pp. 521∼533. [https://doi.org/10.1016/S0096-3003(03)00574-5]
• San Andrés, L., Wu, T., Barajas-Rivera, J., Zhang, J. and Kawashita, P., 2019, “Leakage and Cavity Pressures in an Interlocking Labyrinth Gas Seal: Measurements vs. Predictions,” J. Eng. Gas Turbines Power, Vol. 141, No. 10, pp. GTP-19-1309. [https://doi.org/10.1115/1.4044284]
• Karassic, I. J., Messina, J. P., Copper, P., Heald, C. C., 2001, “Pump Handbook,” 3rd edition, Mc Graw Hill, Chap. 2, pp. 2.52∼2.55.
• Guelich, J., Jud, W. and Hughes, S. F., 1987, “Review of Parameters Influencing Hydraulic Forces on Centrifugal Impellers,” Proc. Inst. Mech. Eng., Part A, Vol. 201, No. A3. [https://doi.org/10.1243/PIME_PROC_1987_201_021_02]
• Li, W., 2013, “Model of Flow in the Side Chambers of an Industrial Centrifugal Pump for Delivering Viscous Oil,” J. Fluids Eng., Vol. 135, pp.051201. [https://doi.org/10.1115/1.4023664]
• Godbole, V., Patil, R. and Gavad, S. S., “Axial Thrust in Centrifugal Pumps-Experimental Analysis,” 15th International Conference on Experimental Mechanics, Porto, Portugal, July, pp. 22∼27.
• Shimura, T., Kawasaki, S., 2012, Uchiumi, M., Kimura, T. and Matsui, J., “Internal Flow and Axial Thrust Balancing of a Rocket Pump,”, J. Fluids Eng., Vol. 134, No. 4 pp. 041103. [https://doi.org/10.1115/1.4006470]
• Kurokawa, J., Sakura, M., 1988, “Flow in a Nattow Gap Along an Enclosed Rotating Disk with Through-Flow,” JSME Int. J., Ser. II, Vol. 31, No. 2, pp. 243∼251. [https://doi.org/10.1299/jsmeb1988.31.2_243]
• Poncet, S., Chauve, M. P. and Legal, P., 2005, “Turblent Rotating Flow with Inward Throughflow,” J. Fluid Mech., Vol. 522, pp. 253∼262. [https://doi.org/10.1017/S0022112004002046]
• Gantar, M., Florjancic, D. and Sirok, B., 2002, “Hydraulic Axial Thrust in Multistage Pumps-Origins and Solutions,” J. Fluid Mech., Vol. 123, No. 2, pp. 336∼341. [https://doi.org/10.1115/1.1454110]
• Kurokawa, J., Kamijo, K. and Shimura, T., 1994, “Axial Thrust Behavior in LOX-Pump of Rocket Engine,” J. Propul. Power, Vol. 10, No. 2. [https://doi.org/10.2514/3.23735]
• Noh, J.-G., Choi, C.-H., Kim, J., 2006, “Numerical Study on the Effect of Cavity Vanes to Control the Axial Thrust of a Turbopump,” The KSFM Journal of Fluid Machinery, Vol. 9, No. 2, pp. 39∼43. [https://doi.org/10.5293/KFMA.2006.9.2.039]
• Choi, C.-H., Noh, J.-G., Kim, D.-J., Kim, J., 2012, “Study on the Control of the Axial Thrust of a Pump for Liquid Rocket Engine Turbopumps,” The KSFM Journal of Fluid Machinery, Vol. 15, No. 1, pp. 36∼40. [https://doi.org/10.5293/kfma..2012.15.1.036]
• Kim, D.-J., Choi, C.-H., Noh, J.-G., Kim, J., 2012, “Axial Thrust Control of High-speed Centrifugal Pump with Cavity Vanes,” The KSFM Journal of Fluid Machinery, Vol. 15, No. 6, pp. 46∼50. [https://doi.org/10.5293/kfma.2012.15.6.046]
• Evgen’ev, S. S., Petrosyan, G. G. and Futin, V. A., 2009, “Calculation of Axial Gasodynamic Forces, Disk Friction Losses and Overflow in Semiopen Impellers of Centrifugal Compressors,” Russian Aeronautics, Vol. 52, No. 3, pp. 319∼326. [https://doi.org/10.3103/S1068799809030106]
• Childs, D. W., 1987, “Force and Moment Rotordynamic Coefficients for Pump-Impeller Shroud Surfaces,” NASA Tech. Rep., No. 87N22226.
• Neumann, K., 1964, “Zur Frage der Verwendung von Durchblickdichtungen im Dampfturbinenbau,” Maschinentechnik, Vol. 13, No. 4, pp. 188∼195.
• John, J. E. A., 1984, “Gas Dynamics”, 2nd ed. Allyn and Bacon, Inc., Boston.
• Wright, D. V., 1983, “Labyrinth Seal Forces on a Whirling Rotor,” NASA Tech. Rep., 83N22198.
• Hirs, G. G., 1973, “A Bulk-flow Theory for Turbulence in Lubricating Films,” ASME J. Lubr. Technol., Vol, 105, pp, 137∼146. [https://doi.org/10.1115/1.3451752]