오리피스에서의 과냉 임계유량 특성 연구
Abstract
A meta-stable effect on a subcooled critical flow in orifice was investigated. For an investigation of the meta-stable effect, two homogeneous nucleation models, e.g., the Alamgir and Lienhard’s model and the Elias and Chambre’s model, and one isentropic model, e.g., the Henry and Fauske’s model, were compared with respect to previous test data performed by Sozzi and Sutherland. From comparisons of throttle pressures, the Alamgir and Lienhard’s model provided a lower bound and the Elias and Chambre’s and the Henry and Fauske’s, an upper bound. The experimental data were lying between the two bounds. The well-known diameter effect in critical flow was investigated and rather, diameter ratio (d/D) effect was found important in critical flow.
Keywords:
Critical Flow, Meta-stabe, Diameter Effect, Orifice키워드:
임계유동, 준안정, 직경효과, 오리피스1. 서 론
원전에서의 누설 평가나 냉각재 상실과 같은 사고 분석을 위하여 임계유량에 대한 연구가 많이 수행되었으며 관련한 이론적 모형의 비교⋅검증을 위한 실험 데이터도 많이 생산되었다. 개발된 이론적 모형은 임계유동 현상 진행에서의 열역학적 성질에 관련한 적절한 가정을 도입하여 모델링이 이루어졌다(1,2). 실제적인 측면에서 생산된 임계유량 실험은 대개 짧은 노즐이나 오리피스와 같은 급격한 면적변화의 단순 형상을 기본으로 하고 길이 효과를 보기 위해 보조배관을 연결하여 길이 효과를 고려하기도 하였다(3). 임계유동에 있어서 기하학적 영향을 보기 위한 대표적인 실험은 Sozzi와 Sutherland에 의한 실험(3)으로서 입구형상, 출구형상, 유로길이, 그리고 직경 변화에 대한 임계유량 데이터를 근거로 기하학적 영향을 검토한 바 있다. 즉, 입구형상은 유선형의 경우 더 큰 임계유량을 보였으며, 출구형상은 아냉유동에서는 급격한 형상 변화에서 그리고, 포화2상 유동에서는 완만한 형상 변화에서 더 큰 임계유동을 보였다. 유로길이에 있어서는 유로 길이가 길어질수록 유동내의 열역학적 성질이 평형상태에 가까워짐에 따라 유로길이가 길어짐에 따른 저항 효과로 임계유동이 감소하는 경향을 보였다. 특이한 것은 직경효과인데 실험자료에 의하면 노즐이나 오리피스의 목(Throat) 직경이 작을수록 임계유동이 큰 경향을 보였다는 것이다. 그런 경향은 저자에 의해서 이루어진 기하학적 효과 검토(4)에서도 확인된 바 있다.
본 논문에서는 임계유동에 대한 일반적인 특성을 논의하고 이어, 이전에 수행되었던 오리피스 임계유량 실험 데이터를 기준으로 임계유동에서의 Meta-stable 효과와 직경 영향 등에 대하여 검토하였다.
2. 임계유동 특성 검토
임계유동 현상은 유동 속도가 음속에 도달하여 발생하거나 유동과정에서 상당한 열역학적 과열(Super-heated) 액체 상태에 이른 유체가 갑자기 비등(Flashing) 하면서 Choking이 발생하는 것으로 이해된다. 본 장에서는 임계유동 현상에 영향을 미치는 구조물에 의한 음속 영향과 과포화 상태와 관련된 Meta-stable 영향, 그리고 Isentropic 영향에 대하여 각각 검토하였다.
2.1 직경에 의한 음속 영향
임계유동은 유동의 음속과 연관된 현상으로서 임계유동이 일어나는 곳은 유체의 음속에 도달한 상태로 이해될 수 있다. 이런 점에서 음속에 대하여 유로 직경이 어떤 영향을 미치는 지를 검토하는 것은 필요하다. 구조물 내에서의 유체의 음속 변화를 Nguyen 등(5)이 정리한 것을 아래에 나타내었다.
| (1) |
여기서, aE는 유효 유체 음속을, a는 유체 음속, EF는 유체의 체적탄성비, EW는 구조물 벽의 체적탄성비, D는 배관의 직경, 그리고 S는 배관의 두께이다. 식 (1)에서 보듯이 노즐이나 오리피스의 목 직경 (D)이 감소하면 유효 유체 음속 (aE)은 증가하는 경향을 나타내는 것을 알 수 있다. 그러나, 강철과 물의 경우 체적탄성비 비율이 거의 102 정도여서 직경 감소에 의한 음속 증가 영향은 미미하다는 것을 알 수 있다. (강철의 EW 는 160 GPa이고 물의 EF 는 2.2 GPa이다.) 즉, 이전 실험데이터에서 보여주는 임계유량의 직경 영향에서 보여주는 현저한 차이를 설명하기에는 부족하다 할 수 있다.
2.2 Meta-stable에 의한 영향
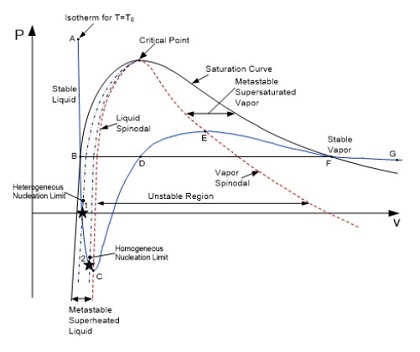
오리피스에서 임계유동이 발생할 때는 목(Throat)에서의 압력이 실질적인 배압으로서의 기능을 한다. 예를 들어, 오리피스가 전후단 압력차가 있는 계통사이에 연결될 경우 전단의 과냉(Subcooled) 상태의 물이 오리피스를 통과할 수 있는 유량은 전후단의 압력차 크기에 따라 증가한다. 그러나, 전후단 압력차가 매우 큰 경우는 오리피스의 목에서 감압에 따른 Flashing이 발생하면 그로 인하여 Choking에 의한 유량이 제한되는데 이것을 임계유량이라 부르며 이때의 Throat 압력이 실질적인 배압의 기능을 하는 것이다. 이와 같이 과냉 상태의 물이 감압이 되면서 변하는 열역학적 물성을 P-v 선도에 나타낼 수 있는데 이를 Fig. 1에 나타내었다. 그림에서 아냉 상태 A의 물이 서서히 감압되면 포화 상태 B에 도달하고 더욱 감압되면 증기 포화상태 F에 도달한다. 과냉 상태의 물이 서서히 감압이 되면서 통과하는 과정 ABF는 열역학적으로 평형상태를 이루면서 진행되는 과정이다. 그러나, 감압의 속도가 매우 빨라지면 포화상태의 물 B에서 과열(Super-heated) 물 상태 즉, Meta-stable의 한계점인 C를 향하는 경로의 물성치 변화를 겪게 된다(6). 그림에서 과정 ABCDEFG는 Van der Waal’s 상태 방정식에서 계산된 커브로서 두 극치 C,E는 각각 Liquid Spinodal과 Vapor Spinodal을 나타낸다. Cary(6)에 의하면 물리적으로 상(Phase)으로서 존재를 위한 필요⋅충분 조건 즉, 안정조건은 이며 이를 만족하는 구간은 ABC와 EFG이며 특히, 포화 상태내의 과정 BC와 EF를 Meta-stable 구간이란 한다. (그림에서 보듯이, 과정 BC는 과열 액체 상태의 구간이고, 과정 EF는 과포화 증기 상태의 구간이다.) 구간 CDE는 안정조건을 만족하지 않는 Unstable 구간으로서 물리적으로 존재할 수 없는 구간이라 할 수 있다. 따라서, 감압과정에 점 C에 도달한 유체는 구간 CDE내 어떤 상태로도 존재하지 못하고 바로 점 E 상태 이후의 과정으로 진입하게 되는 것이다.
구간 BC에서 일어나는 물리적 현상은 두 가지로 구분될 수 있다. 즉, Heterogenous Nucleation Limit 지점 1과 Homogeneous Nucleation Limit 지점 2이다. 개념적으로 후자는 Spinodal Limit에 근접한 액체 상태로 이해된다. 구간 BC는 정도 차이는 있지만 열역학적으로 과열 액체 상태이므로 작은 교란으로도 Flashing이 발생할 수 있는 상태인 것이다. 일반적인 환경에서는 물에는 용존 기체가 있고 또한 용기 벽에는 Cavity와 같이 매우 작은 기포 공간을 가진 흠집 등이 있어서 과열 상태의 물이 빨리 Flashing 할 수 있는 요인을 제공하게 되는데 이런 것으로 인한 Flashing을 Heterogeous Nucleation이라 부른다. 즉, Heterogeneous Nucleation 이란 물 자체에 의한 Flashng이 아니라 주변 환경 요인에 의한 것이기에 ‘Heterogeous’라고 정의된 것이며 일반적으로 감압속도가 작은 경우에 많이 발생하는 현상이다. 이에 반하여 Homogeneous Nucleation은 순수한 물과 주변 흠집이 없는 매우 정교한 실험에서 확인되는 것으로서 매우 큰 감압속도에서 일어나는 현상이다.
본 절에서는 Meta-stable 효과에 대한 최근 검토된 논문(7)에 의거하여 두 가지 Homogeneous Nucleation 모델 즉, Alamgir & Liemhard(8)와 Elias & Chambre(9) 에 대하여 검토하였다.
Alamgir & Lienhard의 모델은 전통적인 Homogeneous Nucleation 이론에 근거하여 초기 정지 유체가 감압되면서 일어나는 Spinodal Line을 Fig. 2와 같은 개념의 감압 실험을 이용하여 다음과 같은 Semi-empirical 상관식을 도출하였다. 즉,
| (2) |
여기서, psat, pFI, kB, T0, TC, Tr, ∑', σ, ρf, ρg는 각각 초기 물 온도에 상응한 포화압력 (Pa), Spinodal Line의 Flashing Inception 압력 (Pa), 볼츠만 상수 (1.3806×10-23JK-1), 초기 물 온도 (K), 물의 임계온도 (647.1K), Reduced 온도 (≡T0/TC), 표면장력 (N/m), 감압율 (Matm/s), 포화 물 밀도 (kg/m3), 그리고 포화 증기 밀도 (kg/m3)를 나타낸다.
식 (2)에서 보듯이 Alamgir & Lienhard의 모델은 초기 물 온도와 감압율로 Homogeneous Nucleation 발생 압력을 예측할 수 있는 모델로서 초기 정지 상태의 감압 현상에 광범위하게 활용되는 상관식이다.
Elias & Chambre의 모델은 정지된 유체나 흐르는 유체에서의 감압이 발생할 때 Flashing이 일어나는 열역학적 조건을 현상학적으로 제시한 관계식으로 다음과 같은 관계식들로 정리된다. 즉,
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
여기서, ∑, ah, ap, hfg, mW, ND, B, Ψ, c1, c2, c3는 각각 감압율 (atm/s), 엔탈피에 대한 물 밀도 변화 (kg/m4-N), 압력에 대한 물 밀도 변화 (kg/m-N), 기화열 (J/kg), 분자 질량 (kg), 물의 Number density (≡NAρf/M, NA: 아보가드로 수 (6.02×1023); M: 몰질량 (kg)), 상수 2/3, Heterogeneity 계수, 상수 1.5061×103, 상수 31.906, 상수 0.3103을 나타낸다. 식 (8)에 포함된 무차원 감압율 S는 다음 식으로 정의된다. 즉,
| (10) |
인데, 식 (3)에서 나타낸 것처럼 감압율 ∑는 atm/s의 단위이다. (참고로, 식 (2)에 있는 감압율 ∑′의 단위는 Matm/s이므로 식 (2)와 (3)을 사용함에 있어서 감압율 단위에 유의할 필요가 있다.)
Alamgir & Lienhard의 모델과 같이 Elias & Chambre의 모델도 초기 물 온도와 감압율로 Homogneneous Nucleation 압력을 예측할 수 있으며 특히, 정지 상태나 유동이 있는 계통에서도 감압율에 따른 Flashing 압력을 예측할 수 있다는 점에서 유용한 개념으로 알려져 있다. (여기서, 한가지 특기할 사항은 식 (2)와 (3)에서 사용되는 감압율에 있어 작은 값에서는 Heterogeneous Nucleation의 경향을 나타내며, 큰 값에서는 Homogeneous Nucleation의 경향이 두드러진다는 사실이다. 본 논문에서는 Homogeneous Nucleation 발생에 초점을 맞추기 위하여 매우 큰 감압율 (1.85×106 atm/s)을 가정하여 평가하였다.
2.3 Isentropic Process에 의한 영향
원전 안전해석에서 사용되는 임계유동 모델은 저자들의 이전 연구(10)에서 제시한 바와 같이 대표적으로 Trapp-Ransom 모델(1)과 Henry-Fauske 모델(2)이 있다. 두 모델에서는 임계유동의 발생 과정을 열역학적으로는 Isentropic Process로 가정한 것으로서 여러 가지 실험 데이터와의 비교에서 타당한 임계유량을 예측하는 것으로 밝혀져 현재까지도 두 모델이 원전의 냉각재 상실사고 및 비냉각재 상실사고를 위한 안전해석에 핵심적인 임계유동 모델로 활용되고 있다. 본 논문에서는 저자의 이전 논문(10)에서 정리된 Henry-Fauske 모델을 Isentropic 모델의 기준으로 삼았다.
Heny-Fauske 모델중 과냉 임계유동 관계식은 다음과 같이 두 가지 관계식으로 정리된다. 즉,
| (11) |
| (12) |
where, C: contraction coefficient
여기서, Gc는 단위면적당 임계유량(kg/m2-s), x는 증기질(Quality), s는 Specific Entropy(J/kg-K), v는 Specific Volume (m3/kg), N은 Experimental Parameter, 그리고 P는 압력(Pa)을 나타낸다. 또한 아래첨자로서 0은 초기 Stagnant Condition, f는 Liquid 상태, g는 Vapor 상태, E는 국부 압력에 따른 Equilibrium 상태, 그리고 t는 임계목(Throat)을 의미한다.
Stagnation 조건이 주어지면 두 관계식 (11)과 (12)의 미지수는 임계유량 Gc와 Throat 압력 Pt이므로 두 관계식을 모두 만족하는 Pt 를 반복계산법으로 먼저 구하고 식 (11)을 이용하여 임계유량을 구할 수 있다.
3. Orifice에서의 임계유동 특성 비교
오리피스 임계유동 특성을 비교⋅검토하기 위해서 먼저 Sozzi & Sutherland의 실험 데이터를 기준으로 모형간 특성을 검토하였으며 이어서 저자의 이전 연구에서 제시된 실험데이터를 기준으로 Orifice 직경 영향에 관련된 정성적인 현상 규명을 정리하였다.
3.1 Sozzi & Sutherland Data(3)
임계유동 특성을 파악하기 위하여 앞장에서 논의된 모형중 Meta-stable 효과에 관련된 두 가지 모형과 Isentropic 모형을 비교⋅검토의 대상으로 삼았다. 특히, 오리피스에서의 임계유동 특성을 검토하기 위하여 Sozzi & Sutherland가 수행한 실험 중에서 오리피스 데이터를 기준으로 각 모델의 임계유동 특성을 비교⋅검토하였다.
Sozzi & Sutherland에 의해서 수행된 오리피스 실험 조건은 Table 1과 같으며 취득된 데이터는 임계유량과 오리피스 목(Throat)에서의 압력이었는데 본 절에서는 Throat 압력을 기준으로 모형간 특성을 비교⋅검토하였다.
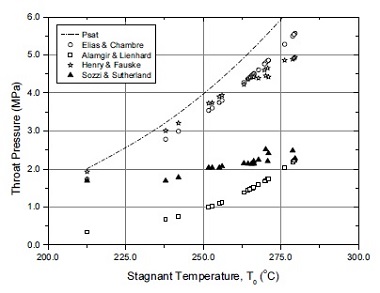
2개의 Homogeneous Nucleation 모델과 Isentropic Process 모델인 Henry & Fauske 모델 등 3개의 모델들의 계산 결과와 Sozzi & Sutherland 실험의 Throat 압력 데이터를 Fig. 3에 비교하여 나타내었다. Meta-stable에 의한 Super-heated 정도를 알아보기 위하여 그림에 초기 물 온도에 상응하는 포화압력도 동시에 표시하였다. 그림에서 보는 바와 같이 Alamgir & Lienhard 모델이 가장 낮은 Throat 압력을 보이고 있어서 Lower Bound를 형성하고 있다. 이는 Alamgir & Lienhard 모델이 매우 큰 Super-heated 값을 예측한다는 의미이다. Elias & Chambre 모델과 Henry-Fauske 모델의 예측은 서로 유사한 경향을 보이고 있는데 두 모델이 Upper Bound를 형성하고 있으며 상대적으로 작은 Super-heated 값을 예측하고 있다. 두 모델이 모두 흐르는 유동에서의 Throat 압력을 예측하는 모델이어서 그런 결과를 보이고 있는 것을 판단된다. 특기할 점은 실험 데이터가 Lower Bound와 Upper Bound 사이에는 존재하지만 초기 물 온도가 낮을 때는 Upper Bound인 Elias & Chambre 모델과 Henry-Fauske 모델에 가까우나, 초기 물 온도가 높아질수록 Lower Bound인 Alamgir & Lienhard 모델에 근접한다는 사실이다. (표 1에서 보듯이 Sozzi & Sutherland 실험에서 초기 압력 범위가 5.8-6.8 MPa인 점으로 미루어 보아 초기 물 온도가 낮다는 것은 초기 Subcooled 값이 크다는 것으로 해석될 수 있고 초기 온도가 높다는 것은 초기 Subcooled 값이 적다는 의미이기도 하다.) 또한, 그림에서 보듯이 실험데이터의 분포가 전반적으로 Lower Bound에 가까운 경향을 보이는데, 이는 Orifice에서의 Meta-stable 특성이 흐르는 유동 특성 보다는 정지된 유동의 급격 감압에 의한 Homogeneous Nucleation 현상에 가까운 것으로 해석된다.
3.2 저자의 이전 데이터(4)
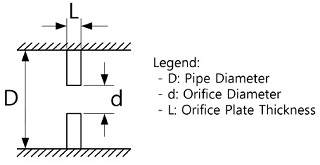
저자의 이전 데이터는 Orifice 형상에 관련된 인자들 즉, 배관 직경과 목 직경, 그리고 목 길이에 대한 임계유동 특성을 알아보기 위한 실험에서 얻은 데이터로서 취득된 인자는 임계유량 뿐이어서 Throat 압력 데이터가 필요한 Meta-stable 효과에 관련한 비교⋅검토는 어려운 상황이다. 그러나, 앞 절의 Throat 압력의 비교⋅검토에서 확인된 사항 즉, Homogeneous Nucleation 모델중 Elias & Chambre 모델과 Isentropic Process 모델인 Henry & Fauske 모델이 매우 유사한 경향을 보였다는 사실에 근거하여 본 절에서는 Henry & Fauske 모델을 오리피스에서의 임계유동 특성 비교⋅검토의 주 모델로 선정하였다. (참고로, 본 절에서 정의된 오리피스의 기하학적 인자를 Fig. 4에 나타내었다.)
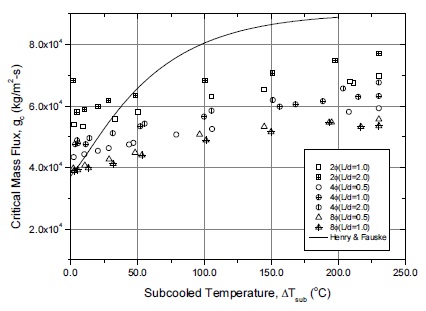
Fig. 5에는 초기 Upstream 압력이 4 MPa에서 넓은 과냉 온도 범위에 대하여 수행한 오리피스 실험 결과를 Henry & Fauske 모델과 비교하여 나타내었다. 그림에서 보듯이 오리피스 목 직경별로는 임계유동의 크기가 확실히 구분됨을 알 수 있다. 즉, 목 직경이 작을수록 큰 임계유량을 보이고 있으며 이는 목 직경이 작을수록 Meta-stable의 효과가 커지는 것을 의미하기도 한다. 실험 데이터와 Herny & Fauke 모델과의 비교에서 Subcooled 값이 작은 경우에 실험에서의 임계유량이 더 크게 나타났는데 이는 Subcooled 값이 적을수록 Meta-stable의 효과가 커지는 것으로 해석할 수 있다. (이러한 경향은 앞 절에서 Sozzi & Sutherland 데이터 비교⋅검토에서 확인된 초기 Subcooled 값의 Meta-stable 경향과도 유사하다.
그림에서 특이한 점은 목 직경별로는 목 형상비 (L/d)가 클수록 임계유량이 크게 나타난다는 것이다. 이전 연구들(3,4)에서 확인된 사항으로 노즐이나 오리피스 목의 길이가 길어질수록 유동내의 열역학적 성질이 평형상태에 가까워지고 길이가 길어짐에 따른 저항 효과가 나타나 임계유동이 감소하는 경향을 보인다는 사실이다. 그러나, 그림 내 직경별 형상비에 따른 임계유량의 경향은 (8mm 경우를 제외하고) 반대의 경향을 보이고 있어서 다른 기하학적 요인이 고려되어야 할 필요성이 제기되었다.
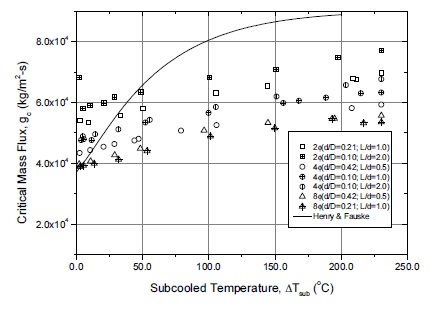
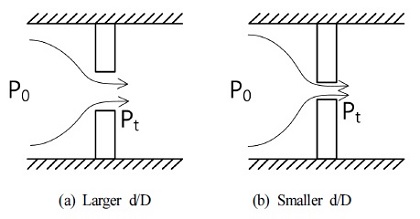
Fig. 6에는 Fig. 5의 실험 데이터에 대해서 인자 하나를 추가하여 데이터를 나타내었다. 추가된 인자는 d/D로 정의된 오리피스 직경비로서 목 직경과 오리피스 입구측 배관의 직경 비율이다. 직경별 실험 결과를 살펴보면 큰 형상비(L/d)에서 역전된 임계유량은 동시에 작은 직경비(d/D)를 가지고 있다는 것을 알 수 있다. 실험에서 임계유량이 크게 계측되었다는 것은 Meta-stable 효과가 더 크게 작용한 연유로 해석되는데 이런 경향은 목 직경이 작은 2가지(2,4mm) 오리피스에서 동일한 경향을 보이고 있음을 그림에서 확인할 수 있다. 이를 통하여 짐작할 수 있는 것은 이제까지 알려졌던 임계유동에 있어서의 직경효과는 절대적 크기의 직경효과이기 보다는 오리피스의 목 직경과 배관의 직경 비율에 따른 Meta-stable 효과의 변화로 해석될 수 있다. Fig. 7에는 직경비에 따른 유동의 움직임을 개념적으로 나타내었다는데 그림에서 보듯이 직경비가 작을수록 유동의 움직임이 커지고 이런 것이 목에서의 Meta-stable (또는 Non-Thermal Equilibrium) 효과를 크게 하는 것으로 판단된다. (참고로, 임계유량에 관한 오리피스 직경비와 형상비의 특성 비교에서 8mm와 같이 비교적 큰 목 지경인 경우는 직경비보다는 형상비가 더 큰 영향을 미치는 것으로 판단된다.
4. 결 론
임계유동에 대한 일반적인 특성을 논의하고 이어, 이전에 수행되었던 오리피스 임계유량 실험 데이터를 근거로 임계유동에서의 Meta-stable 효과를 비교⋅검토하고 또한 기하학적 효과 중에서 직경과 관련된 영향을 검토하였다.
임계유동 현상에 영향을 미치는 구조물에 의한 음속 영향을 검토하였고, 오리피스 임계유동에 있어 과열 상태와 관련된 Meta-stable 영향과 Isentropic 영향에 대하여 검토하였다. Meta-stable 영향에 대해서는 두 가지 Homogeneous Nucleation 모델인 Alamgir and Lienhard’s Model과 Elias and Chambre’s Model을 검토하였으며, Isentropic Process에 의한 영향에 대해서는 Henry and Fauke’s Model을 기준으로 하였다. 본 논문에서 수행된 비교⋅검토에서 발견된 사항들은 다음과 같이 요약할 수 있다.
- - 구조물에 의해 변화된 음속에 의한 임계유동 영향은 미미함
- - Alamgir & Lienhard의 모델은 Meta-stable의 Lower Bound를 예측함
- - Elias & Chambre의 모델과 Heny & Fauske의 모델은 Meta-stable 예측에 있어서 유사한 경향을 나타내며 Upper Bound를 예측함
- - 실험 데이터들은 두 Bound들 사이에 위치하지만 상대적으로 낮은 온도(또는 큰 Subcooled 값)에서는 Upper Bound에, 높은 온도(또는 작은 Subcooled 값)에서는 Lower Bound에 가까운 경향을 보임
- - 오리피스 임계유량은 초기 Subcooled 값이 작을수록 더 큰 Meta-stable 효과로 인한 증가 경향을 보임
- - 오리피스 임계유량에 관련된 직경효과는 실제적으로는 직경비(d/D) 효과임을 확인함
Acknowledgments
The authors would like to gratefully acknowledge the financial support of Korea Government (MOTIE, Ministry Of Trade, Industry and Energy) (No. 20181510102340).
References
-
Trapp, J.A. and Ransom, V.H., 1982, “A Choked-Flow Calculation Criterion for Nonhomogenous, Nonequilibrium, Two-Phase Flows,” Int. J. Multiphase Flow, 8(6), 669-681.
[https://doi.org/10.1016/0301-9322(82)90070-2]

-
Henry, R.E. and Fauske, H.K., 1971, “The Two- Phase Critical Flow of One-Component Mixtures in Nozzles, Orifices, and Short Tubes,” ASME Journal of Heat Transfer, 179-187.
[https://doi.org/10.1115/1.3449782]

- Sozzi, G.L. and Sutherland, W.A., 1975, Critical Flow of Saturated and Subcooled Water at High Pressure, NEDO-13418, General Electric.
-
Kim, Y.-S., 2015, “Overview of Geometrical Effects on the Critical Flow Rate of Sub-Cooled and Saturated Water,” Annals of Nuclear Energy, 76, 12-18.
[https://doi.org/10.1016/j.anucene.2014.09.028]

-
Nguyen, D.L., Winter, E.R.F. and Greiner M., 1981, Sonic Velocity in Two-Phase Systems, Int. J. Multiphase Flow, 7, 311-320.
[https://doi.org/10.1016/0301-9322(81)90024-0]

- Cary, Van Pl, 1992, Liquid-Vapor Phase-Change Phenomena, Hemisphere Publishing Corp., Washington.
-
Liao, Y. and Lucas, D., 2017, Computational modellijg of flash boiling flows: A literature survey, Int. J. Heat and Mass Transfer, 111, 246-265.
[https://doi.org/10.1016/j.ijheatmasstransfer.2017.03.121]

-
Alamgir, Md. And Lienhard, J.H., 1981, Correlation of Pressure Undershoot During Hot-Water Depressurization, J. of Heat Transfer, 103, 52-55.
[https://doi.org/10.1115/1.3244429]

-
Elias, E. and Chambre, P.L., 1993, Flashing Inception in Water During Rapid Decompression, J. of Heat Transfer, 115, 231-238.
[https://doi.org/10.1115/1.2910654]

-
Kim, Y.-S., Euh, D.-J., Kim, W.-S., Kwon, T.-S, 2019, Investigation of Leakage Characteristics on Major Equipment/Component in Reactor System, The KSFM J. of Fluid Machinery (in Korean), 22(6), 30-35.
[https://doi.org/10.5293/kfma.2019.22.6.030]