단일 광섬유 센서 프로브의 국소 기포 변수 측정 성능 평가

1. 서 론

2상 유동은 원자력, 기계공학, 화학공학, 바이오 분야 등 다양한 공학분야에서 발생되며, 비등, 응축 및 관내 압력 강하 증가 등 복잡한 유동 현상을 동반한다. 이러한 2상 유동이 발생되는 시스템을 해석하기 위해서는 각상의 분율(Local phase fraction), 상 속도(Local phase velocity), 계면면적밀도(Interfacial area concentration), 상의 크기(Phase size) 등 2상 유동 변수를 예측하기 위한 물리 모델이 필요하다. 그러나 이러한 변수들은 유동 조건에 따라 변하는 계면 형상에 크게 영향을 받아 이를 예측하는 물리 모델을 개발하고 검증하기 위해서는 다양한 유동조건에서 실험 데이터를 생산하는 것이 필수적으로 요구된다.

일반적으로 2상 유동 변수 측정 기법은 크게 침투식과 비침투식 측정 방법론으로 나뉜다. 이 중 비침투식 측정 방법론으로는 고속 카메라를 이용한 이미지 영상 처리 기법, Laser Doppler Anemometry(LDA), Particle Image Velocimetry(PIV) 등을 들 수 있다. 이러한 비침투식 측정법은 유동에 교란을 주지 않는 장점이 있지만, 기포 빈도수가 높은 유동 조건에서 빛 또는 레이저 빔이 기포들의 경계면에서 산란되거나 감쇄되어 계면을 투과하지 못함으로써 센서까지 도달하지 못하며, 빛 투과를 위한 가시창 재료의 제약으로 고온⋅고압 조건에 적용할 수 없는 등 제한된 조건에만 적용 가능한 한계를 갖는다. 침투식 측정 방법으로는 유체의 임피던스나 레이저빔을 이용하는 다중 센서 프로브와 wire mesh 임피던스 센서 등이 있다. 이들은 유로 내 유동 교란을 발생시키는 문제점이 있지만, 기포 갯수에 제한을 받지 않고 넓은 유동 조건에 적용할 수 있어 2상 유동 변수 측정에 널리 사용되고 있다. 특히 국소지점에서 기포인자 측정에 사용되는 다중 센서 프로브의 경우, 센서 제작 기술의 발달로 수십 마이크론 정도의 직경을 갖는 국소 광섬유 센서 등 유동 교란을 최소화하는 센서들이 개발되고 있다. 대표적으로 사용되는 다중 센서 프로브는 2중 센서 프로브와 4중 센서 프로브를 들 수 있으며, 프로브를 구성하는 센서는 축방향 위치에 따라 전단부 센서와 후단부 센서로 나뉜다. 이때 기포 속도, 기포 직경 등과 같은 기포 변수를 측정하기 위해서는 기포가 모든 센서를 통과해야 한다.^(1-6) 따라서 다중 센서 프로브의 측정 성능은 기포 크기에 영향을 받으며, 정밀한 변수 측정을 위해서는 센서 크기가 최소화되어야 한다.⁽⁶⁾ 그러나 이러한 센서는 프로브의 형상 구현을 위한 최소 크기가 필요해 작은 기포 또는 액적 측정에는 한계가 있다.

이를 해소하기 위해 선행 연구자들은 크기가 작은 단일 광섬유 센서 프로브를 이용한 기포 속도 측정 기술을 개발한 바 있다.^(7-9) Abuaf et al.⁽⁷⁾은 기포가 단일 광섬유 센서를 통과할 때 상승하는 신호의 크기(⊿V)가 기포 속도에 반비례하는 것을 확인하고, 각 상(Phase)에서의 신호 간 최대 크기 차이(⊿V_max)에 대한 기포신호 상승비(⊿V/⊿V_max)를 이용하여 기포 속도 범위 0∼1.5 m/s에서 속도 교정 곡선을 얻었다. 그러나 기포가 센서를 통과하는 동안 신호의 오버슈트(Overshoot) 등과 같은 불안정한 신호가 발생하여 ⊿V_max를 정밀하게 얻는 것에 어려움이 발생하였다. Cartellier⁽⁸⁾는 불안정한 신호의 원인이 프로브 끝단 센서부의 형상과 센서와 기포 계면의 접촉각 등에 있음을 보고하였다. 그리고 기포가 센서를 통과하는 동안 발생하는 신호의 변화율을 이용한 기포 속도 측정 방법론을 제시하였다. Mizushima and Saito⁽⁹⁾는 기포가 센서를 통과하기 직전 기포 계면에서 반사되는 레이저 빔에 의한 선행 기포 신호(Pre-signal)가 발생되는 것을 확인하고, 선행 기포 신호의 기울기 변화율(g_rd)을 이용하는 기포 속도 측정 방법론을 제시하고 검증하였다. 그러나 선행 연구의 단일 센서 프로브 속도 측정 방법론^(7-9)은 속도 범위 0.1∼1.5 m/s인 저속 기포 유동 조건에서 검증되어 고속의 기포 유동에 적용할 경우 불확실성이 따른다. 따라서 단일 광섬유 센서의 고유속 적용성을 확보하기 위해 보다 넓은 유동 조건에서 센서의 측정 성능을 평가하는 것이 필요하다. 최근 Kim et al.⁽¹⁰⁾은 작은 크기의 액적인자 측정을 위한 단일 광섬유 센서를 개발하고, 이를 고속의 기체-액적 혼합 유동 조건(2∼32 m/s)에 적용하여 국소 액적 속도 등 액적 변수들을 성공적으로 측정하였다. 이러한 연구결과는 단일 광섬유 센서 프로브가 고속의 기포 유동 조건에도 적용될 수 있음을 보여준다. 그러나 액적과 기포의 신호의 특성은 다르므로 고속의 기포 유동 조건에 단일 광섬유 센서 프로브를 적용하기 위해서는 고속의 기포 유동 조건에서 기포 속도 측정성을 평가하는 것이 필요하다.

더불어 몇몇 선행연구자들은 상(Phase) 간의 질량, 운동량, 에너지 전달량을 결정하는 주요 변수인 기포 직경을 다중 센서 프로브로 측정할 수 있는 방법론을 통계학적 방법론과 몬테카를로 시뮬레이션을 통해 개발하고 그 성능을 검증하였다.^(2-4) 이를 위해 선행 연구자들은 기포 형상을 구형 또는 타원형(Ellipsoid)으로 가정하였다. 그러나 실제 기포 유동에서는 캡 형상의 기포(Cap bubble)와 불안정한 계면을 가지는 기포 형상(Disk-like or wobbling) 등 구형과 다른 형상의 기포가 나타날 수 있어, 다양한 기포 형상 구성비를 가지는 유동 조건에서 센서의 측정 성능을 정량적으로 평가하는 것이 필요하다.

본 연구에서는 단일 광섬유 센서 프로브의 기포 속도 및 기포 크기 측정 성능을 평가하기 위해 넓은 유속 조건의 물-공기 실험장치에서 성능평가 실험을 수행하였다. 실험에는 단일 광섬유 센서 외 기포인자 측정에 많이 사용되는 2중 광섬유 센서를 동시에 적용하여 비교 평가하였다.

2. 광섬유 센서 프로브의 기포 변수 측정 기법

2.1 광섬유 센서의 작동 원리

광섬유 센서로 입사된 레이저 빔의 일부는 광섬유 내부의 코어를 통과해 센서 끝단에 도달한 후 센서 코어와 센서 외부 유체의 굴절률 차이로 반사된다. 이때 레이저 빔의 방향이 센서 끝단면에 수직한 경우, 반사되어 되돌아오는 레이저의 양은 다음의 식으로 계산할 수 있다.⁽¹¹⁾

$\[ R={\left(\frac{n_1-n_2}{n_1+n_2}\right)}^2 \]$

(1)

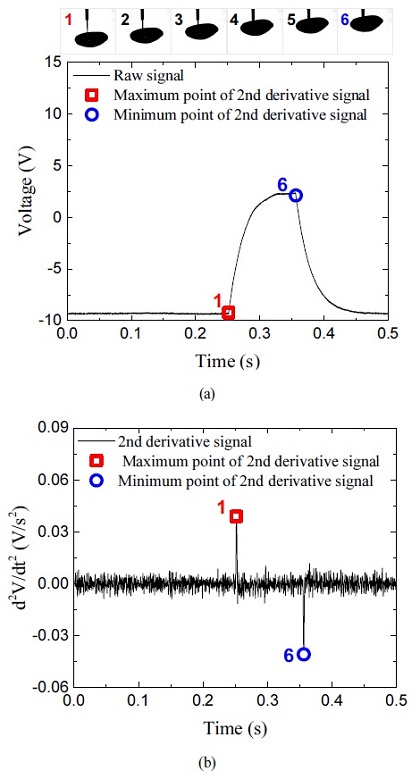
여기서 n₁, n₂는 각각 광섬유 코어와 레이저에 노출되는 유체의 굴절률이다. 광섬유의 굴절률은 본 연구에서 사용된 1,550 nm 파장의 광원 조건에서 1.46이며, 물과 공기의 굴절률은 온도 25℃의 대기압 조건에서 각각 1.33과 1.00이다.^(12,13) 이때, 센서 끝단에서 물과 공기에 의해 반사되는 레이저의 반사율은 Table 1과 같다. 이는 센서 끝단 외부의 유체가 공기인 경우 물인 경우보다 반사되어 되돌아오는 레이저 양이 상대적으로 많음을 나타낸다. Fig. 1은 매질에 따른 레이저의 반사 특성으로, 기포가 센서를 통과하는 경우, 센서 끝단에서 반사되어 돌아오는 레이저양을 광전 다이오드(Photo diode)를 통해 전압으로 변환한 신호이다. 이때 기포와 물의 경계인 계면(interface)은 전압 신호의 2차 미분 신호가 최대값 또는 최소값을 갖는 지점에 해당한다.⁽¹⁰⁾ 이렇게 얻은 광섬유 센서의 출력 신호는 기포 변수 측정에 사용된다.

Table 1

Reflection rate of laser light according to air and water

Fig. 1

(a) Typical bubble signal obtained from single sensor probe and (b) its 2nd derivative

2.2 국소 기포 변수 측정법

2.2.1 기포 속도

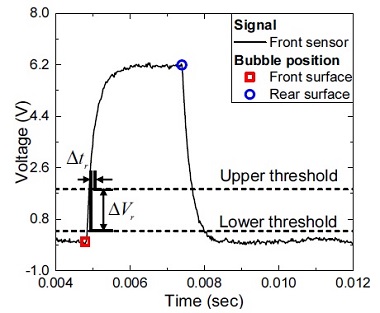
기포 속도 측정법은 프로브를 구성하는 센서의 수에 따라 다르다. 단일 광섬유 센서 프로브는 기포가 센서를 지날 때 발생되는 상승 신호의 단위 시간당 기울기 변화율(g_rd)을 이용하여 속도를 측정한다.^(9,10) 이를 위해서는 기포 속도와 g_rd 간의 관계를 나타내는 교정 곡선이 필요하다. Mizushima & Saito⁽⁹⁾는 Fig. 2에서와 같이 기포가 센서를 통과할 때 상승하는 신호의 특정 구간을 이용하여 다음 식과 같이 g_rd를 계산하고, 기포 속도와 g_rd 간의 선형적인 교정 곡선을 얻었다.

Fig. 2

Slope (grd) of a rising bubble signal

$\[ g_{rd}=\frac{{∆V}_r}{{∆t}_r} \]$

(2)

또 다른 속도 교정 방법론으로 액적입자 속도 측정을 위해 개발된 Kim et al.⁽¹⁰⁾의 방법론이 있다. 저자들은 입자의 속도 교정 곡선은 g_rd 뿐만 아니라 입자 크기에도 영향을 받음을 확인하고, 입자 크기 영향을 고려하기 위해 입자가 센서를 통과하는 시간인 입자 잔류시간과 총 측정시간의 비인 입자의 센서 통과 시간의 비, 그리고 g_rd를 기계학습의 입력변수로 사용하여 훈련시킨 후 이를 액적 속도 결정에 사용하였다.

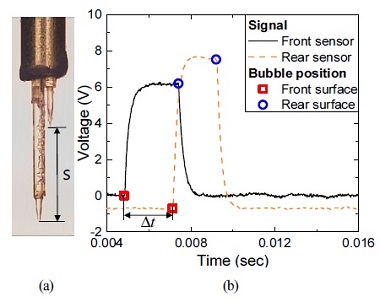
반면, 단일 센서의 비교 대상이 되는 2중 센서 프로브는 Fig. 3과 같이 축방향으로 거리(s) 사이에 배열된 2개의 광섬유 센서에서 측정되는 기포 신호 간의 시간 차이(⊿t)를 이용하여 다음 식과 같이 속도를 측정한다.

Fig. 3

(a) 2-sensor optical fiber probe (2S-OFP) and (b) typical bubble signal from the 2S-OFP

$\[ V_{2S-OFP}=\frac{s}{∆t} \]$

(3)

본 연구에서는 Mizushima and Saito⁽⁹⁾의 교정 방법론과 Kim et al.⁽¹⁰⁾의 방법론에 의한 액적 변수 측정 오차를 계산하고, 이를 2중 센서 프로브와 비교 평가하였다.

2.2.2 Sauter 평균 직경

Sauter 평균 직경(D₃₂)은 단위 부피당 계면면적을 나타내는 변수로 2상 유동에서 상간의 질량, 운동량, 에너지 전달량을 결정하는 주요 변수이다. 선행 연구자들은 국소 지점에서 기포의 시간 평균 Sauter 직경을 측정하기 위해 계면면적밀도(Interfacial Area Concentration, IAC) 기반의 측정 모델^(2-4)과 현의 길이 분포 함수(Chord Length Distribution, CLD)로 부터 얻은 기포 직경 분포(Particle Size Distribution, PSD)로 Sauter 평균 직경을 측정하는 방법론⁽¹⁴⁾을 개발하였다. 계면면적밀도($$ \overline{a_i}$$) 기반의 측정 방법론에서 Sauter 평균 직경은 다음 식과 같이 $$ \overline{a_i}$$와 기포율(α)의 함수로 나타난다.

$\[ d_{32}=\frac{6\alpha }{\overline{a_i}}, where \overline{a_i}=\sum _{j=1}^{N_b}\left|\frac{1}{V_{j,normal}}\right| \]$

(4)

여기서 기포율은 전체 측정 시간에 대해 기포가 전단부 센서를 통과한 시간의 비이다. 상기 식에서와 같이 계면면적밀도는 센서가 닿은 기포의 계면에 수직한 법선 속도(V_j,normal)를 측정함으로써 얻는다. 그러나 단일 광섬유 센서와 2중 광섬유 센서는 법선 속도가 아닌 축방향 속도만을 측정하므로 계면면적밀도 계산에 교정계수 도입이 필요하다. 이를 위해 선행연구자들은 Table 2와 같이 통계학적 접근법을 적용하여 유도한 계면면적밀도 측정 모델을 제시하였다.^(2,4,6)

Table 2

Existing IAC measurement methods for 2 sensor

Sauter 평균 직경을 측정하기 위한 또 다른 모델은 기포가 센서를 통과하는 길이(Traverse distance)인 현의 길이 분포(Chord Length Distribution, CLD)로부터 기포 직경(Particle Size Distribution, PSD)분포를 구하는 방법이다.^(14-17) 이때, 현의 길이는 다음식과 같이 계산된다.

$\[ L_{chord}=V_b\times t_{residence} \]$

(5)

현의 길이는 센서를 지나는 기포의 계면 위치와 기포의 크기에 따라 영향을 받는다. 기존 연구자들은 단일 기포 크기에 대한 현의 길이 분포를 나타내는 다음 식을 유도하였다.^(14-17)

$\[ M_{\overline{Lj}}=p_{\overline{D_i}}\left(L_j,L_{j+1}\right)N\left(\overline{D_i}\right) \]$

(6)

여기서 $$ N\left(\overline{D_i}\right)$$는 측정 시간 동안 평균직경이 D_i인 데이터 갯수, $$ p_{\overline{D_i}}\left(L_j,L_{j+1}\right)$$는 평균직경 D_i인 기포에 대해 측정된 현의 길이 범위가 L_j부터 L_j+1인 확률, $$ M_{\overline{L_j}}$$는 평균 현의 길이가 $$ \overline{L_j}\left(L_j+L_{j+1}\right)/2$$인 현의 갯수이다. 이때 센서가 구형인 기포의 단면을 동일한 확률로 통과한다는 가정을 적용하면 기포 직경 분포에 따라 측정되는 현의 길이 분포는 아래 식과 같다.

$\[ G\left(L\right)=AH\left(D\right) \]$

(7)

여기서 H(D)는 각 기포직경의 개수 분포를 나열한 행렬($$ \left[N\left(\overline{D_i}\right),N\left(\overline{D_2}\right), \dots , N\left(\overline{D_N}\right)\right]$$), A는 각 기포 직경에 따른 현의 길이 변환 행렬($$ p_{\overline{D_i}}\left(L_j,L_{j+1}\right), i=\mathrm{1,2}, \dots N;j=\mathrm{1,2}, \dots M$$), G(L)은 각 직경 분포로부터 변환된 현의 길이 분포($$ \left[M\left(\overline{L_1}\right),M\left(\overline{L_2}\right), \dots , M\left(\overline{L_M}\right)\right]$$)를 나타낸다. 이로부터 직경 분포는 아래 식으로 계산할 수 있다.

$\[ H\left(D\right)={\left(A^{T}A\right)}^{-1}{A}^{T}G\left(L\right) \]$

(8)

이때, Sauter 평균직경은 식 (8)에서 얻은 직경 분포를 이용하여 다음 식으로 구한다.

$\[ D_{32}=\frac{\sum _{i=1}^{N_b}{n}_i{D}_i^3}{\sum _{i=1}^{N_b}{n}_i{D}_i^2} \]$

(9)

여기서 D_i는 현의 길이 분포로부터 변환된 기포 직경, n_i는 각 기포 직경의 수밀도이다.

3. 센서 성능평가 실험

본 연구에서는 자체 제작한 단일 및 2중 광섬유 센서 프로브를 물-공기 실험장치에 적용하여 성능을 평가하였다. 실험장치와 기법은 다음과 같다.

3.1 실험장치

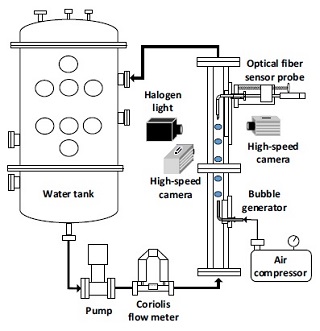
실험장치는 Fig. 4와 같이 물-공기 시험부, 기포 발생기, 물 주입계통으로 구성되었다. 물-공기 시험부는 20 mm x 20 mm 단면적을 가지는 사각유로로 총 길이는 1 m이며, 유동 가시화를 위해 아크릴로 제작되었다. 시험부 하부에는 물 주입구와 기포 발생기가 설치되었다. 기포 발생기는 노즐에서 생성되는 기포의 크기를 조절하기 위해 시험부로 주입되는 물이 일부를 인출하여 공기와 섞어 주입되도록 설계되었다. 시험부 상부에는 광파이버 센서가 설치되며, 동일한 높이에 2대의 고속카메라 시스템이 설치되어 가시화에 의한 기포인자 기준값 측정에 사용된다. 이때 고속 카메라는 정밀한 3차원 기포 형상 데이터 취득을 위해 시험부 전면과 측면에 수직이 되게 배열된다. 실험에서는 광파이버 센서로 취득되는 신호와 고속 카메라를 동기화함으로써 상호 비교할 수 있게 수행되었다. 이때 고속 카메라의 촬영 프레임 수는 초당 10,000장이다. 물 주입계통에서는 시험부로 공급되는 물의 질량 유량을 조절함으로써 다양한 유속 조건에서의 실험이 가능하다. 실험장치에서 실험이 가능한 유속은 최대 5.0 m/s이다.

Fig. 4

Schematic diagram of test facility

3.2 3차원 기포 형상 재구성 및 변수 측정법

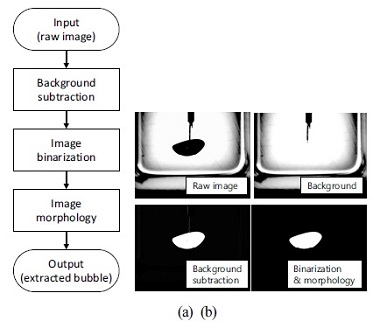
고속 카메라로 얻은 기포 영상은 분석을 통해 시험부 내 기포 속도 및 직경 정보 측정에 사용된다. Kim et al.⁽¹⁸⁾은 2대의 고속 카메라를 이용하여 전면과 측면에서의 기포 이미지를 취득하고, 이를 이용하여 3차원 기포 형상을 재구성한 바 있다. 본 연구에서는 Kim et al.⁽¹⁸⁾의 연구방법론을 기반으로 3차원 기포 형상을 재구성하였다. Fig. 5는 기포 추출을 위한 이미지 처리와 3차원 기포 형상 재구성 과정을 정리한 것이다.

Fig. 5

(a) Flow chart of image processing and (b) Images in the process of image processing

계면 추적을 위한 영상처리의 첫 번째 단계에서는 기포가 측정된 영상에서 기포가 없는 배경 영상을 제거한 후 명암 자동 이진화법을 적용하여 기포 경계를 1차로 구분한다. 두번째 단계에서는 기포의 경계를 보다 명확히 구별하기 위해 모폴로지 연산을 수행하여 계면을 추적한다. 이때 촬영된 각 영상 프레임의 기포 계면 정보로부터 기포 중심의 이동 거리를 계산할 수 있으며, 이를 이용하여 기포 속도를 계산한다.

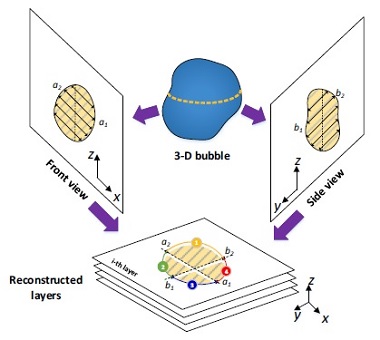
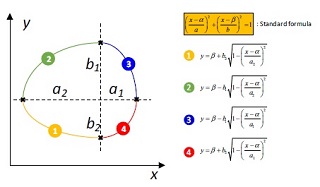
3차원 기포 형상은 Fig. 6과 같이 각 단면을 타원으로 가정하고, 이를 구성하는 각 단면을 층으로 쌓아 재구성한다. 여기서 각 타원은 Fig. 7과 같이 총 4개의 방정식으로 구성된다. 각 타원의 방정식의 장축과 단축은 전면에서 촬영된 이미지와 측면에서 촬영된 이미지로 계산한다. 이때 기포의 Sauter 평균 직경은 각 단면에서의 타원의 넓이(A_suf,i)와 둘레(P_i)를 이용하여 다음 식으로 계산한다.

Fig. 6

3-D reconstruction of bubble shape

Fig. 7

Cross-section of bubble at the layer

$\[ \begin{array}{r}{D}_{32}=\frac{6V}{A_{suf}}, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} A_{suf}=\sum _{i=1}^{N_{layer}}{P}_i\times {dh}_i\\ V=\sum _{i=1}^{N_{layer}}{A}_{suf,i}\times {dh}_i\end{array} \]$

(10)

4. 실험 및 결과

4.1 실험조건

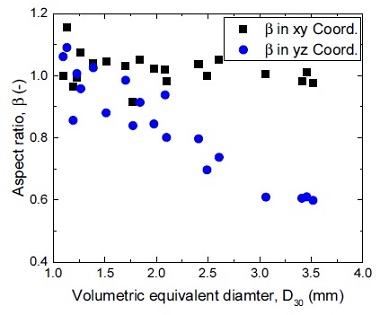
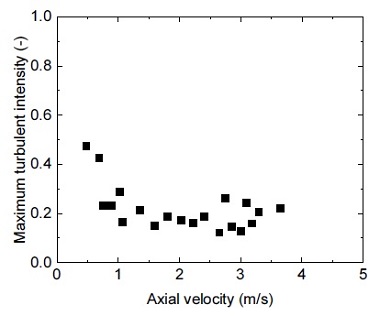
실험에서 유로에 나타나는 기포 형상 및 크기는 물 및 기포 속도에 영향을 받는다. 실험은 시험부에 주입되는 물 속도 조절을 통해 기포 속도 범위 0.2∼4.0 m/s에서 수행되었다. Fig. 8은 실험에서 유속을 변화시키며 수행한 실험에서 가시화 기법을 통해 얻은 기포의 크기와 종횡비를 나타낸다. 그림에서 유속이 작아 직경이 큰 기포가 형성되는 경우 기포 형상은 횡방향으로 넓게 퍼지며, 상대적으로 유속이 커서 기포 직경이 작은 경우에는 기포 형상이 구형으로 바뀐다. 이는 시험부로 주입되는 물의 속도가 큰 경우, 기포 분열(Break-up)이 활발해 기포 크기가 작아지기 때문이다. Fig. 9는 기포 속도에 따른 기포의 최대 난류섭동(Turbulent intensity) 크기를 보여준다. 실험에서 기포의 지그재그(Zigzag) 모션은 기포 속도 약 1 m/s 이하에서 크게 발생하였다. 이때 난류섭동의 최대 크기는 기포 속도가 가장 작은 0.2m/s에서 약 0.5였다. 그리고 물의 속도가 증가하면 기포의 축방향 속도도 증가해 최대 난류섭동은 감소한다.

Fig. 8

Bubble shape according to bubble diameter

Fig. 9

Maximum of turbulent intensity according to bubble velocity

4.2 기포 속도 측정 오차

단일 광섬유 센서 프로브는 기포 속도를 측정하기 위해 기포 상승 신호의 기울기 변화율과 기포 속도의 관계를 나타내는 교정 곡선이 필요하다. 본 연구에서는 2.2.1절에서 논의한 바와 같이 Mizushima and Saito⁽⁹⁾과 Kim et al.⁽¹⁰⁾이 제시한 교정 방법론으로 각각 교정 곡선을 얻고 이로부터 기포 속도를 계산하였다.

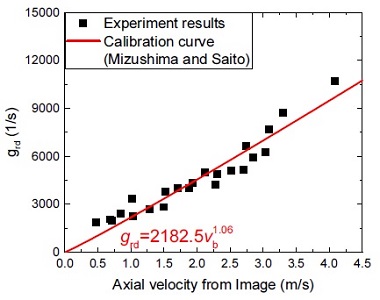
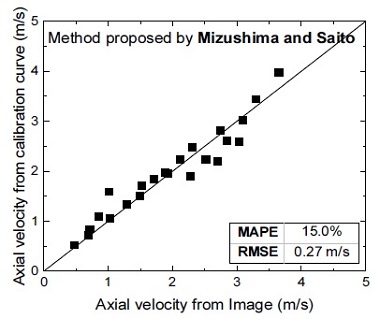
Fig. 10은 Mizushima and Saito⁽⁹⁾가 제시한 교정방법론을 적용하여 얻은 교정 곡선이며 기포 상승 신호의 기울기 변화율(g_rd)은 기포 속도와 선형적인 관계를 보인다. 여기서 g_rd값은 기포가 센서를 지나는 순간을 기준으로 기포와 액체 간 신호 높이 차이의 5%와 30%를 값을 기준으로 계산된다. Fig. 11은 선형 교정 곡선으로부터 계산된 기포 속도의 오차를 보여준다. 선형 교정 곡선을 이용한 경우, 단일 광섬유 센서 프로브는 최대 15%의 오차범위 내에서 기포 속도를 측정할 수 있다.

Fig. 10

Calibration curve for bubble velocity by Mizushima and Saito(9)

Fig. 11

Comparison of measured bubble velocity by calibration curve(Mizushima and Saito(9)) and image

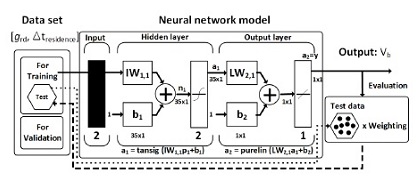
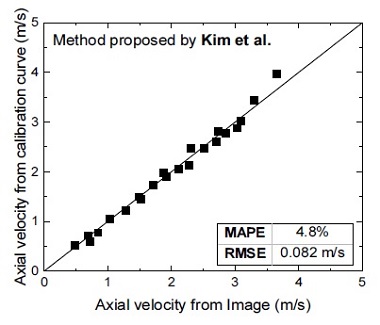
Fig. 12는 Kim et al.⁽¹⁰⁾의 교정방법론을 적용하기 위해 본 연구에서 사용한 기계학습의 구조를 나타낸다. 기계학습을 위한 입력 데이터는 g_rd와 기포 크기 정보를 내포하는 기포 잔류 시간(⊿t_residence)이며 기계학습 모델은 Kim et al.⁽¹⁰⁾이 적용한 베이지안 정규화 오류 역전파 모델(Bayesian regularization backpropagation)을 사용하였다. Fig. 13은 기계학습을 완료한 후 이를 이용하여 계산된 기포 속도 결과이다. 기계학습을 이용한 교정방법론은 4.8%의 속도 오차를 가지며 Mizushima and Saito⁽⁹⁾가 제시한 교정방법론보다 우수한 속도 측정 성능을 보인다. 이는 정밀한 기포 속도 측정을 위해서는 기포 크기 정보를 고려한 교정 곡선이 필요함을 뜻한다. 특히 기포류가 발생하는 유로 내 기포는 기포의 분해(break up)와 기포 간 결합(coalescence)으로 인해 그 크기가 다양하며 기계학습을 이용한 교정 곡선은 이에 따른 직경 효과를 고려할 수 있다. 그러나 단일 센서 교정 방법론은 각 센서에 대해 교정된 유동 범위 내에서만 측정 성능이 보장되므로 교정 범위를 벗어나는 유동 조건에 적용 시 측정 오차가 증가될 수 있다.

Fig. 12

Structure of neural network model(10)

Fig. 13

Comparison of measured bubble velocity by calibration curve(Kim et al.(10)) and image

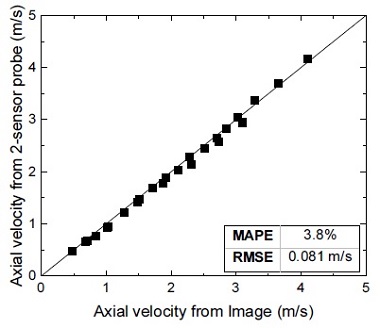
Fig. 14는 2중 광섬유 센서 프로브의 측정 성능 결과를 나타낸다. 그림에서와 같이 2중 광섬유 센서 프로브는 기포 속도를 약 3.8% 오차 범위 이내로 측정한다.

Fig. 14

Measured Velocity using 2-sensor optical fiber probe

4.3 기포 직경 측정 오차

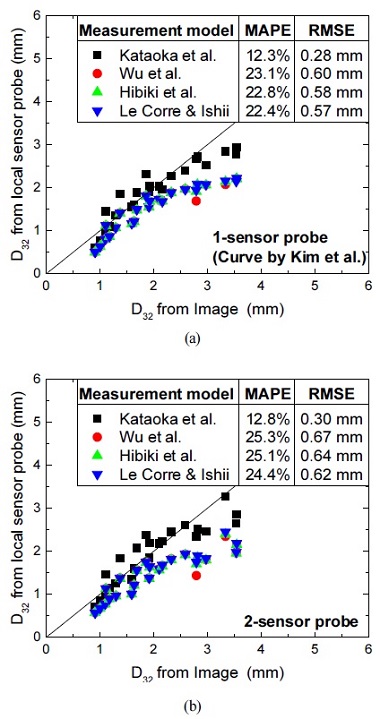
기포 직경 측정 방법론은 2.2.2절에서 논의한 바와 같이 계면면적밀도에 기반한 측정 방법론과 현의 길이 분포를 이용하는 방법이 있다. Fig. 15는 계면면적밀도 측정 모델을 적용한 단일 광섬유 센서와 2중 광섬유 센서 프로브로 측정한 포 직경을 나타낸다. 계면면적밀도 측정 모델의 경우, 단일 및 2중 광섬유 센서 프로브 모두에서 Kataoka et al.⁽¹⁾의 측정 모델은 오차 약 13%로 가장 우수한 성능을 보이고, Hibiki et al.⁽²⁾, Wu et al.⁽⁴⁾, Le Corre and Ishii⁽⁶⁾의 모델의 측정 오차는 모두 약 23% 정도를 보였다. 그러나 Kataoka et al.⁽¹⁾의 모델은 센서가 구형 기포 단면을 균일한 확률 분포로 통과한다는 가정을 적용하지 않기 때문에 사용 시 주의가 필요하다. 그리고 모든 계면면적밀도 기반의 기포 직경 측정 모델은 기포의 크기가 증가함에 따라 측정오차가 증가하였다. 이는 각 측정 모델이 기포를 구형으로 가정하는 반면, 실험에서 나타나는 실제 기포의 형상은 기포의 크기 증가에 따라 구형으로부터 왜곡되기 때문이다. 이와 관련하여 Grace⁽¹⁹⁾은 기포 형상이 Eo와 Re에 영향을 받으며, 이를 이용하여 기포 형상을 예측하는 맵을 제시한 바 있다. 본 실험에서 관측된 기포 형상은 구형에서 벗어난 형태로 Grace⁽¹⁹⁾에 의해 예측된 기포 형상과 동일하다.

Fig. 15

Measured bubble diameter(D32) based on ai¯ : (a) 1-sensor probe and (b) 2-sensor probe

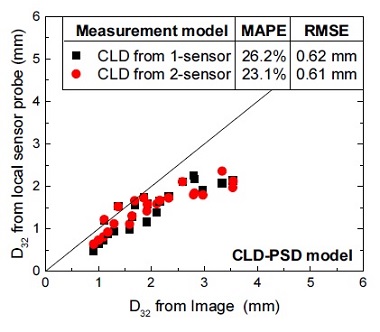
현의 길이 분포를 이용하여 기포 직경을 측정한 결과는 Fig. 16과 같다. 단일 센서 프로브의 직경 측정 오차와 2중 센서 프로브의 측정오차는 각각 26.2%와 23.1%로, 2중 센서 프로브가 단일 센서 프로브보다 우수한 측정 성능을 보인다. 이는 2중 센서 프로브의 기포 속도 측정 오차가 단일 센서 프로브보다 근소하게 작아 2중 센서 프로브에서 측정된 현의 길이 분포가 단일 센서 프로브보다 정확하기 때문이다. 단일 센서 프로브와 2중 센서 프로브는 모두 기포의 크기가 증가함에 따라 측정 오차가 증가한다. 이는 현의 길이 분포를 이용한 모델도 2중 센서 프로브와 같이 구형 기포를 가정하고, 기포 형상도 기포의 크기 증가에 따라 구형으로부터 왜곡되기 때문이다.

Fig. 16

Measured bubble diameter(D32) based on chord length distribution

기포 직경을 측정하기 위한 계면면적밀도 측정 모델과 현의 길이 분포를 이용한 측정 모델을 종합적으로 비교 평가한 결과, 기포 직경 측정 성능은 축방향 속도 분포에 기반하는 측정모델과 현의 길이 분포로부터 기포 직경을 측정하는 밥법론은 서로 비슷한 결과를 보인다. 그리고 두 측정 방법론 모두 기포 형상을 구형으로 가정함으로서 기포 크기가 증가하여 구형기포에서 멀어지는 경우 측정 오차가 증가한다. 이를 개선하기 위해서는 기포 형상을 고려하는 모델의 개발이 필요하다.

5. 결 론

본 연구에서는 단일 광섬유 센서 프로브의 기포 속도와 기포 크기 측정 성능을 실험적으로 평가하였다. 이를 위해 다양한 기포 직경과 형상, 그리고 기포 속도를 갖는 물-공기 유로에서 벤치마크 실험을 수행하였다. 또한, 기존에 널리 사용되는 2중 광섬유 센서를 동시에 적용하여 단일 센서의 측정 성능을 비교 평가하였다. 평가의 기준이 되는 기포 변수는 가시화 기법을 적용하여 얻었다. 본 연구를 통해 도출한 결론은 다음과 같다.

• 1) 단일 광섬유 센서 프로브로 기포 속도를 측정하기 위해서는 속도 교정 곡선이 필요하며, 단일 피팅 곡선보다 기포 크기를 간접적으로 고려하는 기계학습 교정 기법이 우수한 측정 성능을 보였다.
• 2) 단일 광섬유 센서 프로브와 2중 광섬유 센서 프로브는 기포 속도를 각각 4.8%와 3.8%의 평균 오차로 측정하였다.
• 3) 기포 직경 측정 성능은 계면면적밀도에 기반한 모델과 현의 길이 분포를 이용한 측정 모델로 나누어 평가하였으며, 두 모델은 서로 비슷한 성능을 보였으며, 양 센서 간의 측정 오차의 차이는 기포 속도 측정 오차 차이에 기인한다.
• 4) 기포 직경 측정 모델은 기포를 구형으로 가정하고 있어 기포 크기가 증가할수록 오차가 증가한다. 이를 개선하기 위해서는 기포 형상을 고려한 기포 직경 측정 모델의 개발이 필요하다.

Acknowledgments

이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

References

• Kataoka, I., Ishii, M., and Serizawa, A., 1986, “Local formulation and measurements of interfacial area concentration in two-phase flow,” International Journal of Multiphase Flow, Vol. 12, No. 4, pp. 505∼529. [https://doi.org/10.1016/0301-9322(86)90057-1]
• Hibiki, T., Hogsett, S., and Ishii, M., 1998, “Local measurement of interfacial area, interfacial velocity and liquid turbulence in two-phase flow,” Nuclear engineering and design, Vol. 184, No. 2-3, pp. 287∼304. [https://doi.org/10.1016/S0029-5493(98)00203-9]
• Revankar, S. T., and Ishii, M., 1993, “Theory and measurement of local interfacial area using a four sensor probe in two-phase flow,” International journal of heat and mass transfer, Vol. 36, No. 12, pp. 2997∼3007. [https://doi.org/10.1016/0017-9310(93)90029-6]
• Wu, Q., and Ishii, M., 1999, “Sensitivity study on double-sensor conductivity probe for the measurement of interfacial area concentration in bubbly flow,” International Journal of Multiphase Flow, Vol. 25, No. 1, pp. 155∼173. [https://doi.org/10.1016/S0301-9322(98)00037-8]
• Kim, S., Fu, X. Y., Wang, X., and Ishii, M., 2000, “Development of the miniaturized four-sensor conductivity probe and the signal processing scheme,” International journal of heat and mass transfer, Vol. 43, No. 22, pp. 4101∼4118. [https://doi.org/10.1016/S0017-9310(00)00046-6]
• Le Corre, J. M., and Ishii, M., 2002, “Numerical evaluation and correction method for multi-sensor probe measurement techniques in two-phase bubbly flow,” Nuclear engineering and design, Vol. 216, No. 1-3, pp. 221∼238. [https://doi.org/10.1016/S0029-5493(02)00130-9]
• Abuaf, N., Jones Jr, O. C., and Zimmer, G. A., 1978, “Optical probe for local void fraction and interface velocity measurements,” Review of Scientific instruments, Vol. 49, No. 8, pp. 1090∼1094. [https://doi.org/10.1063/1.1135524]
• Cartellier, A., and Barrau, E., 1998, “Monofiber optical probes for gas detection and gas velocity measurements: conical probes,” International journal of multiphase flow, Vol. 24, No. 8, pp. 1265∼1294. [https://doi.org/10.1016/S0301-9322(98)00032-9]
• Mizushima, Y., and Saito, T., 2012, “Detection method of a position pierced by a single-tip optical fibre probe in bubble measurement,” Measurement Science and Technology, Vol. 23, No. 8, 085308. [https://doi.org/10.1088/0957-0233/23/8/085308]
• Kim, T., Ahn, T., Bae, B., Jeong, J. J., Yun, B., and Kim, K., 2019, “Measuring local droplet parameters using single optical fiber probe,” AIChE Journal, VOl. 65, No. 6, e16591. [https://doi.org/10.1002/aic.16591]
• Morris, D., Teyssedou, A., Lapierre, J., and Tapucu, A., 1987, “Optical fiber probe to measure local void fraction profiles,” Applied optics, Vol. 26, No. 21, pp. 4660∼4664. [https://doi.org/10.1364/AO.26.004660]
• Schiebener, P., Straub, J., Levelt Sengers, J. M. H., and Gallagher, J. S., 1990, “Refractive index of water and steam as function of wavelength, temperature and density,” Journal of physical and chemical reference data, Vol. 19, No. 3, pp. 677∼717. [https://doi.org/10.1063/1.555859]
• Ciddor, P. E., 1996, “Refractive index of air: new equations for the visible and near infrared,” Applied optics, Vol. 35, No. 9, pp. 1566∼1573. [https://doi.org/10.1364/AO.35.001566]
• Uga, T., 1972, “Determination of bubble-size distribution in a BWR,” Nuclear Engineering and Design, Vol. 22, No. 2, pp. 252∼261. [https://doi.org/10.1016/0029-5493(72)90167-7]
• Clark, N. N., and Turton, R., 1988, “Chord length distributions related to bubble size distributions in multiphase flows,” International Journal of Multiphase Flow, Vol. 14, No. 4, pp. 413∼424. [https://doi.org/10.1016/0301-9322(88)90019-5]
• Liu, W., and Clark, N. N., 1995, “Relationships between distributions of chord lengths and distributions of bubble sizes including their statistical parameters,” International journal of multiphase flow, Vol. 21, No. 6, pp. 1073∼1089. [https://doi.org/10.1016/0301-9322(95)00039-Z]
• Simmons, M. J. H., Langston, P. A., and Burbidge, A. S., 1999, “Particle and droplet size analysis from chord distributions,” Powder Technology, Vol. 102, No. 1, pp. 75∼83. [https://doi.org/10.1016/S0032-5910(98)00197-1]
• Kim, Y. N., Kim, J. S., Park, G. C., and Cho, H. K., 2017, “Measurement of sliding bubble behavior on a horizontal heated tube using a stereoscopic image processing technique,” International Journal of Multiphase Flow, Vol. 94, pp. 156∼172. [https://doi.org/10.1016/j.ijmultiphaseflow.2017.04.017]
• Grace, J., 1973, “Shapes and velocities of bubbles rising in infinite liquid,” Transactions of the Institution of Chemical Engineers, Vol. 51, pp. 116∼120.