1.5 kW 유도전동기 엔드링 기공이 회전체 진동 및 베어링 내구성에 미치는 영향 분석
Abstract
This paper presents the results of rotordynamic analyzing the effect of the end-ring porosity of a 1.5 kW induction motors on the rotor vibration and the bearing durability. Firstly, the end ring porosity shape of the induction motor was simplified by the porosity cross-sectional area (S) and porosity distribution angle (θ), and a mathematical model was established to calculate the amount of unbalance. The amount of unbalance due to porosity shape was analyzed through a mathematical model. As a result, it was confirmed that the amount of unbalance significantly increased to more than the balancing grade G40 by S and θ. In general, the proper balancing class for induction motors is G2.5. Second, a rotordynamic analysis model was developed that can predict the vibration characteristics of rotor. In addition, the analysis model was validated through the modal test. Finally, the vibration characteristics of the rotor were analyzed according to the amount of unbalance and phase angle through the rotordynamic analysis. As S decreases, the maximum rotor amplitude linearly decreased and the bearing life increased. As θ increases, the maximum rotor amplitude nonlinearly decreased and the bearing life increased. As the phase angle increases, the maximum rotor amplitude decreased by 75% and the bearing life increased 63 times.
Keywords:
Induction motor키워드:
유도전동기1. 서 론
전동기는 전기 에너지를 기계 에너지로 변환하는 기계시스템으로 산업 및 가정용 분야에서 핵심 동력원으로 널리 사용되며 개발된 지 100년 이상의 역사를 가지고 있다. 이 중 유도전동기는 내구성이 우수하고 제조가 비교적 간단하여 산업용과 가전용에서 90%, 50% 이상의 점유율을 차지하고 있다(1). 특히, 유도전동기를 구동하는데 사용되는 전력은 우리나라 전력 소비량의 50% 이상을 차지하고 있어, 유도전동기의 효율 향상은 국가 에너지 사용 절약에 있어 중요한 과제이다(2). 또한 최근 환경오염 문제가 전 세계적으로 대두되고 있으며, 특히 이산화탄소 배출 저감을 위한 에너지 절약 및 기계시스템의 효율 규제 등의 에너지 정책이 급격히 증가하고 있다. 전동기 분야에서는 환경오염 문제의 해결 및 고효율 전동기의 보급 확대를 위해서 고효율 전동기의 생산 판매를 의무화하는 최저효율제(Minimum Energy Performance Standards, MEPS) 정책을 법률로 제정하여 시행하고 있다(2).
유도전동기의 효율 향상을 위해서는 설계기술, 재료기술, 생산기술, 평가기술 등이 함께 개발되어야 한다. 생산기술은 고효율 전동기의 생산성을 높여 고효율 전동기가 널리 사용되기 위한 중요한 기술 중 하나다. 생산기술 분야에서 핵심이 되는 이슈는 회전자 제작기술이다. 유도전동기는 고정자(Stator)와 회전자(Rotor)로 구분되며, 회전자는 크게 샤프트(Shaft), 샤프트 중앙에 로터 코어(Rotor core)와 로터 코어 양 끝에 두 개의 엔드링(End-ring)으로 구성된다. 로터 코어와 엔드링의 제작은 금형주조법(Die casting)으로 제작된다. 금형주조법은 금형에 용융 금속을 주입하여 제작하는 방법이며, 로터 코어와 엔드링 금형주조는 금형에 로터 코어에 해당하는 전기강판을 적층시키고 적층된 로터 코어의 슬롯(Slot)에 융용 알루미늄을 충진시켜 제작된다. 금형주조법은 높은 생산성을 가지는 장점이 있지만 주조품에 기공(Porosity)이 발생한다는 단점이 있다. 따라서 금형주조 시 기공을 줄이는 생산기술 개발 연구과 활발히 진행되고 있다(3).
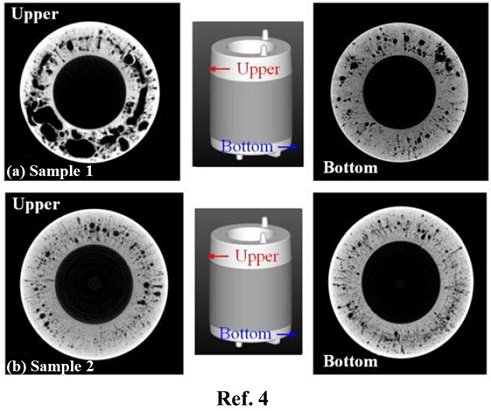
기공은 금형주조 시 용융금속의 유동에 의한 와류에 의해 발생하고, 유도전동기에서는 특히 회전자의 엔드링에 다량으로 발생한다. Fig. 1은 1.5 kW 유도전동기의 엔드링을 엑스선 전산화 단층 촬영(X-ray computed tomography)한 사진을 나타낸다(4). 금형주조 과정 중 발생한 엔드링의 기공은 전자의 흐름을 방해해 전력의 효율을 떨어트리고 질량 불평형(Imbalance)으로 회전체 진동 및 소음을 발생시켜 밸런싱(Balancing)과 같은 추가적인 공정이 요구된다(5). 또한 기공은 해석과 실험의 오차를 발생시키는 요인으로 작용한다. 이러한 문제는 유도전동기 저효율, 과진동 설계 등 다양한 문제를 초례할 수 있다.
엔드링의 기공을 저감시키는 기술 연구로, Park(6)은 금속주조의 충진 흐름을 고려한 새로운 회전자 주조 방법을 제시하였다. 제시된 회전자 주조 방법의 충진 흐름은 충진 해석 결과 용융 금속은 하부 엔드링이 먼저 충진되고 상부 엔드링, 슬롯에서 충진이 완료된다. 또한 실험을 통해 새로운 회전자 주조 방법이 엔드링 기공 단면적이 70% 감소된 양호한 품질의 회전자를 생산할 수 있음을 검증하였다.
Gang 등(7)은 엔드링 충진율을 향상시키는 스퀴즈 바 가압 방식을 제시하였다. 스퀴즈 바 가압 방식은 회전자 주조시 돌출된 스퀴즈 바를 형성한 후 스퀴즈 바를 회전자측으로 가압하는 방식이다. 특히, 스퀴즈 바 가압 방식은 밀도를 향상시키고 기공률을 저하시켜 높은 품질의 회전자 생산이 가능하는 장점을 가진다.
한편 엔드링 기공이 유도전동기의 전기적 효율에도 영향을 미치게 된다. Lee 등(4)은 엔드링 기공률이 19.8%와 5.8% 두 가지 1.5 kW 유도전동기 샘플에 대해서, 엔드링 기공이 전동기의 효율 및 손실에 미치는 영향을 유한요소 해석을 통해 규명하였고 실험을 통해 검증하였다. 특히, 엔드링 기공량과 분포를 측정하기 위해서 엑스선 전산화 단층 촬영 장비를 이용하여 기공량을 추측하였다. 연구결과로, 효율 측정 실험과 유한요소 해석 결과가 1.07% 이내의 오차를 가지고, 엔드링 기공률이 19.8%에서 5.8%로 감소할 때 유도전동기 효율이 1.4% 증가하였다.
Yun 등(8)은 15kW 유도전동기에 대하여 알루미늄 다이케스트 회전자 기공이 유도전동기 효율에 미치는 영향에 대해 연구하였다. 알루미늄 다이케스트 회전자 충진률이 67%부터 100%까지 증가할 때 효율 변화를 해석하였고 효율 90.2%이상(IE3 급) 도달하기 위한 최소한의 회전자 충진률을 제시하였다. 해석결과 충진률 100%가 67%에 비해 효율이 2.04% 증가하였고 효율 90.2% 이상이 되려면 충진률이 93% 이상이 되어야한다고 제시하였다.
이처럼 엔드링 기공을 줄이는 연구와 기공이 유도전동기 효율에 미치는 영향에 대해 연구가 진행되었다. 하지만 엔드링 기공이 유도전동기 진동에 미치는 영향 연구는 진행되지 않은 상황이다. 본 연구에서는 참고문헌 [4]의 1.5 kW 유도전동기를 이용하여 엔드링 기공이 회전체 진동에 미치는 영향을 회전체 동역학 해석을 통해 분석하고자 한다. 이를 위해 복잡한 기공 분포를 단순화 및 정량화 할 수 있는 기공 단순화 모델을 도입하였다. 또한 유도전동기 진동을 예측하기 위해 회전체 동역학 해석을 하였으며, 모드실험을 통해 해석의 정확도를 향상시켰다. 마지막으로 개발한 회전체 동역학 해석 모델을 이용해 엔드링 기공 분포와 위상에 따른 유도전동기 축계의 진동 거동을 해석 및 분석하였다.
2. 기공의 단순화 분석
2.1 기공의 단순화 모델
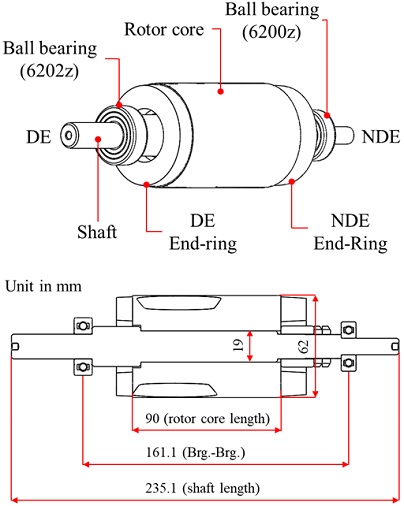
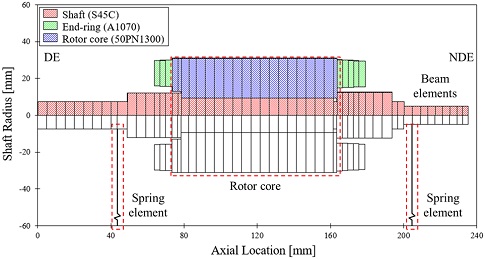
Fig. 2는 1.5 kW 단상 유도전동기 축계 도면을 보여준다. 본 유도전동기는 가전, 산업 등 다양한 분야에서 구동원으로 사용된다. 또한 영구 자석 모터에 비해 구조가 간단해 작은 비용으로 제작이 가능하다(4). 축계는 중심을 기준으로 어플리케이션과 결합되는 좌측 부하단(Driven end, DE)과 우측 자유단(Non driven end, NDE)로 구분된다. 구성은 샤프트(Shaft)와 샤프트 중앙에 로터코어(Rotor core), 로터코어 양 끝에 두 개의 엔드링(End-ring)이 위치되어 있다. 또한 샤프트는 두 개의 볼베어링(Ball bearing)으로 양단 지지된다.
샤프트의 총 길이는 235.1 mm이며 로터코어의 총 길이는 90 mm, 두 베어링간 거리는 161.1 mm이다. 또한 로터코어의 직경은 62 mm이며 샤프트의 직경은 19 mm이다. Table 1은 유도전동기의 전기적 특성을 보여주며, 정격 용량은 1.5 kW이고 동기속도는 60 Hz 입력에서 3420 rpm이다.
Fig. 1과 같이 엔드링 제조 공정 중 발생된 엔드링 내의 기공은 불규칙한 형태 및 분포로 형성된다. 이러한 기공은 엔드링의 질량을 변화시키며 질량중심의 편심을 야기하여, 축계의 회전중심과 무게중심이 일치하지 않는 질량 불평형(Mass unbalance)초래한다. 질량 불평형은 회전 중 축계를 가진하는 주요 가진원에 해당한다.
따라서 기공에 의한 엔드링의 질량중심 이동과 질량감소를 등가의 단순한 형태로 정량화하여 분석하기 위해 단순화 모델을 도입하였다. Fig. 3과 같이 XYZ 좌표계상에서 단순화된 엔드링과 기공은 기하학적 변수 기공 단면적(S)과 기공분포 각도(θ) 변수를 통해 정의된다. 기공 단면적 S는 단순화된 기공 형상의 단면적을 의미한다. 중심거리(R)는 엔드링 중심과 기공 단면적의 중심간 거리로 상수 값을 가진다.
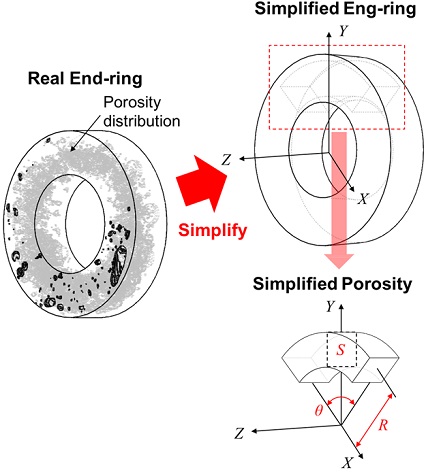
3D drawing of that defines the simplified end ring and porosity in the XYZ coordinate system through geometric variables cross-sectional area(S) and distribution angle(θ)
실제 엔드링을 단순화 하는 과정은 실제 기공의 질량과 질량중심의 위치와 동일한 단순화된 형태의 기공을 기하학적 변수 S와 θ를 이용하여 표현하는 것이다. 따라서 주어진 실제 기공의 질량과 질량중심을 계산하고, 이를 질량 등가 및 질량중심 등가 수식을 통해 S와 θ를 찾는 것이 가능하다.
실제 기공과 단순화된 기공의 질량 등가는 다음 수식을 만족한다.
| (1) |
여기에서 좌변은 실제 기공의 질량, 우변은 단순화된 기공의 질량을 의미하며, ρ는 엔드링의 밀도를 나타낸다. 좌변의 값은 캐드 프로그램을 통해서 계산이 가능하다.
단순화된 기공의 질량중심(yp)은 다음과 같이 계산되며, 실제 기공의 질량중심과 일치한다.
| (2) |
단순화된 기공은 X, Y 축을 기준으로 대칭으로 분포한 것으로 가정하므로, Y 방향 좌표만으로 질량중심의 정의가 가능하다.
한편, 엔드링의 불평형 거리(yep)는 기공의 질량(mp)과 기공을 제외한 엔드링의 질량(mep)의 비율과 기공의 질량중심(yp)의 곱으로 다음과 같이 결정된다.
| (3) |
엔드링의 불평형 방향은 기공의 질량 중심의 반대 방향이다. 엔드링의 불평형 벡터()는 기공의 질량 중심 벡터()의 음의 방향으로 다음과 같이 결정된다.
| (4) |
엔드링 기공에 의한 회전체 동역학적 질량 불평형, 즉 불평형량(eep)은 엔드링의 질량과 불평형 거리의 곱으로 계산이 가능하며, 다음과 같이 정의된다.
| (5) |
2.2 기공에 의한 불평형량 분석
.5 kW 유도전동기 축계의 엔드링 샘플 #1, #2를 대상으로, 변수 S와 θ의 변화에 따라 불평형량의 변화를 분석하였다. 이는 불평형량은 회전체를 가진하는 가진력으로 작용하며, 회전속도의 제곱에 비례한 가진력을 발생시킨다. 따라서 불평형량 분석은 회전체 동역학 해석에 있어 중요한 사전 단계이다.
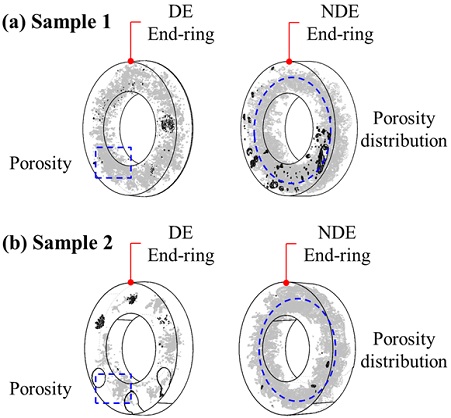
Fig. 4는 1.5 kW 유도전동기 축계 (a)샘플 #1과 (b)샘플 #2의 엔드링 3D 모델링을 보여준다. 엔드링 3D 모델링은 실제 엔드링의 엑스선 전산화 단층 촬영을 통해 2D 사진을 200~400장 촬영하고, 촬영된 2D 사진을 Z 축 방향으로 적층시켜 3D 모델으로 구현하였다. 샘플은 부하단과 자유단 엔드링이 각각 존재하며, 실제 엔드링 기공의 질량과 질량중심 좌표는 캐드 프로그램을 통해 계산하였다.
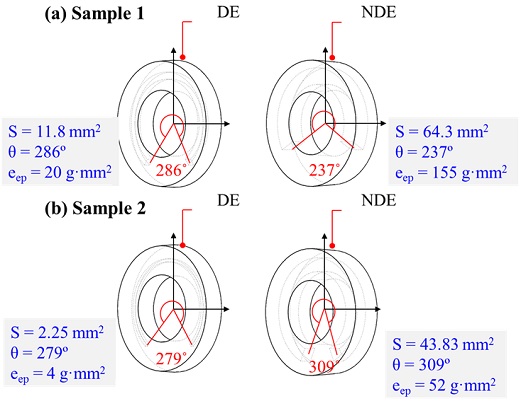
Fig. 5는 (a)샘플 #1과 (b)샘플 #2 의 실제 엔드링 기공을 단순화한 형태를 보여준다. 단순화 과정은 실제 엔드링의 질량과 질량중심 정보를 이용해 식 (3, 4)을 통해 변수 S, θ를 결정하고, 이를 시각적으로 표현하였다. 이때 중심거리(R)은 단순화된 기공의 단면적(S)이 엔드링 단면의 중심에 위치해 있다고 가정하여, DE 22.9 mm, NDE 22.5 mm의 값을 사용하였다.
단순화 결과 두 샘플 모두 DE 엔드링보다 NDE 엔드링에서 S 값이 더 크며, 이는 많은 기공이 형성되었다는 것을 의미한다. 또한 불평형량은 샘플 #1의 경우 NDE가 DE보다 7.75배 크며, 샘플 #2의 경우 13배 큰 값을 가진다. 이는 실제 금형 주조에서 하부에 위치하는 NDE 엔드링은 용융금속의 유동 와류에 의해 많은 기공이 형성되기 때문으로 판단된다(5,6).
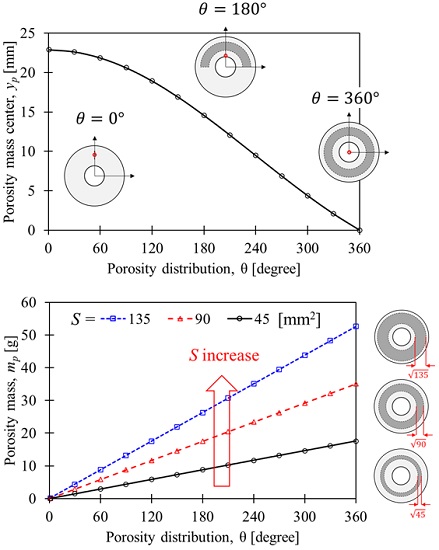
다음으로 변수 S와 θ에 따라 기공의 질량과 질량중심 변화를 예측한 결과를 Fig. 6에 나타내었다. S = 45, 90, 135 mm2이며, θ = 0∼360°로 변화시켰다. 기공의 질량중심(yp) 변화는 θ가 증가할수록 비선형적으로 감소하였으며, 기공이 원주방향으로 고르게 분포할수록 질량중심이 엔드링 끝에서 중심으로 이동한다. 반면, 기공의 질량(mp)은 각각 θ 와 S의 증가에 비례하여 선형적으로 증가하였다. 이는 기공의 질량이 기공 부피에 비례하고 기공 부피가 S와 θ의 증가에 비례하여 증가하기기 때문으로 판단된다.
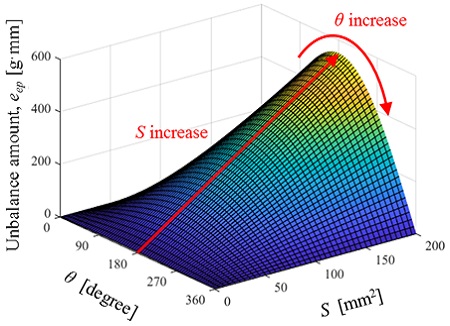
Fig. 7는 기공에 의한 불평형량의 변화를 변수 S와 θ에 대해서 예측한 결과를 보여준다. 불평형량은 S 증가에 따라 비례해서 증가하는 경향이며, 특히 기공분포 각도(θ)에 따라 비선형적 거동을 보인다. θ = 180°일 때 S 변화에 따라 가장 민감하게 불평형량이 변화한다. 반면 θ 가 0° 또는 360°에 수렴할수록 S 변화에 따라 둔감하게 변화한다. 즉, 불평형량을 결정하는 주요 인자는 기공분포 각도(θ)이다. 따라서 축계의 가진력을 저감하는 관점에서 기공의 분포가 고르게 분포하도록 엔드링의 제조 공정을 수정하는 것이 유리하다. 또한 기공이 엔드링의 원주방향으로 고르게 분포할 경우 기공량 자체는 회전체 진동에 크게 영향을 미치지 않는다고 분석할 수 있다.
기공에 의한 불평형량의 수준을 판단하기 위해서 ISO 1940-1기준에 따라 일반적인 회전체 밸런싱 등급(G)에 해당하는 잔류 불평형량(Uper)를 계산하고(9), 이를 기공에 의한 불평형량과 비교하였다. 잔류 불평형량(Uper) 계산에 있어 축계 총질량(m) 2.34 kg, 정격 회전속도(Ω) 358 rad/s(3,420 rpm)의 값을 사용하여, 다음의 수식을 이용하였다.
| (6) |
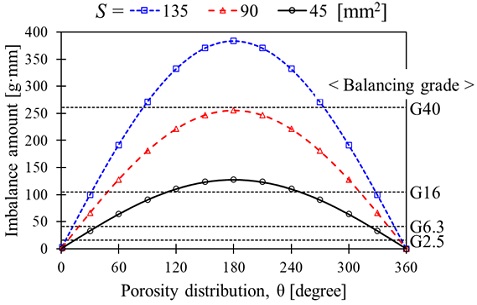
Fig. 8은 S와 θ에 대하여 불평형량 변화와 불평형량에 따른 축계 밸런싱 등급을 나타낸다. θ는 180°에서 불평형량이 최대가 되고, S는 증가할수록 불평형량이 증가한다. 밸런싱 등급은 θ가 180°도 부근에서 최대 G40 이상이 된다. ISO 1940-1(9)에 따르면 80 mm 이하의 샤프트 직경과 최대 정격속도 950 rpm 이하의 유도전동기는 G6.3등급으로 제한되며, 80 mm 이상의 샤프트 직경과 최대 정격속도 950 rpm 이상의 유도전동기는 G2.5등급으로 불평형량을 제한하고 있다. 즉, 기공에 의한 불평형량은 일반적인 회전체 불평형량 기준을 크게 상회하는 수준으로 불평형을 만들 수 있음을 알 수 있다.
3. 회전체 동역학 해석모델
3.1 기본 모델(Baseline) 수립
회전체 동역학 해석모델 수립 과정은 기본 모델 수립과 모델 개선 과정으로 구분된다. 기본 모델 수립 과정은 주어진 축계 형상과 재질정보를 이용해 초기 모델을 생성하는 단계이며, 모델 개선 과정은 생성된 모델의 정확도를 개선하기 위해 모드실험을 수행하고, 모드실험(Modal test)의 결과에 기반해 기본 모델을 개선하는 과정이다.
Fig. 9는 1.5 kW 유도전동기 축계의 2차원 유한요소 회전체 동역학 해석모델을 보여준다. 해석은 2차원 유한요소해석 프로그램인 XLRotor를 이용하여 수행된다(10). 해석모델은 샤프트와 로터코어, 엔드링이 빔 요소로 모델링되었다. 그리고 각 부품에 해당되는 기계적 특성 값을 입력하였으며 그 값은 Table 2에 제시되었다. 샤프트는 강(Steel, S45C), 로터코어는 규소강판(Silicon steel, 50PN1300), 엔드링은 알루미늄(Aluminum, AL1070)으로 제작되었다. 또한 두 개의 볼베어링(6200zz)은 등가의 강성을 가지는 스프링요소로 모델링되었다. 베어링 강성은 XLRotor ball bearing 해석 프로그램을 이용하여 해석되었다(10).
3.2 해석모델 개선
해석모델 개선은 참고논문 [11]에서 제시된 보정계수(Influence factor)를 도입하여 로터코어의 탄성계수 값을 보정하였다. 실제 축계의 로터코어는 0.5 mm 두께의 규소 강판이 적층된 구조다. 이러한 적층구조는 적층된 강판과 강판 사이 슬립(Slip)이 발생해 로터코어 구조를 유연하게 만들어 강성이 감소하게 된다. 따라서 로터코어의 적층구조로 인한 강성감소효과 때문에 탄성계수 보정이 필요하다. 기존 탄성계수(E)에 보정계수(η)를 곱하여 로터코어의 탄성계수를 보정하였다.
| (7) |
여기서, Em은 보정된 탄성계수를 의미한다. 이 때 보정계수는 0부터 1사이의 값을 가지므로 로터코어의 탄성계수는 감소된다. 탄성계수 감소로 인해 로터코어 강성 또한 감소된다. 특히, 적절한 보정계수 값은 해석모델을 통해 예측된 고유진동수가 실제 고유진동수와 일치하도록 선정되었다. 실제 고유진동수는 모드실험을 통해 측정되었다.
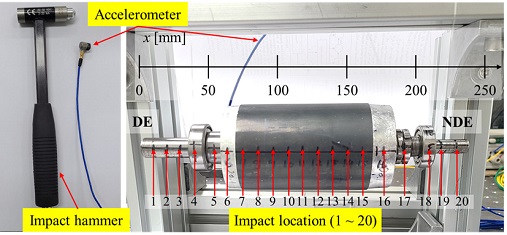
Fig. 10은 1.5 kW 유도전동기 축계의 모드실험의 구성을 나타낸다. 축계의 부하단과 자유단을 끈으로 메달아 자유상태(Free-free condition)에 가깝게 모사하였다. 측정 센서는 충격 하중을 측정하는 충격 망치(Impact hammer)와 충격 후 축계의 진동응답을 측정하는 가속도계(Accelerometer)로 구성된다. 가속도계는 부하단 베어링와 엔드링 사이에 위치시켰다. 실험 방법은 충격 위치를 위치 1부터 위치 20까지 나누어 20개의 위치에서 충격 가진을 가하고, 각 충격 위치에서 5회 반복 측정하였다.
측정된 데이터를 통해 얻을 수 있는 것은 축계의 주파수 응답함수와 모드 형상이다. 주파수 응답 함수는 아래와 같이 정의된다.
| (8) |
여기서 i는 충격 위치이고, Hi는 주파수 응답, Aj는 가속도계로 측정된 진동응답, Fi는 충격 망치로 가진한 하중을 의미한다.
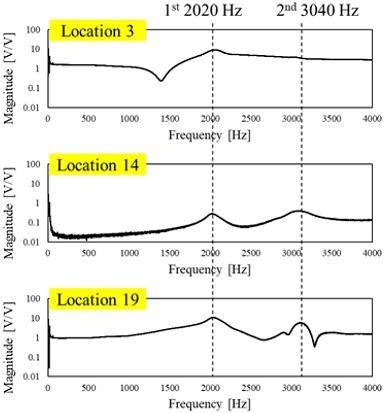
Fig. 11은 충격 실험에서 실험 축계의 측정된 주파수응답 그래프를 보여준다. 주파수 응답 그래프는 축계의 중앙과 양 끝 위치인 위치 3과 14, 19에 대해 나타내었다. 그 결과, 2,020 Hz와 3,040 Hz에서 주요하게 피크가 형성되는 것을 확인할 수 있다. 따라서 실험과 동일 조건에서 고유진동수 해석을 수행하고, 축계의 1차 고유진동수가 실험치인 2,020 Hz와 동일하도록 해석상에서 보정계수를 0.019로 선정하였다. 본 유도전동기의 운전속도는 3420 rpm이므로 1차 고유진동수에 더 가깝다. 따라서 운전속도에서 축계 진동 특성은 1차 고유진동수에 크게 영향을 받기 때문에 보정계수를 0.019로 선정하였다.
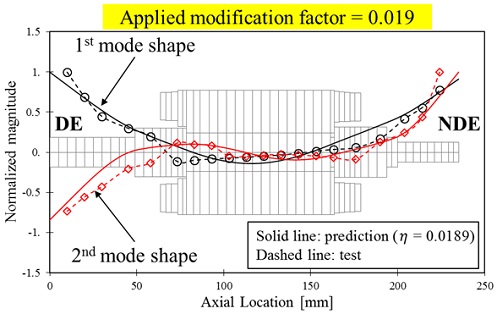
Fig. 12는 보정계수 0.019을 적용해 해석한 1, 2차 축계 모드형상과, 모드실험을 통해 측정한 1, 2차 모드형상을 비교한 그래프이다. 1차 모드 형상은 실험과 해석 결과 모두 2,020 Hz에서 U자 형태로 변형하며, 2차 모드 형상은 실험과 해석 결과 각각 3,040 Hz, 3,750 Hz에서 S자 형태로 변형하였다. 2차 고유진동수 예측에 있어 약 23%의 오차가 존재하지만, 1차 고유진동수 및 모드형상 예측에 있어 높은 정확성을 보여준다. 결과적으로 개선된 해석모델은 축계의 회전체 동역학적 특성 및 거동을 예측하는데 적합함을 확인하였다.
4. 회전체 동역학 해석 및 분석
4.1 DE/NDE 동일 기공 형상
본 장에서는 DE와 NDE 엔드링 기공 형상이 동일하다는 가정 하에서 회전체 동역학 해석을 수행하여, 기공이 회전체 진동 크기 및 베어링 수명에 미치는 영향을 분석하였다.
Fig. 13은 DE와 NDE 엔드링 기공 형상 S와 θ의 수준을 나타낸다. 변화 인자는 기공 형상을 결정하는 파라미터인 θ(x1)와 S(x2)가 된다. 이 때 θ와 S의 수준은 각각 180°, 260°, 340°와 10%, 55%, 100%로 선정하였다. 그 이유는 θ에 대한 불평형량 변화가 180°에 대하여 대칭이므로 180~360°에서 선정하였다. 또한 S와 θ각각 0%와 360°에서 0 g⋅mm이 되므로 가까운 수준인 340°와 10%로 선정하였다. 따라서 2인자 3수준 완전요인배치법(Full factorial design)으로 총 9개의 조건에서 해석을 수행하였다. 해석 결과로 유도전동기 구동속도인 3,420 rpm에서 최대진폭, 부하단 베어링 수명, 자유단 베어링수명을 예측하였다.
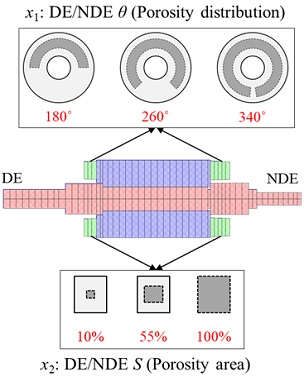
Schematic view showing the level of DE and NDE end-ring porosity distribution(θ) and cross section area(S)
베어링 수명은 회전체 동역학 관점에서 중요한 성능 지표 중 하나에 해당된다(12). 예측된 베어링 수명을 통해 유도전동기의 베어링 교체 주기를 결정할 수 있어 유도전동기 운용에 편리성을 가져다준다. ISO 281규정에 따르면 99% 신뢰도 구간에서 볼베어링 수명은 다음과 같이 정의된다(13).
| (9) |
여기서 L1h는 베어링 수명을 나타내고 단위는 시간이다. 또한 Ω는 회전속도를 의미하고 C는 베어링 동하중용량(Basic dynamic load capacity), P는 베어링 동하중(Dynamic loading)을 의미하고, α1는 신뢰도 계수로 99% 구간에서는 0.25값을 사용한다. 특히 본 볼베어링 수명은 마찰, 작동 환경 등을 고려되지 않은 식이다. 즉, 반경방향 동하중만 고려된 베어링 수명으로 실제 수명은 베어링 마찰, 온도, 외력, 오염 등에 의해 더욱 감소될 것으로 사료된다.
해석 결과를 반응표면도로 나타내어 기공 형상 변화에 따른 최대진폭과 베어링 수명 경향을 파악하였다. Fig. 14는 DE와 NDE 엔드링 기공 형상 S(x1)와 θ(x2)에 따른 최대진폭(y1)과 DE 베어링 수명(y2), NDE 베어링 수명(y3)의 반응표면도를 보여준다. 통계 프로그램인 MINITAB을 이용하여 요인분석을 수행하였다. 요인분석 결과, 수립된 최대진폭과 DE 베어링 수명, NDE 베어링 수명에 대한 반응표면 방정식은 다음과 같다.
| (10.a) |
| (10.b) |
| (10.c) |
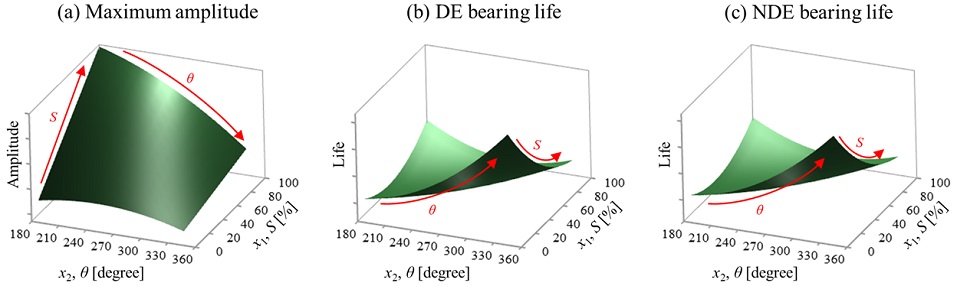
Response surface diagram of (a)maximum amplitude, (b)DE and (c)NDE bearing life according to porosity distribution(θ) and cross section area(S)
최대진폭은 S의 증가에 비례하여 선형적으로 증가하였고 θ의 증가에 비선형적으로 감소하였다. 이 는 S와 θ에 따른 불평형량 변화 경향과 동일하므로 축계 진동은 불평형량 크기에 지배적으로 결정된다고 볼 수 있다. 또한 베어링 수명은 최대진폭과 반대의 경향을 나타낸다. 이는 축계 진동이 증가함에 따라 베어링 동하중이 증가하고, 이에 반비례하게 베어링 수명이 감소한 결과로 보인다. 한편 베어링 수명이 크게 예측된 이유는 외부 하중이 없는 무부하 조건, 즉 이상적으로 회전체 질량 불평형에 의한 하중만 존재하기 때문이다.
4.2 DE/NDE 다른 기공 형상
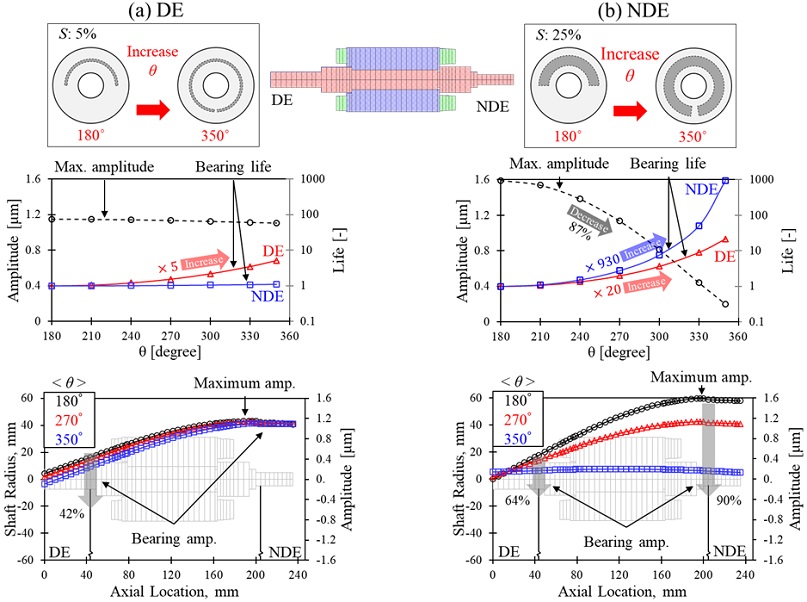
본 장에서는 DE와 NDE 엔드링 기공 형상이 서로 다른 조건에서 기공 형상 변화에 따른 회전체 거동을 파악하였다. 실제 기공은 DE와 NDE에서 서로 상이한 분포로 형성되며, 제조 공정을 고려했을 때 3.2 절의 샘플 #1과 #2처럼 NDE 엔드링에 더 많은 기공이 분포하게 된다. 따라서 DE와 NDE 엔드링의 S를 각각 5%, 25%로 가정하고 θ변화에 따른 회전체 동역학 거동을 파악하였다.
Fig. 15는 (a)DE와 (b)NDE의 θ변화에 따른 회전체 동역학 해석결과를 나타낸다. 회전체 동역학 해석결과는 진동 크기와 베어링 수명이 있으며, 베어링 수명은 θ 180°를 기준으로 상대적인 크기를 비교하였다. 해석결과, DE의 θ가 증가할수록 DE측 진동이 0.43 μm 에서 0.25 μm로 42% 감소하였다. 이에 따라 DE 베어링 수명은 5배 증가하였고, 정격 운전속도에서 축계의 변형 형상도 소폭 감소한다. 따라서 DE 엔드링 기공이 고르게 분포하면, 외부 어플리케이션과 결합되는 DE측의 진동이 감소하게 되는 결과를 얻을 수 있다.
한편, NDE의 θ가 증가할수록 NDE측 진동이 0.47 μm에서 0.16 μm로 90% 감소하였고 DE 베어링측 진동 또한 64% 감소하였다. 이에 따라 NDE 베어링 수명이 930배 증가하였고 DE 베어링 수명이 20배 증가하였다. 또한 최대진폭은 NDE측에 위치하여 87% 감소하였다. 즉, NDE의 θ변화가 전반적인 회전체 진동 및 베어링 수명에 있어 지배적인 변화를 낳는다는 것을 알 수 있다. 또한 NDE 기공분포에 따라 과도한 축계 진동이 발생할 수 있음을 시사하므로, 유도전동기 제작에 있어 엔드링 기공의 발생은 중요하게 고려되어야할 인자이다. 특히 고속으로 운전되는 유도전동기의 경우, 기공에 의한 회전체 진동의 발생은 더욱더 지배적일 수 있다.
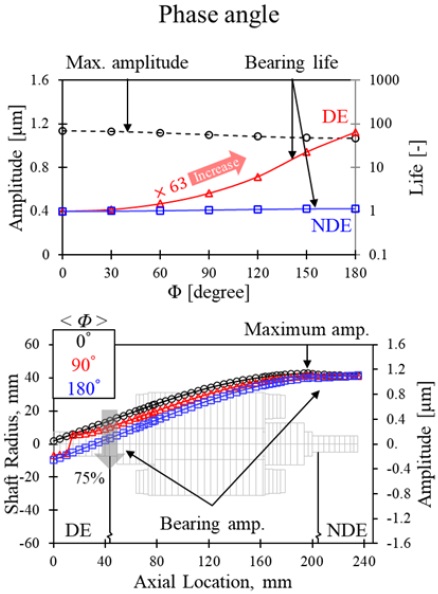
Fig. 16은 DE와 NDE의 위상각 변화에 따른 회전체 동역학 해석 결과를 나타낸다. 위상각이란 DE 엔드링의 질량중심과 NDE 엔드링의 질량중심이 이루는 각도를 의미한다. DE와 NDE 엔드링의 S를 각각 5%, 25%로, θ를 모두 270°로 가정하고, 위상각을 0°부터 180°까지 변화시키며 해석을 수행하였다. 해석결과, 위상각이 증가할수록 DE측 진동이 75% 감소하였다. 이에 따라 DE 베어링 수명이 63배 증가하였다. 즉, 위상각이 증가할수록 유도전동기 DE측 베어링 수명 측면에서 유리하다. 따라서 DE와 NDE 엔드링 위상각을 증가시키면, 외부 어플리케이션에서 DE측으로 전달되는 하중에 의한 베어링 수명감소가 완화될 것으로 사료된다.
5. 결 론
본 논문에서는 1.5 kW 유도전동기의 엔드링 기공 형상을 단순화 및 불평형량을 계산하는 수학모델을 수립하였고 회전체 동역학 해석을 통해 불평형량 크기 및 위상각에 따른 축계 진동 거동을 분석하였다. 그 과정에서 다음과 같은 결론을 얻었다.
- 1) 엔드링의 기공 단면적(S)이 작을수록 축계 최대진폭은 선형적으로 감소하고 베어링 수명은 증가하였다. 기공 단면적(S)이 작을수록 기공에 해당하는 질량(mp)이 선형적으로 감소하며, 기공에 해당하는 질량 감소는 불평형량(eep)을 감소시키기 때문이다.
- 2) 엔드링의 기공 분포 각도(θ)가 클수록 축계 최대진폭은 비선형적으로 감소하고 베어링 수명은 증가하였다. 기공 분포 각도(θ)가 클수록 기공에 해당하는 질량은 증가하지만 불평형 거리(yep)가 0에 가까워져 불평형량을 감소시키기 때문이다.
- 3) DE와 NDE의 기공 단면적(S)이 각각 5%, 25%일 때, 기공 분포 각도(θ)가 증가할수록 축계 최대진폭이 각각 4%, 87% 감소하였고, 베어링 수명이 각각 5배, 930배 증가하였다. S가 더 큰 방향의 θ의 관리가 더 효과적이다.
- 4) DE와 NDE의 위상각은 증가할수록 DE측 진동이 75% 감소하였고, 베어링 수명이 63배 증가하였다.
- 5) 결과적으로 회전체 진동 측면에서, 엔드링 기공 관리는 기공 단면적(S)을 감소시키고 기공 분포 각도(θ)를 증가시켜야 한다. 또한 DE와 NDE 중 기공이 더 큰 엔드링의 관리가 더 효과적이며, 둘 사이 위상각은 증가시켜야 한다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 2018201010633B)
References
-
Jang, K. B., 2016, “Technology Trends to High Efficiency Motors : Focused on Induction Motor,” KIEE, Vol. 65, No. 6, pp. 995∼1000.
[https://doi.org/10.5370/KIEE.2016.65.6.995]

- Han, P. W., Jeon, Y. D., Koo, D. H., 2006, “Premium-Class High Efficiency Induction Motor Technology Trend,” KIPE, Vol. 11, No. 6, pp. 27∼31.
- Lee, S. H., Gang, C. S., Kim, Y. C., 2017, “Rotor Manufacturing Technology for High Efficiency of Induction Motor,” KIEE, Vol. 66, No. 6, pp. 19∼23.
-
Lee, K. S., Lee, S. H., Park, J. H., 2017, “Experimental and Analytical Study of Single-Phase Squirrel-Cage Induction Motor Considering End-Ring Porosity Rate,” IEEE Transactions on Magnetics, Vol. 53, No. 11.
[https://doi.org/10.1109/TMAG.2017.2714190]

- Park, S. C., 2018, “Quality Evaluations of Induction Motor Rotors during Die Casting Process,” Journal of the Korea Academia-Industrial, Vol. 19, No. 10, pp. 115∼120.
- Park, S. C., 2019, “Quality Evaluations of Induction Motor Rotors during Die Casting Process Ⅱ,” Journal of the Korea Academia-Industrial, Vol. 20, No. 7, pp. 347∼352.
- KITECH, 2011, KR Patent No. 10-2011-00165961.
-
Yun, J. H., Lee, S. B., 2018, “Influence of Aluminum Die-Cast Rotor Porosity on the Efficiency of Induction Machines,” IEEE Transactions on Magnetics, Vol. 54, No. 11.
[https://doi.org/10.1109/TMAG.2018.2841912]

- API Standard 611, “General-purpose Steam Turbines for Petroleum, Chemical, and Gas Industry Services,” Fifth Edition, American Petroleum Institute, Washington, D.C., 2008.
- Rotating Machinery Analysis, Inc., https://www.xlrotor.com/index.php/solutions/xlrotor, , Accessed February 25, 2019.
- Park, J. S., Sim, K. H., Lee, S. H., 2019, “Rotordynamic Model Development with Consideration of Rotor Core Laminations for 2.2 kW-Class Squirrel-Cage Type Induction Motors and Influence Investigation of Bearing Clearance,” Tribol. Lubr., Vol. 35, No. 3, pp. 158∼168.
-
Park, J. S., Lee, S. H., Sim, K. H., 2020, “Design Optimization of the Rotor-Bearing System for 2.2 kW-Class Induction Motors via Response Surface Method,” KSFM, Vol. 23, No. 1, pp. 23∼31.
[https://doi.org/10.5293/kfma.2020.23.1.023]

- ISO 281, 1990, “Rolling Bearings-Dynamic Load Ratings and Rating Life,” International Organization for Standardization(ISO), Geneva, Switzerland.