스윕을 가지는 축류 팬의 성능예측 방법

1. 서 론

팬 블레이드의 전진 스윕(forward sweep)은 팬 소음을 줄이기 위해 널리 알려진 기술로서,⁽¹⁾ 많은 팬 업체의 실제 설계 관행에서 광범위하게 적용되고 있으며 전진 스윕을 가지는 축류 팬은 에어컨, 환기 또는 냉각 장비와 같은 저압 공기 처리 시스템에 널리 사용되고 있다. 일반적으로 팬 블레이드의 스윕은 팬 내부 유동 현상으로 인해 발생하는 공기역학적 소음뿐만이 아니라 팬 성능에도 크게 영향을 미치는 것으로 알려져 있다. 따라서 팬 설계 과정에서 블레이드 스윕이 팬 소음과 성능에 미치는 복합적인 영향을 검토하는 것이 매우 중요한 설계과제이다. 최근 들어 CFD(computational fluid dynamics)와 CAA(computational aero-acoustics) 기술의 발전^(2,3)은 팬 성능과 소음에 대한 예측 기능을 제공하고 있지만, CFD와 CAA 모델링에는 여전히 숙련된 전문가와 많은 모델링 작업 및 계산 시간을 필요로 한다. 이러한 이유로, 팬 산업체에서는 CFD 및 CAA 방법보다는 쉽게 사용할 수 있고 팬 음압레벨과 성능을 동시에 예측할 수 있는 신뢰성 있는 설계 및 해석 방법을 요청하고 있는 실정이다.

전진 스윕을 가지는 축류 팬의 성능과 소음에 대한 연구는 많은 연구자들에 의해 수행되었다. Envia와 Nallasamy⁽⁴⁾는 블레이드 스윕을 가지고 있는 축류 팬의 공기역학적 특성과 음향 특성에 대한 문헌 검토를 제시했으며, 소음 테스트를 통해 블레이드 스윕이 팬의 평균 소음을 감소시킴을 보여주었다. Mohammed와 Prithvi Raj⁽⁵⁾는 넓은 입사각 범위에서 블레이드 스윕이 높은 팬 성능을 제공해 주는 3가지 팬 블레이드 모델에 대한 실험 연구를 수행하였다. Bamberger와 Carolus⁽⁶⁾는 CFD 시뮬레이션과 음향 측정을 통해 수정된 블레이드 스윕 전략을 이용하여 전진 스윕 축류 팬(forward swept axial flow fan)의 블레이드 설계를 최적화했다. Hurault 등⁽⁷⁾은 측정 및 CFD 전산 모사를 통해 블레이드 스윕이 축류 팬의 3차원 흐름 및 블레이드 표면 압력 분포에 미치는 영향을 조사하였다. 그러나 앞선 팬 연구들에서 알 수 있듯이, 실험실에서는 정교한 수치와 실험기법이 사용되고 있지만, 이러한 방법들이 실제 팬 산업계의 설계 단계에서 현장 기술자들에게는 적합하지 않을 수 있다.

따라서 본 연구에서는 산업체에서 쉽게 사용할 수 있는 전진 스윕 축류 팬의 관통류 해석(through-flow analysis)을 이용한 성능예측방법을 제안하고자 한다. 본 연구에서는 전진 스윕 축류 팬 내부의 유동 해석을 위해서, 스윕된 블레이드 좌표에 따라 유동변수들을 정의하고, 유동 편차 및 전압력 손실 모델들을 적용하여 관통류 해석을 수행하였다. 팬 블레이드 출구에서의 유동 편차각은 설계점 및 탈설계점을 고려하는 상관관계 모델을 적용하여 계산하였다. 전압력 손실 모델은 블레이드 경계층, 2차 유동, 벽면 경계층 및 팁 간극 유동으로 인한 4가지 압력 손실원을 고려하였고, 날개길이 방향의 전압력손실 분포를 계산하였다. 팬의 성능은 관통류 해석에 의해 계산된 유동예측결과의 질량 평균으로 계산하였다. 또한 본 해석 방법의 예측 정확도를 검증하기 위해서, 본 방법을 서로 다른 설계 사양과 운전 조건을 가지는 7개 팬 모델들에 적용하였고 그 예측 결과를 시험 및 CFD 해석 결과와 비교하였다.

2. 관통류 해석을 이용한 성능예측 방법

본 연구는 전진 스윕된 팬의 성능을 예측할 수 있는 관통류 해석방법과 그에 상응하는 유동 편차각 및 전압력손실 모델들을 기술한다. 팬 산업체에서 3차원 팬 블레이드의 익렬형상 설계와 스윕 설계가 완료되면, 유선곡률방법(SCM: Streamline Curvature Method)을 날개길이 방향으로 적용하고 관통류 해석을 수행하여 유동분포 계산결과를 구한 후 그 결과를 질량가중 평균하여 팬의 성능 예측에 활용한다.

2.1 유선곡률방법

정상 상태 및 축 대칭 팬 내부 유동장은 블레이드 날개길이 방향을 따라 설정되는 여러 개의 유선들에 대해 접선 평균된 유동을 모델링하여 그 결과들을 결합하여 팬 성능을 분석할 수 있다. 이를 위해 유선곡률방법은 오일러 일방정식(Euler’s work equation), 유동 편차(flow deviation), 전압력 손실(total pressure loss) 모델들을 식 (1)-(4)의 반경방향 평형방정식(radial equilibrium equation)과 결합하여, 팬 블레이드 출구에서 날개길이 방향의 유속, 유동각, 압력 분포들을 계산한다. 유선곡률방법의 유도과정, 자세한 계산 과정 및 절차는 Novak의 논문⁽⁸⁾에 잘 설명되어 있다.

$\[ \frac{d{V}_m^2}{dr}+A\left(r\right)V_m^2=B\left(r\right) \]$

(1)

$\[ A\left(r\right)=\begin{array}{l}2{\sin }^2\beta \left[-\frac{\sin \varphi }{V_m}\frac{d{V}_m}{dm}+\frac{\cos \varphi }{r_m}\right.\\ +\frac{{\csc }^2\beta }{2}\left(\frac{1}{Q}\frac{dQ}{dr}\right)+\frac{1}{2}\frac{d\left({\cot }^2\beta \right)}{dr}\\ \left.+\frac{{\cot }^2\beta }{r}+\frac{2\Omega }{V_m}\cot \beta \right]\end{array} \]$

(2)

$\[ B\left(r\right)=2{\sin }^2\beta \left[\frac{1}{Q}\frac{d\left(IQ\right)}{dr}+\frac{{\Omega }^2{r}^2}{2}\left(\frac{1}{Q}\frac{dQ}{dr}\right)\right] \]$

(3)

$\[ Q={\left(p_{o2}/p_{o1}\right)}^{\frac{\gamma -1}{\gamma }}/\left(T_{o2}/T_{o1}\right) \]$

(4)

$\[ V_m^2\left(r\right)=e^{-\int A\left(r\right)dr}\left[\int e^{\int A\left(r\right)dr}B\left(r\right)dr+V_{m,h}^2\right] \]$

(5)

이때 V_m,β,r_m,ϕ 는 자오선면 유속, 상대 유동각, 유선의 곡률 반경 및 기울기를 의미하며, I,T_o,p_o 와 Ω,Q 는 로탈피, 전온도, 전압과 회전수, 엔트로피 함수를 나타내고. 하첨자 1,2, h는 블레이드 입, 출구 조건과 허브를 표현한다. 또한 식 (1)-(4)를 풀기 위해 요구되는 상대 유동각, 전압력 및 전온도는 유동 편차각, 전압력손실 모델 및 오일러 일방정식을 통해 구하며, 반경방향에 따른 속도분포는 질량보존관계를 만족하도록 식 (5)의 적분을 통해 계산된다.

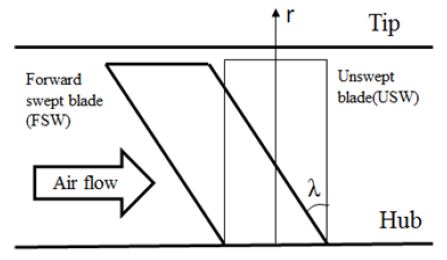
앞서 기술된 유선곡률방법을 전진 스윕 축류 팬에 적용하기 위해서는, 모든 블레이드 설계 인자 및 유동 변수들을 스윕된 블레이드 좌표에 따라 변환해야 한다.⁽⁹⁾ Fig. 1에 도시된 블레이드의 공기역학적 스윕각(λ)을 기준으로, 스윕된 블레이드에서의 상대 유동각(β)은 스윕되기 전의 상대 유동각(β_USW)으로부터 다음과 같이 변환된다.

$\[ \mathrm{t}\mathrm{a}\mathrm{n}\beta =\mathrm{c}\mathrm{o}\mathrm{s}\lambda \times \mathrm{t}\mathrm{a}\mathrm{n}{\beta }_{USW} \]$

(6)

Fig. 1

Blade sweep angle definition of axial flow fan

또한 스윕된 블레이드의 간격(s) 및 시위길이(c)는 다음의 관계식에 의해 계산되며,

$\[ s=s_{USW}\times {\mathrm{s}\mathrm{i}\mathrm{n}}^2\xi /\sqrt{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\xi +{\mathrm{t}\mathrm{a}\mathrm{n}}^2\lambda } \]$

(7)

$\[ c=\sigma \times s \]$

(8)

여기서 σ는 익렬 충실도(solidity)를 나타내고 ξ는 블레이드의 엇갈림각(stagger angle)을 나타낸다.

3. 성능예측 결과 및 검토

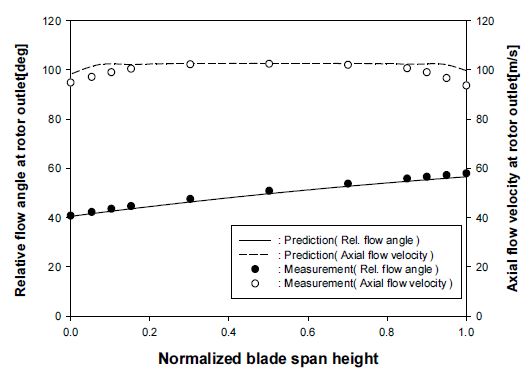
본 방법에 의해 계산된 내부 유동 분포 결과를 NASA 23B 압축기 동익 출구의 측정결과⁽¹⁶⁾와 비교하였다. 참고로 본 방법의 검증대상으로 삼은 압축기는 팁 직경이 0.508 m, 허브/팁 비율이 0.8, 시위길이가 0.05 m인 59개의 동익을 가지며, 블레이드 스윕은 없는 경우이다. Fig. 2에서 볼 수 있듯이, 접선방향으로 평균된 상대 유동각 및 축방향 속도의 예측 값이 블레이드 길이 방향을 따라 측정값과 잘 일치하고 있다. 이러한 좋은 비교 결과는 본 유선곡률방법에 의한 해석 방법이 높은 예측 정확도를 가지고 축류형 압축기 및 팬의 유동장 예측에 매우 적합하다는 것을 보여준다.

Fig. 2

Relative flow angle and axial flow velocity distributions at NASA compressor rotor blade outlet

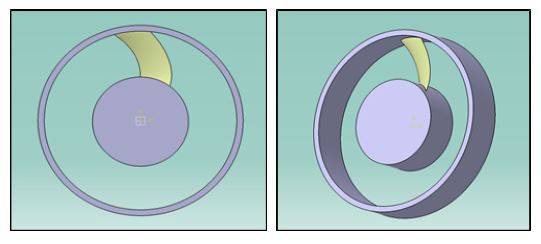
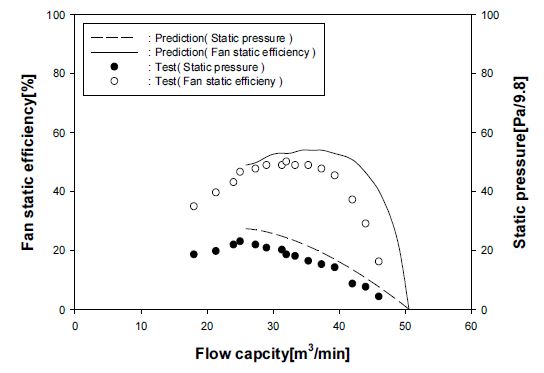
Fig. 3은 2500 RPM으로 회전하며 30°의 전진 스윕각을 가지도록 설계된 팬 블레이드 형상을 보여주고 있으며, 팬 설계 제원은 팁 직경 0.3 m, 허브/팁 비율 0.5, 시위길이 0.06 m, 블레이드 개수가 9개이다. Fig. 4는 팬의 정압 및 효율 곡선에 대한 예측과 측정결과⁽⁶⁾ 간의 비교결과를 보여주고 있으며, 전 유량 범위 내에서 본 예측방법에 의한 계산결과가 측정결과와 잘 일치함을 알 수 있다.

Fig. 3

3-D blade design of forward-swept fan

Fig. 4

Static pressure and efficiency curves of forward-swept fan operating at 2500 RPM

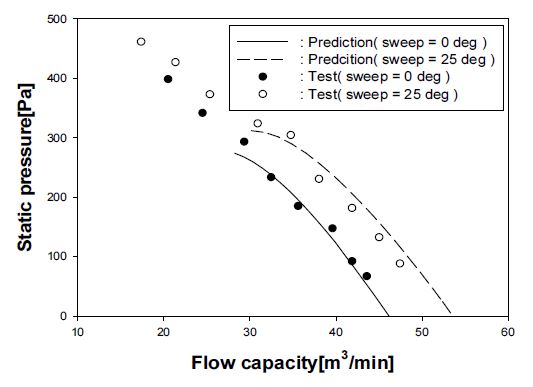
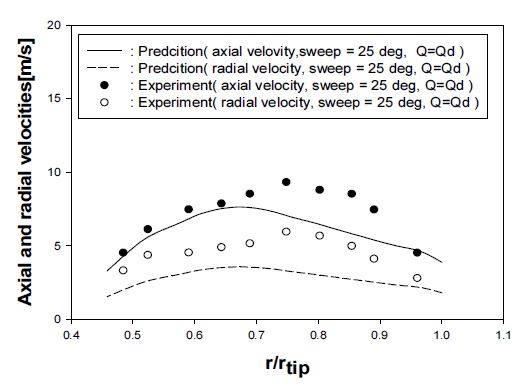
Fig. 5는 3700 RPM에서 작동하는 전진 스윕 또는 스윕을 주지 않은 2가지 팬들의 성능 예측 결과를 보여주고 있다. 팬은 팁 직경이 0.38 m, 허브/팁 비율이 0.46, 팬 블레이드 수가 6개로 설계되었고 스윕각은 25°이다.⁽⁷⁾ Fig. 5의 비교 결과에서 볼 수 있듯이, 2가지 팬의 정압 곡선의 예측 결과가 블레이드 스윕에 관계없이 시험 결과와 잘 일치하고 있다. 또한 Fig. 6 은 설계유량 조건에서 스윕된 팬의 반경 방향 속도분포에 대한 예측과 측정 결과간의 양호한 비교결과를 보여주고 있다. 참고로 유속 측정은 2차원 열선풍속계를 사용하여 챔버형 시험설비에서 수행되었고, 이때 측정의 상대오차는 20 m/s의 고속일 경우는 3%, 4 m/s의 저속일 경우는 13%이다.⁽⁷⁾ 그러므로 이러한 측정오차를 감안한다면, 본 방법이 스윕을 가지는 저압, 저속 팬의 내부 유동장을 예측하는데도 신뢰할 만한 정확도를 가짐을 알 수 있다.

Fig. 5

Static pressure curves of forward-swept and unswept fans operating at 3700 RPM

Fig. 6

Spanwise distributions of axial and radial velocities of forward-swept fan operating at 3700 RPM

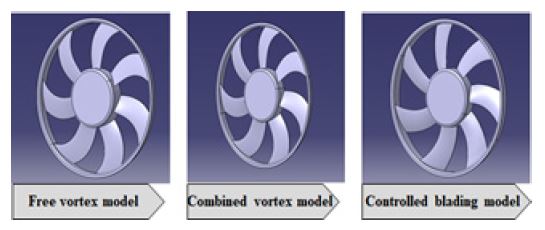
본 성능예측 방법을 서로 다른 익렬 설계방식으로 설계된 3가지 스윕된 축류 팬들에 적용하였다. 3개의 팬 모델은 자유 와류(FV: Free Vortex), 혼합 와류(CV: Combined Vortex) 와 제어 블레이딩(Controlled blading) 설계 방식에 의해 익렬이 설계되었으며, 팬 블레이드의 전진 스윕각은 모두 30°로 설계되었다. 팬의 회전수는 1940 rpm이고, 팬의 시위길이는 0.049 m(허브)에서 0.078 m(팁)까지 변하며 이때 블레이드 개수는 7개이다.⁽¹⁷⁾ 3가지 팬 모델들에 대한 3차원 팬 블레이드 형상은 Fig. 7과 같다.

Fig. 7

Three fan models with different blading designs

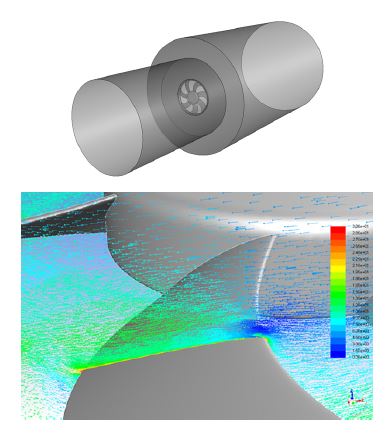
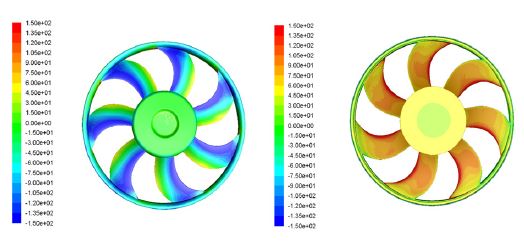
본 성능 예측 방법의 검증을 위해, 자유 와류, 혼합 와류 및 제어 블레이딩 방식으로 설계된 팬들에 대해 CFD 계산을 수행하였다. 본 CFD 계산을 위해 ANSYS CFX 코드를 사용하였고, frozen rotor scheme과 SST κ-ω 난류 모델을 채택하였다.⁽¹⁸⁾ Fig. 8은 본 연구에서 사용된 CFD 모델의 계산영역을 보여주고 있으며, 챔버형 시험설비 측정결과와의 비교를 위해, CFD 모델도 원통형으로 구성하였다. 또한 CFD 방법으로 계산된 블레이드 표면의 공기 흐름이 Fig. 8에 도시되어있다. Fig. 9는 CFD 방법으로 계산된 자유 와류형 팬의 내부 압력 분포를 보여주고 있으며, 흡입면과 압력면의 압력분포가 적절히 예측되고 있음을 알 수 있다. 또한 제어 블레이딩 방식으로 설계된 팬 모델에 대해서는 AMCA 표준 210-16에 따라 다중 노즐(multiple nozzles) 출구 챔버형(outlet chamber setup)설비에서 성능 시험을 수행하였다.

Fig. 8

Computational domain and velocity vectors in fan

Fig. 9

Surface pressure distributions of free-vortex type fan

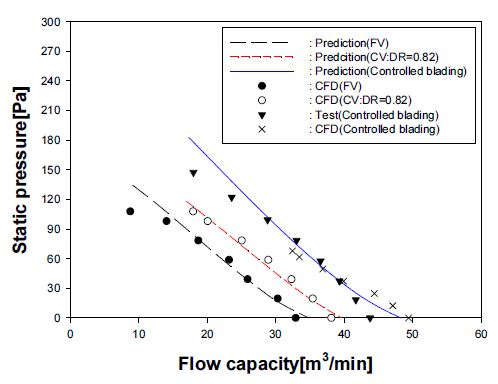
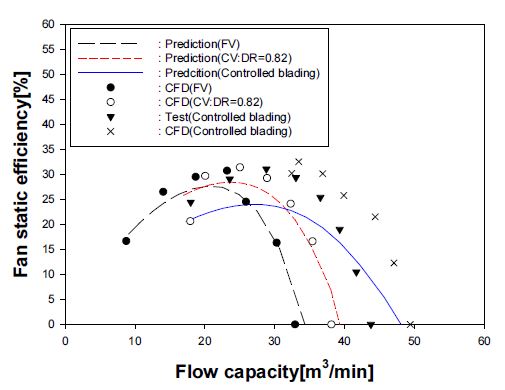
Fig. 10 은 본 방법에 의해 예측된 정압 곡선과 CFD 계산, 측정 결과⁽¹⁷⁾간의 비교를 보여주고 있다. 제어 블레이딩 형태의 팬에 대한 CFD 계산결과가 측정결과와 잘 일치하는 것을 볼 수 있고, 이를 통해 본 CFD 방법의 예측 정확도가 우수함이 검증되었다. 또한 Fig. 10에서 보여지듯이, 전 유량구간에서 본 예측과 CFD 계산, 측정 결과가 매우 양호하게 일치함을 알 수 있다. Fig. 11 역시 본 방법의 효율 예측이 CFD 및 측정 결과와 비교적 잘 일치함을 보여준다. 이러한 결과들로부터, 본 방법이 서로 다른 익렬 설계 방식이 적용된 팬 모델들의 성능 예측에도 적합한 것으로 판단된다.

Fig. 10

Static pressure curves of three fan models with different blading designs

Fig. 11

Efficiency curves of three fan models with different blading designs

4. 결 론

스윕된 축류 팬의 성능예측을 위한 간단하면서도 신뢰성있는 해석방법을 제안하였다. 본 성능예측 방법은 적분형 유선곡률방법을 스윕된 팬 블레이드 좌표계에 적용하고, 유동변수들을 스윕된 블레이드 좌표계의 변수로 변환하여 유동편차각 및 전압력손실 모델들을 결합한 후 팬 내부 유동장 및 성능계산을 수행한다.

본 방법의 예측 정확도 검증을 위해서, 서로 다른 설계 사양, 설계 방식 및 운전 조건을 가지는 다양한 스윕된 축류 팬 모델들에 대해 성능예측을 수행하였고, 성능예측 결과를 시험 및 CFD 결과들과 비교하였다. 다수의 팬들의 시험, CFD 결과들과의 비교를 통해, 본 성능예측 방법이 전 유량 범위 내에서 정압 및 효율 곡선을 예측함에 있어서 적합한 방법임이 입증되었다.

본 성능예측 방법은 간단한 산술 계산과 수치 적분을 통해 해석이 가능하므로, 최근 들어 보편화된 스프레드시트나 수치해석 프로그램을 통해 쉽게 구현할 수 있으며, 이런 계산상의 단순성과 편이성으로 인해 팬 산업체의 실제 설계단계에도 수월히 적용될 수 있을 것으로 기대된다.

Acknowledgments

본 논문은 2020학년도 수원대학교 학술진흥연구비 지원에 의한 논문임.

References

• S.E. Wright, 1976, “The acoustic spectrum of axial flow machines,” J. of Sound & Vibration, Vol. 45, pp. 165-223. [https://doi.org/10.1016/0022-460X(76)90596-4]
• C.Lee, H.S. Kim and H.G. Kil,, 2019, "Evaluation on the Blade Vibration Characteristics of a Plastic Axial Flow Fan Using Flow-Structure Coupled Analysis Technique," The KSFM Journal of Fluid Machinery, Vol.22 No.5, pp.21-27. [https://doi.org/10.5293/kfma.2019.22.5.021]
• A.T. Belamri, S. Kouidri, D. Fedala and R. Rey, 2005, “Comparative study of the aeroacoustic behavior of two axial flow fans with different sweep angles,” Proceedings of ASME FEDSM’05.
• E. Envia and M. Nallasamy, 1999, “Design selection and analysis of a swept and leaned stator concept,” Journal of Sound and Vibration, Vol.228, pp. 793-836. [https://doi.org/10.1006/jsvi.1999.2441]
• K. P. Mohammed and D. Prithvi Raj, 1977 “Investigations on Axial Flow fan Impellers with Forward Swept Blades,” ASME Journal of Fluids Engineering, pp.543-547. [https://doi.org/10.1115/1.3448839]
• K. Bamberger and T. Carolus, 2012, “Optimization of axial fans with highly swept blades with respect to losses and noise reduction,” FAN2012 proceedings. [https://doi.org/10.3397/1.3701043]
• J. Hurault, S. Kouidri, F. Bakir and R. Rey, 2010, “Experimental and numerical study of the sweep effect on three-dimensional flow downstream of axial flow fans,” Flow Measurement and Instrument, Vol.21, pp.155-165. [https://doi.org/10.1016/j.flowmeasinst.2010.02.003]
• R. A. Novak, 1967, “Streamline curvature computing procedure for fluid flow problems,” ASME J. of Eng. for Power, Vol.89, pp. 487-490. [https://doi.org/10.1115/1.3616716]
• S. J. Spuy and T. W. Backstorm, 2002, “Performance of rotor-only axial fans designed for minimum exit kinetic energy,” R&D Journal, Vol.18, pp. 63-69.
• S. L. Dixon, 1998, Fluid Mechanics and Thermodynamics of Turbomachinery, 4th edition, Buterworth & Heinemann.
• O. Adams and O. Leonard, 2005, “A Quasi-one dimensional model for axial compressor,” ISABE proceedings.
• C. C. Koch. and L. H. Smith, Jr., 1976, “Loss sources and magnitudes in axial-flow compressors,” ASME J. of Eng. for Power, Vol.98, pp. 411-424. [https://doi.org/10.1115/1.3446202]
• C. Lee and M. K. Chung, 1991, “Secondary flow loss and deviation models for through-flow analysis of axial flow turbomachinery,” Mechanics Research Communications, pp. 403-408. [https://doi.org/10.1016/0093-6413(91)90053-Y]
• J. H. Horlock and B. Lakshminarayana, 1970, “Secondary flows: Theory, experiment and applications in turbomachinery aerodynamics. Annual Review of Fluid Mechanics,” Vol.5, pp. 247-280. [https://doi.org/10.1146/annurev.fl.05.010173.001335]
• J. F. Simon and O. Leonard, 2006, “Modeling of 3-D Losses and Deviations in a Throughflow Analysis Tool,” Journal of Thermal Science, Vol.16, pp.1-7. [https://doi.org/10.1007/s11630-007-0208-x]
• W. R. Britsch, et al., 1979, NASA TP-1523.
• C. Lee, 2016, Development of the Combined Computer Program for Analyzing the Design, Performance and Noise of Axial Flow Fan Used for Automotive Cooling, Technical Report, Hanon Systems.
• ANSYS Inc., 2011, ANSYS CFX manual, ANSYS Release 16.0.