이류체 노즐 분무 해석을 위한 분열모델 상수 최적화 연구
Abstract
Over the past few decades, investigations on a dual-fluid nozzle for a wafer cleaning process have been actively conducted. Especially, developments of the dual-fluid nozzle using a numerical analysis is attracting many researchers. Breakup model constants, however, must be determined precisely to perform the numerical analysis of the dual-fluid nozzle. To select the suitable breakup model constants, validation study with experiments should be carried out. In this paper, optimization using a multi-objective genetic algorithm (MOGA) was conducted to determine the most suitable breakup model constants to use the discrete phase model (DPM) during the numerical analysis. Then, experimental results using a phase doppler particle analyzer (PDPA) were compared to validate the numerical analysis. For the design parameters, the sheet, ligament, droplet diameter, and breakup time constant, were selected. Also, the Sauther mean diameter (SMD) and mean velocity of the droplets were considered as objective functions. Consequently, the most suitable values of the sheet ligament, droplet diameter and breakup time constants were predicted to be 1.8645, 10.142, 1.4922, and 23.101, respectively.
Keywords:
Discrete phase model, Dual-fluid nozzle, Multi-objective genetic algorithm키워드:
분산입자상 모델, 이류체 노즐, 다목적 유전알고리즘1. 서 론
이류체 스프레이 노즐은 항공 및 기계공학 분야에서 연료분사, 표면 코팅 등과 같은 목적으로 광범위하게 사용되어 왔다. 최근에는 반도체 제조산업에서 집적회로의 초미세 공정이 중요시됨에 따라 웨이퍼(wafer) 세정에도 사용되고 있다. 이에 이류체 노즐을 활용해 CMP(chemical-mechanical polishing) 공정 후 웨이퍼 표면에 잔류하는 오염물질을 효과적으로 제거하기 위한 연구가 활발하게 진행되고 있다.(1) 웨이퍼 세정용 이류체 노즐에서 분무되는 입자의 크기 분포와 속도를 일정하게 유지하는 것이 세정 성능 및 효율을 향상시키는데 중요한 요인이다.(2) 이류체 노즐 분무 특성 및 과정을 정확히 분석하여 웨이퍼 세정 성능을 개선하는 연구가 많은 연구자들에 의해 수행되고 있다.
이류체 노즐의 분무 과정은 분사된 액체가 주변의 고속 기류에 의해 액적(droplet)으로 1차 분해(primary breakup) 되고, 이후 분해되지 못한 액주(liquid core)는 2차 분해(secondary breakup) 과정을 통해 띠(ligament) 형태의 더 작은 액적으로 분해된다. 이와 같은 방법으로 액적을 미립화 하는 노즐을 공기 보조식 분사 노즐(air-assisted atomizer)이라고 한다.(3)
하지만 고속으로 분무된 액적의 특성은 주입되는 유체들의 작동 조건과 노즐의 형상에 따라 달라지며, 그 특성을 예측하기 어렵다. 또한 복잡한 액적의 미립화를 모사하기 위한 수식이 현재까지도 명확히 정의되어있지 않아 정형화된 실험식이 필요하다. 이에 특정 위치를 지나는 액적의 Sauter 평균 직경(SMD), 크기 분포 및 평균 속도 등을 위상 도플러 입자 분석기(phase doppler particle analyzer, PDPA)를 활용하여 분석해왔다.(4) 하지만 노즐 형상에 변화를 주어 세정 성능을 최적화하는데 실험을 통한 연구는 큰 비용과 시간이 소요된다. 따라서 전산 유체 역학 (computational fluid dynamics, CFD)을 통해 노즐 분무 특성을 고찰하고 성능을 개선하는 연구가 최근 활발히 진행되고 있다.
O’Rourke와 Amsden(5)은 액적의 변형을 스프링-질량-감쇠계로 이루어진 시스템에 상사시켜 액적분열을 모사하는 TAB(Taylor analogy breakup) 모델을 제안하였다. TAB 모델은 낮은 웨버 수(weber number, We)를 갖는 분무노즐에 적합하여 보다 높은 We 수를 갖는 미립화 매커니즘은 Reitz(6)가 wave 모델을 사용하여 제안하였다. Wave 모델은 액체제트(liquid jet) 주변에 고속의 공기와의 공기역학적 관계를 액주(liquid core) 표면의 불안정성을 사용하여 미립화를 모사하였다. 노즐 분무 매커니즘을 모사하기 위한 수치해석 기법이 고도화되며 분무 해석을 사용해 노즐의 분무 성능 개선을 위한 연구도 진행되었다. Xiaoyi 등(7)은 적응형 격자 기법을 활용한 다상유동에서의 입자 미립화 과정을 수치적으로 분석하였으며 PDPA를 이용해 검증 연구를 수행하였다. 이진우 등(8)은 분산입자상 모델(discrete phase model, DPM)을 이용해 반도체 세정용 이류체 노즐의 형상이 분무성능에 미치는 영향을 수치적으로 분석하였다. Duangkhamchan 등(9)은 표면 코팅용 이류체 분무 노즐의 분무 과정을 수치해석을 이용해 실험값과 비교 분석하였다.
반도체 세정용 이류체 노즐의 분무 해석을 올바르게 수행하기 위해 적용되어야 하는 경험상수(empirical constant)에 대한 연구는 미미한 상태이다. 특히, 분열 모델에 적용되는 경험 상수는 노즐 형상에 따라 고유값이 존재한다. 경험상수로는 액막(sheet), 띠 형태의 액적(ligament), 분열 시간(breakup time, B1),액적 직경(droplet diameter, B0)으로 구성되어 있다.
Patterson 등(10)은 B1을 30으로 사용했고, Ranger 등(11)은 8로 결정해 사용하였다. 이 외에도 1.73을 사용한 연구 결과도 있어 분열모델에서 노즐 형태에 따른 적절한 B1을 선정하는 것이 중요하다는 것을 알 수 있다. 또한 액적 직경 상수인 B0은 Reitz(12)에 의해 25 < We < 50에서 0.61이 제안되었다. Hwang 등(13)은 B0을 We > 50 구간에서 0.3에서 0.9까지 범위안에서 노즐 형상과 미립화 형태에 따라 다양하게 적용될 수 있음을 보여주었다.
액막 상수는 Fraser(14)가 flat 형태의 노즐 분무 실험을 통해 얻게 된 경험적 수치로서, 사용되는 노즐의 분무형상에 따라 그 값이 상이할 것으로 예상된다.
이와 같이 노즐 형상에 적합한 분열모델 상수를 선정하는 것은 이후 노즐의 공정조건 성능 최적화 등의 연구를 수행하기에 앞서 반드시 선행되어야 한다. 따라서 본 연구에서는 상용프로그램인 ANSYS Fluent에서 DPM 사용 시 요구되는 경험상수를 원뿔형(cone) 이류체 스프레이 노즐에 맞는 값으로 예측하였다. DPM의 여러 분열모델 중 높은 We 수를 갖는 분무 해석에 적합한 wave 분열 모델을 사용하였다. 해당 분열 모델에 적용된 띠 형태의 액적, 액막, 분열 시간, 액적 직경 상수를 설계변수로 선정하였으며, 실험과 수치해석을 통해 얻은 SMD 값의 차이가 최소화되는 것을 목적함수로 설정하였다.
2. 수치해석
2.1 모델 형상 및 경계조건
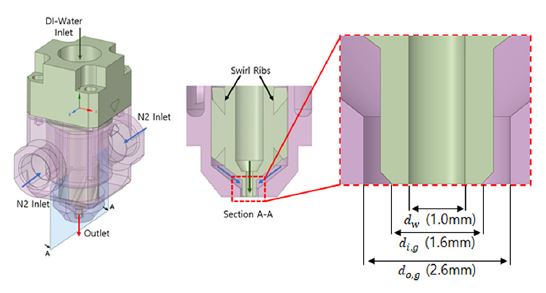
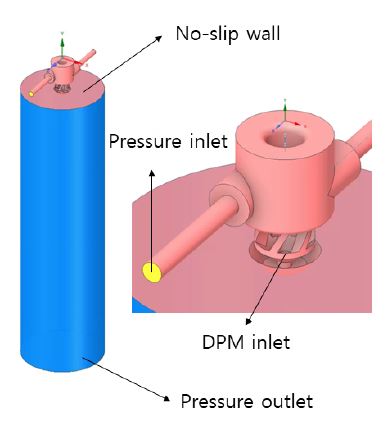
본 연구에서 사용된 이류체 노즐은 국내 H社에서 제공한 모델을 사용하였으며, Fig. 1에 도시하였다. 사용된 이류체 노즐에 대한 경계조건은 Table 1과 Fig. 2에 나타내었다. 수치해석은 질소가스(N2)를 주입 후 정상상태의 유동장을 형성하였고, 이후 DPM의 air-assisted blast 모델을 사용하여 탈이온수(deionized water, DIW)를 모델 중앙을 관통하는 유로에 주입하였다. 또한, 격자수에 따른 차분 오차를 정량화하기 위해 Roache가 제안한 격자수렴지표(grid convergence indicator, GCI)를 사용하여 Table 2에 나타내었다.(15) GCI는 해당 격자모델을 사용해 계산된 해가 점근값(asymptotic value)로부터 얼마나 벗어났는지를 비율로 나타낸 값이다. GCI가 작을수록 해당 격자모델로 예측된 해가 점근 범위 내에 있다고 할 수 있다.
사용된 격자 모델은 총 세 가지로 Case I, Case II, 그리고 Case III로 나뉜다. 세 모델 중 가장 성긴 격자는 Case I 모델에 해당하며 약 1.21백만 개의 격자로 구성되어 있다. 반면, 가장 조밀한 격자는 Case II 모델로 약 1천 4백만 개의 격자로 구성되어 있다. 수치해석 결과의 격자 의존성을 확인하기 위해 노즐 토출구에서의 면평균 속도를 측정하였다. 노즐 토출구에서의 평균 속도를 관찰한 이유는 분산입자상 모델에서 유체의 속도항이 액적의 분열 시간과 궤적을 예측하는데 지배적으로 사용되기 때문이다. 총 세 가지 격자 모델 중 GCI 값이 0.371%인 Case II 모델이 격자의 독립성을 확보하며 경제적인 유동 분석을 수행할 수 있다 판단하여 본 연구를 위한 격자 모델로 선정하였다. 최종 선정된 격자는 Fig. 3에 도시하였다.
2.2 지배방정식
연속체의 영향을 받아 거동하는 액적의 경로를 예측하기 위해 Eulerian-Lagrangian 접근법을 따르는 DPM을 사용하였다. 유체상의 연속체는 연속방정식과 Navier-Stokes 방정식을 사용하여 계산되며, 주입된 입자는 연속체 유동장에 의해 경로가 결정된다. 우선 연속방정식은 질량 보존의 법칙으로부터 유도되며 다음과 같이 표현된다.
| (1) |
여기서 는 유체의 속도 벡터이며, ρ는 유체의 밀도를 나타낸다. 또한 Navier-Stokes 방정식은 운동량 보존 법칙으로부터 유도되며, 외부에서 유체에 가해지는 힘을 고려하면 다음과 같이 표현된다.
| (2) |
여기서 p는 압력, 는 응력 텐서, 는 중력, F는 외력을 의미한다.
2.3 난류모델
노즐에서 초음속 유동 특성과 충격파 및 박리점을 비교적 정확히 예측하는 Realizable k-ε 난류모델을 사용하였다.(16) 이 모델의 난류 운동에너지, k와 난류 소산율, ε은 다음 수송방정식으로부터 도출된다.(7)
| (3) |
| (4) |
위 식에서 Gk와 Gb는 각각 평균 속도 구배에 의해 발생한 난류 운동에너지와 부력에 의해 생성된 난류 운동에너지를 의미한다. 또한 YM는 팽창소산항(dilatation dissipation term)으로 초음속 유동에서 유체의 압축성이 난류에 미치는 영향을 고려하기 위해 추가되었다. Sκ와 Sε는 난류 운동에너지와 난류 소산률의 소스항이다.
2.4 분산입자상 모델
주입된 입자의 경로를 추적하기 위해 ANSYS Fluent의 DPM을 사용하였다. 이 모델은 입자에 작용하는 힘에 대한 평형방정식을 적분하여 입자의 궤적을 예측하며, 다음 지배방정식을 따른다.
| (5) |
여기서 mp는 입자의 질량, 는 연속 유체의 속도, 는 입자의 완화시간(relaxation time)이며 하첨자 p는 입자의 물성치를 의미한다. 또한, 위 방정식에서 우항은 입자에 가해지는 모든 항력의 합을 의미한다.
3. 최적 설계
3.1 설계변수
본 연구에서 수행한 최적 설계는 노즐 분무 수치해석을 위해 사용된 최적의 분열 모델 상수를 찾는 것이며 Table 3에 설계변수를 나타내었다. 변수의 범위는 기존 연구 논문을 참고하여 상수 범위를 선정하였다.
3.2 목적함수
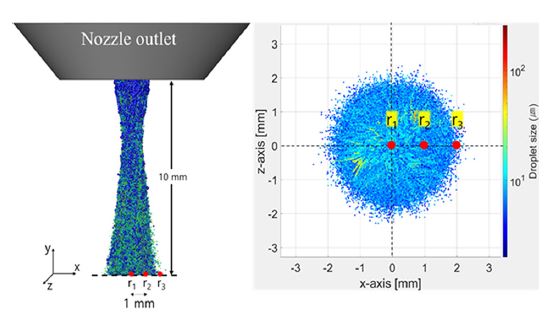
각 독립변수에 대하여 Fig. 4에 표기된 r1, r2, 그리고 r3에서 수치해석과 실험으로 얻은 SMD의 차이를 최소화하는 것을 목적함수로 지정하였으며 아래 관계식으로 나타내었다.
| (6) |
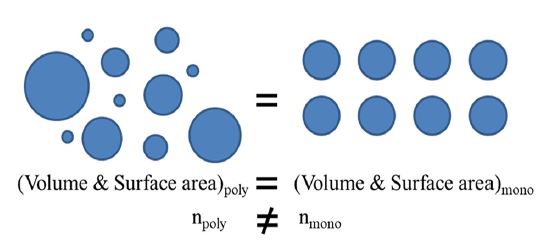
Fig. 4에서 세 지점은 노즐 토출구로부터 10 mm 하류에 위치해 있으며, 웨이퍼 세정 공정에서 노즐과 웨이퍼 사이 거리가 10 mm인 것을 고려하여 선정하였다. 여기서 SMD란 노즐에서 분무된 액적의 산포도 및 평균 직경을 평가하는 요소로, 그 수가 분무된 모든 액적의 산술 평균 직경과 가까울수록 산포도가 작다고 표현될 수 있다(Fig. 5 참조).
SMD를 수식으로 표현하면 분사된 모든 입자의 전체 표면적에 대한 전체 부피로서의 표면적율 대비 동일 부피를 지니는 입자의 직경으로, 아래 식으로 나타낼 수 있다.
| (7) |
3.3 실험계획법
최적 설계를 위해 사용된 실험계획법(design of experiments, DOE)은 데이터가 균일하게 분포되는 특징을 가진 Latin-hypercube sampling(LHS)기법이다.(17) 학습데이터로 부터 LHS 기법을 통해 생성된 25개의 데이터와 무작위 변수로 선정된 5개의 데이터를 추가해 총 30개의 데이터 집단을 생성하였다. LHS 기법은 정해진 변수의 범주 안에서 중복되지 않는 샘플링 데이터를 생성할 수 있다는 장점이 있지만, 변수의 최대 및 최소점에서의 샘플링 데이터를 구하는데 취약하다는 단점도 갖고 있다. 따라서, 각 변수의 최대 및 최소점에서 부근에서 무작위 변수 5개를 추가 생성하여 단점을 보완하고자 하였다. 다음 장에서 다룰 반응표면분석에 있어 실험계획법 내 학습데이터는 많을수록 좋지만, 실험의 신속성과 경제성을 위해 총 데이터 30개를 선정했다. 생성된 데이터에서 목적함수 값은 수치해석을 통해 도출되었으며, Table 4에 나타내었다.
3.4 반응표면분석법
설계변수에 대한 반응표면을 분석하기 위해 ANSYS Design exploration의 genetic aggregation을 사용하였다. Genetic aggregation으로부터 예측된 반응표면의 결정계수(coefficient of determination, R2)와 평균 제곱근 편차(root mean square error, RMSE)는 아래 Table 5에 나타내었다.
3.5 다목적 유전알고리즘
이류체 노즐 분무 해석을 위한 분열모델 상수 최적설계를 위해 다목적 유전알고리즘(MOGA)을 사용했다.
MOGA는 모집단(population)에서 적합도(fitness)를 평가하고, 그 결과의 다양성과 수렴성을 확보하기 위해 선택(selection), 교차(crossover), 돌연변이(mutation) 과정을 반복한다.(17) 사용된 MOGA의 매개변수를 Table 6에 나타내었으며 Design exploration 내 optimization을 사용하였다.
4. 결 과
파레토 해 집단 중 세 목적함수의 표준편차와 변량이 가장 작은 설계변수를 최종 선정하였다. 이 지점에서 설계변수X1, X2, X3, 그리고 X4의 값은 각각 1.8645, 10.142, 1.4922, 그리고 23.101이다. 이를 사용하여 얻은 수치해석 결과와 실험에서 얻은 SMD값을 비교하였다. 비교대상 모델은 기준 모델(Case I)과 노즐에 주입되는 질소가스와 세정액의 유량비(air-to-liquid mass flow ratio, ALR)를 다르게 한 두 실험모델(Case II & Case III)을 사용하였으며, PDPA를 활용하여 분무 액적의 직경을 측정하였다. PDPA는 Laser doppler analyzer(LDA)의 작동원리를 바탕으로 한 액적 속도 및 크기 측정 장비이다. PDPA 시스템를 구성하는 장치로는 레이저, 트랜스미터, 리시버, 신호 처리 장치 등으로 구성되어있다. 우선 트랜스미터를 통해 조사된 한 쌍의 레이저가 분무 입자 측정 구역에 교차하게 된다. 이때 입사광선이 측정하고자 하는 분무 입자를 통과하여 굴절되거나, 입자의 표면에 반사될 때 발생하는 산란광(scattered light)의 위상변화를 리시버가 읽어 액적 크기를 측정하게 된다. 사용된 트랜스미터와 리시버는 2축 traverse를 통해 정밀하게 위치시켰다. PDPA를 사용하여 얻은 결과와 수치해석 결과를 Table 7에 나타냈으며, 분열모델 상수를 적용한 수치해석과 실험의 SMD값이 오차범위 10% 이내로 일치하였다.
실험 결과와 해석 결과의 차이는 실제 분무 과정에서 1차 분열 중 완전히 미립화되지 않고 떨어져 나간 액적들이 수치해석에서 정확하게 계산되지 못해 생긴 원인으로 보인다. 하지만 동일 노즐 형상에서 ALR 조건을 다르게 적용했음에도 실험값과 오차범위가 작기 때문에 검증 결과를 사용하는데 문제가 없을 것으로 판단된다.
5. 결 론
노즐 분무 해석을 수행하기 위해 사용되는 분열 모델에는 노즐 형상에 적합한 경험상수가 적용되어야 한다. 본 연구에서는 반도체 웨이퍼 세정용 이류체 노즐의 분무 과정을 모사하기 위하여 wave 분열 모델을 사용하였다. 이후, 해당 모델에 요구되는 경험상수인 리거먼트, 액막, 액적 직경, 그리고 분열 시간 상수를 설계변수로 선정하여 수치해석과 실험으로 얻은 SMD 값의 차이가 최소화하는 것을 목적으로 최적 설계를 수행하였다.
다목적 유전알고리즘을 사용해 최적 설계한 변수로 노즐의 ALR을 세 가지로 다르게 적용하여 분무해석을 수행하였다. 그 결과 실험값과의 오차가 평균 6.87%로 최적 설계 결과에 대한 신뢰성을 확보하였다. 최종 선정된 설계변수를 토대로 향후 진행될 이류체 세정 노즐의 ALR과 같은 공정조건 최적화를 진행하는데 적용되어 보다 정확한 수치해석기법을 확인하는데 기여할 것으로 기대한다.
Acknowledgments
본 연구는 2021년도 중소벤처기업부의 기술 개발사업 지원에 의한 연구임[S2829696].
References
-
Snow, J. T., Sato, M. and Tanaka, T., 2013, “Dual-fluid spray cleaning technique for particle removal, in developments in surface contamination and cleaning,” Elsevier. pp. 107-138.
[https://doi.org/10.1016/B978-1-4377-7879-3.00003-0]

-
Keswani, M. and Han, Z., 2013, “Post CMP cleaning, in developments in surface contamination and cleaning,” Elsevier. pp. 145-183.
[https://doi.org/10.1016/B978-0-323-29961-9.00004-1]

-
Lefebvre, A. H. and McDonell, V. G., 2017, “Atomization and Sprays,” CRC press.
[https://doi.org/10.1201/9781315120911]

-
Payri, R., Araneo, L. and Shakal, J., 2008, “Phase doppler measurements: system set-up optimization for characterization of a diesel nozzle,” Journal of Mechanical Science and Technology, Vol. 22, pp. 1620–1632.
[https://doi.org/10.1007/s12206-008-0432-7]

-
O’Rourke, P. and Amsden, A., 1987, “The Tab method for numerical calculation of spray droplet breakup,” SAE Technical Paper 872089.
[https://doi.org/10.4271/872089]

- Reitz, R. D., 1987, “Mechanisms of atomization processes in high-Pressure vaporizing sprays,” Atomization and Spray Technology, Vol. 3, pp. 309–337.
- Xiaoyi, L., Arienti, M., Marcos S., Soteriou, M. C. and Sussman, M. M., 2010, “Towards an efficient, high-fidelity methodology for liquid jet atomization computations,” 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Jan 4-7 2010, Orlando, AIAA 2010-210.
- Lee, J. W., Jung, K. J., Sherman, M, Kim, H. S. and Kim, Y. J., “Experimental and numerical analysis on the performance of spiral two-fluid atomizer using DPM method,” Proceedings of the ASME 2020 FEDSM, ASME, Heat Transfer Summer Conference and the ASME, Vol. 3, Virtual, Online. July 13–15, 2020. V003T05A027.
-
Duangkhamchan, W., Ronsse, F., Depypere, F., Dewettinck, K. and Pieters, J. G., 2012, “CFD study of droplet atomisation using a binary nozzle in fluidised bed coating,” Journal of Chemical Engineering Science, Vol. 68, pp. 555-566.
[https://doi.org/10.1016/j.ces.2011.10.022]

-
Patterson, M. A., Kong, S. C., Hampson, G. J. and Reitz, R. D., 1994, “Modeling the effects of fuel injection characteristics of diesel engine soot and NOx emissions,” SAE 940523.
[https://doi.org/10.4271/940523]

-
Ranger, A. A. and Nicholls, J. A., 1969, “Aerodynamic shattering of liquid drops,” AIAA, Vol. 7, No. 2, p. 285.
[https://doi.org/10.2514/3.5087]

- Reitz, R. D., 1987, “Modeling atomization processes in high pressure vaporizing sprays,” Atomisation and Spray Technology, Vol. 3, No. 4, pp. 309-337.
- Hwang, S. S., Liu, Z. and Reitz, R. D., 1996, “Breakup mechanisms and drag coefficients of high speed vaporizing liquid drops,” Atomization and Sprays.
-
Fraser, R., Eisenklam, P., Dombrowski, N. and Hasson, D., 1962, “Drop formation from rapidly moving liquid sheets,” A.I.Ch.E Journal, 8(5), pp. 672-680.
[https://doi.org/10.1002/aic.690080522]

-
Christoper J. R., 2003, “Grid converence error analysis for mixed-order numerical schemes,” Vol.41, No.4, pp.595-604.
[https://doi.org/10.2514/2.2013]

-
Tian, C. and Lu, Y., 2013, “Turbulence models of separated flow in shock wave thrust vector nozzle,” Engineering Applications of Computational Fluid Dynamics, Vol. 7, pp. 192-192.
[https://doi.org/10.1080/19942060.2013.11015463]

-
Boyd, S. and Vandenberghe, L., 2004, Convex optimization, Cambridge university press.
[https://doi.org/10.1017/CBO9780511804441]