90도 모서리와 충돌하는 와류고리의 격자볼츠만 시뮬레이션

1. 서 론

와류(vortex)는 여러 가지 유동 현상 중 흔하게 접할 수 있는 것 중 하나이다. 와류와 관련된 유동 현상 중에서 대표적인 것으로는 와류고리(vortex ring)가 있다. 와류고리는 제트유동, 경계층 유동의 박리를 포함한 많은 상황에서 발생할 수 있다. 그 밖에도, 곤충, 조류 또는 물고기 등의 형상들이 만드는 다양한 와류고리들이 관측되었다.^(1-3) 이러한 현상을 응용한 형상설계 및 와류구조(vortex structure)에 대한 연구 등이 진행되면서 와류고리에 대한 연구는 많은 연구자들의 관심을 받아왔다.⁽⁴⁾

그 중에서 와류고리와 고체표면과의 상호작용은 오랫동안 관심을 받아온 주제 중 하나이다. 특히, 고체표면의 냉각과 같은 열전달효과에 필요한 기초적인 유동가시화 연구결과들을 제공해주기도 하였다.⁽⁵⁾ 이와 관련된 대표적인 연구주제는 평면에 충돌하는 와류고리와 벽면과의 상호작용에 의한 와류구조의 변화에 대한 것이다. 실험 및 수치해법을 통해 연구가 되었으며,^(6-9) 고체표면 근처에서는 새로운 크고 작은 와류구조가 생성되는 것이 밝혀졌다. 또한, 기울어진 면과 충돌하는 와류고리와 같이 상대적인 위치의 변화는 새로운 유동의 형태를 발생시킨다는 것이 입증되었다.^(7-9)

평면뿐만이 아니라 다른 형상의 고체표면에 충돌하는 와류구조에 대해서도 연구가 진행되었다.^(5,10,11) 여러 가지 형상들이 연구되었고, 그 중에서 기본적인 형상 중 하나인 원통은 연구자들의 많은 관심을 받은 형상이다. New et al.⁽⁵⁾는 원통에 충돌하는 와류고리에 대한 실험적 연구를 하였으며, 원통의 직경을 변화시킴으로써 서로 다른 와류구조가 생성된다는 것을 밝혀내었다. 그들의 연구는 고체표면으로 인해 대칭형태의 두 부분으로 나뉘고, 고체면과 계속해서 상호작용을 하며 와류구조가 발달되는 과정을 보여주었다. 하지만, 항상 대칭적인 결과만 나타나는 것은 아니다. Homa et al.⁽¹⁰⁾은 원통과 충돌하는 와류고리의 중심축이 원통의 중심에 일치하지 않을 경우 비대칭적인 와류구조가 생성되는 것을 확인하였다. 두 연구의 차이는 원통의 크기, 그리고 와류고리의 중심과 원통 중심의 상대적 위치에 있었다. 참고논문¹⁰에서는 와류고리와 원통의 직경을 비교했을 때, 원통의 직경이 와류고리보다 상대적으로 작아서 원통에 충돌하는 상대적 위치에 따라 분리된 와류구조의 대칭성에 민감한 결과를 보여주었다. 반면, 참고논문⁽⁵⁾에서는 충분히 큰 직경의 원통을 대상으로 하고 있기 때문에 대칭성에 대해서는 민감한모습을 보이지 않는다. 또한, 직경이 크기 때문에 충돌한 와류고리가 계속해서 고체면과 상호작용을 한다는 차이가 있다. 본 논문에서는 두 연구에서 사용된 형상의 특징들이 나타날 수 있는 형상으로 90° 모서리모양에 대해 조사하였다.

기존에 사용된 적 없는 형상인 90°의 모서리는 작은 직경의 원통과 마찬가지로 모서리부분이 충돌한 와류고리를 두 부분으로 충분히 나눌 수 있는 형상이다. 하지만 작은 원통의 경우와는 다르게, 나눠진 와류고리는 벽면과 상호작용을 하게 되고 이것은 큰 직경의 원통의 특징이다. 더 나아가, 충돌하는 와류고리의 상대적 위치를 다르게 하여서, 서로 다른 와류구조에 대해 수치해석적 연구를 진행하였다.

90°의 모서리에 충돌하는 와류고리의 유동을 시뮬레이션하기 위해 본 연구에서는 격자볼츠만법(Lattice Boltzmann Method, LBM)의 코드를 개발하였다. 격자볼츠만법은 일반적으로 고레이놀즈수(high Reynolds number)의 경우 많은 격자수가 필요하며, 그렇지 않을 경우에는 수치해석적 안정성에 약점을 보여왔다. 이러한 단점을 극복하기 위하여 다중이완시간(Multiple Relaxation Times, MRT)⁽¹²⁾이 제안되었고 와류고리와 벽면과의 상호작용에 대한 연구에서도 검증되었다.⁽⁷⁾ 본 연구에서도 다중이완시간을 이용한 격자볼츠만법을 이용하여 와류고리의 유동현상을 구현하였다.

본 연구에서는 격자볼츠만법을 구현한 코드를 검증하기 위해 3차원 공동유동 (lid-driven cavity flows) 문제와 3차원 와류고리-평면의 상호작용에 대한 문제에 적용하였다. 검증된 코드를 이용하여 와류고리-90도 모서리와의 상호작용에 대해 조사하였다. 또한, 모서리 근처에서 발생하는 와류구조에 대한 형상을 가시화하였다.

2. 다중이완시간을 이용한 격자볼츠만법

격자볼츠만법은 이완시간(τ) 값이 항상 0.5보다 커야하며, 0.5에 근접할수록 수치해석적인 안정성에 문제가 발생할 수 있다. 이러한 약점을 극복하기 위하여 다중이완시간을 사용하는 격자볼츠만법이 개발되었다. 본 논문에서는 줄여서 격자볼츠만법으로 표기하였다.

격자볼츠만법에서는 다음과 같은 식으로 밀도와 운동량을 계산한다.

여기서, f_i는 밀도분포함수 (density distribution function), $$ \overrightarrow{x}$$는 격자 중심의 위치벡터, $$ \overrightarrow{e}$$는 이산속도벡터(discrete velocity vector), i는 이산속도벡터의 인덱스를 나타내고 있다. f_i를 계산하기 위해서 격자볼츠만법은 다음과 같이 충돌(collision), 이송(streaming) 두 부분으로 나뉘어져 있다.

Collision step :

Streaming step :

여기서, m은 밀도분포함수의 모멘트, M은 밀도분포함수를 모멘트로 변환하는 행렬, $$ \widehat{S}$$는 이완시간들 나타내는 행렬이다. m은 다음과 같이 계산한다.

$$ f_i^{eq}$$는 평형상태의 밀도분포함수이고 다음과 같이 정의되었다.

여기서 w_i는 가중치, c는 단위시간스텝당 1개의 격자길이를 이동하는 속도이며 격자볼츠만법에서는 일반적으로 1로 고정한다. 인덱스 i는 이산속도벡터의 개수 또는 방향을 의미하며 3차원 격자볼츠만법에서는 15, 19, 27 세 종류 중 하나를 사용한다. 본 논문에서는 가장 많이 사용되는 19방향의 D3Q19 격자볼츠만법 모델을 사용하고 있다. 19방향의 이산속도벡터는 다음과 같이 정의되어 있다.

또한, D3Q19에서의 가중치 w_i는 다음의 값들을 사용하였다.

i가 0-18까지 정수를 나타내고 있기 때문에, 식 (5)의 M은 19⨯19의 행렬로 표현할 수 있다. 또한, 식 (3)의 $$ \widehat{S}$$ 는 다중이완시간들의 19⨯19 대각행렬로 표현된다. M과 $$ \widehat{S}$$는 참고논문⁽⁷⁾에 나와 있는 값들을 사용하였다.

3. 격자볼츠만법을 구현한 코드의 검증

3.1 3차원 평판이 움직이는 공동유동

이번 섹션에서는 격자볼츠만법에서의 점착조건 알고리즘에 대해 검증하기 위하여 3차원 공동유동 시뮬레이션을 수행하였다. 격자볼츠만법에서 점착조건의 벽면처리를 하는 데 많이 쓰이는 바운스백 (bounce-back) 알고리즘을 사용하였으며, 다음과 같이 표현한다.

$\[ f_i^{\mathrm{*}}\left(\overrightarrow{x},t+\mathrm{\Delta }t\right)=f_{-i}\left(\overrightarrow{x},t\right)+6w_i{\overrightarrow{e}}_i\cdot {\overrightarrow{U}}_0 \]$

(9)

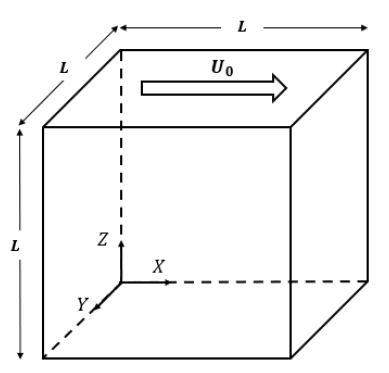
여기서, $$ {\overrightarrow{U}}_0$$는 벽면의 속도벡터, -i는 i방향 이산속도벡터의 반대방향을 의미한다. 즉, 바운스백 알고리즘은 이송되는 밀도분포함수가 벽에 충돌하면 반대방향으로 되돌아오는 것을 의미한다. 이 알고리즘은 공동(cavity)의 여섯 면에 대해 모두 적용되었으며, 벽면 형상은 Fig. 1과 같다.

Fig. 1

Geometry of lid-driven cavity

정육면체 한 변의 길이 L은 128, 256의 격자유닛(lattice unit, lu)으로 설정하였다. 격자유닛은 격자볼츠만법에서 사용하는 정육면체 형태의 균일격자 하나의 길이를 의미하며 일반적으로 1의 값을 사용한다. 시간간(time step, ts)격은 이산속도벡터가 크기 1인 격자를 이동할 때 소요되는 시간이다. 본 논문에서는 격자볼츠만법에서 계산된 값을 무차원화를 하였고, 무차원화를 하기 위한 속도 U₀는 0.05lu/ts의 값을 사용하였다.

이번 검증에서는 레이놀즈수 100, 400, 1000에 대해 계산하였으며, 레이놀즈수는 다음과 같이 정의되었다.

$\[ Re=\frac{U_{0}L}{\nu } \]$

(10)

ν는 유체의 동점성계수를 의미하며, 이완시간을 이용하여 다음과 같이 계산한다.

$\[ {\nu }_{LBM}=\frac{1}{3}\left(\tau -0.5\right) \]$

(11)

속도와 거리는 다음과 같이 무차원화되었다.

$\[ \overrightarrow{R}=X\widehat{i}+Y\widehat{j}+Z\widehat{k}=\frac{x}{L}\widehat{i}+\frac{y}{L}\widehat{j}+\frac{z}{L}\widehat{k} \]$

(12)

$\[ \overrightarrow{U}=U\widehat{i}+V\widehat{j}+W\widehat{k}=\frac{u}{U_0}\widehat{i}+\frac{\upsilon }{U_0}\widehat{j}+\frac{w}{U_0}\widehat{k} \]$

(13)

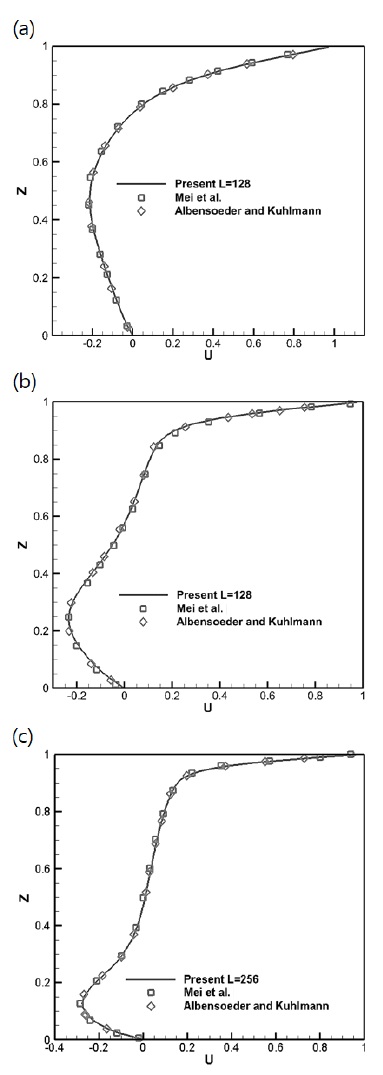
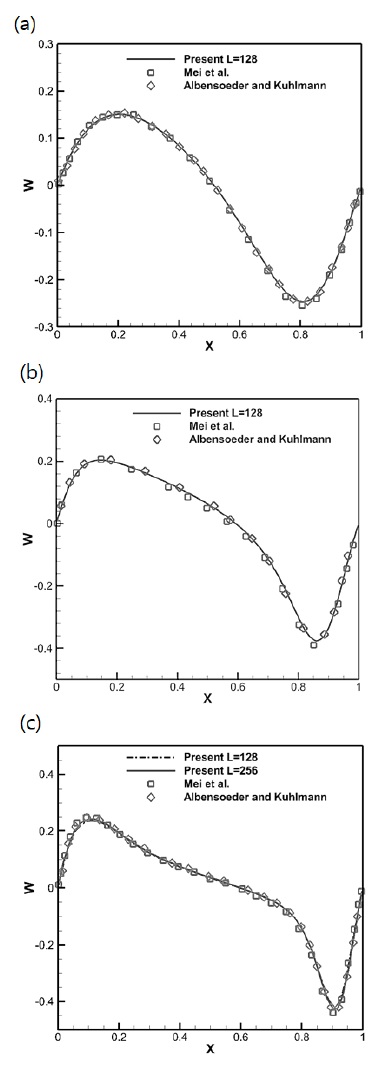
3개의 레이놀즈수에 대해 시뮬레이션을 진행하였으며, 공동 가운데의 X축과 Z축에 대한 속도성분값을 다른 연구자들의 결과와 비교하였다. 결과는 Fig. 2,3에 그래프로 표현되었다.

Fig. 2

X-component of velocity vector along the Z-axis for Re = (a) 100, (b) 400, and (c) 1000

Fig. 3

Z-component of velocity vector along the X-axis for Re = (a) 100, (b) 400, and (c) 1000

속도 결과는 두 방향의 속도성분을 참고논문^(13,14)의 결과와 비교하였다. 레이놀즈수가 상대적으로 낮은 100과 400에서는 세 결과가 매우 근접한 값을 보여주고 있는 것이 그래프에서도 나타나고 있다. 레이놀즈수 1000의 경우에는 격자수를 256⨯256⨯256까지 늘렸으며, 두 참고논문과 매우 근접하고 있는 것을 확인하였다. 이 결과는 바운스백 알고리즘이 적용된 코드의 결과가 기존 연구자들의 결과에 매우 근접한 것을 보여주고 있다.

3.2 평판에 충돌하는 와류고리

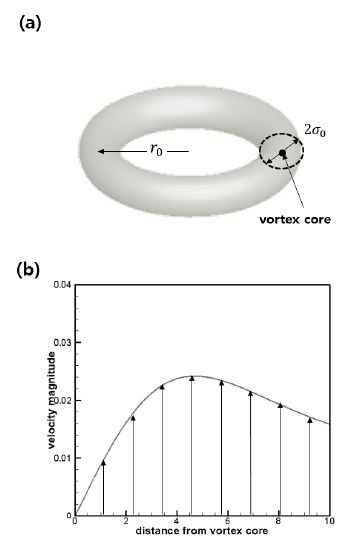
고체면에 충돌하는 와류고리에 대해 검증을 시도하였다. 와류고리 모델은 참고논문⁷에서도 사용한 Oseen-Lamb의 와류모델을 사용하였으며, 다음 식과 같이 정의되었다.⁽¹⁵⁾

$\[ u=\frac{{\Gamma }_0}{2\pi r}\left[1-e^{-{\left(\frac{r}{{\sigma }_0}\right)}^2}\right] \]$

(14)

여기서, σ₀는 와류고리 중심의 반지름, Γ₀는 순환(Circulation), 그리고 r은 와류 중심(vortex core)으로부터 떨어진 거리이다. 식(14)는 와류의 중심으로부터 떨어진 거리에 대해 속도를 나타내고 있으며 Fig. 4와 같이 나타낼 수 있다.

Fig. 4

(a) Vortex ring and (b) the velocity distribution along the distance from the vortex core

와류고리의 레이놀즈수는 참고논문⁽⁶⁾과 같은 식을 사용하였다.

$\[ Re=\frac{{\Gamma }_0}{\nu } \]$

(15)

$\[ R{e}_d=\frac{2u_s{r}_0}{\nu } \]$

(16)

여기서, 식 (15)는 순환을 기준으로 한 레이놀즈수 이며, Re_d는 와류고리의 병진속도(v_s)를 기준으로 한 레이놀즈수이다. Chu et al.⁽⁶⁾는 두 레이놀즈수가 Re≈2.1Re_d를 만족한다는 것을 밝혀내었다. 본 논문의 레이놀즈수는 식 (15)로 계산된 2100의 값을 사용하였고, 참고논문⁶의 Re_d=1000 실험결과 값과 비교하였다. 결과값의 수치를 비교하기 위하여, 다음과 같은 식으로 무차원화하였다.

$\[ \overrightarrow{R}=X\widehat{i}+Y\widehat{j}+Z\widehat{k}=\frac{x}{r_0}\widehat{i}+\frac{y}{r_0}\widehat{j}+\frac{z}{r_0}\widehat{k} \]$

(17)

$\[ T=\frac{{\Gamma }_{0}t}{r_0^2} \]$

(18)

$\[ \overrightarrow{U}=U\widehat{i}+V\widehat{j}+W\widehat{k}=\frac{u{r}_0}{{\Gamma }_0}\widehat{i}+\frac{\upsilon r_0}{{\Gamma }_0}\widehat{j}+\frac{w{r}_0}{{\Gamma }_0}\widehat{k} \]$

(19)

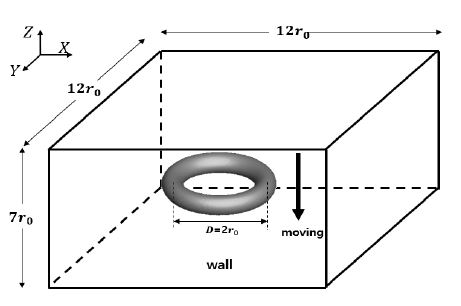
여기서, $$ \overrightarrow{r}$$은 격자중심의 위치벡터, r₀은 와류고리의 반지름이다. 이번 검증을 위해 사용된 순환의 값은 5.6lu²/ts를 사용하였고, 이완시간은 식(11)을 이용하여 계산하였다. 본 연구에서 사용된 격자볼츠만법 코드를 검증하기 위하여 Fig. 5와 같은 형상의 시뮬레이션을 수행하였다. 이번 검증에서 와류고리의 반지름 r₀를 격자볼츠만법에서 정육면체 형태의 균일 격자 30lu로 고정하였고, 전체 계산영역은 12r₀⨯12r₀⨯7r₀으로 설정하였다. σ₀는 0.21r₀의 값을 사용하였다.⁽⁶⁾ 와류고리중심의 초기값은 (X,Y,Z)=(6.0r₀,6.0r₀,3.0r₀)이다. Z=0의 벽면은 바운스백 알고리즘을 적용하였으며, 그 외의 경계면에 있는 밀도분포함수는 내부 영역의 밀도분포함수로부터 외삽법을 이용하여 계산하여 열린경계조건을 구현하였다.

Fig. 5

Computational domain including the vortex ring and the wall

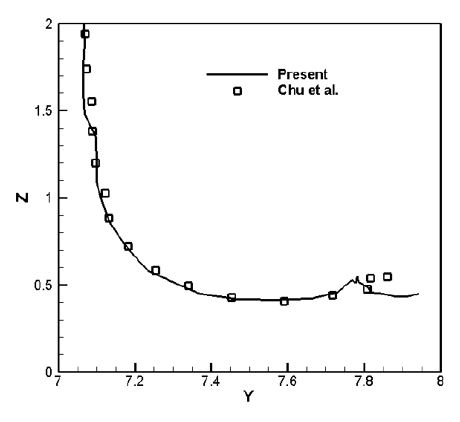
와류고리는 자기유도속도(self-induced velocity)로 인하여 평면에 접근하게 되고, 가까워지면 와류고리의 지름이 커지면서 와류중심은 벽면을 따라 움직이게 된다. 와류중심(vortex core)의 좌표값을 실험결과⁽⁶⁾와 비교함으로써 검증을 시도하였다. 와류중심은 다음과 같은 식으로 계산되었다.⁽¹⁶⁾

$\[ \begin{array}{l}{\Gamma }_x={\int }_A {\Omega }_{x}dA\\ Y_c=\frac{1}{{\Gamma }_x}{\int }_A Y{\Omega }_{x}dA,Z_c=\frac{1}{{\Gamma }_x}{\int }_A Z{\Omega }_{x}dA\end{array} \]$

(20)

여기서, Ω_x는 X축 성분의 와도성분, (Y_c,Z_c)는 와류중심의 좌표축, dA는 x축 방향의 미소면적이다.

Fig. 6에서는 벽면에 충돌하면서 생기는 압력의 상승이 와류고리를 바깥쪽으로 밀어내고 있는 것을 보여주고 있다. 또한, 이 결과에서는 실험값을 잘 따라가고 있는 것을 보여주고 있고 이차와류가 발생하면서 와류중심의 위치가 위로 올라갔다가 다시 내려오는 리바운드현상(rebound) 역시 표현되고 있다. 또한, 전체적으로 좌표값 결과는 Fig. 6에서 보여지고 있는 것처럼 실험 결과에 매우 근접한 값을 보여주고 있다.

Fig. 6

The trajectory of vortex core

4. 90도 모서리에 충돌하는 와류고리

4.1 3차원 와류구조 형상

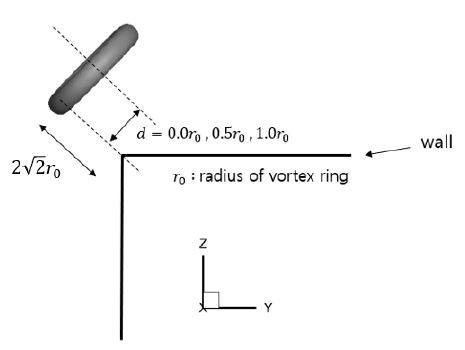
검증된 격자볼츠만법 코드를 이용하여 와류고리와 모서리의 상호작용, 그리고 그 때의 와류구조에 대해 조사하였다. 와류고리와 모서리의 형상은 Fig. 7에서 보여지고 있다. 와류고리의 중심선과 모서리 사이의 거리를 d로 정의하고 0.0r, 0.5r₀, 1.0r₀의 값에 따라 격자볼츠만법 시뮬레이션을 수행하였다. 계산영역의 크기는 10r₀⨯14r₀⨯14r₀으로 설정하였다. 벽면은 바운스백 알고리즘을 적용하여 점착조건을 구현하였고, 계산영역의 외곽에서 필요한 밀도분포함수는 안쪽 유체노드점으로부터 외삽법으로 계산하여 열린경계조건을 구현하였다. r₀은 정육면체 형태의 균일격자기준 30lu로 설정하였다. 레이놀즈수는 식 (15)을 계산되었고 2100의 값을 사용하였다. 와류고리의 순환 역시 두 번째 검증과 마찬가지로 5.6lu²/ts의 값으로 설정하였으며, 이완시간은 식 (11)으로 계산되었다. 와류고리의 중심위치는 초기값으로 (5r₀, 5r₀, 9r₀)에 위치하도록 하였다.

Fig. 7

The vortex ring and the 90 degree edge

와류고리는 자기유도속도에 의해 고체모서리와 충돌하게 되고, 두 부분으로 갈라지게 된다. 분리된 와류들은 수평방향(Y축)과 수직방향(Z축)을 따라 이동하며, 움직이는 와류구조의 형상은 Q-criterion에 의해 표현되었다.

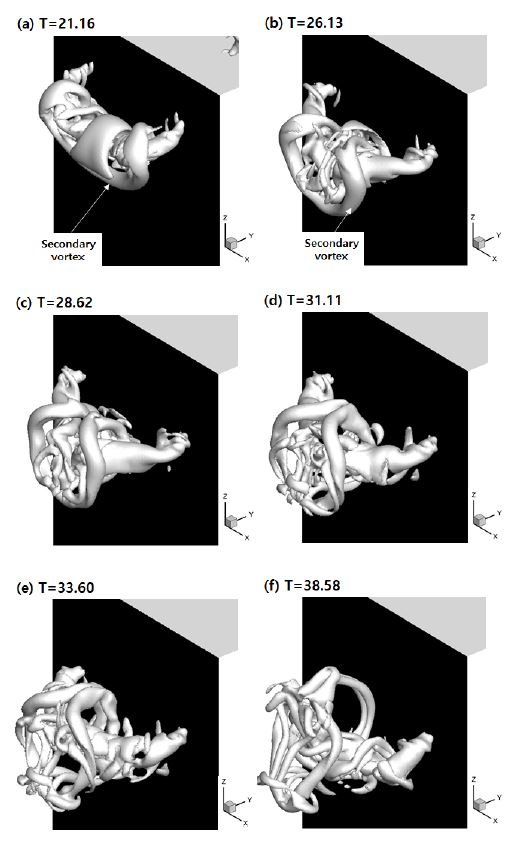
Fig. 8은 d=0.0r₀값에 따른 와류구조의 변화과정을 나타내고 있다. 와류고리는 모서리와 충돌 후 두 부분으로 나뉘어져서 평면을 따라 흐르게 된다. 나뉘어진 와류고리는 평면과 상호작용을 하면서 이차와류를 형성하게 된다. 생성된 이차와류는 Fig. 8 (a)에서 보여지는 것처럼, 주와류와 상호작용을 하면서 주와류 주위를 따라 감겨있는 것을 확인할 수가 있다. 감겨있는 이차와류는 주와류 주위를 돌아나와 T=28.62까지 점점 가까워지게 되고, 가까워진 이차와류는 T=28.62 이후로도 계속해서 상호작용을 하면서 움직인다. 하지만, 모서리에 충돌하고 떨어져 나온 와류고리는 불안정한 상태로 계속해서 움직이고 있고, 동시에 작은 크기의 와류구조들이 계속해서 만들어지면서 복잡한 유동을 보여주고 있다. 결국, 뚜렷한 와류고리 형태를 보여주지 못하는 것을 Fig. 8 (f)에서 볼 수 있다. 하지만 d=0.5r₀의 경우에는 d=0.0r₀의 경우와는 다르게, 충돌하면서 떨어져 나온 수직평면위의 와류고리가 크지 않기 때문에 좀 더 안정적인 흐름을 기대할 수 있다.

Fig. 8

The vortex structures near the wall for d=0.0r0. The gray and black walls are horizontal and vertical walls, respectively. The iso-surface shows Q=0.2

Fig. 9는 d=0.5r₀ 의 경우에 대해, 시간에 따른 와류구조의 변화를 보여주고 있다. 와류고리는 모서리에 충돌 후 d=0.0r₀의 경우와 마찬가지로 두 부분으로 나뉘게 된다. 두 와류 중에서 큰 와류는 d=0.0r₀에서 보여준 와류구조보다 훨씬 불안정하며 수평면 위에서 복잡한 유동을 보여주게 된다. 상대적으로 안정적인 흐름을 보여주고 있는 수직면 위의 와류구조는 Fig. 9에서 보여주고 있다. Fig. 9 (a)는 T=16.18일 때의 와류구조를 나타내고 있으며, 고체 모서리에 충돌하고 떨어져 나온 와류에 의해 형성된 이차와류가 보여진다. 그리고, 이차와류는 평면으로부터 떨어져나와 Fig.9 (a-c)에서 보여지는 것처럼 주와류 주위를 흐르며 돌아나와 점 점 가까워지게 된다. 이 부분까지는 d=0.0r₀의 경우와 크게 다르지 않다. 하지만, 주와류와 이차와류 사이에서 작은크기(small-scaled) 와류구조에서 차이를 보여주고 있다. Fig. 9 (c) T=23.64일 때, 이차와류가 만들어내는 유동방향은 평면의 반대쪽으로 형성되며 안쪽에서 생성된 작은크기의 와류가 야기된 것이 관측되었다. 이 두 작은 와류는 이차와류에 의해 계속해서 늘어나면서 T=26.13이후로는 하나의 와류로 재연결된다. 이 작은와류구조는 시간이 흘러 계속해서 발달하게 되고, 이차와류와 계속해서 상호작용을 한다. 결국, Fig 9(e)와 (f)에서 보여지는 것처럼, 이차와류의 특정부분에 작용하면서 매듭을 짓는 역할을 한다. 그 결과, 그 부분에서 이차와류가 급격하게 가까워 지고, 결국 이차와류고리를 생성시키는 것을 확인할 수가 있었다. 이 과정에서 생성된 작은사이즈의 와류구조가 이차와류의 중간에서 매듭을 짓는 역할을 하게 되었고, 결국, 이 지점에서의 연결은 이차와류고리의 형상을 원형에 가까운 형상으로 만드는 계기가 되었다.

Fig. 9

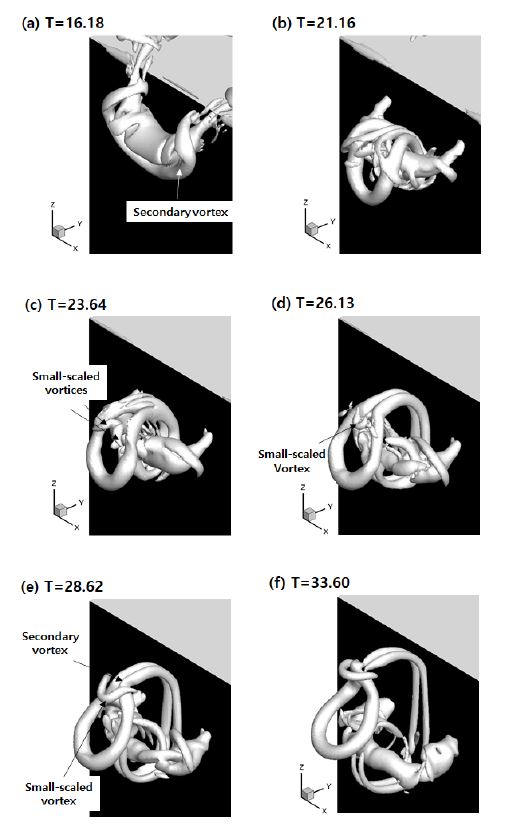
The vortex structures near the wall for d=0.5r0.The gray and black walls are horizontal and vertical walls, respectively. The iso-surface shows Q=0.2

d=1.0r₀의 경우에도 d=0.5r₀와 마찬가지로, 충돌하면서 떨어져 나오는 와류고리의 부분이 작기 때문에, 새로운 형태의 와류구조가 만들어질 수 있다. Fig. 10은 d=1.0r₀의 경우에 대해, 시간에 따른 와류구조의 변화를 보여주고 있다. T=11.20에 와류고리가 모서리에 충돌하면서 바로 모서리 부근에서는 이차와류가 형성이 된다. 모서리 근처에서 생성된 이차와류는 주와류 주위를 따라 움직이면서 T=16.18 이전에 주와류에 의해 바깥쪽으로 돌아 나오게 된다. 그 이후로는 d=0.0r₀와 d=0.5r₀의 경우에서도 나타나는 것처럼, 이차와류는 서로 가까워지며 이차와류고리를 생성시킬 가능성을 보여주고 있다. 하지만, 어느 부분에서 연결되는 지에 따라 이차와류고리의 종횡비가 결정된다. 이 부분에 대한 와류의 거동은 T=21.16에서부터 나타나기 시작한다. 가까워진 와류구조 사이에 빠른 유동을 유도하고, 또한 수평방향으로 이동하는 주와류 역시 이러한 유동에 긍정적인 역할을 하면서 경계층을 발달시키기에 충분하다. 이러한 과정을 거쳐, 모서리근처에서는 작은 사이즈의 와류가 생성된다. 최종적으로, 모서리근처의 와류와 이차와류는 연결되면서 종횡비가 큰 이차와류고리를 생성하였다. d=0.5r₀의 경우에서도 작은 사이즈의 와류가 최종적인 이차와류고리가 만들어지는 형상을 결정지은 것과 마찬가지로, d=1.0r₀의 경우에도 작은 사이즈의 와류가 최종적인 와류고리 형상에 영향을 끼쳤다. 하지만, d=0.5r₀에서는 직접적인 연결다리가 되지 않았지만, d=1.0r₀의 경우에는 직접적으로 이차와류의 연결고리역할을 하면서 최종적인 이차와류의 한 부분이 되었다.

Fig. 10

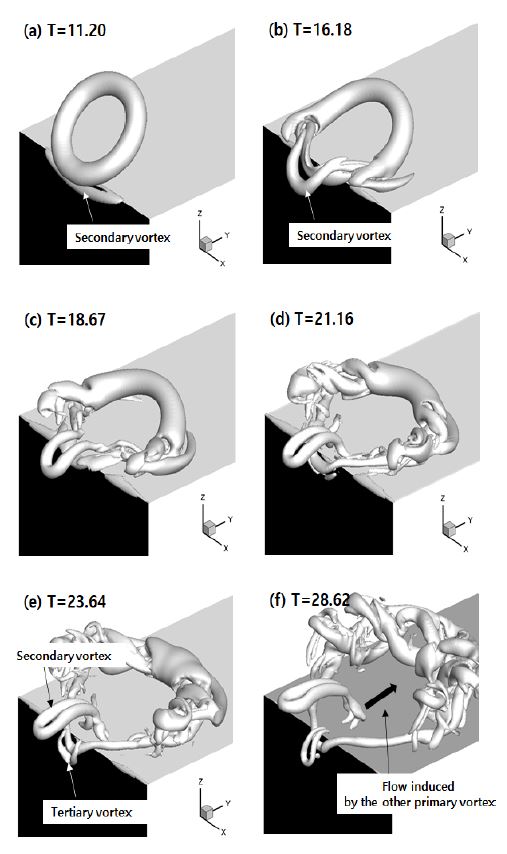
The vortex structures near the wall for d=1.0r0.The gray and black walls are horizontal and vertical walls, respectively. The iso-surface shows Q=0.2

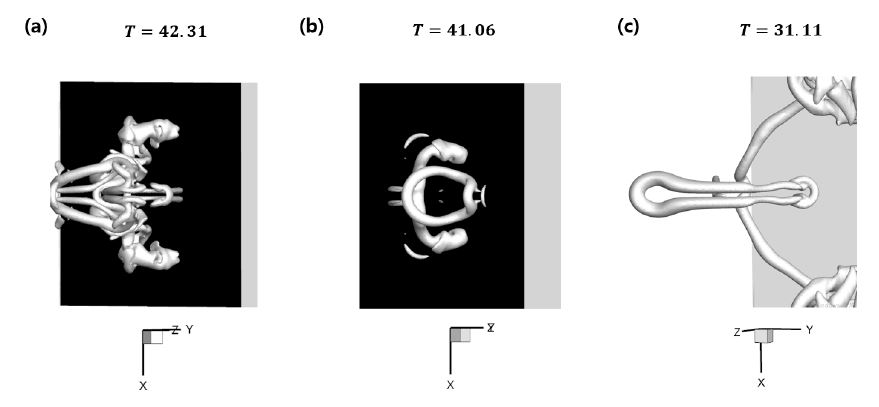
Fig. 11은 최종적인 와류구조의 모습을 보여주고 있다. (a) d=0.0r₀의 경우에는 복잡한 유동을 알 수 있는 복잡한 와류구조의 모습을 계속해서 보여주고 있다. 하지만, (b)와 (c)의 경우에는 뚜렷한 와류고리의 모습을 하고 있는 것이 확인된다. 두 와류고리는 이차와류의 종횡비에서 큰 차이를 보여주고 있으며 이러한 원인은 이차와류를 연결시켜주는 지점이 원인이다.

Fig. 11

The vortex structures for d= (a) 0.0r0 , (b) 0.5r0, and (c) 1.0r0 . The iso-surface shows Q=0.2

4.2 와도벡터의 X축 성분 분포

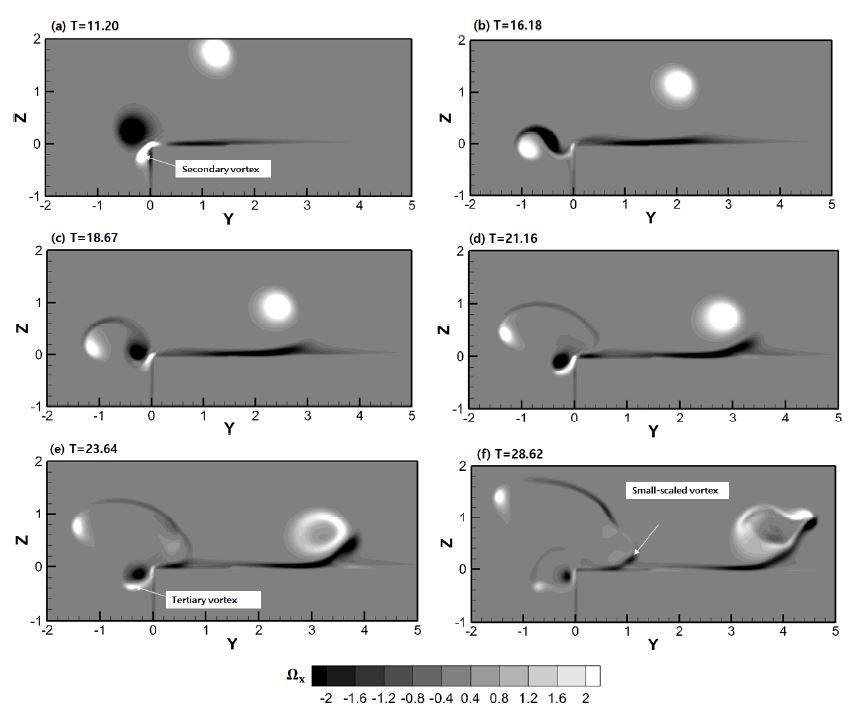
Fig. 12은 d=0.0r₀일 경우에 대해, 시간에 따른 와도 벡터 X성분의 분포를 보여주고 있다. 와류고리가 모서리와 충돌 후 평면과 상호작용을 하면서 이차와류가 떨어져 나오기 시작한다. 떨어져 나온 이차와류 외에도 Fig. 12에서 보여지듯이, 복잡한 와류들이 계속해서 생성되고 기존의 와류들과도 상호작용을 하게 된다. 이 과정에서 복잡한 유동을 보여주며, 최종적으로는 주와류와 이차와류 모두 뚜렷한 형태의 와류고리를 보여주지 못한다. 또한, T=21.16이전에 이차와류가 모서리로부터 박리된 후, 주와류의 구조가 급격히 무너지는 모습을 보여주고 있다. 하지만, d=0.5r₀와 d=1.0r₀의 경우에는 모서리로 인해 나뉘어진 와류고리의 에너지가 작기 때문에, 좀 더 안정적인 와류구조를 보여줄 수 있다.

Fig. 12

The X-component of vorticity vector near the vertical wall for d=0.0r0

Fig. 13은 d=0.5r₀의 경우에 대해, 시간에 따른 와도벡터 X성분의 분포를 보여주고 있다. T=16.18 이전에 생성된 이차와류는 평면으로부터 떨어져 나와 주와류 주위를 돌아 나오게 된다. 동시에 주와류는 불안정적인 유동의 구조를 보여주며 d=0.0r₀의 경우와 마찬가지로 불명확한 형태를 보여주고 있다. 하지만, d=0.0r₀보다는 좀 더 명확한 주와류의 형태가 와도벡터분포에서는 나타나고 있다. 특히, T=23.64부터는 Fig. 9(c)에서 관측된 작은 사이즈의 와류가 와도분포로도 나타나고 있으며, 시간이 흐르며 점점 그 세기가 커지고 있다. 이러한 결과는 3차원적인 와류구조로도 나타나고 있는 작은 와류의 연결에 의한 것이다. 또한, T=26.13과 28.62에서 나타나는 것처럼, 새로운 양의방향 와류구조는 시계반대방향의 유동을 야기시키며 이차와류의 접촉을 가속화시켰다. 이러한 과정을 거쳐, T=33.60에서는 이차와류의 재연결로 인한 음수의 와도성분값이 계산되었다. 결국, 작은와류로 인해 그 지점에서 이차와류고리가 생성되었고 종횡비는 1:1에 가까운 원형의 와류구조가 만들어졌다.

Fig. 13

The X-component of vorticity vector near the vertical wall for d=0.5r0

Fig. 14는 d=1.0r₀의 경우에 대해, 시간에 따른 와도벡터 X성분의 분포를 보여주고 있다. 이 경우에는, 와류고리의 끝부분이 모서리에 충돌하면서 바로 이차와류가 생성된다. T=11.20일 때, 모서리 부근에서 이차와류가 생성되면서 주와류 주위를 돌아 나오게 된다. 동시에, 오른쪽 또는 수평방향으로 흐르는 주와류로 인해 수직방향의 주와류는 계속해서 모서리 부근에 붙어있게 된다. 이러한 현상은 T=18.67 이후에 관측되는 모서리 근처에서의 삼차와류(tertiary vortex)생성의 원인이 된다. d=0.0r₀와 d=0.5r₀의 경우에는 수평방향성분의 주와류가 모서리의 형상으로 인해 서로 영향을 크게 주지 않는다. 하지만, d=1.0r₀는 서로 큰 영향을 주고받고 있으며, 상대적으로 크기가 큰 수평방향 주와류가 모서리 부근에 발생한 주와류와 이차와류에 직접적인 영향을 끼치고 있었다. 그 결과, 삼차와류의 생성과 동시에 Fig. 14 (f)에서는 수평면 위의 경계층에서 발달하는 작은 사이즈의 와류로 인해 새로운 와류고리가 형성되는 것을 알 수가 있다. 여기서, 삼차와류는 경계층유동의 반대방향으로 유동을 야기시키고 있기 때문에, 삼차와류가 작은 크기의 와류에 끼치는 영향은 작다고 할 수 있다. 최종적으로는, d=0.5r₀의 경우와는 다르게 종횡비가 매우 큰 새로운 와류고리로 형성되고, 평면 근처에서 생긴 새로운 와류가 연결다리 역할을 직접적으로 하고 있는 것이 와도벡터의 분포에서도 확인된다.

Fig. 14

The X-component of vorticity vector near the walls for d=1.0r0

5. 결 론

본 연구에서는 다중완화시간을 이용한 격자볼츠만법을 이용하여 90° 모서리에 충돌하는 와류고리의 와류구조를 조사하였다. 먼저, 격자볼츠만법을 이용하여 개발된 코드를 3차원 공동유동에 적용하여 점착조건 처리 알고리즘에 대해 검증하였다. 그 다음, 와류고리와 벽면사이의 상호작용에 대해 검증하기 위하여 Chu et al.⁽⁶⁾의 실험결과와 비교하였다. 두 가지 검증시도에서 모두 기존의 실험결과 및 수치해석결과에 근접한 결과를 보여주고 있는 것을 확인하였다.

검증된 코드를 이용하여 90° 모서리와 충돌하는 와류고리와 면을 따라 움직이는 와류구조에 대해 시뮬레이션하였다. 레이놀즈수는 2100으로 고정, 와류고리의 중심축과 모서리 사이의 거리는 d로 정의하였으며 0.0r₀,0.5r₀,1.0r₀ 세 가지 경우에 대해 조사하였다. 수치해석결과로부터 세 가지 조건에 대해서 각기 다른 와류구조를 보여주는 것을 확인하였다.

모서리와 충돌한 와류고리는 두 부분으로 분리되었으며, 분리된 와류고리는 평면을 따라 서로 멀어져갔다. 모서리와의 상호작용으로 이차와류가 생성되었고, 이 와류는 d값에 따라 수직면위에서 다른 특징들을 보여주었다. d=0.0r₀인 경우에는 분리된 와류가 제일 컸으며, 모서리로부터 멀어진 거리 역시 가장 길었다. 이동하면서 평면과 상호작용을 하였고, 마지막에는 뚜렷한 고리를 남기지 않으며 소산되었다. d=0.5r₀는 최종적으로 와류고리가 형성되는 것을 확인할 수가 있다. 주와류고리가 평면을 따라 움직이면서 형성되는 작은 크기의 와류들로 인해 이차와류고리가 생성되었다. 와류구조들이 재연결되면서 이차와류고리가 생성될 수 있는데, 이 경우에는 작은 사이즈의 와류가 매듭을 짓는 역할을 하였다. 그 결과 종횡비가 1에 가까운 와류고리가 형성되었다. d=1.0r₀의 경우에는 모서리 부분에서 이차와류고리가 형성되었으며, d=0.5r₀의 경우와는 다르게 종횡비가 매우 큰 형상을 보여준다. d=0.5r₀의 경우에는 이차와류고리 안쪽에서부터 형성된 작은 사이즈의 와류가 중요한 역할을 했지만, 직접적인 이차와류고리의 연결다리는 되지 않았다. 하지만, d=1.0r₀은, 수평면위에서 발달한 작은 사이즈의 와류가 직접적으로 연결다리가 되면서 종횡비가 큰 이차와류고리가 형성되었다.

References

• Brücker, C. and Bleckmann, H., 2007, “Vortex dynamics in the wake of a mechanical fish”, Experiments in Fluids, Vol. 43, No. 5, pp. 799∼810. [https://doi.org/10.1007/s00348-007-0359-2]
• Hedrick, T. L., Tobalske, B. W., and Biewener, A. A., 2002, “Estimates of circulation and gait change based on a three-dimensional kinematic analysis of flight in coctatiels (Nymphicus hollandicus) and ringed turtle-doves (Streptopelia risoria)”, Journal of Experimental Biology, Vol. 205, No. 10, pp. 1389∼1409. [https://doi.org/10.1242/jeb.205.10.1389]
• Fuchiwaki, M., Kuroki, T., Tanaka, K., and Tababa, T., 2013, “Dynamic behavior of the vortex ring formed on a butterfly wing”, Experiments in fluids, Vol. 54, No. 1, pp. 1450∼1461. [https://doi.org/10.1007/s00348-012-1450-x]
• Gupta, D., Sane, S. P., and Arakeri, J. H., 2020, “Design and development of a vortex ring generator to study the impact of the ring as a gust”, bioRxiv. [https://doi.org/10.1101/2020.10.12.331777]
• New, T. H. and Zang, B., 2017, “Head-on collisions of vortex rings upon round cylinders”, Journal of Fluid Mechanics, Vol. 833, pp. 648∼676. [https://doi.org/10.1017/jfm.2017.599]
• Chu, C., Wang, C., and Chang, C., 1995, “A vortex ring impinging on a solid plane surface-Vortex structure and surface force”, Physics of Fluids, Vol. 7, No. 6, pp.1391∼1401. [https://doi.org/10.1063/1.868527]
• Cheng, M., Lou, J., and Luo, L.-S., 2010, “Numerical study of a vortex ring impacting a flat wall”, Vol 660, pp. 430∼455. [https://doi.org/10.1017/S0022112010002727]
• New, T. H., Shi, S., and Zang, B., 2016, “Some observations on vortex-ring collisions upon inclined surfaces”, Experiments in Fluids, Vol 57, No. 6, pp. 109. [https://doi.org/10.1007/s00348-016-2196-7]
• Verzicco, R., and Orlandi, P., 1994, “Normal and Oblique Collisions of a Vortex Ring with a Wall”, Meccanica, Vol. 29, No. 4, pp. 383∼391. [https://doi.org/10.1007/BF00987573]
• Homa, J., Lucas, M., and Rockwell, D., 1988, “Interaction of impulsively generated vortex pairs with bodies”, Vol. 197, pp. 571∼594. [https://doi.org/10.1017/S0022112088003374]
• New, T. H., Long, J., Zang, B., and Shi, S., 2020, “Collision of vortex rings upon V-walls”, Journal of Fluid Mechanics, Vol. 899, A2. [https://doi.org/10.1017/jfm.2020.425]
• d’Humieres, D., 1992, “Generalized Lattice-Boltzmann Equations”, Rarefied Gas Dynamics: Theory and Simulations AIAA, pp. 450-458.
• Mei, R., Shyy, W., Yu, D., and Luo, L., 2000, “Lattice Boltzmann Method for 3-D Flows with Curved Boundary”, Journal of Computational Physics, Vol. 161, No. 2, pp. 680∼699. [https://doi.org/10.1006/jcph.2000.6522]
• Albensoeder, S., and Kuhlmann, H. C., 2005, “Accurate three-dimensional lid-driven cavity flow”, Journal of Computational Physics, Vol. 206, No. 2, pp. 536∼558. [https://doi.org/10.1016/j.jcp.2004.12.024]
• Saffman, P. G., 1992, “Vortex Dynamics”, Springer. [https://doi.org/10.1017/CBO9780511624063]
• Kim, D., Hussain, F., and Gharib, M., 2013, “Vortex dynamics of clapping plates”, Journal of Fluid Mechanics, Vol 714., pp. 5∼23. [https://doi.org/10.1017/jfm.2012.445]