냉각성능 향상을 위한 고압터빈 노즐의 막냉각홀 배치설계

1. 서 론

막냉각 기술은 냉각유체를 블레이드 표면에 흘려 얇은 막을 만듦으로써 블레이드가 직접적으로 고온의 가스와 접촉하지 않도록 하는 방법이다. 이는 터빈 입구온도를 보다 높게 할 수 있어 터빈엔진의 효율을 더 향상시킬 수 있도록 도움을 준다. 이러한 막냉각 기법은 블레이드 내부유로의 냉각유체가 막냉각홀을 거쳐 날개 표면으로 분사되는데 이 홀의 형상, 위치 등에 따라 냉각성능에 차이를 보인다⁽¹⁾.

이와 관련된 연구는 지난 수 십 년간 수행되어 왔으며 하나의 막냉각홀에 대한 형상설계가 주를 이뤘지만, 최근에는 막냉각 홀 간의 상호작용, 설치 위치에 대해서도 고려하고 있다^(2-5). Johnson 등⁽⁶⁾은 노즐베인 압력면의 냉각홀 형상과 패턴을 최적화하였고, Al-Zurfi 등⁽⁷⁾은 3종류의 냉각홀을 1-1/2 터빈단에 배치하여 LES 해석을 통해 와류를 감소시킬 수 있는 방법을 연구했다. Liu 등⁽⁸⁾은 끝벽(endwall) 전연(leading edge) 부근에 6종류의 막냉각홀 배열을 설치하였고 토출비(blowing ratio)와 난류강도에 따라 이들 배열이 가지는 냉각유체의 확산범위(coverage)를 조사하였다. 한편 Lee 등⁽⁹⁾은 냉각홀 제작 시 발생할 수 있는 형상의 차이를 불확실성으로 고려하여 표면 평균온도가 균일하도록 강건최적설계를 이용한 배치설계를 수행하였다. 냉각 시스템이 모델링된 터빈형상을 대상으로 하였고, 비록 계산비용이 큰 수치해석을 이용하였지만 근사모델로 이를 보완하면서 배치설계를 수행하였다. 이와 같이 실제 터빈을 대상으로 수치해석을 이용한 냉각홀 설계연구에는 컴퓨팅 자원이 많이 필요하거나, 설계변수의 수를 늘리기 어려운 약점을 여전히 가지고 있기 때문에 보다 효과적인 설계방법이 필요한 상황이다.

본 연구에서는 E3(Energy Efficient Engine) 고압냉각터빈^(10-12)의 1단 노즐베인을 대상으로 막냉각홀 배치설계를 수행하고자 한다. 이 때 효과적인 설계를 위해 냉각홀을 실제 모델링하지 않고 그 효과를 모사할 수 있는 injection region⁽¹³⁾ 기법을 적용한 수치해석을 이용할 것이고, 냉각홀 위치에 따라 토출되는 냉각유량을 반영할 수 있는 모델을 구축할 것이다. 또한 이로부터 도출된 배치설계안에 대해 기존의 형상과 비교, 검토할 것이다.

2. 막냉각홀 배치설계 과정

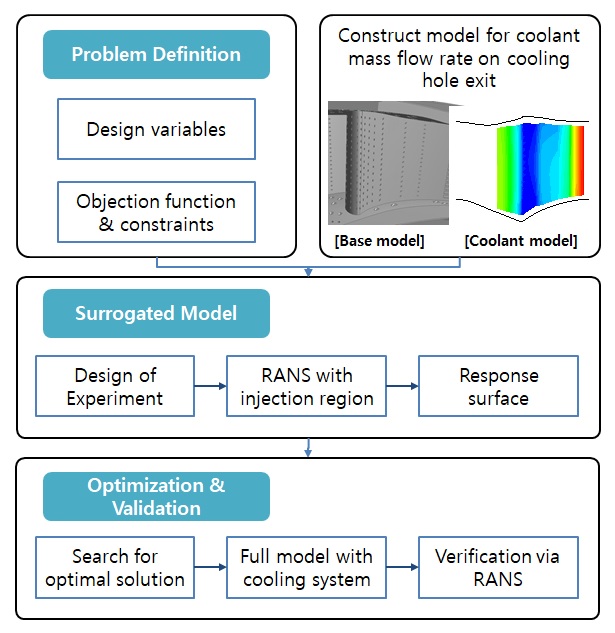
본 연구에서 수행한 막냉각홀 배치설계 과정은 Fig. 1과 같다. 우선 기본모델 선정 및 설계문제를 정의하고, 냉각유량 분포모델 구축하여 근사모델 기반의 배치 최적설계를 수행한다. 이 과정을 거쳐 도출된 결과물을 토대로 내부 냉각유로, 냉각홀 등의 냉각 시스템을 포함한 전체모델을 만들고 수치해석을 통해 최종 개선안을 검토한다. 이러한 일련의 과정을 아래 장에서 보다 자세히 설명하겠다.

Fig. 1

Cooling hole arrangement design

2.1 기본모델 – E3 고압터빈 1단 베인

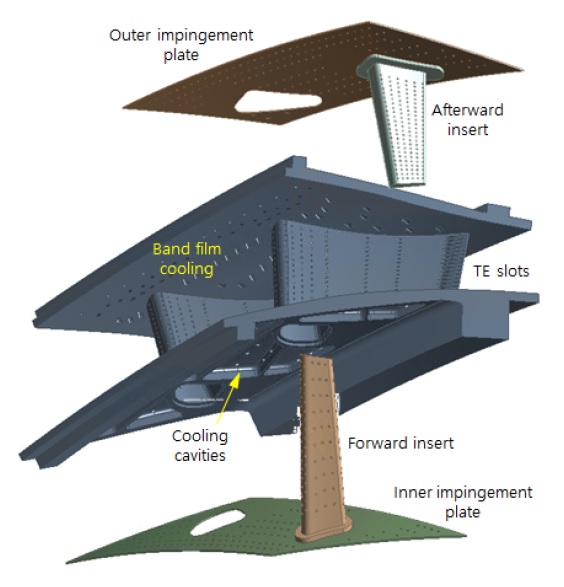
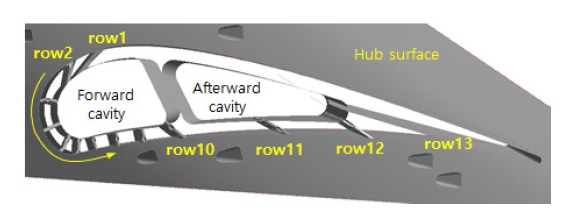
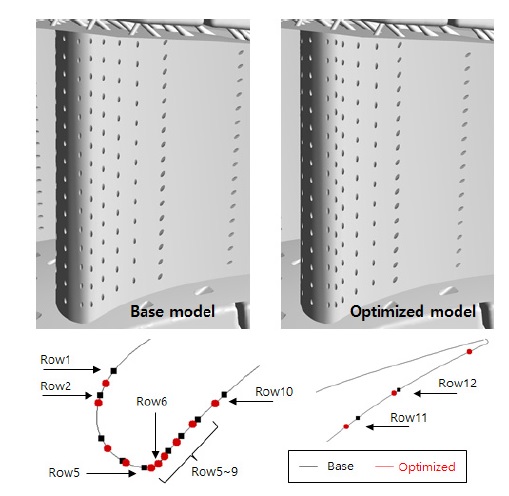
냉각홀 배치설계 대상이자 기본모델(base model)은 E3 고압터빈의 1단 노즐 베인으로 그 형상은 참고문헌^(10,11)에서 제시하고 있는 에어포일 및 자오면 정보를 바탕으로 하였다. 냉각 시스템도 같은 NASA 보고서를 참고하였지만 그 정보가 충분하지 않아 다른 터빈형상과 1차원 해석을 통해 이를 보완하여 Fig. 2와 같이 모델링하였다⁽¹²⁾. 베인 내부에는 2개의 캐비티(cavity)가 있고, 내부에 충돌판(impingement plate)이 구성되어 있다. 냉각유체가 유입되는 끝벽에도 5∼6개 정도의 공간(compartment)과 충돌판이 구비되어 있다. 냉각유체는 허브쪽 유로(inner band)를 통해 앞쪽 캐비티(forward cavity)로, 쉬라우드쪽 유로(outer band)로 뒤쪽 캐비티(afterward cavity)로 공급된다. 베인에서의 냉각홀은 Fig. 3과 같이 총 13열로 구성되어 있고, 흡입면의 2열에는 확산형(diffusion type), 전연과 압력면에는 실린더형, 후연(trailing edge)에는 슬롯(slot) 형태를 가지고 있다. 편의상 이들을 Fig. 3에 표기한 것과 같이 흡입면의 홀부터 압력면 후연부까지 반시계방향으로 Row1∼13의 번호로 표기하였다.

Fig. 2

Base model–the 1st stage nozzle vane

Fig. 3

Cooling hole array

2.2 문제정의 및 냉각유량 분포모델

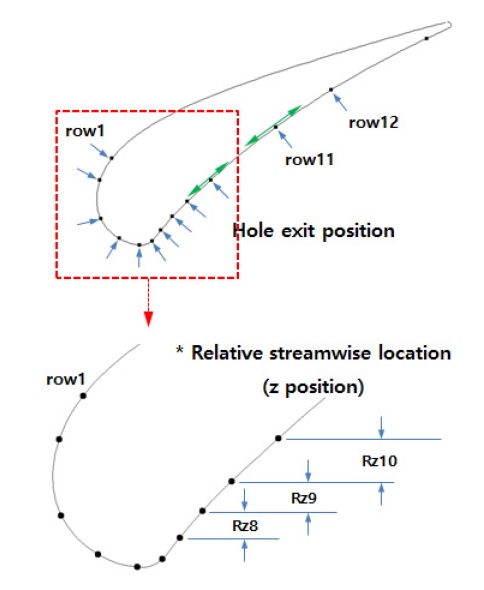
냉각홀 출구의 위치를 설계변수로 선정하였고, 냉각홀 열의 순서가 역전되는 현상을 방지하기 위해 Fig. 4와 같이 상대적인 유동방향 위치로 표시하였다. 이 때 후연의 슬롯 형태의 냉각홀은 제외하였다. 또한 냉각홀 Row1∼10까지는 앞쪽 캐비티에서, Row11∼13은 뒤쪽 캐비티에서 냉각유체가 공급되고 있기 때문에 설계변수의 범위는 이를 고려하여 Table 1과 같이 선정하였다. 목적함수는 날개표면에서의 평균온도(T_averaged)를 낮추고, 고온부분을 가능한 많이 제거하여 균일도(σ(T), deviation T)를 높일 수 있도록 표면의 온도편차를 설정하였으며, 하나의 형상이 도출될 수 있도록 1:1 비율의 가중치를 주었다. 한편 날개표면에서의 최대온도(T_max)는 기본모델보다 낮도록 제약조건으로 설정하였다. 이 배치설계 문제정의를 식 (1)에 나타내었다.

$\[ \left\{\begin{array}{ll}min.& T_{averaged}+\sigma \left(T\right)\\ subject to& T_{max}\le T_{max, base}\end{array}\right. \]$

(1)

Fig. 4

Definition of design variables

Table 1

Range of design variables

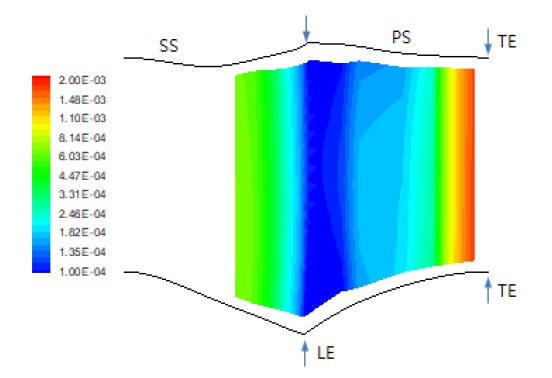
본 연구에서는 냉각 시스템이 포함된 모델을 대상으로 배치설계를 수행하지 않고 냉각효과를 나타낼 수 있도록 냉각홀 위치에 소스(source term)를 적용한 모델을 기반으로 하였기 때문에 냉각홀 위치에 따른 냉각유량을 반영해야 한다. 이를 위하여 냉각홀의 위치가 바뀌어도 내부유로의 압력과 날개표면의 압력은 크게 바뀌지 않는다는 가정 하에 냉각 시스템이 모두 모델링된 기본모델을 대상으로 수치해석을 수행⁽¹²⁾하였고, 이로부터 도출된 각 냉각홀 위치에서의 냉각유량을 바탕으로 날개표면에 대한 냉각유량 분포모델을 신경망 모델로 구축하였다. 이와 같이 만들어진 모델을 이용하여 날개표면에서의 냉각유량 분포를 Fig. 5에 나타내었다. 결정계수, R²은 0.9994이고 RMSE(root mean square error)는 1.09×10^-4로 해당 모델은 냉각홀 위치에 따른 냉각유량을 높은 신뢰도로 제공할 수 있음을 확인하였다.

Fig. 5

Definition of design variables (Unit: kg/s)

이상으로 냉각홀 배치설계를 위한 기본모델, 문제정의 및 준비과정을 설명하였고, 다음 장에는 근사모델을 사용하는 최적설계 과정으로 베인 표면온도를 구하기 위한 수치해석 및 injection region 방법, 근사모델 구성과정에 대해 설명하고자 한다.

2.3 배치설계 및 냉각성능 평가 방법

주어진 설계공간에서 목적함수 및 제약조건을 잘 설명할 수 있는 근사모델을 만들기 위해 실험계획법이 이용된다. 본 연구에서는 설계공간에 실험점이 고르게 분포할 수 있도록 실험점간 거리 편차를 최소로 하는 D-optimal 방법을 이용하였고, 12개의 설계변수를 가지고 있어 총 137개의 실험점이 추출되었다. 이들 실험점 각각에 대해 수치해석을 수행하고, 이로부터 구하여진 베인 표면의 온도정보를 기반으로 근사모델을 구축하였다.

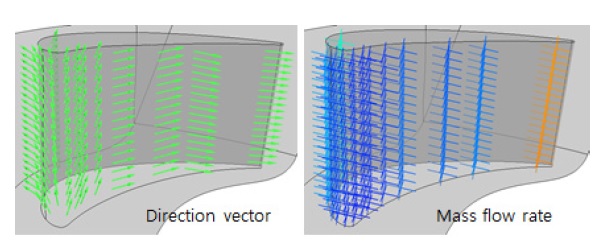
수치해석에는 상용 소프트웨어인 ANSYS CFX v2020을 이용하였고, Navier-Stokes 방정식과 SST 난류모델을 적용하였다. Table 2에 정리된 경계조건을 사용하였고, 이 때 Re수는 4.7×10⁶이다. 계산 도메인은 무냉각 베인 형상으로 셀 기준 588만 개의 정렬격자가 사용되었다. Injection region 기법⁽¹³⁾은 Fig. 6과 같이 막냉각 유동을 모사할 수 있도록 지정된 냉각홀 위치와 직경에 냉각유체가 원하는 각도로 토출되도록 소스항을 부여하는 방법이다. 실제 냉각홀을 모델링 하지 않기 때문에 무냉각 베인 형상의 계산 도메인을 바로 사용할 수 있다. 이러한 까닭에 수치해석에 소요되는 계산 비용을 상당부분 절감할 수 있고, 이는 곧 높은 설계 자유도를 가질 수 있게 해준다. 하지만 냉각홀의 위치가 변하게 되면 냉각유량이 달라지므로 이를 고려해야 한다. 본 연구에서는 앞서 설명한 냉각유량 분포모델을 구축하여 적용하였다.

Table 2

Boundary condition

Fig. 6

Injection region in the computational domain (Eject direction & mass flow rate of the coolant)

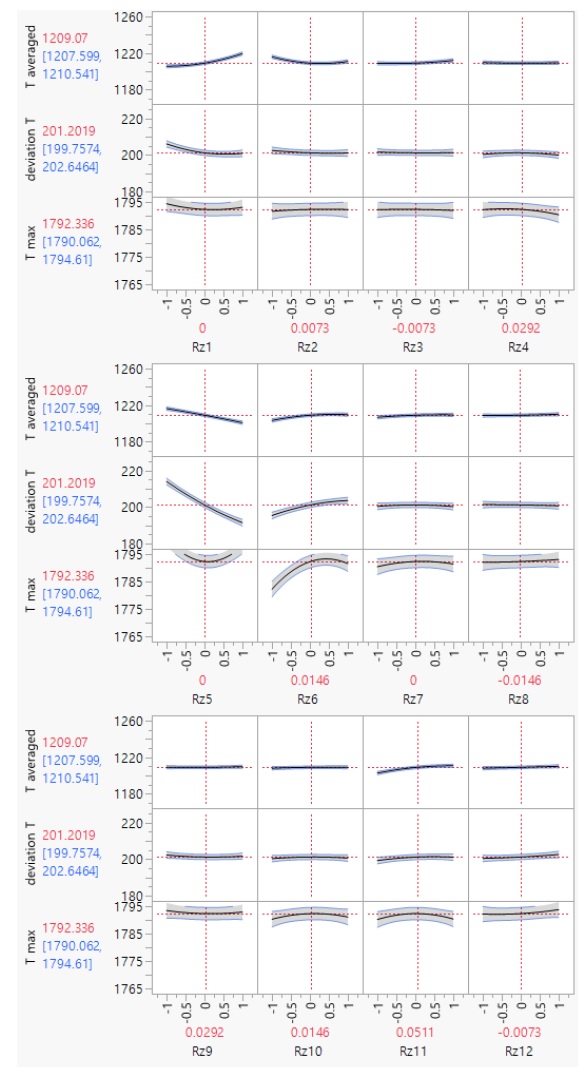
이와 같이 각 실험점에 대해 수치해석을 수행하여 구해진 날개표면의 평균온도, 최대온도, 온도의 편차를 2차 다항식의 근사모델로 구축하였고, 설계변수에 대한 온도들의 민감도 그래프를 Fig. 7에 도시하였다. 전반적으로 변수 Rz1, 5, 6에 의해 베인 표면의 평균온도, 균일도, 최대온도가 크게 영향을 받음을 확인할 수 있다. 이들 중 Rz5와 6은 전연부에 있으며, 정체점(stagnation point)이 형성되는 부분의 설계변수로 유입되는 고온의 작동유체가 바로 부딪히기 영역이기 때문에 이를 극복하기 위한 조치가 필요한 지점이다. Table 3에 정리된 근사모델의 신뢰도 지수에서 결정계수의 값이 0.9 이상이므로 만들어진 모델을 이용하여 냉각홀 배치설계를 수행하기 타당한 것으로 판단된다.

Fig. 7

Sensitivity chart

Table 3

Reliability index for response surface

3. 막냉각홀 배치설계 결과

이상의 과정을 거쳐 도출된 설계안에 대한 표면온도 결과를 Table 4에 정리하였다. 여기서 전체모델(full model) 행은 냉각 시스템을 포함한 형상에 대한 수치해석 결과를, 근사모델(surrogated model) 행은 최적설계에 사용된 근사모델에서 도출된 결과를 나타낸다. 전체모델과 근사모델의 온도와 균일도는 약간의 차이를 보이고 있지만 그 경향성은 유지되고 있어 배치설계에 사용된 근사모델이 설계공간을 적절히 모사하고 있음을 알 수 있었다. 이를 통해 근사모델을 구축할 때 사용한 수치해석 방법-injection region이 적용된 해석 역시 막냉각 성능을 충분히 모사했다고 판단되어 진다. 또한 배치 개선안(Optimized model)은 기본모델에 비해 베인 표면 평균온도가 10K 낮고, 온도 균일도는 6% 개선된 것을 전체모델의 수치해석을 통해 확인할 수 있었다.

Table 4

Design results: Surface temperature(Unit: K)

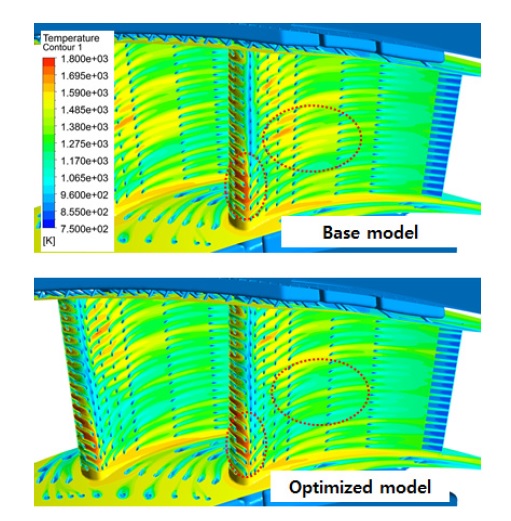
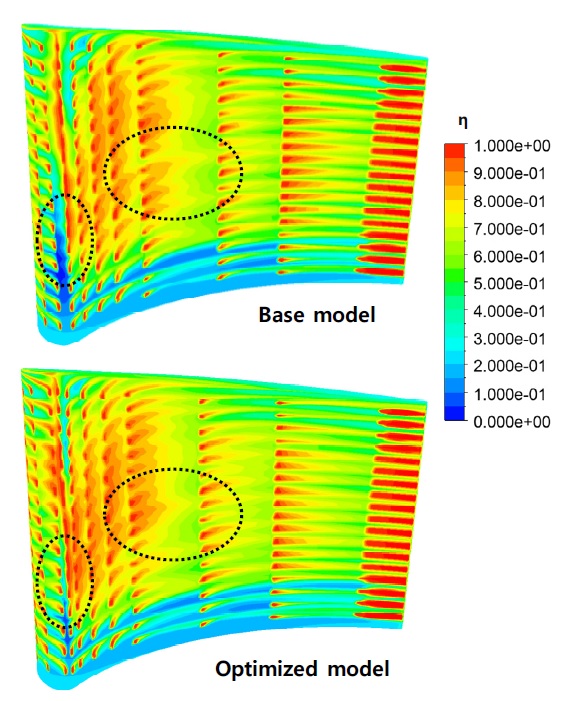
Fig. 8은 두 모델의 베인 표면온도 분포를 나타낸 것으로 기본모델에 비해 개선안은 전연부와 압력면의 고온영역이 상당부분 감소된 것을 알 수 있다. 이것은 설계변수인 냉각홀의 유동방향 위치가 Table 5와 Fig. 9에 정리된 것처럼 전체적로 전연부 쪽으로 이동을 했기 때문이다. Row6 냉각홀의 위치에서 주유동이 압력면과 흡입면으로 갈라지기 때문에 해당 홀은 기본모델과 개선안이 거의 동일한 위치를 보이고 있지만, 개선안은 인근의 Row5와 7 냉각홀이 Row6과 보다 더 가깝게 위치하고 있다.

Fig. 8

Temperature distribution for the base & optimized models

Table 5

Design results: Design variables (Normalized with respect to the axial length of the airfoil)

Fig. 9

Comparison of cooling hole positions

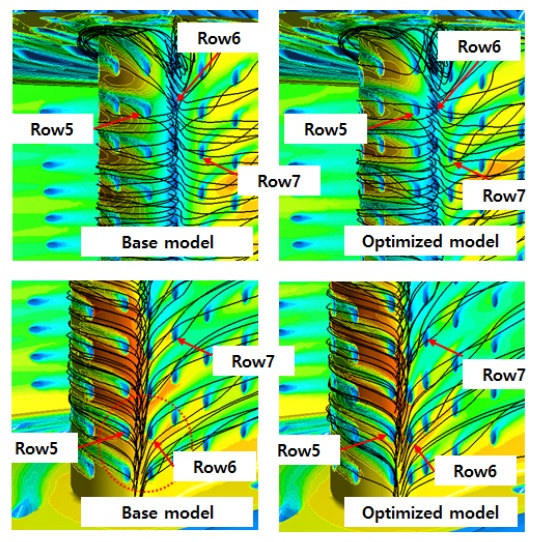
이와 같은 냉각홀 배치로 인한 기본모델과 개선안의 표면온도분포 차이는 Fig. 10에서 더 잘 볼 수 있다. 쉬라우드 부근에서는 Row6 냉각홀의 위치에 정체점이 형성되어 고온의 주유동와 토출된 냉각유체가 바로 만나게 되지만, 허브 근처에서는 정체점이 Row5와 6사이에 존재해 베인의 고온영역이 그 부분에 존재하게 된다. 이것은 막냉각홀의 영향이 작은 영역에 고온의 주유동이 지나는 공간을 가능한 최소한으로 줄여야 함을 의미한다. 개선모델은 기본모델보다 Row5 냉각홀이 Row6에 더 가깝게 위치함으로써 정체점이 형성된 고온영역이 줄어든 것을 볼 수 있다. Row7 역시 Row6에 가까워짐으로써 압력면에 냉각유체를 보다 앞선 위치에서 공급하게 되어 개선안이 낮은 평균온도를 가질 수 있도록 한 것으로 보인다.

Fig. 10

Temperature distribution and streamline around the leading edge

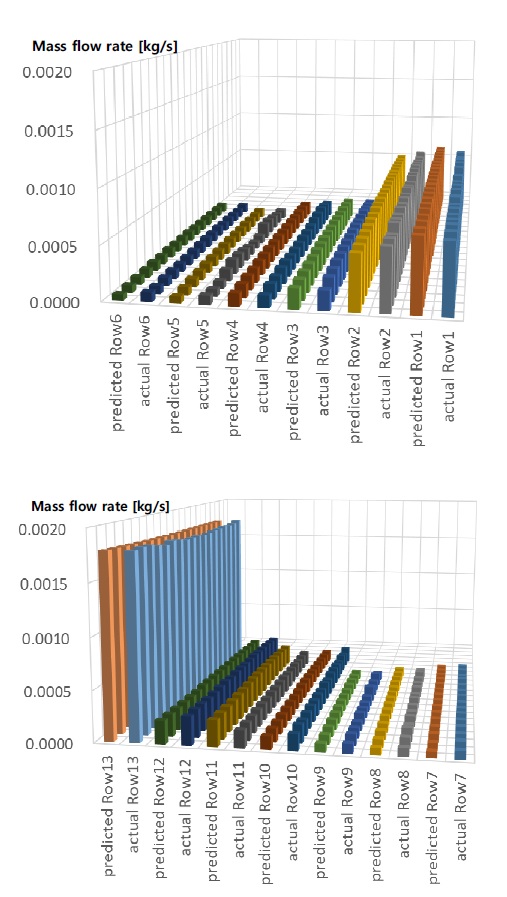
앞서 언급하였던 냉각유량 분포모델의 신뢰성을 확인하기 위해서 Fig. 11과 같이 각 냉각홀에서 토출되는 유량을 비교하였다. 여기서 actual은 냉각 시스템을 포함한 전체모델의 수치해석을 통해 구해진 값이고, predicted는 신경망으로 기 구축된 냉각유량 분포모델의 값을 의미한다. 두 값들을 비교했을 때 평균 3%의 오차를 보이고 있으며, RMSE는 4.02x10^-5로 냉각홀의 위치 변화에 따라 냉각유량을 잘 예측하고 있음을 확인하였다.

Fig. 11

Coolant mass flow rate for the optimized model

한편 injection region 방법과 냉각유량 분포모델을 적용한 해석이 냉각홀을 포함한 모델의 해석 결과와 유사한 경향을 보이는지 확인하기 위해 Fig. 12에 베인 표면에서의 막냉각 효율분포를 도시하였다. 이 때 식 (2)를 이용하였고, T_surface는 베인 표면온도, T_gas는 주유동의 입구온도, T_coolant는 냉각유체의 입구온도를 나타낸다.

Fig. 12

Film cooling effectiveness for vane surface

Injection region을 사용한 해석의 경우 베인 표면온도를 전반적으로 낮게 예측하여 높은 막냉각 효율을 보이고 있다. 하지만 기본모델과 비교할 때 전연의 아래쪽(허브쪽)과 압력면 중앙 부분에서 배치 개선안이 더 높은 막냉각 효율을 가지는 것을 알 수 있고, Fig. 8의 냉각홀을 포함한 전체모델의 해석 결과와 그 경향성이 일치하는 것을 확인할 수 있다. 이러한 까닭에 냉각홀 배치설계를 수행하는 데 있어서 injection region 방법을 적용하는 것은 적절한 것으로 보인다. 이 근사적인 방법은 설계의 효율성을 위해 사용한 것이므로 도출된 설계안에 대해 냉각홀을 포함하는 전체모델을 만들어 이에 대한 해석을 반드시 수행하여 검토할 것을 추천한다.

4. 결 론

이상에서 살펴본 바와 같이 E3 고압터빈의 1단 노즐베인의 냉각성능을 향상시키기 위해 냉각홀 배치설계를 수행하였고, 최종 배치 개선안에 대해 냉각 시스템을 포함한 전체모델을 구성하여 설계 결과와 비교, 검토하였다.

이 과정에서 도출된 냉각홀 배치 개선안은 기본모델과 비교하여 베인 표면의 평균온도가 10 K 낮고, 균일도는 6% 향상되었다. 정체점이 형성되는 전연부근으로 냉각홀이 이동함으로써 고온영역이 상당부분 감소한 것을 확인하였다. 또한 기본모델의 냉각유량 데이터를 기반으로 구축된 냉각유량 분포모델이 배치 개선안에 대해서도 평균 3%의 오차를 가지고 있어 냉각홀 배치설계 적용에 적절하였음을 확인하였다. 마지막으로 설계 자유도를 높이기 위해 도입한 injection region 방법은 전체모델의 수치해석 결과와 비교해 봤을 때 그 경향성을 잘 따르고 있어 막냉각홀 유동 모사에 보다 활용이 가능할 것으로 판단된다.

Acknowledgments

이 논문은 과학기술정보통신부의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다. (과제번호: NRF-2019K1A3A1A2009299)

References

• Bunker, R. S., 2005, “A Review of Shaped Hole Turbine Film-Cooling Technology,” Journal of Heat Transfer, Vol. 127, No. 4, pp. 441∼453. [https://doi.org/10.1115/1.1860562]
• Lee, S., Rhee, D. H., Cha, B. J., and Yee, K., 2016, “Film Cooling Performance Improvement with Optimized Hole Arrangements on Pressure Side Surface of Nozzle Guide Vane - Part I: Optimization & Numerical Investigation,” Proceedings of ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, GT2016-57975. [https://doi.org/10.1115/GT2016-57975]
• Jun, S., Rhee, D. H. and Kang, Y. S., 2020, “Application of Large Eddy Simulation to Turbine Nozzle with Film Cooling Holes,” The KSFM Journal of Fluid Machinery, Vol. 23, No. 4, pp. 5∼12. [https://doi.org/10.5293/kfma.2020.23.4.005]
• Kang, Y. S., Jun, S., and Rhee, D. H., 2018, “Large Eddy Simulation on Film Cooling Flow from a Fan-Shaped Cooling Hole on a Flat Plate,” The KSFM Journal of Fluid Machinery, Vol. 21, No. 6, pp. 1∼9. [https://doi.org/10.5293/kfma.2018.21.6.005]
• Wang, Z., Wang, Z., Zhang, W., and Feng, Z., 2019, “Numerical Study on Turbine Rotor Blade Unsteady Film Cooling Performance with Consideration of Inlet Non-Uniformities and Upstream Coolant,” Proceeding of ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, GT2019-90723.
• Johnson, J. J., King, P. I., Clark, J. P., and Ooten, M. K., 2013, “Genetic Algorithm Optimization of a High-Pressure Turbine Vane Pressure Side Film Cooling Array,” Journal of Turbomachinery, Vol. 136, No. 1, Paper 011011. [https://doi.org/10.1115/1.4023470]
• Al-Zurfi, N., Turan, A., Nasser, A., and Alhusseny, A., 2019, “A numerical study of anti-vortex film-cooling holes designs in a 1-1/2 turbine stage using LES,” Propulsion and Power Research, Vol. 8, No. 4, pp. 275∼299. [https://doi.org/10.1016/j.jppr.2019.10.001]
• Liu, J., Du, W., Hussain, S., Xie, G., and Sundén, B., 2021, “Endwall film cooling holes design upstream of the leading edge of a turbine vane,” Numerical Heat Transfer, Part A: Applications, Vol. 79, No. 3, pp. 222∼245. [https://doi.org/10.1080/10407782.2020.1835110]
• Lee, S., Yee, K., and Rhee, D. H., 2017, “Optimum Arrangement of Film Cooling Holes Considering the Manufacturing Tolerance,” Journal of Propulsion and Power, Vol. 33, No. 4, pp. 793∼803. [https://doi.org/10.2514/1.B36210]
• R. W. Claus, T. Beacg, M. Turner, K. Siddappaji, and E. S. Hendricks, 2015, “Geometry and Simulation Results for a Gas Turbine Representative of the Energy Efficient Engine (EEE),” NASA/TM-2015-218408.
• L. P. Timko, “Energy Efficient Engine High Pressure Turbine Component Test Performance Report,” NASA CR-168289.
• Jun, S., Rhee, D. H., Kang, Y. S., Chung, H., and Kim, J. H., 2021, “Validation of Numerical Analysis for the 1st Stage Nozzle of E3 High Pressure Turbine,” The 2021 KSFM summer conference.
• ANSYS CFX-Solver Modeling Guide 2020R1, ANSYS, Canonsburg, PA, 2020.