Laboratory–Scale 펌프수차 모델의 수차 모드에서 흡출관 내 와류 특성
Abstract
The pump-turbines as a flexible power generation facility have being operated within the off-design conditions for ensuring the constant power supply to respond to intermittent renewable energy sources such as solar and wind power. Especially, under the low flow rates of the off-design conditions, the complicated internal flows with vortex ropes in the draft tube destabilize the pump-turbine system. Therefore, in order to expand the reliable operating range, it is necessary to understand the internal flow and pressure phenomena under low flow rate conditions of the pump-turbines. In this study, the experiments of a laboratory-scale pump-turbine model were conducted to investigate the vortex characteristics according to the cavitation number at the turbine mode under low flow rate condition. Based on the experimental results, a two-phase (water and vapor) unsteady state RANS analyses were performed using SAS-SST turbulence model. Experimental and numerical investigations showed that the behavior and magnitude of visible vortex rope in the draft tube were in good agreement, and when the visible vortex rope was generated, a relatively higher swirl number and unsteady pressure were shown in the draft tube.
Keywords:
Pump-turbine, Model experiment, Numerical analysis, Draft tube, Cavitation number, Vortex Characteristic키워드:
펌프 터빈, 모델 실험, 수치해석적 분석, 흡출관, 캐비테이션 수, 와류 특성1. 서 론
세계적으로 기후변화 위기에 대응하기 위해 온실가스 감축 전략 및 정책을 확대하고 있는 추세이며, 국내에서도 2030년까지 2017년 온실가스 배출량 대비 24.4% 감축 목표와 2050년까지 탄소중립을 실현하는 장기저탄소발전전략을 추진하고 있다.(1)
또한, 정부의 재생에너지 3020 비전에 따라 탄소를 발생하지 않는 신재생에너지의 발전량 비중은 2030년 기준 20%, 설비용량은 60GW 수준으로 확대 및 보급될 전망이며, 특히, 태양광 및 풍력 발전의 설비용량이 51GW로 확대될 것으로 전망된다. 하지만, 외부 환경의 변화에 따라 출력이 일정하지 않고 변동성이 높은 태양광 및 풍력 발전은 설비용량 증가 및 계통 유입 시 불안정적인 전력공급을 야기할 수 있다. 이와 같은 간헐성 발전 특성을 가진 신재생에너지원의 출력의 변동성과 불확실성에 대한 전력계통의 안정성을 확보하기 위해, 발전량 변동에 따라 대응할 수 있는 유연성 발전설비가 필요하다.(2)
양수발전 시스템은 빠른 기동 및 신속한 부하 증ㆍ감발 운전 특성으로, 간헐성 발전 특성을 지닌 신재생에너지원의 계통 유입에 대응하여 전력 시스템의 안정을 위한 전력 계통 백업 및 주파수 조정을 담당하고 있으며, 그 역할이 더욱 중요해지고 있다.(3) 유연성 발전 담당을 위한 양수발전 시스템의 운전 환경 변화로 고효율 설계 범위보다 저유량 및 고유량 영역의 탈설계 운전 범위에서 작동이 지속되고 있다. 한편, 저유량 운전 영역에서는 양수발전 시스템의 펌프수차 내 복잡한 유동 및 와류가 유발되며, 이는 시스템 운전을 불안정하게 하는 진동과 소음의 발생으로 이어진다. 이러한 운전이 지속될 시 잦은 고장의 발생으로 시스템 설비의 수명감소로 이어 질 수 있다.(4,5)
펌프수차의 수차 모드에서 저유량 영역 운전 시 흡출관(Draft tube, DT) 내에서 발생하는 와류(Vortex rope)는 러너 콘에서 흡출관으로 중심선 축으로 그 둘레를 회전하며, 러너의 회전 주파수의 약 0.2∼0.4배의 주파수 특성으로 압력 맥동을 유발한다. 이러한 압력 특성은 양수발전 시스템과 공진을 일으키는 경우, 출력 맥동을 유발하여 성능 저하의 원인이 될 수 있다.(6) 따라서, 양수발전 시스템의 안정적인 유연성 발전 담당을 위한 탈설계 범위 운전의 안정성 확보를 위해, 저유량 운전 시 유발되는 복잡한 유동 및 압력 특성에 대한 이해가 필요하다.
펌프수차의 탈설계 영역에서 유발되는 유동과 압력 특성에 관련된 연구로써, Yu 등(7)은 펌프수차 모델의 부분부하 조건에서 흡출관 내 와류의 발생 거동을 다양한 유량조건에서 수치해석을 통해 검토하였으며, 이에 유발되는 압력 맥동 특성을 규명하였다. Lai 등(8)은 고낙차 펌프수차 모델의 수차 및 펌프 모드에서 흡출관 내 발생하는 와류에 대해 Laser Doppler Velocimetry를 통해 가시화하였으며, 시간 평균된 축 방향 및 원주 방향 속도 성분의 분석을 통해 흡출관 내부의 스월(Swirl) 강도 및 패턴을 검토하였다. Yang 등(9)은 수치해석을 통해 펌프수차의 부하 감발 시 흡출관에서 발생하는 압력 특성을 검토하였으며, 측정된 압력 특성을 통해 캐비테이션 발생을 검증할 수 있는 기법을 제시하였다. Li 등(10)은 펌프수차의 펌프모드에서 저주파수 영역의 고진폭 특성 메커니즘 규명을 위해 비정상 상태 수치해석을 수행하였고, 저유량 영역 운전 영역에서 압력 맥동의 전파 특성을 규명하였다. 이와 같이 펌프수차의 탈설계 영역의 내부 유동 및 압력 특성에 대한 다양한 연구가 수행되고 있지만, 펌프수차의 수차 모드에서 저유량 영역 운전 시 캐비테이션 수에 따른 흡출관 내 와류 거동 특성 및 비정상 압력 특성에 대한 실험과 수치해석을 통한 비교 연구는 수행되고 있지 않다.
따라서, 본 연구에서는 저유량 운전 조건에서 캐비테이션 수에 따른 흡출관 내 유동 및 비정상 압력 특성 검토를 위해, Laboratory-scale 펌프수차 모델의 실험을 수행하였다. 실험 결과를 토대로, 적용된 캐비테이션 수에 따른 경계 조건을 적용하여 물과 증기를 고려한 2상 비정상 상태 Reynolds-averaged Navier-Stokes(RANS) 해석을 수행하였다. 실험과 수치해석을 통해 나타낸 흡출관 내 내부 유동 및 와류 특성을 비교 검토 하였고, 펌프수차 모델의 수차 모드에서 캐비테이션 수에 따라 발생하는 가시화된 와류와 그에 따른 유동 및 압력 특성에 대해 규명하고자 하였다.
2. 펌프수차 제원 및 Laboratory-scale 모델
2.1 펌프수차 제원(수차 모드)
모델 시험과 비정상 상태 수치해석이 수행된 Lab-scale 펌프수차 모델은 수차 모드에서 비속도 120급으로, 이전 연구인 펌프수차의 기하학적 상사 영향에 따른 S-곡선의 비교 연구에서 사용된 모델을 해당 연구의 모델로 선정하였다.(11) 펌프수차의 수차 모드에서 상세 제원인 에너지, 회전속도, 및 유량은 IEC60193 규격에서 제시된 계수를 사용하여 계산하였으며, Table 1과 같다.(12) 펌프수차 모델은 스테이 베인(Stay vane, SV), 가이드 베인(Guide vane, GV) 및 러너 수는 각각 20매, 20매, 및 7매로 구성되어 있다.
2.2 Laboratory-scale 펌프수차 모델 실험 기법
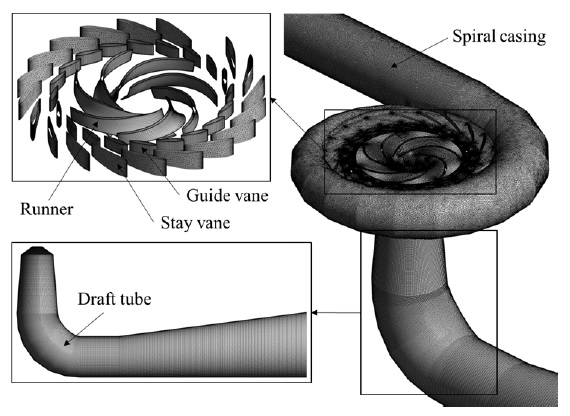
Lab-scale 펌프수차 모델 시험 장치는 Fig. 1과 같으며, 수차 및 펌프 모드를 포함하여 모든 운전 조건에서 작동할 수 있도록 구성되어있다. 또한, 4방 밸브를 통해 다양한 운전조건에서도 일정한 유동 방향을 유지할 수 있도록 하였고, 펌프수차(스파이럴 케이싱, 스테이 베인, 가이드 베인, 러너, 및 흡출관) 구성을 포함하여 메인 탱크, 부스터 펌프, 4방 밸브, 인버터, 발전기, 압력 센서, 및 진공 펌프로 구성되어있다.(11,13)
유량 조절은 가이드 베인 각도와 유량 제어 밸브를 통해 제어하였으며, 메인 유동의 안정화를 위해 펌프수차 모델 입구에 서지탱크를 설치하였다. 압력과 유량의 정확한 측정을 위해 직관의 직경에 따라 적용된 10개의 측정점을 적용하였으며, 흡출관 내 유동의 가시화 관찰을 위해 흡출관 콘 영역을 아크릴로 제작하였다. 가이드 베인 각도는 링크로 연결되어 조정되며, 러너와 발전기 사이 축에 토크 미터를 설치하여 측정하였다. 또한, 실험 중 발생하는 압력을 측정하기 위해 가이드 베인과 러너 사이 공간인 베인리스(Vaneless, VL) 영역에 압전 압력 센서를 일정한 간격으로 4개를 장착하였다. 차압계 및 토크 미터를 포함한 데이터 측정 장치의 제원과 불확실성은 Table 2와 같다. 출력 데이터는 데이터 수집 시스템(Data acqusition system)을 통해 측정하였으며, Lab VIEW 소프트웨어를 통해 실시간 모니터링을 수행하였다.(11,13)
Lab-scale 펌프수차 모델의 저유량 영역은 최고효율점의 약 70% 유량 조건에서 측정하였으며, 진공 펌프를 사용하여캐비테이션 수를 조절하였다. 캐비테이션 수는 유체의 캐비테이션 특성을 나타내는 무차원수로 IEC60193 규격에 제시된 식 (1)을 통해 계산되었다.(12)
| (1) |
여기서, patm, ρ, Hs, pi, 및 H는 각각 대기압, 물의 밀도, 펌프수차 모델의 흡입 수두, 유체의 정압, 및 낙차를 나타낸다. 본 연구에서 실험된 캐비테이션 수 조건은 Table 3과 같으며, 진공 펌프를 작동하지 않은 진공도 0%의 Case 1과 흡출관 내 가시화된 와류가 관찰되는 Case 2에 대한 실험 결과를 토대로 비정상 상태 수치해석을 수행하였다.
3. 수치해석 기법
Lab-scale 펌프수차 모델의 비압축성 내부 유동장은 상용 소프트웨어인 ANSYS CFX-19.1을 사용하여 비정상 상태 RANS 수치해석을 통해 유한체적법을 사용한 이산화된 지배방정식에 의해 계산되었다.(14) ICEM-CFD 기능을 사용하여 스파이럴 케이싱(Spiral casing, SC), 스테이 베인, 및 흡출관의 수치해석을 위한 격자를 생성하였으며, TurboGrid 기능을 사용하여 가이드 베인 및 러너의 격자를 생성하였다. 경계 조건은 CFX-Pre 기능을 통해 설정하였으며, 지배 방정식 계산은 CFX-Solver 기능을 사용하여 해석하였고, CFX-Post 기능을 사용하여 분석을 위한 후 처리를 수행하였다.
스파이럴 케이싱과 스테이 베인의 유동 도메인은 일체형 도메인으로 사면체 격자(Tetrahedral grid)와 프리즘 격자(Prism grid)를 사용하여 작성되었으며, 가이드 베인, 러너, 및 흡출관은 육면체 격자(Hexahedral grid)를 사용하여 작성되었으며, Fig. 2와 같다. 본 연구에 사용된 scale-adaptive simulation shear stress transport(SAS-SST) 난류 모델에 대해 벽 함수 처리 조건을 적용하지 않고 직접 계산하기 위해 러너 블레이드 표면에 O형 격자계를 적용하여, y+값을 약 1로 유지 하였다. 또한, 최적의 격자계 선정을 위해 지난 연구를 통해 수행한 격자 의존성 테스트를 통해 서로 다른 격자 수 5.3☓106, 6.6☓106, 10.4☓106, 및 12.5☓106의 비교를 통해, 계산 시간 및 비용을 고려하여 최적의 격자 수 10.4☓106을 선정하여 수치해석을 수행하였다.(15)
Lab-scale 펌프수차 모델의 수치해석을 위한 경계조건으로, 입구 및 출구는 모델 실험 결과를 토대로 각각 질량 유량과 정압 조건을 부여하였다. 또한, 수치해석 내 캐비테이션 특성을 고려하기 위해 증기의 발생 및 붕괴 과정을 묘사하는 Reyleigh Plesset 모델을 사용하였고,(16) 캐비테이션의 평균 직경 및 포화 압력은 각각 2.0☓10-6 m 및 3,169.9 Pa로 설정하였으며, 작동 유체는 25℃ 물과 증기를 사용하였다. 난류 모델은 유동 박리의 영향을 정확하게 예측하는 SAS-SST 모델을 사용하였다.(17,18) 회전자인 러너와 고정자인 가이드 베인 및 흡출관 사이의 경계면 조건은 transient rotor-stator 조건을 부여하여 실제 순간적인 유동에 대한 상호작용을 예측하고자 하였다. 비정상 해석의 총 해석 시간(Total time)은 러너 8회전에 해당하는 0.26667 s로 설정하였고, 타임 스텝(Time step)은 러너 3° 간격인 0.00027775 s로 설정하여 해석을 수행하였다. 비정상 수치해석의 Loops coefficient는 5회 반복 횟수를 부여하여 수렴성을 향상시키고자 하였다. 또한, 본 연구에서 분석된 결과 값 중 시간 평균값은 총 러너 8회전 중 수치해석의 초기 노이즈를 회피하고자, 마지막 러너 3회전에 대한 시간 평균값을 계산하여 사용하였다.
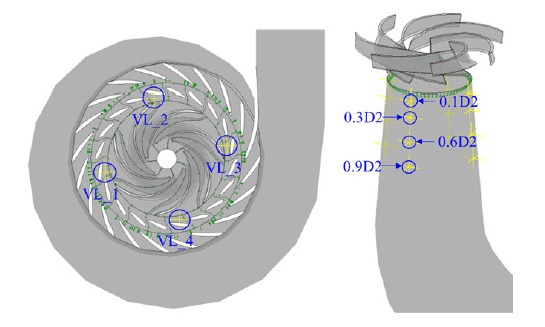
비정상 상태 수치해석 시 발생하는 압력 특성에 대한 검토와 모델 실험의 압력 결과와 비교를 위해 Fig. 3과 같이 압력 측정점을 추가하였다. 베인리스 구간에 적용한 측정점은 lab-scale 펌프수차 모델의 실제 압전 압력 센서와 동일한 위치에 적용하였고, 흡출관은 콘 벽면에 유동 진행 방향으로 0.1D2, 0.3D2, 0.6D2, 및 0.9D2에 압력 측정점을 부여하여 비정상 압력 특성을 비교 분석하였다. 또한, 흡출관 벽면의 각높이에서 일정한 간격으로 4개의 압력 측정점을 적용하여, 각 높이에서 발생하는 압력 특성 중에서 가장 높은 압력값을 사용하여 비교하였다.
4. 결 과
4.1 비정상 상태 수치해석 결과의 타당성 검토
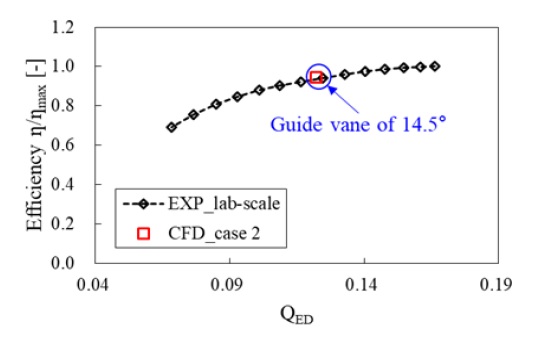
비정상 상태 수치해석 결과의 타당성 검토를 위해, lab-scale 펌프수차 모델의 실험 결과와 수치해석 결과를 Fig. 4와 같이 비교하였고, 효율은 실험 결과의 최대 효율 값으로 무차원화 하였다. 모델 실험은 동일한 낙차와 진공도(Case 2) 조건에 대해 가이드 베인 각도 조절을 통한 유량 조절로 효율 특성을 검토하였다. 최고효율점에서 약 70%인 저유량 영역(가이드 베인 각도 14.5°)의 해석 결과가 실험 결과의 경향과 잘 일치하므로, 수치해석의 성능에 대한 결과는 타당하다고 볼 수 있다.
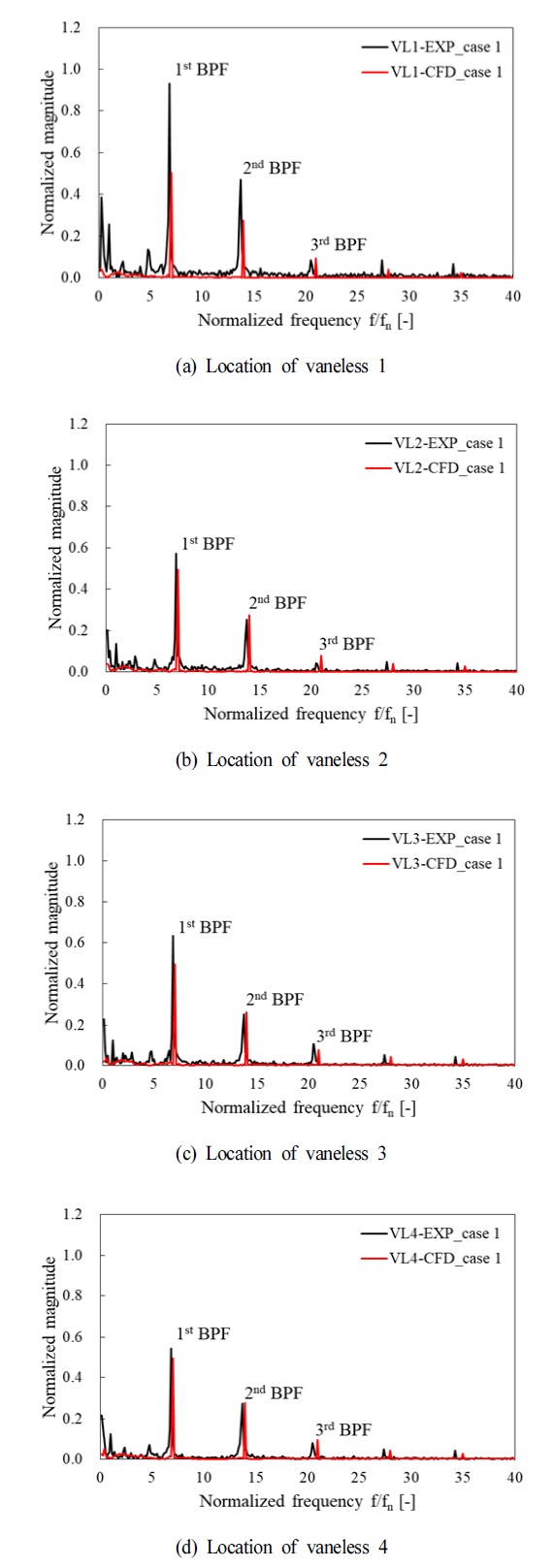
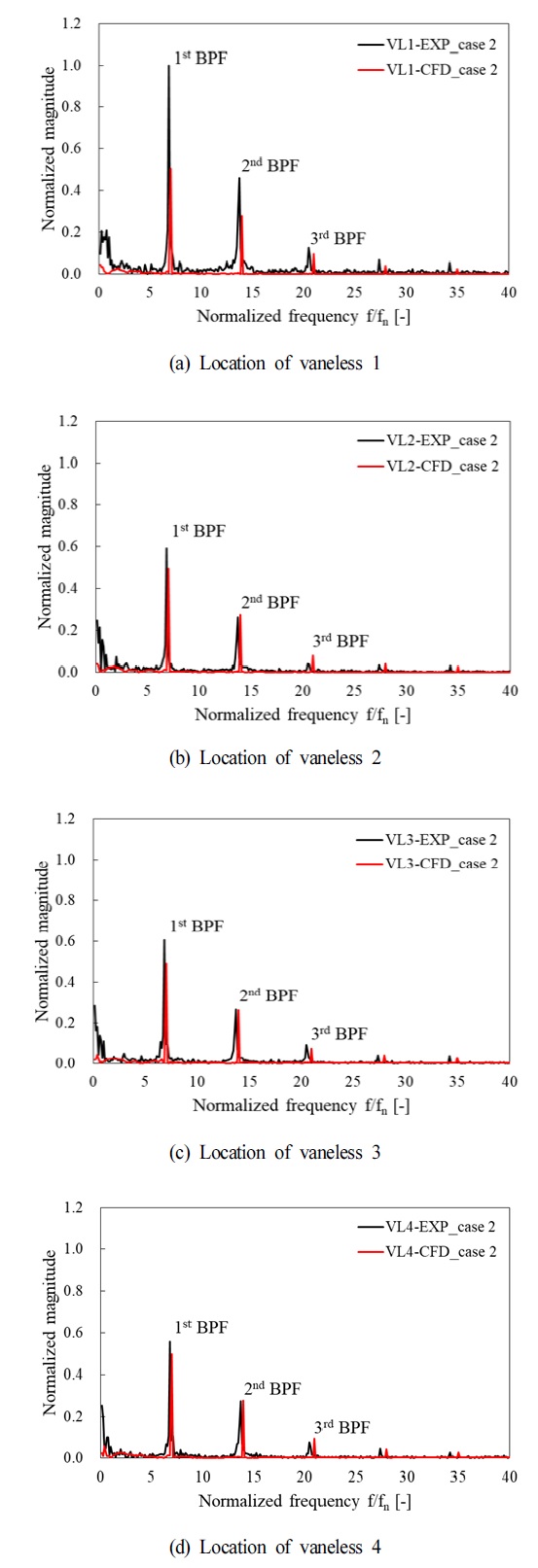
Lab-scale 펌프수차 모델 실험과 비정상 상태 수치해석에서 발생하는 비정상 압력에 대한 비교를 통해, 수치해석의 압력 특성 결과에 대한 타당성을 검토하고자, Fig. 5 및 Fig. 6과 같이 Case 1 및 Case 2의 베인리스 구간에서 비정상 압력을 비교하였다. 베인리스 구간에서 VL1∼VL4 측정점에 대한 비정상 압력 값으로부터 고속퓨리에변환(Fast Fourier transform, FFT) 분석을 통해 비교하였다. Magnitude는 실험 압력 값 중 최대값으로 무차원화하였고, 주파수는 펌프수차 모델의 러너 회전 주파수(fn)로 무차원화하였다. Fig. 5는 모델 시험 및 수치해석 결과의 관찰된 모든 측정 위치에서 1차, 2차, 및 3차 날개통과주파수(Blade passing frequency, BPF) 특성을 나타내고 있다. 한편, VL1 위치에서 실험 결과의 BPF가 상대적으로 큰 Magnitude가 발생한 반면, 나머지 위치인 VL2∼VL4에서는 실험과 수치해석 Magnitude의 크기가 발생한 BPF에서 모두 유사한 크기를 나타냈다.
Fig. 6의 Case 2 경우, Case 1에서 발생한 특성과 유사하게, VL1 위치에서 실험 결과의 큰 Magnitude를 제외하고 관찰된 모든 측정 위치에서 실험 및 수치해석 결과 모두 유사한 크기의 Magnitude를 나타냈다. 또한, Case 1 및 Case 2는 캐비테이션 수가 다름에도 불구하고, 각 측정 위치에서 실험 및 수치해석 결과 모두 유사한 Magnitude 특성을 나타냈다. 따라서 베인리스 구간에서는 캐비테이션 수에 따라 두드러진 비정상 압력 특성의 차이를 발생하지 않았고, VL1 측정점의 실험 결과의 큰 Magnitude를 제외하고, 전반적으로 발생하는 BPF의 특성과 Magnitude의 크기가 유사하므로 수치해석 결과의 비정상 압력 특성에 대해 타당성이 있다고 볼 수 있다.
4.2 Lab-scale 펌프수차 모델 흡출관 내 와류 특성
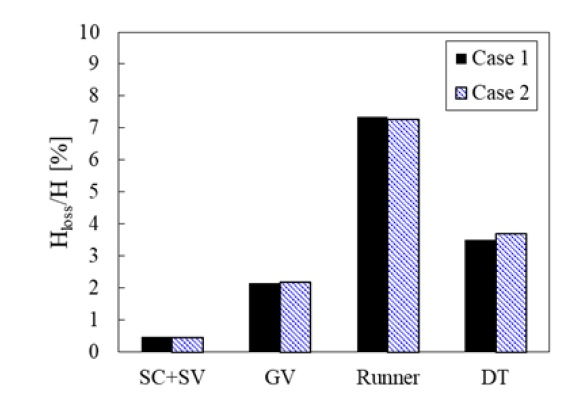
Fig. 7은 Lab-scale 펌프수차 모델의 각 구성요소의 Head 손실을 나타내며, 저유량 운전 조건에서 캐비테이션 수에 따른 성능 비교를 위해 각 구성요소에 대한 Head 손실을 검토하였다. 러너를 제외한 펌프수차 모델의 구성요소에 대한 Head 손실은 식 (2)를 사용하였고, 러너는 식 (3)을 사용하여 계산하였다.(5)
| (2) |
| (3) |
여기서, ∆p, T, ω, 및 Q는 각각 구성요소의 전압력 차, 러너의 토크, 각속도 및 유량을 나타낸다. 펌프수차 모델은 캐비테이션 수에 따라 흡출관을 제외한 각 구성요소에서 Head 손실은 유사하게 발생하였으며, 캐비테이션 수가 감소함에 따라 흡출관의 Head 손실이 약 0.2% 증가하였다.
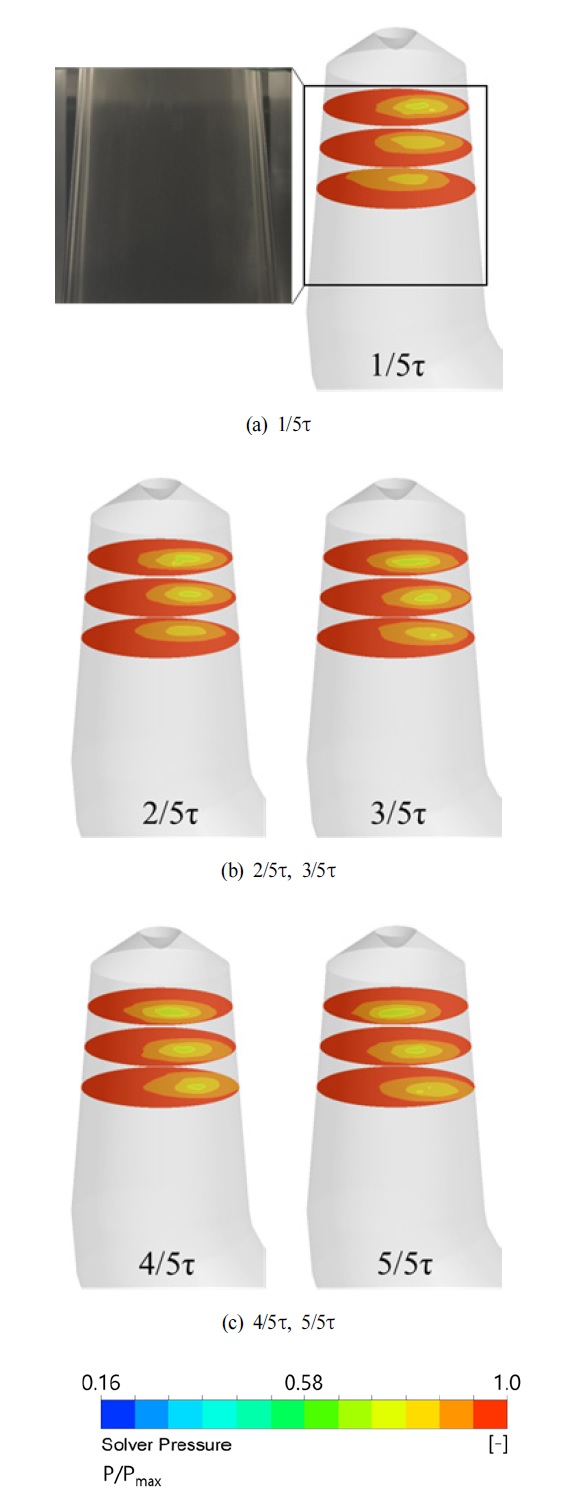
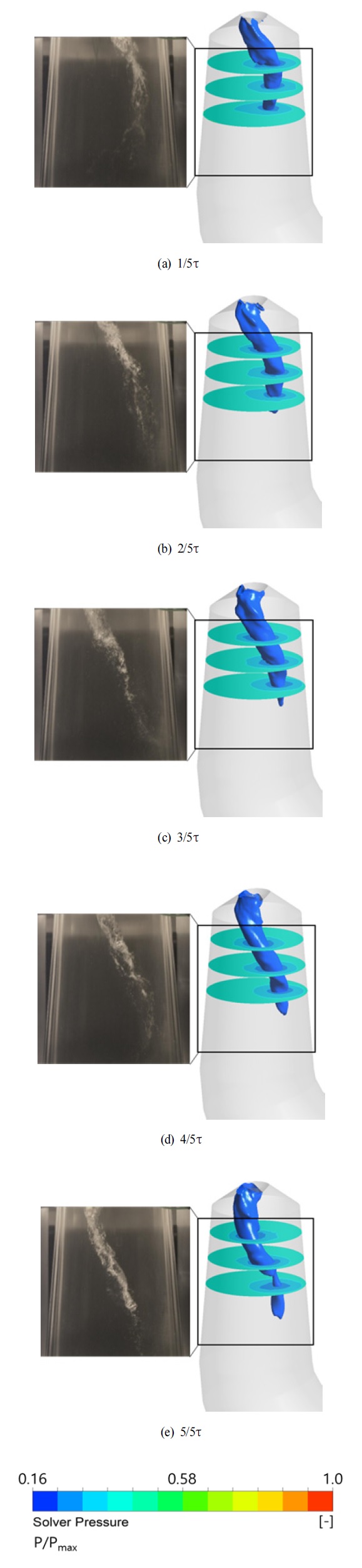
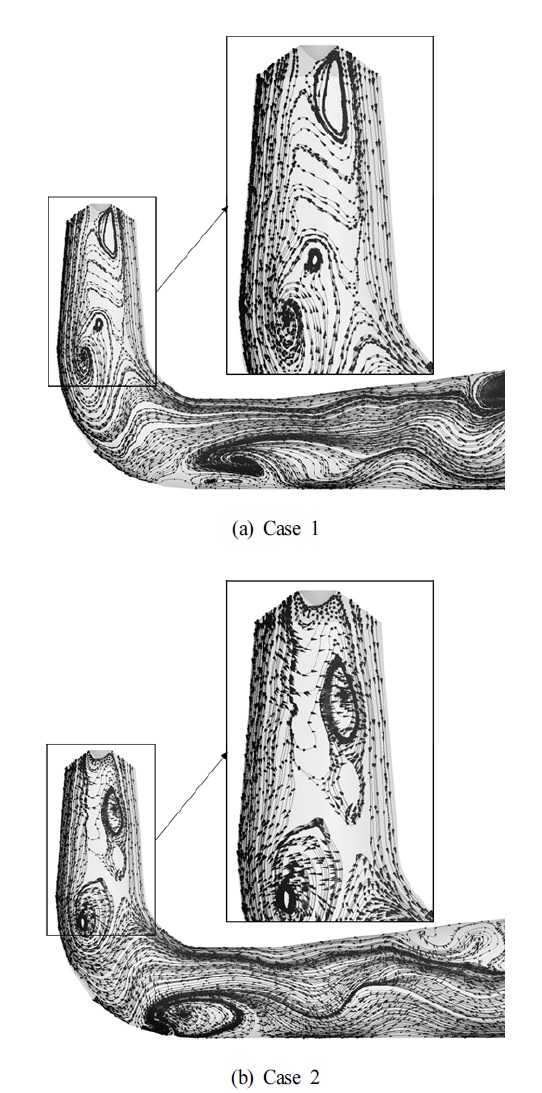
Fig. 8 및 Fig. 9는 lab-scale 펌프수차의 흡출관 내 와류특성을 검토하기 위해 러너 마지막 1회전에 대해 iso-surface 압력 분포와 흡출관 입구로부터 0.3D2, 0.6D2, 및 0.9D2의 관찰단면에서 압력 분포를 나타냈다. 관찰된 iso-surface 압력 분포의 압력 값은 물의 포화 압력을 적용하였으며, 단면의 압력 분포는 최대 압력 값으로 무차원화 하였다. 또한, 가시화된 와류의 거동에 대해 lab-scale 펌프수차 모델의 흡출관 콘에 설치한 아크릴 창에서 초고속 카메라를 통해 촬영한 와류와 수치해석 결과를 비교하였다.
Fig. 8(a)는 저유량 영역임에도 흡출관 내 가시화된 와류가 발생하지 않았지만, 흡출관 내 각 관찰 단면에서 흡출관의 벽면 보다 흡출관 중심 인근에서 상대적으로 저압구간이 발생함을 볼 수 있으며, Fig. 8(a)∼(c)와 같이 시간이 지남에 따라 저압 구간이 러너 회전축을 중심으로 회전함을 볼수 있다. 이는 캐비테이션 수 조건에 따른 흡출관 내 압력 조건으로 인해 가시화된 와류는 발생 하지 않았으나, 저유량 조건에서 흡출관 내 발생하는 원주방향 속도 성분과 스월 성분으로 인해 상대적으로 낮은 저압구간이 형성된 것으로 볼 수 있다.
Fig. 9는 펌프수차 모델의 흡출관 내 가시화된 와류가 발생하였고, Fig. 9(a)∼9(e)에 나타난 바와 같이 러너 마지막 1회전에서 발생하는 와류의 거동과 크기 특성이 실험 결과와 수치해석 결과가 잘 일치하는 것을 볼 수 있다. 특히, 관찰 단면의 압력 분포를 보면, Fig. 8과 달리 전반적으로 압력 수준이 감소함을 알 수 있으며, 이에 따라 포화 압력 아래로 감소하여 가시화된 와류가 발생하였다. 따라서 동일한 낙차 및 유량 조건임에도 불구하고, 캐비테이션 수에 따라 펌프수차 모델의 흡출관 내 가시화된 와류가 발생하며, 압력 수준에서 차이가 발생한다. 이는 Fig. 7에서 Case 2의 흡출관 내 손실 증가의 원인으로 볼 수 있다.
Lab-scale 펌프수차 모델의 흡출관 내 캐비테이션 수에 따른 내부 유동 특성 검토를 위해, Fig. 10과 같이 흡출관 내 관찰 평면에서 속도 유선 분포를 비교하였다. Case 1 및 Case 2는 모두 복잡한 내부 유동 특성을 가지고 있으며, 흡출관 입구 인근의 중간 영역에서 유동 진행의 역방향으로 회전하는 역류 분포를 나타내고 있다. 이러한 역류 발생은 유동 정체 구간의 발생으로 인한 폐색 효과로 펌프수차 시스템 성능의 손실을 야기할 수 있다. 이와 같이, Case 1은 가시화된 와류가 발생하지 않았지만, 저유량 영역으로써 흡출관 내 복잡한 유동 특성을 가지고 있으므로 Fig. 7에서 가시화된 와류의 차이로 인해 Head 손실에 차이를 나타냈지만, 그 차이가 두드러지게 크게 발생하지 않은 이유를 알 수 있다.
흡출관 내 와류 발생의 원인이 되는 스월 특성의 검토를 위해, Case 1 및 Case 2에 대해 흡출관 입구 인근인 0.1D2에서부터 0.9D2까지의 유동 진행방향에 따른 스월 수(Swirl number) 분포를 Fig. 11과 같이 비교하였다. 스월 수는 식 (4)를 사용하여 계산하였다.(19,20)
| (4) |
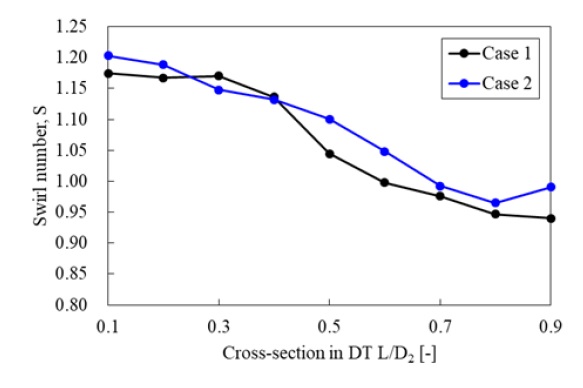
Swirl number distribution along the flow direction in the draft tube of a lab-scale pump-turbine model
여기서, Cm, Cu, 및 r은 각각 축 방향, 원주 방향 및 반경을 의미하며, 본 연구에서는 스월 수에 계산된 축 방향 및 원주 방향은 시간 평균된 값을 사용하여 계산하였다. 가시화된 와류가 발생하는 Case 2가 유동 진행 방향에 따라 전반적으로 높은 스월 수를 나타내지만, Case 1의 경우, 입구 인근인 0.3D2에서 Case 2보다 높은 스월 수를 나타냈다. 이는 Fig. 10에서 나타낸 바와 같이 가시화된 와류가 발생하지 않아도 흡출관 내부의 복잡한 유동으로 인해 높은 스월 수 특성이 나타난 것으로 볼 수 있다. 한편, Case 1은 유동 진행방향에 따라 스월 수가 점차 감소하는 반면, Case 2는 0.9D2에서 스월 수가 상승함을 볼 수 있다. 이는 Fig. 9에 나타낸 가시화 된 와류가 내부 유동에 영향을 주어 스월 수가 증가한 것으로 볼 수 있다.
4.3 펌프수차 모델 흡출관 내 비정상 압력 특성
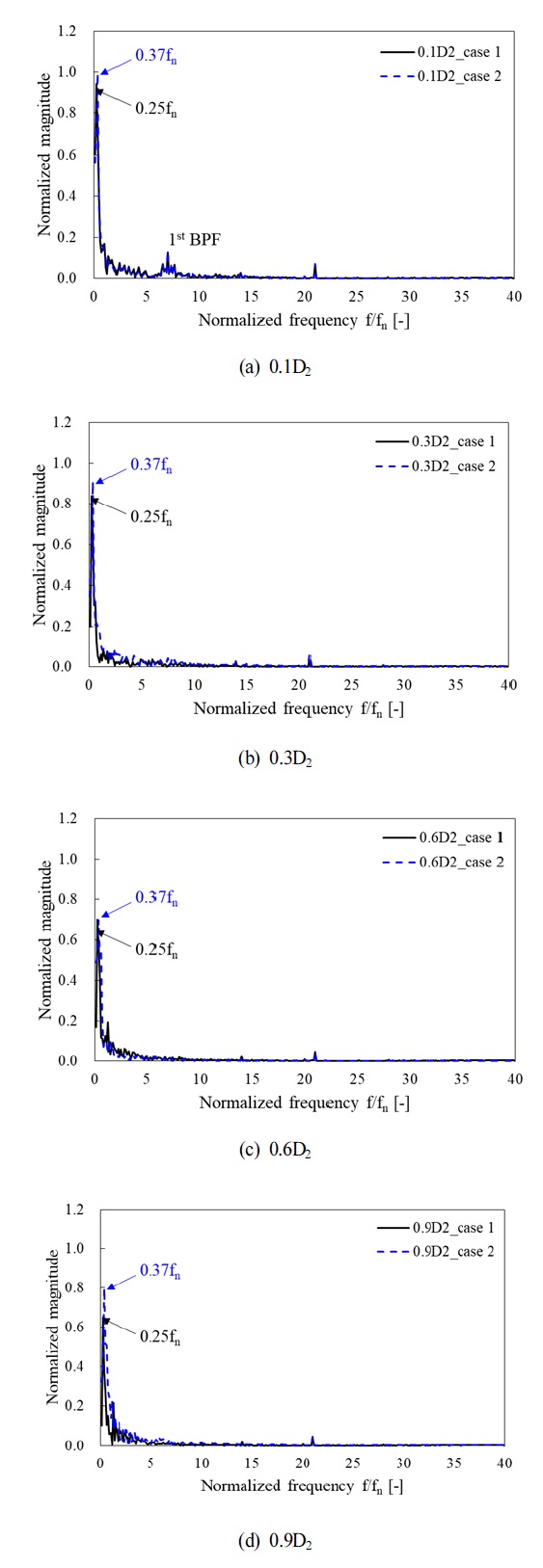
Fig. 12는 Lab-scale 펌프수차 모델의 흡출관 내 캐비테이션 수에 따른 수치해석 결과의 비정상 압력 특성을 비교 검토하였다. Fig. 5 및 Fig. 6에 적용된 FFT 분석 기법을 통해 특성을 검토하였으며, Magnitude는 흡출관 내 발생하는 최고 압력 값으로 무차원화 하였다. Case 1은 저주파수 영역 내 0.25fn에서 높은 Magnitude 특성을 나타냈으며, Case 2는 0.37fn에서 높은 Magnitude 특성을 나타냈다. 이는 흡출관 내 선회 성분과 가시화된 와류 발생으로 인해 발달되는 저주파수 영역의 차이로 볼 수 있다. Fig. 12(a)에서는 Case 1과 Case 2에서 BPF 특성을 나타냈으나, 유동 방향으로 진행함에 따라 BPF 특성은 사라졌다. Case 1은 유동 진행방향에 따라 Magnitude가 점차 감소하였으며, 0.6D2까지는 Case 2와 유사한 Magnitude 크기를 나타냈다. 하지만, Case 2의 경우, 0.6D2 위치까지 유동 진행방향에 따라 Magnitude가 감소하다가, 0.9D2에서 Magnitude가 증가하였다. 이는 Fig. 9의 와류 거동 특성 및 Fig. 11의 스월 수 분포에서 나타냈듯이, 가시화된 와류가 발생했을 때 흡출관 내 스월 성분과 압력 특성에 영향을 미치는 것으로 볼 수 있다. 따라서 펌프수차 모델의 저유량 영역에서 흡출관 내 유동 및 압력 특성은 캐비테이션 수에 따라 전반적으로 유사하게 발생하지만, 가시화된 와류가 발생하는 조건에서는 유동 진행방향에 따라 운전에 불안정한 요소인 스월 강도와 비정상 압력이 감소하지 않고 증가하는 경향을 나타냈다.
5. 결 론
본 연구에서는 laboratory-scale 펌프수차 모델의 수차 모드에서 저유량 조건 운전 시 캐비테이션 수에 따른 내부 유동과 압력 특성의 비교를 위해, 모델 실험을 수행하였다. 실험 결과를 토대로 비정상 상태 RANS 수치해석을 수행하였으며, 효율 및 베인리스 구간의 FFT 분석을 통한 비정상 압력 특성의 비교를 통해 수치해석 결과의 타당성을 확인하였다. 캐비테이션 수에 따른 펌프수차 모델의 각 구성요소에 대한 Head 손실을 통해 성능을 검토하였으며, 흡출관 내 가시화된 와류는 압력 수준 차이에 의해 발생함을 확인하였다. Case 1은 가시화된 와류가 발생하지 않았음에도 흡출관 내 상대적으로 낮은 압력구간이 시간에 따라 회전함을 확인하였고, 역류 특성을 포함한 복잡한 내부 유동 특성이 발생함을 확인하였다. 또한, 흡출관 내 유동진행 방향에 따라 스월 수와 비정상 압력 특성이 점차 감소하는 특성을 나타냈다. 반면, Case 2는 흡출관 내 가시화된 와류의 발생 및 그에 따른 내부 유동 특성의 영향으로 Case 1과 다른 저주파수 구간의 비정상 압력 특성을 나타냈으며, 흡출관 내 유동진행 방향에 따라 스월 수 및 비정상 압력 특성이 감소하였으나, 0.9D2에서 스월 수와 비정상 압력 특성이 증가함을 확인하였다.
이와 같은 결과를 토대로 펌프수차의 수차 모드에서 저유량 영역 운전 시 발생하는 와류로 인한 복잡한 내부 유동과 비정상 압력 특성은 캐비테이션 수에 따라 달라지며, 탈설계 범위인 저유량 영역의 운전 시 상대적으로 안정적인 운전 환경을 확보하기 위해 낮은 스월 강도와 비정상 압력 특성을 위한 캐비테이션 수를 고려해야 한다. 추후 연구에서는 펌프수차 모델의 수차 모드에서 고유량 운전 영역에 대한 모델 실험과 수치해석을 통해, 내부 유동 및 압력 특성에 대한 검토를 수행하고, 저유량 운전 특성과 비교 분석할 예정이다.
Acknowledgments
본 연구는 한국수력원자력의 연구비(L17S029000)와 한국생산기술연구원의 연구비(JE210011) 지원에 의해 수행되었습니다.
References
- Hong, Y. K., 2021, “The task of industrial complexes according to the national greenhouse gas reduction goal,” Korea Industrial Complex Corporation, No. 27.
- Jang, H. S., and Cho, J. H., 2018, “Economic analysis of flexible facilities due to the increase in the proportion of renewable energy generation in the era of energy conversion,” Korea Energy Economic Institute 18-02.
-
Olimstad, G., Nielsen, T., and Børresen, B., 2012, “Stability limits of reversible-pump turbines in turbine mode of operation and measurements of unstable characteristics,” Journal of Fluids Engineering, Vol. 134.
[https://doi.org/10.1115/1.4007589]

-
Kim, S. J., Suh, J. W., Choi, Y. S., Park, J. G., Park, N. H., and Kim, J. H., 2019, “Precessional Vortex Characteristics according to the Swirl Number in the Draft Tube at Turbine Mode of a Pump-Turbine,” The KSFM Journal of Fluid Machinery, Vol. 22, No. 5, pp. 05∼12.
[https://doi.org/10.5293/kfma.2019.22.5.005]

-
Kim, S. J., Cho, Y., Choi, J. W., H, J. J., Kim, S. W., and Kim, J. H., 2021, “Flow Characteristics according to the Air-injection in the Draft Tube of a Francis Turbine Model,” Vol. 24, No. 3, pp. 24∼31.
[https://doi.org/10.5293/kfma.2021.24.3.024]

-
Arpe, J., Nicolet, C., and Avellan, F., 2009, “Experimental evidence of hydroacoustic pressure waves in a Francis turbine elbow draft tube for low discharge conditions,” Journal of Fluid Engineering, Vol. 131, No. 8, pp. 081102∼081109.
[https://doi.org/10.1115/1.3155944]

-
Yu, A., Wang, Y., Tang, Q., Lv, R., and Yang, Z., 2021, “Investigation of the vortex evolution and hydraulic excitation in a pump-turbine operating at different conditions,” Renewable Energy, Vol. 171, pp. 462∼478.
[https://doi.org/10.1016/j.renene.2021.02.131]

-
Lai, X. D., Liang, Q. W., Ye, D. X., Chen, X. M., and Xia, M. M., 2019, “Experimental investigation of flows inside draft tube of a high-head pump-turbine,” Renewable Energy, Vol. 133, pp. 731∼742.
[https://doi.org/10.1016/j.renene.2018.10.058]

-
Yang, J., Lv, Y., Liu, D., and Wang, Z., 2021, “Pressure Analysis in the Draft Tube of a Pump-Turbine under Steady and Transient Conditions,” Energies, Vol. 14, No. 16, pp. 4732.
[https://doi.org/10.3390/en14164732]

-
Li, D., Wang, H., Qin, Y., Li, Z., Wei, X., and Qin, D., 2018, “Mechanism of high amplitude low frequency fluctuations in a pump-turbine in pump mode,” Renewable Energy, Vol. 126, pp. 668∼680.
[https://doi.org/10.1016/j.renene.2018.03.080]

-
Suh, J. W., Kim, S. J., Yang, H. M., Kim, M. S., Joo, W. G., Park, J. G., and Choi, Y. S., 2021, “A Comparative Study of the Scale Effect on the S-Shaped Characteristics of a Pump-Turbine Unit,” Energies, Vol. 14, No. 3, pp. 525.
[https://doi.org/10.3390/en14030525]

- IEC 60193 Ed. 2.0 b: 1999, “Hydraulic Turbines, Storage Pumps and Pump-Turbines Model Acceptance Tests,” American National Standards Institute (ANSI), New York.
-
Suh, J. W., Yang, H. M., Kim, J. H., Joo, W. G., Park, J. G., and Choi, Y. S., 2021, “Unstable S-shaped characteristics of a pump-turbine unit in a lab-scale model,” Renewable Energy, Vol. 171, pp. 1395∼1417.
[https://doi.org/10.1016/j.renene.2021.03.013]

- ANSYS CFX-19.1, 2019, ANSYS CFX Manager User’s Guide, Ansys Inc.
-
Suh, J. W., Kim, S. J., Kim, J. H., Yang, H. M.,, Joo, W. G., Hwang, T. G., ... and Choi, Y. S., 2019, “Establishment of Numerical analysis method of Pump-turbine for Pumped Storage,” The KSFM Journal of Fluid Machinery, Vol. 22, No. 2, pp. 22∼29.
[https://doi.org/10.5293/kfma.2019.22.2.022]

- Zwart, P. J., Gerber, A. G., and Belamri, T., 2004, “A two-phase flow model for predicting cavitation dynamics,” In Fifth international conference on multiphase flow, Vol. 152.
-
Egorov, Y., and Menter, F., 2008, “Development and application of SST-SAS turbulence model in the DESIDER project,” In Advances in Hybrid RANS-LES Modeling, pp. 261∼270.
[https://doi.org/10.1007/978-3-540-77815-8_27]

-
Meter, F. R., and Egorov, Y., 2010, “The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1:theory and model description,” Flow, turbulence and combustion, Vol. 85, No. 1, pp. 113∼138.
[https://doi.org/10.1007/s10494-010-9264-5]

-
Senoo, Y., Kawaguchi, N., and Nagata, T., 1978, “Swirl flow in conical diffusers,” Bulletin of JSME, Vol. 21, No. 151, pp. 112∼119.
[https://doi.org/10.1299/jsme1958.21.112]

- Gupta, A. K., Lilley, D. G., and Syred, N., 1984, “Swirl flows,” Tunbridge Wells.