습식 압축 기술이 원심압축기 공력성능에 미치는 영향
Abstract
Wet compression technology reduces the temperature inside the compressor by spraying water droplets at the inlet of the compressor to improve the turbine output. This technology improves compressor performance and efficiency by reducing compression work and compressor exit temperature. Wet compression technology affects compressor aerodynamic performance depending on variables such as droplet sizes and mass flow rate. This analysis has concentrated on the aerodynamic performance with droplet diameter in wet compression technology. As a result, the centrifugal compressor applied with wet compression technology showed lower exit temperature and increased pressure ratio than the conventional centrifugal compressor. In addition, the compressor performance varied by droplet diameter, and the best performance was shown when the droplet diameter was 2μm. These results confirmed that wet compression technology improves the performance and efficiency of centrifugal compressor.
Keywords:
Centrifugal Compressor, Droplet Evaporation, Wet Compression, Aerodynamic Performance키워드:
원심압축기, 액적 증발, 습식 압축, 공력 성능1. 서 론
일반적으로 가스터빈 입구 온도가 1도 올라가면 출력이 0.54~0.90% 떨어진다고 알려져 있다.(1) 사계절이 뚜렷한 국가에서는 계절마다 발생하는 온도차에 의해 출력변동이 발생하며, 이로 인해 전력수급 문제가 발생한다. 이러한 문제를 해결하기 위해 발전설비의 출력 및 효율 향상을 위한 연구가 활발히 진행되고 있다. 특히 압축기 입구영역에서의 공기온도를 저감시키는 방법이 가스터빈 성능 개선에 효과가 크다고 보고되었으며, 다양한 연구들이 진행되고 있다.
터빈 입구 온도(turbine inlet temperature, TIT)를 낮추는 방법으로는 중간냉각(intercooling), 입구분무 냉각(inlet fog cooling) 등이 있으며, 압축기 출구 온도를 낮추는 방법으로는 습식 압축(wet compression)이 있다.(2) 중간냉각은 압축기나 다단압축기 사이를 냉각시켜 가스터빈 출력을 높이고 압축일을 효과적으로 줄일 수 있는 방법으로 알려져 있다. 액적이 압축기 입구에서 완전증발되는 경우를 입구 분무 냉각방식이라고 하며, 미증발된 액적이 압축기 내부로 유입되어 압축되는 과정을 습식 압축 기술이라고 한다. 이러한 기술들 중에 습식 압축 기술은 다른 기술들보다 출력 증대 효과가 크다고 보고되었다.(1) 이 기술은 다른 기술들과 달리 액적이 압축기 내부로 들어가 증발되기 때문에 외기 조건의 영향을 거의 받지 않는다는 장점이 있다. 또한 기존 발전 설비를 그대로 사용하기 때문에 저비용으로 출력 증대 효과를 얻을 수 있다.
습식 압축 기술은 1940년대에 Kleinschmidit(3)에 의해 처음 제안되었으며, 많은 연구자에 의해 효과를 입증받았다. Jolly(4)는 실험적으로 습식 압축 기술을 가스터빈에 적용하여 9%의 출력 향상을 가져왔다. Bettocchi 등(5)은 습식 압축과 기존 공기압축의 성능곡선을 비교하였으며 습식 압축방식을 사용한 경우 압력비가 2% 상승함을 실험적으로 입증하였다. Neupert 등(6)은 압축기 내부를 부유하는 액적 유동을 입자분석기를 사용하여 가시화하였다. 최근에는 수치해석 기술이 발달함에 따라 3차원으로 습식 압축 기술을 적용한 원심압축기 내부에 대한 연구가 가능해졌다. Surendran 등(7)은 수치해석을 이용하여 저속의 원심압축기에 습식 압축 기술을 적용하였으며, 액적 분무량이 3% 이상일 때 압축일이 감소함을 보였다. Sun 등(8)은 수치적으로 압축기 내부의 액적 거동에 대해 연구하였으며, 이를 통해 습식 압축이 성능향상에 미치는 영향을 고찰하였다. 더 나아가 Sun 등(9)은 액적과 블레이드 간의 물리적인 상호작용에 대한 수치해석을 진행하였다.
습식 압축 기술은 다양한 연구들에 의해 효과를 입증받았지만, 액적거동과 같은 복잡한 압축기 내부 유동현상에 의해 성능예측이 어렵다. 따라서 본 연구에서는 습식 압축 기술이 원심압축기 공력성능에 미치는 영향에 대해 수치해석 기법을 사용하여 분석하였다.
2. 수치해석
2.1 해석모델
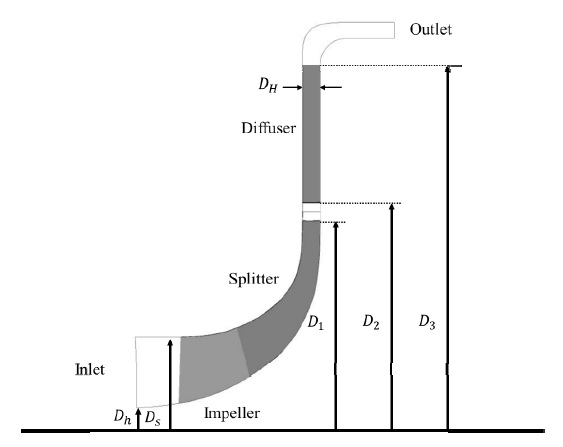
본 연구에서는 선행연구자료를 참고하여 수치해석 정확성을 높이기 위하여 NASA에서 개발한 NASA CC3 모델을 사용하였다. NASA CC3 모델은 산업용 공기압축기로 이용되고 있으며 실험을 통해서 성능과 효율이 입증된 바 있다.(10) Fig. 1에 실제 실험에 사용한 모델과 수치해석에 사용된 3차원 형상을 나타내었다.(11) CC3 모델은 임펠러 영역과 디퓨저 영역으로 나누어져 있으며, 임펠러에는 15개의 블레이드와 스플리터, 디퓨저에는 24개의 베인으로 구성되어있다. 해석 모델의 설계점은 압력비가 4, 회전수는 21,789 rpm 그리고 작동유량은 4.54 kg/s이다. 모델 제원에 대한 형상 변수를 Fig. 2에 표시하였으며, 자세한 제원값은 Table 1에 기술하였다.

(a) Configuration of centrifugal compressor(NASA CC3) and (b) computational modeled of centrifugal compressor
2.2 격자계 구성
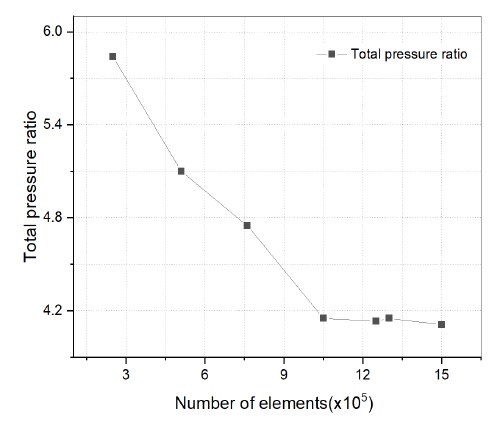
임펠러와 디퓨저 격자계 생성은 TurboGrid를 이용하여 정렬 격자(structured grid)를 사용하였다. 블레이드 근처 표면은 O-격자계를 사용하였으며, 이 외의 영역은 H-격자계를 사용하였다. 격자에 따른 수치해석 결과의 영향을 최소화하기 위하여 격자 의존성 시험(grid dependency test)을 수행하였으며, Fig. 3에 나타내었다. 격자 크기를 변화시키며 수치해석을 진행하였으며, 압축기 성능 평가 지표인 압력비의 변화를 확인하였다. 약 127만개에서부터 압력비 변화가 크지 않음을 확인하였다. 최종 격자계는 벽면 조건을 고려하여 임펠러 영역 706,543개, 디퓨저 영역에 571,128개를 구성하여 수치해석을 수행하였다.
2.3 경계조건
수치해석 연구에서는 정상상태 해석을 수행하였다. 압축기 회전에 대한 해석은 MRF(moving reference frame)기법을 사용하였다. 난류 모델은 유동 박리 등의 특성을 잘 모사하는 SST(shear stress model)모델을 사용하였다. 습식 압축 기술은 압축된 공기와 함께 액적이 분사되는 2상 유동(two-phase flow)이기 때문에 유체와 분무되는 액적에 대한 경계조건이 필요하다. 연속된 상인 유체는 Eulerian방법을 사용하였고, 분사되는 액적은 Lagrangian방법을 사용하여 계산하였다. Eulerian-Lagrangian식을 통한 계산 방식은 양방향 연계(two-way couple)방식으로 계산함에 따라 유동과 함께 액적 온도 및 궤적(trajectory) 등을 계산하였다. 자세한 경계조건은 Table 2에 기술하였다. 습식 압축기술은 압축기 내부에서 기체 흐름에 액적이 노출되어있기 때문에 기상(gas phase)와 액상(liquid phase)의 속도 차이로 인해 분열(breakup)이 발생한다.(14) 본 연구에서는 기상과 액상의 속도차이를 고려하기 위하여 CAB(Cascade atomization and breakup) 모델을 사용하였다. CAB 모델은 액적의 분열이 스피링-질량 감쇠계로 이루어진 시스템에 상사시킨 TAB (Taylor analogy breakup) 모델에서 개발되었으며, 일반적으로 액체 분무 해석에 적합하다고 알려져 있다.(15) 또한 액적 간 충돌과 블레이드에 충돌에 의해 발생하는 영향을 고려하기 위하여 확률적 충돌 모델인 Sommerfeld Collision model을 사용하였다. 병합 모델은 액적이 블레이드에 충돌하게 되면 더 작은 물방울로 부서지고 다른 벽에 충돌하는 물방울들은 제거된다는 가정을 바탕으로 진행된다.(8)
2.4 지배방정식
원심압축기 내부 유동을 해석하기 위해서는 지배방정식인 3차원 Reynolds Averaged Navier-Stokes 방정식(RANS)의 해를 구해야한다. 수치해석은 상용프로그램인 ANSYS CFX 2020R2를 사용하였으며, 유체는 연속체로 가정하였다. RANS 방정식은 연속방정식, 운동량 방정식, 에너지 방정식으로 이루어져 있으며 다음과 같이 표현된다.
- 연속방정식:
| (1) |
여기서 ρ는 유체밀도, 그리고 는 유체의 속도벡터를 말한다.
- 운동량 방정식:
| (2) |
위 식에서 p는 압력, 는 중력항, 그리고 는 응력텐서를 뜻한다. 또한 응력텐서는 다음과 같이 표현된다.
| (3) |
여기서 μ는 점성이며, I는 단위 텐서(unit tensor)이다.
- 에너지 방정식:
| (4) |
여기서 E는 총에너지, keff는 유효 열전도계수, 그리고 는 유효 응력텐서이다.
습식 압축 기술에서 액적의 움직임은 입자수송방정식(particle transport equation)을 통해서 계산이 되는데, 고속으로 회전하는 원심압축기 특성상 부력(buoyancy force)값은 항력(drag force)과 코리올리력(Coriolic force)에 비해 상대적으로 매우 작기 때문에 고려하지 않았다. 따라서 본 연구에서는 항력(FD)과 코리올리력(FR)만을 고려하여 다음과 같이 표현하였다.(12)
| (5) |
위 식에서 md는 액적 하나의 질량을 뜻하며, ud는 액적속도를 뜻한다. FD와 FR은 각각 다음과 같다.
| (6) |
| (7) |
여기서 d는 액적지름, u는 유체속도, Ω은 각속도 그리고 r은 위치 벡터를 뜻한다. CD는 항력계수를 의미하며 실험상관식에 의해 다음과 같이 표현된다.(13)
| (8) |
위 식에서 Red는 액적의 레이놀즈 수(Reynolds number)로 다음과 같이 표현된다.
| (9) |
여기서 μair는 공기의 점성계수이다.
3. 결과 및 고찰
3.1 해석 모델 유효성 검사
수치해석 결과를 검증하기 위해 기존에 존재하는 실험값(10)과 성능곡선을 비교하였으며, Fig. 4에 나타내었다. 성능곡선은 원심압축기가 설계회전수인 21,789 rpm에서 100%의 성능으로 작동될 때 무차원 압력비와 등엔트로피 효율을 보여준다. 압력비와 등엔트로피 효율은 다음과 같은 식으로 정의된다.
| (10) |
| (11) |
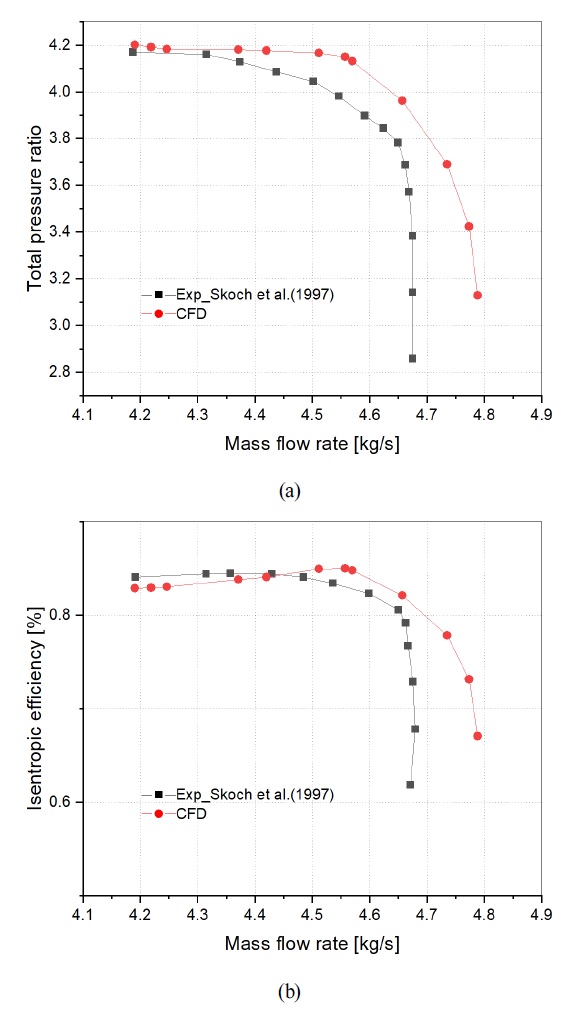
Comparison results of the total pressure ratio (a) and isentropic efficiency (b) vs. mass flow rate between experiment(10) and CFD
실험결과와 비교하여 수치해석 결과는 전반적으로 비슷한 경향을 보였으며 설계점(21,789 rpm, 4.54 kg/s)에서 압력비와 등엔트로피 효율의 상대오차는 각각 3.416%, 0.864%으로 나타났다. 이를 통하여 수치해석 결과들에 대한 정확성을 확보하였음을 알 수 있다. 저유량에 비해 고유량에서 실험값과 계산값이 큰 차이가 발생하였는데 이는 고유량에서의 압력손실을 정확하게 예측하지 못한 것에 기인한다. 하지만 계산된 오차율은 모두 5% 이내의 값을 가지기 때문에 본 연구의 수치해석 기법에 대한 타당성을 검증할 수 있었다.
3.2 성능 및 효율 선도
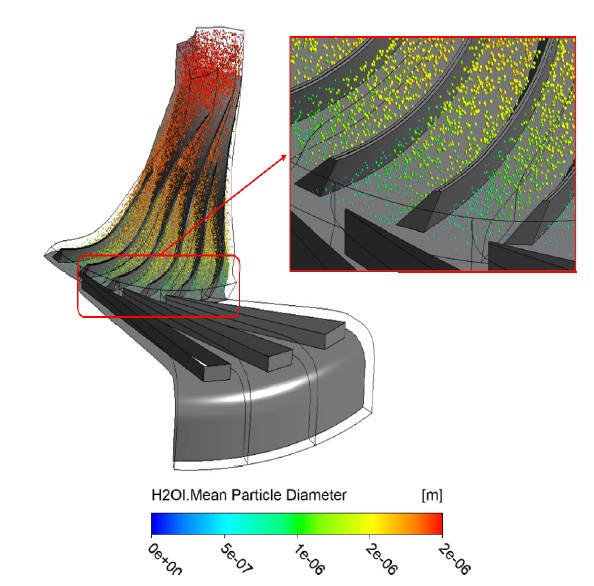
설계점에서 습식 압축기술이 적용된 압축기 내부 액적거동을 Fig. 5에 나타내었다. 특히 원심압축기 내부에서 부유하고 있는 액적의 크기를 나타내었다. 입구에서 분사된 액적은 임펠러 영역을 지나 디퓨저 앞에서 대부분의 액적이 증발됨을 알 수 있다. 액적 증발은 압축기 내부 온도를 감소시키고 결과적으로 압축기 성능을 향상시킨다. 이러한 영향을 확인하기 위하여 압축기 성능곡선에 습식 압축기술이 적용된 원심압축기와 기존 원심압축기 성능을 비교하였다. 비교를 위해서 습식 압축은 직경 2μm인 액적을 설계 운전점인 공기유량(4.54 kg/s)의 0.2%를 압축기 입구 영역에서 분사하였다. 성능곡선은 출구 영역의 정압을 변화시켜 운전점을 다르게 하면서 압력비와 등엔트로피 효율을 유량에 따라 도출하였다.
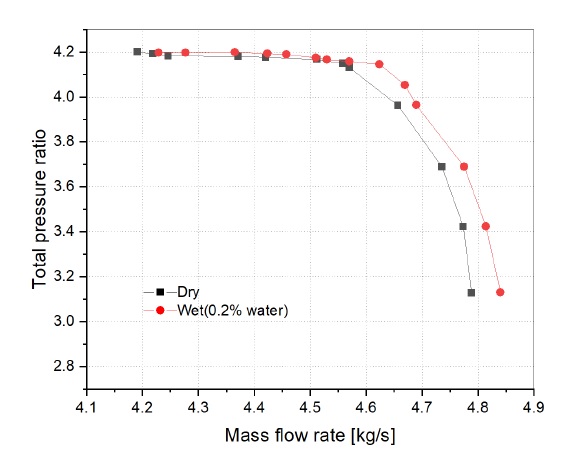
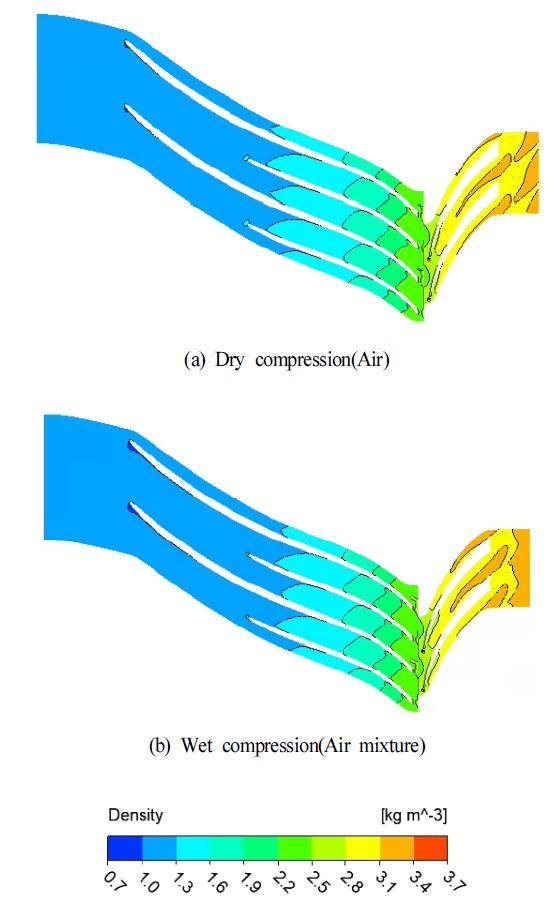
압력비에 대한 성능 곡선을 Fig. 6에 나타내었다. 습식 압축이 적용된 압축기의 성능곡선이 기존 공기 압축에 의한 성능 곡선보다 우측으로 이동하는 것을 볼 수 있다. 설계점에서 압력비는 기존 공기 압축에 비해 0.12% 향상되었다. 또한 동일 유량에서 더 큰 압력비를 가지는 것을 볼 수 있다. 이것은 액적이 분사됨에 따라 액적이 가지고 있는 잠열 크기만큼 압축기 내부 온도가 감소하여 공기 밀도를 증가시키기 때문에 공기 혼합물의 질량 유량이 증가하는 것을 알 수 있다. Fig. 7은 압축기 내부의 공기 혼합물 밀도 분포를 나타낸다. 기존 공기 압축에 비해 습식 압축을 통한 압축기 디퓨저 영역에서 더 높은 공기 혼합물 밀도 분포가 나타남을 알 수 있다.
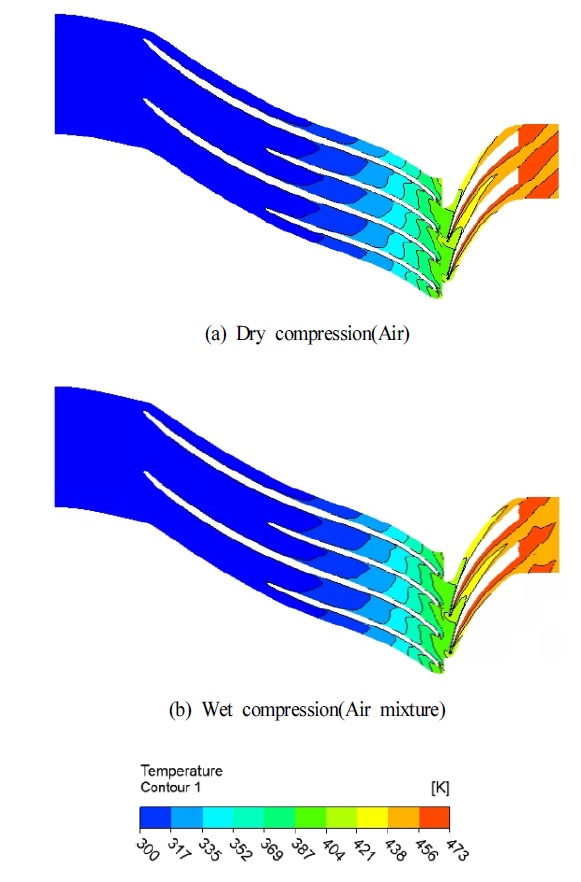
등엔트로피 효율은 압축기 내부 온도가 어느 정도 감소하는가에 의해 결정된다. 따라서 액적의 잠열로 인해 발생하는 흡열 반응이 뚜렷할수록 효율이 상승함을 알 수 있다. 등엔트로피 효율의 원심압축기 성능곡선을 Fig. 8에 나타내었다. 압력비와 마찬가지로 습식 압축이 적용된 원심압축기의 등엔트로피 효율은 기존 공기 압축보다 질량유량이 상승하는 것을 볼 수 있으며 이는 곧 성능 향상을 의미한다. 잠열에 의해 발생하는 액적의 흡열 정도를 보기 위해 Fig. 9에 압축기 내부 온도 분포를 나타내었다. 임펠러 영역을 지나 디퓨저 영역으로 가면서 기존 공기 압축과의 온도 차이가 나는 것을 볼 수 있다. 이것은 고속으로 움직이는 임펠러 영역보다 운동에너지가 압력으로 변화하는 디퓨저 영역에서 액적의 영향을 많이 받아 낮은 온도 분포를 가지는 것으로 사료된다.
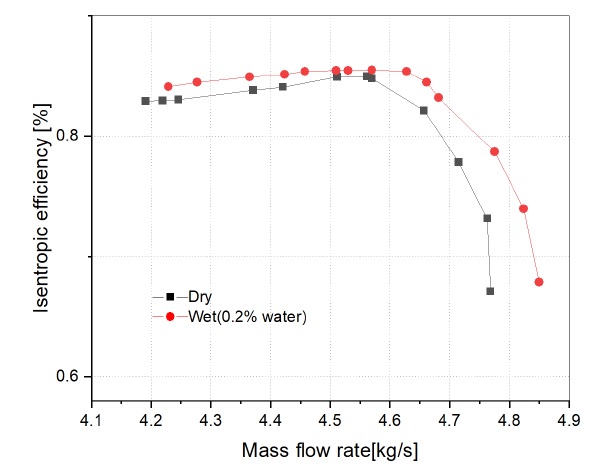
Comparison results of the total isentropic efficiency vs. mass flow rate between dry and wet compression
3.3 입자 크기에 따른 압축기 성능 및 효율
액적은 압축기 내부의 유로를 따라 이동하면서 증발하게 된다. 이때 액적 직경은 증발율과 밀접한 관련이 있어 성능에 영향을 준다. 액적 직경에 따른 원심압축기 성능에 미치는 영향을 고찰하기 위해 액적 직경을 1∼10μm까지 변화시켜 유량, 출구온도, 압력비, 그리고 엔트로피 효율을 고찰하였다. 결과 비교의 편의성을 위하여 정규화된 결과들을 입자 직경에 따라 나타내었으며, Fig. 10에 나타내었다. 정규화는 각각의 변수들이 가지는 최고값을 분모로 결과값으로 나타냈다. 유량과 등엔트로피 효율과 압력비는 액적 크기가 2μm에서 최고값을 가졌으며 다른 액적 직경의 값을 2μm기준으로 정규화하였다. 출구 온도는 6μm를 기준으로 무차원화하였으며 다음 식으로 계산된다.
| (12) |
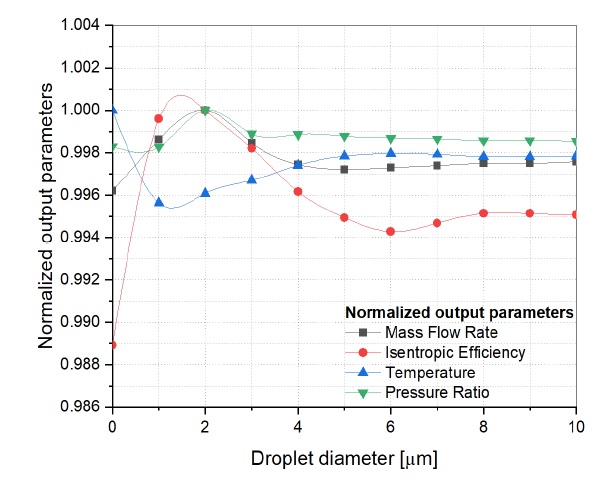
Effects of the different droplet size on the centrifugal compressor performance(injecting mass flow rate 0.2%)
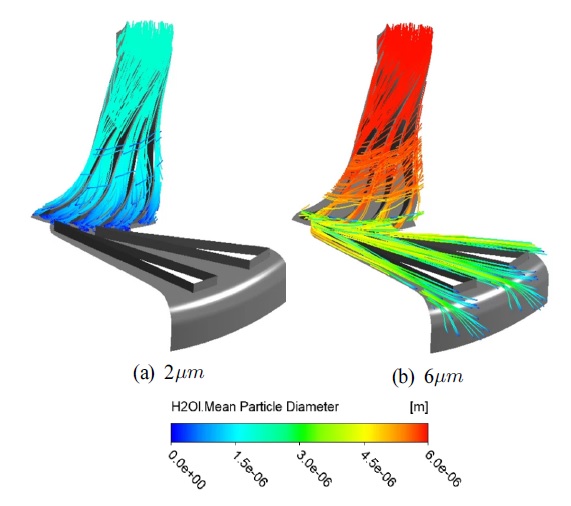
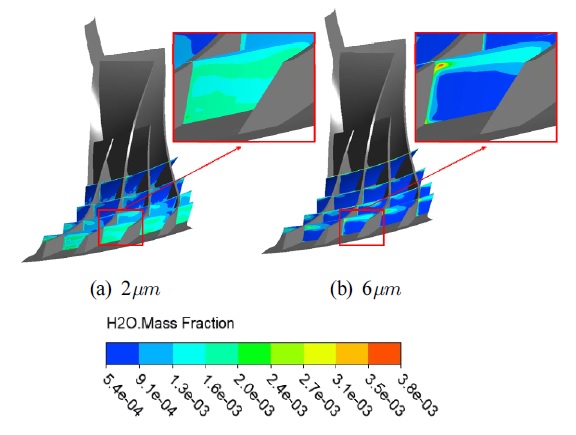
설계점에서는 2μm의 액적 크기를 가질 때 가장 낮은 출구 온도와 높은 압력비, 그리고 등엔트로피 효율을 가졌다. 반면 6μm의 액적 크기를 가질 때 가장 낮은 등엔트로피 효율을 가짐을 확인하였다. 이를 고찰하기 위하여 2μm와 6μm의 입자 궤적을 Fig. 11에 나타내었다. 2μm인 경우 임펠러 출구영역에서 모두 증발되는 것을 알 수 있다. 6μm인 경우에는 디퓨저 출구 영역에서 액적이 모두 증발되는 것을 알 수 있는데, 이것은 동일 질량유량을 가졌을 때 액적의 표면적이 9배가 더 크기 때문으로 이해할 수 있다. 또한 6μm의 크기를 가지는 액적은 주 유동에서 더 빨리 이탈하는 것을 볼 수 있다. 이것은 질량이 더 크기 때문에 더 큰 원심력이 발생하여 슈라우드 방향으로 액적이 몰리는 것을 알 수 있다.[8][15] 원심압축기 내부에 있는 액적은 반경 방향으로 원심력을 받게 된다. 액적 직경이 클수록 입자 반응 시간(particle response time)이 길어지게 됨에 따라 원심력의 영향을 많이 받게 된다. 입자 반응 시간은 입자가 유체 흐름 변화에 반응하는데 필요한 시간을 의미한다. 따라서, 큰 물방울들은 기체 유동장의 영향을 받지 않기 때문에 주 유동에서 더 빨리 이탈하게 된다. 이를 확인하기 위하여 Fig. 12에 유동방향으로 액적의 질량분율분포를 확인하였으며, 6μm의 액적 크기를 가진 모델이 큰 원심력에 의해 간극 쪽으로 집중되는 것을 확인할 수 있다. 대부분의 액적이 간극 쪽으로 이동하게 되어 더 많은 누설유동을 발생시켜 불안정한 내부 유동장을 형성함을 알 수 있다. 결과적으로 질량 유량이 감소하는 결과를 가져왔다. 이를 통해 액적 직경에 따라 압축기 내부 유동 특성이 변화하였고 압축기 성능에 영향을 미침을 확인하였다.
4. 결 론
본 연구에서는 원심압축기 입구 영역에 액적을 분사하여 압축기 내부에서 증발하는 습식 압축 기술에 대한 연구를 수행하였다. 이를 통해 원심압축기 공력성능에 습식 압축 기술이 미치는 영향에 대해 고찰하였으며 그 결과를 요약하면 다음과 같다.
1) 습식 압축 기술을 적용하기 위하여 공기유량(4.54 kg/s)의 0.2%를 압축기 입구 영역에서 분사한 결과 기존 공기 압축과 비교하여 100% 회전속도 영역에서 압력비와 등엔트로피 효율이 상승하는 것을 확인하였다.
2) 습식 압축 기술을 적용한 결과 설계점에서 기존 공기 압축보다 압력비는 0.12%, 등엔트로피 효율은 1.14% 상승하였다.
3) 액적 직경을 1∼10 μm변화시켰을 때 압력비는 크게 차이가 나지 않았으며, 등엔트로피 효율은 2μm에서 최고값을, 6μm일 때 최소값을 나타내었다. 액적 직경에 따라 내부 유동특성이 변화하였으며 압축기 성능에 큰 영향을 미침을 확인하였다.
Acknowledgments
본 연구는 국토교통과학기술진흥원의 국토교통기술촉진연구사업의 지원으로 수행되었음(Grant 21CTAP-C157760-02).
References
-
Sun, L., Zheng, Q., Li, Y., and Bhargava, R., 2011, “Understanding effects of wet compression on separated flow behavior in an axial compressor stage using CFD analysis,” Journal of Turbomachinery, 133(3).
[https://doi.org/10.1115/1.4003003]

-
Jonsson, M. and Yan, J., 2005, “Humidified gas turbines-a review of proposed and implemented cycles,” Energy, 30(7), pp. 1013-1078.
[https://doi.org/10.1016/j.energy.2004.08.005]

- Kleinschmidt, R. V., 1947, “Value of wet compression in gas-turbine cycles,” Mechanical Engineering, 69(2), pp. 115-116.
- Jolly, S., 2002, “Wet compression–a powerful means of enhancing combustion turbine capacity,” Power-Gen International, 1-12.
-
Bettocchi, R., Morini, M., Pinelli, M., Spina, P. R., Venturini, M. and Torsello, G., 2011, “Setup of an experimental facility for the investigation of wet compression on a multistage compressor,” Journal of Engineering for Gas Turbines and Power, 133(10).
[https://doi.org/10.1115/1.4002947]

-
Neupert, N., Ober, B. and Joos, F., 2015, “Experimental investigation on droplet behavior in a transonic compressor cascade,” Journal of Turbomachinery, 137(3).
[https://doi.org/10.1115/1.4028351]

-
Surendran, A. and Kim, H. D., 2014, “Effects of wet compression on the flow behavior of a centrifugal compressor: a CFD analysis,” In Turbo Expo: Power for Land, Sea, and Air, Vol. 45639, p. V02DT42A002.
[https://doi.org/10.1115/GT2014-25035]

-
Sun, J., Zhou, X., Liang, Q., Zuo, Z. and Chen, H., 2019, “The effect of wet compression on a centrifugal compressor for a compressed air energy storage system,” Energies, 12(5), 906.
[https://doi.org/10.3390/en12050906]

-
Sun, L., Zheng, Q., Luo, M., Li, Y. and Bhargava, R., 2011, “On the behavior of water droplets when moving onto blade surface in a wet compression transonic compressor,” Journal of Engineering for Gas Turbines and Power, 133(8).
[https://doi.org/10.1115/1.4002822]

-
Skoch, G. J., Prahst, P. S., Wernet, M. P., Wood, J. R. and Strazisar, A. J., 1997, “Laser anemometer measurements of the flow field in a 4: 1 pressure ratio centrifugal impeller,” In ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition. American Society of Mechanical Engineers Digital Collection.
[https://doi.org/10.1115/97-GT-342]

- Yamauchi, G. K. 2012, Fundamental Aeronautics Program.
-
Khan, J. R. and Wang, T., 2011, “Three-dimensional modeling for wet compression in a single stage compressor including liquid particle erosion analysis,” Journal of Engineering for Gas Turbines and Power, 133(1).
[https://doi.org/10.1115/1.4001828]

- Naumann, Z. and Schiller, L., 1935, “A drag coefficient correlation,” Z. Ver. Deutsch. Ing, 77(318), e323.
-
Liu, C., Zheng, Q., Wang, Q., Li, A., Jiang, Y. and Luo, M., 2019, “Sensitivity analysis of multistage compressor characteristics under the spray atomization effect using a CFD model,” Energies, 12(2), p.301.
[https://doi.org/10.3390/en12020301]

-
White, A.J. and Meacock, A.J., 2011, “Wet compression analysis including velocity slip effects,” Journal of engineering for gas turbines and power, 133(8).
[https://doi.org/10.1115/1.4002662]