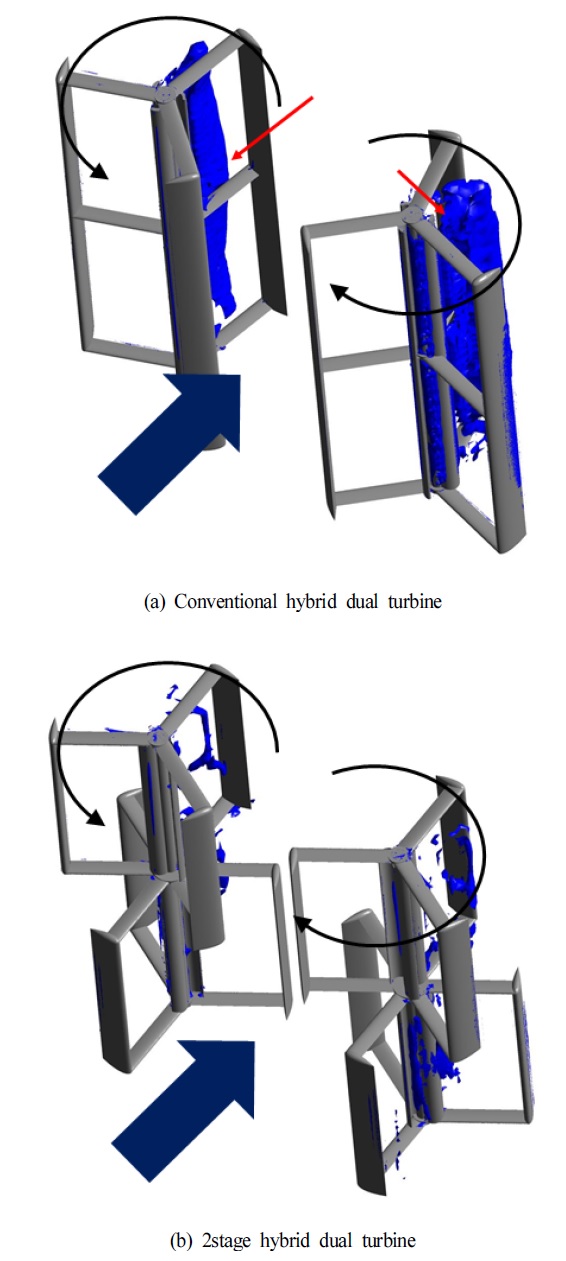
다리우스와 사보니우스를 결합한 하이브리드 타입의 조류발전 터빈 설계

2.1 유동해석방법

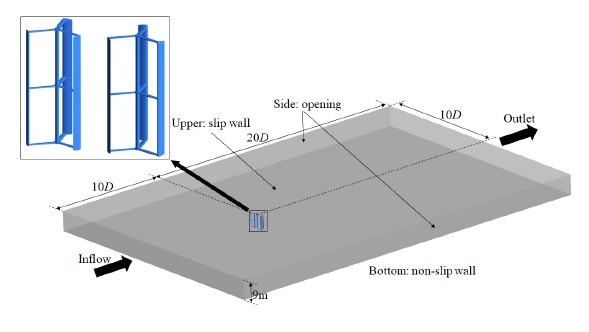
본 연구에서는 100kW급 조류발전시스템을 설계하기 위하여, 50kW급 수직축 터빈 2기를 고려하고 조류방향에 대해 좌우로 배치한 듀얼 터빈을 설계하였다. 이러한 듀얼 수직축 터빈에 대한 설계 및 수력학적 성능 특성을 분석하기 위하여 유동장을 비압축성 3차원 비정상상태로 가정하고 상용 CFD코드인 ANSYS CFX-19.2⁸⁾를 사용하여 비정상 RANS해석을 수행하였다. 본 연구 대상인 조류발전용 수직축 듀얼 터빈의 유동해석을 위한 계산영역을 Fig. 1에 도식화하였다. 단일 터빈의 직경(D)과 높이(H)는 각각 3 m 및 6 m이고, 계산영역의 높이는 대상해역의 수심을 고려하여 9 m로 고려하였다. 그리고 계산영역의 폭과 길이는 터빈 직경에 대해 각각 20배와 30배로 설정하였으며, 듀얼 수직축 터빈은 입구부로부터 10D의 위치에서 바닥면과 2 m의 거리를 두도록 하였다.

Fig. 1

Computational domain of a dual vertical axis turbine

유동해석을 위해 작동유체는 물로 가정하였고, 속도 및 압력을 계산영역의 입구와 출구에 각각 경계조건으로 부여하였다. 계산영역의 바닥면은 점착(non-slip)조건을 부여하고, 상부면과 좌우의 양 옆면은 각각 미끄럼(slip)조건과 opening 조건을 적용하였다. 수직축터빈은 로터의 회전으로 발생하는 후류가 로터 성능에 비정상상태로 영향을 미치기 때문에 수직축 터빈의 유동특성을 분석하기 위하여 비정상해석을 수행하였다. 수치해석은 로터가 총 10회전할 때까지 수행되었으며, 반복해석(iteration) 당 로터가 3°씩 회전할 수 있도록 설정하였다. 로터의 회전영역과 고정영역의 경계면에는 transient rotor stator interface 방법으로 처리하였고, 로터 블레이드와 지지대(spoke) 및 축(shaft) 등에는 점착조건으로 경계조건을 부여하였다. 지배방정식의 난류항을 계산하기 위하여 shear stress transport(SST) k-ω 난류모델을 사용하였다. SST 난류모델은 k-ω모델과 k-ε모델의 장점을 결합한 것으로, 벽 근처 영역에서는 k-ω모델을 사용하고 이외의 영역에서는 k-ε모델을 사용한다.

비정상 계산을 수행하기 위해서 Intel Xeon E5-2690 CPU를 사용하였고 단일 계산 당 약 80시간이 소요되었다.

2.2 격자의존성시험

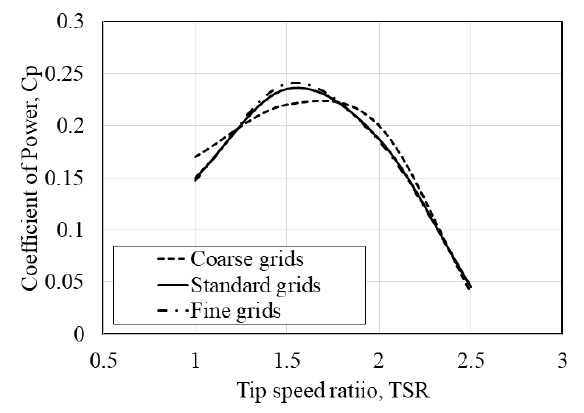
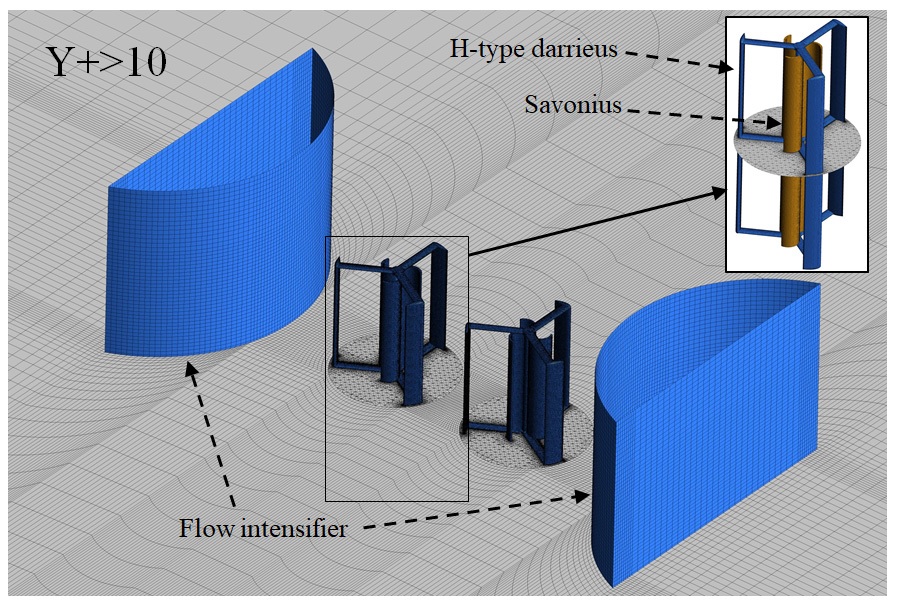
유동해석 결과에 대한 격자의 영향성을 배제시키기 위한 격자의존성시험을 수행하여 Fig. 2에 결과를 나타내었다. Fig. 1에 나타낸 H-type 다리우스형 수직축 듀얼터빈에 대해 격자수의 변화에 따른 출력효율의 변화를 비교하여 Fig. 2에 그래프로 나타내었으며, 계산영역에 대한 격자수는 약 5백만~23백만 개의 범위에서 평가하였다. 격자의존성시험의 결과를 바탕으로 격자수가 약 15백만 개 이상에서 결과 값이 약 2% 미만의 변화를 보이는 것을 확인하여 이를 계산영역에 대한 최적의 격자 크기로 정하였다. 격자의존성시험을 통해 결정한 최적 격자 크기를 바탕으로 하이브리드 듀얼터빈과 유속강화장치를 적용한 계산영역에 대한 격자계를 Fig. 3에 나타내었다. 주유동의 정지영역 및 듀얼터빈의 회전영역은 각각 육면체 및 사면체 격자계로 구성하였고, 벽면의 첫 번째 격자점에서의 y+ 값은 10이상을 유지시켜 high-Re SST모델이 적용되도록 하였다.

Fig. 2

Grid dependency test result

Fig. 3

Structure of the grid system

3.1 수직축 듀얼터빈의 기초설계

본 연구에서는 100 kW급 조류발전시스템을 개발하기 위하여 수직축 듀얼터빈을 설계하였다. 우선 터빈을 설계하기 위해서는 시스템을 설치하기 위한 해역의 입지조건을 분석해야 한다. 적지 후보지들을 분석하여 2.6 m/s의 유속 조건을 터빈 설계를 위한 정격유속으로 결정하였다.

조류발전용 듀얼터빈에 대한 성능함수로서 출력 및 출력효율을 고려하였고, 출력효율은 다음의 식으로 정의한다.

여기서, ρ, A, 그리고 V는 각각 작동유체의 밀도, 터빈의 투영면적, 그리고 작동유체의 유입속도를 의미하며, 식 (1)을 터빈 직경(D)에 대한 식으로 변환하면 아래의 식으로 정리할 수 있다.

여기서 H는 수직축 터빈의 높이를 의미하며, 본 연구에서는 수심 9 m에 대해 수면 및 바닥으로부터 각각 1 m와 2 m의 간격을 두고 터빈을 설치하는 것으로 고려하여 H는 6 m로 결정하였다.

기초설계 단계에서는 식 (2)로부터 듀얼터빈의 출력 및 효율 값을 각각 100 kW 및 30%로 가정하였으며, 이로부터 D는 약 3 m로 계산되었다. NACA00xx계열의 익형을 갖는 수직축 H-type 다리우스 터빈은 약 25~35%의 출력 효율을 가지며⁹⁾, 본 연구에서는 NACA0025 익형을 사용하여 기초설계 단계에서 단일 터빈의 출력 효율을 30%로 가정하여 기초설계를 수행하였다. 기초설계한 형상에 대한 상세정보는 Table 1에 정리하였다. 기초설계한 터빈은 듀얼로 배치시켜 발전하도록 하였고, 두 터빈 사이의 거리는 1.375D로 간격을 유지시켰다. 듀얼 터빈의 회전방향은 서로 반대 방향으로 회전시키는 것이 같은 방향으로 회전하는 듀얼 터빈과 비교하여 출력성능이 증가한다는 것을 Li와 Calisal¹⁰⁾ 및 Heo 등¹¹⁾의 연구를 통해 확인하였고, 이 결과를 바탕으로 본 연구에서는 듀얼 터빈을 서로 반대방향으로 회전시키도록 하였다.

Table 1

Design specifications of vertical axis dual turbine for tidal current convertor

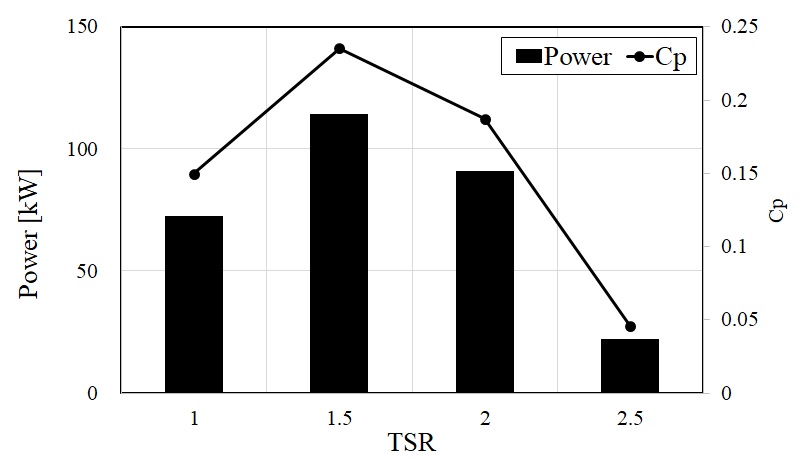
기초설계를 바탕으로 도출한 수직축 듀얼 터빈에 대해 3차원 비정상 RANS해석을 수행하여 듀얼 터빈의 출력 및 효율 값을 주속비(tip speed ratio, TSR)의 변화에 따라 Fig. 4에 나타내었다. 터빈의 회전에 따라 출력 값이 변하기 때문에 터빈의 마지막 10바퀴 회전에서 평균한 출력 값을 성능함수로서 고려하였다. 듀얼 터빈의 최대 출력 및 효율 값은 1.5의 TSR에서 약 114 kW 및 23.5%를 예측하였다. 날개 수와 익형의 차이는 있으나 NACA0018의 익형을 사용한 H-type 다리우스 듀얼터빈의 출력 효율은 약 20%로 Vergaerde 등3)의 연구에서 확인되었고, 본 연구에서는 기초설계한 듀얼터빈의 효율이 23.5%으로 계산되었으므로 설계 결과가 타당한 것으로 사료된다.

Fig. 4

Performance data of the preliminary design of the vertical axis dual turbine

3.2 유속강화장치 적용의 영향성 분석

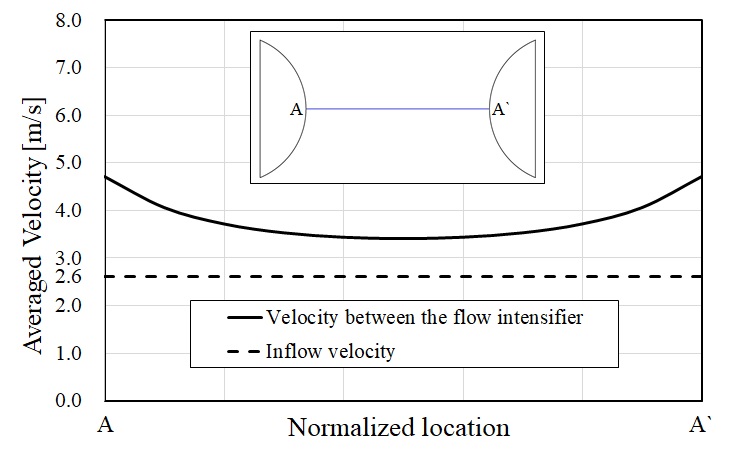
수직축 듀얼 터빈의 기초설계 형상에 대한 3차원 유동해석을 수행하여 최대 출력 값은 약 114 kW로 예측되는 것을 확인하였다. 그러나 조류발전 시스템 손실을 고려하면 목표 출력 값을 달성하기 위해서는 터빈의 출력을 향상시키는 것이 요구된다. 터빈의 출력을 향상시키기 위해서는 터빈 형상에 대한 최적설계를 통한 방법도 있지만, 본 연구에서는 터빈의 기초형상에 대해 동일 유속 경계조건(2.6 m/s)에서 터빈이 받는 유속만 증가시킬 수 있도록 유속강화장치 개념을 제안하고자 한다. 제안하는 유속강화장치를 Fig. 3에 도식화하였으며, 이러한 유속강화장치를 통해 동일한 유속 환경조건에서 벤츄리 효과를 바탕으로 터빈이 실제로 받는 조류속을 증가시킬 수 있다. Fig. 5에 유속강화장치 사이(A-A')에서의 높이 방향으로 평균한 유속 분포를 나타내었다. 조류속이 2.6 m/s의 조건에서 유속강화장치 사이에서 벤츄리 효과에 의한 유속이 증가하는 것을 확인할 수 있다. 듀얼 터빈을 설치할 위치에서는 유속이 상대적으로 약 30% 증가하는 효과가 있지만 실제 터빈을 설치하면 유속은 다소 감소할 것으로 사료된다.

Fig. 5

Velocity distribution averaged in vertically between the flow intensifier(A-A`)

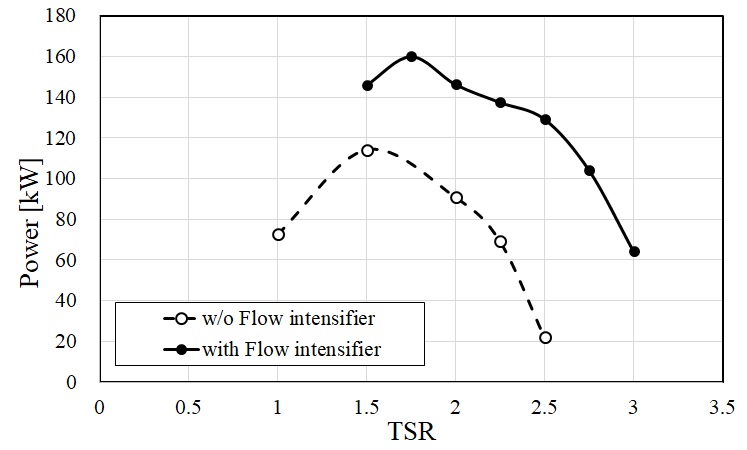
Fig. 6에 유속강화장치의 적용에 따른 출력 성능의 변화를 그래프로 비교하여 나타내었다. 유속강화장치를 적용함으로써 전반적으로 출력 성능이 증가하는 것을 확인하였고, 최대 출력 값이 약 160 kW로 예측되어 상대적으로 약 40.3%의 출력상승 효과를 보였다. 또한 최대 출력 값이 나타나는 주속비는 1.5에서 1.75로 변경되어 터빈의 회전수가 증가하는 것을 확인할 수 있었다.

Fig. 6

Power of vertical axis dual turbines with and w/o the flow intensifier

3.3 사보니우스 터빈의 영향성 분석

수직축 터빈들 중에서 H-type 다리우스 터빈의 경우에는 일반적으로 출력 성능은 높지만 자가 구동(self-starting) 성능이 좋지 않다는 특징¹²⁾이 있다. Fig. 7에 기초설계한 조류터빈의 회전에 따른 토크 값의 변화를 나타내었다. 터빈 회전에 따라 토크 값이 거의 0 Nm에 가까운 구간들이 존재하며, 해당 구간에서는 터빈의 회전력이 상쇄되기 때문에 출력이 거의 발생하지 않게 된다. 또한 터빈의 회전에 따라 토크 값이 최대 약 50,000 Nm에서 최소 0 Nm 이하로 급격히 변경되기 때문에 발전기에 급격한 부하의 변동을 야기한다.

Fig. 7

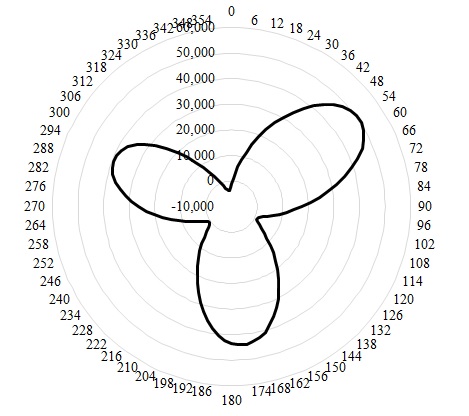
Instantaneous torque with respect to azimuth angle during the last revolution for the preliminary design of the vertical axis turbine at TSR of 2.0 (@rated speed=2.6 m/s)

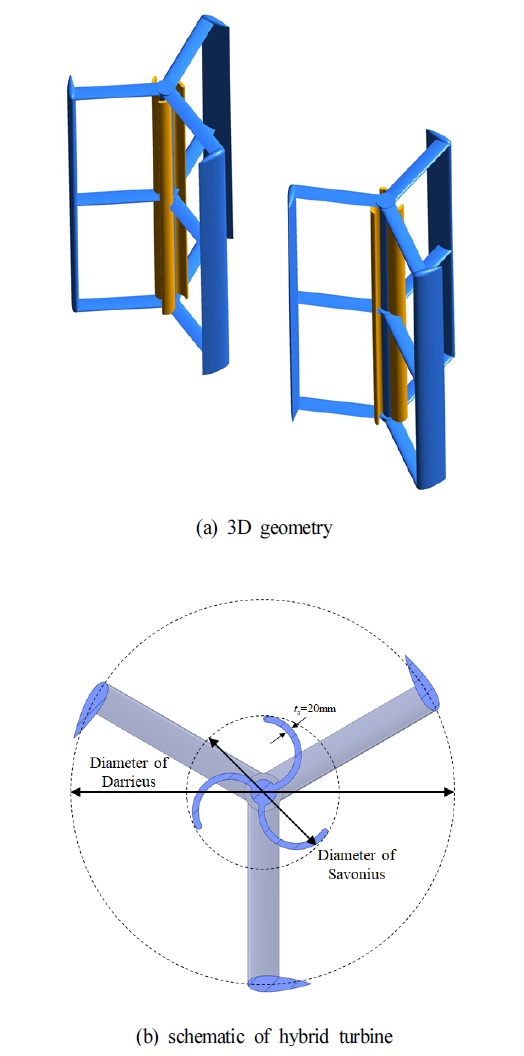
사보니우스 터빈의 경우에는 출력 효율이 상대적으로 작지만 자가 구동 성능이 우수하다는 장점¹²⁾이 있다. 이러한 특성을 고려하여 본 연구에서는 다리우스 터빈의 상대적으로 높은 출력 성능 특성과 사보니우스 터빈의 상대적으로 높은 자가 구동 성능 특성을 결합하고자 다리우스 터빈과 사보니우스 터빈을 결합한 하이브리드 터빈의 성능 특성을 분석하였다. 하이브리드 터빈의 기본형상을 Fig. 8에 도식화하였다. 기본형상의 사보니우스 터빈은 다리우스 터빈과 같이 3엽의 날개를 갖고 다리우스 터빈의 직경보다 작게 설계하였다. Table 1에 나타낸 것과 같이 다리우스 터빈에는 NACA0025 익형으로 설계하고 사보니우스 터빈은 일반적인 반원형으로 설계하였다.

Fig. 8

Hybrid turbine combining darrieus(blue color) and savonius(orange color) turbines

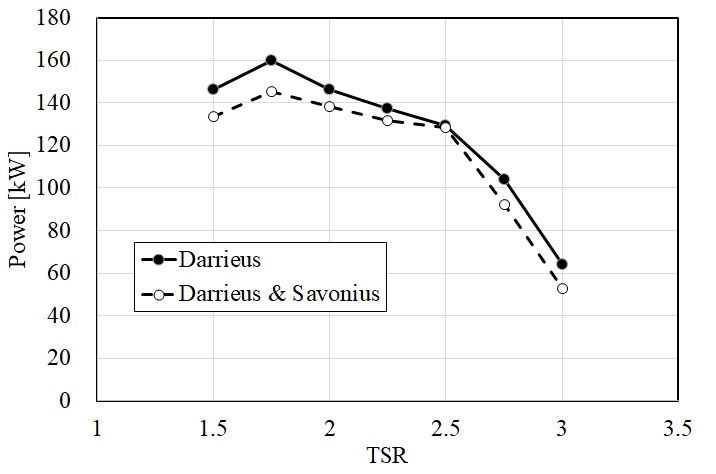
조류발전 수직축 하이브리드 듀얼 터빈의 출력 성능을 다리우스 듀얼 터빈의 출력과 비교하여 Fig. 9에 그래프로 나타내었다. 다리우스 터빈과 사보니우스 터빈을 결합한 하이브리드 터빈 기본형상의 출력 값은 다리우스 터빈과 비교하여 전반적으로 감소한 경향을 보였고 최대 출력 값은 TSR=1.75에서 약 9.3% 감소하였다. 또한 하이브리드 터빈은 주속비 1.5∼2.5의 구간에서 출력의 변화가 작은 경향을 보였다. 이러한 경향은 조류발전시스템의 발전기가 안정적으로 작동할 수 있는 요인으로 작용하기 때문에 매우 중요하다. 주속비 2.5에서는 다리우스 듀얼 터빈의 출력과 하이브리드 듀얼 터빈의 출력이 거의 같은 값을 갖는 것을 확인할 수 있다.

Fig. 9

Power performance comparison of darrieus turbine and hybrid turbine

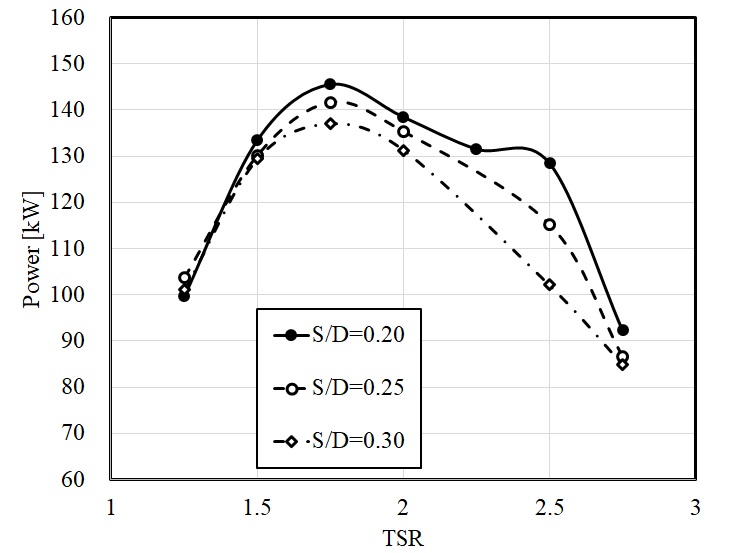
하이브리드 터빈 내의 사보니우스 터빈의 직경(S) 변화가 출력 성능에 미치는 영향을 분석하기 위하여 Fig. 10에 S의 변화에 따른 터빈 출력 값의 변화를 비교하였다. 사보니우스 터빈의 직경과 다리우스 직경의 비(S/D)가 20%의 경우가 전반적으로 높은 출력 성능을 나타냈으며, S/D의 증가에 따라 주속비에 따른 출력 성능 곡선이 전반적으로 감소하는 경향을 보였다. 그리고 S/D가 25% 및 30%의 경우에는 TSR=2.5의 구간에서 출력 값이 급격히 감소하는 것을 확인할 수 있었다.

Fig. 10

Power of vertical axis hybrid dual turbines with different the S/D

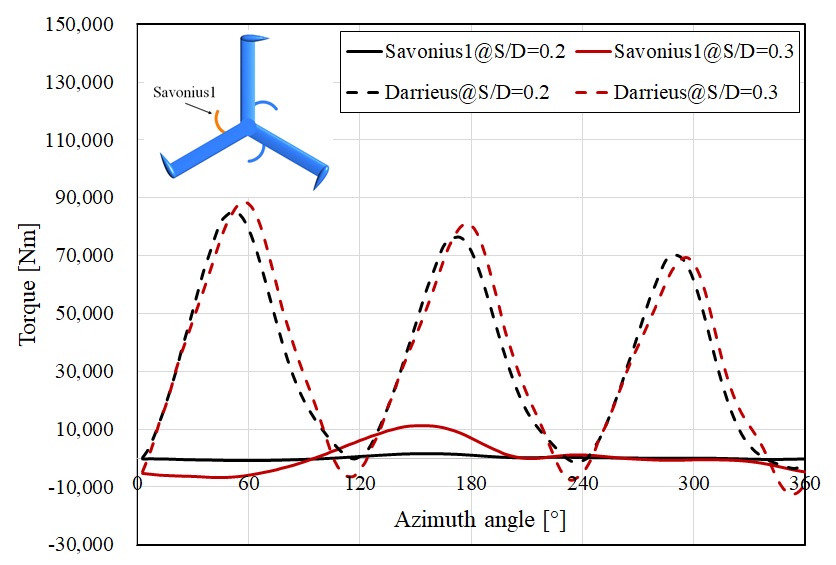
Fig. 11은 하이브리드 터빈의 사보니우스 1엽 및 다리우스 터빈의 회전에 따른 토크의 변화를 보여준다. S/D가 20% 및 30%의 터빈에 대해 비교하였으며, S/D가 증가함에 따라 사보니우스 1의 회전에 따른 토크의 변동 폭이 큰 것을 확인할 수 있었다. 사보니우스 1이 음(-)의 토크 값을 나타내는 경우에는 S/D=0.3에서의 최대 작은 값이 S/D=0.2와 비교하여 약 610% 더 작은 값을 나타내었다. 또한 다리우스 터빈의 경우에도 S/D가 증가함에 따라 회전에 따른 토크의 변동 폭이 상대적으로 커지는 것을 확인하였고, 음의 토크를 갖는 영역에서의 값이 더 작은 값을 나타내었다. 이러한 영향으로 Fig. 10에서와 같이 TSR>1.5 구간에서 S/D의 증가에 따라 출력이 감소한다는 것을 확인할 수 있었다.

Fig. 11

Instantaneous torque for Savonius 1 and Darrieus turbine with respect to azimuth angle during the last revolution@TSR=1.75

3.4 유속강화장치 사이 거리의 영향성 분석

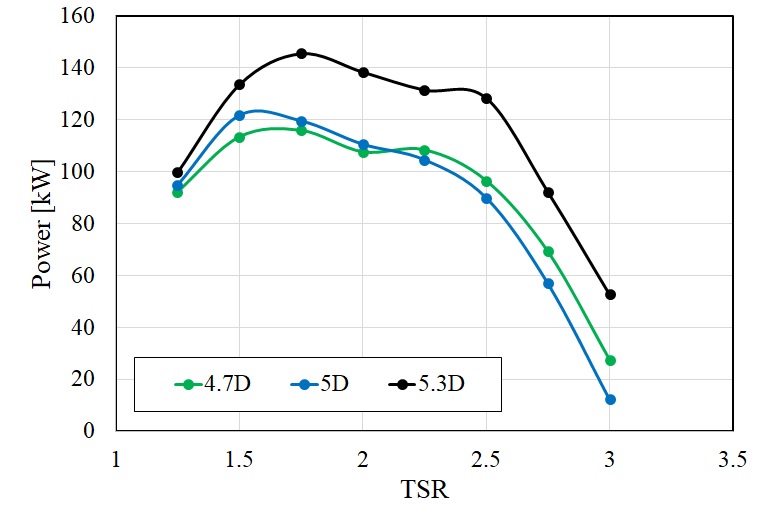
조류발전 수직축 듀얼 터빈의 성능에 대한 유속강화장치의 영향을 분석하기 위하여 유속강화장치 사이 거리의 변화에 따른 하이브리드 듀얼 터빈의 출력 성능 변화를 Fig. 12에 그래프로 비교하였다. 유속강화장치 사이 거리를 수직축 터빈의 직경에 대하여 4.7, 5.0, 그리고 5.3배의 거리만큼 변화시켰으며, 4.7D∼5.3D의 범위에서는 유속강화장치 사이 거리가 가장 먼 5.3D의 경우에 가장 높은 출력 성능을 보였다. 유속강화장치 사이 거리가 4.7D의 경우에는 5.0D의 경우와 비교하여 TSR<2.0 구간에서 상대적으로 작은 출력 성능을 보였지만 TSR이 2.25 이상에서는 더 큰 출력 값을 나타내었다.

Fig. 12

Power of vertical axis hybrid dual turbine with different distances between the flow intensifiers

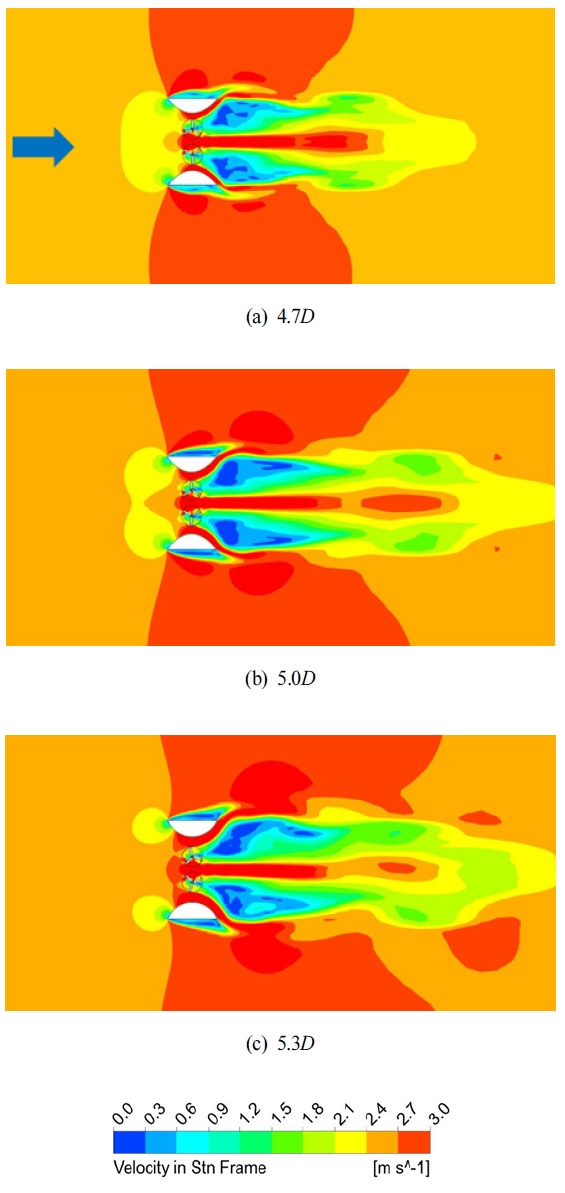
유속강화장치 사이 거리의 변화에 따른 터빈 주변에서의 속도장 비교를 Fig. 13에 나타내었다. 터빈 입구부에서는 유속이 줄어드는 것을 확인할 수 있는데 유속강화장치의 거리가 터빈과 가까우면 봉쇄효과(blockage effect)에 의해 유속강화 효과가 감소되고 이로 인해 듀얼 터빈의 출력이 줄어드는 것을 확인할 수 있다. 그리고 유속강화장치 사이 거리는 자켓 구조물의 크기와 연계되어 계속 증가할 수 없으므로, 유속강화장치는 수직축 터빈의 직경에 대해 5.3D의 거리를 유지시키는 것으로 설계하였다.

Fig. 13

Velocity contour around vertical axis hybrid dual turbine with different distances between the flow intensifiers at TSR=1.75

3.5 2단 하이브리드 듀얼 터빈 설계

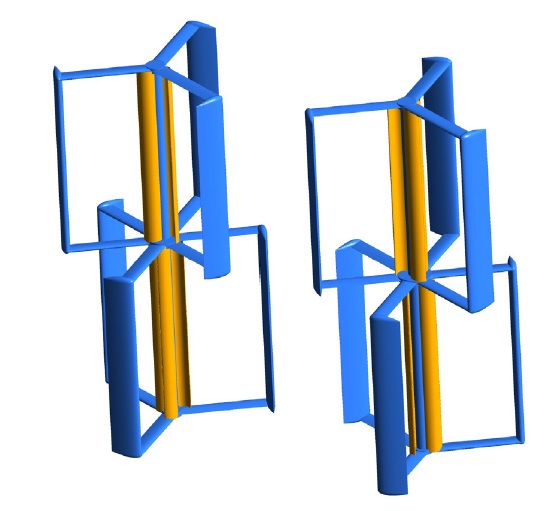
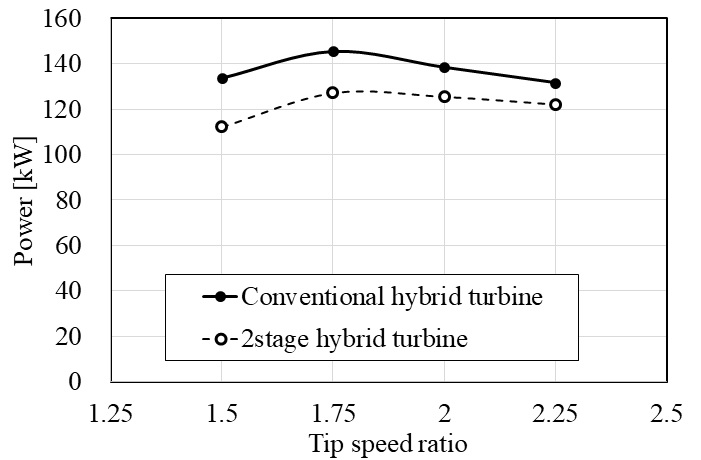
수직축 터빈은 Fig. 7에 나타낸 것과 같이 터빈 회전에 따라 터빈의 토크 값이 급격히 변하며 국부적으로는 음의 값을 나타내기도 한다. 이러한 구간에 의해 터빈의 회전에 따른 출력 값의 변동이 크며, 발전기의 부하를 증가시키는 요인으로 작용한다. 이러한 문제를 해결하고자 Fig. 14에 도식화한 것과 같이 수직축 터빈을 상부와 하부로 구분한 2단 하이브리드 듀얼 터빈을 제안하였다. 상부와 하부 터빈은 60°의 위상 차이를 주어 구분하였으며, 이러한 2단 하이브리드 듀얼 터빈의 출력 성능을 Fig. 15에 나타내었다. 기존의 하이브리드 듀얼 터빈의 출력과 비교하여 전반적으로 출력이 다소 감소하는 경향을 나타내었다. 최대 출력을 나타내는 TSR=1.75에서 약 12.4%의 출력 감소를 보였고 TSR=2.0에서는 약 9.4%만큼 출력이 감소하였다. 그러나 주 발전이 이루어지는 TSR<2.0의 구간에서는 목표 출력 값인 100 kW를 상회하는 결과를 보여주었다.

Fig. 14

Hybrid turbine combining darrieus(blue color) and savonius(orange color) turbines

Fig. 15

Comparison of power between the conventional hybrid dual turbine and the 2stage hybrid dual turbine

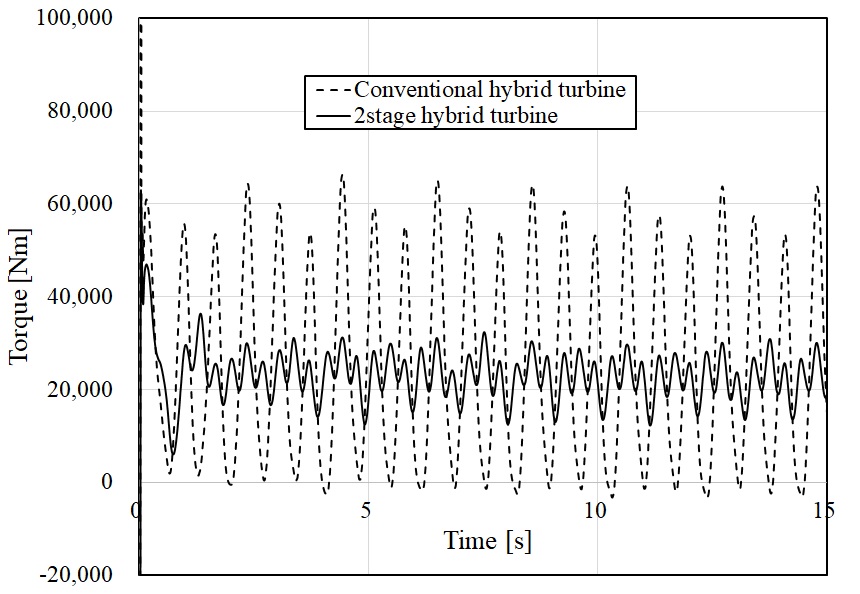
시간의 변화에 따라 회전하는 하이브리드 듀얼 터빈의 출력 값 변화를 Fig. 16에 나타내었다. 기존의 하이브리드 듀얼 터빈의 경우에는 토크 값의 변동 폭이 매우 크게 나타나며, 음의 값을 갖는 매우 낮은 토크 값의 구간이 있는 것도 확인된다. 그러나 2단 하이브리드 듀얼 터빈의 경우에는 전반적으로 토크 값이 약 20,000 Nm 부근에서 작은 변동 폭으로 변하는 것을 확인할 수 있다. 이러한 변동 폭이 작은 터빈 설계는 조류발전 터빈 지지구조물 및 발전기 시스템의 설계에도 영향을 주는 요소로서 매우 중요하게 평가된다. 최종적으로 2단 하이브리드 듀얼 터빈을 본 연구의 최종설계 형상으로서 도출하였다.

Fig. 16

Time history of torque of conventional and 2stage hybrid dual turbines at TSR=1.75

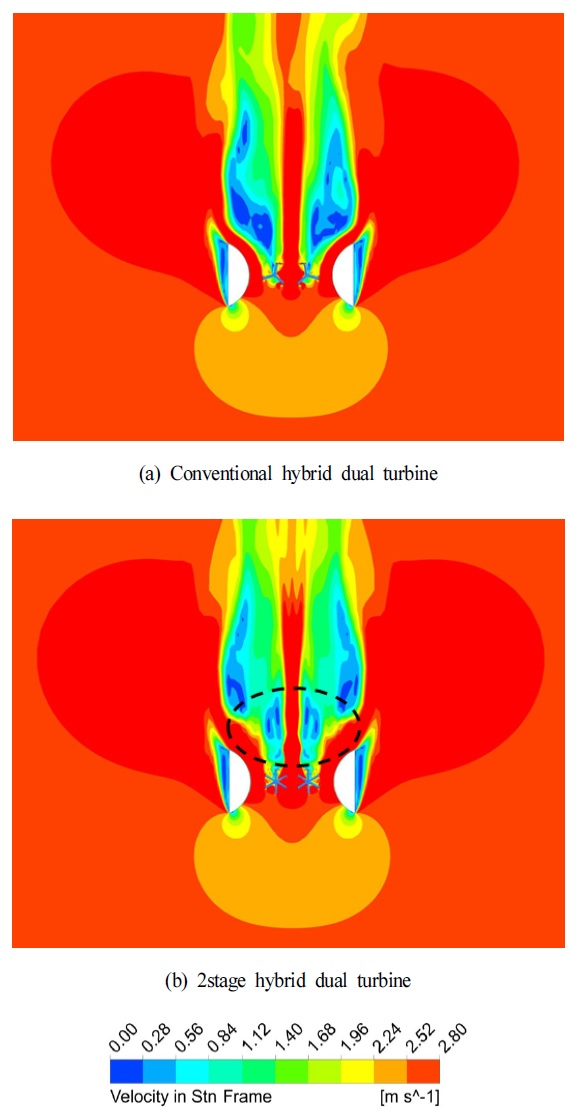
Fig. 17는 기존의 하이브리드 듀얼 터빈이 가장 낮은 음의 토크 값을 갖는 위치에서 터빈 주위의 속도 분포를 2단 하이브리드 듀얼 터빈의 것과 비교하여 보여준다. 기존의 하이브리드 터빈은 후류에 매우 복잡한 유동을 보이며 낮은 속도 영역이 넓게 분포하였다. 이것은 터빈이 음의 토크 값을 갖는 위치에서 터빈의 후류에 낮은 속도분포가 넓게 발생하는 것이며, 2단 하이브리드 터빈의 적용으로 인해 개선된 것을 Fig. 17(b)에서 확인할 수 있다. Fig. 15에 나타낸 것과 같이 기존 하이브리드 듀얼 터빈의 출력은 2단 하이브리드 듀얼 터빈의 출력보다 높은 경향을 보이지만, 터빈의 회전에 따른 토크의 변화를 고려하면 기존의 하이브리드 듀얼 터빈은 매우 작은 음의 토크 값을 나타내는 구간이 발생하지만 2단 하이브리드 듀얼 터빈에서는 크게 개선되어 전체적으로 토크의 변동 폭이 작은 것을 확인할 수 있었다.

Fig. 17

Velocity contour of conventional and 2stage hybrid dual turbines at TSR=1.75

2단 하이브리드 듀얼 터빈의 적용에 따른 터빈 내부의 유동 특성을 비교하기 위하여 Fig. 18에 터빈 내부에서 발생하는 저속도(0.2 m/s) 영역을 비교하여 나타내었다. Fig. 18(a)에서 보는 것과 같이 터빈의 회전에 따라 발생하는 와류가 터빈 내부에 길이 방향으로 길게 분포하는 것을 확인하였다. 이러한 터빈 내부에 발생하는 저속도 영역은 터빈의 성능을 저하시키는 요인으로 작용할 수 있으며, 터빈을 2단으로 설계함에 따라 저속도 영역이 상당히 줄어든다는 것을 Fig. 18(b)를 통해 확인할 수 있었다.

Fig. 18

Low velocity region(0.2 m/s) in conventional and 2stage hybrid dual turbines at TSR=1.75