OpenFOAM을 이용한 평판 팬 형상 막냉각 홀 하류에서의 막냉각 특성 연구

2.1 계산 환경 및 오픈폼 버전

본 연구는 KISTI에서 제공하는의 슈퍼컴퓨터 누리온(Nurion)을 이용하여 계산을 수행하였다. 누리온은 Knight Landing (이하 KNL)과 Skylake (이하 SKL) 시스템으로 이루어져 있으며, 이론성능 25.7 PFlops 규모로 고성능, 대용량의 계산환경을 제공하는 슈퍼컴퓨터이다.⁽¹²⁾ 누리온에서는 오픈폼을 비롯한 각종 소프트웨어를 제공하며 대용량 병렬연산 기능을 이용할 수 있어 이를 이용하여 해석을 수행했다.

오픈폼은 현재 여러 버전이 있으며, 사용자 인터페이스나 특정 해석에 적합한 기능을 추가하는 패치 등이 배포되어 있다. ESI Group과 CFD Direct Ltd.에서 개발 및 제공하는 버전이 주로 사용되고 있으며, foam-extend 버전의 경우 기존의 오픈폼에서 지원하지 않는 유체기계 인터페이스 등의 기능을 제공한다. foam-extend 버전의 경우 앞선 두 기관에서 제공하는 버전과는 호환이 잘 이뤄지지 않으며, 다른 버전에 비해 불안정적인 요소가 있어 사용 시 주의가 필요하다. 본 연구에서는 CFD Direct Ltd.에서 개발 및 제공하는 OpenFOAM v7을 사용하여 전산해석을 수행했다.

2.2 막냉각 홀 형상 및 해석 영역

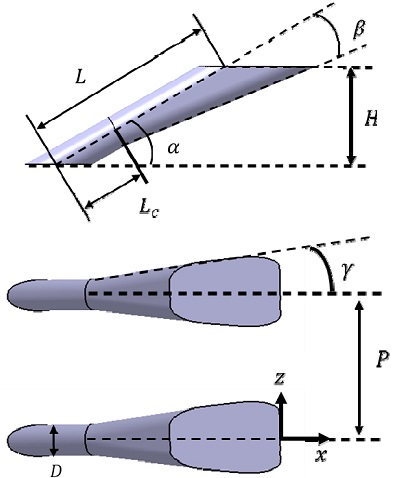
동일한 유동 조건이라도 막냉각 홀의 형상에 따라 막냉각 홀의 냉각성능은 큰 차이를 나타낸다. 막냉각 홀의 형상에 대한 연구는 다방면으로 진행되었으며,⁽¹³⁾ 그중 가장 대표적인 막냉각 홀 형상이 팬 형상 막냉각 홀이다. 팬 형상 막냉각 홀은 기존의 원형 홀에서 홀의 출구 부분의 형상을 확장하여 막냉각 성능을 향상시킨 형상으로 본 연구에서는 Kim 등⁽¹¹⁾이 실험한 팬 형상 막냉각 홀에 대해 수치해석을 수행했으며, 해당 홀의 형상 및 정보는 Table 1과 Fig. 1에 제시되어 있다.

Table 1

Geometry parameters of fan-shaped film cooling hole

Fig. 1

Configurations of fan-shaped film cooling hole

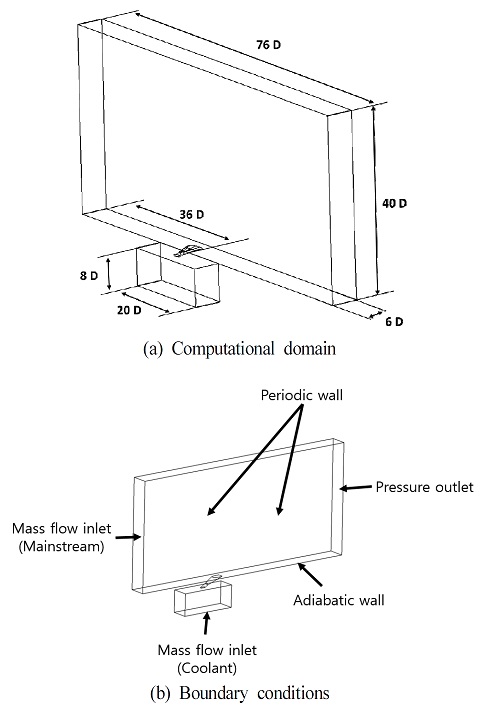
Fig. 2(a)는 수치해석의 영역을 나타냈으며 Fig. 2(b)는 해석영역의 경계조건을 나타내었다. 막냉각 홀의 직경(D)을 기준으로 주유동이 통과하는 영역의 길이는 76D이며, 높이는 40D, 폭은 6D로 해석영역을 정의하였다. 주유동과 냉각 유체가 유입되는 영역을 질량 유량 조건으로 정의했으며 평판에 해당하는 부분은 단열 벽면 조건으로 정의하였다.

Fig. 2

Computational domain and boundary conditions

주유동과 냉각 유체의 분사비(Blowing ratio, M)는 식(1)에 정의하였으며, 분사비에 따른 입구 경계조건을 Table 2에 나타내었다. 경계조건이 실제 가스터빈 막냉각 유동 상황과 차이가 있으나, 본 연구는 평판에서의 막냉각 홀에 따른 특성을 파악하기 위한 연구로 Kim 등⁽¹¹⁾의 상온에서의 실험조건을 기반으로 적용했다. 작동 유체는 상온의 공기로 Cengel과 Cimbala의 저서⁽¹⁴⁾의 물성치를 사용했으며, 난류 Prandtl 수는 Ansys Fluent Theory Guide⁽¹⁵⁾와 Kays⁽¹⁶⁾에 나타낸 값을 적용했다.

Table 2

Inlet boundary conditions for mainstream and coolant chamber

막냉각 홀에 대한 열유동해석을 진행함에 있어 적합한 공간차분법을 선정하기 위해 분사비가 1.0인 조건에서 서로 다른 공간차분법을 적용하여 해석을 수행하였으며, 선정된 공간차분법을 적용하여 분사비를 0.5, 1.0, 2.0으로 변경하여 해석을 진행하였다. Ansys CFX 또한 동일한 분사비 조건에 대해 해석을 진행하였고, 해석결과에 대해서 오픈폼의 결과와 비교분석하였다.

2.3 해석 기법

수치해석에 사용된 지배방정식은 3차원 압축성 Navier-Stokes 방정식을 사용했으며 수식은 다음과 같다.

Table 3에는 오픈폼과 Ansys CFX의 해석 조건을 정리하였다. RANS 해석을 기준으로 하여 오픈폼은 압축성 정상유동 해석에 사용되는 솔버인 rhoSimpleFoam을 사용했으며, Ansys CFX의 경우 Ansys CFX 19.0의 압축성 유동해석 솔버를 사용했다. 두 소프트웨어 모두 동일하게 난류 모델은 k-ω SST model⁽¹⁷⁾을 사용했으며, 난류항의 공간차분법은 1차 정확도를 갖는 차분법을 사용했다. 오픈폼에서는 다양한 공간차분법을 제공하고 있어 본 연구에서는 Ansys CFX와의 비교를 통해 적절한 공간차분법을 선정하기 위해 1차 정확도를 갖는 공간차분법인 Upwind와 Upwind 계열의 2차 정확도를 갖는 공간차분법인 linearUpwind, 그리고 중앙차분법을 이용한 2차 정확도를 갖는 공간차분법인 Linear와 linearUpwind를 결합한 LUST (Linear-Upwind Stabilised Transport)차분법을 사용하여 해석을 수행하였다. Upwind와 linearUpwind 차분법은 각각 식(5), (6)과 같이 정의되며, LUST와 Linear 차분법에 대한 정의는 식(7), (8)과 같다. 식(6)의 d_f는 격자의 중심과 인근 격자와의 접촉면에서의 중심점과의 거리이며, 식(8)의 ψ는 격자의 중심과 인근 격자와의 접촉면 사이의 거리와 두 격자의 중심점 사이의 거리의 비율을 뜻한다. Ansys CFX에서 사용된 공간차분법인 High Resolution은 2차 정확도를 갖은 공간차분법으로 식(9)에 정의하였다. High Resolution은 linearUpwind와 유사한 공간차분법으로 β∙(∇ϕ_P)∙d_f항의 β는 0에서 1사이의 값이며 Barth 등⁽¹⁸⁾에 기반한 경계 원칙에 의해 값이 결정된다.

where,

where, β∈[0,1]

Table 3

Numerical schemes of CFD

2.4 격자 선정

본 연구에서는 Ansys를 통해 격자를 생성했으며, .msh 파일 형태로 저장하였다. 저장된 파일을 오픈폼의 격자변환(Mesh conversion) 유틸리티인 fluent3DMeshToFoam를 통해 오픈폼의 해석에 적용할 격자 파일을 생성하였다.

막냉각 홀의 열유동해석에 있어 격자 의존성을 검증하기 위해 홀 내부와 주변부에서의 격자 크기를 변경해가며 격자를 생성하였다. 벽면격자의 수는 15개이며, 격자의 밀집도가 높은 부분(Fine Section)에서의 격자 크기는 직경(D) 대비 0.2∼0.09로 변경하며 5개의 격자계를 생성하였다. 생성한 격자계의 정보는 Table 4와 Fig. 3에 제시되어 있다.

Table 4

The number of computational meshes for mesh sensitivity test

Fig. 3

CFD mesh configurations (Table 3 - No. 4)

생성된 격자는 M=1.0의 조건에에서 2차 공간차분법인 linearUpwind를 이용한 해석을 수행하였으며, 각 해석결과의 면적 평균 단열 막냉각 효율을 비교하였다. 막냉각 홀의 단열 막냉각 효율을 정의하는 식(10)은 다음과 같다.

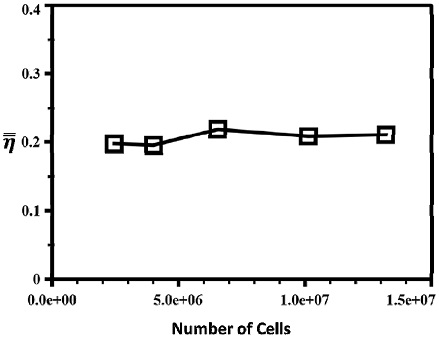
면적 평균 단열 막냉각 효율은 x/D=3에서 x/D=25 사이의 영역에서 평균된 값이며, 격자 수에 따른 면적 평균 단열 막냉각 효율값은 Fig. 4에 나타냈다. 격자 수가 1 천만개 이상인 경우, 면적 평균 막냉각 효율값은 격자 수가 증가함에도 유사한 값을 보여주어 홀 주변부가 직경(D)의 0.1배의 크기인 격자계(No. 4, 총 격자수 약 1,000만개)를 선정하여 이후 수치해석을 수행하였다.

Fig. 4

Area-averaged film cooling effectiveness from the mesh sensitivity test at M=1.0

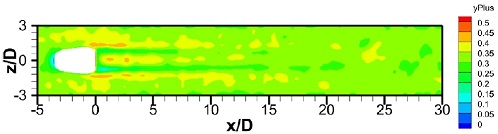
벽면에서의 열유동 해석을 위해서는 해석영역에 대해 전체적으로 y⁺값이 1 전후의 수치를 갖도록 격자계를 구성할 필요가 있다. Fig. 5는 격자 수렴성 검증에서 해석을 수행한 총 격자수가 1 천만개인 격자계에 대한 해석결과에서 단열 벽면의 y⁺값을 나타내었다. 해석결과에서 y⁺값이 1이하의 값을 충족하여 벽면의 열유동해석에 적합한 격자계임을 확인하였다.

Fig. 5

y+ value around the film cooling hole at M=1.0

3.1 공간차분법의 영향성

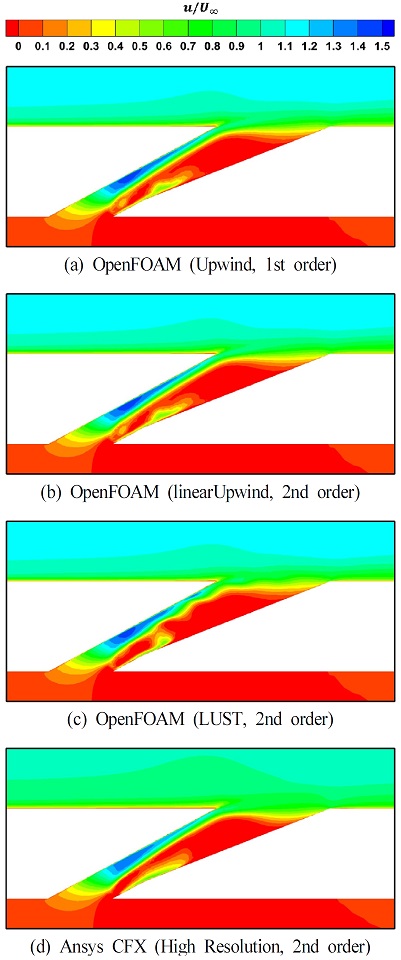
Fig. 6은 선정된 격자계에 대해 M=1.0 조건에서 오픈폼 해석 시 공간차분법에 따른 해석결과와 CFX의 해석결과의 단열 막냉각 효율 분포를 나타내고 있다. Fig. 6(a)는 오픈폼의 1차 공간차분법인 Upwind를 사용한 해석결과이다. Fig. 6(a)는 2차 정확도의 공간차분법을 사용하여 나타난 결과인 Fig. 6(b)와 (c), (d)에 비해 높은 효율의 영역이 길게 나타나는데, 이는 1차 정확도의 공간차분법이 2차 정확도의 공간차분법에 비해 소산율이 낮기에 나타나는 결과로 보인다.

Fig. 6

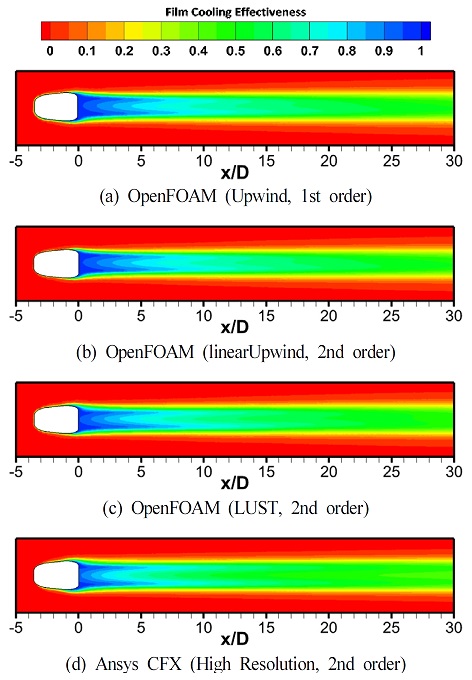
Contour plots of film cooling effectiveness from CFD results for various spatial discretization schemes

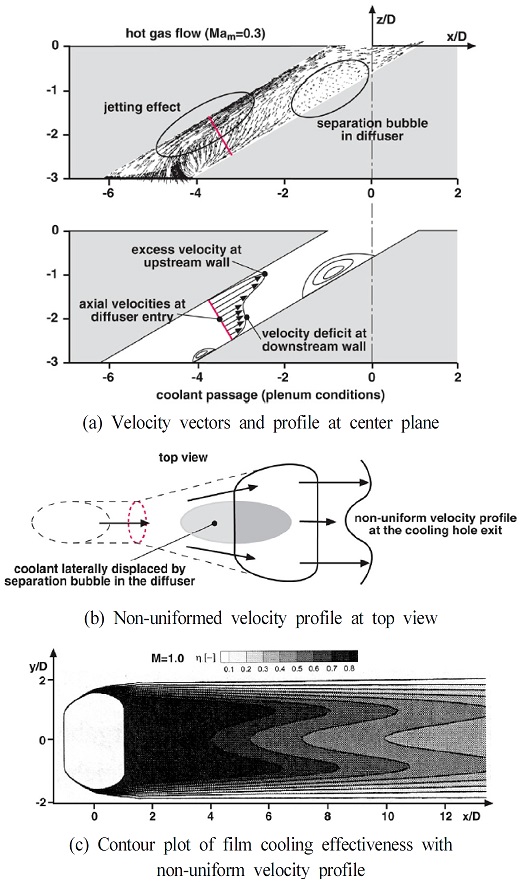
각 효율 분포의 패턴이 홀의 중심부가 낮고 홀 출구의 양끝단이 높은 경향을 보이는데, 이는 난류 모델에 k-ω SST model을 사용하여 팬 형상 막냉각홀에 대한 해석을 수행할 시에 생기는 결과이다. Saumweber 등⁽¹⁹⁾의 연구에서는 막냉각 홀의 해석에서 난류 모델을 k-ω SST model로 사용하는 경우, Fig. 7(a)와 같이 팬 형상의 막냉각 홀의 내부에서 유동의 가속 영역과 홀의 확장부에서의 박리로 인한 감속에 의해 불균일한 속도장이 생성됨을 보였다. 불균일한 속도장으로 인해 단열 벽면에는 Fig. 7(b)와 같은 홀의 양끝단에서 높고 중심에서 낮은 속도장이 생성된다. 벽면에서의 불균일한 속도장은 Fig. 7(c)와 같은 막냉각 효율 분포를 만들며, Fig. 6의 해석결과 또한 유사한 패턴의 분포를 보여준다.

Fig. 7

Schematic of characteristic flow phenomenon in fan-shaped film cooling holes(19)

Fig. 8(a)와 (b)는 각각 해석결과의 x/D=3과 x/D=25에서의 횡방향 막냉각 효율 분포를 나타내었다. 1차 정확도의 공간차분법을 사용한 오픈폼의 Upwind는 단열 막냉각 효율의 값이 다른 해석결과에 비해 전체적으로 높은 값을 보여준다. Fig. 6에서의 막냉각 효율 분포에서와 같이 Upwind는 다른 공간차분법에 비해 소산율이 낮아 냉각유체가 하류까지 잘 유지되어 전체적으로 높은 막냉각 효율값을 보여준다.

Fig. 8

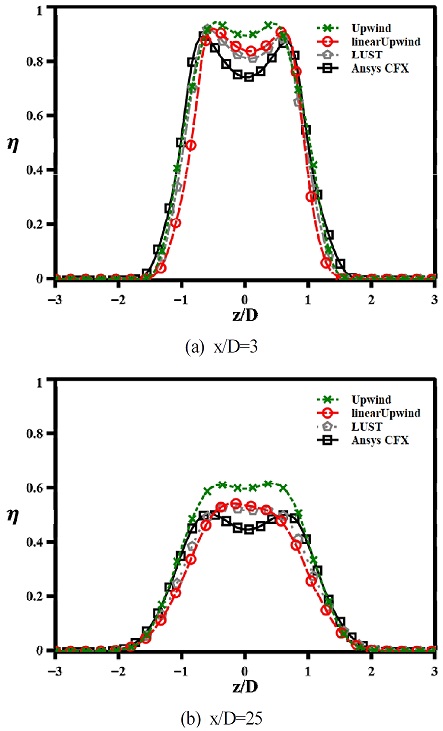
Lateral distributions of film cooling effectiveness for various spatial discretization schemes at M=1.0

Fig. 8(a)에서 홀 출구 부분의 막냉각 효율 분포를 보면 전체적으로 중심부가 낮게 나오며 CFX의 해석결과가 가장 낮은 값을 보여준다. 하류에서의 막냉각 효율 분포를 보여주는 Fig. 8(b)에서는 CFX의 해석결과는 Fig. 8(a)와 같이 홀의 출구와 같은 형태를 유지하지만, 오픈폼의 해석결과는 상류에서의 형태와는 다른 분포를 보여준다. CFX에서 사용된 공간차분법인 High Resolution은 2차 정확도를 갖고 있으나, 다른 2차 차분법과는 달리 추가로 주변 유동과의 상호작용이 식(6)의 β(0≤β≤1)에 영향을 받는다. β값이 1인 오픈폼의 linearUpwind와 LUST는 High Resolution에 비해 해석과정에서 주변 유동과의 상호작용이 더 크게 예측되고, 그로 인해 상류에서 생성된 CRVP(Counter Rotating Vortex Pairing)가 소산되어 Fig. 8(b)와 같은 중심부의 효율값이 높은 결과를 보여준다.

Fig. 9는 각 해석결과에서 횡방향으로 평균한 단열 막냉각 효율값을 비교하고 있다. 오픈폼에서 Upwind를 사용한 결과는 다른 2차 정확도의 공간차분법을 사용한 결과에 비해 전체적으로 높은 값을 보이며, 2차 정확도의 공간차분법을 사용한 오픈폼 해석결과는 CFX의 해석결과와 유사한 값을 보이는 것을 확인할 수 있다.

Fig. 9

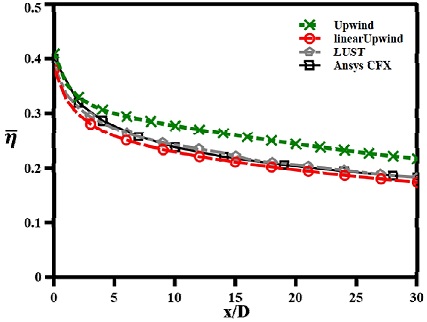
Comparison of laterally averaged film cooling effectiveness for various spatial discretization schemes at M=1.0

Fig. 10에는 홀의 중심부를 기준으로 나눈 단면에서의 주유동의 유속대비 무차원 속도장을 나타내었다. Fig. 10(a), (b), (d)는 거의 유사한 결과를 보여주나 LUST를 이용한 해석결과인 Fig. 10(c)는 홀 내부에서 가속영역이 물결치는 패턴을 확인할 수 있다. 이는 LUST의 특징으로 서로 유속이 다른 유체 사이의 Shear layer 영역에서 LUST에 사용된 중앙차분법인 Linear에 의해 부자연스러운 진동 패턴이 발생한다.⁽²⁰⁾ 또한, LUST의 경우 같은 2차 정확도의 차분법인 linearUpwind와 막냉각 효율에 대한 해석결과는 유사하지만 수치해석에 있어 동일 조건에서 CPU time이 약 53%가 더 소모된다.⁽²¹⁾ 위와 같은 특징으로 리소스를 적게 소모하며 해석결과 또한 유사한 linearUpwind를 공간차분법으로 선정하여 이후 분사비 별 해석결과를 CFX와 비교하였다.

Fig. 10

Non-dimensional velocity contour plots on the center plane for various spatial discretization schemes at M=1.0

3.2 분사비 별 해석결과 비교

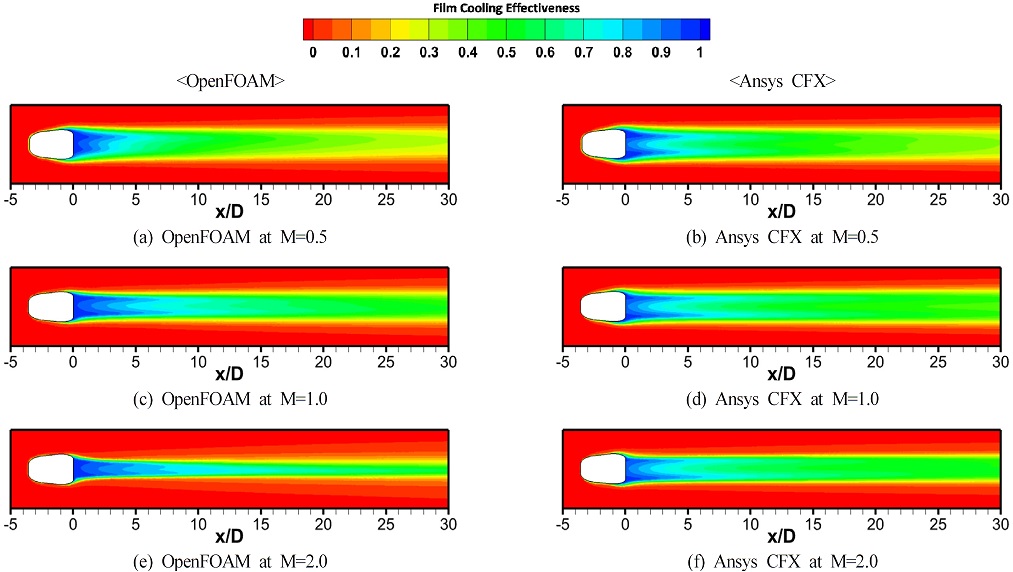
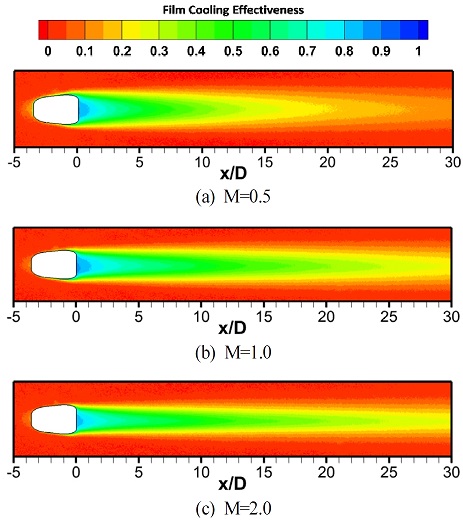
Table 2에서의 각 분사비 별 조건을 동일 격자계(No.4)에 적용 하여 오픈폼과 Ansys CFX을 이용하여 해석을 진행하였고, 수치해석의 결과로부터 계산한 단열 막냉각 효율 분포를 Fig. 11에 나타냈다. 전체적으로 분사비가 증가하면서 홀 출구 부분의 높은 효율값의 영역이 하류방향으로 더 길게 확장되는 것을 볼 수 있다.

Fig. 11

Comparison of film cooling effectiveness for various blowing ratios between OpenFOAM and Ansys CFX

Fig. 11(a)와 (b)는 M=0.5 조건에서의 단열 막냉각 효율 분포를 보여준다. 낮은 분사비 조건에서의 냉각유체는 주유동에 비해 운동량이 낮아 높은 분사비 조건에 비해 주유동과의 상호작용이 활발하다. CFX에 비해 오픈폼에 사용한 공간차분법이 주유동의 간섭을 더 많이 받는 특징이 있으며, 낮은 분사비 조건으로 인해 주유동과 상호작용 또한 활발하기 때문에 CFX에 비해 오픈폼의 막냉각 효율이 동일 위치에서 더 낮은 값을 보인다.

Fig. 11(e)와 11(f)와 같은 M=2.0 조건에서의 단열 막냉각 효율을 M=1.0 조건의 결과인 Fig. 11(c), 11(d)와 비교할 때, 효율 분포의 횡방향 폭이 가늘어지는것을 볼 수 있다. 분사비가 증가하면서 막냉각 홀로부터 분사되는 냉각유체가 단열 벽면을 보호하는 것이 아닌 표면으로부터의 이탈하는 현상이 생긴다. 이러한 냉각유체의 벽면으로부터 이탈은 단열 막냉각 효율의 횡방향 분포폭을 점차 좁아지게 만든다. 두 해석결과 또한 단열 막냉각 효율 분포의 폭이 좁아지는 결과를 보여주나 오픈폼의 막냉각 효율 분포의 횡방향 폭 감소는 CFX에 비해 크게 나타난다. 오픈폼은 CFX에 비해 앞서 언급한 linearUpwind와 High Resolution의 차이로 주변 유동과의 간섭이 더 크게 일어난다. 높은 분사비 조건에서 발생하는 냉각유체의 벽면으로부터 이탈은 주유동과의 상호작용을 더 크게 계산하는 오픈폼의 경우 CFX에 비해 비교적 높은 위치에 CRVP가 존재하게 된다. 높은 위치에 있는 오픈폼의 CRVP는 벽면의 영향을 덜 받게 되어 더 많은 양의 주유동을 홀의 중심방향으로 끌어들인다. 와류와 주유동의 영향으로 인해 분사된 냉각유체가 벽면과 접촉하는 면적을 좁혀져 막냉각 효율의 횡방향 분포가 CFX보다 오픈폼의 해석 결과가 더 크게 감소한다.

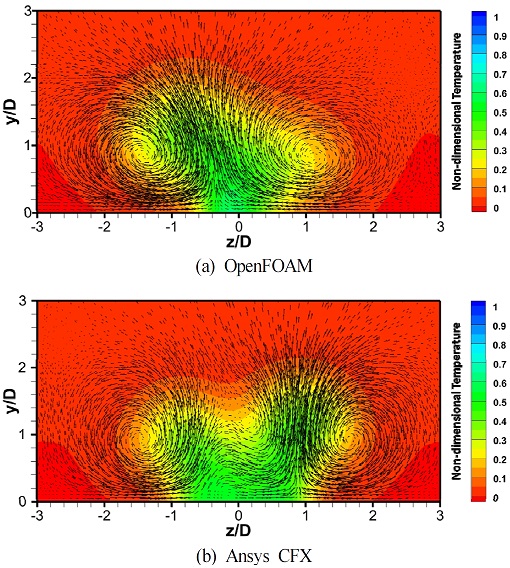
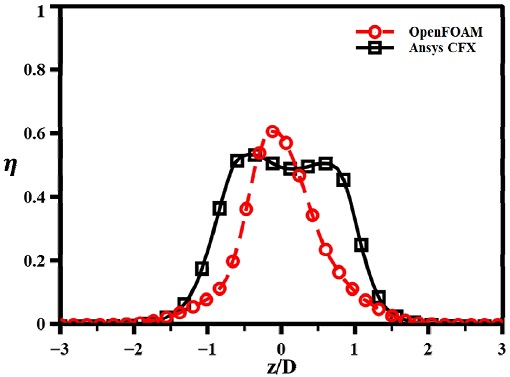
냉각유체의 단열 벽면으로부터의 이탈과 차분법의 차이는 막냉각 효율분포의 폭뿐만 아니라 하류에서의 횡방향 분포 패턴에도 영향을 미친다. Fig. 12은 M=2.0에서 x/D=25 지점에 위치한 단면에서의 속도장과 무차원 온도장을 나타내었고, Fig. 13에는 x/D=25에서의 횡방향 단열 막냉각 효율 분포를 나타냈다. Fig. 12(b)의 CFX 결과는 두 개의 와류가 z/D=0을 기준으로 대칭되는 위치에 있으나, 오픈폼의 결과인 Fig. 12(a)에서는 두 개의 와류가 z/D=0 부근에서 결합하는 것을 볼 수 있다. 오픈폼의 해석결과는 CFX의 결과보다 주변 유동간의 상호간섭이 크다는 점으로 인해 주유동이 와류로 인해 z/D=0 방향으로 이동하며, z/D=0 방향으로 흘러들어온 유동은 y/D 방향으로 상승하여 와류가 z/D=0 부근에서 접촉하는 형태를 보인다. 이런 와류 패턴의 변화로 인해 Fig. 13과 같은 막냉각 효율의 횡방향 분포 패턴이 변화한다는 점을 알고 차후 Ansys CFX를 대체하여 오픈폼을 사용하여 수치해석을 수행 시 위와 같은 점을 고려하며 사용 및 분석해야 한다.

Fig. 12

Velocity vectors and non-dimensional temperature contour plots at x/D=25

Fig. 13

Lateral distributions of film cooling effectiveness between OpenFOAM and Ansys CFX at x/D=25

3.3 실험 및 수치해석결과 비교

Fig. 14에는 Kim 등⁽¹¹⁾이 수행한 압력감응페인트를 이용한 막냉각 효율 측정 결과를 분사비별로 나타냈다. 측정된 결과에서의 막냉각 효율 패턴은 오픈폼과 CFX의 해석 결과와는 다른 형상이 나타났다. 이는 난류모델로 사용된 k-ω SST model로 인한 결과이며, 전체적으로 동일 위치에서 해석을 통한 결과값이 측정값에 비해 높은 값을 보여준다.

Fig. 14

Contour plots of film cooling effectiveness measured by experiments for various blowing ratios(11)

Fig. 15에는 Kim 등의 측정결과와 해석결과의 횡방향 평균 단열 막냉각 효율을 비교하였다. Fig. 15(a), (b)에서는 오픈폼과 CFX의 해석결과는 Kim 등의 실험결과에 비해 높은 횡방향 평균 효율값을 보인다. 앞선 단열 막냉각 효율 분포의 비교에서 분포의 패턴 차이와 더불어 난류모델을 통한 해석의 경우, 와류를 비롯한 유동의 섭동을 직접 계산이 아닌 모사를 한다는 점에서 차이가 있으며, 해석의 결과가 전체적으로 높은 효율값을 나타내어 평균시 해석의 결과가 더 높은 값을 보여준다.

Fig. 15

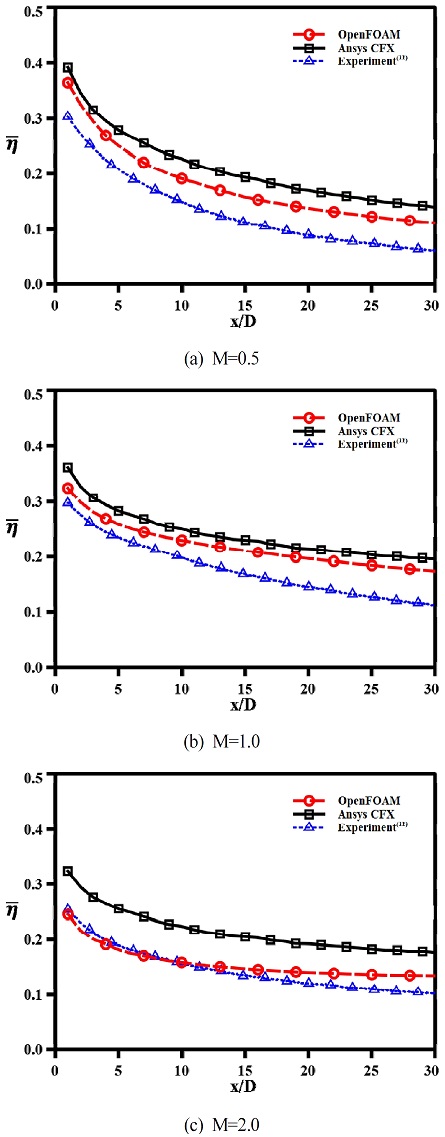
Comparison of laterally averaged film cooling effectiveness between CFD results and experiment results(11)

Fig. 15 (c)에서는 CFX의 경우, 앞선 Fig. 15(a), (b)와 같이 실험결과보다 높은 값을 보이나 오픈폼의 결과는 측정결과와 유사한 값을 보인다. M=2.0조건에서 오픈폼 해석결과는 CFX의 결과와 같은 난류모델에 영향을 받은 효율 분포의 패턴을 보인다. 그러나 오픈폼의 해석결과에서 막냉각 효율의 분포가 횡방향으로 폭이 협소하여, 평균을 계산시 실험결과와 유사하게 계산된 것을 확인할 수 있다.

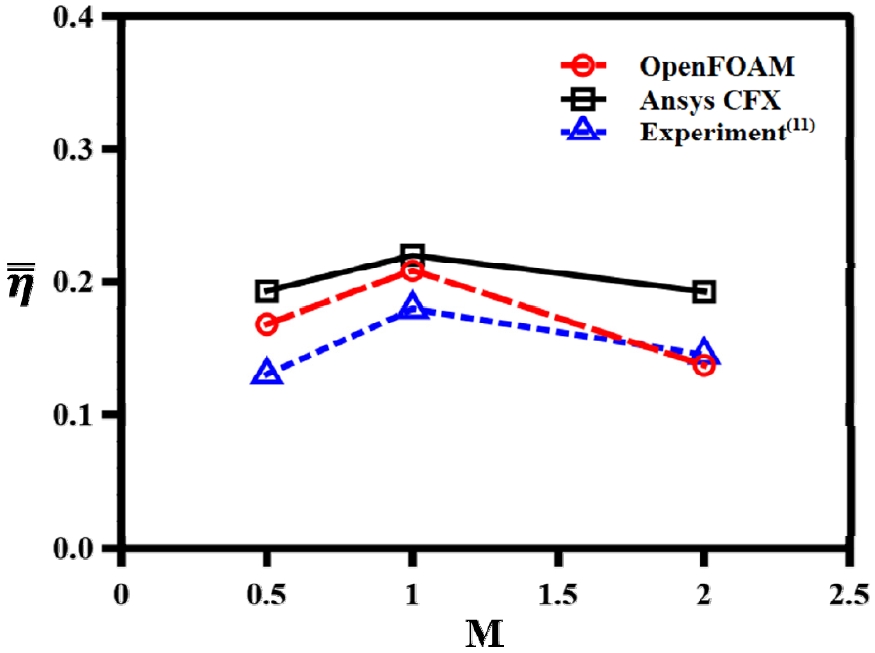
이러한 결과는 면적평균된 막냉각 효율값에서도 확인할 수 있다. Fig. 16은 분사비에 따른 x/D=3에서 x/D=25 범위의 막냉각 효율값의 평균값을 나타냈다. 측정결과와 CFX의 값은 분사비에 따른 변화의 패턴이 비슷한 양상을 보이는 반면, 오픈폼의 결과는 M=2.0에서 막냉각 효율분포 폭의 감소로 인해 급격한 저하가 나타난다. 급격한 저하로 인해 오픈폼의 값이 측정값과 유사한 결과를 보이며, 횡방향 평균을 비롯하여 면적평균시 M=2.0 조건에서 측정값과 비슷한 결과를 나타낸다.

Fig. 16

Comparison of area-averaged film cooling effectiveness between CFD and experiment results