비정렬 유입 유동을 가지는 고 레이놀즈 수 조건 하 유동 균일도 향상을 위한 벨마우스의 형상 최적화

1. 서 론

가스터빈 엔진은 그 구조적 특성상 주유동이 연소실에서 빠져나온 직후의 온도인 터빈입구온도(turbine inlet temperature, TIT)가 높아져야 효율을 높일 수 있다.⁽¹⁾ 이에 따라 근래의 가스터빈은 과거와 비견하여 눈부신 발전을 이루었으나 부차적으로 높은 온도의 유동을 견디는 내구성능을 요구하게 되었다. 엔진의 내구도를 향상시키기 위해 냉각성능에 대한 다양한 연구가 수행되었다. Gunther 등⁽²⁾은 가스터빈 제트엔진에 4가지 종류의 와류 감소기(vortex reducer)를 적용하여 각속도에 따른 압력손실 측정 실험을 수행했다. 링과 노즐 등 간단한 구조를 통해 난류를 제거하여 냉각유동의 압력손실을 감소시켜 기존 구조와 동일한 성능을 확인하였다. Mucci 등⁽³⁾은 회전하는 가스터빈 압축기 디스크 사이의 공간에 6가지 와류 감소기를 통해 공동(cavity)을 따라 분배되는 내부 냉각유동의 압력강하 감소와 질량유량 증가를 연구하였다. Da soghe 등⁽⁴⁾은 In-house 1-D Network를 사용하여 충돌제트가 가스터빈 케이싱으로 분사되는 Active clearance control (ACC) 시스템에서 노즐 직경, 압력비와 매니폴드 단면을 바꾸어가며 냉각공기를 분사하는 부위의 대류 열전달 계수 프로파일에 대한 영향을 수치적으로 분석했다. Goldstein 등⁽⁵⁾은 교차 유동 여부에 따라 충돌냉각 제트의 냉각판 도달거리를 달리하며 열전달 계수를 실험했다. 먼 거리의 교차 유동은 열전달 계수의 극댓값을 없앴으나 가까운 경우 극댓값을 증가시켰고 교차 유동이 없을 때 평균 열전달 상관식을 제시했다.

가스터빈 냉각용 공기는 보통 저압 터빈부 또는 압축기에서 추출되어 사용될 수 있다. 주로 압축기에서 추출된 냉각공기(bleed air)는 유량이 많을수록, 압력이 높을수록 비용 증가로 연결된다. 효율을 높이기 위해서는 동력의 손실을 야기하지 않으면서도 엔진 내부 요소를 냉각할 만큼의 양의 공기가 충분히 배분되어야 한다.^(6-7)

유동의 분배에 관한 산업적 연구는 중요도가 높기 때문에 다양한 분야에서 연구되고 있다. Bajura 등⁽⁸⁾은 매니폴드를 4가지 형상별로 바꾸어 가며 유동 분배를 확인하기 위해 2 - equation 모델로 압력과 질량유량 관점에서 수치적, 실험적으로 연구했다. 최종웅 등⁽⁹⁾은 물 흡입 펌프 시스템에서 Anti-submerged Vortex Device (AVD)의 다양한 형상에 대한 수치적, 실험적으로 연구했다. 이재호 등⁽¹⁰⁾은 단일 입구이며 이중 출구인 덕트 시스템에서 유동의 분배에 블록구조물의 위치, 설치여부와 세장비 등의 조합에 따른 시스템 성능을 평가했다.

유동 분배 구조를 가진 시스템은 형상 구조 변화를 통해 유동 균일도(uniformity)를 개선하여 냉각 성능을 향상 시킬 수 있다. 이는 유동이 벨마우스를 지나 관 내 균일한 분포로 통과하면 압력 손실을 감소시킬 수 있다. 특정 위치의 균일 유동을 위한 목적으로 연구된 문헌으로 Simon Martinez 등⁽¹¹⁾은 자동차 배기 매니폴드의 유동 균일도를 향상시키기 위해 전산유체역학을 수행하였다. 차량의 촉매변환기 직전의 유동을 균일하게 공급하기위해 주물 매니폴드, 4-2-1 분지관, L자 형의 3가지 형상에 따른 전압력 손실과 유동 균일도 변화를 파악했다. 최창규 등⁽¹²⁾은 6가지 형상의 돌출부를 포함하는 분배기에서 유동 균일도의 변화를 해석했다. 각 형상에서 속도와 압력분포를 국소 유속으로 정의한 유동 불균일도로 살펴보았다. 가장 유동 불균일도가 낮은 형상은 물방울 형태의 돌출부를 포함하는 분배기임을 확인하였다.

본 논문에서는 가스터빈의 균일한 냉각유동분배를 통한 효율 향상을 위해 터빈 케이싱 벨마우스의 형상 최적화를 수행했다. 유다미 등⁽¹³⁾은 임펠러의 풍량을 높이기 위해 블레이드 개수, 각도, 길이를 변수로 하여 형상최적화를 진행하였고 최적안의 실험 및 CFD 결과를 비교하였다. 형상 최적화를 벨마우스에 적용한 사례로 김종수 등⁽¹⁴⁾은 유량조건을 만족하면서 정압이 최적화된 원심팬 블레이드를 설계하기 위하여 CFD와 형상 최적화를 진행했다. 다수의 설계변수를 정의하고 특성별로 분류하는 단계별 최적화 기법을 사용했다. 도출한 최종 최적형상을 실험결과와 비교 검증했다. Sevinc⁽¹⁵⁾는 CFD와 유전자 알고리즘(genetic algorithm)에 기반한 최적화법으로 엔진 시험시설 입구용 벨마우스를 설계했다. 변수는 벨마우스 높이, 타원길이, 직선부 길이, 호 반경, 말단부 각도가 선정되었다. 목적함수로는 최저 전압력 손실계수와 최대 축 방향 속도 등이 선택되었고 최종형상을 제작하여 실험하여 성능을 평가했다.

현재 벨마우스 최적화의 연구수준은 설계용 가이드라인과 연구결과가 여럿 존재하지만 유동 방향과 입구 방향이 동일 한 연구가 주를 이루고 있으며, 유동 방향과 입구 방향이 다른 경우 냉각 성능에 미치는 영향에 대한 연구가 필요하다. 또한, 극한환경과 제한된 설계 공간을 가진 가스터빈 이차유로 영역의 벨마우스 설계 연구는 부족한 실정이다.

따라서 본 논문에서는 베인으로 외부 냉각유동을 공급하는 가스터빈 케이싱 내 벨마우스 설계를 수치 기법을 이용하여 연구하였다. 계산 시간을 줄이기 위해 실제 가스터빈 형상을 단순화한 모델로 수정하였고, 벨마우스 내부 반경, 외부 반경, 높이, 각도의 4가지 형상 변수를 조합하여 해석하였다. 81가지 결과로 그린 파레토 프론트(Pareto front)에서 선택한 개선형상을 기준형상과 비교하고, 성능을 추가 개선하기 위해 압력강하의 최소화와 유동 균일도의 최대화를 목적함수로 정하여 형상최적화를 수행했다. 반응표면을 도출하고 설계변수에 따른 변화를 설명하였으며, 등고선 겹치기(overlaid plot)법을 통해 최종 최적형상을 제시한다.

2. 수치해석 방법

2.1 지배방정식 및 경계조건

본 연구의 3차원 정상상태, 압축성 조건에서 연속 방정식, 운동량 보존 방정식, 에너지 보존 방정식은 다음과 같다.

$\[ \frac{\partial }{\partial x_i}\left(\rho u_i\right)=0 \]$

(1)

$\[ \frac{\partial }{\partial x_j}\left(\rho u_i{u}_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\rho \overline{{u^{\text{'}}}_i{u^{\text{'}}}_j}\right] \]$

(2)

$\[ \frac{\partial }{\partial x_j}\left(\rho c_p{u}_{j}T\right)=-\frac{\partial }{\partial x_j}\left(-k\frac{\partial T}{\partial x_j}+\rho c_p\overline{{u^{\text{'}}}_{j}T}\right) \]$

(3)

시간 평균 된 식 (1)-(3)은 정상상태 난류 유동 해석에 적용하는 Reynolds-Averaged Navier-Stokes (RANS) 방정식이다. 여기서 u_i는 i-방향 속도 성분, u_j는 j-방향 속도 성분, p는 정압, ρ는 밀도, μ는 점성 계수, c_p는 정압비열, k는 열전도도, T는 온도를 의미한다. 식 (2)에서 $$ \rho \overline{{u^{\text{'}}}_i{u^{\text{'}}}_j}$$항은 Reynolds 응력항이다.

본 연구에는 무차원화된 물리량을 사용하였다. 무차원화의 기준이 되는 값들을 Table 1에 나타내었다. 아래 식 (4)-(5)에 온도와 압력을 무차원화 하기 위한 식을 나타냈다.

$\[ {\theta }^{\text{*}}=\frac{T-T_{in}}{T_{TIT}-T_{in}} \]$

(4)

$\[ C_p=\frac{P-P_{vane0}}{\frac{1}{2}{\rho }_{vane0}{V}_{vane0}^2} \]$

(5)

Table 1

Reference values for nondimensionalization

위 Table 1에서 R_in0, R_out0, H₀, M_FR0 는 순서대로 기준형상의 내부 반경, 외부 반경, 높이, 질량유량을, T_TIT, T_in, ΔP₀, P_vane0 는 터빈입구 온도, 유입유동 온도, 베인 압력강하, 베인 압력을, γ₀, ρ_vane0, V_vane0, V_in 은 유동 균일도, 베인 출구유동밀도, 베인 출구유동 속도, 입구유동 속도를 나타낸다. 식 (4)의 θ^*는 무차원 온도, T는 국소 온도, 식 (5)의 C_p는 압력계수, P는 국소 정압을 의미한다.

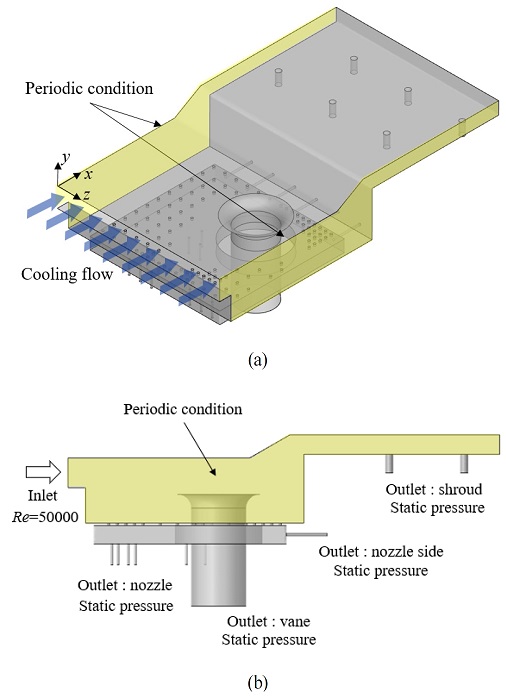
Fig. 1(a)는 본 연구에서 해석한 3차원 계산영역이다. 입구로 들어온 냉각공기는 베인, 쉬라우드, 주유로 등 각 출구로 빠져나간다.

Fig. 1

Computational domain of baseline (a) ISO view, (b) Side view

Fig. 1(b)와 Table 2은 측면에서 본 계산 영역 및 경계조건을 나타낸다. 계산 시간을 줄이기 위해 케이싱 모델의 좌우 벽면에 주기조건(periodic condition)을 적용했다. 벽에는 단열조건을 부여하였고 입구 유동의 온도는 700K를, 입구 Reynolds 수는 5×10⁴을, 출구 조건은 각 출구별 static pressure outlet 조건을 부여하였다. 입구 Reynolds 수는 아래 식 (6)-(7)로 정의된다.

$\[ {Re}_{in}=\frac{\rho V_{in}{D}_h}{\mu } \]$

(6)

$\[ D_h=\frac{4A}{P}=\frac{4\left(w_{in}\times h_{in}\right)}{2w_{in}}=2h_{in} \]$

(7)

위 식의 V_in은 입구유동 속도, D_h는 수력직경, w_in는 입구 폭, 그리고 h_in는 입구높이를 의미한다.

Table 2

Boundary condition used in CFD

전산해석을 위해 pressure-based solver로 SIMPLE 알고리즘을 사용하였고, 지배방정식 이산화를 위해 2차원 풍상 차분법(second-order upwind difference scheme)을 선택했다. 정압비열, 열전도도는 Kuldeep 등⁽¹⁶⁾의 선행연구에서 제시한 방정식을 참고하였다. 입구 밀도는 이상기체 상태방정식을 적용한 10.243 kg/m³로 계산했으며, 점도는 식 (8)을 사용하여⁽¹⁶⁾ 3.51×10^-5 Pa⋅s를 부여했다.

$\[ \begin{array}{c}\mu =\left(1.7020\times {10}^{-14}\right)T^3-\left(4.0405\times {10}^{-11}\right)T^2\hfill \\ +\left(6.8539\times {10}^{-8}\right)T+1.0616\times {10}^{-6}\hfill \end{array} \]$

(8)

2.2 검증 및 격자 의존성 검사

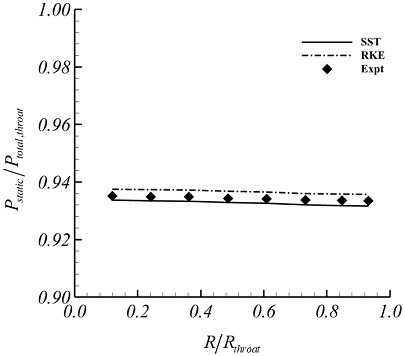
엔진 시험 시설(engine testing facility, ETF)에서 벨마우스 내부 위치별 무차원 정압 분포를 확인한 Beale 등⁽¹⁷⁾의 선행문헌을 기반하여 본 연구의 수치 해석 기법을 검증하였다. 계산에는 상용 소프트웨어 ANSYS Fluent 2019 R2를 사용했다. Fig. 2는 압력 및 난류 모델에 대한 선행 문헌과 본 연구의 해석 기법 결과 비교를 나타낸다. Realizable k-ε모델은 0.26%차이를, SST k-ω모델은 0.16%차이를 보였으며 본 연구에서는 SST k-ω모델을 차용했다.

Fig. 2

Validation result

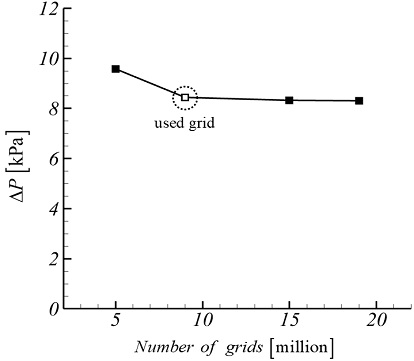
Fig. 3은 베인 압력강하를 격자수에 따라 그래프로 나타낸 격자 의존성 검사 결과이다. 해석 영역의 격자 수는 0.5, 0.9, 1.5, 1.9×10⁷개의 4가지 경우의 계산 결과를 비교하였다. 계산 시간 및 정확도를 고려하여 오차가 1.53%를 가지는 0.9×10⁷개의 격자를 선정하였다.

Fig. 3

Grid dependency test result

3. 결과 및 토의

3.1 최적화 조건

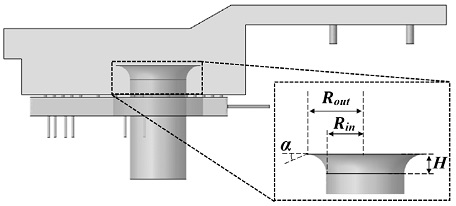
Fig. 4는 본 연구에서 사용된 벨 마우스의 형상을 나타내며, 벨마우스의 내부 반경, 외부 반경, 높이 그리고 각도 (순서대로 R_in, R_out, H, α)를 설계변수로 선정하였다. 각도를 제외한 3개 변수는 기준형상 대비 ±10%로, 각도는 0°, 5°, 10°로 구분하였다. Table 3은 전술한 변수들을 나타내며, 변수별 치수 비를 조합하여 81가지 완전요인배치법(full factorial case study)으로 전산해석을 진행하였다.

Fig. 4

Design variables in baseline domain

Table 3

Three levels of design variables for case study

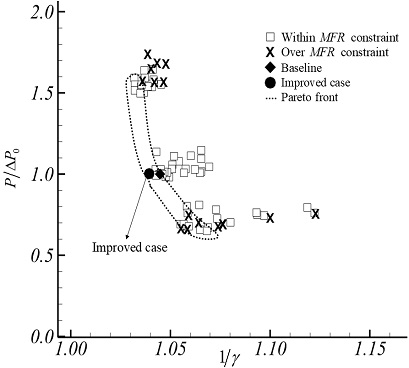
Fig. 5에 81개 조합으로 압력강하와 유동 균일도를 축으로 하는 기존 질량유량의 ±1%를 초과하지 않는 파레토 프론트(Pareto front)를 나타냈다. 유동 균일도는 아래 식 (9)와 같이 정의한다.⁽¹⁸⁾

$\[ \gamma =1-\left(\frac{1}{2}\sum _{i=1}^n\frac{\left|v_i-v_{mean}\right|A_i}{v_{mean}A}\right) \]$

(9)

Fig. 5

Pareto front from 81 cases

식 (9)의 v_i는 y-방향 속도, A_i는 국소면적, v_mean은 y-방향 평균 속도, A는 전체면적을 나타낸다.

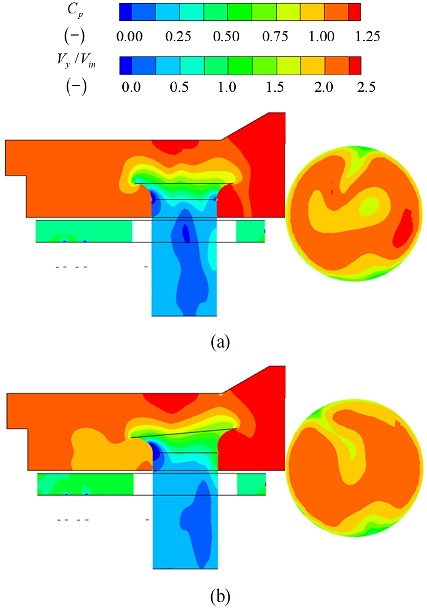
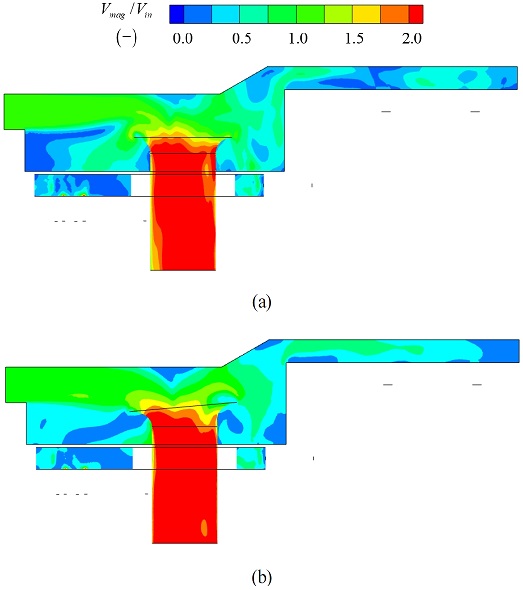
파레토 프론트 내 벨마우스의 외부 반경이 10% 증가하고 각도는 5°일 때, 기존 대비 유동 균일도가 증가하였다. Fig. 6-7은 기준 및 개선 모델에 대한 압력 계수, 유동균일도, 및 속도 분포도를 나타낸다.

Fig. 6

Compared pressure contour and uniformity distribution: (a) Baseline, (b) Improved case

Fig. 7

Compared velocity magnitude contour: (a) Baseline, (b) Improved case

Fig. 6에 나타나있듯이, 외부 반경 및 각도가 증가함에 따라 입구 유동에서 관 내로 유입되는 유량은 상승하기 때문에 개선 모델의 벨마우스 주위의 압력 계수는 감소하고 관 내 압력 분포는 기존 대비 균일하였다. 따라서 Fig. 6(b)의 유동 균일도에서 관 중심부의 속도 편차와 Fig. 7(b)의 관 내 속도 분포는 전술한 압력 분포로 인해 기존 대비 향상되었다.

Table 4는 기준 및 개선 형상의 설계 변수와 전산해석 결과 비교를 나타낸다. 외부 반경이 커짐에 따라 벨마우스 전단부에서 기존 대비 저압 영역의 분포가 증가하여 압력 강하값은 기준형상과 동일하였다. 하지만 유동 균일도는 유입되는 유량이 증가하여 균일해진 속도 분포로 인해 증가하였다.

Table 4

Design variables and objective functions for best cases in 81 case study

3.2 최적화 문제 정의

선정된 개선형상은 유동 균일도는 향상되었지만 압력강하 값은 기준형상 대비 동일수준을 유지하였다. 두 목적함수를 다 향상시키기 위해 형상 최적화를 진행하였다. 무차원화된 수식으로 표현한 본 연구의 최적화 목표는 아래 식 (10)과 같다.

$\[ Minimize \Delta P \text{and} 1/\gamma =f\left(R_{in}, R_{out}, H, \alpha \right) \]$

(10)

최대 유동 균일도와 최소 압력강하 결과로부터 기준형상의 목적함수 사이로 구속조건의 범위를 지정했다. 질량유량은 기준형상의 ±1% 조건으로 부여했다. 아래 식 (11)-(13)은 전산해석 결과로부터 선형회귀법으로 구한 유동 균일도, 압력강하, 질량유량의 관계식이다. 설계변수(Rin, Rout, H, α)를 순서대로 A, B, C, D로 간단히 표기했으며 모든 상관식의 결정계수는 0.92 이상이다. Table 5는 관계식별 계수를 나타낸다.

$\[ \begin{array}{c}Uniformity\hfill \\ \gamma =c_1+c_{2}A+c_{3}B+c_{4}C+c_{5}D\hfill \\ +c_{6}AB+c_{7}AC+c_{8}AD+c_{9}BC+c_{10}BD+c_{11}CD\hfill \\ +c_{12}{A}^2+c_{13}{B}^2+c_{14}{C}^2+c_{15}{D}^2\hfill \\ +c_{16}ABC+c_{17}ABD+c_{18}ACD+c_{19}BCD\hfill \\ +c_{20}{A}^{2}B+c_{21}{A}^{2}C+c_{22}{A}^{2}D+c_{23}A{B}^2\hfill \\ +c_{24}A{C}^2+c_{25}A{D}^2+c_{26}{B}^{2}C+c_{27}{B}^{2}C\hfill \end{array} \]$

(11)

$\[ \begin{array}{c}Pressure drop\hfill \\ \mathrm{\Delta }P=c_1+c_{2}A+c_{3}B+c_{4}C+c_{5}D\hfill \\ +c_{6}AB+c_{7}AC+c_{8}AD+c_{9}BC+c_{10}BD+c_{11}CD\hfill \\ +c_{12}{A}^2+c_{13}{B}^2+c_{14}{C}^2+c_{15}{D}^2\hfill \end{array} \]$

(12)

$\[ \begin{array}{c}Mass flow rate\hfill \\ \dot{m}=c_1+c_{2}A+c_{3}B+c_{4}C+c_{5}D\hfill \\ +c_{6}AB+c_{7}AC+c_{8}AD+c_{9}BC+c_{10}BD+c_{11}CD\hfill \\ +c_{12}{A}^2+c_{13}{B}^2+c_{14}{C}^2+c_{15}{D}^2\hfill \end{array} \]$

(13)

Table 5

Coefficients of fitted equations

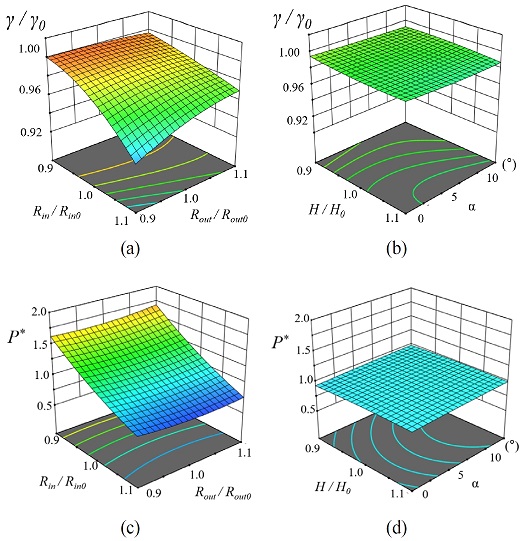
Fig. 8은 설계변수별 변화가 목적함수에 미치는 영향을 나타낸 반응표면이다. Fig. 8(a)의 유동 균일도에는 내부 반경이 제일 영향이 크고, 치수가 낮을수록 개선된 성능을 보였다. 외부 반경은 클수록 유동을 균일하게 만든다. 외부 반경이 크면 관 내로 유입되는 유량이 상승하기 때문이다. Fig. 8(c)의 압력강하에는 내부 반경이 가장 영향이 크며 치수가 클수록 더 개선된 성능을 보인다. 이는 베인으로 토출되는 유동에 병목 현상이 영향을 미치기 때문이다. 각도는 커질수록 압력강하를 개선시킨다. Fig. 6에서 전술하였듯이, 유동장의 입구쪽으로 기운 벨마우스는 주변의 압력계수 분포를 고르게 하기 때문이다. 81개 결과 중 압력강하와 유동 균일도에 공통적으로 내부 반경이 제일 큰 영향을 끼쳤다. 내부 반경이 크면 압력강하는 개선되지만 유동 균일도는 악화되는 상반되는 경향을 보인다. 이는 유동이 유입되는 단면이 크면 병목 현상은 줄어들지만 관 내부에서 와류(vortex)가 커지기 때문이다.

Fig. 8

Response surface of two objective functions: (a) Response of Rin and Rout on γ, (b) Response of H and α on γ, (c) Response of Rin and Rout on ΔP, (d) Response of H and α on ΔP

3.3 등고선 겹치기법(overlaid plot)

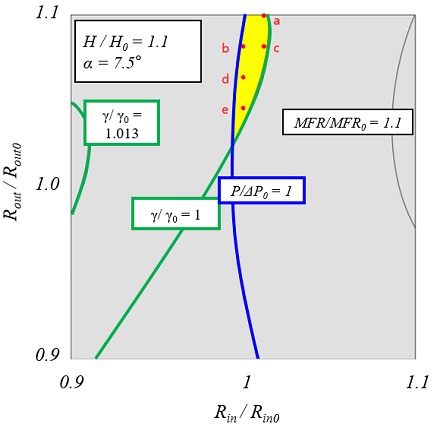
4개의 설계변수 영향을 고려한 최적영역 내 최적점을 찾기 위해 기준 형상 대비 ±10% 높이와 2.5씩 각도 변화를 조합하였다. Fig. 9는 최적 영역이 존재하지 않는 설계 변수들의 조합을 제외하고 가장 넓은 최적영역을 가지는 높이 +10%, 각도 7.5°의 조합을 나타낸다. 설계변수에 따라 압력 강하 및 유동 균일도에 영향을 미치기 때문에 최적영역 내 5개의 최적점을 선별하였다.

Fig. 9

Five optimal candidates in H 1.1 and α 7.5

Table 6은 5개의 최적점의 해석 결과를 나타낸다. 외부반경이 증가함에 따라 유동 균일도에 영향을 미치는데, 외부 반경이 10% 증가하였을 때 Fig. 8(a)의 상승곡선은 완만하여 각 최적점간 유동 균일도 차이는 1% 미만이다. 그러나 압력강하 측면에서는 Fig. 8(c)에서 볼 수 있듯이 내부 반경에 따라 벨마우스 이후 관 내 마찰 압력손실이 급격하게 감소하기 때문에 유동 균일도 대비 큰 변화율로 압력강하가 감소한다. 따라서 유동 균일도가 가장 높고 압력강하도 가장 적은 C 지점을 최적점으로 선정하였다.

Table 6

Design variables and objective functions of five optimal candidates in H 1.1 and α 7.5

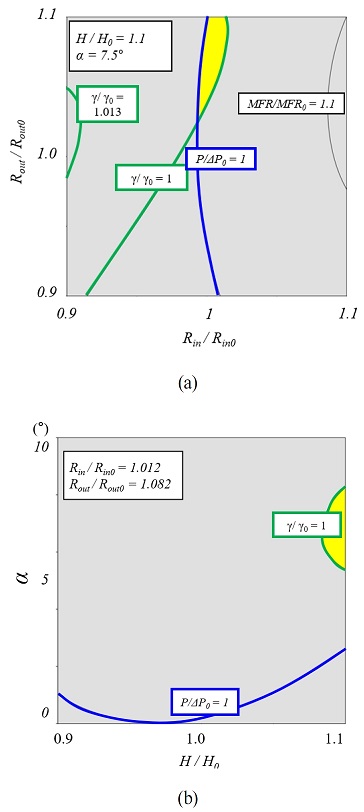
Fig. 10은 최적 영역을 나타내는 목적함수의 등고선이다. Fig. 10(a)는 외부 반경과 내부 반경의 관계를 나타낸 최적영역이다. 가로방향의 내부 반경의 영향이 크기 때문에 영역의 폭이 좁은 것을 확인할 수 있다. 이는 반응표면에서 내부 반경이 유동 균일도와 압력강하에 공통적으로 제일 큰 영향을 미치기 때문이다. Fig. 10(b)는 높이와 각도의 상관관계를 나타낸 최적영역이다. 벨마우스가 입구로 기울수록 유량 증가로 인해 유동 균일도가 개선되므로 최적영역은 5°이상에 위치한다. Fig. 10(a)에서 외부반경은 기준형상보다 더 클 때 최적영역을 가지는데, 이는 전술하였듯이 넓어진 외부 반경이 유량을 증가시켜 유동의 분포를 고르게 하기 때문이다.

Fig. 10

Overlaid plot of objective functions: (a) Plot of Rin and Rout, (b) Plot of H and α

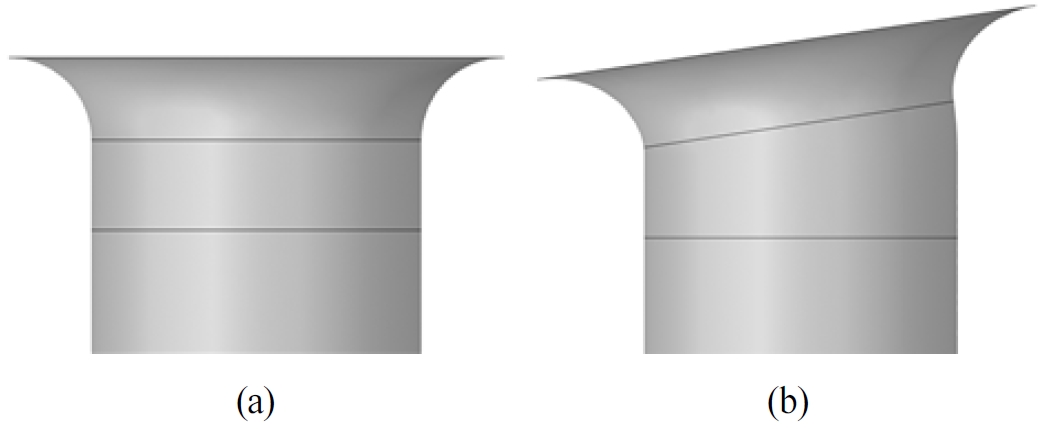
Fig. 11은 등고선 겹치기 방법으로 찾은 벨마우스 최적형상과 기준형상의 비교이다. 내부 반경은 기준형상 대비 1.2% 증가했다. 외부 반경은 8.2% 증가하였고 높이는 10% 상승하였다. 각도는 0°인 기준형상 대비 7.5°로 증가하였다.

Fig. 11

Bellmouth shape comparison: (a) Baseline, (b) Optimized shape

3.4 최적화 결과 고찰

3.4.1 압력강하

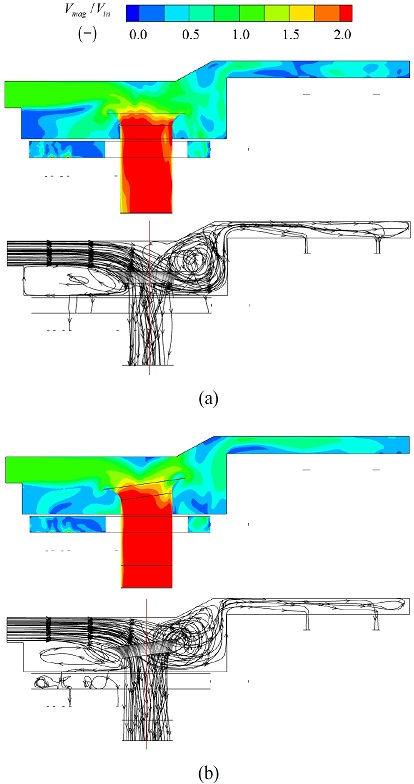
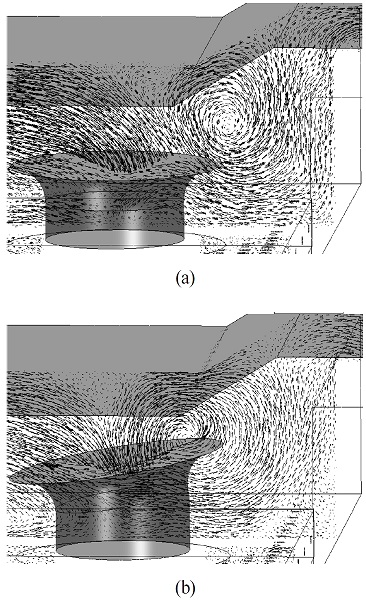
등고선 겹치기법으로 찾은 최적형상에서 전산해석을 수행했다. Fig. 12는 기준형상과 최적형상에서 속도 분포와 유선이다. Fig. 12(a)의 속도 분포에서 벨마우스 전단부의 유동 일부는 아래로 재순환 하는데, Fig. 12(b)의 기울어진 벨마우스 형상은 전단부 재순환을 줄여 관 내부로 진입하는 유량을 증가시킨다. 이로부터 최적형상에서 관 내부 속도 분포는 기준형상 대비 균일하게 변화함을 알 수 있다.

Fig. 12

Compared velocity magnitude contour and streamline: (a) Baseline, (b) Optimized shape

Fig. 12의 유선에서 나타나있듯이, 벨마우스를 통과하는 유동은 두 가지 성분으로 나뉜다. 입구유동이 벨마우스 전단부를 통해 들어오는 성분과 벨마우스 주변영역을 재순환하다가 벨마우스 후단부로 유입되는 성분이다. Fig. 12(a)의 기준형상에서 유선은 관 내를 통과할 때 전술한 두 성분 간 중심선을 넘는 간섭이 발생하여 병목현상으로 압력강하가 생긴다. 그러나 Fig. 12(b)에서 최적형상의 유선은 기울어진 벨마우스 각도와 넓어진 벨마우스 외부 반경으로 인해 재순환 성분의 진입각이 개선되어 두 성분 사이의 간섭 없이 빠져나감을 확인할 수 있다.

개선된 진입각은 재순환 영역의 중심을 앞으로 이동시킨다. Fig. 13은 재순환 유동이 벨마우스 후단부로 진입하는 흐름을 확인하기 위한 z = 4.4R_in0 에서의 벡터장이다. 기준형상인 Fig 13(a)에서는 재순환 성분이 벨마우스로 유입되지 않지만, 최적형상인 Fig 13(b)에서는 벨마우스로 진입한다. 케이싱 입구로 들어온 유동의 경로는 최적화된 벨마우스의 바깥벽을 따라서 위쪽 방향으로 기울어져 순환을 시작한다. 따라서 기준형상보다 앞에서 생성된 재순환 중심은 유동이 벨마우스로 진입할 때 안쪽 벽을 타고 간섭 없이 유입될 수 있게 된다.

Fig. 13

Vector field showing recirculated flow goes into the bellmouth at z = 4.4Rin0 : (a) Baseline, (b) Optimized shape

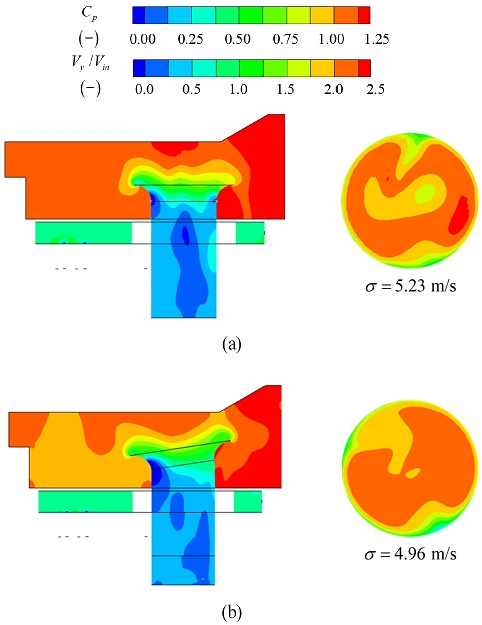
Fig. 14는 기준형상과 최적형상에서 압력계수 및 유동 분포이다. 벨마우스 전단부에서 줄어든 재순환과 벨마우스 후단부에서 중심이 앞으로 이동한 재순환은 Fig 14(b) 좌측처럼 압력 분포를 기존 대비 균일하게 만든다. 이는 기준형상 대비 더 적은 입구 압력으로도 케이싱 출구에 유동을 분배할 수 있게 하고, 관 내 압력 분포도 균일하게 되어 압력강하도 적어지게 된다. 그 결과 최적화된 형상에서 압력강하는 기준형상보다 9% 개선되었다.

Fig. 14

Compared pressure contour and uniformity distribution: (a) Baseline, (b) Optimized shape

3.4.2 유동 균일도

식 (14)는 유동 균일도 표준편차의 정의를 나타낸다.

$\[ \sigma =\sqrt{\frac{\sum _{i=1}^n{\left(v_i-v_{mean}\right)}^2}{n}} \]$

(14)

여기서 v_i는 y-방향 속도, v_mean은 y-방향 평균 속도, n은 격자 개수를 의미한다. 표준편차는 기준형상 대비 5.2% 최적화되었다.

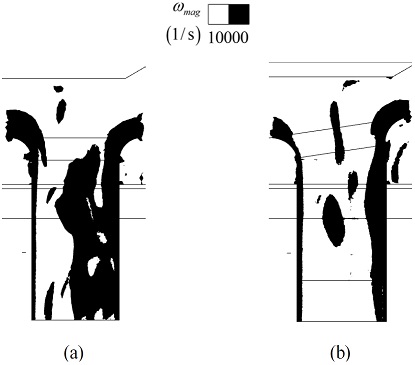
Fig. 14 우측 그림은 기준형상과 최적형상의 y-방향 속도 분포이다. Fig. 14(b)의 최적형상이 관 내 단면의 중심부에서 더 균일한 속도 분포를 띤다. 이는 앞서 설명한 유선 Fig. 12(b)에서 기울어진 형상으로 인해 벨마우스 유입 이후 유동분포가 더 균일하게 변했기 때문이다. Fig. 13(b)에서 앞으로 이동한 벨마우스 후단부 재순환 성분의 중심이 관 내 유입 유동을 더 고르게 하여 관 내부 이차와류(secondary vortex)의 강도가 감소하였음을 알 수 있다. Fig. 15는 기준형상과 최적형상의 측면 와도장이다. 관 내부의 와도 감소량을 비교하기 위해 x = 3.8R_in0 부터 6.9R_in0 사이에서 벨마우스 중심면 z = 5.6R_in0 의 와도를 나타냈다. 최적형상인 Fig. 15(b)에서 와도의 강도가 10000이상인 검정색 영역이 줄었음을 확인할 수 있다. 이로 인해 Fig. 14(b) 우측의 관 내 유동 분포에서 중심부 와도가 감소하고, 최적형상의 벨마우스 유동 균일도 표준편차가 5.23 m/s 에서 4.96 m/s 로 5.2% 감소하여 유동 분포가 균일하게 개선되었다.

Fig. 15

Vorticity contour: (a) Baseline, (b) Optimized shape

4. 결 론

본 연구에서는 냉각유동의 효율적인 분배가 필요한 가스터빈 케이싱에서 벨마우스를 최적화하여 압력강하와 유동 균일도를 개선하고 그 최종 형상을 제시하였다. 요약된 연구의 결론은 다음과 같다.

• 1) 완전요인배치법(full factorial case study)의 결과를 활용하여 유동 균일도, 압력강하 및 질량유량에서 상관식을 도출하였고 벨마우스를 최적화하였다.
• 2) 도출한 상관식으로부터 반응 표면을 그려 변수와 목적함수간의 영향을 살펴보았다. 압력강하 개선 목적으로는 내부 반경이 가장 연관성이 컸고 이는 벨마우스로 나가는 유동의 병목현상과 관련이 있다.
• 3) 유동 균일도 개선 목적으로는 내부 반경이 작을수록, 외부 반경이 클수록 큰 반응을 보였다. 단, 압력강하와 유동 균일도는 서로 trade-off관계이므로 설계시 복합적으로 고려되어야 한다.
• 4) 최적형상에서 압력강하는 벨마우스 전방과 후방에서 유입되는 유동의 진입각이 개선되고 두 성분사이의 간섭이 줄어듦으로 개선된다. 유동 균일도의 개선 이유는 벨마우스 내 유동의 와도가 줄어서이다.
• 5) 파레토 프론트와 등고선을 겹쳐 그린 결과로부터 최적화된 형상을 제시하였고 압력강하와 유동 균일도 양방향에서 개선된 효과를 확인하였다. 파레토 프론트는 직관적으로 최적안을 고를 수 있으나, 정밀한 설계안인지 판단에는 주의가 필요하다. 등고선 겹치기법은 상관식을 통해서 최적화를 수행해야 하지만 정교한 설계가 가능함을 확인하였다. 최종적으로 압력강하는 기준형상대비 9% 개선되었고 유동 균일도의 표준편차는 5.2%개선되었다.

본문에서 기술한 최적형상의 전산해석 결과를 향후 실험으로 검증하는 것이 추가 진행될 수 있을 것으로 판단된다.

Acknowledgments

본 연구는 방위사업청과 국방과학연구소가 지원하는 무인기용 고효율 터빈기술 특화연구센터 사업의 일환으로 수행되었습니다.

References

• Saravanamuttoo, Herbert IH, Gordon Frederick Crichton Rogers, and Henry Cohen., 2001, Gas turbine theory, Pearson Education, London.
• Gunther, A., Uffrecht, W., Kaiser, E., Odenbach, S. and Heller, L., 2008, “Experimental analysis of varied vortex reducer configurations for the internal air system of jet engine gas turbines,” Turbo Expo: Power for Land, Sea, and Air, Vol. 43147, pp.1563∼1570. [https://doi.org/10.1115/GT2008-50738]
• Mucci, A., Kholi, F. K., Sibilli, T., Min, J. K., Ha, M. Y., and Cho, G. H., 2021, “Numerical Analysis of Secondary Airflow in a Rotating Cavity of a Gas turbine at High Operating Points with Vortex Reducer Implementation,” Heat Mass Transfer, Vol.57, No.8, pp.1363∼1378. [https://doi.org/10.1007/s00231-021-03029-6]
• Da Soghe, R., Facchini, B., Micio, M., and Andreini, A., 2012, “Aerothermal Analysis of a Turbine Casing Impingement Cooling System,” International Journal of Rotating Machinery, pp.1∼10. [https://doi.org/10.1155/2012/103583]
• Goldstein, R. J., and Behbahani, A. I., 1982, “Impingement of a Circular Jet with and without Cross Flow,” International Journal of Heat and Mass Transfer, Vol.25, No.9, pp.1377∼1382. [https://doi.org/10.1016/0017-9310(82)90131-4]
• Breeze, Paul., 2016, Gas-Turbine power generation. Academic Press, Massachusetts, pp.43∼53. [https://doi.org/10.1016/B978-0-12-804005-8.00005-7]
• Sungwan Park and Nakwon Sung, 2011, “The effects of a bleed air from the compressor on the performance of a Turbojet Engine,” Proceedings of the KSME Conference, pp.199∼204
• Bajura, R.A., and Jones, E.H., Jr., 1976, “Flow Distribution Manifolds,” Journal of Fluids Engineering, Vol.98, No.4, pp.654∼665. [https://doi.org/10.1115/1.3448441]
• Choi, J.W., Choi, Y.D., Kim, C.G., and Lee, Y.H., 2010, “Flow Uniformity in a Multi-Intake Pump Sump Model,” Journal of Mechanical Science and Technology, Vol.24, No.7, pp.1389∼1400. [https://doi.org/10.1007/s12206-010-0413-5]
• J.H. Lee, B.J. Kim, D.J. Cho and S.J Yoon, 2005, “Effect of a Variation of a Main Duct Area on Flow Distribution of Each Branch,” Korean Journal of Air-Conditioning and Refrigeration Engineering, Vol.17, No.4, pp.386∼395.
• Simon Martinez-Martinez, Ruben D. Leal-Garza, Fausto A. Sanchez-Cruz and Esteban Baez Villarreal, 2010, “CFD analysis of the effect of the exhaust manifold design on the close-coupled catalytic converter performance,” Journal of KONES Powertrain and Transport, Vol.17, No.4, pp.303∼311.
• Choi, C., Lee, C., Park, N.-S., and Kim, I. S., 2019, “Numerical Study of Fluid Behavior on Protruding Shapes within the Inlet Part of Pressurized Membrane Module Using Computational Fluid Dynamics,” Environmental Engineering Research, Vol.25, No.4, pp.498∼505. [https://doi.org/10.4491/eer.2018.423]
• Yu, D.-M., Kim, S., Jang, H.-L., Han, D.-H., and Kang, L.-H., 2019, “Optimal Design of Impeller according to Blade Shape Variation Using CFD Simulation,” Journal of Aerospace System Engineering, Vol.13, No.1, pp29∼37.
• Lee, H., Lee, J., Kim, D., and Cho, J., 2017, “Pre-Swirl Nozzle Geometry Optimization to Increase Discharge Coefficient Using CFD Analysis,” The KSFM Journal of Fluid Machinery, Vol.20, No.1, pp21∼28. [https://doi.org/10.5293/kfma.2017.20.1.021]
• Sevinc, K., 2021, “Aerodynamic Design Optimization of a Bellmouth Shaped Air Intake for Jet Engine Testing Purposes and Its Experiment Based Validation,” Journal of Physics: Conference Series, Vol.1909, No.1, pp. 012028. [https://doi.org/10.1088/1742-6596/1909/1/012028]
• Kuldeep Singh, B. Premachandran, and M. R. Ravi, 2014, “A Numerical Study on the 2D Film Cooling of a Flat Surface,” Numerical Heat Transfer, Part A: Applications, Vol.67, No.6, pp.673∼695. [https://doi.org/10.1080/10407782.2014.949131]
• D.K. Beale, T.L. Hand, and C.L. Sebourn, 2001, “Development of a Bellmouth Airflow Measurement Technique for Turbine Engine Ground Test Facilities,” 37th Joint Propulsion Conference and Exhibit, American Institute of Aeronautics and Astronautics, pp3676 [https://doi.org/10.2514/6.2001-3676]
• ANSYS Inc., 2011, ANSYS Fluent 14.0 Theory Guide, ANSYS Inc., Pennsylvania.