곡면 델타 윙렛 와류발생기를 이용한 핀 휜의 열전달 및 유동 특성 개선
Abstract
A numerical analysis was carried out to investigate the effects of curved delta winglet vortex generator on the heat transfer and flow characteristics of pin fin arrays. The steady RANS simulation has been performed with k-w SST turbulence model by using Fluent 18.0. The effects of the curved delta winglet vortex generators installed upstream of each pin of the staggered array 8 row pins were confirmed, and the cases where the curved delta winglet vortex generators were located on one endwall(Case 1) and on both endwalls(Case 2) were considered. The results showed that the curved delta winglet vortex generators induce the generation of mixed vortices that reduce the size of the wake region of the pin and improve the heat transfer of the pins. In addition, the pressure loss is reduced due to the effect of decreasing the size of wake occurring in the pin, and this tendency becomes stronger as the Reynolds number increases. As a result, the thermal performance factor(η) increases according to the Reynolds number, and when the Reynolds number is 30000, η of Case 1 and Case 2 increased by 11.3% and 12.2%, respectively, compared to the baseline.
Keywords:
Turbine Cooling, Pin Fin Array, Numerical Analysis, Vortex Generator, Mixed Vortices, Heat Transfer, Pressure Loss, Thermal Performance Factor키워드:
터빈 냉각, 핀 휜 배열, 전산해석, 와류발생기, 혼합 와류, 열전달, 압력 손실, 열 성능 팩터1. 서 론
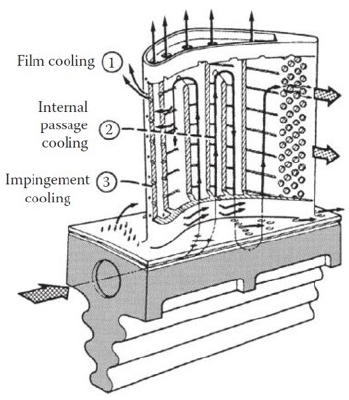
일반적으로 항공기 가스터빈 엔진의 성능 향상은 사이클 압력비와 연소기 출구 온도 상승을 동반한다.(1) 이에 따라 터빈 블레이드는 작동 중에 큰 열 하중에 노출되며, 이를 해결하기 위해 블레이드 내부와 외부를 냉각하는 방법들이 고안되어져 왔다. Fig. 1은 항공기 가스터빈 블레이드에 이용되는 전형적인 냉각 방법들을 보여준다. Fig. 1에서 알 수 있듯이 핀 휜은 유로의 폭이 좁은 블레이드 뒷전에 주로 설치되며, 열전달 면적을 늘리고 냉각 공기를 뒤섞어, 벽면 온도를 낮추는데 효과적인 것으로 알려져 있다.(2)
터빈 블레이드 뒷전에 이용되는 핀은 좁은 유로 형상과 제작의 어려움 때문에 핀의 지름 대비 채널 높이(H/D)가 4미만인 형상이어야 하고, 이를 고려한 연구에 대한 필요성이 VanFossen(3)에 의해 대두되었다. 이후 H/D<4인 짧은 핀 배열의 대한 다양한 연구들이 수행되었다. Metzger 등(4-6)은 H/D가 1인 10열의 핀들의 유동방향 간격과 횡 방향 간격이 전열성능에 미치는 영향을 실험으로 확인하였다. 그 결과, 핀의 유동방향 간격은 열전달이 가장 강하게 일어나는 핀의 위치와 전반적인 난류강도와 연관이 있음을 확인하였다. Chyu 등(7)은 H/D가 1인 7열의 핀과 끝벽이 열전달에 기여하는 정도를 확인하기 위해 나프탈렌 승화법을 이용하였으며, 엇갈림 배열일 때, 끝벽에 의한 열전달의 비중이 핀에 의한 것에 비해 20% 높은 것을 확인하였다. Ames 등(8,9)은 실험을 통해 H/D가 2인 8열의 엇갈림 핀 배열에 의한 난류 발달 및 전열성능 변화 과정을 자세히 확인하였으며, 이를 전산해석 결과와 비교하였다. 이를 통해, 대칭형 전산해석 도메인은 핀에서 발생하는 쉐딩 효과를 반영하지 못하며, 정확한 성능 예측에 이용하기 어렵다는 것을 확인하였다.
최근에는 제작 기술이 발전함에 따라 보다 복잡한 냉각유로 형상도 제작이 가능해질 전망이며, 기존의 냉각 방법을 두 가지 이상 조합하는 방식이 새로운 전열성능 향상 방법으로서 각광 받고 있다.(10) 그 예로, Siw 등(11)은 핀 휜과 립이 조합된 냉각유로에 대해 실험적 연구를 수행했으며, 립이 끝벽 열전달 향상에 기여함을 확인하였다. Rao 등(12,13)은 핀 휜에 딤플 추가된 유로에 대한 실험을 수행하였으며, 핀 휜만 있는 경우에 비해 전열성능 향상과 손실 감소에 효과 있음을 확인하였다. Murata 등(14)은 핀 모양의 돌기, 딤플과 립을 조합한 유로에 대해 실험을 수행하였으며, 전열성능은 최대 40%, 압력 손실은 최대 32% 증가함을 확인하였다. 이와 같이 두 가지 이상의 냉각 방식을 조합하는 개념은 냉각유로를 설계하고자하는 연구자들에게 여러 가능성을 열어주었으나, 일반적으로 손실 증가 또한 야기하게 된다.(10) 따라서 단순히 전열 면적을 늘리거나 유로의 구조를 복잡하게 하는 것이 아닌 보다 효율적이고 새로운 냉각 유로 개념이 필요하다.
와류발생기는 일반적으로 소형 휜 튜브 열교환기 이용되며, 슬릿(Slits), 옵셋 스트립(Offset strips)과 루버(Louvers) 등과 같은 단속 표면 방식에 비해 전열상승 효과 대비 낮은 손실을 유발하는 것으로 알려져 있다.(15) 특히 곡면 델타 윙렛 와류발생기는 튜브 전방에 설치될 때, 평면형 와류발생기 수준의 전열 상승을 일으키며, 손실 증가는 미미한 수준으로 나타나는 것으로 확인되었다.(16) 그러나 곡면 델타 윙렛 와류발생기를 핀 휜 냉각유로에 이용한 연구 사례는 거의 없으며, 휜 튜브 열교환기에서의 경우(16)와 유사한 효과를 기대해 볼 수 있다. 이에 본 연구에서는 곡면 델타 윙렛 와류발생기가 핀 휜 냉각유로의 전열 특성에 미치는 영향에 대해 확인하고자 와류발생기가 한쪽 끝 벽에 위치한 경우, 양쪽 끝 벽에 위치한 경우에 대해 3차원 전산해석을 수행하였다. 또한, 전반적인 전열성능과 각 열별로 전열성능 변화를 비교하였으며, 유동 패턴을 상세히 분석하였다.
2. 본 론
2.1 수치해석 모델
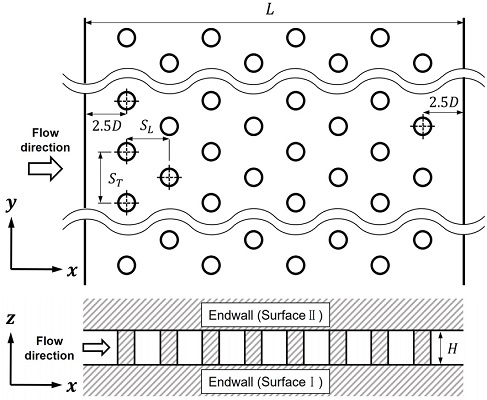
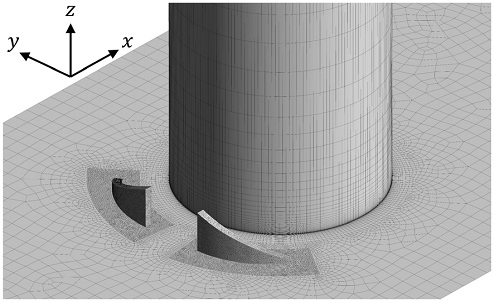
Fig. 2는 해석대상이 되는 핀 휜 배열을 나타낸 것이며, 이 형상은 Ames 등(16)의 실험에서의 형상과 같다. Fig. 2에서 x축은 유동방향, y축은 유동방향에 수직한 횡 방향이며, 두 끝벽이 z축에 수직하게 위치한다. 8열의 핀 휜은 엇갈림 배열로 배치되어 있으며, SL과 ST은 각각 핀의 유동방향 간격과 횡 방향 간격을 의미한다. 그 밖에 D, H와 L은 각각, 핀의 지름, 유로의 높이와 해석모델의 길이이다. 그리고 첫 번째 핀의 상류방향과 마지막 핀의 하류 방향으로 2.5D씩 끝벽이 연장되어 있다.
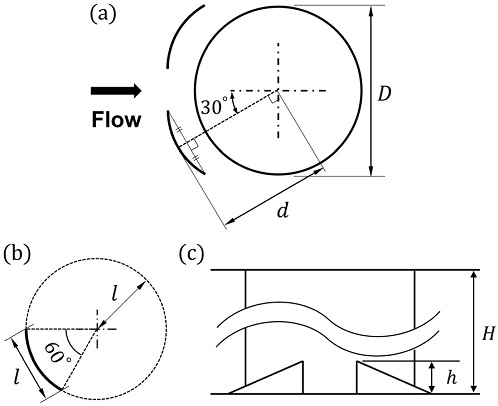
Fig. 3는 본 연구에서 이용한 곡면 델타 윙렛 와류발생기의 형상에 대해 나타낸 것이다. Fig. 3(a)는 핀의 중심을 기준으로 와류발생기의 위치를 표현한 것이며 d는 와류발생기의 반경방향 위치이다. 또한 와류발생기의 곡률은 Fig. 3(b)와 같이 가상의 원호로 표현되며, 가상의 원의 반지름과 와류발생기의 길이는 l과 같다. 그리고 Fig. 3(c)에서 h는 와류발생기의 높이이다. 와류발생기의 l/D와 h/D는 Oh와 Kim(16)의 와류발생기 형상과 동일하게 결정되었으며, 두 경우 각각 핀 혹은 튜브 지름을 기준으로 같은 비율을 가진다. Fig. 2와 Fig. 3에서 언급된 형상 관련 자세한 정보는 Table 1에 구체적으로 표기되어 있다.
2.2 변수 정의
레이놀즈수(Re), 대류 열전달계수(h)와 대수평균온도차(ΔTlm)의 정의는 식 (1)∼(3)과 같다.
| (1) |
| (2) |
| (3) |
ρ, Vmax, μ, Q와 A는 각각 입구 공기 밀도, 단면적이 가장 작은 위치의 평균 유속, 입구 공기의 점성, 벽면의 열전달량과 전열면적을 의미한다. 단면적이 가장 작은 위치란, 같은 열에 위치한 두 핀 사이의 유로에서 유동 단면적이 최소가 되는 위치를 의미한다. 그리고 Tw, Ti와 To는 각각 벽면의 온도, 입구와 출구의 온도를 의미한다. 누셀트 수(Nusselt number, Nu)와 마찰인자(Friction factor, f)에 대한 정의는 식 (4)와 (5)와 같으며, 종합적인 열전달 성능을 비교하기 위해 Webb(23)에 의해 제시된 열 성능 인자(Thermal performance factor, η)를 식 (6)과 같이 정의하였다.
| (4) |
| (5) |
| (6) |
위의 마찰인자(f)와 누셀트 수(Nu)는 Ames 등(8)이 정의한 식과 동일하며, 검증과정에서 Ames 등(8)의 실험 결과와의 비교를 위해 위의 식을 이용하였다. 그리고 통일성을 위하여 전산해석 결과 분석에서도 위의 식을 이용하였다.
k, Δp와 N은 각각 공기의 열전도 계수, 압력 강하량과 핀의 열 개수를 의미하며, 아래첨자 ‘0’는 와류발생기가 없는 단순 핀 휜에 관한 값을 의미한다. 압력 강하량은 첫 번째 열 핀의 중심으로부터 상류로 5D인 위치와 마지막 열 핀의 중심으로부터 하류로 5D인 위치 사이의 값을 이용하였으며, 이는 Ames 등(8)이 압력 강하를 측정한 위치와 동일하다.
2.3 경계조건
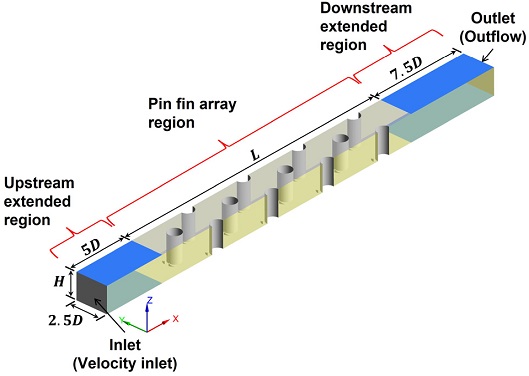
Fig. 4는 전산해석을 위한 도메인을 나타낸 것이다. Ames 등(8)이 제안한 것처럼 도메인은 Fig. 2의 해석모델을 횡 방향으로 한 주기에 해당하는 영역으로 설정하였으며, 도메인의 높이는 유로의 높이, H와 동일하다. 또한, Ames 등(17)의 실험 조건을 고려하여 핀 휜 배열 영역(Pin fin array region)의 상류와 하류방향으로 각각 핀 지름의 5배와 7.5배의 연장구간(Extended region)을 설정하여 도메인을 구성하였다. 도메인의 y축 방향으로는 주기조건이 부여되었으며, 핀 휜 배열 영역의 와류발생기, 핀, 양쪽 끝벽을 비롯해 끝벽과 동일 평면상에 위치한 상류와 하류 연장구간의 면에 모두 점착조건의 벽으로 설정하였다. 그리고 Ames 등(17)의 실험을 모사하기 위해 핀 휜 배열 영역에 위치한 벽들에 한하여 325K의 등온 조건이 부여되었으며, 상류와 하류 연장구간의 벽면은 모두 단열조건이다. 작동 유체는 공기이며, 물성치가 일정하다고 가정하였다. 또한, Ames 등(17)의 실험 조건에 따라 비압축성 유동으로 가정할 수 있으며, 계산 비용의 효율을 위해 정상상태유동으로 가정하였다. 입구로 유입되는 공기의 온도는 300K이고, x축 방향 외의 다른 방향으로 속도 성분은 없다고 가정하였다.
2.4 격자의존도
본 연구에서는 곡면 델타 윙렛 와류발생기의 주변의 일부 영역과 나머지 영역으로 구분하여 격자를 구성하였다. 와류발생기 주변의 영역은 비정렬 격자, 그 외 영역은 z축 방향으로 스윕(Sweep) 방법을 이용하여 육면체 격자로 구성하였으며, 벽면 주변의 격자의 질을 개선하기 위해 모든 벽면에 인플레이션(Inflation) 기법을 이용하였다. 그 결과 와류발생기의 벽면 근처는 여러 층의 프리즘(Prism/Wedge) 격자로 구성되고, 그 외 남은 공간은 사면체 격자로 채워진다. 스윕이 적용된 영역에서는 핀과 양 끝벽 주변에 격자가 조밀하도록 하였으며, 레이놀즈수가 30000인 조건에서 모든 벽면에서 y+가 1보다 작은 것을 확인하였다.
격자의존도를 확인하고, 도메인의 격자 요소 개수를 결정하기 위해, Celik 등(18)이 제시한 방법을 통해 격자 수렴 지수(Grid Convergence Index)를 확인하였다. 격자 수렴 지수는 해가 점근값으로부터 얼마나 멀리 떨어져 있는지에 대한 차이를 나타내며, 이산화 오류 추정을 위해 권장되는 방법이다.(24)각 격자계의 격자 크기(h)의 정의는 식 (7)과 같으며, n과 ∆Vi는 각각 격자계를 구성하는 총격자의 수와 i번째 격자의 체적을 의미한다.
| (7) |
그리고 격자 조정 계수(rrefine)는 k-1번째 격자계에 대한 k번째 격자계의 격자 크기 비를 의미하며, 식 (8)과 같다.
| (8) |
Grid 2과 Grid 1간 rrefine를 r21, Grid 3와 Grid 2간의 rrefine를 r32라고 할 때, Apparent order(p)와 관련 식들은 다음과 같다.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
여기서, ϕk는 k번째 격자계의 주요 변수를 의미한다. 위 관계식들을 이용하여 고정점 반복법(Fixed-point iteration)을 수행할 경우 p를 구할 수 있으며, GCI 값을 얻기 위해 필요한 Approximate relative error ()와 GCI의 정의는 다음과 같다.
| (14) |
| (15) |
와류발생기가 한쪽 끝벽에 설치된 Case 1과 양쪽 끝벽에 설치된 Case 2에 대하여 레이놀즈수가 30000인 조건에서 각각 세 가지 격자를 이용하여 격자 수렴 지수를 확인하였으며, 그 결과는 Table. 2와 같다.
Table. 2를 통해 Case 1과 Case 2에서 Nu와 f에 대한 격자 수렴 지수(GCIfine)가 모두 1% 이하로 나타나는 것을 알 수 있으며, 이는 Grid 1 수준의 격자가 본 전산해석에 사용하기에 충분히 적합하다는 것을 의미한다. Fig. 5는 Case 1의 Grid 1 격자를 나타낸 것이다.
3. 결과 및 고찰
3.1 해석기법 검증
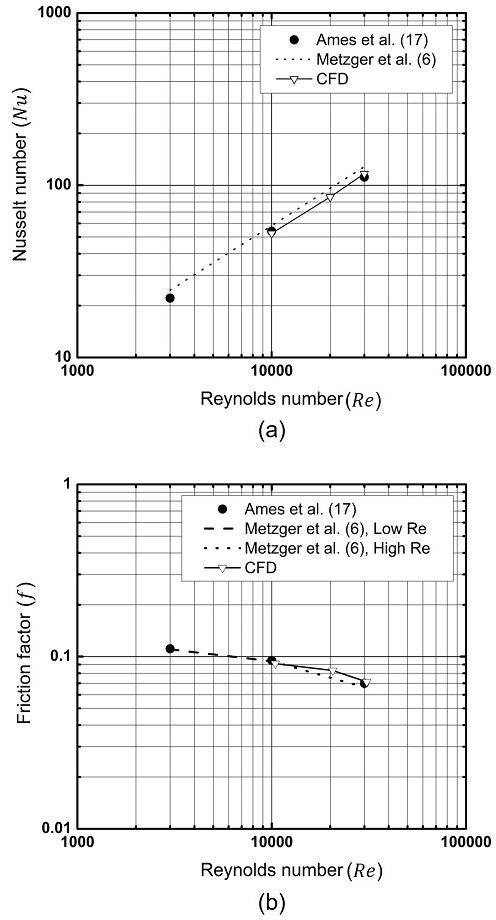
본 연구에서는 Reynolds Averaged Navier-Stokes(RANS)방정식을 풀기위해 유한체적법 기반의 상용 전산해석 프로그램인 Fluent 18.0을 이용하여 전산해석을 수행하였으며, k-ω Shear Stress Transport(SST) 난류모델을 사용하였다. k-ω SST 난류모델은 핀 휜 및 립 등에 의해 발생하는 유동과 열전달 특성 예측에 높은 정확도를 보여주는 것으로 알려져 있다.(19-22) 또한, 압력-속도 커플링에 Coupled, 공간차분법에는 2차 상류 차분법을 이용하였다. 수치해석기법의 타당성을 검증하고자 Ames 등(17)의 형상을 이용한 전산해석 결과를 실험 결과 및 관계식들과 Fig. 6과 같이 비교하였다. Fig. 6(a)의 Nu의 경우, Ames 등(17)의 실험 결과와의 오차가 약 2-12%로 나타나며, Metzger 등(6)의 관계식과는 약 2-10%의 오차를 보인다. Fig. 6(b)의 f의 경우, 해석 결과가 실험 결과와 약 2-4%의 오차를 보이며, Metzger 등(6)의 관계식과의 차이는 약 3-10%로 나타난다. 그리고 Fig. 6(a)와 (b)에 나타난 바와 같이 레이놀즈수 변화에 따른 Nu와 f의 변화 경향도 실험 및 관계식의 경향과 잘 일치하며, 이는 본 전산해석기법이 핀 휜 유동을 모사하기 적합함을 의미한다.
3.2 전열 성능 및 압력 손실
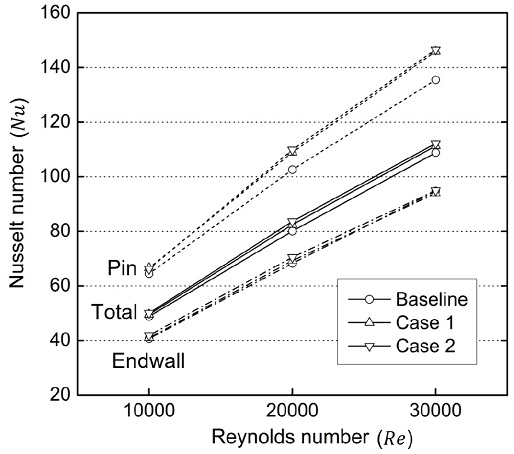
곡면 델타 윙렛 와류발생기가 핀 휜 배열의 전열 성능에 미치는 영향을 확인하기 위해 레이놀즈수 변화에 따른 누셀트 수(Nu)를 Fig. 7과 같이 나타내었으며, 전체, 끝벽과 핀에 대해 각각 평균한 누셀트 수를 각각 따로 도시하였다. 전체 평균한 누셀트 수의 경우, 레이놀즈수가 10000일 때, Case 1과 Case 2는 Baseline에 비해 각각 1.5% 와 2.5% 높게 나타나며, 레이놀즈수가 20000일 때는 누셀트 수 증가 폭이 3.0%와 4.5% 로 커진다. 그러나 레이놀즈수가 30000일 때는 소폭 감소하여 각각 Baseline보다 2.3%와 3.1% 높게 나타난다. 끝벽에 대해 평균한 누셀트 수를 살펴보면, Case 1의 경우 레이놀즈수와 관계없이 기존 대비 변화폭이 약 1.0% 수준을 넘지 못한다. 반면, 와류발생기가 양쪽 끝벽에 설치된 Case 2의 경우, 레이놀즈수가 10000와 20000일 때 끝벽의 전열이 약 3.0% 씩 증가한다. 그러나 레이놀즈수가 30000일 때는 차이가 미미하다. 핀에 대해 평균한 누셀트 수를 살펴보면, 레이놀즈수가 10000일 때 Case 1과 Case 2가 기존 대비 각각 3.2%와 2.7% 상승하였다. 이 폭은 레이놀즈수가 상승함에 따라 커지며, 레이놀즈수가 30000 일 때는 Case 1과 Case 2 의 전열이 기존 대비 7.7%와 8.2% 까지 상승하였다.
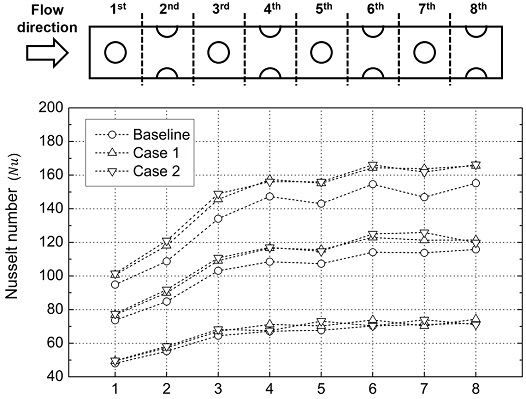
유동방향으로 흐르는 동안의 누셀트 수의 경향을 확인하기 위해 각 열의 핀들을 기준으로 등 간격으로 나눈 구간에서 각 구간에 속한 핀과 끝벽에 대해 평균한 누셀트 수를 Fig. 8과 같이 나타내었다. 앞서 살펴본 경향과 유사하게 레이놀즈수가 10000일 때는 전반적으로 누셀트 수의 차이가 크게 두드러지지 않으며, 각 열별로 살펴보아도 차이가 두드러지는 곳은 찾기 어렵다. 그러나 레이놀즈수가 20000과 30000인 경우, Case 1과 Case 2의 누셀트 수가 Baseline에 비해서 전반적으로 높아졌음이 확연히 드러난다. 비록 초기 구간에서는 누셀트 수 상승이 비교적 작으나 하류로 갈수록 상승 정도가 커지는 경향을 보이며, 이 경향은 레이놀즈수가 20000일 때 보다 30000일 때 더 두드러진다. 열별로 상승한 정도를 비교해볼 때, 레이놀즈수가 20000인 경우, Case 1과 Case 2는 공통적으로 4-7열 부근에서, 레이놀즈수가 30000인 경우, 3열,5열과 7열에서 비교적 전열 증가가 높게 나타난다. 그리고 Case 1과 Case 2를 비교할 때, 기존 대비 누셀트 수 증가 정도는 서로 비슷한 수준으로 나타난다.
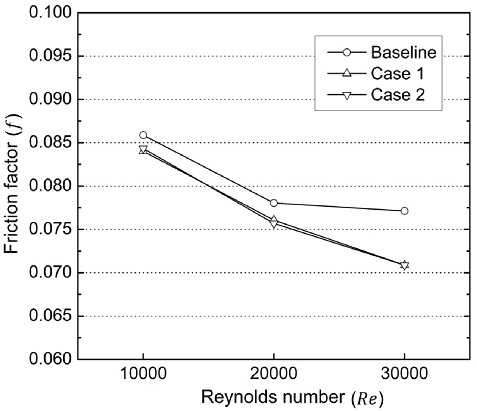
곡면 델타 윙렛 와류발생기가 압력 손실에 미치는 영향을 확인하고자 레이놀즈수에 따른 마찰인자(f)를 Fig. 9와 같이 나타내었다. Fig. 9에서 확인할 수 있듯이, Case 1과 Case 2의 기존 대비 마찰인자는 모든 레이놀즈수에서 전반적으로 낮게 나타나며, 레이놀즈수가 커짐에 따라 손실 감소가 더욱 두드러진다. 그러나 Case 1과 Case 2 간의 정량적 차이는 크게 나타나지 않는다.
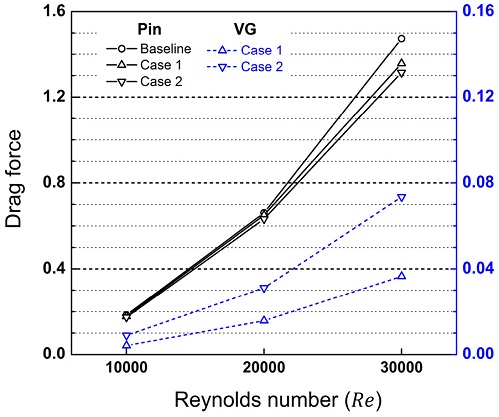
곡면 델타 윙렛 와류발생기가 존재하는 경우, Baseline에 비해 마찰인자를 감소시키는 효과를 보이지만 레이놀즈수에 따른 Case 1과 Case 2의 마찰인자 수준은 크게 차이가 나지 않는다. 이러한 경향의 원인을 상세히 살펴보기 위해 핀과 와류발생기의 항력을 Fig. 10과 같이 나타내었다. 핀에서 발생하는 항력의 경우, 레이놀즈수가 10000일 때, 핀에서 발생하는 항력의 차이가 크지 않다. 그러나 레이놀즈수가 증가함에 따라 Baseline에 비해 Case 1과 Case 2의 항력이 낮게 발생하는 경향이 잘 확인되며, Case 2의 항력이 Case 1에 비해 낮은 경향이 두드러진다. 와류발생기에서 발생하는 항력의 경우를 살펴보면, 와류발생기에서 발생하는 항력은 레이놀즈수에 따라 꾸준히 상승하는 것을 알 수 있다. 그리고 레이놀즈수에 관계없이 Case 2가 Case 1에 비해 두 배가량 높게 항력이 발생하는데, 이는 Case 1과 Case 2에 설치된 와류발생기 개수 차이에 따른 경향이다.
보다 정량적으로 비교하기 위해 Fig. 10의 정보를 Table. 3과 같이 나타내었다. Case 1과 Case 2의 핀과 와류발생기의 항력 변화를 비교하면, 레이놀즈수가 10000인 경우에는 핀에서 발생하는 항력의 감소 정도보다 와류발생기에 의한 항력 증가 수준이 높게 나타나며, 이는 Fig. 9에서 10000일 때, Case 2의 마찰인자가 Case 1 보다 높게 나타난 이유로 볼 수 있다. 레이놀즈수가 20000일 때와 30000일 때는 와류발생기가 늘어남에 따른 항력 증가치 대비 핀에서의 항력 감소 수준이 높은 것을 알 수 있으나, 차이가 비교적 미미한 수준이다. 따라서 Fig. 9에서 Case 1과 Case 2의 마찰인자의 차이가 크지 않은 것은 핀에서의 항력 감소 효과가 와류발생기 수 증가에 따른 항력 증가와 상쇄되어 나타나는 경향으로 볼 수 있다.
3.3 곡면 델타 윙렛 와류발생기에 의한 유동 구조
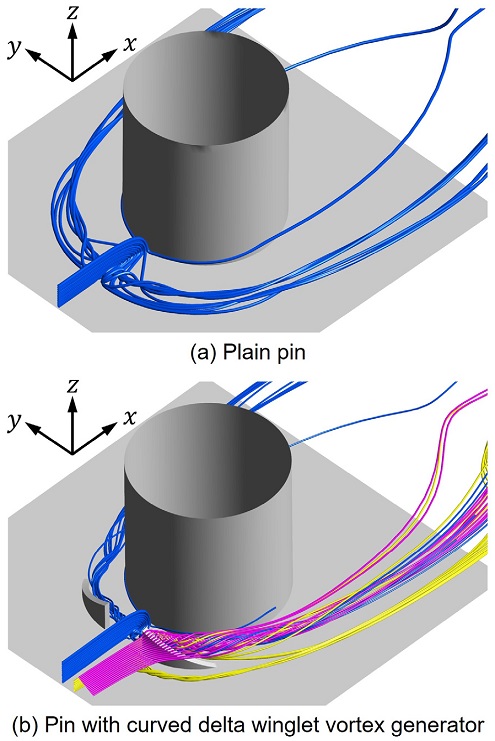
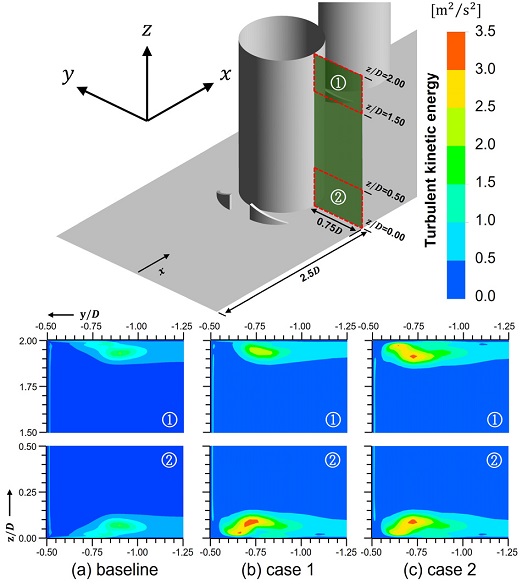
앞서 살펴본 바와 같이 곡면 델타 윙렛 와류발생기가 핀 휜 배열에 설치될 때, 전열 성능 증가와 더불어 손실 감소가 일어난다. 이와 같은 효과가 나타나는 원리를 파악하고자 Fig. 11과 같이 와류발생기가 설치된 경우(Case 1)와 단순 핀(Baseline) 주변의 3차원 유선을 비교하였다. 차이가 명확하게 드러나도록 Fig. 11(b)와 같이 와류발생기 전단과 상단부 모서리에 부딪치는 유동을 핀의 전단에 부딪히는 유동과 구분하여 다른 색으로 표현하였다. 곡면 델타 윙렛 와류발생기가 핀의 상류에 설치된 경우, Oh와 Kim(16)에 의해 확인된 것과 유사하게, 와류발생기에서 생성된 와류가 핀 전단에서 발생한 말굽와류와 혼합되어 하나의 와류로 흘러가는 것을 확인할 수 있다. 또한 이 혼합된 와류는 Fig. 11(a)의 말굽와류에 비해 튜브에 인접한 경로로 흐르는 것이 명확히 관찰된다. Fig. 12은 첫 번째 열 핀의 중심축과 동일 평면상에 위치하며, 유동방향에 수직한 면에서의 난류 운동에너지(Turbulent kinetic energy)를 나타낸 것이다. Fig. 12에서 확인할 수 있듯이 와류발생기가 있는 경우, 난류 운동에너지가 상대적으로 큰 혼합 와류가 생성되며, 이 혼합와류는 기존의 말굽와류에 비해 튜브에 인접하게 흐른다는 것을 알 수 있다.
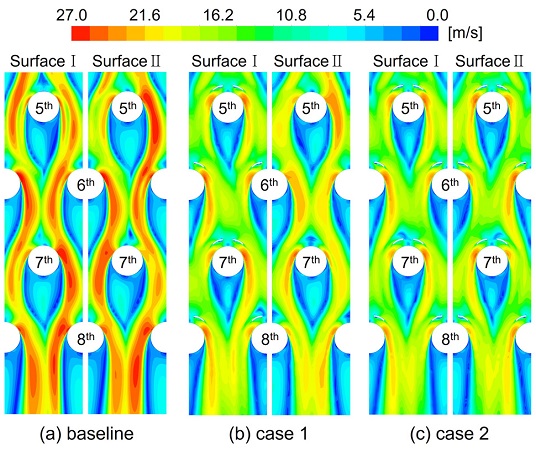
곡면 델타 윙렛 와류발생기와 핀에 의해 생성된 혼합와류에 의한 효과를 추가적으로 확인하고자 양 끝벽에 인접한 면에서의 속도 분포를 Fig. 13과 같이 나타내었으며, 주 유동을 기준으로 -z와 +z 방향에 위치한 끝벽을 각각 surfaceⅠ과 surfaceⅡ로 명명하였다. Fig. 13(b)의 surfaceⅠ이나 Fig. 13(c)의 surfaceⅠ과 surfaceⅡ를 Fig. 13(a)의 경우와 비교하면, 각 핀에서 발생한 박리에 의한 후류 영역 크기가 감소하였음을 관찰할 수 있다. 이는 델타 윙렛 와류발생기에 의한 혼합와류가 기존의 말굽와류보다 튜브에 인접하게 흐르게 됨으로써 핀 주위의 유동 박리영역을 축소시키는 것으로 볼 수 있다. Fig. 9에서 Case 1과 Case 2의 f가 기존에 비해 낮게 나타난 것 또한 박리영역 축소에 따른 효과로 판단된다.
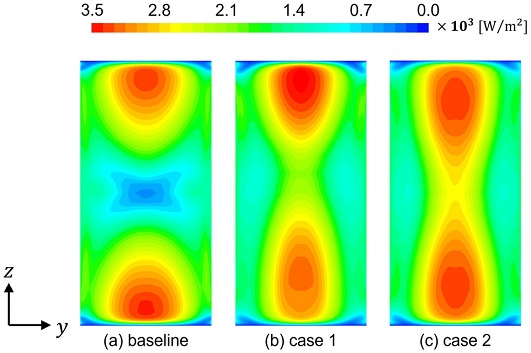
Fig. 14은 레이놀즈수가 30000일 때, 6번째 핀의 후방부의 열유속(Heat flux) 분포를 예시로서 나타낸 것이다. Fig. 14(b)와 (c)의 경우, Fig. 14(a)에 비해 전열이 나쁜 영역이 줄어들었으며, 전반적으로 전열 성능이 개선되었음을 알 수 있다. 이는 와류발생기에서 발생한 혼합와류는 핀에 의한 박리영역의 크기를 축소시킬 뿐만 아니라 핀의 전열 성능도 개선함을 의미한다. 그리고 Fig. 7에서 Case 1과 Case 2의 핀 누셀트 수가 기존 대비 높게 나타난 것도 핀의 후방부 전열 성능이 개선되어 나타난 결과로 볼 수 있다.
3.4 열 성능 팩터(Thermal performance factor)
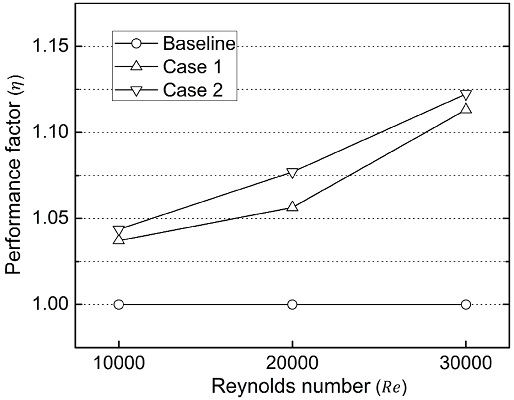
핀 휜 냉각 유로에 곡면 델타 윙렛 와류발생기가 설치됨에 따른 전열 성능 증가와 압력 손실 변화를 종합적으로 평가하기 위해, 각 해석 케이스의 열 성능 팩터를 Fig. 15와 같이 나타내었으며, 정량적 수준은 Table 4과 같다. Fig. 15에 따르면, 핀 휜 냉각 유로에 곡면 델타 윙렛 와류발생기가 부착될 경우, 열 성능 팩터가 기존 대비 향상됨을 알 수 있으며, 레이놀즈수가 높을수록 향상 정도가 높게 나타난다. 그리고 와류발생기가 유로의 한쪽 끝벽에 설치된 Case 1보다 양쪽 끝벽에 설치된 Case 2가 각 레이놀즈수에서 더 높은 열 성능 팩터를 보인다. 각 레이놀즈수별로 열 성능 팩터를 Table 4을 통해 자세히 살펴보면, 레이놀즈수가 10000일 때는 Case 1과 Case 2의 열 성능 팩터가 각각 기존 대비 3.7%와 4.4% 높게 나타난다. 레이놀즈수가 20000일 때, Case 1과 Case 2의 열 성능 팩터는 각각 기존 대비 5.6%와 7.7% 상승하였으며, 레이놀즈수가 30000인 경우에는 각각 11.3%와 12.2% 상승하였다.
4. 결 론
본 연구에서는 휜 튜브 열교환기의 전열 성능을 향상시키는데 효과가 있는 것으로 알려진 곡면 델타 윙렛 와류발생기가 핀 휜 냉각 유로에 부착될 때 발생하는 효과를 확인하기 위해 전산해석을 통한 연구를 수행하였다. 곡면 델타 윙렛 와류발생기가 한쪽 끝벽에 설치된 경우(Case 1)와 양쪽 끝벽에 설치된 경우(Case 2)에 대해 레이놀즈수가 10000, 20000과 30000인 조건에 대해 해석을 수행하였으며, 전열성능 변화를 확인하기 위해 전체 전열 면적, 핀과 끝벽 면적에 대해 평균한 누셀트 수를 확인하였다. 또한, 각 해석 결과의 유동방향 누셀트 수 변화를 비교하였으며, 압력 손실 차이를 확인하기 위해 마찰인자를 비교하였다. 그리고 형상에 따라 성능 차이가 발생하는 원인을 파악하고자, 3차원 유동경로, 난류 운동에너지, 속도 등고선과 핀 후방부 열유속을 확인하였으며, 열 성능 팩터를 이용하여 곡면 델타 윙렛 와류발생기가 부착된 형상들의 종합적인 열전달 성능을 평가하였다. 그 결과, 도출된 결론은 다음과 같다.
- 1) 곡면 델타 윙렛 와류발생기가 핀의 상류에 부착될 경우 핀과 와류발생기에서 생성된 와류들이 뒤섞여 혼합 와류를 형성하게 된다. 이 와류는 기존의 말굽와류에 비해 난류강도가 강하며, 튜브에 인접하게 흐른다.
- 2) 혼합 와류의 영향으로 핀의 후류 박리영역의 크기가 감소하며, 시스템 전반의 압력 손실 또한 감소된다. 압력 손실 감소 효과는 레이놀즈수가 클수록 강하다.
- 3) 곡면 델타 윙렛 와류발생기가 있는 경우, 유로 전반의 전열이 소폭 상승하며, 특히, 핀의 전열 성능이 상당히 향상된다. 이는 핀의 후방부 전열 성능이 개선되어 나타나는 효과로 판단된다.
- 4) Case 1과 Case 2의 전체 평균 누셀트 수와 마찰인자는 정량적으로 크게 차이나지 않는다. 두 경우는 공통적으로 레이놀즈수가 높을수록 높은 열 성능 팩터를 보이는데 이는 전열 증가보다는 손실 감소 효과에 기인한 것으로 판단된다.
Acknowledgments
이 논문은 2021년도 4단계 두뇌한국21 사업(4단계 BK21 사업)에 의하여 지원되었음.
이 논문은 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
- Gladden, H. J., and Simoneau, R. J., 1989, “Review and Assessment of the Database and Numerical Modeling for Turbine Heat Transfer,” Toward Improved Durability in Advanced Aircraft Engine Hot Sections, Vol. 2, pp. 39-55.
- Wright, L. M., and Han, J. C., 2006, “Enhanced internal cooling of turbine blades and vanes,” The gas turbine handbook, Vol. 4, pp. 1-5.
-
VanFossen, G. J., 1982, “Heat-transfer coefficients for staggered arrays of short pin-fins,” Journal of Engineering for Power, Vol. 104, No. 2, pp. 268–274.
[https://doi.org/10.1115/1.3227275]

-
Metzger, D. E., Berry, R. A., and Bronson, J. P., 1982, “Developing Heat Transfer in Rectangular Ducts With Staggered Arrays of Short Pin Fins,” ASME. J. Heat Transfer, Vol. 104, No.4, pp. 700–706.
[https://doi.org/10.1115/1.3245188]

-
Metzger, D. E., and Haley, S. W., 1982, “Heat transfer experiments and flow visualization for arrays of short pin fins,” ASME, In Turbo Expo: Power for Land, Sea, and Air, Vol. 79597, p. V004T09A007.
[https://doi.org/10.1115/82-GT-138]

-
Metzger, D. E., Fan, Z. X., and Shepard, W. B., 1982, “Pressure Loss and Heat Transfer Through Multiple Rows of Short Pin Fins,” Heat Transfer 1982, Hemisphere, Washington, DC, Vol. 3, pp. 137-142.
[https://doi.org/10.1615/IHTC7.1600]

-
Chyu, M. K., Hsing, Y. C., Shih, T. P., and Natarajan, V., 1999, “Heat transfer contributions of pins and endwall in pin-fin arrays: effects of thermal boundary condition modeling,” ASME. J. Turbomach., Vol. 121, No. 2, pp. 257–263.
[https://doi.org/10.1115/1.2841309]

-
Ames, F. E., Dvorak, L. A., and Morrow, M. J., 2005, “Turbulent augmentation of internal convection over pins in staggered-pin fin arrays,” J. Turbomach., Vol. 127, No. 1, pp. 183-190.
[https://doi.org/10.1115/1.1811090]

-
Ames, F. E., and Dvorak, L. A., 2006, “Turbulent Transport in Pin Fin Arrays: Experimental Data and Predictions,” ASME. J. Turbomach, Vol. 128, No. 1, pp. 71–81.
[https://doi.org/10.1115/1.2098792]

-
Chyu, M. K., and Siw, S. C., 2013, “Recent Advances of Internal Cooling Techniques for Gas Turbine Airfoils,” ASME. J. Thermal Sci. Eng. Appl., Vol. 5, No. 2, 021008.
[https://doi.org/10.1115/1.4023829]

-
Siw, S. C., Chyu, M. K., and Alvin, M. A., 2013, “Effects of Pin Detached Space on Heat Transfer in a Rib Roughened Channel,” ASME. J. Turbomach., Vol. 135, No. 2, 021029.
[https://doi.org/10.1115/1.4006567]

-
Rao, Y., Wan, C., and Zang, S., 2010, “Comparisons of flow friction and heat transfer performance in rectangular channels with pin fin-dimple, pin fin and dimple arrays,” Turbo Expo: Power for Land, Sea, and Air, Vol. 43994, pp. 185-195.
[https://doi.org/10.1115/GT2010-22442]

-
Rao, Y., Wan, C., Xu, Y., and Zang, S., 2011, “Local heat transfer characteristics in channels with pin fin and pin fin-dimple arrays,” ASME Paper GT-2011-45449.
[https://doi.org/10.1016/j.ijthermalsci.2011.06.013]

-
Murata, A., Nishida, S., Saito, H., Iwamoto, K., Okita, Y., and Nakamata, C., 2011, “Heat transfer enhancement due to combination of dimples, protrusions, and ribs in narrow internal passage of gas turbine blade,” Turbo Expo: Power for Land, Sea, and Air, Vol. 54655, pp. 1173-1182.
[https://doi.org/10.1115/GT2011-45356]

-
Wang, C. C., Lo, J., Lin, Y. T., and Liu, M. S., 2002, “Flow visualization of wave-type vortex generators having inline fin-tube arrangement,” Int. j. heat and mass transfer, Vol. 45, No. 9, pp. 1933-1944.
[https://doi.org/10.1016/S0017-9310(01)00289-7]

-
Oh, Y., and Kim, K., 2021, “Effects of position and geometry of curved vortex generators on fin-tube heat-exchanger performance characteristics,” Applied Thermal Engineering, Vol. 189, 116736.
[https://doi.org/10.1016/j.applthermaleng.2021.116736]

-
Ames, F. E., Nordquist, C. A., and Klennert, L. A., 2007, “Endwall heat transfer measurements in a staggered pin fin array with an adiabatic pin,” Turbo Expo: Power for Land, Sea, and Air, Vol. 47934, pp. 423-432.
[https://doi.org/10.1115/GT2007-27432]

-
Celik, I. B., Ghia, U., Roache, P. J., and Freitas, C. J., 2008, “Procedure for estimation and reporting of uncertainty due to discretization in CFD applications,” Journal of fluids Engineering-Transactions of the ASME, Vol. 130, No. 7, 078001.
[https://doi.org/10.1115/1.2960953]

-
Ye, L., Liu, Z., Gao, C., Yang, X., and Feng, Z., 2017, “Numerical Study on Heat Transfer Performance of a New-Proposed Pin-Fin in an Internal Channel,” ASME, In Turbo Expo: Power for Land, Sea, and Air, Vol. 50879, p. V05AT11A014.
[https://doi.org/10.1115/GT2017-64573]

-
Zhang, F., Wang, X., Li, J., Zheng, D., and Zhou, J., 2017, “Numerical Study on the Flow and Heat Transfer Characteristics in Rectangular Channels With Grooves and Different Protrusions,” ASME, In Turbo Expo: Power for Land, Sea, and Air, Vol. 50879, p. V05AT11A005.
[https://doi.org/10.1115/GT2017-63737]

-
Singh, P., Ji, Y., and Ekkad, S. V., 2018, “Experimental and numerical investigation of heat and fluid flow in a square duct featuring criss-cross rib patterns,” Applied Thermal Engineering, Vol. 128, pp. 415-425.
[https://doi.org/10.1016/j.applthermaleng.2017.09.036]

-
Liu, J., Hussain, S., Wang, J., Wang, L., Xie, G., and Sundén, B., 2018, “Heat transfer enhancement and turbulent flow in a high aspect ratio channel (4: 1) with ribs of various truncation types and arrangements,” International Journal of Thermal Sciences, Vol. 123, pp. 99-116.
[https://doi.org/10.1016/j.ijthermalsci.2017.09.013]

-
Webb, R. L., 1981, “Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design,” international journal of heat and mass transfer, Vol. 24, No. 4, pp. 715-726.
[https://doi.org/10.1016/0017-9310(81)90015-6]

-
Kim, S. J., Choi, Y. S., Cho, Y., Choi, J. W., Hyun, J. J., Joo, W. G., and Kim, J. H., 2020, “Analysis of the Numerical Grids of a Francis Turbine Model through Grid Convergence Index Method,” The KSFM Journal of Fluid Machinery, Vol. 23, No. 2, pp. 16-22.
[https://doi.org/10.5293/kfma.2020.23.2.016]