대형 유체기계 최적화 문제의 차원 축소를 위한 스크리닝 방식에 관한 연구

1. 서 론

최근 다양한 분야의 특성을 고려한 최적설계가 중요시되면서 설계 과정에서 반드시 필요한 성능지수의 종류가 다양해지고 있다. 이에 따라 엔지니어가 고려해야하는 설계변수 개수도 많아지고 있다.

일반적으로 설계변수 개수가 많아질수록 최적설계 과정에서 필요로 하는 해석, 실험 횟수가 기하급수적으로 증가하게 된다. 그러므로 설계변수 개수가 많은 대형 최적화 문제는 주요 설계변수를 찾는 스크리닝 과정이 필수라고 할 수 있다. 스크리닝이란 성능지수에 영향을 크게 끼치는 설계변수의 조합을 찾는 것으로 스크리닝 결과에 따라 최적설계 솔루션과 솔루션을 도출하는 시간이 달라지게 된다.

기존 스크리닝 방식은 민감도 기준을 설정하여 설계변수를 선정하는 방식과 성능별로 주요 설계변수의 합집합을 취하는 방식, 이렇게 크게 두 종류로 나눠볼 수 있다. 민감도 기준을 설정하는 방식의 경우, 특정 성능지수에 영향을 크게 끼치는 설계변수들이 집중적으로 선정되면서 각 성능지수들의 설계자유도가 균등하지 않을 수 있다는 단점이 존재한다. 또한 합집합 방식의 경우는 성능 별로 주요 설계변수를 모두 취하다보니, 사용자가 스크리닝을 통해 원하는 설계변수 개수만큼 조절이 어려울 수 있으며, 상대적으로 많은 설계변수가 선정될 수도 있어서 스크리닝의 효과가 반감할 수 있다.

이러한 단점들을 보완하기 위해 공학 분야에서는 다양한 스크리닝 연구가 진행되어 왔다. 차량의 충돌내구성 설계를 위해 스크리닝 과정에서 선형 근사모델을 사용한 경우도 있으며⁽¹⁾, 수력 터빈의 최적 설계 과정에서 전역 민감도 분석을 이용하여 스크리닝을 수행한 연구도 있었다⁽²⁾. 또한 신뢰성 기반 최적설계에 적합하도록 성능지수 변동량을 고려한 스크리닝 연구도 있었다⁽³⁾.

고려해야 하는 성능지수와 설계변수가 많은 대형 최적화 문제의 경우, 각 성능지수들이 균등하게 설계자유도를 가질 수 있도록 스크리닝을 수행하는 것이 중요하다. 그러므로 본 연구에서는 사용자가 원하는 설계변수 개수만큼 선택 가능하고, 동시에 특정 성능지수에 설계 자유도가 집중되지 않도록 하는, 즉 모든 성능지수들이 최대한 균등하게 설계 자유도를 가질 수 있도록 하는 새로운 스크리닝 방식을 제안하려고 한다.

2. 스크리닝 방법론 소개

2.1 민감도 분석

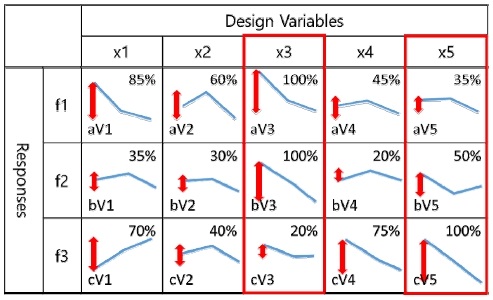
실험계획법 결과를 이용하여 Analysis of Mean (ANOM)⁽⁴⁾ 분석을 수행하면 Fig. 1과 같이 각 설계변수에 의한 각 성능지수의 변동량을 계산할 수 있다. 변동량이란 성능지수의 최대값과 최소값 사이의 크기 차이를 의미한다.

Fig. 1

Design sensitivity matrix

특정 성능지수에 대해 각 설계변수에 의한 변동량 중 가장 큰 값을 100%로 설정하여 이 값을 기준으로 나머지 변동량에 대해서도 상대적인 %값을 계산한다. 이와 같은 방식으로 나머지 성능지수에 대해서도 %값을 계산하면 Fig. 1과 같이 Design Sensitivity Matrix를 도출할 수 있다.

2.2 중요 설계변수 선정

본 연구에서는 각 설계변수에 의한 성능지수의 변동량 선형합을 설계자유도 정의에 사용하였다. 우선, Design Sensitivity Matrix에서 각 성능지수에 대해 변동량 값이 100%인 설계변수를 모두 주요 설계변수로 선정한다. 특정 성능지수에 대해 주요 설계변수의 변동량 선형 합을 동일한 특정 성능지수에 대한 모든 설계변수의 변동량 선형 합으로 나눠준다. 이것을 특정 성능지수가 갖는 설계자유도라 정의한다. 예를 들어, Fig. 1에서 각 성능지수에 대해 변동량 값이 100%인 설계변수는 x3, x5 이며, 이 두 설계변수가 주요 설계변수로 선정된다. 이 경우, 성능지수 f1의 설계자유도는 식 (1)과 같이 계산되어진다.

$\[ \frac{a V3+a V5}{a V1+a V2+a V3+a V4+a V5}=\frac{100+35}{85+60+100+45+35} \]$

(1)

즉, 설계자유도란 주요 설계변수만을 사용하는 경우, 전체 설계변수를 사용하는 경우 대비 상대적으로 해당 성능지수가 변동할 수 있는 비율을 의미한다. 설계자유도 값이 클수록 더욱 넓은 범위에서 성능지수 값을 변화시킬 수 있는 것이다.

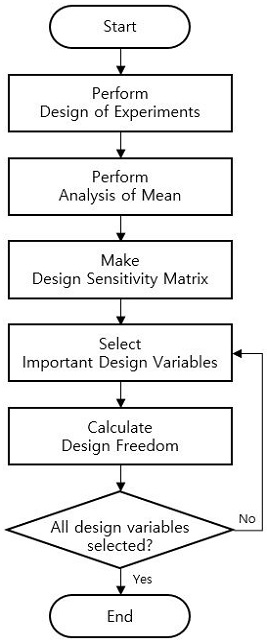
동일한 방식으로 나머지 성능지수에 대해서도 설계자유도를 계산한다. 가장 작은 설계자유도 값을 갖는 성능지수에 대해 이미 주요 설계변수로 선정된 설계변수 외에 나머지 설계변수 중 해당 성능지수에 대해 가장 높은 변동량 값을 갖는 설계변수를 주요 설계변수에 추가한다. 그 후, 모든 주요 설계변수를 이용하여 각 성능지수에 대해 다시 설계자유도를 계산한다. 예를 들어, Fig. 1에서 가장 작은 설계자유도 값을 갖는 성능지수가 f3인 경우, 기존 주요 설계변수인 x3, x5를 제외한 나머지 설계변수 중에서 가장 큰 변동량 값을 갖는 x4가 주요 설계변수에 추가되는 것이다. 그리고 x3, x4, x5를 주요 설계변수로 하여 다시 각 성능지수에 대해 설계자유도를 계산하는 것이다.

Fig. 2와 같이 위의 과정을 모든 설계변수가 선정될 때까지 반복하며, 선정되는 순서대로 설계변수 중요도 랭킹이 부여된다.

Fig. 2

Flow chart of the proposed screening

3. 스크리닝 성능 평가

3.2. 평가 예제

주요 제원이 Table 1과 같은 축류팬 설계문제를 사용하였다. Fig. 3에 나와 있는 해석 소프트웨어 FanDAS, CFturbo를 이용하여 각각 모델링하였으며, 서로 다른 설계변수를 적용하였다. 그리고 PIDO (Process Integration and Design Optimization) 소프트웨어인 PIAnO⁽⁶⁾를 이용하여 Fig. 4와 같이 FanDAS, CFturbo와 각각 통합하여 해석 자동화를 하였으며, 이렇게 구성된 두 가지 예제를 이용하여 스크리닝 성능 평가를 진행하였다.

Table 1

Design specification of the axial fan

Fig. 3

(a) FanDAS and (b) CFturbo

Fig. 4

Automation using PIAnO

3.2.1 축류팬 예제 1

Total efficiency, Total pressure, Noise, Power 이렇게 네 가지 성능지수를 선정하였다. FanDAS의 공력음향학적 해석방법에 따라 소음은 Sound pressure level[dBA]을 계산하였고, 동력은 전압손실을 감안한 유체동력(Fluid power)을 계산하였으며, 이를 통해 유체동력과 입력동력(Input power)의 비율인 전압 효율도 계산하였다. 상세한 해석방법과 계산절차는 참고문헌^(7),(8)에 기술되어 있다.

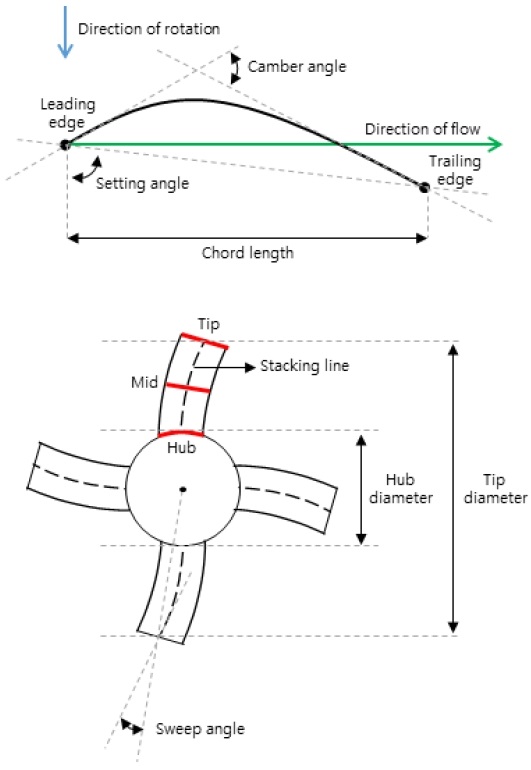
FanDAS가 포함하고 있는 입력변수 중에서 유체역학적으로 Axial fan 성능에 큰 영향을 끼치는 것으로 이미 잘 알려진 21개의 설계변수를 선정하였다. Tip 직경 대비 Hub 직경의 비율을 의미하는 Hub to tip ratio, Rotor와 Stator의 Hub, Mid, Tip 위치에서 Leading edge와 Trailing edge 사이의 축방향 길이를 뜻하는 chord length, 회전 방향으로 Blade의 휘어진 정도를 의미하는 Sweep angle, Mid 위치에서의 Chord length 대비 Blade의 최대 두께의 비율을 의미하는 Maximum blade thickness to mid chord length ratio, Rotor와 Stator의 Blade 개수, 회전 방향과 Blade의 엇갈린 정도를 의미하는 Setting angle, Blade 단면의 휘어진 정도를 의미하는 Camber angle을 설계변수로 선정하였다.

설계변수의 초기 값들은 Free vortex method를 이용하여 선정하였고, 이렇게 선정된 초기 값들을 기준으로 Setting angle 및 Camber angle의 설계 범위는 블레이드에 사용되는 airfoil의 유효입사각을 감안하여 ±5%로 설정했으며, 블레이드 시위길이는 약 ±15%, Maximum blade thickness to mid chord length ratio는 ±5%로 설정하였다. 그리고 Hub to tip ratio, Sweep angle, 동익과 정익의 개수는 Axial fan의 작동 환경과 기하학적인 면을 고려하여 상, 하한 범위를 결정하였다. 설계변수의 상, 하한 범위는 Table 2에 정리하였으며, Fig. 5에 설계변수를 도식화하였다.

Table 2

Initial values, lower bounds and upper bounds of design variables in the axial fan design problem 1

Fig. 5

Geometric design variables of the axial fan

해석 소프트웨어 FanDAS에서는 Hub에서 Tip까지 16등분을 하여 각 위치에서의 Setting/Camber angle 값들을 입력할 수 있다. 본 연구에서는 Setting/Camber angle 1, 5, 9, 13, 17을 설계변수로 사용하였으며, 이 5군데 값을 이용하여 4차 다항식을 생성하여 설계변수로 선정되지 않은 위치에서의 Setting/Camber angle 값을 계산하였다. 그리고 이 값들이 각 위치에 자동으로 입력되도록 설정하였다.

3.2.2. 축류팬 예제 2

Total efficiency, Total pressure 이렇게 두 가지 성능지수를 선정하였다. 그리고 CFturbo가 포함하는 입력 변수 중 Axial Fan 성능에 큰 영향을 끼치는 것으로 이미 잘 알려진Rotor의 blade 개수, Chord length, Setting angle, Camber angle과 Hub 직경 총 17개의 설계변수를 선정하였다.

축류팬 예제 1과 동일하게 설계변수의 초기 값들은 Free vortex method를 이용하여 선정하였고, 이렇게 선정된 초기 값들을 기준으로 Setting angle 및 Camber angle의 설계 범위는 ±5%, 블레이드 시위길이는 약 ±16%로 설정하였다. 또한 Hub diameter, 동익 개수는 Axial fan의 작동 환경과 기하학적인 면을 고려하여 상, 하한 범위를 결정하였다. 설계변수의 상, 하한 범위는 Table 3에 정리하였으며, Fig. 5에 설계변수를 도식화하였다.

Table 3

Initial values, lower bounds and upper bounds of design variables in the axial fan design problem 2

해석 소프트웨어 CFturbo를 통해 Hub에서 Tip까지 8등분을 하여 각 위치에서의 Chord length, Setting/Camber angle 값들이 입력되도록 설정하였다. 본 연구에서는 Chord length, Setting/Camber angle 1, 3, 5, 7, 9를 설계변수로 사용하였으며, 축류팬 예제 1과 같이 이 5군데 값을 이용하여 4차 다항식을 생성하고, 설계변수로 선정되지 않은 위치에서의 Chord length, Setting/Camber angle 값들이 자동으로 계산되어 입력되도록 설정하였다.

4. 결 과

4.1. 축류팬 예제 1

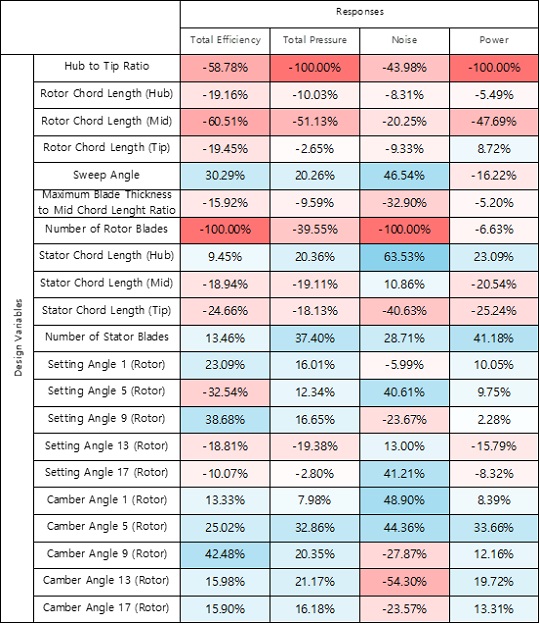
Fig. 6은 제안한 스크리닝 방식을 이용하여 얻은 축류팬 예제 1의 Design sensitivity matrix이다. 바탕색이 적색인 경우는 설계변수 값이 커질수록 성능지수 값이 감소하는 것을 의미하며, 청색은 설계변수 값이 커질수록 성능지수 값도 증가하는 것을 의미한다. 흰색에 근접할수록 설계변수 변화에 따른 성능지수의 변동량이 적다는 것을 의미한다.

Fig. 6

Design sensitivity matrix of the axial fan design problem 1

Design sensitivity matrix를 이용하여 모든 설계변수에 중요도 랭킹을 부여하고, Table 4와 같이 제안한 스크리닝 방식을 통해 상위 7개의 설계변수가 선정되었다. 기존 스크리닝 방식을 통해 선정된 상위 7개의 설계변수도 Table 4에 정리하였다. 5개의 설계변수는 동일하며, 2개가 서로 다르게 선정되었다.

Table 4

Selected design variables of the axial fan design problem 1

각각 선정된 설계변수만을 이용하여 3 Level FFD를 수행하였으며, Table 5와 같이 FFD 데이터를 통해 성능지수의 최대-최소값(Diff.)을 계산하였다. 본 연구에서 제안한 스크리닝 방법을 이용하는 경우, 4개의 성능지수 중 3개에서 최대-최소값이 더 크게 나왔다. 최대-최소값은 변동량을 의미하며, 변동량이 크다는 것은 설계 자유도가 높다는 것을 의미한다.

Table 5

Comparison of FFD results in the axial fan design problem 1

평균 변동량과 변동량의 표준편차를 계산하기 위해 각 성능지수들의 변동량 크기를 서로 비슷한 크기로 맞춰줄 필요성이 있다. 그러므로 각 성능지수들의 변동량 중 큰 값으로 스케일링을 수행하였으며, 그 결과(Norm. Diff.)를 Table 5에 정리하였고, 스케일링한 값을 이용한 변동량의 평균(Ave.)과 표준편차(St. Dev.) 값도 Table 5에 같이 정리하였다.

본 연구에서 제안한 스크리닝 방법을 통해 설계변수를 선정하는 경우, 성능지수들의 평균 변동량이 기존 대비 약 3% 증가하였다. 또한 변동량의 표준편차는 기존 대비 약 63% 감소하였다. 즉, 기존 방법 대비 각 성능지수들의 평균적인 설계자유도가 향상되었으며, 상대적으로 균등하게 설계자유도가 분포됨을 확인할 수 있었다.

4.2. 축류팬 예제 2

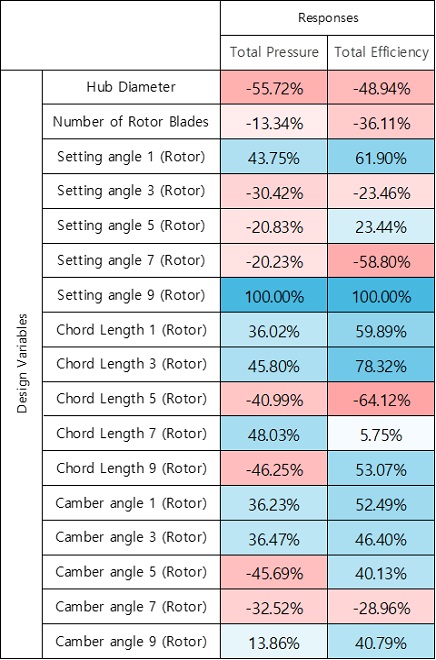
Fig. 7은 제안한 스크리닝 방식을 이용하여 얻은 축류팬 예제 2의 Design sensitivity matrix이다. 축류팬 예제 1과 동일하게 색상 스펙트럼을 통해 설계변수 변화에 따른 성능지수의 변동량 방향을 나타내고 있다.

Fig. 7

Design sensitivity matrix of the axial fan design problem 2

Design sensitivity matrix를 이용하여 모든 설계변수에 중요도 랭킹을 부여하고, Table 6과 같이 제안한 스크리닝 방식을 통해 상위 5개의 설계변수가 선정되었다. 기존 스크리닝 방식을 통해 선정한 상위 5개의 설계변수도 Table 6에 정리하였다. 4개의 설계변수는 동일하며, 1개가 서로 다르게 선정되었다.

Table 6

Selected design variables of the axial fan design problem 2

축류팬 예제 1과 동일하게 제안한 방법과 기존 방법을 비교하였으며, FFD를 통해 도출한 각 성능지수의 최대-최소(Diff.), 스케일링한 최대-최소(Norm. Diff.), 변동량의 평균(Ave.)과 표준편차(St. Dev.)를 Table 7에 정리하였다.

Table 7

Comparison of FFD results in the axial fan design problem 2

본 연구에서 제안한 스크리닝 방법을 통해 설계변수를 선정하는 경우, 2개의 성능지수 모두에서 최대-최소 값이 더 크게 나왔으며, 평균 변동량은 기존 대비 약 47% 증가하였다. 제안한 방법을 통해 성능지수들의 평균적인 설계자유도를 크게 향상시킬 수 있었다.

스케일링한 변동량 값이 제안한 방법에서 모두 ‘1.00’이므로 변동량의 표준편차는 ‘0.00’으로 계산되었다. 그러므로 수치적으로는 기존 대비 변동량의 표준편차가 100% 감소한 것으로 계산되었다.

5. 결 론

본 연구에서는 2가지 축류팬 예제를 이용하여 새로운 스크리닝 방법을 검증하였다. 실험계획법을 이용하여 각 성능지수의 평균 변동량, 변동량의 표준편차를 계산하고, 이를 통해 설계자유도를 비교하는 방식으로 검증을 진행하였다.

첫 번째 축류팬 예제의 경우, 기존과 제안한 스크리닝 방식 모두 총 21개 설계변수 중 상위 7개를 선정하였다. 본 연구에서 제안한 스크리닝 방식을 통해 설계변수를 선정하는 경우, 성능지수들의 평균 설계자유도가 기존 대비 약 3% 증가하였으며, 설계자유도의 표준편차는 기존 대비 약 63% 감소하였다.

두 번째 축류팬 예제의 경우, 기존과 제안한 스크리닝 방식 모두 총 17개 설계변수 중 상위 5개를 선정하였다. 본 연구에서 제안한 스크리닝 방식을 통해 설계변수를 선정하는 경우, 성능지수들의 평균 설계자유도가 기존 대비 약 47% 증가하였다. 제안한 방식에서 두 성능지수의 스케일링 된 변동량이 모두 동일하게 ‘1.00’이 나온 관계로 설계자유도의 표준편차는 기존 대비 수치적으로 100% 감소한 것으로 나왔다.

본 논문에서 제안한 Screening 방법론은 단순히 영향력 순서대로 주요 설계변수를 선정한 것이 아니기 때문에 주요 설계변수로 선정되지 못한 다른 설계변수가 성능지수에 더 큰 영향력을 끼칠 수 있다. 하지만 단순히 영향력 순서대로 주요 설계변수를 선정했다면 특정 성능지수들의 설계자유도는 개선되겠지만 다른 성능지수들의 설계자유도는 악화될 것이다. 이러한 현상이 향후 모든 성능지수들을 고려해야 하는 최적설계 단계에서는 좋지 않을 것이라 판단되어 모든 성능지수들의 설계자유도를 균등하게 향상시킬 수 있는 방향으로 주요 설계변수를 선정하였다.

두 결과를 통해, 본 연구에서 제안한 새로운 스크리닝 방식을 사용한다면 사용자는 원하는 설계변수 개수만큼 선택하면서 동시에 모든 성능지수들의 설계자유도를 균등하게 향상시킬 수 있음을 확인하였다.

Acknowledgments

2021 한국유체기계학회 동계학술대회 발표 논문, 2021년 12월 1일~12월 3일, 휘닉스 제주

이 논문은 2021년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구입니다(No. 20212020800261, 가변형 고효율 유체기계 핵심 기술 및 운영 시스템 개발).

References

• Craig K.J., Stander N., Dooge D.A., and Varadappa S., 2005, "Automotive crashworthiness design using response surface-based variable screening and optimization," Engineering Computations: International Journal for Computer-Aided Engineering and Software, Vol. 22, No. 1, pp. 38~61. [https://doi.org/10.1108/02644400510572406]
• U. Shrestha, Y.D. Choi, J.W. Park, and H.K. Cho, 2021, "Reduced-dimensional design optimization of stay vane and casing of reaction hydro turbines using global sensitivity analysis," KSME Journal of Mechanical Science and Technology, Vol. 35, No. 4, pp. 1487~1499. [https://doi.org/10.1007/s12206-021-0314-9]
• H.K. Cho, S.J. Bae, K.K. Choi, Lamb D., and R.J. Yang, 2014, "An efficient variable screening method for effective surrogate models for reliability-based design optimization," Struct Multidiscip Optim, Vol. 50, No. 5, pp. 717~738. [https://doi.org/10.1007/s00158-014-1096-9]
• P.F. Ramig, 1983, "Applications of the analysis of means," J. Qual. Technol., Vol. 15, No. 1, pp. 19~25. [https://doi.org/10.1080/00224065.1983.11978837]
• Montgomery, D.C., 2005, Design and Analysis of Experiments 6th edition, John Wiley & Sons.
• PIDOTECH, 2021, PIAnO User's Manual, Korea.
• C. Lee, and H.G. Kil, 2010, “A Computerized Design System of the Axial Fan Considering Performance and Noise Characteristics,” The KSFM Journal of Fluid Machinery, Vol. 13, No. 2, pp. 48~53. [https://doi.org/10.5293/KFMA.2010.13.2.048]
• C. Lee, 2021, “A Performance Prediction Method of the Axial Flow Fans with Blade Sweep,” The KSFM Journal of Fluid Machinery, Vol. 24, No. 5, pp. 24~29. [https://doi.org/10.5293/kfma.2021.24.5.024]