A Study of Supersonic Nozzle Design for Partial Admitted Turbine Used on Organic Rankine Cycle

1. 서 론

가용한 화석연료의 자원이 고갈되어 감에 따라 전 세계적으로 재생에너지의 활용에 관한 많은 연구가 수행되고 있다. 이러한 재생에너지로 활용되는 것으로는 풍력, 태양열, 지열 등 다양한 종류가 있으므로 이들로부터 유용한 에너지를 얻게 된다. 태양전지의 경우에는 바로 전기에너지를 얻을 수 있으며, 풍력의 경우는 풍력터빈으로 부터 전기에너지를 생산하게 된다. 반면에 태양열이나 산업체에서 발생되는 폐열, 지열 등은 열원이므로 열로써 직접이용하거나, 유기랭킨 사이클을 이용하여 전기를 생산하기도 한다.

일반적으로 유기랭킨 사이클에 사용되는 작동유체는 증발 온도가 수증기에 비하여 낮고, 응축온도는 높기 때문에 비교적 낮은 온도의 열원이 있는 경우에도 사이클 형성이 용이하므로 저온의 열원이 있더라도 전기에너지로의 변환이 가능한 장점이 있다. 이러한 용도로 사용되는 작동유체는 기본적으로 오존을 파괴하지 않아야 하며, 지구 온난화 지수가 낮으며, 가연성이 낮고, 효율이 높으며, 인체에 무해하고, 저비용이 요구되는 냉매를 사용하여야 한다. 이러한 용도로 CO₂와 같은 자연냉매를 사용하기도 하나 추가적인 장치의 필요로 비용적 측면에서 불리하므로, 현재에는 CFC/HFC 계열의 단점을 개선한 대체냉매를 많이 사용하고 있다. 유기랭킨 사이클에 사용될 수 있는 적절한 작동유체에 대한 연구((1^-8))들이 많이 수행되었다.

저온의 열원을 이용하여 유기랭킨 사이클을 작동하는데 있어서 수 MW 급에서 수 W 급까지 열원의 종류에 따라 다양한 출력을 얻고 있으며, 열원도 지열(9), 바이오매스(10), 산업체 폐열(11), 태양열(12) 등 다양한 열원을 이용하고 있다. 이러한 열원으로부터 전기에너지를 생산하기 위한 팽창기도 스크롤(13), 스크류(14), 왕복피스톤(15), 베인(16), 터보형(17) 등 여러 종류가 적용되고 있다. 출력이 큰 경우에는 터보형이 주로 많이 사용되고 있으므로 출력이 적어지는 경우에는 용적식의 팽창기가 많이 사용되고 있다.

유기랭킨 사이클을 이용하여 재생에너지를 회수하는 경우에 충분한 열원이 있는 경우에는 대형으로 설치하여 일정한 출력을 얻을 수 있겠지만, 일반적으로 재생하고자 하는 열원들은 일정하게 공급되지 않는다. 이러한 경우에 터보형 팽창기는 탈설계점에서의 작동에 대하여서도 적절히 대응하는 장점이 있기 때문에 용적식 팽창기보다는 변동열원을 가진 시스템에 적용할 수 있는 이점이 있다. 하지만 터보형의 경우는 대용량의 경우에 높은 효율을 나타내지만 소용량의 경우에는 높은 회전속도에서 작동되며, 부분분사율에 따라 낮은 효율을 보여주기도 한다.

국내 산업단지를 기준으로 배출되는 폐열의 수준을 고려하면 30 kW 이하의 출력을 얻을 수 있는 유기랭킨 사이클의 구성이 적절하다. 이러한 용량의 터보팽창기가 변동열원에서 작동하는 경우에 열원의 가용한 용량에 따라서 수십 W에서 수십 KW까지 출력을 얻기위하여서는 터빈은 부분분사에서 작동할 수 밖에 없다. 터빈이 부분분사에서 작동하는 경우에는 분사되는 속도가 회전속도를 좌우하므로 고효율에서 작동하도록 하는 분사속도를 얻기 위한 노즐의 설계가 중요하다. 따라서 노즐의 설계는 시스템의 성능에 영향을 미치는 핵심부품이 된다. 따라서 본 연구에서는 유기랭킨 사이클에 사용되는 노즐 설계(18)에 대한 구체적인 연구를 수행하였다.

2. 유기랭킨 사이클

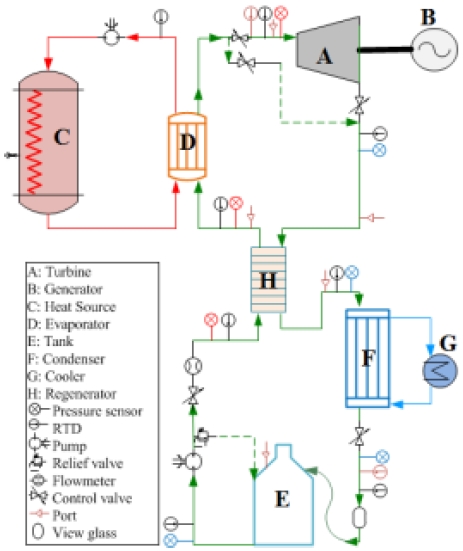
열원으로부터 동력을 얻는 유기랭킨 사이클의 작동원리를 나타내기 위한 구성도를 Fig.1에서 보여주고 있다. 그림에서의 가열기(C)는 일반적으로 산업체에서 발생되는 100 °C 전후의 낮은 온도를 가진 폐열, 태양열, 지열 등을 활용할 수 있다. 가열기에 사용되는 열매체로는 실리콘오일, 고압수 등이 사용되는데, 가열된 열매체는 열교환기(D : 증발기)에서 작동유체를 가열하여 액체상태에서 증기상태로 만든다. 증기상태인 작동유체는 고온고압의 상태에서 터빈(A)을 구동하게 되고 터빈의 출구에서 나온 저온저압의 증기는 열교환기(F:응축기)에서 액화된다. 액화된 작동유체는 탱크를 지나서 펌프에 의하여 가압되어 다시 증발기(D)로 들어가는 사이클의 과정이 이루어진다. 재생기(H)를 사용하는 경우에는 터빈에서 나온 고온의 작동유체가 펌프를 지나 고압이 된 저온의 작동유체를 가열기에 들어가기 전에 예열하는데 사용되므로 시스템의 효율을 증가할 수 있다.

Fig. 1.

Schematic diagram of an organic Rankine system

터빈은 전분사의 경우에는 정익과 동익으로 구성되어지나, 부분분사의 경우에는 동익으로 분사되어지는 분사영역이 제한되어지므로 일반적으로 전분사에서 적용하는 정익으로 구성하는 것보다는 정익을 대신하여 노즐로 구성하는 것이 효과적이다. 특히 가용한 열원이 일정하게 공급되지 못하는 경우에, 이에 대응하여 터빈을 운전하기 위하여서는 열원의 용량에 따라 작동유체의 질량유량을 조절하여야 하므로 여러 개의 노즐을 사용하여 선택적으로 사용할 수 있도록 하면 변동하는 열원에 대응할 수 있다. 따라서 노즐의 개수에 따라서 터빈은 여러 부분분사율에서 작동하게 된다.

유기랭킨사이클에 적용할 작동유체는 많은 연구결과를 참조하여 본 연구에서는 여러 종류의 작동유체 중에서 증기상태에서 터빈의 작동에 유리한 R245fa 를 작동유체로 선정하였다. 작동유체로 선정된 R245fa의 음속은 대략 공기의 1/3수준 정도이다.

3. 노즐설계

3.3 노즐축소영역설계

유기랭킨사이클이 작동하는데 가용한 열원에서 얻어진 노즐 입구에서의 전압력과 전온도를 기준으로 노즐이 쵸크되는 위치에서 압력과 온도를 구하여야 한다. 노즐 내에서의 유동장 예측을 위하여 노즐 형상과 함께 노즐 내부에서의 물성치룰 파악하여야 하므로, 노즐에서의 유동을 1차원적 유동, 단열, 균일유동으로 가정하고, 연속방정식, 모멘텀방정식, 총엔탈피, Gibbs 방정식 기준으로 다음과 같은 방정식을 지배방정식으로 사용한다.

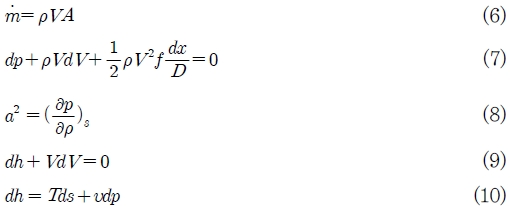
식(6-10)로부터 노즐에서의 유동으로 인한 압력손실식을 식(11)과 같이 구할 수 있게 된다.

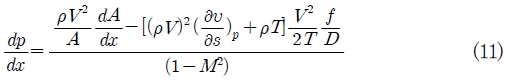
마찰계수 f 는 Fang et.al(19)이 제안한 식(12)을 사용하였으며, 표면거칠기는 30 μm 로 설정하였다.

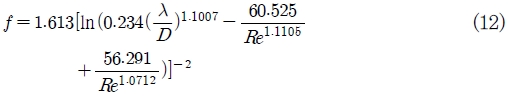
주어진 입구조건에서 노즐목에서의 쵸크상태값을 얻기 위하여서는 노즐목 앞부분에서의 형상이 필요하다. 이를 위하여 노즐이 쵸크되는 경우에 질량유량을 구하여야 한다. 하지만 쵸크상태의 물성치를 모르기 때문에 대략적으로 노즐이 쵸크되는 상태의 값을 적용하여, 쵸크 될 때의 질량유량을 구한다. 이를 위하여 식(4,5,13)를 사용하여 노즐목에서의 압력과 온도를 구하고, 이상기체의 가정으로부터 유도된 식을 적용하였으므로 이 결과를 보정하기 위하여 식(4,5,14)를 사용하여 노즐목에서 구한 압력과 온도를 앞서 구한 결과와 각각 평균하여 노즐목에서의 면적으로부터 질량유량을 구하게 된다. 계산상에서 작동유체인 R245fa의 물성치는 Refprop(20)을 사용 프로그램과 연동되도록 하였다.

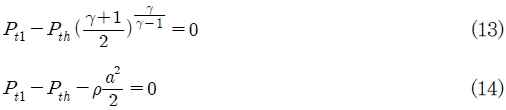
질량유량이 정하여지면 노즐입구에서 마하수를 0.2 정도할 수 있는 노즐의 입구 직경을 정하게 된다. 노즐의 축소영역에서의 형상을 만들기 위하여 목의 영역은 반경(r_up)을 기준으로 원형으로 하고, 상류부분은 1과 1a 의 위치를 기준으로 각각의 기울기와 좌표를 사용하여 3차 다항식으로 나타낼 수 있다. Fig. 2는 노즐의 축소되는 영역에서의 향상을 보여주고 있다.

Fig. 2.

Shape of nozzle converging region

이렇게 얻어진 형상을 기준으로 식(11-12)를 사용하여 재계산을 수행하여야 한다. 가정한 노즐목에서의 압력과 온도를 기준으로 얻어진 질량유량으로부터 노즐입구에서의 압력을 얻고, 이 압력을 초기조건으로 식(11)의 결과로 노즐목에서 압력과 온도를 얻게 되는데 이 압력과 온도가 일치될 때까지 계산을 수행하게 된다. 이렇게 구한 온도와 압력으로부터 최종적으로 노즐에서의 질량유량을 구하게 된다. 초기에 노즐입구 직경을 결정하였던 질량유량이 변경되었으므로 노즐입구에서의 마하수는 다소 변하게 된다. 만일 입구의 마하수를 원하는 속도로 한정하고자 한다면, 다시 입구직경을 계산하여 형상의 변경과 함께 반복계산을 하여야 한다.

3.4 노즐확대영역설계

초음속 노즐의 설계는 단상(single-phase)인 경우에는 특성곡선법을 이용하여 설계하는 방법(2122)이 많이 이용되고 있다. 따라서 작동유체의 물성치와 함께 특성곡선법으로 초음속 노즐의 형상설계가 가능하다. 팽창과정에서 작동유체가 이상(two-phase)유체로 되는 경우에는 일차원적인 해석법을 사용하여 설계(2324)를 할 수 있다. 본 연구 사용되는 R245fa 의 경우는 포화증기 선도의 변화가 dT/ds>0의 특성을 가지므로 dry 냉매로 분류된다. 따라서 팽창 시에 과열(superheated) 상태를 유지하므로 작동유체는 노즐 출구까지 단상을 유지하게 된다. 따라서 노즐의 기본 형상을 특성 곡선법으로 원형(circular)의 형상을 가진 초음속 노즐을 설계하였으며, 설계된 형상에서 난류경계층(25)의 두께를 추가하였다. 계산상에서 작동유체의 물성치는 Refprop(20)을 사용하였다.

원형의 노즐에서 특성곡선법을 적용하기 위하여서는 원형은 축대칭이므로 축대칭의 관계를 적용한다. 노즐목에서의 초기조건을 분포하여야 하는데 이를 위하여 이미 얻어진 노즐목에서의 압력과 온도를 2차원 설계를 위하여 음속(sonic)선에 분포하여야 한다. 2차원의 음속선을 설정하기 위하여 음속선은 이상기체의 가정으로 얻어진 Sauer’s 해석결과(21)를 도입하여 노즐목을 기준으로 분포하고 음속선에서의 위치에 따라 압력과 온도를 초기조건으로 분포한다.

노즐의 확대영역 형상은 초기에는 위치 1b와 2의 좌표값과 각각의 위치에서의 기울기와 함께 3차원 다항식으로 나타내지만 특성곡선법 계산으로 노즐의 형상이 유선을 따르도록 변경하고, 출구에서 원하는 마하수가 얻어지도록 노즐 확대영역의 길이와 노즐출구에서의 직경이 변경된다. Fig. 3은 노즐입구에서의 전온도가 100 °C 이고, 출구마하수가 1.6인 경우에 난류경계층을 고려하여 얻어진 형상을 보여주고 있다.

Fig. 3.

Shape of nozzle diverging region

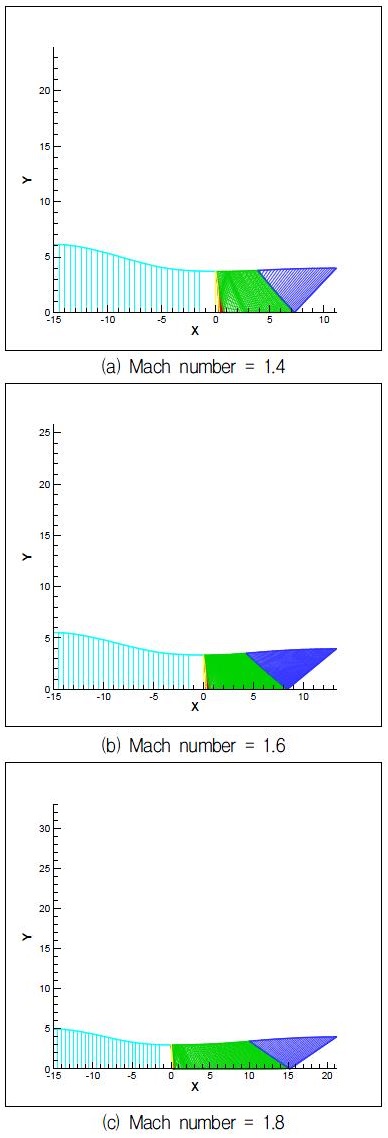
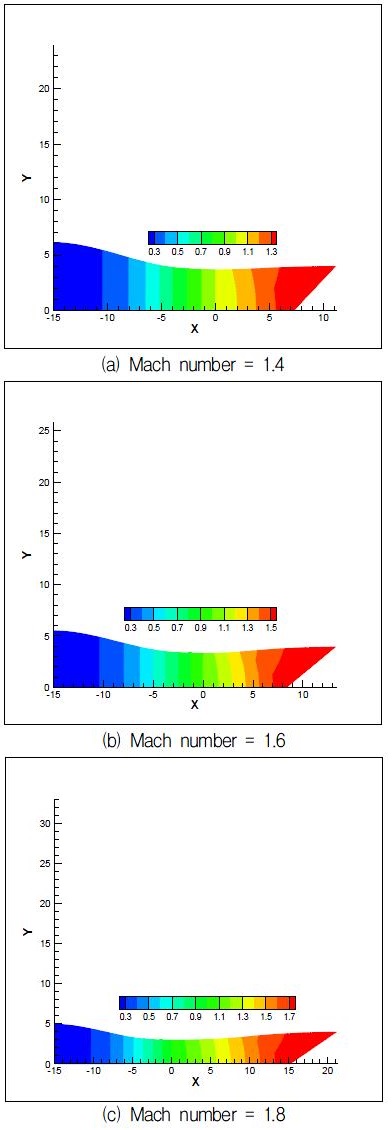
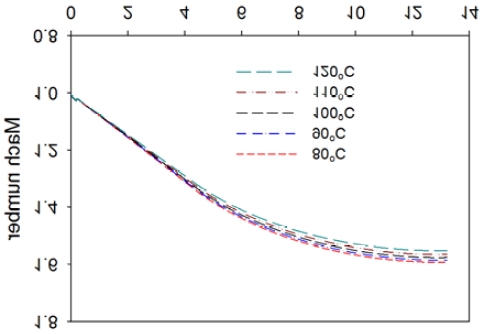
Fig. 4는 터빈에 적용하기 위하여 노즐출구의 직경을 동일하게 하면서 출구에서의 마하수가 1.4, 1.6, 1.8인 경우에 대하여 노즐확대 영역에서의 특성곡선들을 보여주고 있다. 출구에서의 직경을 동일하게 설정하였으므로 높은 출구마하수를 얻기 위하여서는 노즐목에서부터 출구까지 확대각도가 커져야 한다. 하지만 노즐출구에서의 직경이 동일하므로 반대로 마하수가 증가하기 위하여서는 노즐목이 축소되어야 한다. 따라서 노즐 출구에서의 마하수가 1.8인 경우에 노즐목이 축소되었음을 보여주고 있다. 또한 노즐목이 축소되면 동일한 입구조건에서 노즐에서 쵸크되어지는 질량유량이 감소하게 된다. 따라서 노즐입구에서의 마하수를 0.2 정도로 유지하게 되면 질량유량이 줄어들게 되는 경우에 노즐입구의 직경이 줄어들게 된다. 따라서 출구마하수가 1.8인 경우에 얻어진 노즐입구의 직경이 줄어든 것을 보여주고 있다. Fig. 5는 마하수의 분포를 보여주고 있는데 출구에서 요구하는 마하수에 도달하고 있음을 보여주고 있다.

Fig. 4.

Nozzle shape designed by characteristic method

Fig. 5.

Mach Number Contours on a Nozzle shape designed by characteristic method

3.5 노즐확대영역해석

유기랭킨 사이클을 작동하는데 있어서 일정하게 열원이 공급되지 않는 경우에 설계점 작동기준으로 설 계된 노즐을 입구조건의 변화에 따라서 매번 변경할 수는 없다. 단지 노즐의 개수를 조정하여 질량유량의 조정은 가능하다. 동일 노즐이 사용되는 경우에 쵸크가 발생되는 경우에 질량유량은 노즐출구의 압력을 낮추어도 질량유량은 증가하지 않는다. 하지만 노즐입구의 온도가 올라가면 압력이 상승하고, 압력 상승에 따라 밀도증가를 초래하여 동일노즐에서도 질량유량은 증가하게 된다. 따라서 초기조건의 변경에 따라 동일노즐에서의 출구변화를 확인하여야 한다.

노즐에서 압력감소는 설계점 작동기준으로 설계된 노즐형상과 함께 식(11-12)를 사용하여 구할 수 있다. 또한 노즐에서의 초크위치는 식(11)의 분자로부터 마하수가 1일 때의 값으로부터 구하게 된다.

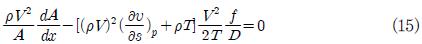
초크 위치에서의 압력 구배식은 식(11)의 분자를 미분하여(L’hopital의 정리로부터) 식(16)과 같이 구하게 된다.

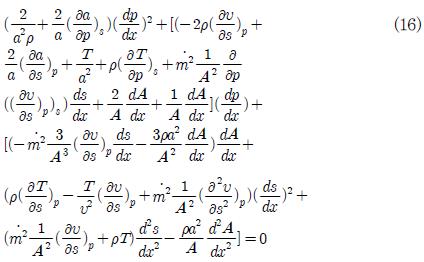
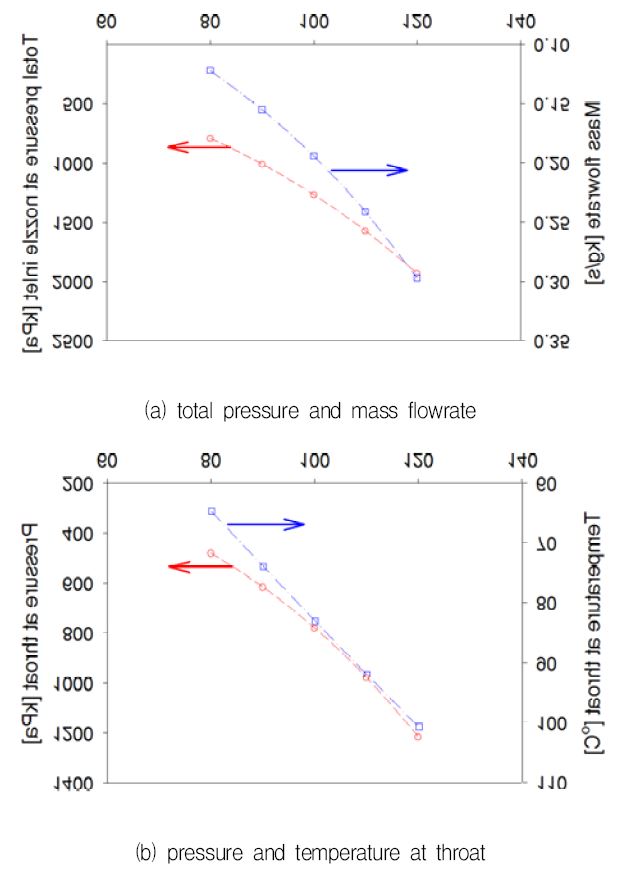
여기서 구한 압력구배와 쵸크위치에서의 물성치를 초기조건으로 하여 노즐의 주어진 형상과 함께 식(11)로부터 노즐의 확대영역을 따라서 압력을 얻게 되고, 전엔탈피의 조건과 함께 노즐 내부에서의 물성치를 얻게 된다. Fig. 6은 노즐입구 전온도가 변하는 경우에 예측되어지는 노즐확산영역에서의 마하수의 변화를 보여주고 있다. 출구에서의 마하수가 변하는 것을 확인할 수 있으며, 이러한 변화의 발생은 고정된 노즐형상에서 노즐입구의 온도가 변경됨으로 질량유량의 변화가 발생되었기 때문이다.

Fig. 6.

Variation of Mach Number along nozzle streamwise direction

노즐입구에서 온도증가에 따라 전압력의 변화를 Fig. 7에서 보여주고 있으며, 압력의 증가로 인하여 밀도가 상승하여 질량유량이 동일 노즐에서 쵸크가 되었을 경우에 증가됨을 보여주고 있다. 또한 노즐목에서 쵸크될 때의 압력과 온도도 노즐입구의 전온도의 증가에 의하여 증가함을 보여주고 있다.

Fig. 7.

Variation of thermodynamic properties versus total temperature at nozzle inlet

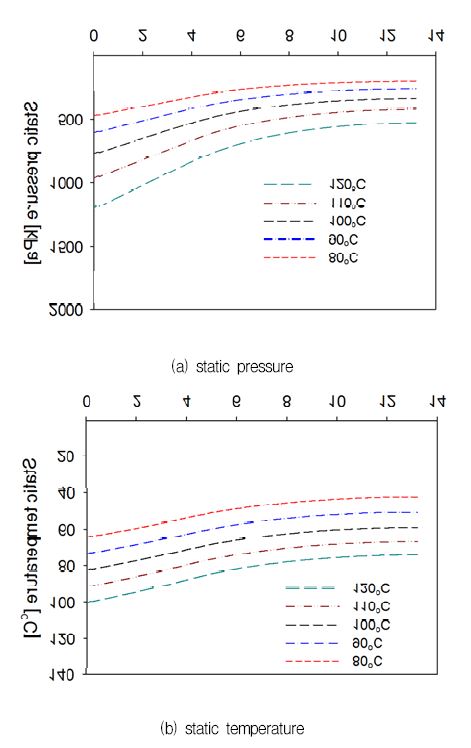
Fig. 8은 노즐 확산영역에서의 정압력과 정온도의 변화를 보여주고 있으며, 노즐입구 전온도의 증가에 따라 증가함을 보여주고 있다.

Fig. 8.

Variation of pressure and temperature along streamwise direction

3.6 노즐유동장해석

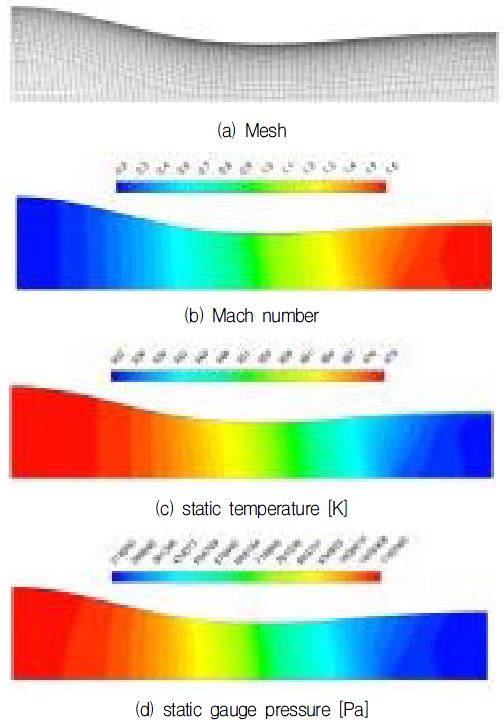
노즐 내부의 유동장을 해석하기 위하여 노즐입구에서의 전온도가 100 °C 인 경우를 기준으로 상용코드인 Fluent(26)를 사용하여 수행하였다. Density-based solver 를 사용하고, 난류모델은 k-ε을 적용하였다. 계산은 implicit Roe- FDS scheme을 적용하고, 2nd order의 정확도를 갖도록 공간을 이산화 하였다. 경계조건은 입구에 질량유량을 고정하고, 출구에는 압력을 고정하였다.

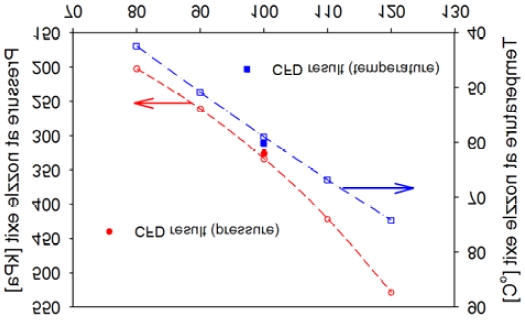
Fig. 9는 계산에 적용된 격자의 형상을 보여주고 있는데, 벽면에서의 격자는 y+ 값이 1근처의 값을 갖도록 하였다. 마하수의 변화에서는 출구에서 1.61의 평균 마하수가 얻어졌으며, 출구에서의 압력과 온도는 325.7 kPa 와 60.3 °C의 값을 얻었다. 노즐확산영역에서의 예측결과와의 비교를 나타내고 있는 Fig. 10에서 보여주는 것과 같이 일치하는 경향을 보여주고 있다. 입구에서의 전압력도 1265 kPa 이 얻어졌으므로 R245fa의 특성과도 일치하는 결과를 얻었다.

Fig. 9.

Flow structures within the nozzle

Fig. 10.

Comparison of predicted results and CFD results

4. 결 론

폐열, 지열, 태양열 등의 열원으로부터 재생에너지로 활용하기 위한 유기랭킨 사이클의 핵심부품인 초음속노즐의 설계에 대한 연구를 작동유체 R245fa 기준으로 연구를 수행하였으며, 시스템의 작동조건이 변경되는 경우를 고려하여, 우선 설계점 기준으로 특성곡선법으로 노즐을 형상화하였다. 형상화된 노즐을 기준으로 작동조건이 변경되는 경우에 대한 사이클수행을 위한 해석기섭을 확보하였으며, 형상화된 노즐에서의 CFD 결과와 비교하여 보았을 때 노즐에서의 예측 값과 잘 일치하는 결과를 얻었다. 따라서 재생하고자 하는 열원의 변동에 대한 사이클 해석뿐만 아니라 부분분사에서 작동하는 터빈의 고효율 시스템의 구성이 가능하게 되었다.

Acknowledgments

본 연구는 산업통상자원부, 한국산업기술진흥원, 호남지역사업평가원의 광역경제권 선도산업 육성사업으로 수행된 연구결과입니다.

References

• Maizza, V., and Maizza, A., (1996), Working Fluids in Non-Steady Flows for Waste Energy Recovery Systems, Applied Thermal Engineering, 16(7), p579-590. [https://doi.org/10.1016/1359-4311(95)00044-5]
• Hung, T. C., Shai, T. Y., and Wang, S. K., (1997), A Review of Organic Rankine Cycles for the Recovery of Low-Grade Waste Heat, Energy, 22(7), p661-667. [https://doi.org/10.1016/S0360-5442(96)00165-X]
• Liu, B. T., Chie, K. H., and Wang, C. H., (2004), Effect of Working Fluids on Organic Rankine Cycle for Waste Heat Recovery, Energy, 29, p1207-1217. [https://doi.org/10.1016/j.energy.2004.01.004]
• Tchanche, B. F., Papadakis, G., Lambrinos, G., and Frangoudakis, A., (2009), Fluid Selection for a Low- Temperature Solar Organic Rankine Cycle, Applied Thermal Engineering, 29, p2468-2476. [https://doi.org/10.1016/j.applthermaleng.2008.12.025]
• Hung, T. C., Wang, S. K., Kuo, C. H., Pei, B. S., and Tsai, K. F., (2010), A Study of Organic Working Fluids on System Efficiency of an ORC Using Low-Grade Energy Sources, 35, p1403-1411. [https://doi.org/10.1016/j.energy.2009.11.025]
• Chen, H., Goswami, D. Y., and Stefanakos, E. K., (2010), A Review of Thermodynamic Cycles and Working Fluids for the Conversion of Low-Grade Heat, Renewable and Sustainable Energy Reviews, 14, p3059-3067. [https://doi.org/10.1016/j.rser.2010.07.006]
• Vélez, F., Segovia, J. J., Martín, M. C., Antolín, G., Chejne, F., and Quijano, A., (2012), A Technical, Economical and Market Review of Organic Rankine Cycles for the Conversion of Low-Grade Heat for Power Generation, Renewable and Sustainable Energy Reviews, 16, p4175-4189. [https://doi.org/10.1016/j.rser.2012.03.022]
• Bao, J., and Zhao, L., (2013), A Review of Working Fluid and Expander Selections for Organic Rankine Cycle, Renewable and Sustainable Energy Reviews, 24, p325-342. [https://doi.org/10.1016/j.rser.2013.03.040]
• Hettiarachchi, H. D. M., Golubovic, M., Worek, W. M., and Ikegami, Y., (2007), Optimum Design Criteria for an Organic Rankine Cycle Using Low-Temperature Geothermal Heat Sources, Energy, 32, p1698-1706.
• Qiu, G., Shao, Y., Li, J., Liu, H., and Riffat, S., (2012), Experimental Investigation of a Biomass-Fired ORCBased Micro-CHP for Domestic Applications, Fuel, 96, p374-382.
• Navarro-Esbrí, J., Peris, B., Collado, R., Molés, F., (2013), Micro-Generation and Micro Combined Heat and Power Generation Using ‘Free’ Low Temperature Heat Sources Through Organic Rankine Cycles, ICREPQ’13, Bilbao, Spain.
• Twomey, B., Jacobs, P. A., and Gurgenci, H., (2013), Dynamic Performance Estimation of Small-Scale Solar Cogeneration with an Organic Rankine Cycle Using a Scroll Expander, Applied Thermal Engineering, 51, p1307-1316. [https://doi.org/10.1016/j.applthermaleng.2012.06.054]
• Quoilin, S., Lemort, V., and Lebrun, J., (2010), Experimental Study and Modeling of an Organic Rankine Cycle Using Scroll Expander, Applied Energy, 87, p1260-1268. [https://doi.org/10.1016/j.apenergy.2009.06.026]
• Wang, W., Wu, Y., Ma, C., Liu, L., and Yu, J., (2011), Preliminary Experimental Study of Single Screw Expander Prototype, Applied Thermal Engineering, 31, p3684-3688. [https://doi.org/10.1016/j.applthermaleng.2011.01.019]
• Zhang, B., Peng, X., He, Z., Xing, Z., and Shu, P., (2007), Development of a Double Acting Free Piston Expander for Power Recovery in Transcritical CO² Cycle, Applied Thermal Engineering, 27, p1629-1636. [https://doi.org/10.1016/j.applthermaleng.2006.05.034]
• Qiu, G., Liu, H., and Riffat, S., (2011), Expanders for Micro-CHP Systems with Organic Rankine Cycle, Applied Thermal Engineering, 31, p3301-3307. [https://doi.org/10.1016/j.applthermaleng.2011.06.008]
• Yamamoto, T., Furuhata, T., Arai, N., and Mori, K., (2001), Design and Testing of the Organic Rankine Cycle, Energy, 26, p239-251. [https://doi.org/10.1016/S0360-5442(00)00063-3]
• Cho, S. Y., and Cho, J. H., (2014), A Study on the Organic Rankine Cycle for the Fluctuating Heat Source, J. of Fluid Machinery, 17(1), p12-21. [https://doi.org/10.5293/kfma.2014.17.1.012]
• Fang, X., Xua, Y., and Zhou, Z., (2011), New Correlations of Single-Phase Friction Factor for Turbulent Pipe Flow and Evaluation of Existing Single-Phase Friction Factor Correlations, Nuclear Engineering and Design, 241(3), p897-902. [https://doi.org/10.1016/j.nucengdes.2010.12.019]
• NIST, (2010), Reference Fluid Thermodynamics and Transport Properties, Refprop version 9.0.
• Zucrow, M. J., and Hoffman, J. D., (1976), Gas Dynamics, 1,2, John Wiley & Sons Inc.
• Hodge, B. K., and Koenig, K., (1995), Compressible Fluid Dynamics, Prentice hall.
• Elliott, D. G., and Weinberg, E., (1968), Acceleration of Liquids in Two-Phase Nozzles, Jet 666 Propulsion Laboratory, Technical Report 32-987.
• Elliott, ., (1982), Theory and Tests of Two-Phase Turbines, Jet Propulsion 668 Laboratory, DOE/ER-10614-1, JPL Pub B1-105.
• Granville, P. S., (1959), The Determination of the Local Skin Friction and the Thickness of Turbulent Boundary Layers from the Velocity Similarity Laws, David W. Taylor Model Basin Rept, p1340.
• Fluent, (2011), Ansys Fluent Ver. 14, ANSYS Inc.