Numerical Study of Agitation Performance in a Drilling Mud Mixing Tank to Non-Newtonian Rheological Properties
Non-Newtonian fluid mechanics takes charge of an important role in the oil industries. Especially in the oil well drilling process, the drilling fluid such as mud keeps the drill bit cool and clean during drilling, with suspending drill cuttings and lubricating a drill bit. The purpose of this study is to examine the effect of fluid mud rheological properties to predict different characteristics of non-Newtonian fluid in the mud mixing tank on offshore drilling platforms. In this paper, ANSYS fluent package was used for the simulation to solve the hydrodynamic force and to evaluate mud mixing time. Prediction of the power consumption and the pumping effectiveness has been presented with different operating fluid models as Newtonian and non-Newtonian fluid. The comparison between Newtonain mud model and non-Newtonian mud model is confirmed by the CFD simulation method of drilling mud mixing tank. The results present useful information for the design of the drilling mud mixing tanks and provide some guidance on the use of CFD tool for such non-Newtonian fluid flow.
Keywords:
Newtonian fluid, Non-Newtonian fluid, Drilling mud mixing tank, Bingham plastic fluid, CFD, Drilling facilities, Agitator, Power consumption, Pumping effectiveness, 뉴턴 유체, 비뉴턴 유체, 시추용 머드 혼합 탱크, 빙햄 소성 유체, 전산유체역학, 시추설비, 교반기, 소요 동력, 토출 유용도1. 서 론
드릴쉽(Drillship), 반잠수식 시추선(Semi-submersible rig) 등의 시추 구조물에는 권상 시스템(Hoisting system), 파이프/라이저 핸들링 시스템(Pipe/Riser Handling system), 머드 순환 시스템(Mud circulating system) 및 회전시스템(Rotating system)으로 구성되는 시추 시스템을 구비하고 있다. 여기서, 머드 순환 시스템은 벌크 시스템, 머드 혼합 시스템, 고압 머드 시스템, 솔리드 컨트롤 시스템으로 구성되며 재사용을 위한 순환 시스템으로 운영되는 것이 일반적이다. 머드 순환 시스템은 시추공의 바닥 청소, 드릴 비트(Drill bit)와 드릴 스트링(Drill string)의 냉각 및 윤활, 커팅 제거 및 표면으로 이송, 압력조정 및 유정의 함몰이나 붕괴 방지 등의 목적으로 시추공으로 머드를 공급하기 위한 장치이며 사용이 끝난 머드를 재사용할 수 있도록 정제하기 위한 장치이다. 머드 순환 시스템에서 사용하는 머드는 물 또는 오일에 바라이트(Barite), 벤토나이트(Bentonite) 등을 섞어 특정 점도와 밀도를 갖도록 만든 혼합물이다. 여기에서 바라이트는 머드의 중량을 조절하는 역할을 하고 머드의 밀도를 증가시킨다. 벤토나이트는 머드의 점도를 증가시켜 시추시에 발생된 커팅을 회수하기 쉽게 하는 역할을 하며 머드의 부피를 증가시켜주는 역할도 한다.(12) 해양시추 설비의 머드 탱크와 임펠러는 일반적인 교반기에 비하여 크기 때문에 교반 소요동력, 머드 주입구 및 배출구의 위치 등이 중요한 설계 요소이다. 또한 형상이 정형화되어 있지 않기 때문에 상관식으로 설계 및 평가하기가 어렵고 토크 측정 및 입자 주입 등의 실측 정보를 얻기가 곤란하다. 따라서 시스템의 설계 및 평가를 위하여 CFD 해석을 채용하는 경우가 많다.
일반적으로 교반기의 교반 성능을 나타내는 지표로는 유동패턴, 동력, 펌핑, 전단력, 방해판 효과, 솔리드 유동화, 액적 확산 등이 있다. 본 논문에서는 머드 탱크의 주요한 교반 특성으로 동력특성, 혼합특성, 물질 이동특성을 비교 검토하였다. 각각 소요동력, 혼합시간, 물질이동 계수 및 액적 혹은 기포 직경으로 나타나는 특성이다. 이들 성능지표는 점도가 관여하는 대표적인 특성 지표이다.
머드 탱크는 벤토나이트의 비율에 따라 다양한 점도를 가질 수 있으므로 이 점도가 해석에 잘 반영되어야 하지만 머드 물성의 정보 부족과 해석의 편의 등의 이유로 뉴턴 점성 유체로 가정하여 해석하는 경향이 많다. 빙햄 소성 유체(Bingham plastic fluid)로 알려진 시추용 머드는 일정한 항복 응력 τ0을 가지며 항복 응력을 넘어서는 구간에서는 전단속도의 증가에 대해서 전단응력의 증가가 직선으로 변화하는 소성 점도의 기울기를 가지는 모델이다.(34)
교반기의 실험 및 수치 시뮬레이션 연구는 오래 전부터 많은 연구자들에 의해 수행되었지만 주로 뉴턴 유체로 가정한 점성유동해석이 주를 이루며 교반기의 소요동력을 추정하는 실험적 연구가 대부분이다. Valachakis는 러시턴(Rushton) 타입의 임펠러를 사용한 교반기의 난류 특성에 대한 연구를 수행하였으며 작동유체를 물로 하여 PIV(Particle Image Velocimetry) 실험을 수행하였고 SKE(Standard k-ε), RNG-KE(Renormalization Group k-) 및 RSM(Reynolds Stress Model)의 3가지 난류모델을 이용한 CFD해석의 결과를 PIV 실험 결과와 비교하여 RSM 난류 모델을 사용한 CFD 해석이 교반기 유동특성을 잘 추정함을 보였다.(5)
Huang등은 4장의 방해판을 가지는 교반기의 동력수를 CFD해석을 통하여 산정하였다. RSM 및 RKE(Realizable k-ε)의 난류모델을 이용하여 해석을 수행하였으며 Rushton과 Murthy의 실험결과에서 동력수 평균값과 해석 결과를 비교하였다. 이들은 RSM이 0.98%, RKE가 2.42%의 오차로 실험 결과와 유사함을 보였다.(6)
Mununga 등은 수치해석을 이용하여 방해판이 없는 패들(Paddle) 타입 임펠러의 블레이드 크기가 토출 유용도에 미치는 영향을 파악하였다. 작동유체는 뉴턴 유체로 가정한 실리콘 오일을 사용하였으며 난류 모델로 SKE, RNG-KE, RSM의 3가지를 이용한 수치해석을 수행하였다. 해석 결과, RSM모델에 비하여 RNG-KE모델과 SKE 모델은 동력 계수, 유동 계수등의 유동 특성이 5 %~25 % 높게 추정한다는 결과를 제시하였다.(7)
본 논문에서는 안전 및 효율을 중시하는 최근의 해양플랜트 사업의 경향에 따라 시추용 머드를 비뉴턴 유체로 모사하여 작동 유체의 모델링 방법에 따른 교반 특성의 차이를 비교 검토하고자 한다. 비교검토를 위하여 3가지 수치 시뮬레이션을 수행하였고 머드의 거동 및 머드 탱크 교반 특성을 검토하였다. 시뮬레이션1을 통하여 머드의 점도를 모델링하는 방법에 따른 머드의 거동을 파악하였고 시뮬레이션2는 단순화한 방해판이 없는 교반기의 정상 유동해석을 수행하여 교반 특성을 비교하였으며 시뮬레이션3은 시추설비의 머드 탱크를 해석하여 토크, 소요동력 및 토출 유용도, 혼합시간 등을 계산하였다. 이를 통하여, 뉴턴 유체 및 비뉴턴 유체로 가정한 머드를 작동유체로 하여 시뮬레이션 하는 경우 머드의 유동 특성을 파악하기 위한 적합한 방법은 어떤 것인지에 대해서 검토하였다. 이러한 검토 결과는 수치 시뮬레이션을 통하여 얻어진 상세한 기술정보를 바탕으로 신뢰성이 높은 머드 탱크의 설계 및 평가를 가능하게 할 것으로 기대된다.
2. 수치해석
2.1 지배방정식 및 수치해석 모델
머드를 주입하여 거동을 비교하는 비정상 유동해석을 수행하기 위하여 VOF(Volume Of Fluid)법을 이용하였다. 또한 머드 탱크 성능특성을 비교하는 해석을 수행하기 위하여 정상 및 비정상 유동해석을 수행하였다. 머드 탱크의 정상 및 단상 유동해석에는 MRF(Multiple Reference Frame)를 이용하였고, 비정상 및 다상유동 해석에는 슬라이딩 격자법(Sliding Mesh Method)과 VOF법을 이용하였다. 머드의 CFD 해석에 사용한 유동해석의 지배방정식은 식(1), 식(2)에 나타내었다. 이들은 각각 질량 보존 및 운동량 보존을 표현하는 것으로 일반적인 Navier-Stokes방정식을 표현하는 것이다.
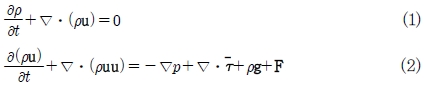
여기서, ρ는 밀도[kg/m3], u는 속도[m/s], p는 압력[Pa], τ는 응력 텐서[Pa], ρg 및 F는 중력[N/m3] 및 외력이다.
전단 응력 τ를 식(3)과 같이 뉴턴의 점성법칙으로 모사하는 것은 일반적인 점성유동 해석으로 가능하다. 그에 반해, 비뉴턴 유체의 리올로지(Rheology)에 관하여는 몇 가지 모델이 존재하며 비뉴턴 유체의 특성에 따라서 그에 맞는 모델을 선택하여야 한다. 점도는 식(3)의 뉴턴유체로 가정하여 전단 속도의 변화에 대해서 고정된 기울기를 가는 것으로 모사할 수 있고 식(4)와 같이 일정한 항복 응력을 가지도록 빙햄 소성 유체(Bingham Plastic Fluid)로 모사 할 수 있다.


여기서 μ는 유효 점도(effective viscosity), τγ 는 항복점(yield point)[Pa], μp는 소성점도(plastic viscosity)[kg/ms], γ는 전단 속도(Shear rate)[s-1], τ는 전단 응력[Pa]이다.
시뮬레이션1, 시뮬레이션3에서는 자유수면을 포함한 머드의 해석을 수행하였다. 공기와 머드 사이의 자유수면을 추적하기 위하여 식(5)과 같은 연속방정식 형태의 체적분율(Volume fraction)에 대한 추가방정식을 구성한다. 상간의 질량 전달 및 생성을 무시하는 경우 해당 항은 0이다.
체적분율(Volume fraction equation)
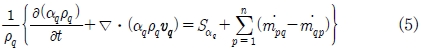
여기서 m.qp는 상q에서 상p로의 질량 전달량, Sαq는 생성항, ρ는 밀도[kg/m3], α는 각상의 체적분율이다.
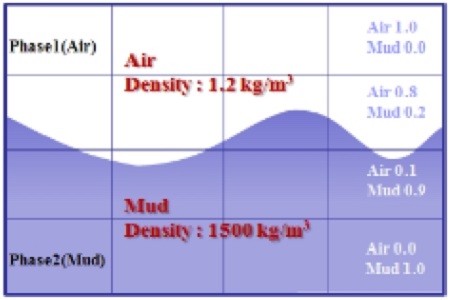
본 논문에서는 범용 유동해석 프로그램인 ANSYS Fluent 15.0을 사용하였으며 ANSYS Fluent에서는 제1상을 제외한 상에 대하여 방정식을 풀고 식(6)과 같이 셀에서의 체적분율이 1이 되도록 계산하는 방법을 사용한다. Fig. 1에 식(6)의 이미지를 표시하였다.(8)

Fig. 1에 나타낸 바와 같이 본 논문에서 다루고자 하는 머드는 실선 사용가능한 물성으로 가정하였고 공기는 대기에 노출된 상태로 가정하였다.
이미 언급한 바와 같이, 교반기의 성능을 나타내는 중요한 지표 중 하나는 혼합 성능이다. 교반기가 내부 유체를 잘 섞어주는지를 판단하기 위하여 혼합 시간을 측정하였다. 혼합 시간을 측정하기 위하여 머드에 식(7)과 같은 가상의 추적 입자를 분포시키고 이를 추적하여 체적분율이 일정하게 수렴하는 시간을 혼합 시간으로 판단하였다. 식(7)은 추적 입자의 수송 방정식이다. 결국, 상기 기본 방정식에 임의의 스칼라 함수를 하나 더 추가하는 것으로 혼합 시간을 추정할 수 있다.

여기서 C는 추적 입자의 농도, u는 머드의 속도장, D는 질량확산 계수이다.
문제를 간단히 하기 위하여 식(7)에서 확산항을 제거하였다. 확산항을 제거하여 모델링한 근거는 식(8)에 나타낸 바와 같이 페클레수를 기준으로 하였다.
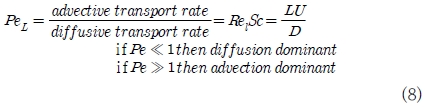
여기서 L은 특성길이, U는 대표속도, D는 질량확산 계수이다.
일반적인 액체의 확산 계수는 10-9정도이기 때문에 Pe≫1이다. 따라서 본 논문의 경우 질량확산은 무시하고 대류가 지배적인 유동장이라고 판단하여 추적 입자의 수송방정식에서 대류항만을 고려하여 추적하는 것으로 하였다.
2.2 교반 특성의 산출
교반 소요동력을 결정할 때 중요한 무차원 수는 식(9)의 교반 레이놀즈 수와 식(10)의 동력 수이다. 식(11)은 임펠러가 머드를 토출하는 능력을 평가하기 위한 지표로 사용하는 무차원 수인 유동 계수이다. 식(12)는 유동 계수와 동력 수의 비율로 표시되는 토출 유용도(Pumping effectiveness)이다. 이는 소요 동력 대비 임펠러의 토출 능력을 나타내는 지표로 임펠러의 작동 효율을 평가하는 무차원 수이다. 실제 적용되는 교반기의 교반 성능은 액체의 용량 및 점도, 교반기의 회전수, 교반기 임펠러의 종류 이외에도 교반조의 형상 및 방해판과 같은 다양한 변수가 적용되기 때문에 엄밀하게 실험 및 해석을 통하여 산정하여야 한다. 교반 소요동력은 식(13)으로부터 산정하거나 식(14)를 이용하여 실험 시에 토크 메타로 읽은 토크 값 혹은 CFD 해석에 의한 토크를 이용하여 산정할 수 있다.(9)

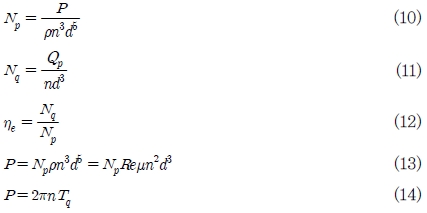
여기서 ρ는 밀도[kg/m3], d는 임펠러 직경[m], n은 회전수[rps], Qp는 펌핑 유량[m3/s], μ는 점성 계수[kg/ms], Τq는 토크[Nm]이다.
2.3. 해석 조건 및 해석 케이스
Table 1에 수치해석에 공통적으로 사용한 계산 방법을 나타내었다. 운동에 따른 내부 유체의 거동을 파악하기 위하여 정상 및 비정상해석을 수행하였고 다상유동해석을 위해서 VOF법을 사용하였으며 해석의 안정성을 위한 압력과 속도의 커플링을 위해 Coupled법을 사용하였다.
시뮬레이션1은 전단 속도가 낮은 영역에서의 자유수면을 비교하기 위하여 상부에서 뉴턴, 비뉴턴 유체를 주입하여 바닥면을 따라서 이동하는 머드의 표면 형상 및 거동을 비교하였고 시뮬레이션2는 간단한 교반기 모델을 이용하여 밀도와 점도에 따른 토크, 소요동력, 혼합 유용도 및 유동패턴 등을 비교하였다. 마지막으로 시뮬레이션3은 실제 시추설비에서 사용하는 머드 탱크를 모델링하여 소요동력 및 혼합시간을 비교하였다. 이상의 3가지 수치 시뮬레이션을 통하여 머드 탱크의 수치해석에 적합한 방법을 비교 검토하였다. 뉴턴 및 비뉴턴 유체의 점도 값은 시추 설비에 적용하고 있는 점도 범위에서 선정하였고 점도 측정기인 Fann VG meter 35A의 측정값인 Table 2를 이용하였다.(1011)
식(15)는 뉴턴 유체의 점도를 산정하기 위한 식이다. 이때 θN은 각각 300 rpm, 600 rpm에서 측정한 점도 측정기의 전단 응력 값이다. 식(16)은 비뉴턴 유체의 소성 점도를 산정하기 위한 식이다. 본 논문에서는 N1은 300, N2는 600이다. 식(17)은 항복 응력을 산정하기 위한 식이다. 300 rpm의 전단 응력 측정값에서 소성 응력을 뺀 값으로 산정한다.
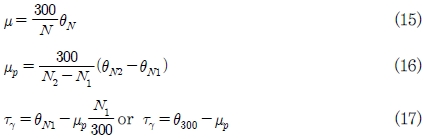
여기서 N은 Fann VG meter 35A의 회전속도[rpm], θN은 회전속도 N일 때 Fann VG meter에서 읽은 전단 응력[Pa], μp는 소성 점도[kg/ms]이다.
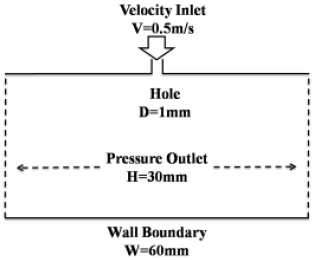
Fig. 2에는 작은 구멍을 통해 머드 액적을 주입하는 경우의 자유수면의 변화를 비교하기 위한 모델이다. Table 3는 뉴턴 유체로 가정한 경우 및 빙햄 소성 유체로 가정한 경우의 밀도 및 점도를 나타내고 있다. 뉴턴 유체로 가정한 경우에는 300 rpm 및 600 rpm의 전단응력 θ를 이용하여 식(15)로 산정하였다. 비정상 유동해석을 수행하였으며 머드 표면을 추적하기 위하여 VOF법을 이용하였다.
Fig. 3은 점도 및 밀도에 따른 교반 특성을 비교하기 위한 모델이다. 가장 단순한 방해판이 없는 원통형 교반조이며 45도 피치 각을 가지는 4장의 블레이드로 구성되어 있다. 임펠러의 회전속도는 60 rpm으로 계산하였다. 뉴턴유체 및 비뉴턴 유체의 거동을 비교하였고 상관식에 의한 소요동력과 비교하였다. 각 케이스의 레이놀즈 수는 15,000~32,000 정도이다. 각 케이스는 단상의 정상해석을 수행하였고 MRF법을 이용하였다. Table 4에 시뮬레이션2에서 사용한 밀도, 점도 및 항복응력을 나타내었다.
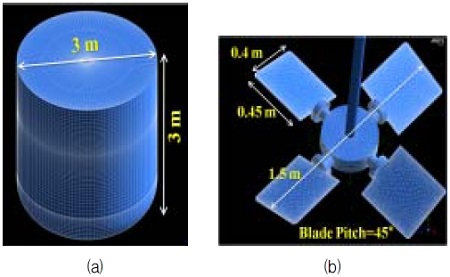
시뮬레이션3에서 사용한 머드 탱크의 형상과 임펠러를 Fig. 4에 나타내었다. Fig. 4(a), (b)는 드릴쉽의 머드탱크 및 교반기 임펠러를 나타내고 있다. 머드 탱크의 체적이 아주 크기 때문에 임펠러는 4개를 사용하고 있고 탱크내의 모든 곳에 유동을 형성하기 위하여 중심으로부터 대칭인 두 개의 축을 사용하고 있다. 탱크의 바닥면에는 x방향으로 약간의 경사를 배치하였는데 이는 실제 사용하는 선체의 형상을 그대로 모사한 것이다. 축의 직경은 0.06 m로 하였고 머드는 통상 운용 조건으로 약 93 %를 채운 상태로 하였다.
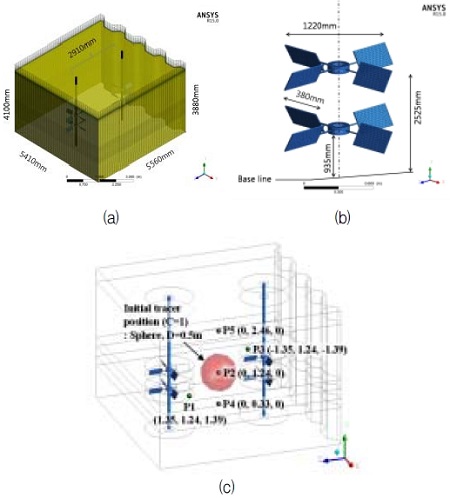
Geometry of mud tank with two axes and multi-impellers, (a) Schematic iso-view of mud tank, (b) Pitched paddle type impeller, (c) Initial tracer sampling position and tracer concentration
Fig. 4(c)는 혼합시간을 산정하기 위한 추적 입자의 초기 분포 및 측정 점의 좌표를 나타내고 있다. 총 5점에서 추적 입자의 농도 변화를 측정하는 것으로 하였다. 또, 두 개의 축과 각 축에 설치된 임펠러는 반시계방향으로 동일한 회전수 57 rpm으로 회전하는 것으로 하였다. Table 5에 시뮬레이션 3에서 사용한 밀도, 점도 및 항복응력을 나타내었다.
혼합시간의 산정을 위하여 비정상 계산을 수행하여야 하므로 교반기의 회전부인 임펠러는 4면체 격자를 적용하고 나머지 머드 탱크 영역은 6면체 격자를 배치하여 수렴성 및 계산시간을 고려하였다. 해석에 사용한 전체 격자수는 약 80만 개이다.
3. 수치해석 결과 및 고찰
3.1. 머드 액적 주입 해석 결과(시뮬레이션1)
Fig. 5(a)~(c) 는 머드를 상부에서 주입 할 때 자유수면의 변화를 해석한 결과이다. 각각 점도가 0.035 Paㆍs, 0.028 Paㆍs인 경우의 그리고 비뉴턴 유체로 0.021 Paㆍs인 결과이다.
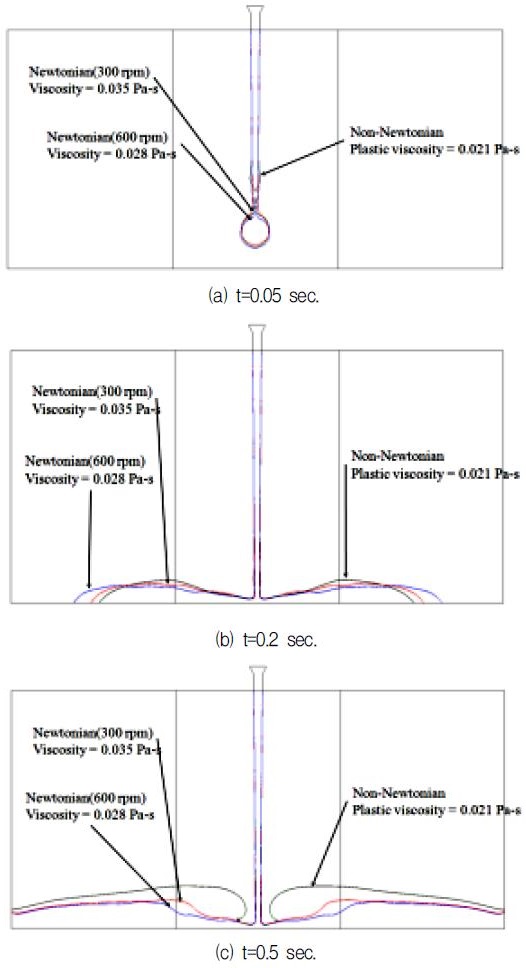
Comparison of free surface between newtonian and non-newtonian fluid, (a) at 0.05 sec, (b) at 0.2 sec, (c) at 0.5 sec.
600 rpm에서 측정한 유효 점도로 계산한 경우의 전단 속도가 가장 빠르며 300 rpm, 비뉴턴 유체로 모사한 경우에 비하여 이동거리가 길다. 비뉴턴 유체는 전단력이 작은 영역에서는 고체에 가까운 거동을 보이기 때문에 주입되는 지점에서 일정 거리에 다다르면 흐르지 않고 쌓여 부풀어 오르는 형태가 된다. Fig. 5(a)의 결과와 같이 상부에서 주입한 머드는 중력가속도의 영향을 주요하게 받고 밀도가 동일하기 때문에 낙하 시에는 거의 유사한 프로파일을 가지고 있다. 점도가 높은 300 rpm의 경우는 연속적인 액적의 형태를 유지하지만 600 rpm 및 비뉴턴 유체의 경우는 액적이 끊어져 있는 것을 확인할 수 있다. Fig. 5(b)의 0.2초의 공기와 머드의 경계면을 비교하면 뉴턴 유체로 가정한 경우에는 면을 따라 자연스럽게 퍼져가는 거동을 보이며 비뉴턴 유체는 벽면을 따라 흐르지 않고 적체되어지고 있는 것을 볼 수 있다. Fig. 5(c)의 0.5초에서는 비뉴턴 유체로 가정한 경우, 낙하지점 상부로 쌓여 부풀어 오르는 것과 같은 형상을 볼 수 있다. 이는 전단 응력과 전단 속도가 작은 영역에서 비뉴턴 유체의 항복 응력의 영향이라고 판단된다.
3.2. 교반기 교반특성 비교(시뮬레이션2)
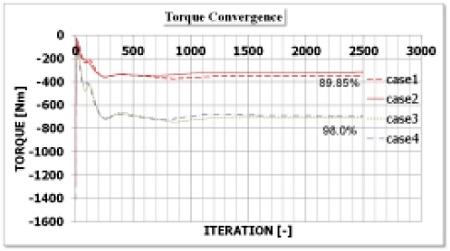
교반기의 교반 특성을 평가하기 위한 CFD해석은 정상 상태 해석을 수행하였고 MRF 모델을 이용하여 임펠러의 회전시의 토크를 계산하였다. Fig. 6은 토크의 수렴 상태를 나타내고 있다. 토크 및 임의의 포인트에서 속도가 일정한 값으로 수렴하는 상황을 보고 유동장의 수렴판정을 하였다.
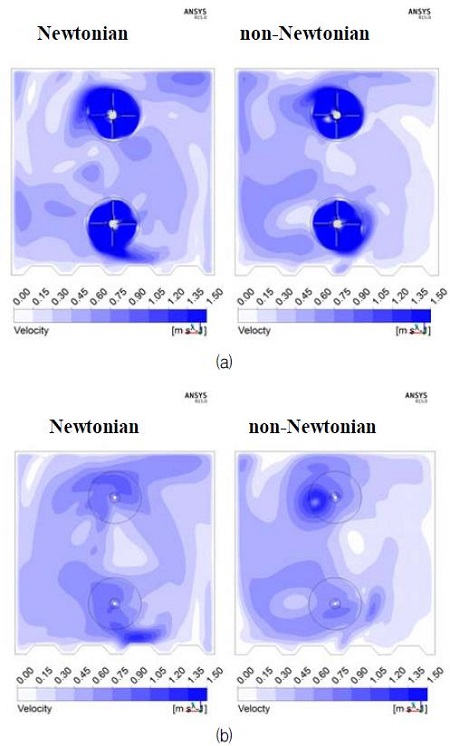
Fig. 7에 뉴턴 유체 및 비뉴턴 유체의 유동장을 나타내었다. Fig. 7(a)에 나타난 것과 같이 비뉴턴 유체로 가정한 case2, case4의 경우, 상부 및 교반기 벽 부근의 임펠러에서 먼 곳에는 상대적으로 저속의 영역이 존재한다. 또, Fig. 7(b), (c)의 뉴턴 유체로 가정한 case1, case3은 벽면 근처에서 유속분포가 비교적 불균일하고 고속의 영역이 넓게 분포하고 있다. 비뉴턴 유체는 운동량의 전달이 항복응력 만큼 저하되어 블레이드 근방의 유속에 비하여 교반조의 벽근처, 상부와 같이 블레이드에서 먼 지점의 유속은 상대적으로 느리게 분포 하고 있는 것을 볼 수 있다. Fig. 7과 같이 계산된 유속의 분포가 다르기 때문에 머드 탱크의 입구 및 출구 조건을 결정해야 하거나 유속 및 전단력의 분포를 파악해야 하는 문제에 대해서는 유체 모델의 선정을 신중히 하여야 한다.
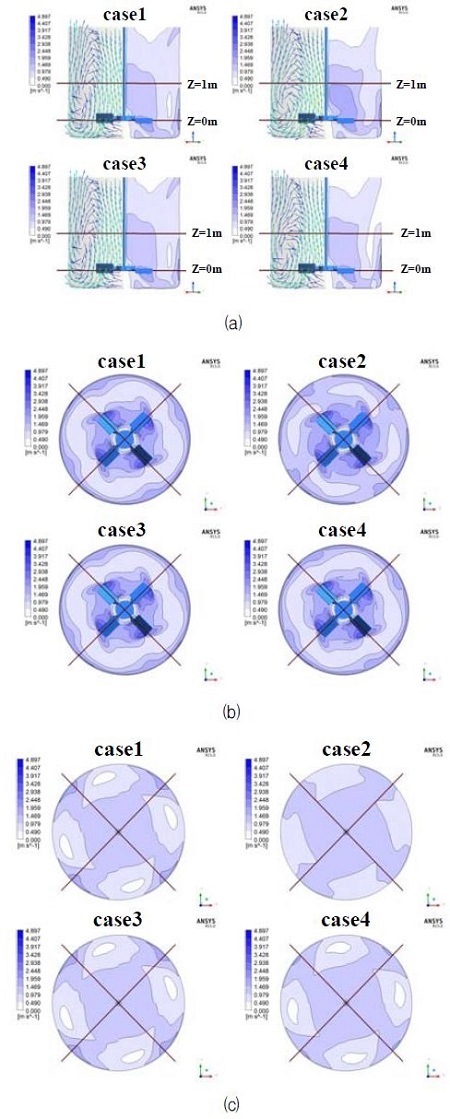
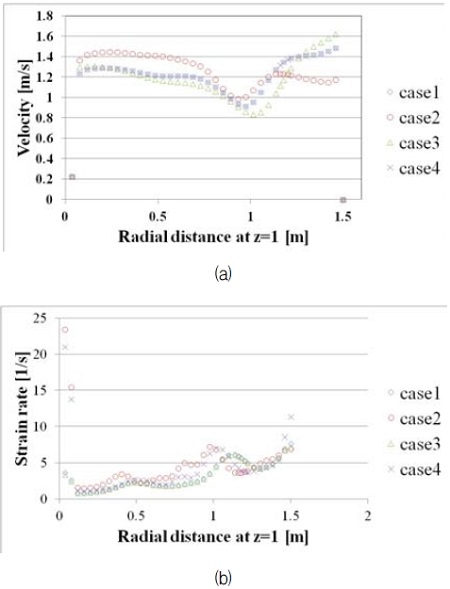
Velocity distribution, (a) elevation view, (b) plan view of z=0 m height, (c) plan view of z=1 m height.
Table 6에는 뉴턴 유체 및 비뉴턴 유체의 소요동력과 토크를 나타내었다. 동일한 밀도에 대해서 비뉴턴 유체로 모델링하는 경우 대비 뉴턴 유체로 가정한 케이스는 각각 case1이 case2에 비하여 19%, case3이 case4에 비하여 15% 높은 소요동력을 추정하였다.
Fig. 8에는 임펠러 블레이드의 높이 블레이드 중심에서 반경 방향의 속도 분포 및 전단 속도의 분포를 나타내고 있다. Fig. 7의 속도 분포와 비슷한 경향으로 임펠러 중심부근에서는 비뉴턴 유체로 가정한 경우의 속도가 크고 임펠러에서 멀어질수록 뉴턴 유체로 가정한 경우의 속도가 크게 분포하는 것을 볼 수 있다. 운동량 전달의 경향이 다르기 때문에 비뉴턴 유체를 뉴턴 유체로 가정하고 계산하였을 경우 모든 결과 값은 상당한 차이를 보이는 것을 알 수 있다. 비뉴턴 유체의 경우 Fig. 8의 유속 프로파일과 같이 임펠러 반경인 0.75 m까지는 비뉴턴 유체의 유속이 높다. 이 결과 비뉴턴 유체의 경우 토출유량이 많고 토출 유용도가 높은 계산 결과를 보인 것으로 추정된다.
3.3. 드릴쉽 머드 탱크의 교반 특성 비교(시뮬레이션3)
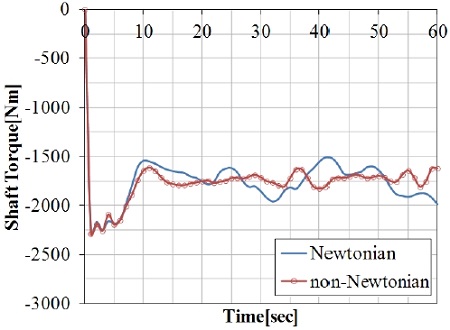
Fig. 9는 CFD 해석을 통하여 계산된 shaft13(방해판 반대편 축)의 토크를 비교한 것이다. 비뉴턴 유체에 비해서 뉴턴 유체로 가정하는 경우의 계산 값들은 변동이 크게 산정되었지만 비슷한 수준의 값을 유지하고 있다.
Table 8에 두 가지 케이스에서 계산되어진 shaft13의 소요 동력, 토출 유용도 등의 교반성능을 표시하였다. 비정상 시뮬레이션을 수행하여 40~60초의 평균값을 표시하였다. 작은 차이이지만 시뮬레이션2와 비슷한 경향을 보이고 있으며 뉴턴 유체로 가정하는 경우와 비뉴턴 유체로 가정하는 경우 모두 비슷한 동력을 필요로 하는 것으로 계산되었다.
Fig. 10은 60초 순시의 x-y평면 속도분포를 나타낸 것이다. Fig. 10에 나타난 바와 같이 시뮬레이션2의 결과와 비슷한 경향을 보인다. 비뉴턴 유체의 경우 임펠러의 중심에서 멀수록 저속의 분포가 넓어지는 유동 영역이 비교적 많다.
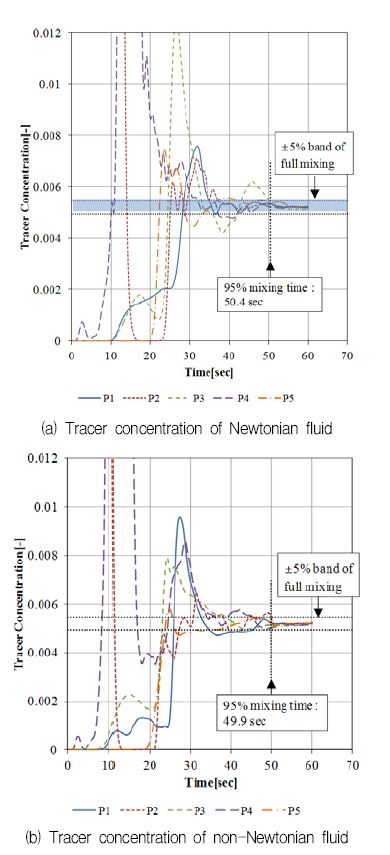
Fig. 11은 두 가지 케이스의 혼합 시간을 나타내고 있다. Fig. 4(c)에 나타낸 것과 같이 전체 체적의 5 % 농도에 해당하는 추적 입자를 초기 분포하였다. 각 계측 포인트의 추적 입자의 농도는 5 %의 95 %인 4.94 %까지 수렴하는 시간을 측정하였다. 혼합시간을 추정한 결과, 모든 포인트의 수렴시간은 거의 동일하게 계산되었다. 이는 추적 입자의 초기 분포 위치가 임펠러와 가까운 곳에 위치하여 Fig. 10의 유속분포와 같이 운동량 전달 패턴이 뉴턴 유체와 비뉴턴 유체 모두 비슷하게 계산 된 것으로 생각된다.
4. 결 론
본 논문에서는 뉴턴 유체 및 비뉴턴 유체로 가정하는 경우 의 소요동력의 차이, 유동 패턴, 토출 유용도와 혼합 시간 등의 교반기의 성능을 검토하였다. 이상의 검토결과, 동력 및 토크 등의 물리량과 운동량의 전달 패턴 및 분포가 다르게 계산되므로 시추 설비의 머드 탱크를 수치 시뮬레이션 하는 경우 머드 물성을 비뉴턴 유체로 모델링 할 필요가 있음을 알 수 있다. 작동 유체를 뉴턴 유체로 모델링 하는 경우에는 통상 임펠러가 소비하여야 하는 동력을 높게 추정하고 임펠러의 토출 성능을 저평가 하는 것을 알 수 있다. 본 논문의 3가지 시뮬레이션을 수행하여 머드를 뉴턴 유체와 비뉴턴 유체로 가정하여 비교 해석을 수행한 결과, 다음과 같은 결론으로 정리할 수 있다.
- 1) 작동 유체의 모델링 방법에 따라 뉴턴 유체로 모델링하는 경우 임펠러 근방과 원방에서 운동량의 전달 패턴이 차이가 나기 때문에 소요동력을 과대평가하므로 엄밀한 해석을 위하여 시추설비의 머드는 비뉴턴 유체 모델로 가정하여 해석하여야 한다.
- 2) 시추설비의 머드 탱크 해석을 수행하는 경우, 작동 유체를 뉴턴 유체로 모델링하면 토출 성능을 과소평가하기 때문에 임펠러로부터 원방에 배치되는 입/출구의 선정과 관련된 문제는 머드 물성을 비뉴턴 유체 모델로 해석하여야 한다.
Acknowledgments
This work was supported by the Industry Convergence Fundamental Technology Development program (10045234, Bulk and LP Mud Handling System for Deep Sea Drilling System) funded by the Ministry of Trade, Industry & Energy(MI, Korea)
References
- Guo, B., and Liu, G., (2011), Applied Drilling Circulation System, HYDRAULICS, CALCULATIONS, and MODELS, Elsevier Inc, Oxford.
- Edward, L. P., Victor, A. A., and Suzanne, M. K., (2004), Handbook of Industrial Mixing. Science and Practice, John Wiley & Sons, Inc, New Jersey.
- Chhabra, R. P., and Richardson, J. F., (2008), Non-Newtonian flow and applied rheology, 2nd Edition, Elsevier Inc, Oxford.
- Kolev, N. I., (2011), Multiphase Flow Dynamics 1 fundamentals, 4th edition, Springer-Verlag, Berlin Heidelberg.
- Valachakis, V. N., (2007), Turbulent Characteristics in Stirring Vessels, Virginia Polytechnic Institute and State Univ, Virginia.
- Weidong, Huang, Kun, Li, (2013), Nuclear Reactor Thermal Hydraulics and Other Applications Chapter 5, Intech, USA.
- Mununga, L., Hourigan, K., and Thompson, M., (2003), Numerical study of the effect of blade size on pumping effectiveness of a paddle impeller in an unbaffled mixing vessel, Third International Conference on CFD in the Minerals and Process Industires CSIRO, Melbourne, Australia.
- ANSYS Inc, (2013), ANSYS Fluent version 15.0 Documentation, ANSYS Inc, Pennsylvania.
- Japan Society for Chemical Engineers, (2011), Handbook of Chemical Engineering, Maruzen, Tokyo.
- Drillingformulas.com, (2012), Effective Viscosity calculation, http://www.drillingformulas.com/effective-viscositycalculation.
- Rachain, J., and Shyne, C., (2010), Plastic viscosity, http://www.drilling-mud.org/plastic-viscosity-pv.