Design Optimization of Fan-shaped Film Cooling Hole Array on Pressure Side Surface of High Pressure Turbine Nozzle
In the present work, design optimization of film-cooling hole array on the pressure side of high pressure turbine nozzle was conducted. There are four rows of fan-shaped film cooling holes on the nozzle pressure side surface and each row has a straight array of holes in the spanwise direction for baseline model. For design optimization, hole distributions in streamwise and spanwise directions for three rows of holes except first row are parameterized as a 2nd-order shape function. Three-dimensional compressible RANS equations are used for flow and thermal analysis around the nozzle surface and optimization technique using Design of Experiment, Kriging surrogate model and Genetic Algorithm is used . The results shows that averaged adiabatic wall temperature at the whole nozzle surface decreases about 2.7% and averaged film cooling effectiveness at the pressure side of nozzle increased about 8.2%.
Keywords:
Gas turbine, High pressure turbine, Film-Cooling, Design optimization, 가스 터빈, 고압 터빈, 막냉각, 최적설계1. 서 론
가스터빈 엔진의 성능 및 효율의 향상과 함께 터빈 입구온도(Turbine Inlet Temperature, TIT)는 지속적으로 증가되어왔다. 이 때문에 고온 고압의 유동조건을 견디기 위한 재료 및 냉각기법에 대한 많은 연구가 수행되었다.
막냉각(Film-cooling)기법은 냉각공기를 물체 표면으로 분사시켜 냉각기체에 의한 막을 형성함으로서 금속표면을 보호하는 외부냉각 기법이다. 막냉각 성능에는 분사각, 홀 사이의 간격, 홀의 형상과 같은 분사형상과 분사비, 밀도비, 난류강도 등의 유동조건이 영향을 미친다. 따라서 다양한 분사형상 및 분사조건에 대한 연구를 통한 막냉각 홀의 냉각성능 향상 시도가 있어왔으며 그 결과 다양한 형상의 막냉각 홀이 제시되었다.(12) 그러나 이러한 연구 대부분은 단일냉각 홀에 대해 수행되어 막냉각 홀의 형상에 대한 연구에 비해 막냉각 홀의 배열에 대한 연구는 상대적으로 미흡한 편이다. 또한 막냉각 홀의 배열에 대해 수행된 연구 대부분도 평판으로 단순화한 형상에서 홀 간 간격의 영향 등에 대해 제한적으로 이루어졌다(34) 한편 Johnson 등(5)은 수치해석과 최적화 기법을 사용해 실제 노즐 벽면에서 최적화된 냉각성능을 가지는 막냉각 홀 배열을 찾는데 성공하였으나 해석자의 낮은 해석 정확도와 몇 가지 제한된 형태의 배열 타입만을 사용하였다는 한계가 있다.
본 연구에서는 가스터빈 고압 냉각터빈 노즐 형상에 적용된 부채꼴 확장 형상(fan-shaped) 막냉각 홀의 배열 최적화를 수행하였다. 최적화를 위해 압력면에 설계된 4개열의 막냉각 홀 중 3개열을 2차 함수 형태로 매개화 하여 높은 자유도의 배열 형태를 가질 수 있게 하였고 실험계획법 및 근사모델을 이용한 최적화 기법을 적용하여 노즐 압력면에서의 냉각성능을 향상시키기 위한 최적화를 수행하였다.
2. 대상 모델
대상이 되는 모델은 10,000 lbf급 항공기용 가스터빈 엔진의 고압터빈 1단 노즐이며 기본 공력 성능 및 냉각 계통 설계형상은 강영석 등(6)과 서종철 등(7)에 의해 제시되어 있다.
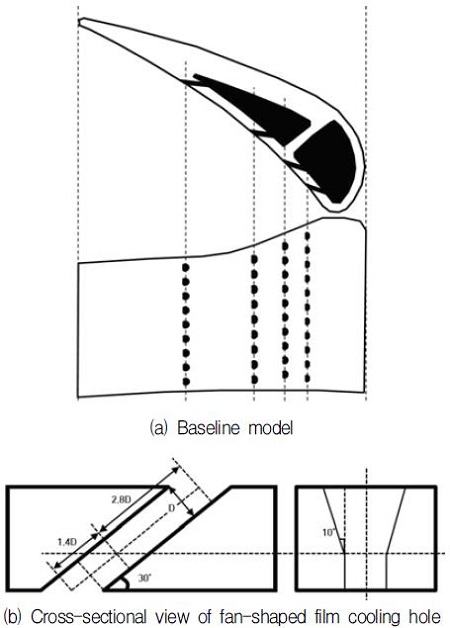
Fig. 1은 최적화 대상 노즐의 기본형상 냉각 계통에 대한 그림으로, Fig. 1(a)에 제시된 기본 형상의 단면을 보면 막냉각 홀로 냉각기체를 공급하기 위한 2개의 내부 냉각 유로와 냉각유로에 연결되어 있는 4개 열의 막냉각 홀이 있다. 첫 번째 열은 총 11개, 두 번째 열에는 10개, 세 번째 및 네 번째 열에는 9개의 막냉각 홀이 있으며, 이때 평균 막냉각홀 간 간격은 3.6D이다. 모든 막냉각홀은 Fig. 1(b)에 제시된 바와 같이 확장 형상의 단면 형상을 갖는다.
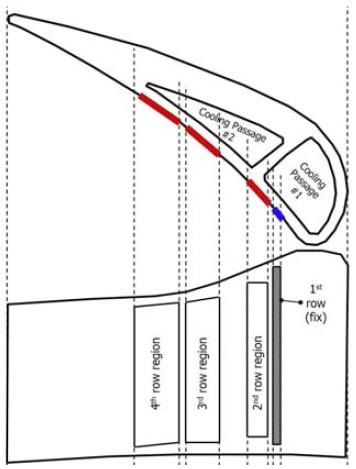
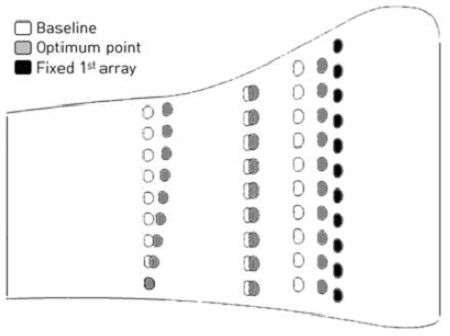
Fig. 2는 막냉각홀 배열 최적화를 위한 설계공간을 제시한 그림이다. 유동 상류에 위치한 첫 번째 열은 고정되어 있으며 나머지 3개열의 경우 각 막냉각 홀들이 위치할 수 있는 영역이 표시되어 있다.
3. 해석 기법 및 성능 평가
3.1. 유동 해석 및 냉각 성능 평가
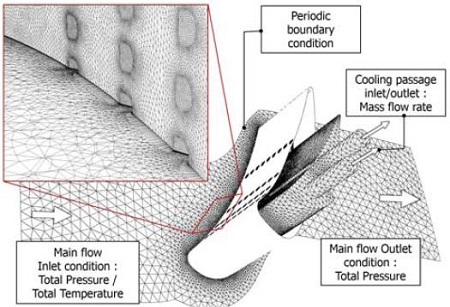
유동해석에는 압축성 정상 RANS 방정식과 κ-ω SST 난류모델을 사용했으며, 상용코드인 ANSYS CFX 14.5을 사용하여 해석을 수행하였다. 이 때 사용된 격자의 형상 및 경계조건은 Fig. 3에 제시되어 있다. 총 격자수는 약 800만개 이며, 서종철 등(7)의 연구결과와 비교하여 격자 의존성을 확인하였다. 계산 효율을 위해 주기조건을 이용하여 노즐을 포함한 한 개 유로에 대한 해석을 수행하였으며, 내부 냉각 유로 입/출구에는 각각 질량유량 조건을 주어 막냉각 홀의 위치가 변하더라도 기본설계형상과 동일한 냉각유량이 공급되도록 하였다. 이를 통해 홀 배열 최적화에 따른 영향성을 고찰하였다. 기본형상의 1~4열 막냉각홀에서의 평균 분사비(blowing ratio)는 각각 1.05, 0.84, 0.65, 0.52이다.
기본 형상 및 최적화 형상의 막냉각 홀의 냉각 성능을 평가하기 위해 막냉각 효율을 사용하였으며 이는 식(1)을 통해 구할 수 있다.

이 때, Tw은 주유동의 온도이고 Tw은 벽면에서의 온도, Tc는 냉각기체의 온도이다. 실제 주 유동의 온도는 평균 약 1700 K, 최고 약 1830 K의 포물선 형태의 온도 프로파일을 가지고 있어 대표온도를 결정하기 힘들고, 천음속의 조건에서 운용되기 때문에 Tm의 경우 막냉각 홀이 없는 노즐에 대한 해석을 통하여 획득한 노즐 단열벽면의 온도를 사용하였다. 냉각기체의 온도 Tc는 840 K이다.
3.2. 최적화 기법 및 과정
본 연구에서는 근사모델을 이용한 최적설계 기법을 사용하였다. 근사모델로는 비선형적인 응답을 표현하는데 효과적인 것으로 알려진 크리깅(Kriging) 모델을 사용하였다. 크리깅 모델은 대표적인 내삽 기법(interpolation method)의 하나로 전산 실험계획으로 얻어진 정보를 바탕으로 다음과 같이 전역 모델(global model)과 국부 편차(localized deviation)의 합으로 구성된다.

여기서 f(x)는 주어진 실험 데이터를 이용해서 구할 수 있는 전역 모델이며 많은 경우 상수항으로 처리한다. Z(x)는 평균이 0이고 분산이 σ2인 정규분포를 따르며 크리깅 모델이 주어진 실험점들을 보간할 수 있도록 국소적인 변동을 만들어내는 부분으로 응답 모델의 불확실성을 나타낸다. Z(x)의 공분산은 다음과 같이 표현할 수 있다.
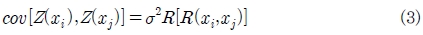
여기서 R은 상관행렬(correlation matrix)이며 R(xixj)는 임의의 두 점 xi, xj 사이의 상관함수(correlation function)이다. 상관함수는 설계자에 의해 결정된다. 크리깅 모델을 구성할 실험점을 결정하기 위해 사용된 실험계획법(Design of Experiment)은 LHS(Latin Hypercube Sampling) 기법이고 크리깅 모델의 신뢰도는 교차검증법(cross-validation)방법을 사용하여 검증하였다.(89)
최적해 탐색에는 유전 알고리즘(Genetic Algorithm, GA)과 EI(Estimated Improvement)를 사용하였다. 유전 알고리즘이란 자연 진화(natural evolution)와 자연 유전(natural genetics)을 최적화에 적용한 것으로써, 여러 개체를 동시에 이용하여 여러 탐색경로를 거쳐 최적해를 구하는 특징을 가지고 있다. 이 때 사용되는 여러 개체의 특성 중 우수한 성질을 다음 단계에서의 개체로 전해 줌으로써 최종적으로 최적해에 도달하도록 하는 방법이다. 유전 알고리즘은 목적함수의 기울기 정보를 이용하지 않으므로 비선형성이 매우 큰 공간에서도 전역 최적점을 찾아낼 가능성이 크다.(10)
크리깅 모델 기반의 유전알고리즘을 사용할 경우 EI(Expected Improvement)라는 평가값을 사용하여 최적해를 탐색할 수 있으며 식(4)을 통해 구할 수 있다.
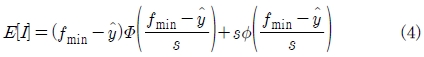
fmin은 실험점 중 최소값,
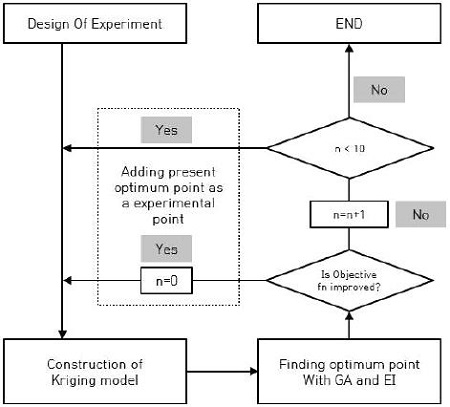
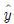 는 크리깅 모델의 예측치, s는 크리깅 모델의 평균오차제곱근, Φ와 φ는 누적분포함수, 확률밀도함수를 의미한다. 즉, EI가 높은 부분은 fmin 보다 낮은 값이 존재할 확률이 높거나 근사함수의 불확실성이 높기 때문에 EI가 최대값이 되는 점을 추가 샘플점으로 선택하여 근사모델을 재구축하면, 근사모델의 정확도 향상과 전역 최적점 탐색이 동시에 가능하게 된다.(11) 이상의 최적화 과정을 플로우차트로 나타내면 Fig. 4과 같다.
는 크리깅 모델의 예측치, s는 크리깅 모델의 평균오차제곱근, Φ와 φ는 누적분포함수, 확률밀도함수를 의미한다. 즉, EI가 높은 부분은 fmin 보다 낮은 값이 존재할 확률이 높거나 근사함수의 불확실성이 높기 때문에 EI가 최대값이 되는 점을 추가 샘플점으로 선택하여 근사모델을 재구축하면, 근사모델의 정확도 향상과 전역 최적점 탐색이 동시에 가능하게 된다.(11) 이상의 최적화 과정을 플로우차트로 나타내면 Fig. 4과 같다.
4. 최적화 결과 및 분석
4.1. 최적화 문제 정의
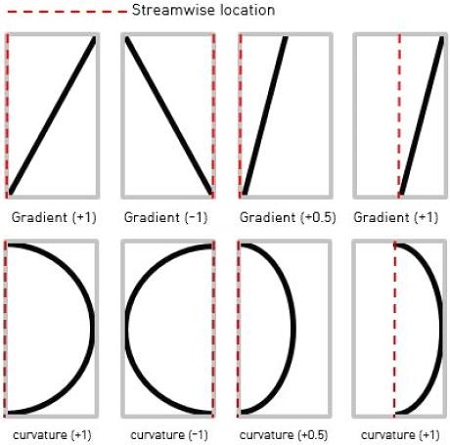
Fig. 2에서 설명했던 것과 같이 4개열의 막냉각 홀들은 냉각유로의 크기, 위치 및 분사각에 의해 노즐 압력면의 좁은 영역에서 제한적으로 배치된다. 이 때 주어진 영역을 최대한 활용하여 다양한 형상의 막냉각 홀 배열을 표현하기 위해 Fig. 5와 같이 각각의 열을 유동방향 위치(streamwise location, rowi,x), 기울기(gradient, rowi,grad), 곡률(curvature, rowi,curve)의 3개의 변수로 정의하였다. 이 때 유동방향 위치는 실제 해석도메인의 x좌표 값을 사용하였으며 가장 허브쪽에 위치한 막냉각홀의 위치를 기준으로 하였다. 각각의 막냉각 홀은 해당하는 x좌표에 따라 y좌표값이 함께 변하여 항상 노즐 표면에서 움직일 수 있도록 조치하였다. 기울기와 곡률은 –1부터 +1까지의 값을 가질 수 있으며 기울기가 +1을 갖는 경우(rowi,x, ymin)과 (xmax, ymax)를 잇는 직선이 되고 –1을 갖는 경우 (rowi,x, ymin)과 (xmin, ymax)를 잇는 직선이 된다. 이 때 xmin, xmax, ymin, ymax는 각각 각 열의 설계영역의 유동 방향 및 스팬 방향 최소/최대값을 의미한다. 곡률변수의 경우도 이와 비슷하게 +1일 땐 (rowi,x, ymin), (xmax, ymax/2), (rowi,x, ymax)의 3점을 지나는 곡선이되고, –1일땐 (rowi,x, ymin), (xmin, ymax/2), (rowi,x, ymax)의 3점을 지나는 곡선이 된다. 이렇게 만들어진 각각의 배열을 수식으로 나타내면 식(5),(6)과 같고, 이 두 수식을 합치면 하나의 배열타입이 완성된다.
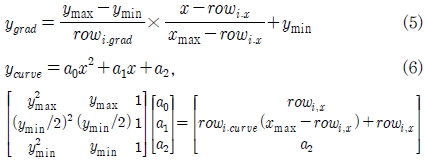
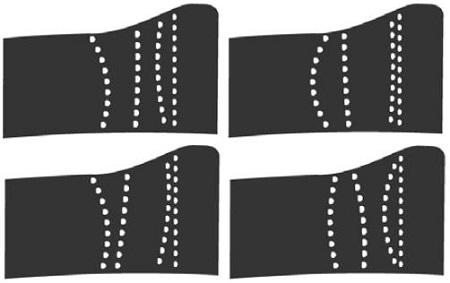
이와 같은 방법을 사용하면 각 변수들이 서로 어떤 값을 가지는지에 관계없이 주어진 설계영역을 최대한 활용하는 배열 형상을 만들 수 있다. Fig. 6은 이렇게 만들어진 배열형상을 노즐 압력면에 적용한 몇 가지 예시이다.
노즐 압력면의 냉각성능 최적화를 위해 다음과 같은 목적함수를 정의하였다.
objective.
min. [Averaged nozzle surface temperature]
목적함수는 노즐 벽면 전체에서의 평균 온도를 최소화하는 것으로 다른 제한조건은 두지 않았다. 최적화 결과는 압력면에서의 막냉각 효율 분포와 노즐 벽면 전체에서의 평균 온도, 첫 번째 홀 이후 압력면에서의 평균온도로 제시하였다.
4.2. 결과 및 분석
근사모델 구성을 위해 총 9개 설계변수에 대해 36개의 초기 실험점을 선정하여 계산을 수행하였다. EI를 이용해 추가점을 선정, 계산 후 실험점에 포함시켜 근사모델의 정확도를 향상시켜가며 최적화를 반복하였다.
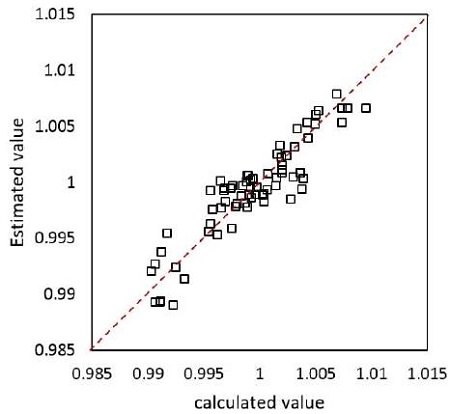
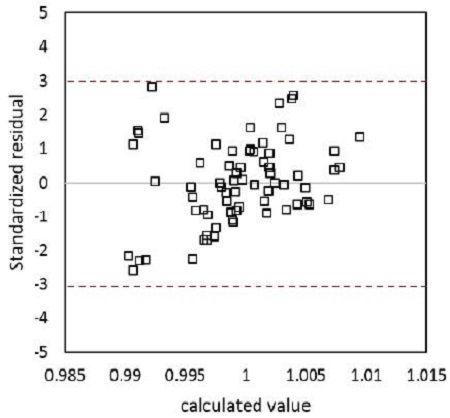
총 12번의 추가점 계산 후 더 이상 성능향상이 없다고 판단하여 최적화 과정을 종료하였으며 이 때 구성된 크리깅 모델의 정확도를 교차검증법을 이용하여 검증하였다. Fig. 7은 계산 값과 교차검증을 통해 구한 값의 적합정 검정(Goodness of Fits) 결과이고 Fig. 8은 이를 좀 더 정량적으로 검증하기 위해 계산값과 교차검증값의 표준잔차를 나타낸 것이다. 이를 통해 모든 실험점이 99.7 %의 신뢰구간에 분포하여 최적화에 사용된 크리깅 모델이 충분한 정확도를 가지고 있다고 판단할 수 있다.
Table 1은 기본 막냉각 홀 배열 형상과 최적화 결과 얻어진 배열 형상의 변수를 비교한 것이다. 2번열과 3번열의 경우 유동방향 변수가 설계하한에 걸렸기 때문에 기울기 변수와 곡률변수 값이 음수가 아닌 어떤 값을 가지더라도 수직인 배열 형태에 영향을 미치지 않기 때문에 크게 의미가 없다. 4번열의 경우 유동 방향 변수가 설계 상한에 걸렸으나 기울기 변수와 곡류변수가 양수이기 때문에 배열타입에 변화가 생기게 된다. 기울기 변수가 0.43이므로 첫 번재 막냉각 홀이 설계 영역의 43% 만큼 앞으로 이동하였고 곡률변수가 0.13이므로 첫 번째 막냉각 홀과 마지막 막냉각 홀을 제외한 모든 막냉각 홀이 약간씩 유동상류로 이동하였다.
Fig. 10은 기본 막냉각 홀 배열 형상과 최적화 결과 얻어진 배열 형상을 비교한 것이다. 2번째와 3번째 열의 경우 설계 공간 내에서 가장 유동 상류에 가까운 영역으로 이동하여 설계 영역의 가장자리에 걸쳤기 때문에 특이할만한 배열형태가 나타나지 않았다. 4번째 열의 경우 슈라우드 근처의 막냉각 홀들만 유동 상류로 약간씩 이동하는 배열 형태를 보였다.
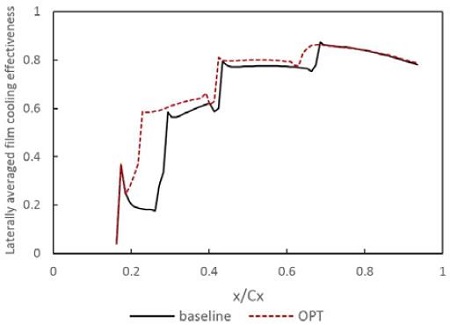
Fig. 9는 기본 배열 형상과 최적화 결과 얻어진 배열 형상을 해석한 결과를 막냉각 효율 분포로 제시한 것이며, Fig. 11은 첫 번째 열 이후 스팬방향으로 평균한 막냉각 효율을 축방향 코드길이에 대해 무차원화해 나타낸 그래프이다. 2, 3번째 열의 이동을 통해 1번째 열과 3번째 열 사이, 냉각이 되지 않는 영역을 최소화 하여 상당한 막냉각 효율 상승이 있음을 알 수 있다. 4번째 열의 경우 슈라우드 근처의 막냉각 홀들이 유동상류로 이동하면서 노즐 중간 부분의 냉각 성능은 좋아졌으나 이로 인해 유동 하류의 냉각성능이 다소 떨어지게 되므로 중간면의 냉각 성능이 향상되면서 노즐 익단에서의 냉각 성능은 떨어지지 않는 위치에서 배열 형태가 결정된 것으로 판단된다.
이와 같이 모든 열이 유동 상류로 이동하려는 경향을 보이는 것은 계산의 효율성을 위해 노즐 선단의 막냉각과 내부유로, 즉 전도에 의한 냉각이 고려되지 않았기 때문으로 판단된다. 따라서 최적화에 노즐 선단에서 막냉각 및 내부유로에 의한 냉각효과가 고려된다면 이와는 다른 배열 형태를 보이게 될 것으로 예상된다.
Table 2는 기본 형상 및 최적화 형상에서 목적함수였던 전체 노즐 표면에서의 평균 온도와 막냉각에 의해 영향을 받고 있는 첫 번째 홀 이후 압력면에서의 평균 막냉각 효율을 비교한 것이다. 전체 표면에서의 평균온도는 최적화 형상에서 기본형상 대비 약 40도가 감소하였고 첫 번째 홀 이후 압력면에서의 평균 막냉각 효율은 약 5.5 %가 증가하였다. 이는 각각 기본형상 전체 표면온도의 약 2.7 %, 기본형상의 압력면 평균 막냉각 효율의 약 8.2 %에 해당하는 값이다.
Table 3은 기본 형상 및 최적화 형상의 각 열에서 구한 평균 분사비를 나타낸 것이다. 두 형상에서 1,3,4번열의 분사비가 거의 동일한 반면 2번열의 분사비가 크게 증가하였다. 이는 막냉각 홀이 앞으로 이동하면서 외부 유동 조건이 변하였기 때문이다. 유동은 노즐을 지나면서 가속되기 때문에 막냉각 홀이 유동 상류로 이동하면 외부유동의 속도가 줄어 상대적으로 분사비가 증가하게 된다. 분사비가 증가했다는 것은 2번 열의 막냉각 효율은 오히려 최적화 형상에서 감소하였음을 의미하나 그만큼 냉각면적 증가에 의한 냉각효과 상승이 크다는 것을 알 수 있다.
5. 결 론
본 연구에서는 고압터빈 노즐 압력면에서 막냉각 홀 배열 최적화를 수행하였다. 이를 위해 직선형태였던 3개열의 막냉각 홀을 위치, 기울기, 곡률의 3개 변수를 이용해 2차 함수 형태로 매개화 하였고 실험계획법을 이용해 각 변수에 대한 근사모델을 구성하였다. 구성된 근사모델과 유전알고리즘을 이용한 최적화 결과 2, 3열은 유동 상류로 이동함으로서 냉각 면적 증가를 통해 노즐 압력면에서의 막냉각 효율을 향상시켰으나 설계영역 경계에 위치해 특이할만한 배열형상을 보이지 않았다. 유동 하류에 위치한 4번째 열의 경우, 3번째 열이 유동 상류로 이동하면서 감소된 노즐 중간면의 냉각성능 감소를 보완하기 위해 일부 막냉각 홀이 유동 상류로 이동하면서 노즐 익단의 냉각성능 역시 감소되지 않도록 하는 위치에서 배열형상이 결정되었다. 그 결과 노즐 압력면에서 평균 8.2 %의 막냉각 효율이 향상되었다.
Acknowledgments
본 연구는 산업통상자원부 항공우주부품기술개발사업(과제번호: KA000157)의 ‘중소형 항공기용 터보팬 엔진의 고압터빈 냉각설계기술 개발 및 시험평가기술 구축’ 연구과제(한국항공우주연구원)에 의하여 지원되었습니다.
References
-
Bunker, R. S., (2005), A Review of Shaped Hole Turbine Film-Cooling Technology, J. Heat Transfer, 127(4), p441-4532.
[https://doi.org/10.1115/1.1860562]

- Lu, Y., (2007), Effect of Hole Configurations on Film Cooling from Cylindrical Inclined Holes for the Application to Gas Turbine Blades, Ph. D Thesis, Luoisiana State University.
- Kim, Y. B., Rhee, D. H., Lee, Y. S., and Cho, H. H., (2004), The Effects of Staggered Rows of Rectangular Shaped Holes on Film Cooling, Trans. of the KSME (B), 28(3), p304-314.
- Ahn, J., Jung, I. S., Lee, J. S., (2001), Film Cooling from Two Rows of Holes with Opposite Orientation Angles (I), Trans. of the KSME (B), 25(8), p1122-1130.
-
Johnson, J. J., King, P. I., Clark, J. P., and Ooten, M. K., (2013), Genetic Algorithm Optimization of a High-Pressure Turbine Vane Pressure Side Film Cooling Array, Journal of Turbomachinery, 136(1), p011011.
[https://doi.org/10.1115/1.4023470]

- Kang, Y. S., Rhee, D. H., Cha, B. J., (2012), Aerodynamic design of high pressure turbine for aircraft turbofan engine, Proceeding of the 7th National Congress on Fluids Engineering, p246-247.
- 서종철, 김김경우, 황선우, 손창민, 김귀순, 이동호, 차봉준, (2013), 가스터빈 엔진 고압 터빈 1단 노즐의 내각계통 설계, 한국유체기계학회 학술대회, p137-138.
-
R. H. Myers, D. C. Montgomery, C. M. anderson-cook, (2009), Response Surface Methodology, Wiley.
[https://doi.org/10.3109/9781439822463.187]

-
T. W. Simpson, T. M. Mauery, J. J. Korte, F. Mistree, (2001), Kriging Models for Global Approximation in Simulation-Based Multidisciplinary Design Optimization, AIAA Journal, 39(12).
[https://doi.org/10.2514/2.1234]

-
K. Deb, A. Pratap, S. Agarwal, Metarivan, (2002), A Fast and Elitist Multiobjective Genetic Algorithm : NSGA-II, IEEE Transactions On Evolutionary Computation, 6(2), p182-198.
[https://doi.org/10.1109/4235.996017]

- 채상현, 양충모, 정신규, TakashiAoyama, ShigeruObayashi, 이관중, (2009), 헬리콥터의 고속충격소음 감소를 위한 블레이드 평면형상 최적화, 한국전산유체공학회지, 14(1), p53-61.