Computational Studies on the Performance of Flow Distributor in Tank
The optimal design of the flow distributor is very important to ensure the structural integrity of the reactor system and their safe operation during some transient or accident conditions. In the present study, we numerically investigated the performance of a flow distributor in tank with different shape factors such as the total number of the holes, the pitch-to-hole diameter ratios (p/d), the diameter of the hole and the area ratios. These data will contribute to a design of the flow distributor.
Keywords:
Flow Distributor, CFD, Pitch-to-hole diameter ratios, 유동 분사장치, 전산유체역학, 피치-구멍 직경비1. 서 론
유동 분사장치는 원자로건물내 재장전수탱크(In-Containment Refueling Water Storage Tank : IRWST) 또는 노심보충탱크(Core Makeup Tank : CMT)내 압력평형배관에 설치되는 등 원자력 발전 산업에서 일반적으로 사용하는 장치이다. 재장전수탱크 내부 유동분사장치는 탱크 내에 잠겨있으며, 유동분사장치를 통해 나온 증기가 냉각수와 직접 닿아 응축되게 된다. 이때 증기 유량 분포를 조절하여 탱크 구조물에 과도하게 부과되는 동하중을 막기 위해 재장전수탱크 내부 유동분사장치가 설치된다. 노심 보충탱크 내부 유동분사장치는 과도한 동하중 방지뿐만 아니라 안정적인 냉각수 주입을 위해 설치된다. 노심보충탱크의 경우 냉각재상실사고 또는 비냉각재상실사고 시 작동되며, 작동시 원자로 내부 증기가 압력평형배관을 통해 노심보충탱크 내부로 유입되어 노심보충탱크와 원자로냉각재계통의 압력평형이 이루어지면 중력 수두에 의해 노심보충탱크의 냉각수 주입이 시작된다. 냉각수 주입 시 뜨거운 증기가 차가운 노심보충탱크 벽면 및 물에 접촉될 경우 탱크 내부에서 급격한 응축현상이 발생하면서 탱크 내부 압력이 떨어지게 되고 냉각수 주입이 중지된다. 따라서 탱크 내부 응축 현상을 완화시켜 노심보충탱크의 냉각수를 안정되게 주입시키기 위해 탱크 내부 상부 압력평형배관 연결노즐에 분사장치를 설치하게 된다.
이러한 유동분사장치에 대한 연구는 많은 연구자들에 의해 활발하게 이루어져 왔다. Song 등(1)은 유동 분사장치 형상이 직접 접촉에 의한 증기의 응축 효과 및 이로 인해 원자로 배수탱크에 미치는 영향을 비교 분석하였다. 이 실험을 통해 증기의 응축에 영향을 미치는 주요변수는 응축수의 평균 온도, 증기의 질량 유속임을 확인하였다. 응축 수조 벽면에서의 동압은 응축수의 평균 온도와 증기 유량의 증가에 따라 커진다고 보고하고 있다. Tuunanen 등(2)은 경수로에서 소형냉각재상실사고시 노심보충탱크의 성능을 실험을 통해 평가하였으며, 노심보충탱크 내부 응축 완화를 통한 안정적인 주입을 위해 유동분사장치 설치가 필요함을 확인하였다. Cho 등(3)은 분사장치의 피치와 구멍 직경비(P/D)를 2~5로, 구멍 배열을 Staggered, Parallel type으로 바꾸어 가며 열적 혼합 현상을 평가하였다. 그 결과 P/D가 작을수록(P/D=2), 열적 혼합이 덜 활발하게 이루어져 탱크 밑 부분 온도와 평균 온도와의 차이가 증가함을 확인하였으며, Staggered-type 분사장치가 Parallel type보다 열적 혼합이 덜 일어나 열성층화에 유리함을 확인하였다. AP 1000 DCD(4)에서는 노심보충탱크 내부로 들어가는 증기의 속도를 줄여 잠재적인 수격작용을 최소화하고, 노심보충탱크작동 초기의 혼합 현상을 줄이기 위해, 노심보충탱크 내부의 유동 분사장치를 설치하며 분사장치의 유량 면적은 1064.51 cm2 이상이 되도록 설계하였다.
기존 연구 결과들을 바탕으로 본 연구에서는 수직 탱크 분사장치로 적절하고 노심보충탱크 내부에 설치가 용이한 I-형 분사장치를 선택하였으며, 분사장치 구멍 배열은 Staggeredtype으로 정하였다. 본 계산에서는 노심보충탱크 내부 분사장치의 형상별 유동 특성을 살펴보고, 탱크 내부 상부 유동의 교란을 효과적으로 완화시킬 수 있는 최적의 분사장치 형상을 도출하고자 한다.
2. 수치해석 접근
상용 CFD 해석 프로그램인 FLUENT 13.0 코드를 이용하여 노심보충탱크 작동 초기에 발생되는 응축현상을 완화시킬 수 있는 최적의 분사장치 형상을 도출하고자 하였다. 실제 응축현상을 정확히 모사하기 위해서는 증기와 물의 속도, 압력, 온도를 모두 해석할 수 있는 다상유동 모델뿐만 아니라, 정확한 응축현상을 해석할 수 있는 증기응축 모델이 필요하다. 하지만 현재 FLUENT 프로그램으로는 증기응축현상을 정확히 해석하는데 한계가 있으며, 증기와 물의 유동을 해석할 수 있는 다상유동 모델을 이용하여 탱크 내 증기응축현상을 파악하기 위해서는 필연적으로 비정상상태를 풀어야 한다. 하지만 다상유동 모델을 비정상상태로 계산하기 위해서는 많은 계산 시간이 소요되어 여러 설계 인자를 바꾸어가며 최적 현상을 파악하는 것이 거의 불가능하다. 따라서 본 계산에서는 노심보충탱크 상부에 연결되어 있는 압력평형배관을 통해 들어오는 증기의 유량(kg/s)과 동일한 유량의 물이 노심보충탱크 내부로 들어갈 때, 탱크 내부 상부의 유동현상을 살펴보고, 탱크 내부 상부 유동의 교란을 효과적으로 완화시킬 수 있는 최적의 분사장치 형상을 도출하고자 한다. 노심보충탱크 내 설치되는 유동 분사장치의 3차원 유동해석을 위해 사용된 지배방정식 및 경계조건은 다음과 같다.
2.1 지배방정식
본 계산에서는 탱크 내부 유동분사장치 유동 해석을 위하여 RANS 방정식을 사용하였다. RANS 방정식은 아래와 같다.
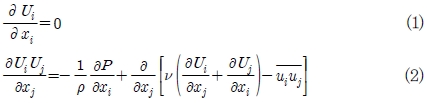
여기서 uiuj는 시간평균을 의미하며, ρ는 유체 밀도, ν는 동적 점성도, Ui는 평균 속도, Ρ는 압력을 나타낸다. twoequation eddy viscosity 모델에서는 Reynolds stress tensor를 식 (3)과 같이 사용한다.
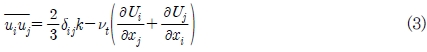
여기서 δij 는 Kronecker delta, κ는 난류 운동에너지, νi는 난류 점성이다. 본 계산에서 사용한 realizable κ ε 난류모델의 경우, 난류 운동에너지 κ 는 식 (4)와 같이 쓸 수 있으며, 난류 소멸률 ε는 식 (5)와 같이 나타내어진다.
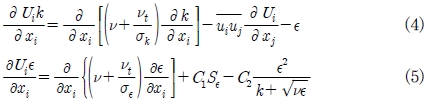
여기서
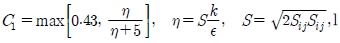
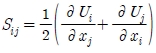과 Cs = 1.9 는 모델 상수, δκ, δε는 난류 Prandtl 수이다.
난류 점성 νt 은 식 (6)과 같이 정해진다.
여기서 계수 Cμ 는 Reynolds(5)와 Shih 등(6)이 제안한 공식으로 계산한다. 난류모델에 대한 더 자세한 내용은 참고문서(7)에서 확인할 수 있다.
유동 해석을 위하여 유한체적 해석 방법을 기반으로 한 FLUENT 13.0 CFD 해석 코드를 이용하였다. 압력 기반 solver를 사용하였으며, 압력-속도 coupling을 위하여 SIMPLEC(Semi-Implicit Method for Pressure-Linked Equations Consistent)알고리즘을 사용하였다. Momentum, turbulence 이산화방법으로는 second order upwind 방법을 사용하였으며, pressure 보간법으로는 Standard 방법을 사용하였다. 난류 모델은 realizable κ-ε 모델을 사용하였으며, 벽 근처 처리를 위해 Standard 벽 함수를 사용하였다.
2.2 경계 조건
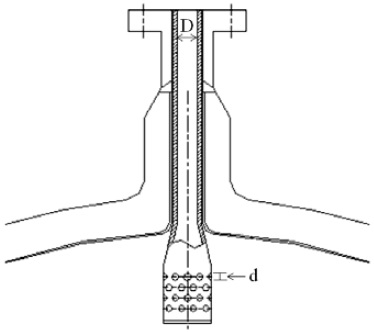
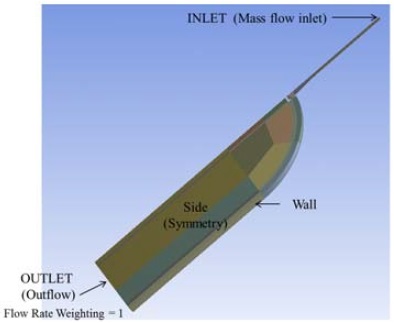
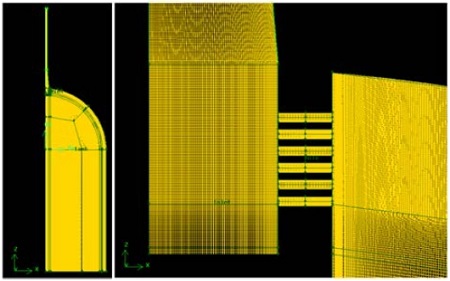
Fig. 1은 유동 분사장치의 형상을 나타낸 그림이다. 유동분사장치는 탱크 입구 배관에 설치되게 되며 유동분사장치의 구멍 배열은 Fig. 1 과 같이 staggered 형상이다. 탱크 입구 배관의 지름은 D로, 유동 분사장치 구멍의 지름은 d로 명하였다. 계산 영역은 Fig. 2에서 볼 수 있듯이, 입구 배관, 유동 분사장치, 탱크 상부로 구성된다. 입구 배관에는 입구유량 경계조건을 사용하였으며, 탱크 출구에는 출구압력 경계조건을 사용하였다. 배관, 유동 분사장치, 탱크의 벽면에는 no-slip 경계조건을 사용하였으며 계산 영역의 양쪽 면에는 대칭 경계조건을 사용하였다. 격자는 Gambit 2.4.6을 이용하여 생성하였으며, 모두 육면체 격자로 구성하였다. 유동 분사장치의 형상별로 약간의 차이는 있지만 300만개 정도의 격자수를 사용하였다. Fig. 3은 형상 F의 격자 형상(280만개 격자 사용)을 나타낸 그림이다.
Schematic of the flow distributor
Schematic of the computational domain
Schematic of the grid system
3. 결과 및 토론
3.1 분사장치 형상에 따른 유동 평가
분사장치 형상 인자의 영향을 살펴보기 위해 형상 A, B, C를 선정하였다. 설계시 고려해야 하는 주요 설계인자는 구멍 배열, 구멍 총 개수 (행 x 열), 구멍 직경과 입구배관 직경의 비 (d/D 비), 피치와 구멍 직경비 (p/d 비), 면적비(구멍 총 면적과 입구 배관 면적의 면적비)이며 형상별 설계인자 값들은 Table 1과 같다. 모든 분사장치의 구멍 배열은 Staggered type 이고, 구멍 총 개수는 형상 A와 B는 40 개(10x4배열), 형상 C는 60개 (10x6배열)이다. 구멍과 배관 직경비 d/D 의 경우 형상 A 는 0.15, 형상 B와 C는 0.31를 사용하였다. 형상 A와 형상 B를 통하여 구멍 직경의 영향을 볼 수 있으며, 형상 B와 형상 C를 통하여 면적비 영향을 볼 수 있다.
Parameters of three types of flow distributors
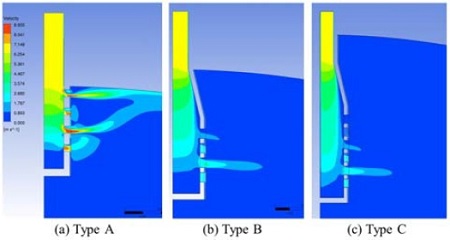
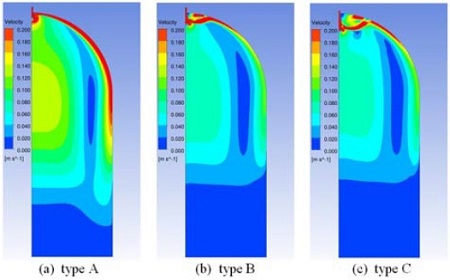
Fig. 4는 유동 분사장치 부근에서 xz평면에서의 유동 속 Contour를 나타낸 그림이다. 형상 A, B, C 모두 inlet mass flow 가 동일하므로 분사장치 구멍의 총 면적이 작을수록 구멍 내 유속은 증가하게 된다. 형상 A의 경우 면적비가 0.88로 형상 B와 C의 면적비(3.96, 5.95)보다 작으므로 구멍 내 유속이 빠름을 확인할 수 있다. 분사장치 형상 B와 형상 C를 비교해보면, 직관적으로 형상 C의 면적비가 형상 B보다 크기 때문에 형상 C의 속도가 작아야 하지만, Fig. 4 (b), (c)에서 볼 수 있듯이 형상 B 와 C의 속도가 상당히 유사한 것으로 보인다. Fig. 4 (c)에서 볼 수 있듯이, 분사장치 형상 C의 경우 구멍 6개 중에서 위 2개에서는 유속이 상당히 작은 것을 알 수 있으며 아래 4개의 구멍에서 대부분의 유속이 나오는 것을 알 수 있다. 그 결과 형상 C(구멍 6개)와 형상 B(구멍 4개)인 경우가 유사한 속도 분포를 보임을 알 수 있다. 즉 구멍 직경비가 0.31 인 경우, 분사장치 구멍 행 개수를 6개, 8개 등으로 증가시켜 분사장치의 구멍 총 면적을 늘리더라도 총 면적이 늘어난 만큼 비례적으로 분사장치 유속이 감소하지는 않을 것으로 예산된다. 또한 형상 A의 경우 구멍으로 나가는 유속이 빠르고, 구멍 직경이 작아 구멍의 유로저항계수(압력손실계수)가 크기 때문에 위 아래 구멍 간의 유속 차이가 형상 B, C보다 작음을 알 수 있다. 구멍 유속, 구멍 유로저항 계수와 구멍 간 유속 차이 관계는 3.1.3절 (식 9)에 자세하게 서술하고 있다.
Fluid velocity contours around the distributors
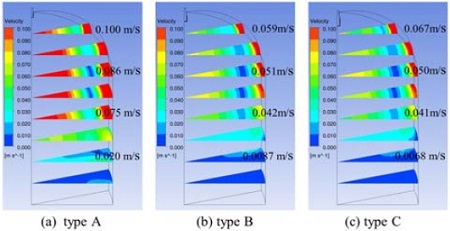
Fig. 5는 계산 도메인 전체에서 xz평면에서의 유동 속도를 나타낸 그림이다. Fig. 5에서 볼 수 있듯이 형상 A의 구멍 내 유속이 형상 B, C보다 크므로 전반적인 탱크 내 유속도 형상 A가 형상 B, C보다 크게 나옴을 확인할 수 있다. 노심보충탱크 내 상부 유동의 열성층화 측면에서는 탱크 내 유속이 작은 것이 유리하므로 형상 A보다 형상 B, C가 분사장치로 더 적합함을 유추할 수 있다. Fig. 6에서는 형상 B, C의 유속 값을 탱크 높이별로 좀 더 자세히 살펴보았다. 형상 C의 분사장치 길이가 형상 B보다 길기 때문에 탱크 상부에서는 형상 C의 유속이 B보다 크게 나옴을 알 수 있었으며, 탱크 아래 부분은 형상 B와 C의 유속이 유사하게 나왔다. 분사장치의 구멍 총 면적을 늘리기 위해 분사장치 구멍의 행 개수를 4개(형상 B)에서 6(형상 A)개로 증가시켰지만, 유속의 감소는 많이 이루어지지 않았고, 오히려 분사장치 구멍의 위치를 밑으로 이동시킨 효과를 주어 탱크 상부의 유속을 증가시키는 결과를 얻었다. 즉, 형상 B가 형상 A와 C보다 적합함을 알 수 있었다.
Fluid velocity contours in computational domain
Fluid velocity contours in computational domain
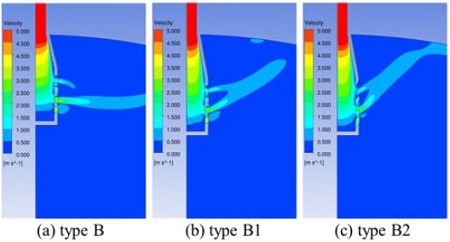
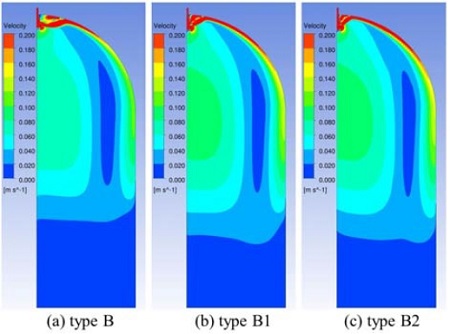
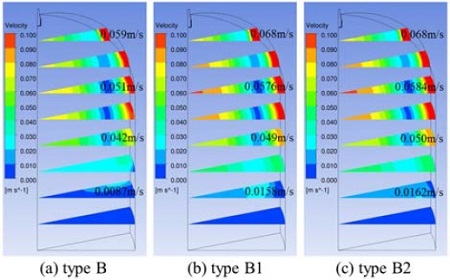
본 절에서는 분사장치 구멍에서 나오는 유동의 방향을 가능한 탱크 상부 벽 쪽으로 유도하면 탱크 상부의 유동 안정화에 유리할 가능성이 있다는 측면에서 분사장치 구멍의 각도를 바꾸어 가며 그 영향을 살펴보았다. 3.1.1의 결과를 바탕으로 형상 A, B, C 중 분사장치로 가장 적합한 형상인 형상 B에서 구멍 뚫는 방향의 각도를 30도, 60도로 기울인 새로운 형상을 제안하였으며 각각 형상 B1, 형상 B2라고 정하였다. 각 분사장치 형상의 주요 설계 인자는 Table 2에 정리하였다. 각도를 제외한 나머지 조건(구멍 배열, 총 개수, 직경, 면적비 등)은 형상 B와 동일하게 사용하였다. Fig. 7은 분사장치 구멍 주위에서 xz평면에서의 유동 속도 Contour를, Fig. 8은 계산 도메인 전체에서 유동 속도 Contour를, Fig. 9는 탱크 높이(z)별 xy 평면에서의 유동 속도 Contour를 나타낸 그림이다. 형상 B1과 B2와 같이 각도를 주어 유동 방향을 탱크 상부 벽 쪽으로 유도할 경우 주 유동이 생기는 부분이 형상 B보다 탱크 위쪽으로 이동되었지만, 벽 쪽으로 모인 대부분의 유동이 분산되지 않고 벽면을 따라 이동하게 되어, 혼합으로 인한 속도 감소 등이 생기지 않아 상당히 빠른 유속이 벽면을 타고 내려오게 되었다. 그 결과 탱크 상부의 평균 유속 값이 오히려 형상 B보다 크게 나옴을 알 수 있다. 탱크 상부(z=0)에서 높이 방향으로 0.5 m 아래 지점에서 xy 평면에서의 유동 속도 크기의 평균값을 살펴보면, 형상 B는 0.059 m/s 인 반면 형상 B1과 B2는 각각 0.068 m/s, 0.068 m/s 으로 미세하게 큼을 알 수 있다. 형상 B1과 B2의 경우 분사장치 구멍의 각도를 주어 유동을 탱크 위로 뿌려주어서 어느 정도 유동이 생기는 부분을 형상 B보다 탱크 위쪽으로 이동시켰지만, 탱크 상부의 유속은 오히려 형상 B보다 빠르게 나옴을 알 수 있었다. 결과적으로 각도를 주면서 구멍 뚫는 것이 제작도 힘들 뿐만 아니라 결과 면에서 큰 향상을 주지 않을 수 있음을 알 수 있었다. 직관적인 예상으로는 각도를 주어 유동을 탱크 상부 벽으로 유도하는 것은 탱크 상부 벽 온도를 빠르게 증가시켜 벽에 의한 응축을 완화시키고 탱크 윗부분부터 물의 온도를 높여 초기 응축 현상 완화에 유리하게 된다. 반면 본 CFD 해석 결과를 바탕으로 각도에 따른 영향을 보면, 유동 방향을 탱크 상부 벽으로 유도할 경우 유동의 분산이 거의 없이 대부분의 유동이 벽면을 타고 내려옴에 따라 탱크 상부 내 유속이 빨라 열 혼합 작용 이 활발해져 열성층화 유지 면에서 불리하게 된다.
Parameters of three types of flow distributors
Fluid velocity contours around the distributor
Fluid velocity contours in computational domain
Fluid velocity contours in computational domain
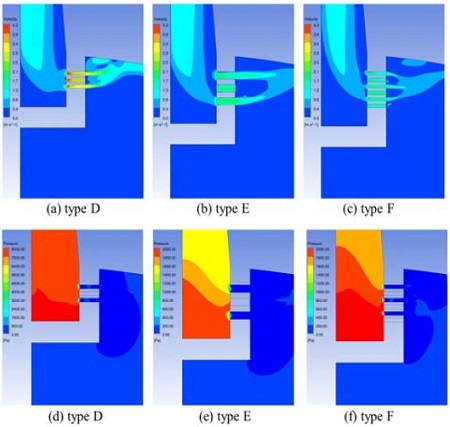
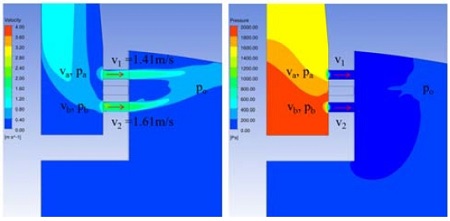
본 절에서는 구멍 직경을 줄여 구멍과 배관 직경비를 0.13으로 감소시켰으며, 구멍 총 면적비는 기존 계산들과 유사하게 유지하기 위해, 구멍 개수를 늘려 총 125~252개의 구멍을 뚫어 면적비가 2.1~4.2가 되게 했다. 분사장치 형상 D, E, F 의 설계 인자들은 Table 3과 같다. 형상 D와 E를 통해 면적비의 영향을 관찰하였으며, 형상 E와 형상 F를 통해 구멍 직경의 영향을 다시 살펴보았다. Fig. 10은 분사장치 구멍 주위에서 xz평면에서의 유동 속도와 압력분포를 나타낸 그림이며, Fig. 11을 통해 구멍 간 속도 차이를 구해보았다. Fig. 11에 표시된 a 위치와 b 위치에서 베르누이 원리를 적용하면 아래 식과 같다.
Parameters of three types of flow distributors
Fluid velocity contours around the distributors
Fluid velocity contours around the distributors
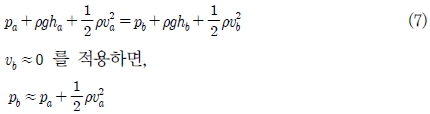
a 위치와 b 위치에서의 압력차는 아래 식과 같이 구할 수 있다.
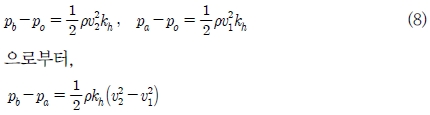
위 식을 속도 차이에 대한 항으로 정리하고, 베르누이 원리를 적용하여 구한 식을 이용하여 정리하면 아래 식과 같이 구멍 간 속도차를 구할 수 있다.
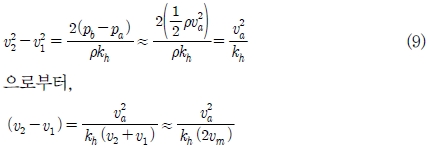
식 (9)를 살펴보면 분사장치 구멍간의 속도차이와 관련된 인자를 알 수 있으며, 그 인자들이 구멍 간 유속 차이에 미치는 영향을 유추할 수 있다. 분사장치 구멍 간의 유속을 고르게 분배하기 위해서는 확대관을 이용하여 분사장치의 면적(Αα)을 증가시켜 분사장치 내 유속(να)을 감소시켜야 효과적임을 알 수 있고, 분사장치 구멍의 직경(d)을 작게 하여 구멍의 압력손실계수(kh)를 증가시킬 경우 구멍 내 속도 차이가 감소함을 알 수 있다. 분사장치 구멍 사이의 높이를 줄여 구멍 사이의 압력차(Ρb - Ρa)가 감소할 경우에도 구멍 내 속도 차이가 감소함을 유추할 수 있다. 또한 유동 분사장치 구멍으로 빠져나가는 평균 유속(νm)이 빠를 경우, 열성층화 유지가 잘 안 되어 응축현상 완화에는 안 좋은 반면, 위의 식과 같이 구멍 간 유속 차이를 감소시켜 유동 분배에는 유리하다는 것도 확인하였다. 위의 수 계산을 검증하기 위해, CFD 해석 결과 값과 비교 및 검증을 수행하였다. 한 예로 형상 E 에서의 구멍 사이의 속도 차를 구하면 아래 식과 같다.
이와 유사하게 다른 유동 분사장치 구멍 내 유속차이를 수계산을 통해 구하였으며, 결과를 Table 4에 정리하였다. 또한 CFD 계산 결과를 이용하여 분사장치 구멍 내 유속차이를 구하였으며(Table 5), 수계산과 CFD 해석결과를 비교한 결과, 두 경우에서의 유속차이 값이 유사하게 나옴을 확인하였다.
Velocity difference between holes of flow distributors
Velocity difference between holes of flow distributors (CFD)
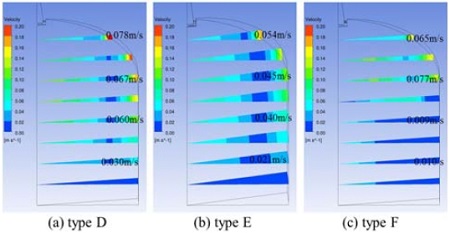
Fig. 12는 탱크 높이(z)별 xy 평면에서의 유동 속도 Contour를 나타낸 그림이다. 형상 D 의 경우 구멍 전체 면적이 형상 E 보다 0.5 배 작기 때문에 구멍 내 유속이 이론적으로는 2배 크게 되며, 그에 비례해서 탱크 내 유속도 전체적으로 증가하게 된다. 다만, 형상 D 가 구멍 간 유속 차이가 형상 E 보다 작고 분사장치 구멍마다 고르게 유동이 분사되어 탱크 내 높이 별 평균 속도의 크기 차이는 2 배가 아닌 1.5 배정도 됨을 확인하였다. 형상 E 와 F 를 살펴보면, 전체적인 탱크 내 유동이 다르게 나옴을 확인하였다. 좀 더 자세히 살펴보면, 탱크 상부에서 0.5 m 깊이에서는 형상 E 의 평균 유속(0.054 m/s)이 형상 F(0.065 m/s) 보다 작았으며 2 m 깊이 밑으로는 형상 F의 평균유속이 형상 E보다 많이 감소됨을 확인하였다. CFD 해석 결과에서는 형상 E가 탱크 상부의 유속이 가장 작아 노심보충탱크 열성층화 안정화 측면에서 가장 유리한 것으로 나왔다.
Fluid velocity contours in computational domain
3.2 CMT 분사장치 설계의 최적화
본 계산에서는 노심보충탱크 작동 시 발생되는 응축현상을 완화시킬 수 있는 최적의 분사장치 형상을 도출하기 위해 유동 분사장치의 여러 설계 인자를 바꾸어가며 유동해석을 수행하였다. 노심보충탱크 내부 열성층막을 유지하기 위해서는 압력평형배관을 통해 노심보충탱크 내부로 들어오는 증기 혹은 물의 유속이 작아야 한다. 이를 위해 가능한 분사장치 구멍의 총면적 혹은 면적비를 크게 하고, 분사장치의 모든 구멍에서 유량이 균등하게 분배되어야 한다. 해석 결과에서 확인할 수 있듯이, 유동이 구멍마다 고르게 분배되지 않을 경우, 분사장치 구멍의 총 면적을 늘리더라도 총 면적이 늘어난 만큼 비례적으로 분사장치 유속이 감소하지는 않음을 알 수 있었다. 구멍마다 고르게 분배하기 위해 구멍 직경을 작게 하거나, 구멍 열 수를 줄여, 맨 위 구멍과 맨 아래 구멍 위치의 높이 차를 줄이는 것이 좋음을 확인할 수 있었다. 다음으로, 포화증기가 압력평형배관을 통해 노심보충탱크 탱크 내부로 유입될 때, 차가운 탱크 벽면 혹은 내부의 냉각수 상부를 만나면 급격한 응축이 발생되게 된다. 이러한 초기에 생기는 응축 현상의 경우, 보수적인 관점에서 보면, 뜨거운 증기와 만나게 되는 탱크 벽면의 온도 및 냉각수 상부가 유입되는 뜨거운 증기에 의해 포화 증기 온도로 가열되어야 더 이상 응축현상이 발생되지 않게 된다. 분사장치 구멍의 각도를 위쪽으로 주어 유동의 방향을 가능한 탱크 상부 벽 쪽으로 유도할 경우 뜨거운 포화 증기와 접촉되는 물의 범위가 줄어들어 초기 응축현상을 완화시킬 수 있다. 또한 탱크 구조물의 열용량이 냉각수보다 크기 때문에 탱크 벽면으로 뜨거운 증기가 분사되는 것이 구조물과 냉각수의 온도를 유사하게 상승시킬 수 있어 열성층막을 빠르게 형성시키는데 유리하다. 또한 분사장치 길이를 애초에 짧게 할 경우, 분사장치 구멍의 각도를 주지 않더라도 분사장치 구멍이 탱크 상부 벽면 쪽에 유동을 분사하게 된다. 따라서 분사장치 구멍의 각도를 주는 것보다는 분사장치 길이를 짧게 하는 것이 더 바람직하다. 본 연구에서 수행한 단상 모델 해석 결과에서는 각도를 위쪽으로 기울여 유동 방향을 탱크 상부 벽 쪽으로 유도할 경우, 주 유동이 생기는 부분을 탱크 위쪽으로 이동시켰지만, 벽 쪽으로 모인 대부분의 유동이 분산되지 않고 벽면을 따라 이동하게 되어, 혼합으로 인한 속도 감소 등이 생기지 않아 상당히 빠른 유속이 벽면을 타고 내려오게 되었으며 그 결과 탱크 상부의 평균 유속 값이 크게 나왔다. 하지만 실제 노심보충탱크 내부에서는 탱크 내부 냉각수 수면이 조금만 내려와도 분사장치에서 나온 증기가 벽면을 따라 속도를 유지하면서 냉각수(물)로 침투하기보다는 탱크 수면 위의 증기 영역에서 순환되는 현상이 더 강할 것으로 예상된다. 또한 초기 응축 현상이 멈추어 주입이 시작될 경우 수위 하강에 따라 노심보충탱크 구조물이 추가적으로 노출되게 되는데, 이때 증기 분사 방향이 벽 쪽으로 유도 될 경우, 뜨거운 증기가 구조 벽을 따라 이동하면서 추가 노출된 구조물의 온도를 상승시켜 주입이 시작된 이후에 추가 노출되는 구조물 벽에 의한 응축 현상을 완화시킨다. 따라서 CFD 해석 결과에서는 유동이 상부 벽 쪽으로 분사될 경우 벽면을 타고 상당히 빠른 유속으로 내려와 열성층화에 불리해 보이지만, 실제 현상에서는 증기의 침투 현상이 CFD 해석 결과만큼 강하게 나타나지 않을 것으로 예상되고, 오히려 유동 방향을 탱크 상부 벽 쪽으로 유도할 경우, 초기 및 주입 중 생길 수 있는 응축현상을 완화시키고 열성층화를 안정화시키는 등 긍정적인 측면이 더 많다고 예상할 수 있다.
4. 결 론
본 연구의 해석 결과 및 고찰을 바탕으로 최적의 분사장치의 형상을 위한 설계 포인트를 요약하면 다음과 같다. 분사장치 구멍마다 고르게 유동을 분사시키기 위해, 확대관을 이용하여 분사장치의 면적을 증가시켜 분사장치 내 유속을 감소시켜야 하며, 구멍 직경을 작게 하고 구멍 행 수를 줄여 맨 위 구멍과 맨 아래 구멍 위치의 높이 차를 줄여야 한다. 또한 분사장치 길이를 짧게 하여 구멍의 각도를 주지 않더라도 유동이 탱크 상부 벽면으로 분사되게 한다. CFD 해석 모델의 한계로, 실제 CMT 내부 현상은 CFD 결과와 다를 수 있으며 최종 분사장치가 CMT 초기 응축현상 완화에 미치는 영향은 추후 시험을 통해 비교 검토되어야 한다.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) funded by the Korea government (MSIP) (No. NRF-2012M2A8A4025974).
References
- Song, C.-H., Cho, S., Won, S.-Y., Chun, S.-Y., Chung, M.-K., (1998), Thermal-hydraulic phenomena in a reactor drain tank, KAERI.
- Tuunanen, J., Vihavainen, J., D’auria, F., Kimber, G., (1999), Assessment of Passive Safety Injection Systems of ALWRs, Final report of the European Commsion 4th framework programme project FI4I-CT95-0004 (APSI).
- EPS-GW-GL-700, AP1000 European Design Control Document.
-
Cho, S., Chun, S.-Y., Baek, W.-P., and Kim, Y., (2004), Effect of multiple holes on the performance of sparger during direct contact condensation of steam, Experimental Thermal and Fluid Science, 28, p629-638.
[https://doi.org/10.1016/j.expthermflusci.2003.10.002]
- Reynolds, W.C., (1987), Fundamentals of turbulence for turbulence modeling and simulation, Lecture Notes for Von KarmanInstitute, Agard Report No. 755.
- Shih, T.H., Zhu, J., Lumley, J.L., (1994), A new Reynolds stress algebraic equation model, NASA TM, 106644.
- ANSYS Inc, (2011), Fluent 13.0 Theory Guide.