영구자석 배열이 사각 공동 내부 자성나노유체의 열유동 특성에 미치는 영향

1. 서 론

자성나노유체(ferrofluid)는 물, 미네랄 오일 등의 유체에 10 nm 크기 자성나노입자를 분산시킨 현탁액으로, 자성체와 유체의 특성을 모두 나타낸다. 자성나노유체는 외부 자기장 인가 시 내부 나노 입자들이 자기장 방향을 따라 배열되며 자기체적력(magnetic body force)에 의해 일반 유체와는 다른 열유동 특성이 나타난다. 또한, 기저 유체(base fluid)에 고체 나노 입자를 분산시킨 자성나노유체와 같은 나노입자현탁액은 입자 농도에 따라 열전도도가 향상되어 기존 유체 대비 열적 특성이 우수하다.⁽¹⁾ 열전달 효율을 높이는 것은 다양한 산업 분야에서 중요한 관심사이며, 자성나노유체를 열전달 매체로 사용할 경우 기존 유체보다 열전달 효율을 높일 수 있고 자기장을 통한 유동 제어가 가능해진다. 이에 따라 자성나노유체의 열유동 특성에 대한 다양한 연구가 진행되고 있다. Mousavi 등⁽²⁾은 네오디뮴 영구자석의 자기장이 자성유체 내부유동에 미치는 영향을 수치적으로 해석하였으며, Reynolds 수가 230인 층류 유동에 자기장을 인가시 Nusselt 수가 약 2배 향상되는 것을 확인하였다. Shojaeizadeh 등⁽³⁾은 외부 자기장이 자성나노유체를 이용한 평판형 태양광 집열기 효율에 미치는 영향에 대해 실험 및 수치해석을 통해 연구하였으며, 물 대신 자성나노유체를 열전달 매체로 적용시 열효율이 최대 52.15% 향상될 수 있음을 확인하였다. Pattanaik 등⁽⁴⁾은 자기장과 자성나노유체를 이용한 폐루프 방식의 폐열회수 및 냉각장치를 개발하고 실험 및 수치해석을 통해 냉각 성능을 고찰하였다. Kumar 등⁽⁵⁾은 전류가 흐르는 마이크로 와이어 주위 자성나노유체의 열자기대류현상에 대해 실험 및 수치적으로 연구하였다. Zanella 등⁽⁶⁾은 변압기 냉각에 절연유 대신 자성유체를 사용할 때 자기체적력 영향에 의해 열전달이 향상됨을 수치적으로 분석하였다. Sirikasemsuk 등⁽⁷⁾은 자성나노유체와 열전냉각 모듈을 이용한 배터리 팩 냉각 장치를 구성하고 배터리 팩 과도 열특성 변화에 대한 연구를 수행하였다. Cheng 등⁽⁸⁾은 영구자석 자기장이 수평 채널 자성유체 자연대류에 미치는 영향을 실험적으로 조사하였다. Chinnasamy 등⁽⁹⁾은 고온 열원이 내부에 위치한 정방형 공동내 나노유체의 자연대류를 수치적으로 분석하였다.

본 연구에서는 2개의 영구자석 위치 배열에 따라 달라지는 직방형 공동(rectangular cavity) 내부 자성나노유체의 열유동 특성을 수치적으로 해석하였다. 해석모델은 고온의 열원을 포함한 밀폐 공동 내 자연대류 열유동 문제이며, 영구자석없이 자연대류만을 고려한 기준 모델과 좌측 및 우측 영구자석의 높낮이를 달리한 6개 경우의 자기-열유동 연성해석을 수행하였다. 영구자석이 형성하는 불균일 자기장 위치 변화가 공동(cavity) 내 자성나노유체 자연대류 열전달 특성에 미치는 영향을 고찰하였으며, 열원 표면에서의 Nusselt 수를 계산해 영구자석 위치에 따라 공동 내 자성나노유체가 갖는 대류열전달 특성을 비교 분석하였다.

2. 수치해석

2.1 해석모델

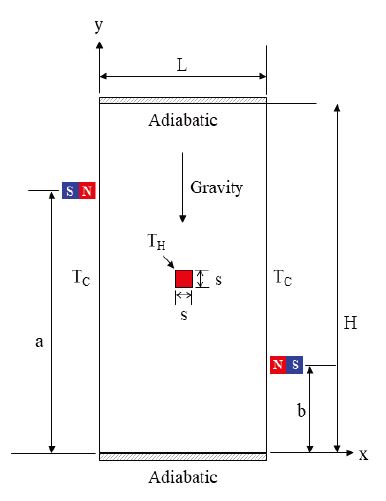
해석모델은 상부 및 하부에 단열 표면을 갖는 밀폐된 직방형 공동으로 설정하였다. 좌측 및 우측면 수직 벽은 저온(T_C)의 등온 표면이며, 고온(T_H)의 등온 표면을 갖는 정방형 열원이 중심부에 위치한다. 불균일 자기장을 형성하는 2개의 영구자석이 직방형 공동 측면벽 외부에 각각 한 개씩 위치한다. 영구자석 높이와 중력의 작용 방향, 해석모델에 대한 정보는 Fig. 1에 도시하였다. 해석모델과 유체 물성에 기반한 Grashof 수는 7.17*10⁷이며 Prandtl 수는 70.4이다.

Fig. 1

Schematic of rectangular cavity model

2.1.1 유효성 검증 및 격자계 구성

수치 모델 유효성 검증을 위해, 본 논문에 적용한 방법을 이용하여 열원이 존재하는 정방형 공동 내 Fe₃O₄-water 나노유체의 자연대류를 수치적으로 연구한 Chinnasamy 등⁽⁹⁾의 결과를 비교 분석하였다. 일정한 Rayleigh 수에 대해서 공동 내 열원의 종횡비 및 Fe₃O₄ 나노입자의 체적분율을 달리하고 열전달 변화를 분석한 연구이다. 본 연구의 해석모델이 참고 논문과 유사한 열전달 양상을 보이는 것을 확인하였으며 Fig. 2에 등온선 결과, Table 1에 물성을 기술하였다.

Fig. 2

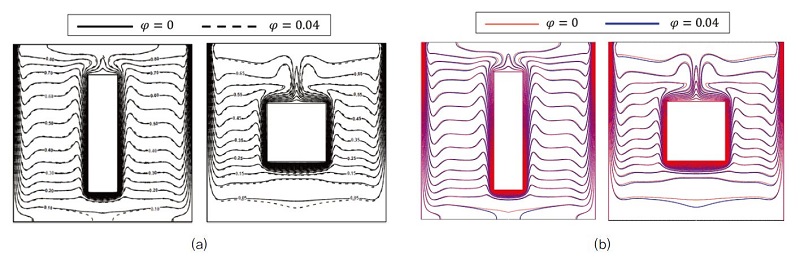
Comparison of isotherms of (a) Chinnasamy et al.9 with (b) present study at a fixed Rayleigh number(Ra=107) and various nanoparticle volume fraction ϕ

Table 1

Physical properties of the validation study

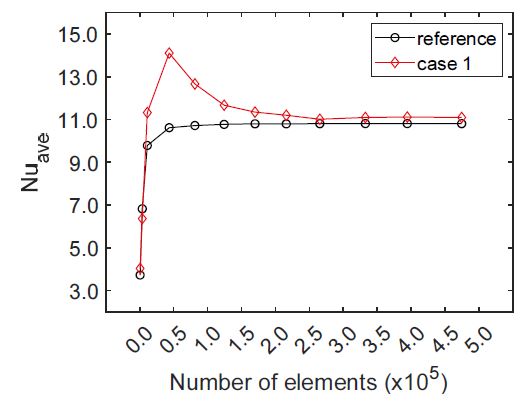
해석모델의 격자계는 비정렬 삼각형 격자로 구성하였다. 격자 의존성 파악을 위해 기준 모델과 magnet case 1의 격자 크기를 감소시키며 10800 sec 동안의 과도해석(transient anlaysis)을 수행하였다. 열원 4개 표면 평균 Nusselt 수의 time-averaged 값을 기준으로 격자 의존성 분석을 수행하였으며 결과는 Fig. 3에 도시하였다. 해석 결과, 수렴 또는 주기적 수렴 구간으로 판단되는 9800 sec 이후에 열원 표면 평균 Nusselt 수의 time-averaged 값이 격자 개수 21만개부터 상대오차 약 1 % 이내로 계산되어 본 해석의 격자계로 설정하였다.

Fig. 3

Results of grid dependency test of reference model and magnet case 1

2.1.2 영구자석 배열

직방형 공동 외부 좌측 및 우측에 위치한 영구자석을 고온 열원 주위에 위치시키고 높낮이를 달리하여 6개의 해석모델을 설정하였다. Case 별 좌측 및 우측 영구자석 위치에 대한 정보는 공동의 수직 길이(H)에 대해 무차원화하여 Table 2에 기술하였다.

Table 2

Arrangements of permanent magnet

2.3 자화

나노입자의 크기를 고려한 자성나노유체의 자화는 식 (9)의 Langevin 함수⁽¹⁰⁾로부터 유도된다.

$\[ L\left(\zeta \right)=\coth \zeta -\frac{1}{\zeta }, \zeta =\frac{\pi {\mu }_0{M}_{d}H{d}^3}{6k_{B}T} \]$

(9)

$\[ M=M_{s}L\left(\zeta \right) \]$

(10)

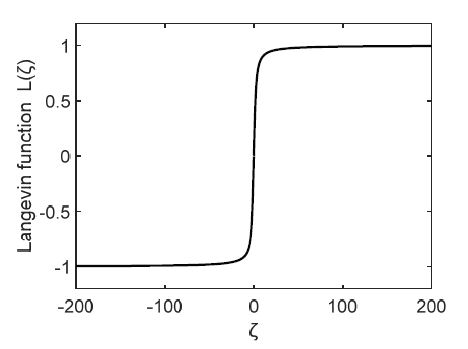
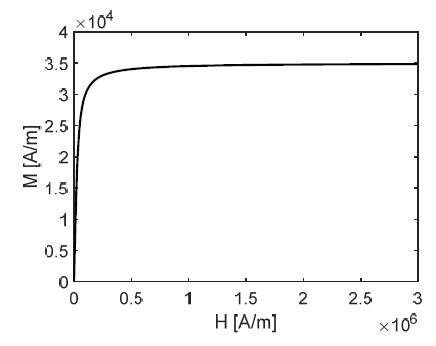
위 식 (10)은 자성나노유체의 자화이며 M_s는 자성나노유체의 포화 자화(saturation magnetization)이다. M_d는 10 nm Fe₃O₄ 입자의 domain magnetization,⁽¹⁰⁾ k_B 는 Boltzmann 상수, H 는 자기장 세기를 의미한다. T 는 절대 온도이며, μ₀ 는 진공의 투자율이다. 본 해석에 적용한 자성나노유체인 EFH-1의 물성은 Table 3에 기술하였으며, 계산된 유체의 Langevin 함수는 Fig. 4에 도시하였다. Langevin 함수로부터 유도된 자화 계산 결과는 Fig. 5에 도시하였다. 계산시 시스템 평균 온도인 300 K 을 적용하였다. Fig. 5는 유체의 자화 곡선이며 자기장 세기가 증가함에 따라 자화 강도가 증가하는 것을 확인할 수 있고, 포화 자화인 35 kA/m 이상부터는 자기장 세기를 증가시켜도 더 이상 자화되지 않았다.

Table 3

Physical properties of the EFH-1 ferrofluid

Fig. 4

Langevin function of EFH-1

Fig. 5

M-H curve of EFH-1

3. 결과 및 고찰

자연대류만을 고려한 기준 모델의 열유동 해석과 자석 영향을 고려한 6개 모델의 자기-열유동 연성해석 결과를 분석하였다. 모든 해석 case에 대해 과도해석의 마지막 time step인 10800 sec 에서의 속도 컨투어와 유선, 등온선을 도시하였다. 등온선 범위는 293.15-308.15 K이며 간격은 0.5 K이다.

또한, 자석 자기장에 의한 열원 주위 대류열전달 특성 분석을 위해 식 (11)의 국소 Nusselt 수를 계산하였다. 국소 Nusselt 수는 식 (12)의 국소 대류열전달계수로부터 도출되며 정방형 열원 벽면 길이(s)로 무차원화한 변수 X = x/s, Y = y/s 에 대해 도시하였다. 도시된 국소 Nusselt 수는 9800 sec 이후부터 마지막 time step까지 1000 sec 동안의 time-averaged 값이다.

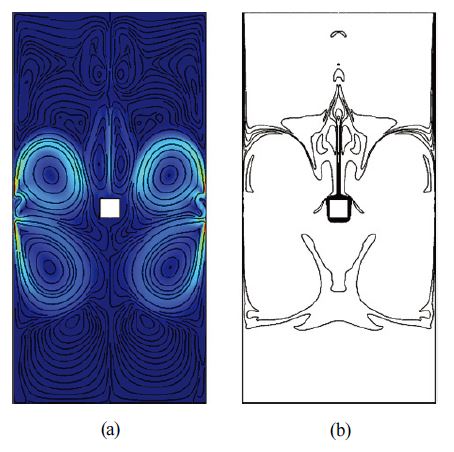
3.1 기준모델

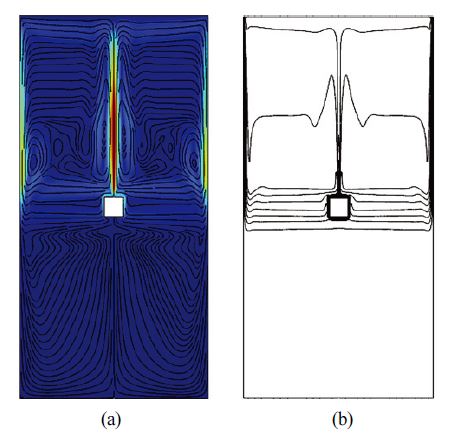
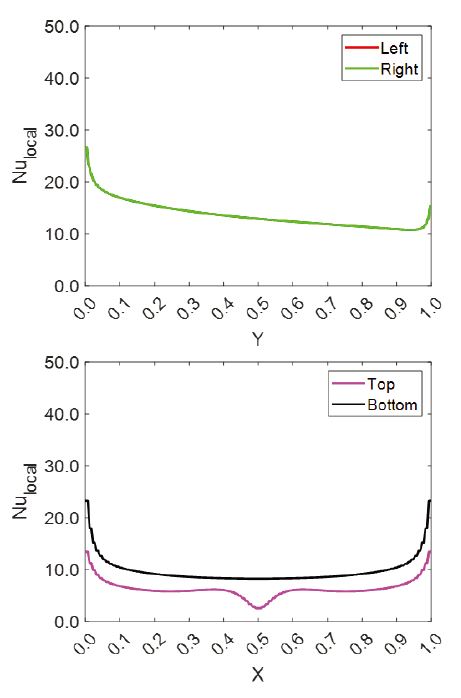
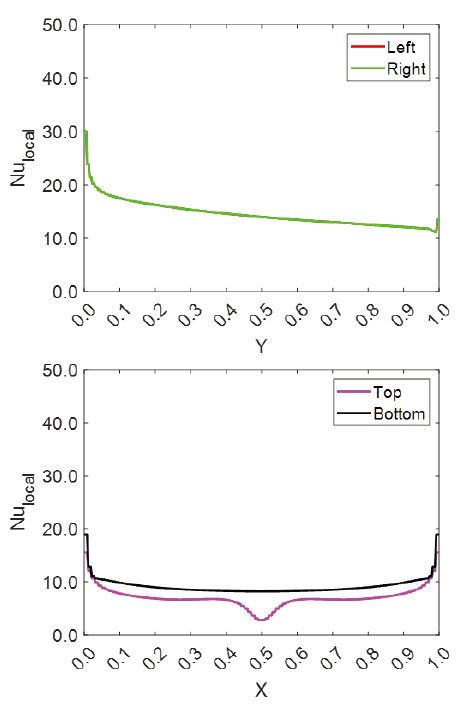
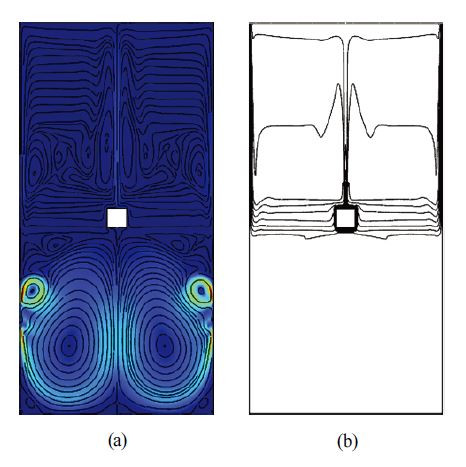
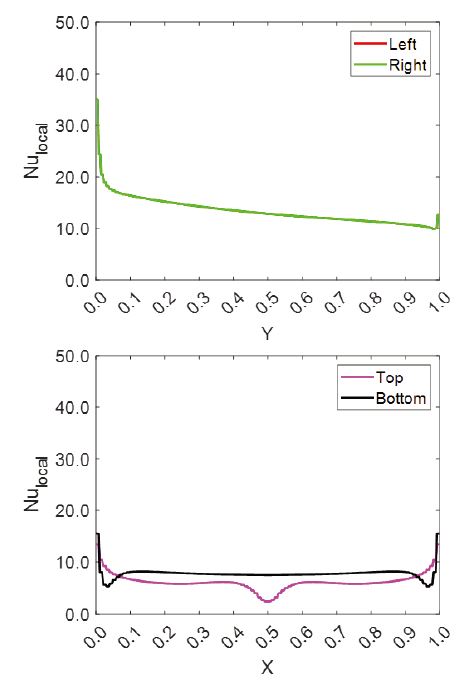
자연대류만을 고려한 기준 모델에 대한 결과는 Fig. 6에 도시하였는데, 중심부 고온 열원으로부터 부력에 의해 유동이 발달되면서 유선은 대칭형상을 나타내었다. 또한, Fig. 7의 국소 Nusselt 수 결과를 통해 열원 측면 수직 표면에서는 아래로 갈수록 Nusselt 수가 증가하여 대류열전달이 활발한 것을 확인할 수 있다. 열원 상부 및 하부에 위치한 수평 표면에서는 가장자리로 갈수록 Nusselt 수가 증가하였고, 특히 상부 수평 표면 중앙에서 국소 Nusselt 수가 가장 낮은 결과를 나타낸다. 기준 모델 상하좌우 4개 열원 표면의 평균 대류열전달계수는 138.51 W/m²K 이고 평균 Nusselt 수 계산 결과는 10.94를 나타내었다.

Fig. 6

(a) streamline, velocity contour, and (b) isotherms of reference case at t=10800 sec

Fig. 7

Time-averaged local Nusselt number of reference case (9800-10800 sec)

3.2 Magnet case 1

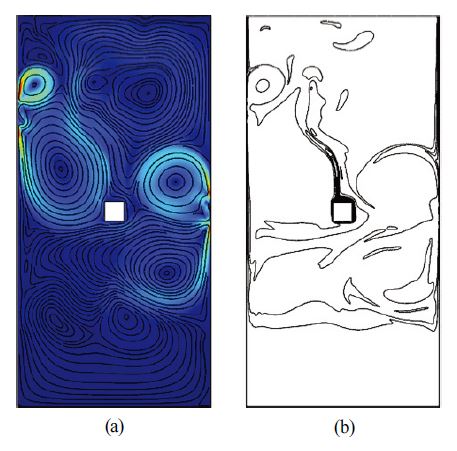
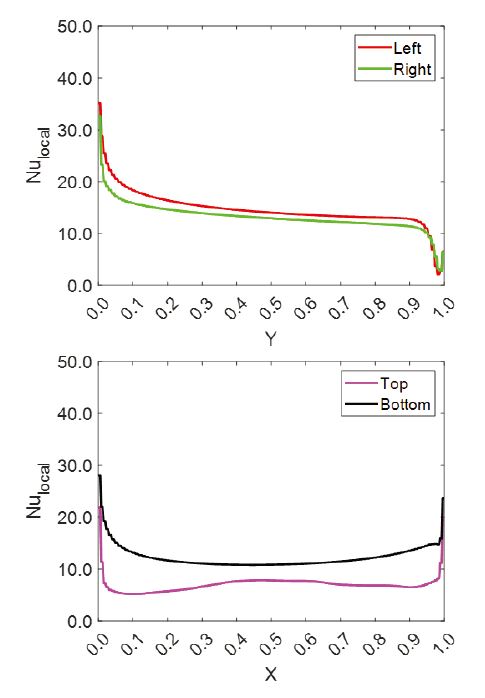
Magnet case 1의 결과는 Fig. 8에 도시하였다. 좌측 및 우측 자석의 위치는 모두 열원보다 상부에 위치하며 두 자석은 동일 선상에 있다. Fig. 9에 국소 Nusselt 수 결과를 도시하였다. 유동은 열원 상부에서 활발하다. 열원 좌측 및 우측 표면과 상부 표면에서 평균 Nusselt 수가 증가하였으며, 하부 표면에서는 감소하였다. 열원 좌우측의 회전 유동장이 측면 및 상부에서 부력에 의한 상승류를 촉진시키고 하부의 부력에 의한 상승 유동은 억제한 결과로 판단된다. 계산 결과 case 1의 열원 4개 표면 평균 대류열전달계수는 143.15 W/m²K 이고, 평균 Nusselt 수는 11.30으로 기준 모델 대비 3.3 % 증가하였다.

Fig. 8

(a) streamline, velocity contour, and (b) isotherms of magnet case 1 at t=10800 sec

Fig. 9

Time-averaged local Nusselt number of magnet case 1 (9800-10800 sec)

3.3 Magnet case 2

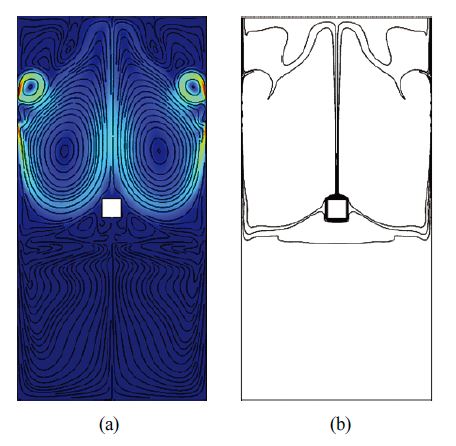
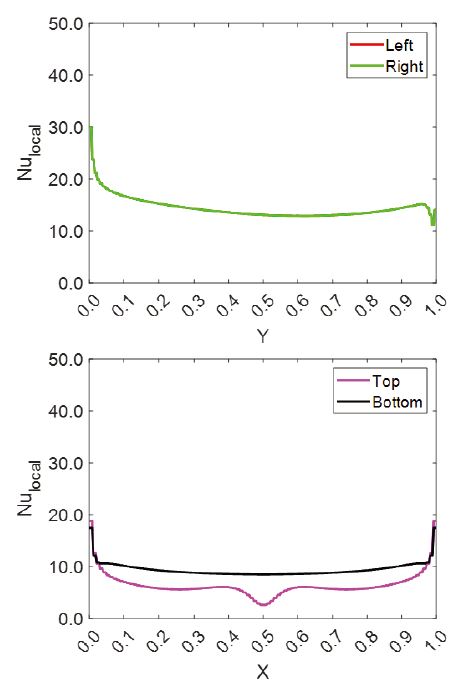
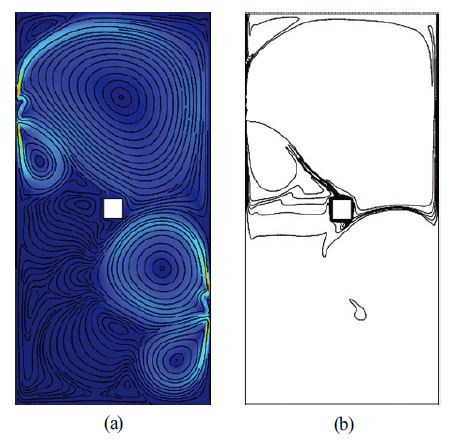
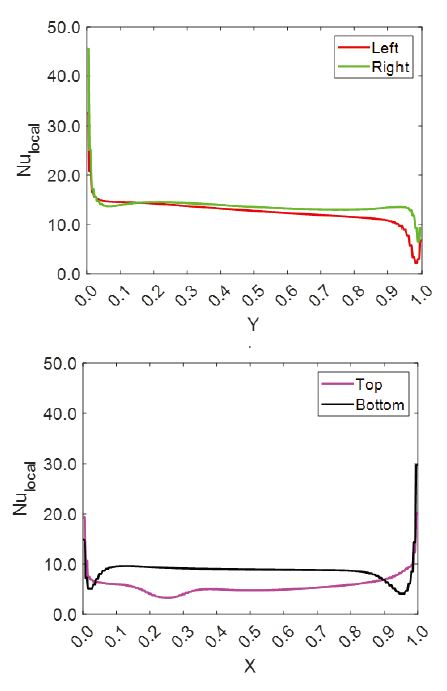
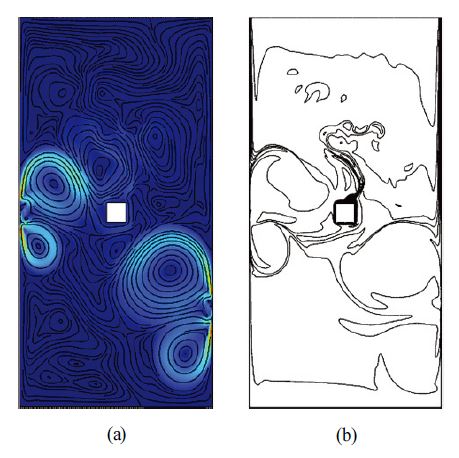
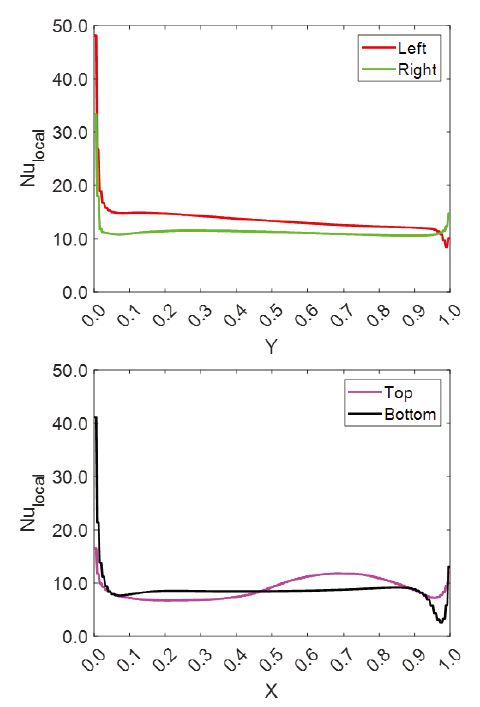
Magnet case 2의 결과는 Fig. 10에 도시하였다. 좌측 자석은 열원보다 상부에 위치하고 우측 자석은 열원과 동일선상에 위치한다. Fig. 11에 국소 Nusselt 수 결과를 도시하였다. 열원 좌측 표면과 상부 및 하부 표면에서 평균 Nusselt 수가 증가하였으며, 우측 표면에서는 감소하였다.

Fig. 10

(a) streamline, velocity contour, and (b) isotherms of magnet case 2 at t=10800 sec

Fig. 11

Time-averaged local Nusselt number of magnet case 2 (9800-10800 sec)

좌측 자석에 의한 회전 유동장 방향이 부력에 의한 상승 유동 방향과 일치하여 좌측 표면의 대류열전달을 증가시킨 것으로 판단된다. 우측 자석에 의한 회전유동장의 방향은 부력에 의한 상승 유동을 억제하는 중력과 같은 방향으로 작용하여 기준모델 대비 우측 표면의 대류열전달을 감소시킨 것으로 판단된다. 열원 4개 표면 평균 대류열전달 계수는 151.83 W/m²K 이고, 평균 Nusselt 수는 11.99로 기준모델 대비 9.6 % 증가하여 6개 자석 배열 중 기준 모델 대비 대류열전달 향상 효과가 가장 높은 영구자석 배열로 판단된다.

3.4 Magnet case 3

Magnet case 3의 결과는 Fig. 12에 도시하였다. 좌측 자석은 열원보다 상부에 위치하고 우측 자석은 하부에 위치한다. Fig. 13에 국소 Nusselt 수 결과를 도시하였다. 좌측 및 우측 자석에 의한 회전 유동장 방향이 부력에 의한 상승 유동을 억제하는 것으로 판단된다. 열원 표면 평균 대류열전달 계수는 131.37 W/m²K 이고, 평균 Nusselt 수는 10.37로 기준 모델 대비 5.2 % 감소하였다.

Fig. 12

(a) streamline, velocity contour, and (b) isotherms of magnet case 3 at t=10800 sec

Fig. 13

Time-averaged local Nusselt number of magnet case 3 (9800-10800 sec)

3.5 Magnet case 4

Magnet case 4의 결과는 Fig. 14에 도시하였다. 좌측 및 우측 자석은 모두 열원과 동일 선상에 위치한다. Fig. 15에 국소 Nusselt 수 결과를 도시하였다. 열원 주위에서 대칭 유동장이 발달한 것을 확인하였으며 열원 좌측, 우측 및 상부에서 기준모델 대비 평균 Nusselt 수가 증가하였다. 하부에서는 평균 Nusselt 수가 감소하였다. 열원 표면 평균 대류열전달계수는 144.89 W/m²K 이고, 평균 Nusselt 수는 11.44로 기준 모델 대비 4.6 % 증가하였다.

Fig. 14

(a) streamline, velocity contour, and (b) isotherms of magnet case 4 at t=10800 sec

Fig. 15

Time-averaged local Nusselt number of magnet case 4 (9800-10800 sec)

3.6 Magnet case 5

Magnet case 5의 결과는 Fig. 16에 도시하였다. 좌측 자석은 열원과 동일 선상에 위치하며, 우측 자석은 열원보다 하부에 위치한다. Fig. 17에 국소 Nusselt 수 결과를 도시하였다. 열원 상부에서 기준모델 대비 평균 Nusselt 수가 증가하였으나 우측 및 하부에서 평균 Nusselt 수가 감소하였다. 열원 표면 평균 대류열전달계수는 136.85 W/m²K 이고, 평균 Nusselt 수는 10.80으로 기준 모델 대비 1.2 % 감소하였다.

Fig. 16

(a) streamline, velocity contour, and (b) isotherms of magnet case 5 at t=10800 sec

Fig. 17

Time-averaged local Nusselt number of magnet case 5 (9800-10800 sec)

3.7 Magnet case 6

Magnet case 6의 결과는 Fig. 18에 도시하였다. 좌측 및 우측 자석은 열원 하부 동일 선상에 위치한다. Fig. 19에 국소 Nusselt 수 결과를 도시하였다. 열원 4개 표면 모두 기준모델 대비 평균 Nusselt 수가 감소하였다.

Fig. 18

(a) streamline, velocity contour, and (b) isotherms of magnet case 6 at t=10800 sec

Fig. 19

Time-averaged local Nusselt number of magnet case 6 (9800-10800 sec)

열원 표면 평균 대류열전달계수는 130.46 W/m²K 이고, 평균 Nusselt 수는 10.30으로 기준 모델 대비 5.8 % 감소하여 6개 영구자석 배열 중 기준모델 대비 대류열전달 감소 효과가 가장 큰 배열로 판단된다. Magnet case 1과 유사한 대칭 유동장이 형성되나 발달된 유동장의 위치가 열원 하부에 위치한다.

4. 결 론

본 연구에서는 직방형 공동 외부 영구자석 배열이 공동 내 자성나노유체 자연대류 열유동 특성에 미치는 영향에 대해 수치적으로 해석하였다. 자연대류만을 고려한 기준 모델에 대해 열유동 해석을 수행하였고, 자기체적력 영향이 고려된 6개의 영구자석 배열 모델에 대해 자기-열유동 연성해석을 수행하여 대류열전달 특성을 비교 분석하였다. 그 결과를 요약하면 다음과 같다.

• (1) 자연대류만을 고려한 기준 모델 해석 결과 중심부 고온 열원으로부터 부력에 의해 유동이 발달하고 유선이 대칭 형상을 나타내는 것을 확인하였다. 열원 좌우측 수직 벽면에서의 국소 Nusselt 수는 위쪽으로 갈수록 감소하였는데, 상부보다 하부에서 대류열전달이 활발한 것을 의미한다.
• (2) 자기체적력 영향을 고려한 영구자석 배열 모델에 대한 해석 결과 case 2, case 4의 열원 표면 평균 Nusselt 수가 각각 11.99, 11.44로 가장 높은 결과를 보였다. 기준 모델의 평균 Nusselt 수 대비 각각 9.6 %, 4.6 % 증가한 수치이다. 불균일 자기장에서 기인하는 자기체적력이 공동 내 회전 유동장을 발달시키고 열원 표면에서 부력과 방향이 같은 상승류를 만들어내어 열원 표면 대류열전달을 향상시킨 것으로 판단된다.
• (3) 영구자석 배열 모델 case 3, 5, 6의 Nusselt 수 감소 결과는 열원 표면에서 자기체적력에 의해 발달한 유동장이 중력과 같은 방향으로 작용하여 부력에 의한 상승 유동을 감쇠시키고 국소 대류열전달을 감소시킬 수도 있음을 의미한다.
• (4) 따라서 온도차에서 기인하는 자연대류 유동의 특성과 자기체적력에 의해 발달하는 유동장의 방향을 적절히 고려하면, 영구자석 배열에 따라 국소 대류열전달 계수를 변화시킬 수 있고 국소 냉각 효과를 높일 수 있다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2021R1A2C1010499).

References

• Altan, C. L., Bucak, S., 2011, “The effect of Fe3O4 nanoparticles on the thermal conductivities of various base fluids,” Nanotechnology, Vol. 22, No. 28, Article 285713. [https://doi.org/10.1088/0957-4484/22/28/285713]
• Mousavi, S. M., Darzi, A. A. R., & Li, M., 2022, “Modelling and Simulation of Flow and Heat Transfer of Ferrofluid under Magnetic Field of Neodymium Block Magnet,” Applied Mathematical Modelling, Vol. 103, pp.238∼260. [https://doi.org/10.1016/j.apm.2021.10.019]
• Shojaeizadeh, E., Veysi, F., Zareinia, K., & Mansouri, A. M., 2022, “Thermal efficiency of a ferrofluid-based flat-plate solar collector under the effect of non-uniform magnetic field,” Applied Thermal Engineering, Vol. 201, Article 117726. [https://doi.org/10.1016/j.applthermaleng.2021.117726]
• Pattanaik, M. S., Cheekati, S. K., Varma, V. B., & Ramanujan, R. V., 2022, “Superior cooling performance of low footprint, hybrid magneto-fluidic heat transfer devices,” International Journal of Heat and Mass Transfer, Vol. 183, Article 122082. [https://doi.org/10.1016/j.ijheatmasstransfer.2021.122082]
• Kumar, V., Casel, M., Dau, V., & Woodfield, P., 2021, “Effect of axisymmetric magnetic field strength on heat transfer from a current-carrying micro-wire in ferrofluid,” International Journal of Thermal Sciences, Vol. 167, Article 106976. [https://doi.org/10.1016/j.ijthermalsci.2021.106976]
• Zanella, R., Nore, C., Mininger, X., Bouillault, F., & Guermond, J. L., 2021, “Numerical Study of Cooling by Ferrofluids in an Electrical Transformer using an Axisymmetric Model,” IEEE Transactions on Magnetics, Vol. 57, No. 7, Article 9380208. [https://doi.org/10.1109/TMAG.2021.3066412]
• Sirikasemsuk, S., Wiriyasart, S., Naphon, P., & Naphon, N., 2021, “Thermal cooling characteristics of Li‐ion battery pack with thermoelectric ferrofluid cooling module,” International Journal of Energy Research, Vol. 45, No. 6, pp.8824∼8836. [https://doi.org/10.1002/er.6417]
• Cheng, Y., & Li, D., 2019, “EExperimental investigation on convection heat transfer characteristics of ferrofluid in a horizontal channel under a non-uniform magnetic field,” Applied Thermal Engineering, Vol. 163, Article 114306. [https://doi.org/10.1016/j.applthermaleng.2019.114306]
• Chinnasamy, S., Priyadharsini, S., & Sheremet, M., 2020, “Thermal convection and entropy generation of ferrofluid in an enclosure containing a solid body,” International Journal of Numerical Methods for Heat & Fluid Flow, Vol. 31(9), pp.2940∼2961. [https://doi.org/10.1108/HFF-08-2020-0494]
• Rosensweig, R. E., 2013, Ferrohydrodynamics., Courier Corporation.