축류펌프의 입구 안내깃 모사에 따른 성능 및 내부 유동장에 관한 수치해석적 연구
Abstract
In this study, an absolute flow angle was numerically assigned to the inlet of an axial pump in order to predict its performance and internal flow field prior to the design process of an inlet guide vane. The finite volume method, which is an approximate analysis method based on the three-dimensional Reynolds-averaged Navier-Stokes (RANS) equation, was applied for discretization of governing equations. The shear stress transport (SST) model was used as the turbulence model and the hexahedral grid system was selected as the appropriate number of nodes through the grid dependency test. The change in the performance curve and internal flow field was found with respect to the difference in the absolute flow angle at the impeller inlet. When installing a variable inlet guide vane of an axial flow pump, an efficient operation plan by adjusting the angle of an inlet guide vane might be established with the results of this study.
Keywords:
Axial pump, Inlet guide vane, Hydraulic performance, Energy saving키워드:
축류펌프, 입구 안내깃, 수력성능, 에너지 저감1. 서 론
기계적 에너지를 이용하여 유체의 운동 에너지를 상승시키는 유체기계의 일종인 축류펌프는 원심 또는 사류펌프에 비해 비교적 저양정을 발생시키는 특성을 가지며, 유체의 대용량 이송에 적합하여 급수, 배수 및 하수처리장 등에서 주로 이용되고 있다. 축류펌프의 구성은 일반적으로 입구 안내깃(inlet guide vane)과 벨마우스(bell mouth)를 포함하는 형태의 흡입 케이싱, 프로펠러 깃 형태의 임펠러(impeller) 및 정압 회복을 위한 출구 안내깃(diffuser vane; DV) 등으로 이루어져 있다. 여기서 입구 안내깃은 임펠러 날개 입구에서 절대 유동각에 변화를 줄 수 있는 요소로서, 수요 변화가 잦은 현장에서 펌프의 효율적인 운용에 기여한다. 일반적으로 축류펌프를 적용하는 현장의 경우 유체의 대용량 이송을 필요로 하나, 상황에 따라 유연하게 운영을 하지 않기 때문에 필요 이상의 전력을 소모하는 경우가 많다. 이 경우 입구 안내깃의 역할은 매우 중요하다. 즉, 입구 안내깃으로 인한 절대 유동각의 부여는 입사각에 영향을 미치며, 이는 곧 펌프의 성능 특성에 변화를 주어 수요 변화에 대응할 수 있는 제어를 이룬다. 결과적으로 입구 안내깃은 펌프의 성능을 결정할 수 있는 요소이며, 따라서 그 가변형 구조는 필수적인 것으로 사료된다.
펌프의 입구 안내깃에 관한 선행연구는 활발하다. Chan 등(1)은 입구 안내깃을 설치함에 따라 펌프 내의 유동 상태와 전단 응력에 미치는 영향에 대해 연구를 하였다. Kaya 등(2) 및 Kim 등(3)은 축류펌프의 입구 안내깃 설치 유무에 따라 펌프 성능변화를 실험적인 방법으로 증명하였고, 입구 안내깃 두께가 펌프의 성능에 미치는 영향을 분석하였다. Yang 등(4)은 펌프 내부에서 설치된 가변형 입구 안내깃의 각도에 따라 성능 곡선 및 최고효율점 변화에 관한 수치적 분석을 수행하였다. 언급된 연구 결과에 따르면 축류펌프 내부 구성품 중 하나인 입구 안내깃 설치 유무 및 각도 등이 내부 유동특성 변화에 영향을 미치는 것을 알 수 있고, 깃 각도에 따른 와류(swirl) 발생 및 최고효율점 변화에 미치는 영향에 관한 고찰이 가능하다. 한편, Choi 등(5)은 유체기계의 효율적인 운전의 측면에서 최적가변운전을 제안하기도 하였으며, Draghici 등(6)은 부하 변동에 따라 펌프의 회전수 조절을 통한 에너지 소비 저감을 분석하였다. 또한 Ahmed 등(7) 및 Junaidi 등(8)은 입구 안내깃 설치 유무에 따라 펌프의 효율성 향상 및 내부 유동특성을 분석하였다.
반면 이들은 모두 입구 안내깃이 실제로 설치된 후의 시점을 기준으로 두었다. 따라서 입구 안내깃의 설계 시점에서 펌프의 성능 및 내부 유동 특성을 예측하는 것에 대한 시도가 필요하며, 이는 설계 및 시제품 제작에 대한 소요 시간과 시행착오로 인한 시제품의 반복 생산에 대한 경제적 손해 등을 최소화하는데 기여할 수 있다.
본 연구에서는 입구 안내깃 후단에 발생하는 선회유동 rotating flow)을 수치적 모사를 통해 펌프 입구부에 절대 유동각으로 부여하여 성능 및 내부 유동을 예측하였다. 이를 통해 세부 설계 및 생산 공정 과정에서 발생되는 손실을 예방할 수 있다. 펌프의 설계 과정에서 가변형 입구 안내깃과 이를 통해 에너지 저감을 위한 효율적인 운영 방안에 대한 체계적인 연구는 아직 찾아보기 어렵다. 따라서 본 연구에서는 축류펌프의 가변형 입구 안내깃 후단 선회유동을 수치적으로 모사하여 성능 및 내부 유동장을 분석하였고, 이를 바탕으로 효율적인 펌프 운영 방안에 대해 연구하였다.
2. 연구대상 및 범위
2.1 축류펌프 사양
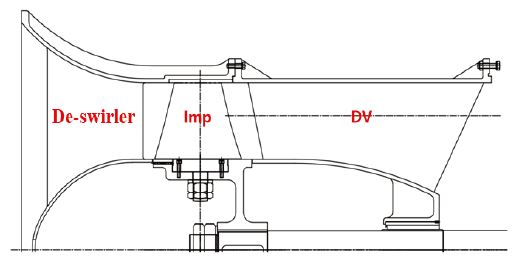
본 연구에서 사용된 축류펌프 모델의 내부 구성품은 입구 케이싱을 지지하면서 임펠러 내부로 불순물의 유입을 차단함과 동시에 저유량 영역에서 임펠러 날개 입사각 증가에 기인하여 깃 선단(leading edge)에 형성되는 박리(separation)및 선회실속(rotating stall)을 방지할 수 있는 와류방지판(de-swirler), 유체의 압력을 상승시키는 임펠러(impeller) 및 정압을 회복 시켜주는 출구 안내깃(diffuser vane; DV)으로 구성되어있으며, 그 자오면 시점을 Fig. 1에 나타내었다. 설계사양과 관련한 자세한 사항은 Table 1에 나타나 있으며, 비속도는 식 (1)을 통해 계산하였다. 유량, 전양정 및 축동력 은 식 (2), (3) 및 (4)를 기반으로 하여 무차원화하였다.
| (1) |
| (2) |
| (3) |
| (4) |
여기서 Q, H, L은 유량, 전양정 및 축동력을 의미하며 단위는 각각 m3/s, m 및 W 이다. ω, g, Cm2, u2, ρ 및 A는 각각 각속도, 중력가속도, 자오면 성분의 임펠러 출구부 절대속도, 임펠러 출구부 회전속도, 밀도 및 단위면적을 나타내며 단위는 각각 rad/s, m/s2, m/s, m/s, kg/m3 및 m2이다.
2.2 안내깃 모사
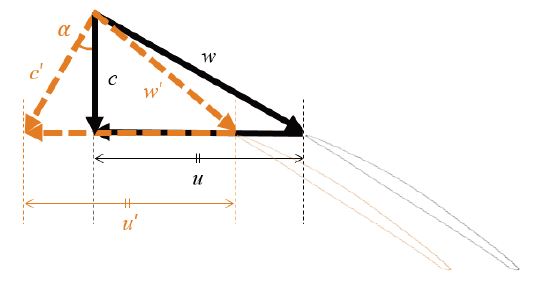
Fig. 2는 임펠러 입구 부분에서의 속도 삼각형 개략도를 나타낸 것이다. 각 벡터(vector)에 대하여, c, u 및 w는 절대속도, 회전속도 및 상대속도이다. 유량과 회전수가 동일한 조건에서 입구 안내깃이 적용되지 않은 경우를 실선(검정)으로 이해하면 입구 안내깃이 적용되는 경우는 점선(주황)으로 도식될 수 있다. 본 연구에서는 입구 안내깃이 실제로 적용되기 전에 그 영향성을 예측하기 위해 펌프 입구부에 유동각을 부여하였다. 임펠러의 회전방향으로 각각 0, 5, 15, 25, 35 및 45°의 유동각이 부여되었으며, 여기서 유동각은 절대 유동각(α)이고 각도 기준은 축방향이다. 상기의 입구부 절대 유동각은 후술되는 수치해석 영역의 입구에 부여되었다.
3. 수치해석 방법
3.1 수치해석 영역 및 격자계
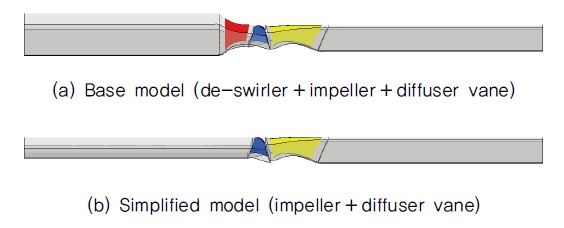
본 연구의 수치해석 영역은 Fig. 3에 나타내었다. 기본 모델은 좌로부터 우로 유동 방향에 따라 입구부, 와류방지판, 임펠러, 출구 안내깃 및 출구부로 이루어져있으며, 여기서 오직 임펠러만이 회전부에 해당한다. 그러나 본 연구는 첫째로 입구부 절대 유동각 변화에 따른 영향성을 분석하기 위함이며, 둘째로 추후 입구 안내깃이 와류방지판의 위치에 구비될 것이므로, 입구부 절대 유동각 변화에 따른 영향성 분석 시 와류방지판에 해당하는 형상을 제외하여 수치해석 영역을 단순화하였다. 단순화 모델은 내부 구성품인 와류방지판을 배제한 후 임펠러 입구와 동일한 직경으로 유로를 연장한 것이며, 이때 수치해석 영역의 전체 축방향 길이는 단순화 전과 동일하게 유지하였다. 입⋅출구부는 수치적 수렴성을 고려하여 직경의 4배에 해당하는 길이를 갖도록 연장하였다. 기본 모델의 단순화에 따른 영향성은 3.3절에서 후술된다.
수치해석에 사용된 격자계는 Fig. 4에 나타낸 바와 같이 육면체 정렬 격자계로 구성되었으며 선행연구(9)에서 제시한 Grid Convergence Index(GCI) 방법으로 검증하였다.
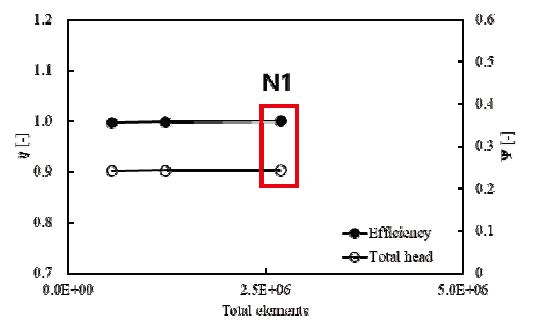
Fig. 5는 Fig. 3의 기본 모델에 대한 격자계 검증 결과를 나타내며, 설계 유량점에서 총 3개의 관찰된 격자에 대해 효율 및 전양정의 수치해석적 오류를 비교하였다. 이때 효율은 N1에 해당하는 격자계로부터 수행된 수치해석 값으로 표준화하였다. 약 2.68⨯106의 수를 갖는 최적 격자계(N1)에 대한 GCIfine21 값은 약 0.0043으로 나타났고, 이 값은 선행연구(9)가 제시하는 격자계에 대한 수렴 기준을 만족한다. 따라서 본 연구에서는 N1의 격자계를 적용하였다.
3.2 수치해석 기법 및 난류모델
본 연구의 대상인 축류펌프에 적용된 수치해석 방법은 아래에 서술된 바와 같다. 상용 소프트웨어인 ANSYS CFX 19.2(10)를 기반으로 난류 해석을 위한 3차원 정상 RANS 방정식이 적용되었고, 이산화는 유한 체적 기법에 기반한다. 입구 및 출구 조건은 전압력 및 유량 조건으로 설정하였으며, 계산시간을 단축하고 수렴기준을 향상시키기 위해 단일 통로(one-passage) 영역의 회전방향에 주기적인 조건을 적용하였다. 고정자와 고정자 사이에는 Frozen rotor, 회전자와 고정자 사이는 Stage average 기법을 적용하였다. 작동유체는 등온(25 °C)의 물이다. 난류 모델은 유동 박리현상을 정밀하게 파악하기 위해 Shear Stress Transport(SST) 모델(11)이 사용되었고, 벽에는 미끄럼 방지 및 자동 벽함수가 부여되었다. 시뮬레이션에는 32코어 듀얼 프로세서 Xeon (2.8GHz) 중앙 처리장치를 사용하였고, 하나의 시뮬레이션에 대한 계산처리에는 약 5시간이 소요되었다.
3.3 수치해석 검증
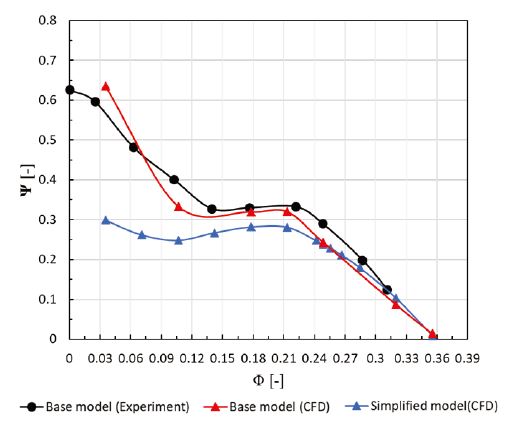
Fig. 6은 기본 및 단순화 모델의 수치해석 결과와 기본 모델에 대한 성능시험 결과에 대한 성능곡선을 나타낸다. 기본 모델에 대한 각 결과로부터, 수치해석 및 성능시험 결과는 대체로 유사한 경향을 보인다. 특히 유량계수 약 0.12 및 0.21에서 성능곡선상 변곡점이 공통적으로 확인되었다. 한편 기본 및 단순화 모델의 각 수치해석 결과는 설계 유량점 근처와 고유량 영역에서 거의 같은 예측을 보이나 저유량 영역에서 유의미한 차이가 있었다. 그 차이는 특히 성능곡선이 양의 기울기를 형성하는 유량 영역, 즉 유량계수 약 0.2 이하에서 두드러지며, 이는 와류방지판이 저유량 영역에서 성능에 영향을 미치고 있음을 암시하는 결과이다. 성능곡선이 양의 기울기를 형성하는 유량 영역은 펌프의 새들(saddle) 현상에 기인하는 것으로서 입사각 증가에 따라 형성되는 박리 및 선회실속 등의 불안정 유동 현상이 펌프의 성능을 저하시키는 것으로 이해되어진다. 이와 관련한 선행연구(12)에 따르면, 상기의 불안정 유동 현상 등이 유체기계의 입구부에 형성되는 경우 본 연구의 와류방지판과 흡사한 구조를 갖는 실속방지휜(anti-stall fin; ASF)이 그 성능과 안정성을 개선할 수 있는 것으로 보고된 바 있으며, 따라서 본 연구의 와류방지판 역시 저유량 영역에서 불안정 유동 현상 등을 일부분 억제할 수 있었던 것으로 분석될 수 있다.
본 연구에서 입구부 절대 유동각에 따른 영향성 분석은 Fig. 3의 단순화 모델을 기준으로 하므로 후술되는 결과가 포함하는 성능곡선은 새들 영역과 같은 저유량 영역에서 다소 낮은 예측을 보일 수 있다. 그럼에도 불구하고 새들 영역은 펌프를 실제로 운용하는 경우 고려되어지는 영역이 아니며 유량계수 약 0.21 지점의 변곡점 예측이 대체로 일치하므로, 단순화 모델을 기준으로 분석을 수행하는 것에 무리가 없을 것으로 보인다.
4. 결 과
4.1 성능곡선
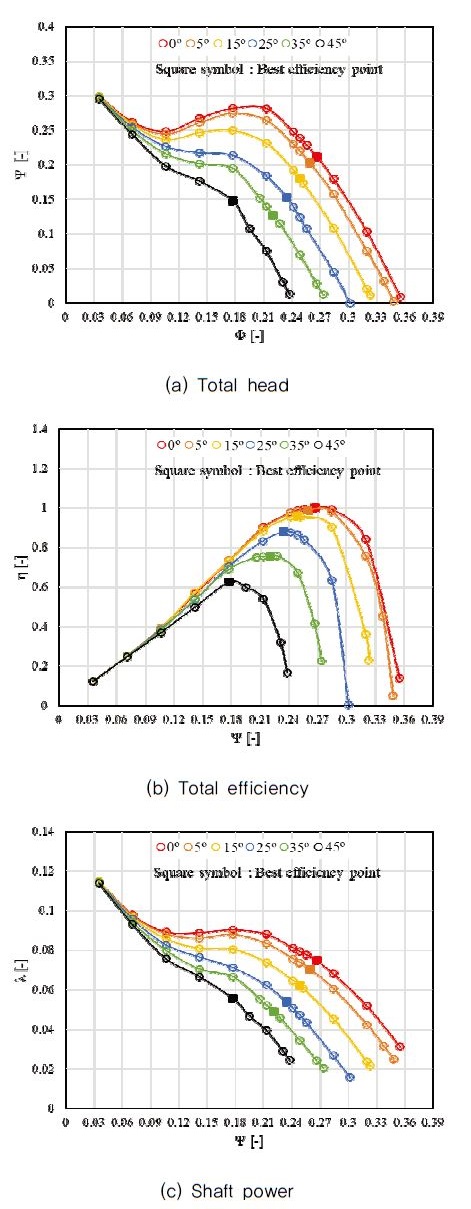
본 연구에서 해석 대상으로 선정한 단순화 모델을 기준으로 입구부 절대 유동각 변화에 따라 성능곡선을 비교하였다. Fig. 7은 각 입구부 절대 유동각에 따른 (a) 전양정, (b) 효율및 (c) 축동력에 대한 성능곡선이다. 각 성능곡선에서 최고 효율 지점은 사각 기호(square symbol)로 나타내었다. 전양정에 대한 성능곡선으로부터, 절대 유동각이 0°로부터 점차 증가할수록 설계 유량점 포함 전체 유량 영역에서 성능은 점차 감소했다. 설계 유량점을 기준으로 0°의 경우에 입사각 증가에 기인하는 양의 기울기는 유량계수 약 0.2 이하부터 확인되었고, 이는 절대 유동각이 증가할수록 점차 낮은 유량점부터 형성되다가 25° 이상의 절대 유동각이 부여되는 경우부터 더 이상 관찰되지 않았다. 반면 양의 기울기의 형성으로부터 야기되는 가장 깊은 새들(saddle)점은 유량계수 약 0.1에서 관찰되었고, 이는 절대 유동각에 따라 영향을 거의 받지 않았다. 양의 기울기 및 새들 영역을 제외하고 펌프가 실제 운용되어질 수 있는 운전 유량 영역은 대체로 절대 유동각이 부여되지 않을수록 넓었고, 이는 절대 유동각 증가에 따라 점차 감소하였다. 여기서 절대 유동각 25∼45°의 경우 운전 유량 영역은 유량계수 약 0.18 이상인 것으로 고려할 수 있다.
절대 유동각 변화에 따른 효율 곡선을 보면 최고효율점의 이동이 현저히 확인된다. 절대 유동각이 증가함에 따라서 최고효율점에 해당하는 유량점이 감소하는 것을 확인할 수 있다. 또한 절대 유동각이 증가할수록 최고효율점에 해당하는 효율의 절대값 역시 감소하였다. 효율 곡선의 변화는 전반적으로 저유량 영역보다 고유량 영역에서 두드러지는 경향이었다. 한편 축동력 곡선은 전양정에 관한 경향과 거의 흡사했다.
절대 유동각이 증가함에 따라 최고효율점에서의 작동유량, 전양정 및 축동력이 감소하는 것을 알 수 있다. 결과로부터, 절대 유동각은 최고효율점, 전양정 및 축동력에 영향을 미치고, 0°에서 45°까지 유동각이 증가할 때 최고효율점에서 표준화된 유량계수는 약 0.358 감소되고, 이는 최고효율점에서의 유량계수와 설계 유량점에서의 유량계수를 사용하여 표준화하였다. 즉, 추후 축류펌프에 가변형 입구 안내깃을 설치하는 경우 유입되는 유량에 따라 각도를 변경함으로써 불필요하게 소모되는 축동력을 감소시켜 효과적인 펌프운용이 가능할 것으로 판단된다.
4.2 내부 유동장
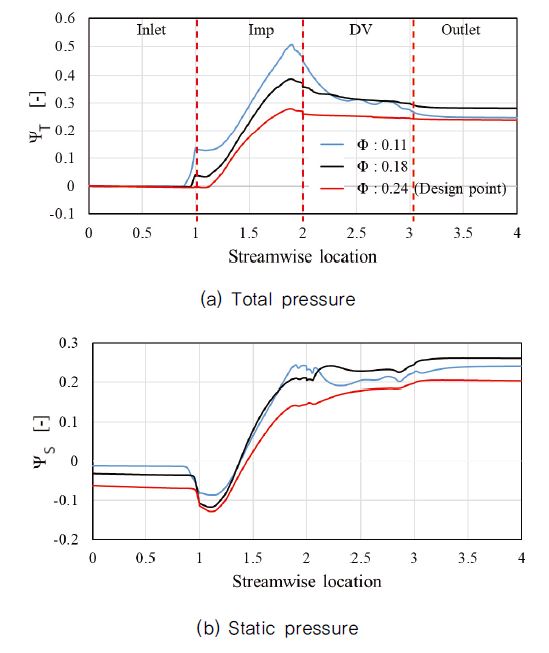
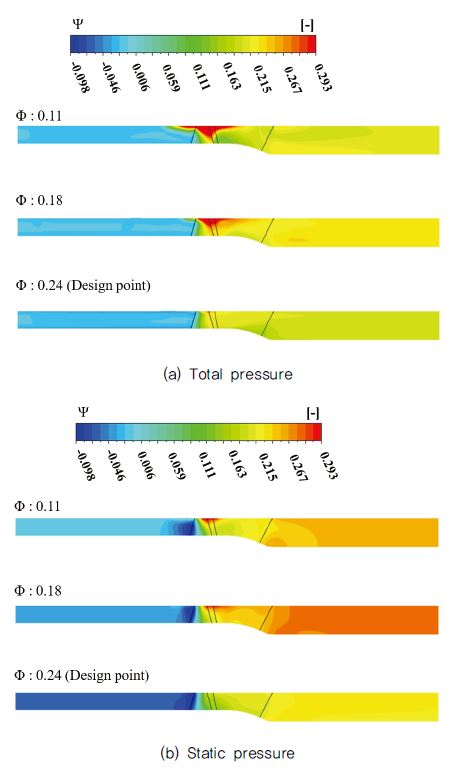
Figs. 8, 9, 10 및 11은 입구부 절대 유동각이 0°인 경우 유량에 따른 내부 유동장 분포를 정량 및 정성적인 방법으로 나타낸 것이다. 먼저 Fig. 8은 수치해석 영역의 입구에서 출구까지 압력 상승 곡선이고, ΨT 및 Ψs는 전압 및 정압에서의 압력계수를 나타낸다. 유량이 감소함에 따라 임펠러 입구에서 전압의 급격한 상승이 뚜렷하다. 이는 동압의 증가에 기인하며 즉, 축류펌프가 저유량 영역에서 작동하는 경우 입사각 증가에 따른 유동 박리로 인한 현상인 것으로 이해할 수 있다. 임펠러를 통과하는 동안 전압은 유량이 감소할수록 대체로 더 높은 상승 폭을 보이나 임펠러 이후의 출구 안내깃을 거치는 동안 감소하였으며 그 폭은 유량이 감소할수록 더 현저한 경향을 보였다. 특히 유량계수 약 0.11의 경우 정압은 출구 안내깃 영역을 통과하는 동안 적절히 회복되지 못하였다. Fig. 8의 경향은 그 자오면 시점에서의 전압 및 정압 분포를 나타낸 Fig. 9에서 동일하게 확인되며, 허브(hub) 보다는 쉬라우드(shroud) 부근에서 지배적인 영향을 받는 것으로 보인다.
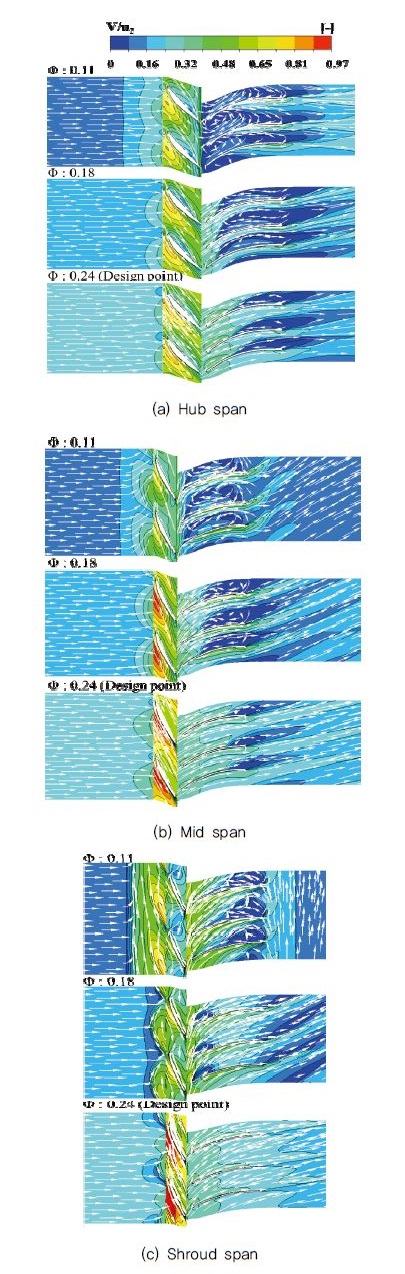
Fig. 10은 절대 유동각이 0°인 경우 각 스팬(span)에서 유량에 따른 유속 분포이며, 속도 등고선(velocity contour)과 벡터로서 나타내었다. 먼저 쉬라우드 스팬을 기준으로, 설계 유량점으로부터 유량 감소에 따른 유동장 분포의 변화는 현저하다. 유량이 점차 감소함에 따라 임펠러 깃 선단(leading edge)에서 박리는 더욱 뚜렷하게 형성되었고, 특히 유량계수 약 0.11에서 이는 임펠러 전단에서 회전방향과 동일한 방향성을 갖는 선회실속을, 임펠러 후단의 출구 안내깃에서 재순환 유동을 각각 야기하였다. 여기서 유량계수 약 0.11, 0.18 및 0.24는 유량과 양정에 관한 성능곡선상에서 각각 가장 깊은 새들점, 양의 기울기가 시작되는 유량점, 그리고 설계 유량점에 해당한다. 따라서 새들과 같은 성능저하의 원인을 박리, 선회실속 및 재부착 유동 등에 둘 수 있으며, 이에 해당하는 유량 영역은 축류펌프 운용 시 회피되어야 한다. 한편 저유량 영역에서 확인되었던 내부 유동장의 불안정 특성은 쉬라우드 스팬에서 가장 두드러지며 허브 스팬을 향할수록 완화되는 경향이 있으나, 출구 안내깃 유로의 저속 영역은 허브 스팬에서 가장 넓게 확인되었다.
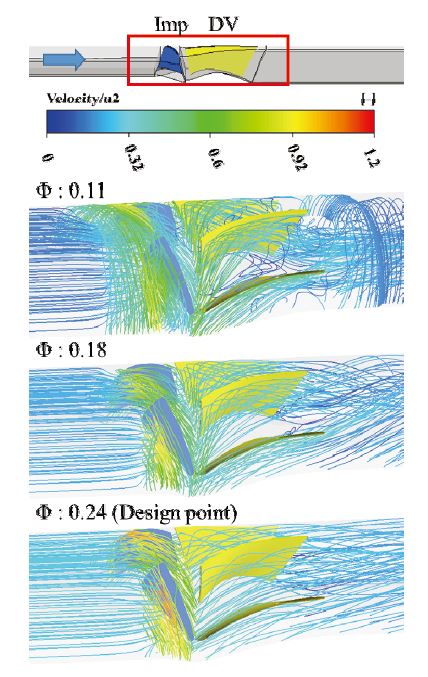
Fig. 11은 절대 유동각이 0°인 경우 각 유량에 대한 3차원 유동 흐름을 나타낸 것이다. 설계 유량점에서 유동은 안정적으로 보이는 반면, 유량계수 0.18에서 날개의 흡입면에 유동 박리가 관찰되며 유량계수 0.11에서는 날개 입구부 및 출구 안내깃 후단에 선회유동이 확인되었다. 유량계수 0.11은 새들 영역에서 운전되고 있고, 이에따라 출구 안내깃 주위로 재순환유동이 발생하기 때문이다. 재순환유동은 쉬라우드 근처에 분포하였으며 원주를 따르는 방향성을 갖고 있었다.
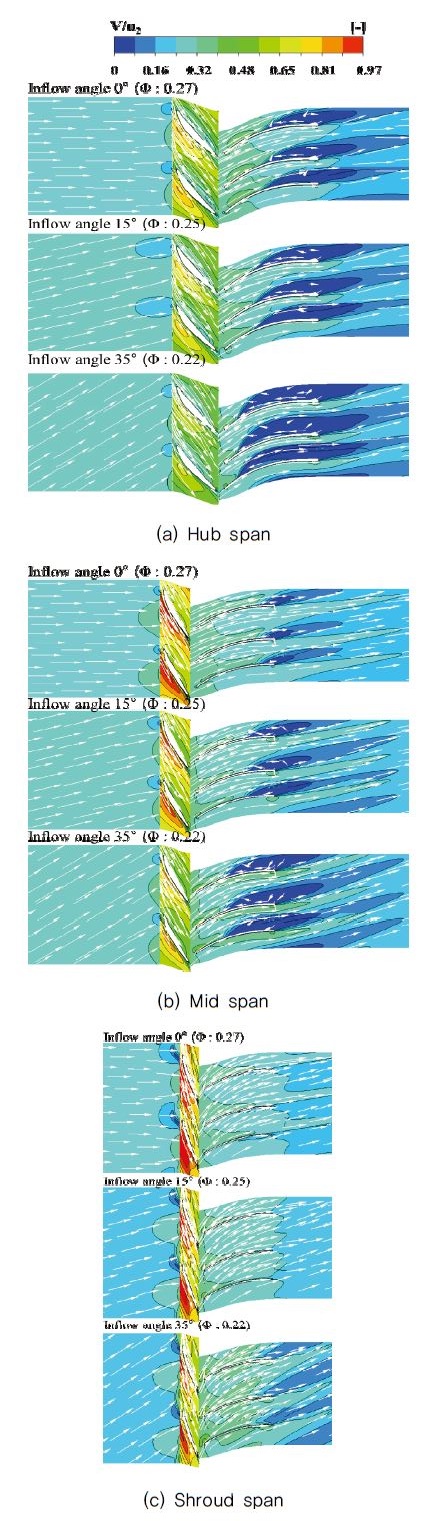
특히 출구 안내깃 후단에서의 선회 유동은 저유량 영역에서 관찰될 수 있는 현상이다(13). Fig. 12는 Fig. 10과 동일한 시점을 기준으로 입구부 절대 유동각이 0, 15 및 35°인 경우 최고효율점에서의 유속 분포이다. 최고효율점에서는 절대 유동각과 작동유량에 관계없이 허브, 미드(mid) 및 쉬라우드 스팬에서 내부 유속 분포가 유사했다. 또한 Fig. 10에서 설계 유량점 대비 유량이 감소할 수록 입사각 증가에 따른 박리 등 불안정 현상이 심화되었으나, 이는 절대 유동각을 부여함으로써 각 최고효율점에서 더 이상 확인하기 어려웠다. 각 절대 유동각의 최고효율점에서 유량의 감소는 다시 입사각의 증가를 야기하므로 펌프 운용 시 별도의 주의를 요하는 반면, 목표 양정 및 작동유량을 만족하는 범위에서 절대 유동각을 부여하는 것은 불필요한 동력 소비를 예방함과 동시에 안정적인 운용을 위한 대책으로 이해될 수 있다. 한편 입구 유동각 0°의 경우 최고효율점에서 유속 분포는 대체로 Fig. 10의 경향과 유사하며, 이는 본 연구의 축류펌프 설계에 대한 타당성을 의미한다.
5. 결 론
본 연구에서는 축류펌프의 입구 안내깃에 대한 실제 적용 전 성능예측을 목표로 수치해석상 입구부에 절대 유동각을 부여하였으며, 이에 따른 성능 및 내부 유동장 분석을 수행하였다. 결과는 다음과 같이 요약될 수 있다.
- 1) 입구부 절대 유동각이 증가할수록 양정, 축동력 및 작동유량 범위가 감소하며, 최고효율점은 0°에서 45°까지 유동각이 변화하는 경우 유량계수가 약 0.358 감소된다.
- 2) 본 연구의 성능곡선 및 내부 유동장 분석 결과를 참조하여 실제 유입되는 유량에 따라 가변형 입구 안내깃의 각도 조절을 통해 효율적이고 안정적인 운영 방안을 수립할 수 있다.
- 3) 본 연구에서는 입구부 형상을 단순화하였으므로 추후 입구 안내깃이 실제로 적용되는 경우에 임펠러 입구에서 절대 유동각 분포가 균일하지 않을 수 있으며, 이에 대한 추가적인 고찰이 요구된다.
Acknowledgments
이 논문은 2022년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임(2021202080026D, AI/ICT 기반 가변형 유체기기 설계⋅상태진단을 위한 기반⋅플랫폼 기술 및 운영관리 시스템 개발)
References
-
Chan, W. K., Wong, Y. W., Yu, S. C. M., and Chua, L. P., 2002 “A computatuinal study of the effects of inlet guide vanes on the performance of a centrifugal blood pump,” International Socity for Artificical Organs, Vol. 26, No. 6, pp. 534∼542.
[https://doi.org/10.1046/j.1525-1594.2002.06917.x]

-
Kaya, D., 2003, “Experimental study on regaining the tangential velocity energy of axial flow pump”, Energy Conversion and Management, Vol. 44, No. 11, pp. 1817∼1829.
[https://doi.org/10.1016/S0196-8904(02)00187-5]

-
Kim, S. W., and Kim, Y. J., 2016, “The effect of the thickness and angle of the inlet and outlet guide vane on the performance of axial-flow pump,” ASME 2016 Fluids Engineering Division Summer Meeting, FEDSM2016-7939.
[https://doi.org/10.1115/FEDSM2016-7939]

- Yang, H. M., Kim, Y. I., Son, Y. J., Lee, K. Y., Choi, Y. S., 2022, “Analysis of energy consumption of the axial-flow pump applying operational scenario,” Sumer Conference of The Korea Society of Fluid Machinery.
- Choi, Y. S., Suh, J. W., Lee, K. Y., and Yang, H. M., 2021, “Analysis of operational scenarios for sites where variable fluid machinery will be applied,” Winter Conference of The Korea Society of Fluid Machinery.
-
Draghici, I. A., Rus, I. D., Cococeanu, A., and Mutean, S., 2022, “Improved operation strategy of the pumping system implemented in timisoara municipal water treatment station,” Sustainability.
[https://doi.org/10.3390/su14159130]

- Ahmed, S. A., Muiz, A., Mubashir, M., Ahmed, W., 2016, “Efficiency enhancement of centrifugal water pump by using inlet guided vanes,” European Journal of Advances in Engineering and Technology., No. 3, pp.1-3.
- Junaidi, MD. A. R., LaksmiKumari, N. B. V., Samad, M. A., SayeedAhmed, G. M., 2015, “CFD Simulation to enhance the efficiency of centrifugal pump by application of inner guide vanes,” ICMPC2015.
- Celik, I. B., Ghia, U., Roache, P. J., Freitas, C. J., Coleman, H., and Raad, P. E., 2008, “Procedure for estimation and reporting of uncertainty due to discretization in CFD application,” Journal of Fluids Engineering.
- ANSYS CFX-19.2. ANSYS CFX-Solver Theory Guide & ANSYS CFX-Training. 2018. ANSYS Inc.
-
Brown, G. J., Fletcher, D. F., Leggoe, J. W., & Whyte, D. S., 2018, “Investigation of 618 turbulence model selection on the predicted flow behaviour in an industrial crystalliser—619 RANS and URANS approaches,” Chem. Eng. Res. Des., No. 140, pp. 205-220.
[https://doi.org/10.1016/j.cherd.2018.10.007]

-
Kim, Y. I., Lee, S. Y., Yang, H. M., Lee, K. Y., Yang, S. H., Choi, Y. S., 2022, “Suppression of stall-induced in stability and positive slope at low flow rates of an axial fan with two-dimensional anti-stall fin” Journal of Fluids Engineering.
[https://doi.org/10.1115/1.4055541]

-
Kim, Y. I., Choi, Y. U., Jeong, C. Y., Lee, K. Y., Choi, Y. S., 2021, “Effect of two-and threee-dimensionally designed guide vanes with different camber length on static pressure recovery of a wall-mounted axial fan,” Process
[https://doi.org/10.3390/pr9091595]