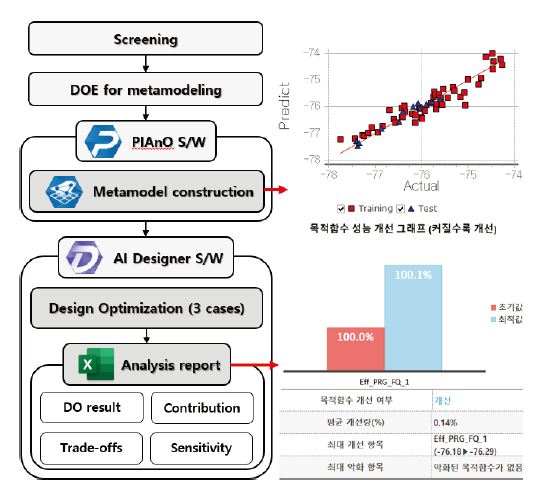
다단계 최적화 프로세스를 활용한 축류 펌프 임펠러 설계

1. 서 론

펌프는 전동기 등의 기계적 에너지를 이용하여 유체의 위치에너지를 상승시키는 유체기계의 일종이다. 그 중에도 축류 펌프는 물을 작동유체로 하며 주 유동의 방향이 회전체의 축 방향과 개략적으로 평행한 펌프로써 요구양정이 크지 않으면서 대용량의 수송을 하여야 하는 선박 등에서 사용된다. 최근 들어 이러한 대용량 운송이 필요한 유체기기의 성능 개선에 대한 수요와 관심도가 증가하고 있으며, 비용이 많이 드는 실험을 통한 성능 평가를 대체할 방법이 강구되고 있다.

유체기계에서 실험을 대신하여 전산유체역학을 이용한 성능예측은 이미 광범위하게 연구되고 있다. 이러한 해석을 이용한 성능 평가의 유효성은 Kim 등⁽¹⁾을 포함한 여러 연구자들에 의해 검증된 바 있으며, PC 성능의 발전에 따라 비용 또한 감소하여 일련의 과정들이 더욱 원활하게 진행될 수 있게 되었다. 그러나 그러한 비용 감소에도 불구하고, 설계 최적화의 관점에서 수많은 실험점을 이용하여 해석하는 과정에는 여전히 소요 시간을 위시한 많은 해석 비용이 발생한다⁽²⁾. 이러한 문제의 해결을 위하여 Wahba 등⁽³⁾은 유전알고리즘을 통하여 펌프 설계 최적화를 시도한 바 있으며, 그 이외에도 기존의 데이터를 이용하여 예측모델(Metamodel)을 구축하고, 그를 기반으로 최적화를 진행하는 방법이 대두되고 있다. Lian 등⁽⁴⁾은 보간법 기반 방사기저함수 예측모델을 이용하여 원심펌프의 양정과 축동력을 예측하였고, Song 등⁽⁵⁾은 반응면 회귀 기법을 이용하여 단일채널 펌프의 효율과 반력을 최적화 한 바 있다. Jung 등⁽⁶⁾은 다항회귀 예측모델을 이용하여 축류펌프의 양정과 효율을 최적화 한 바 있으며, 이외에 사류 펌프, 홴 등에서도 유사한 연구가 진행된 바 있다^(7,8). 그러나 이러한 연구들 또한 예측모델을 통하여 최적화 결과 제시에 방점을 두어, 추가적인 설계 개선에 관한 연구는 부족한 실정이다.

다음 Fig.1에는 본 연구에서의 다단계 최적화 프로세스가 제시되어 있다. 축류 펌프 임펠러의 주요 설계변수 추출과 함께 성능 예측을 위하여 여러 예측모델을 구성하고 이 중 가장 적합한 예측모델을 선정하였다. 또한 선정된 예측모델을 기반으로 펌프 성능 최적화를 진행하여 이를 검증하고, 이를 통하여 축류펌프 설계 최적화에의 예측모델 도입에 대한 타당성을 평가하였다. 이를 기반으로 각 설계변수 별 성능지수에의 영향성 평가를 진행하고 더 나은 성능지수 획득을 위한 설계변수 개선 방향을 제안하였다.

Fig. 1

Multi-stage optimization process

2. 펌프 형상

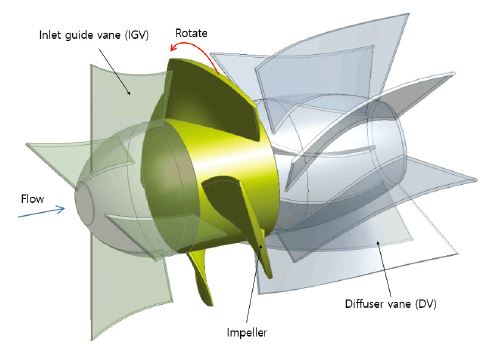
축류 펌프는 입구 안내깃(Inlet Guide Vane, IGV), 임펠러(Impeller, IMP), 디퓨저 베인(Diffuser Vane, DV)으로 구성되어 있으며 이 중 임펠러는 회전자이며 입구 안내깃과 디퓨저 베인은 고정자이다. 다음 Fig.2에는 펌프의 초기 형상이 도시되어 있다. 입구 안내깃에서는 점차 슈라우드 반경이 감소한다. 여기서 입구 안내깃은 임펠러로 입사하는 유동을 정렬하는 기능을 갖는다. 임펠러에서는 허브 반경과 슈라우드 반경이 일정한 값을 가지며, 축동력을 통하여 압력수두를 공급받는다. 임펠러 후방의 확산 영역에서는 유동의 스월(Swirl)을 감소시켜 축 방향으로 재정렬시키는 디퓨저 베인이 설치되어 있다. Table 1에는 펌프의 기본 패러미터가 제시되어 있다. 슈라우드와 연결된 입구 안내깃과 디퓨저와는 달리 임펠러는 회전을 위하여 슈라우드와 약간의 간격을 가진다. 이를 팁 간극(Tip clearance)라 하며 약 0.5(mm)의 값을 갖는다. 본 연구에서는 임펠러 입사유동이 입구 안내깃에 각도가 설정되어 있지 않아 별도의 프리스월(Pre-Swirl)을 갖지 않으며, 임펠러의 형상 최적화를 우선적으로 수행하기 위해 디퓨저 베인이 없는 조건에서 해석을 진행하였다.

Fig. 2

Shape of axial pump

Table 1

Design specification of axial pump

3. 수치해석 기법

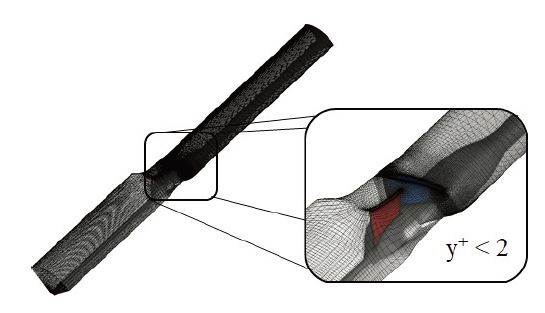
본 연구에서는 수치해석을 위하여 상용 프로그램인 Ansys CFX⁽⁹⁾를 사용하였다. 지배방정식으로 정상상태에서 3차원 레이놀즈 평균된 Navier-Stokes 방정식(RANS)을 이용하였고, 회전체 벽면의 바른 모사를 위하여 k-ω SST 난류모델⁽¹⁰⁾을 적용하였다. 또한 이를 위하여 벽면 주위의 최대 y⁺를 2로 설정하였다. SST 난류모델은 벽면 모사에 유리한 k-ω와, 벽면 주변의 격자에 크게 구애받지 않는 k-ϵ의 장점을 동시에 가지며, 블렌딩 함수를 통하여 벽면 주위와 같이 낮은 y⁺를 갖는 영역에서는 k-ω 난류모델을 적용하고 그렇지 않은 영역에서는 점진적으로 k-ϵ난류모델을 적용한다.

다음 Fig.3에는 수치해석을 위한 격자의 벽면 형상이 제시되어 있다. 격자는 TurboGrid를 이용하여 정렬격자로 구성하였으며 총 530,472개의 셀(Cell)을 갖는다. 형상의 반복에 기인하여 4개의 블레이드 중 하나만을 이용하여 격자를 형성하였다. 임펠러와 허브, 슈라우드는 점착조건을 갖는 벽면(No-slip wall) 경계조건을 가지며 형상 반복면의 경우 회전 주기조건(rotational periodic)을 주었다. 임펠러 전단, 후단의 비등각 격자(nonconformal mesh) 전후 물성치 전달은 출구면 전체의 물성치 평균을 다음 영역으로 전달하는 Stage 기법을 이용하였다.

Fig. 3

Grid system

해석 결과에 격자 영향성을 배제하기 위하여 격자 수렴성 지표(Grid Convergence Index)를 확인하였고, 그 결과가 다음 Table 2에 제시되어 있다.

Table 2

Grid convergence index for the grid dependency test

4. 예측모델 구성

4.1 설계변수와 성능지수

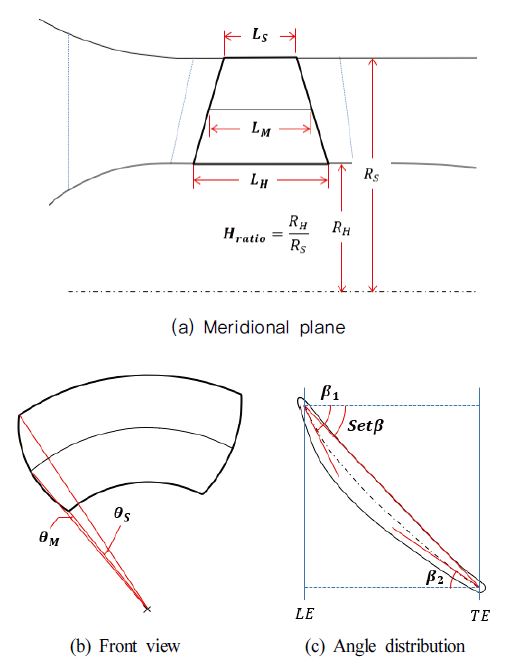
예측모델의 구성에 앞서, 적합한 설계변수와 성능지수의 선정 과정이 선행되어야 하며, 이를 선정하기 위하여 스크리닝(Screening)을 수행하였다. 다음 Fig.4에는 임펠러 형상 변경을 위한 설계변수 목록이 도시되어 있다. 자오면 상에서 임펠러의 허브, 미드스팬, 슈라우드면 길이 L_H, L_M, L_S, 허브 반경과 슈라우드 반경의 비인 허브팁비를 H_ratio = R_H/R_S로 정의하여 총 4개의 설계변수를 선정하였다. 또한 날개 형상 설계변수로 임펠러의 허브, 미드스팬, 슈라우드에서 입사각을 각각 β_1,H, β_1,M, β_1,S, 출구각을 β_2,H, β_2,M, β_2,S, 비틀림각을 Setβ_H, Setβ_M, Setβ_S로 정의하여 9개의 설계변수, 이에 더하여 허브를 기준으로 한 스윕각 차이를 θ_M, θ_S로 정의하여 2개의 설계변수를 추가, 최종적으로 15개의 설계변수를 스크리닝 대상으로 선정하였다.

Fig. 4

Design variables of axial pump

축류펌프는 전양정(Total head, Ht), 정압 양정(Static head, Hs), 축동력 (Power, P), 효율(Efficiency, Eff), 그리고 비속도(Ns) 등을 성능지수로 가지며, 펌프 설계 과정에서는 일반적으로 전양정과 효율을 성능지수로 선택한다. 이 중 효율은 다음 식 (1)과 같이 표현할 수 있다.

$\[ {\eta }_t=\frac{\rho gQ{H}_t}{P} \]$

(1)

여기서 Q, Ht, P는 각각 설계유량(m³/s), 전양정(m), 축동력(W)를 의미한다.

4.3 스크리닝

스크리닝은 효율적인 설계 개선을 위하여 실험계획법을 이용하여 중요한 설계변수를 추출하는 일련의 과정을 의미한다. 이를 통하여 중요한 설계변수 획득 뿐 아니라, 설계변수들의 자세한 경향성 파악과 예측모델 구성에 필요한 실험점 수를 줄이는 효과를 기대할 수 있다. 본 연구에서는 스크리닝 과정을 위한 실험계획법으로 직교배열법을 이용한 2^k 부분요인배치법인 L₃₂(2¹⁵)를 채택하였다. 다음 Table 3에는 각 설계변수의 범위와 Nominal 값이 제시되어 있다. 스크리닝 이후, 선택되지 않은 설계변수들의 Nominal은 2^k 부분요인배치법을 이용한 반응 최적화를 통하여 획득된 변수값으로 고정되었다. 여기서 허브팁비의 변경은 슈라우드 반경(R_S)이 91mm으로 고정시키고 허브 반경(R_H)을 변경하는 방식으로 이루어졌다.

Table 3

Range of design variables

설계변수의 중요도와 적합한 설계변수 선정 방법으로 민감도 분석과 ANOVA를 이용한 스크리닝 기법을 활용하였고, 이를 위해 부분요인법을 이용한 실험계획법으로 실험점들에 대한 데이터를 획득하였다. 해당 기법은 해상도 IV 수준으로 주 효과는 교락되어 있지 않으나 2차 상호작용이 상호간 교락되어 있는 기법이다. 이 32개의 실험점 중 4개의 실험점에서 블레이드 형상에 기인한 해석 불능점이 발생하였고, 이 지점들을 배제하고 변수의 중요도 분류를 진행하였다.

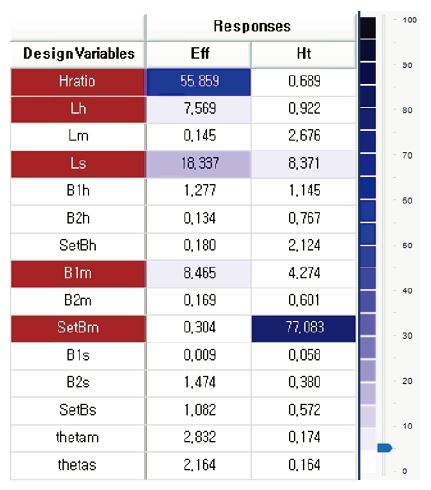
다음 Fig.5에는 ANOVA 기반의 스크리닝 결과와 이러한 과정을 통하여 선정된 설계변수들이 도시되어 있다. 효율의 경우 H_ratio, L_S, β_1,M, L_H, 양정의 경우 Setβ_M, L_S, β_1,M, L_M 순으로 높은 값을 갖으며, 이들 중 Setβ_M, H_ratio, L_S, β_1,M, L_H 순으로 중요한 설계변수로 파악되었다. 이 중 허브팁비 는 기존 연구들을 통하여 중요도가 익히 알려져 있으며(15), 변경에 따라 펌프의 특성 또한 달라질 수 있어 본 연구에서는 해당 변수를 배제하였다. 이에 의하여 Setβ_M, L_S, β_1,M, L_H 등의 총 4개의 변수가 주요 설계변수로 선정되어 예측모델 구성에 이용되었다. 다음 Table 4에는 스크리닝을 통하여 선정된 주요 설계 변수들의 범위가 제시되어 있다. 설계변수 L_S와 L_H는 스크리닝 전 설계변수 범위와 스크리닝 후 설계변수 범위가 다른데, L_S의 경우 여타 변수들과 달리 경험적으로 슈라우드 길이 증가 시 성능의 개선을 보이므로, Upper bound(L_S=33)을 기준으로 설계변수 범위를 재설정하였다. 반면 L_H의 경우 현재 범위를 유지할 경우 펌프의 설계 한계에 의하여 불능점이 발생할 수 있어, Lower bound(L_H=49)를 기준으로 재설정하였다. 두 경우 모두 기존 설계변수들의 그것과 동일한 변량을 갖는다.

Fig. 5

Screening based on ANOVA

Table 4

Range of design variables after screening

4.4 최적 예측모델 선정

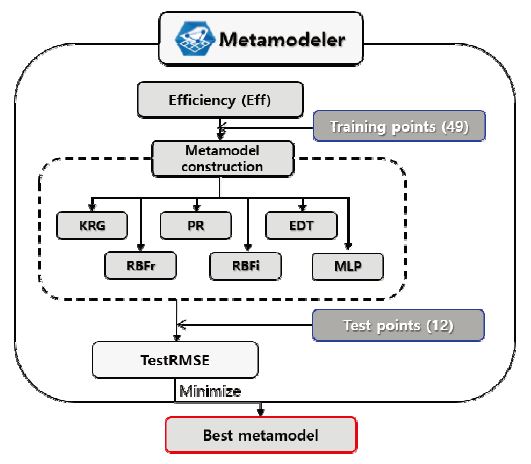
예측모델(Metamodel)은 실험 또는 해석의 결과물을 기반으로 실제 관측이 이루어지지 않은 영역에서의 성능을 예측하는 기법으로, 근사모델(Approximation model), 대리모델(Surrogate model)이라고도 한다. 이러한 예측모델은 크리깅 기법(Kriging)과 같이 예측모델이 실험값들을 지나가도록 설계되는 보간법(Interpolation)과, 다항회귀분석법(Polynomial regression) 등 실험값들이 예측모델을 지나가는 지와 무관하게 최소오차를 갖도록 설계되는 회귀법(regression)으로 나뉜다. 본 연구에서는 PIDOTECH의 상용 프로그램인 PIAnO⁽¹¹⁾을 이용하여 여러 종류의 예측모델을 구성하고 오차율 분석을 통하여 가장 적합한 모델을 선정하였다. 예측모델들의 객관적 비교를 위하여, 예측모델 구성에 데이터 획득 과정에서 사용되는 훈련 데이터셋(training set) 이외에도 훈련에 사용되지 않고 예측모델의 오차비교에 사용되는 테스트 데이터셋(test set)을 획득하였다.

예측모델 수립을 위하여 이에 대하여 실험계획법을 진행하였다. 4개 설계변수에 대하여 2수준 완전요인배치법으로 Upper Bound/Lower Bound에서의 실험점을 설정하고, 2차 이상의 관계도 파악을 위하여 라틴 하이퍼큐브 샘플링(Latin Hypercube Sampling, LHS)을 통하여 32개의 실험점을 추가하였다. 추가로, 이 48개의 데이터에 설계의 초기 지점을 더하여 총 49개의 데이터를 훈련 데이터셋으로 이용하여 예측모델을 구성하였다. 또한, 예측모델의 평가를 위하여 설계변수 범위 내에서 임의의 12개 지점을 테스트 데이터셋으로 구성하여 예측모델의 성능을 평가하였다.

다음 Fig.6에는 예측모델의 오차비교 과정이 도시되어 있다. 적합한 모델을 찾기 위하여 구성된 예측모델은 총 6종류로, 이 중 크리깅 기법(KRG)과 방사기저함수 보간법(Radial Basis Function-interpolation, RBFi)은 보간법 기반, 다항회귀분석법(PR), 방사기저함수 회귀법(Radial Basis Function-regression, RBFr), 앙상블 결정 트리 기법(Ensemble Decision Tree, EDT), 다층 퍼셉트론 기법 (Multi-Layer Perceptron, MLP)은 회귀법 기반의 예측모델이다. 예측모델을 선정하기 위하여 먼저 훈련 데이터셋만을 이용하여 이들을 효율과 양정 각각에 대하여 구성하였다. 그리고 테스트 데이터셋에서 예측모델로 예측된 성능지수와 해석결과를 비교하는 과정을 거쳤다. 여기서 오차는 제곱 평균 제곱근 오차(Root Mean Square Error, RMSE)를 의미하며 다음 식 (2)와 같이 표현된다.

Fig. 6

Process of best metamodel selection

$\[ \begin{array}{l}RMSE=\sqrt{\frac{1}{n}\sum _{j=0}^n{\left(x_{j,real}-x_{j,prd}\right)}^2 }\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{n}\mathrm{ }\mathrm{i}\mathrm{s}\mathrm{ }\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{ }\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{s}\end{array} \]$

(2)

효율과 양정 각각에서 계산된 RMSE가 가장 낮은 예측모델을 선정하였다. 일련의 과정을 모두 수행하는 데에는 훈련 데이터셋 49개 기준 5분 가량의 시간이 소요되었다. 예측모델들 중 EDT는 하이퍼 패러미터(Hyperparameter) 최적화 여부에 따른 결과 비교를, MLP는 최적 네트워크 아키텍쳐(Network architecture)의 탐색 여부에 따른 결과 비교를 추가적으로 진행하였고, 총 8가지의 예측모델의 비교를 진행하였다. 다음 Table 5에는 예측모델별 testRMSE가 제시되어 있다. 먼저 효율의 경우 예측모델 간의 편차가 크며 전반적으로 인공신경망 기반 예측모델들은 높은 오차를 보임을 확인할 수 있다. 특히 최적의 네트워크 아키텍쳐를 탐색하지 않고 구성된 MLP 예측모델의 경우 효율에서 매우 큰 오차를 보이며 경향성을 제대로 반영하지 못하고 있다. 이러한 결과를 종합하여, 구성된 모델들 중 오차가 가장 작은 다항회귀분석법을 효율의 예측모델로 선정하였다. 둘째로 양정의 경우 효율에 비하여 편차가 작으나 효율과 마찬가지로 인공신경망 기반 예측모델들이 전통적인 모델들보다 높은 오차를 보임이 확인된다. 양정에서는 오차가 가장 작은 크리깅 기법을 예측모델로 선정하였다.

Table 5

Test point RMSE of metamodels

5. 설계 최적화

설계 최적화 기법은 목적함수의 수에 따라 단일목적함수 최적화, 다중목적함수 최적화로 분류되며 구속조건 여부에 따라 비구속 최적화, 구속 최적화로 분류된다. 본 연구에서는 단일목적함수, 구속 최적화를 진행하였다. 또한 펌프의 설계 최적화 결과뿐 아니라 민감도, 상충성 등 최적화 과정에서 각 설계변수가 성능지수들에 미치는 영향을 분석하고, 이를 통하여 현재의 설계변수 범위뿐 아니라 더 나은 성능지수 획득을 위한 설계변수 개선 방향을 제시하고자 한다. 설계변수의 용이한 분석을 위하여 본 연구에서는 효율과 양정의 값에 –1을 곱하고 이를 최소화하는 방향으로 목적함수를 설정하였고, 스크리닝 데이터를 이용하여 획득된 결과들을 이용하여 새로운 초기점을 획득, 이 지점을 기반으로 설계 최적화를 진행하였다.

성능지수에 대한 개별 설계변수들의 영향을 평가하고 추가적인 개선책을 도출하기 위하여 단일목적함수 최적화를 진행하였다. 다음 식 (3)에는 단일목적함수 최적화의 설계문제 정식화가, Table 6에는 이에 대한 구속조건이 제시되어 있다.

Table 6

Constraints of total head

최적화 수행을 위해 AIDesigner S/W를 사용하였고, 순차적 국부 최적화 기법인 PQRSM(Progressive Quadratic Response Surface Method)⁽¹⁴⁾을 사용하였다. 본 연구에서는 해당 기법을 이용하여 세 가지 요구양정에서 설계 최적화를 진행하고, 이에 대하여 AIDesigner S/W가 생성한 결과 보고서를 토대로 요구양정의 변화에 따른 설계변수 변화와 각 변수들의 상관관계를 파악하였다. 또한, 이를 이용하여 설계변수 변화에 따른 추가적인 성능 개선 방향을 제시하고자 한다.

6. 최적화 수행 결과 및 분석

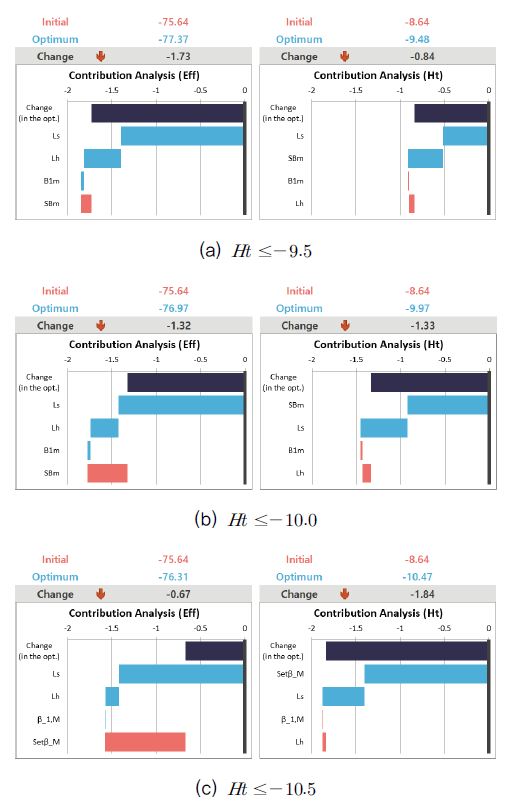
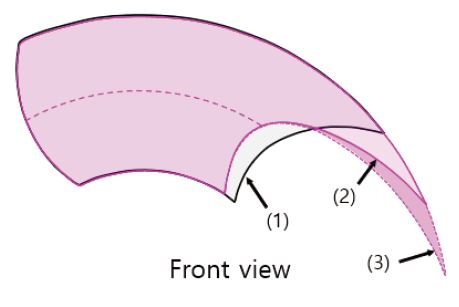
Table 7에는 각 요구양정에 대한 최적화 결과값이 제시되어 있다. 또한 다음 Fig.7에는 Table 7의 결과값에 대응되는 임펠러의 정면 뷰 형상이 도시되어 있다. 기준모델에서의 효율과 양정은 각각 75.44%, 8.64m으로 계산되었고, 최적화 과정을 통하여 효율의 개선과 요구양정 만족이 이루어졌다.

Table 7

Initial vs Optimal shape

Fig. 7

Optimized blade shapes (front view) ((1): Ht≤-9.5, (2): Ht≤-10.0, (3) Ht≤-10.5)

저양정 조건(1)에서 효율 1.93%, 양정 0.84m, 중간 양정 조건(2)에서 1.53%. 1.33m, 고양정 조건(3)에서 0.88%, 1.83m의 개선을 보여 요구양정의 증가에 따른 효율 개선 정도가 감소함이 확인되며, 이를 통하여 요구양정과 효율 최적값이 상호간 상충성을 갖는 성능지수임을 파악할 수 있다. 요구양정의 변경에 대한 최적점에서의 설계변수 변화 또한 확인 가능한데, 요구양정과 관계없이 L_S는 Upper Bound에 근접하였고, L_H와 β_1,M은 증가, Setβ_M은 감소하는 경향을 확인할 수 있다. 특히 L_S의 경우 성능지수의 변화와 무관하게 Upper Bound에 근접하는 특성을 통하여 이 변수의 증가에 따라 효율과 양정 모두 개선되는, 상충성을 가지지 않은 변수임이 확인된다.

6.1 설계변수 영향성 분석

설계변수의 영향은 크게 설계변수 기여도와 민감도로 나뉜다. 설계변수 기여도는 최적화 수행 후 변경된 개별 설계변수가 성능지수에 미치는 영향(개선 또는 악화)으로 정의된다. 이 값을 통하여 최적화 과정에서 각 설계변수가 각 성능지수를 개선하였는지 악화하였는지 파악할 수 있다. 설계변수 민감도는 설계변수 변화에 따른 성능지수의 변화 정도로 정의되는데 이는 크게 전역민감도(Global sensitivity)와 국부민감도(Local sensitivity)로 나뉜다. 이 중 전역민감도는 실험계획법을 이용하여 여러 실험점들을 획득하고, 이들을 이용하여 파악된 전체 설계 영역에서의 설계변수와 성능지수 간의 관계를 의미한다. 전역민감도 정보를 이용하여 설계변수 전반의 성능 개선에 있어 중요한 설계변수 정보와 이들의 개선 방향을 파악할 수 있다. 반면 국부민감도란 특정 실험점을 기준으로 개별 설계변수들을 각각 변화시켰을 때, 개별 성능지수의 변화 정도로, 특정 실험점의 파라메트릭 스터디(Parametric study, PS)를 통하여 이를 파악한다. 시스템의 교호작용이 많지 않은 경우, 통상적으로 전역민감도와 유사한 경향을 보인다. 본 연구에서는 최적화 과정에서 AIDesigner S/W를 이용하여 생성된 보고서를 통하여 이들에 대한 분석을 진행하였다.

6.1.1 기여도 분석

다음 Fig.8에는 AIDesigner S/W를 이용하여 분석된 설계변수 변화에 대한 성능지수 기여도가 도시되어 있다. 각 기여도의 총합은 Table 7에서 도시된 개선 정도와 동일하다. 저양정 조건에서는 Fig.8a와 같이 효율과 양정 모두에서 L_S가 가장 큰 기여도를 보인다. 효율의 경우 이외에도 L_H가 개선에 약간의 기여를 보이며 β_1,M의 경우 거의 변화를 보이지 않고, Setβ_M은 성능지수 악화에 기여한다. 양정의 경우는 Setβ_M이 L_S와 비슷한 수준의 개선 기여도를 보이고, β_1,M과 L_H는 미미한 수준의 성능지수 악화 기여도를 보인다. Fig.8c와 같은 고양정 조건에서는 Setβ_M의 효율 악화 기여도가 증가하고 양정의 개선 기여도 또한 증가, 기타 설계변수들의 경우 L_H의 효율 개선 기여도가 소폭 감소하는 것 이외에 큰 변화를 보이지 않는다. 이를 통하여, 축류 펌프의 설계에서 L_S가 성능 개선을, Setβ_M가 요구양정에 대한 효율을 결정하는 주요 변수임을 알 수 있다.

Fig. 8

Contribution analysis result

6.1.2 전역민감도 분석

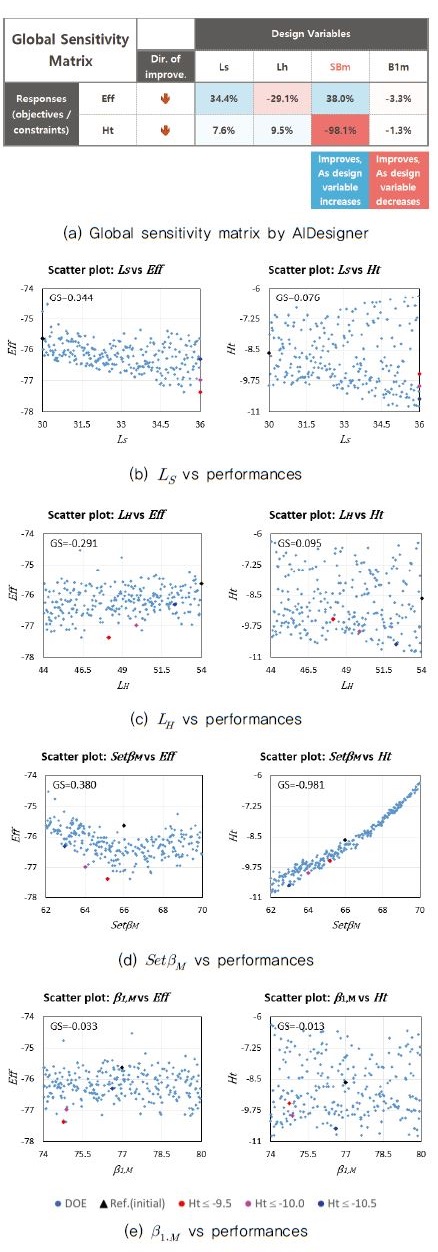
다음 Fig.9에는 전역민감도 분석에 이용된 실험점과 파악된 전역민감도가 도시되어 있다. 본 연구에서는 전역민감도 분석을 위해 실험계획법 중 최적 라틴 하이퍼큐브 설계 (Optimal Latin Hypercube Design, OLHD)⁽¹⁶⁾ 기법을 통하여 500개의 실험점을 획득하였고, 이 실험점들에서의 성능지수를 기 선정된 예측모델을 이용하여 예측하였다. 파악된 전역민감도는 Fig.9a의 전역민감도 매트릭스로 나타내었다. 해당 값들의 예측에 이용된 데이터셋이 Fig.9b-e에 산점도로 표현되었으며 각 설계변수 별 성능지수와의 관계 표현을 위하여 총 8개의 그래프로 도시하였다. 민감도 값의 경우 AIDesigner S/W를 통하여 상관관계분석(correlation analysis) 기법으로 계산되었으며 설계변수 값 증가에 따라 성능지수가 개선되는 경우 양의 값, 설계변수 값 감소에 따라 성능지수가 개선되는 경우는 음의 값을 갖도록 하였다. 이들 중 민감도의 절대값이 높은 변수는 Setβ_M으로 효율에 대하여 0.38, 양정에 대하여 -0.98의 값을 갖는다. 이 중 효율에 대하여는 산점도 상에서 증가-개선 후 Setβ_M=66 이상에서 감소-개선으로 변하고, 양정에 대하여는 전역에서 감소-개선하는 뚜렷한 경향성을 보인다. 그 외 L_S와 L_H가 효율에 대하여 각각 약한 증가-개선, 감소-개선 경향성을 보이고, 나머지 네 경우에 대하여는 유의미한 관계를 보이지 않는다. 이를 통하여 기존의 스크리닝 결과에서와 같이 Setβ_M의 중요도가 상대적으로 높으며, 성능지수에 큰 영향을 줌이 확인된다.

Fig. 9

Scatter plot and global sensitivity of performances (GS: Global Sensitivity)

6.1.3 국부민감도 분석

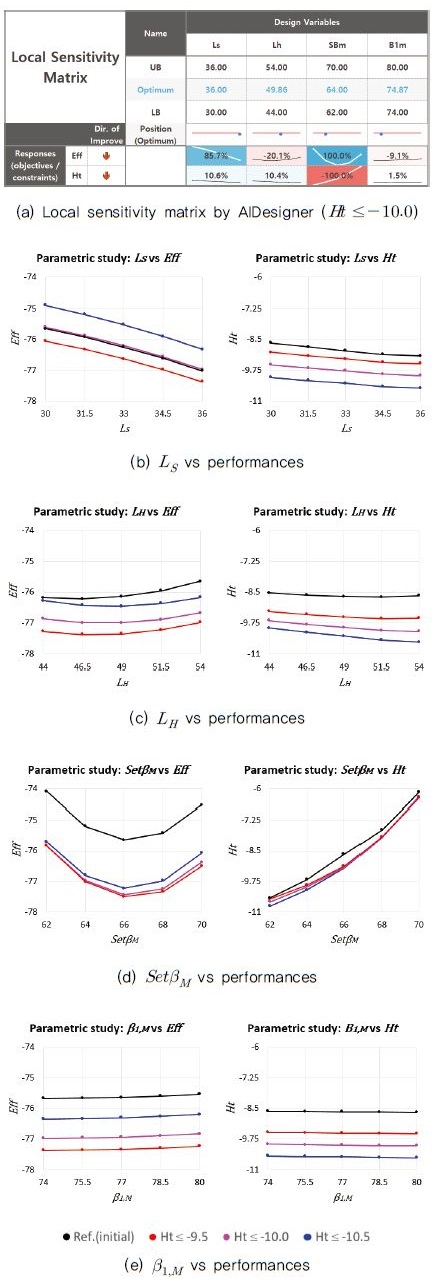
국부민감도 분석을 위하여 초기조건에서의 결과와 함께, 세 요구양정에서 진행된 설계 최적화 결과에 대하여 PS를 진행하였다. PS는 특정 지점에서 특정 설계변수의 변화에 대하여 성능지수의 변화를 획득하고 이를 통하여 해당 설계변수의 영향성을 평가하는 과정이다. 이를 위하여 확인하고자 하는 변수 이외의 설계변수들을 모두 특정값으로 고정하고(Nominal), 확인하고자 하는 변수를 Lower Bound에서 Upper Bound까지 변화시키면서 성능지수를 획득하는 과정을 거친다. 본 연구에서는 설계변수별로 Lower Bound, Upper Bound 포함 5개 지점에서의 데이터를 통하여 영향성을 평가하였으며 효율과 양정에 대하여 총 20번의 예측을 진행하였다.

다음 Fig.10에는 요구양정 10m 조건에서의 국부민감도 값들과(Fig.10a), 각 설계변수들에 대한 PS결과(Fig.10b-e)가 꺾은선 그래프를 통하여 도시되어 있다. 국부민감도 값은 PS를 통하여 계산된 설계변수 변화에 따른 최대값-최소값이 가장 큰 값에 대한 상대적인 값으로 표현되었으며, 세 요구양정들에 대하여 전반적으로 비슷한 수준으로 나타난다. Nominal 값은 각 요구양정에서의 설계변수 최적값으로 설정하였다. PS를 통하여 그려진 꺾은선 그래프(Fig.10b-e) 또한 대체적으로 Fig.9의 경향을 따라감을 확인 가능하다. 전반적으로 교호작용이 크지 않고 설계변수 증감에 대하여 실험점 별 경향성이 유사함이 확인된다. Fig.9의 산점도에서 확인하기 힘든 L_S와 효율의 관계 또한 국부민감도 분석을 통하여 증가-개선 경향성이 명확하게 파악되며, 기타 변수들의 미미한 경향성 또한 파악 가능하다. 효율에 대한 L_S와 Setβ_M의 영향성은 유사한 수준의 전역민감도를 갖던 L_H보다 더욱 지배적이며, β_1,M의 경우 미약한 감소-개선 경향이 확인된다. 양정에 대하여는 Setβ_M이 가장 지배적임은 전역민감도 분석결과와 동일하고, L_S, L_H 등이 약한 증가-개선 경향을 보인다. β_1,M의 경우와 같이 스크리닝을 통하여 획득된 변수라 하더라도 성능지수에 대한 영향이 미미할 수 있음 또한 확인 가능하다.

Fig. 10

Parametric study result of performances

6.2 설계변수 개선 제안

6.2.1 상충성

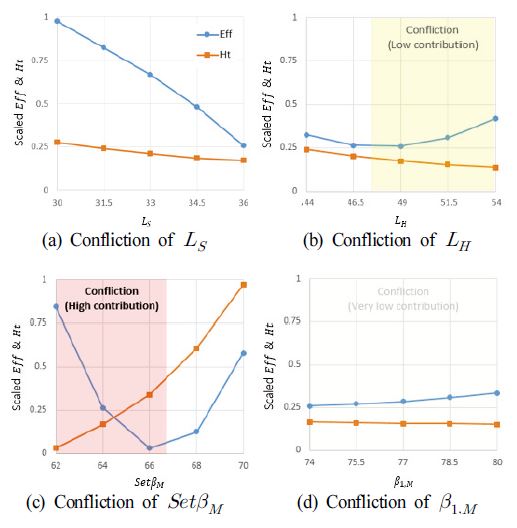
다음 Fig.11에는 Fig.10의 국부민감도 분석결과를 기반으로 한 요구양정 10m에서 성능지수 간의 상충성이 도시되어 있다. 전역민감도에서 확인 가능한 62≤ Setβ_M ≤66에서의 상충성 외에도 47.5≤ L_H ≤54에서 또한 약한 상충성을 보인다. β_1,M의 전역에서도 미약하게 상충성이 확인되나, 해당 변수의 기여도가 매우 낮아 설계 개선에 큰 영향을 주지는 못하였다.

Fig. 11

Confliction on medium required total head

6.2.2 설계변수 개선

단일목적함수 최적화 결과에서 상충성 있는 설계변수들의 최적값은 상충성 발생 영역 내에 위치하며, 요구양정의 변화에 따라 이를 만족하면서 효율의 희생을 최소화하는 방향으로 거동하였다. 따라서, 상충성을 갖는 설계변수들은 설계변수 Lower Bound, Upper Bound가 확장되더라도 현재의 값에서 크게 벗어나지 않는 값으로 결정되며, 범위의 변화에 따라 큰 개선을 기대하기 어렵다. 그렇다면 개선 가능한 변수는 최적값이 Upper Bound/Lower Bound로 고정되면서 상충성을 가지지 않는 설계변수로, 본 연구에서는 L_S가 이에 해당하였다.

다음 Fig.12에는 요구양정 10m 조건(Ht≤-10.0) 에서 개선 제안된 임펠러 형상이 도시되어 있다. 기타 설계변수 변경 없이 L_S만 변경된 형태로, 해당 설계변수가 예측모델 범위 외부에서도 PS의 경향성을 그대로 따른다면 L_S 1당 약 0.3%의 효율 개선과 추가적으로 약 0.03m의 양정 증가가 예측된다.

Fig. 12

Blade shape with suggested parameters (Front view) ((1): new reference. (2): Ht≤-10.0, (3): Suggested)

7. 결 론

PIAnO와 AIDesigner의 multi-stage optimization process를 통해 효과적으로 축류펌프 임펠러의 설계 개선 안을 도출할 수 있었고, 최적화 결과 분석 단계에서 설계 개선의 근거와 상충 관계를 분석함으로써 최적화 결과의 당위성을 이해하고, 추가 개선 방향을 모색할 수 있었다.

Acknowledgments

2022 한국유체기계학회 하계학술대회 발표 논문, 2022년 6월 29일~7월 1일, 휘닉스 평창

본 연구는 2022년도 산업통상자원부(MOTIE)의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제(2021202080026D, AI/ICT 기반 가변형 유체기기 설계·상태진단을 위한 기반·플랫폼 기술 및 운영관리 시스템 개발)입니다.

References

• Kim, M. H., Kim, J. I., and Park, J. S., 2001, “Prediction of Axial Pump Performance Using CFD Analysis,” Journal of Computational Fluids Engineering, Vol. 6, No. 1, pp. 14∼20.
• Wright, T. and Gerhart, P. M., 2010, Fluid Machinery, Application, Selection, and Design, Second edition, CRC press, Florida.
• Wahba, W. A., and Tourlidakis, 2001, “A genetic Algorithm Applied to the Design of Blade Profiles for Centrifugal Pump Impellers, “AIAA 2001-2582. [https://doi.org/10.2514/6.2001-2582]
• Lian, Y. S., Liou, M. S., and Oyama, A., 2004 “An Enhanced Evolutionary Algorithm with a Surrogate Model,” Proceedings of Genetic and Evolutionary Computation Conference, Seattle, WA.
• Song. W. G., Ma, S. B., Choi, Y. S., Lee, K. Y., Kim, Y. S., Kim, K. Y., and Kim, J. H., 2018, “Multiobjective Optimization for Designing a High-Efficiency and Low-Fluid-Induced-Vibration Single-Channel Pump,” The KSFM Journal of Fluid Machinery, Vol. 21, No. 4, pp. 30∼38. [https://doi.org/10.5293/kfma.2018.21.4.030]
• Jung, I. S., Jung, W. H., Baek, S. H., and Kang, S., 2012, “Shape Optimization of Impeller Blades for a Bidirectional Axial Flow Pump using Polynomial Surrogate Model,” International Journal of Mechanical and Mechatronics Engineering, Vol. 6, No. 6, pp. 1097∼1103.
• Kim, J. H., and Kim, K. Y., 2011, “Optimization of Vane Diffuser in a Mixed-Flow Pump for High Efficiency Design,” International Journal of Fluid Machinery and Systems, Vol. 4, No. 1, pp. 172∼178. [https://doi.org/10.5293/IJFMS.2011.4.1.172]
• Samad, A., Kim, K. Y., Goel, T., Haftka, R. T., and Shyy, W., 2008, “Multiple Surrogate Modeling for Axial Compressor Blade Shape Optimization,” Journal of Propulsion and Power, Vol. 24, No. 2, pp. 301∼310. [https://doi.org/10.2514/1.28999]
• ANSYS CFX 19.0, ANSYS Inc.
• Menter, F. R., 2009, “Review of the shear-stress transport turbulence model experience from an industrial perspective,” International Journal of Computational Fluid Dynamics, Vol. 23, No. 4, pp. 305-316. [https://doi.org/10.1080/10618560902773387]
• PIAnO (Process Integration, Automation and Optimization) 2022 User’s Manual, 2022, PIDOTECH Inc.
• AIDesigner 2022 User’s Manual, 2022, PIDOTECH Inc.
• Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T., 2002, “A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II,” IEEE Transactions of Evolutionary Computation, Vol. 6, No. 2, pp. 182∼197. [https://doi.org/10.1109/4235.996017]
• Hong, K. J., Kim, M. S., and Choi, D. H., 2000, “Progressive Quadratic Approximation Method for Effective Constructing the Second-Order Response Surface Models in the Large Scaled System Design,” Trans.Korean Soc. Mech. Eng. A, Vol. 24, No. 12, pp.3040∼3052.
• Park, H. C., Kim, S., Yoon, J. Y., and Choi, Y. S., 2012, “A Numerical Study on the Performance Improvement of Guide Vanes in an Axial Pump,” The KSFM Journal of Fluid Machinery, Vol. 15, No. 6, pp. 58∼63. [https://doi.org/10.5293/kfma.2012.15.6.058]
• Park, J. S., 1994, “Optimal Latin-Hypercube Designs for Computer Experiments,” Journal of Statistical Planning and Inferences, Vol. 39, pp. 95∼111. [https://doi.org/10.1016/0378-3758(94)90115-5]