Effect of Air Layer on the Performance of an Open Ducted Cross Flow Turbine
Abstract
Recently, the cross flow turbines attract more attention for their good performance over a large operating regime at off design point. This study employs a very low head cross flow turbine, which has open inlet duct and has barely been studied before, to investigate the performance of the cross flow turbine with air suction from the rear part of the runner. Unlike conventional cross flow turbines, a draft tube is attached to the outlet of runner to improve the turbine performance. Water level and pressure in the draft tube are monitored to investigate the influence of air suction. Torque at local blade passage of three parts of runner is examined in detail under the conditions of different air suction. Consequently, it is found that with proper air suction in the runner chamber, the water level in the draft tube gradually drops to Stage 2 of the runner and the efficiency of the turbine can be raised by 10%. Overall, the effect of air-layer on the performance of the turbine is considerable.
Keywords:
Open Ducted Cross-Flow Turbine, Air Layer, Very Low Head, Performance, Internal Flow키워드:
개방 덕트형 횡류수차, 공기층, 초저낙차, 성능, 내부유동1. Introduction
Cross flow turbine is ideal for the hydraulic environment of small river runoff plants. Not only because it is easily structured and least expensive, but also because its efficiency is much less dependent on flow rate than other hydro turbines. Unlike conventional hydro barrage installations, cross flow turbine with open duct can generate power over a wide range of sites than those available for conventional power generation with less environmental impact, which is quite suitable for remote rural areas. Consequently, a very low head cross flow turbine with open inlet duct is taken into consideration in this study. However, the relatively low efficiency remains a problem. Though invented in 1900(1), only the value of efficiency 84% have been cited in the literature(2) while the predicted maximum efficiency is 87.8% according to current theory(3).
In order to increase the efficiency, Tamil Chandran(4) conducted an experiment on a cross flow turbine and it was suggested to improve the efficiency by modifying the guide vane profiles. Nasir(5) proved that optimization of the nozzle shape can be a good method.
An extensive bibliographical review results on the development of the cross flow turbine can be found in the works of Khosrowpanah et al.(6), Durgin(7) and Costa Pereira(8). The works included details concerning the influence of the number of blades, outside diameter of the runner and admission arc of the nozzle on the turbine efficiency, which offers a guideline for the turbine design. However, in this study, as this turbine has a very low head of below 1.5m and open inlet duct is applied to guide water into the runner, the effects of the above methods are limited.
As this kind of cross flow turbine has a very low head, the power generated from the kinetic energy is relatively small. Thus, a draft tube is essential to improve the performance of the turbine. Here the draft tube plays the role of utilizing the level difference between runner and downstream water level. Moreover, the velocity of water at the runner outlet is very high. By employing a draft tube, this part of kinetic energy is recovered as a gain in the pressure head, and this increases the efficiency of the turbine. However, during the turbine operation the air in the runner and draft tube moves out along with the discharged water, creating a vacuum at the rear part of runner, causing the water level in the draft tube to rise above the runner. This creates the negative torque at the rear part of the runner. In order to solve the accompanying problem, Choi et al.(9) proposed to employ an air suction hole to the draft tube, which has been proved to be effective for medium head cross flow turbine by the methods of experiment and CFD analysis.
This study tries to employ an air suction pipe behind the rear part of the runner. The purpose of this study is not only to investigate the effect of air layer for a 1.5m head of cross flow turbine which is barely studied before, but also to verify the effectiveness of air layer formation in the runner passage. Two-phase flow transient analysis is conducted under the condition of gravity to embody the air-layer effect. Efficiencies by different air flow rates from the air suction pipe are traced. For further study on the influence of the air flow rate, pressure and velocity distributions in the runner are investigated and compared in detail. The interaction of water level in the draft tube and torque generation of the runner is also discussed.
2. Cross Flow Hydro Turbine Model with Open Inlet Duct
2.1. Runner
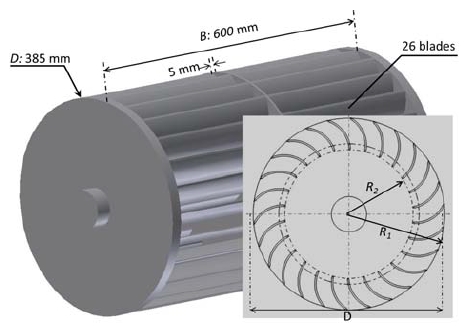
The runner is the heart of the cross flow turbine. For low head cross flow turbine, there are two important specific factors in the runner design: D/B and R2/R1. D is the runner outer diameter and B is the runner breadth. R1 and R2 are outer runner radius and inner runner radius, respectively.
To get a high efficiency, a low ratio of D/B and a high ratio of R2/R1 are needed. However, with a high R2/R1, the runner blade will suffer a lot of stress that may result in structural problems. All considered, a runner breadth of 600 mm with a ratio of R2/R1=0.67 is employed. As shown in Fig. 1, outer runner diameter D=2R1=385 mm; inner runner radius R2=129 mm.
Runner of the very low head cross flow turbine with open inlet duct
To enhance the strength of the blades in the runner, two circular side plates and a mid-plate of 5 mm thickness are used. The number of the blade is 26.
2.2. Shapes of open duct and nozzle
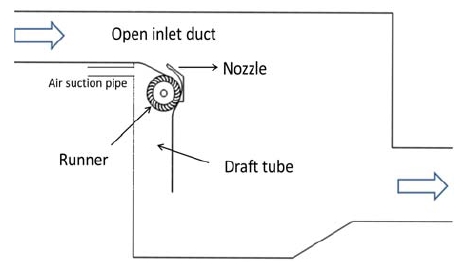
Figure 2 presents the overall view of the turbine model for CFD analysis. Open inlet duct, other than closed duct, is used to avoid blockage by small particles, e.g., wood blocks. To reduce the cost, the structure is simplified with only a nozzle to guide the water running into the runner. The schematic view of the developed cross flow turbine is shown in Fig. 3. The circumferential location starts from the runner inlet in clockwise direction. Water coming from the upstream runs into the runner by the guide of nozzle and passes through the runner twice, i.e., water flow is directed towards the centre of the wheel and then again crossing other blades before exiting. Power is transferred to the runner when the water is leaving the turbine. Moreover, particles such as wood blocks are washed away with the over flow from the outside passage.
Whole view of 2-D flow field including the turbine model for CFD analysis
Schematic view of cross flow turbine with open inlet duct
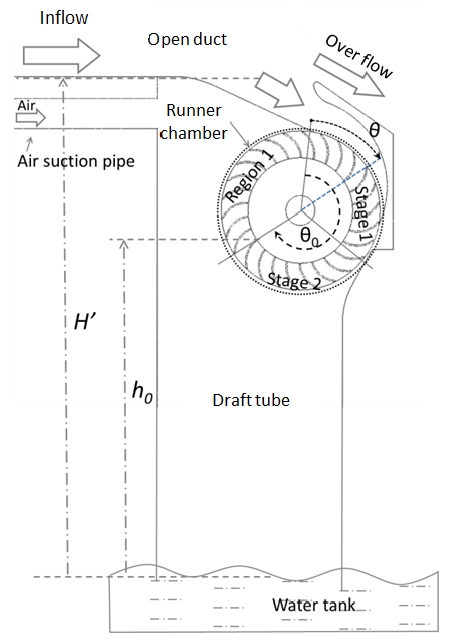
To improve the performance of the turbine, an air suction pipe is attached to the rear part of the runner in this study. The runner is divided into three parts: Stage 1, Stage 2 and Region 1. The following symbols occur in the figure:
θ:circumferential location starting from the inlet of runner;
H:water level in the draft tube;
2.3. Cases for study
The design parameters for the cross flow turbine are as follows: the inflow low rate is 0.25 m3/s, the head is 1.5 m and rotating speed is 132 min-1.
Table 1 shows the studied cases for performance improvement of the cross flow turbine. Case 0 is the designed case, which has no air suction pipe included in the design. From Cases 1 to 5, the air flow rate increases step by step to check the influence of air suction. In particular, for Case 6, the air flow rate is not controlled, and only the pressure at the runner chamber determines the air flow rate. The ratio of air suction ranges from 0.21 to 1.40.
Cases of the CFD analysis
3. Numerical Methods and Boundary Condition
This study employs a commercial CFD code of ANSYS CFX(10) to conduct CFD analysis. Two-dimensional CFD analysis is applied to shorten the calculating time and reduce the computational cost, which means that the transverse flow along the thickness direction is not considered in this study.
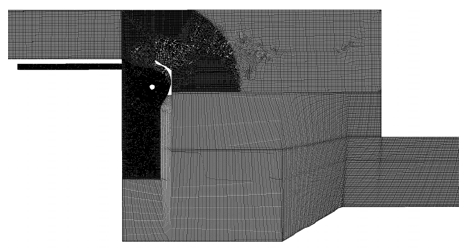
Non-dimensional distance from the mesh wall, y+, is a very important factor in transient analysis(11,12). It is recommended to have a small first cell height to cover the log-law region. In order to diminish the y+, hexahedral grids are applied with high density around the region near the surface of runner blades.
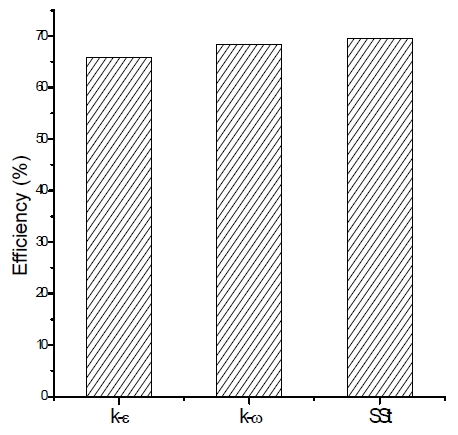
In order to enhance the accuracy of the analysis, turbulence model dependence and mesh dependence tests are conducted as shown in Fig. 4 and Table 2. Finally the hexahedral grids which contain nodes number of 0.87×106 and elements of 0.69×106 are employed to mesh the fluid domain of the cross flow turbine. The whole mesh of the fluid domain can be refered to Fig. 5. Turbulence model of SST is adopted because of its relatively good convergence in the complicated flow field of turbo machinery and has been well known to estimate both separation and vortex occurring on the wall of a complicated blade shape.
Turbulence model dependence test
Mesh dependence test
Whole view of numerical mesh of the turbine model
As the upstream water is separated at the inlet of nozzle and more detail fluid characteristics in these areas are needed to understand as well as that in draft tube and runner chamber, relatively high density grids are used comparing to that of inlet and water tank.
Furthermore, two-phase flow calculation using shear stress transport turbulence model is carried out. A free surface between the air and water layer is used. The detailed boundary condition and numerical method are shown in Table 3.
Numerical methods and boundary condition
4. Results and Discussion
4.1. Efficiency curves
Actual efficiency can be determined by either measurement or computational simulations of the fluid passing through the turbine runner. In this study, as the velocity at the outlet is unstable, the efficiency is simply calculated based on the potential energy difference between the upstream water and downstream water. Namely
| (1) |
where η is the efficiency of the cross flow turbine, T is the torque at runner; ω is the rotational speed of runner rotating on its own axis; H is the turbine head.
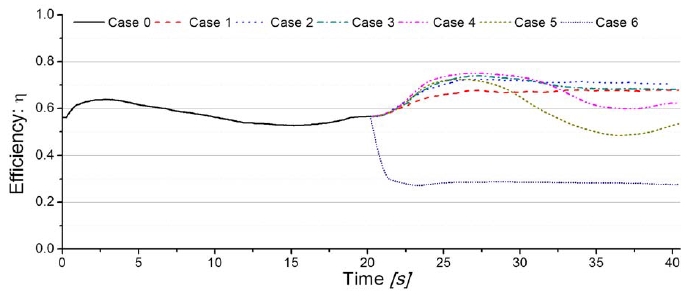
Time serial efficiency curves of the turbine are shown in Fig. 6. To shorten the calculating time, a water level close to the bottom of the runner is set at the beginning in Case 0. The efficiency starts to increase at first, and then decreases. The final efficiency is about 0.6. Taking the final state of Case 0 as initial condition, Cases 1 to 6 are calculated to investigate the effect of air suction through the pipe behind the runner chamber.
Time serial efficiency curves versus time by different cases
According to Fig. 6, efficiencies of Cases 1 to 5 start to increase and the growth ratios get larger with the increasing of the air suction ratio, indicating that the air suction has the effect of improving turbine efficiency. Finally, the efficiency reaches the maximum point up to 0.75 in Case 4. Case 2 is also found to have the optimal air suction ratio of 0.09 with the maximum efficiency of 0.7.
However, when the opening condition is applied to the pipe inlet, which means no control of air flow rate through the air suction pipe, the efficiency curve suddenly decreases to a very low level around 0.3, which is half of that at the beginning. In other words, the excessive air suction also results in energy loss of tail water in the draft tube, which simultaneously causes the efficiency to decrease.
4.2. Time serial distributions of water volume fraction of the fluid domain
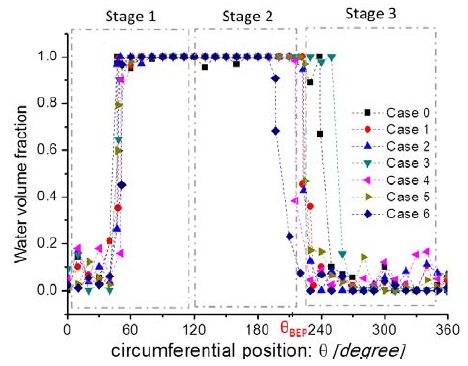
The distributions of water volume fraction in the fluid domain are shown in Fig. 7. A value 1 means that the covered region is only water and a value 0 means there is only air. Between 0 and 1 means is a mixture. Since variations of water volume fraction distributions with time in Cases 1 to 5 are quite similar, and Case 6 includes all the variation process of water level in the draft tube. Case 6 is chosen for description of the change of water level in the draft tube with air suction.
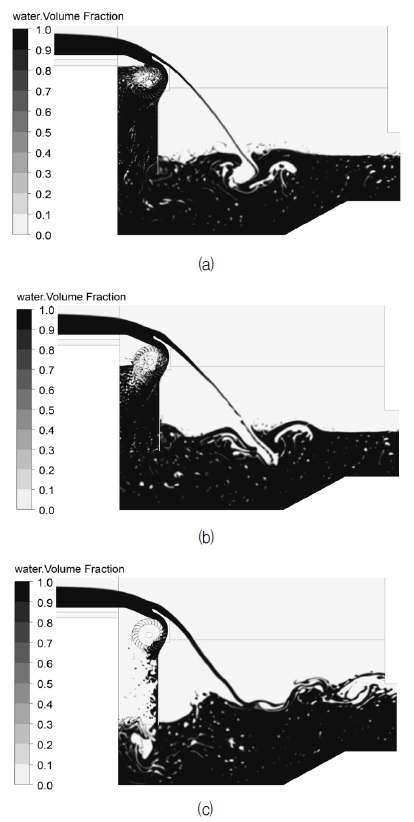
Distributions of water volume fraction at (a) beginning (b) maximum efficiency point and (c) final state in Case 6
From Fig. 7, it can be found that part of the water runs into the runner by the guide of nozzle, and part of the water passes over the nozzle and overflows on the water tank (in Fig. 7(a)). The air in the draft tube is rushed out with the water, forming a vacuum. Thus water level in the draft tube rises and finally the draft tube is filled with water. With constant air suction, water level gradually drops down to a certain level. When the water level drops until Stage 2, the efficiency of the cross flow turbine reaches its maximum point, as shown in Fig. 7(b). However, at the final state of Case 6, the water level in the draft tube equals to that of water tank (in Fig. 7(c)), since too much air is sucked into the draft tube, thus the efficiency decreases.
4.3. Velocity distribution in the runner passage
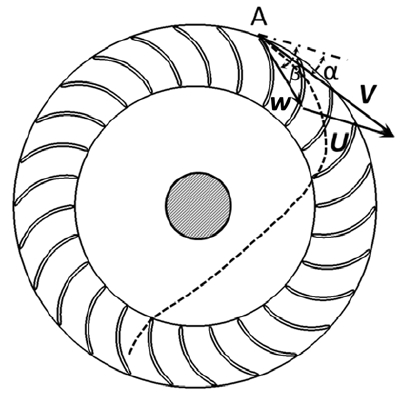
Figure 8 shows the approximate path (dash line) of jet through cross flow turbine. The water enters into the runner at point A at an angle of α, with the velocity tangent to the periphery. The absolute velocity of the water is V. u is the peripheral velocity of the runner at point A, which is known as R1ω. w is the relative velocity. β is the angle in the forward direction of the w and u, and α is the angle between V and u.
Velocity triangle at the entrance of a water path
To calculate the torque transmitted by a blade channel, the following equation can be used [13]:
| (2) |
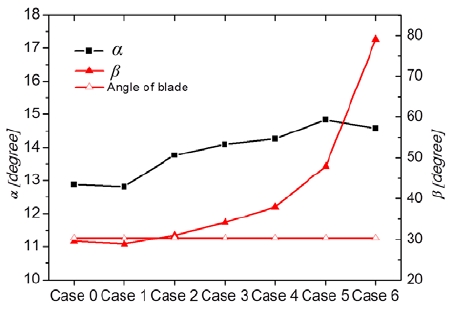
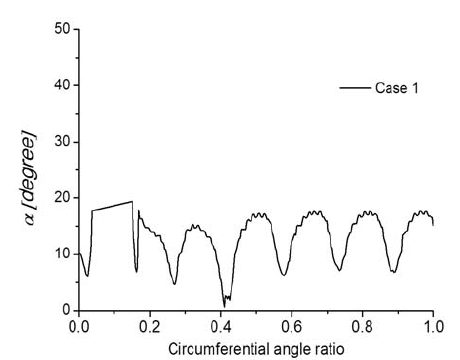
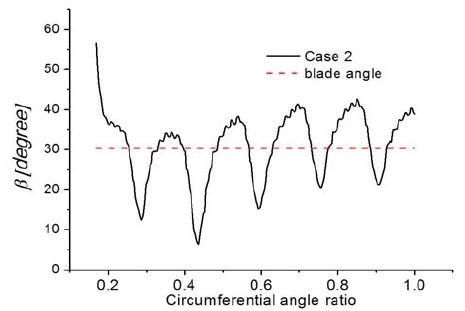
where Tc is the theory output torque, and Qmc is the mass flow per blade channel, R1 and R2 are outer runner radius and inner runner radius, respectively, and ω is the angular velocity. Therefore, to get a large torque, a small α is needed. Moreover, for maximum efficiency, β should be equal to the angle of the blade. Figure 9 presents the averaged α and β at the entrance of Stage 1. It is observed that as air suction flow rate increases, α shows an increasing trend by almost 2 degrees. Case 1 shows to have the minimum α but the distribution fluctuates by circumferential angle as shown in Fig. 10. The 0 of circumferential angle ratio means the starting point at Stage 1, and the 1of that means the ending point at the Stage 1. With air suction, the averaged β at the entrance of Stage 1 increases. However, because of excess air suction, the difference between β and blade angle become larger, and energy loss in the blade channel increases.
Averaged α and β at the entrance of Stage 1 versus air suction
Distribution of α at the entrance of Stage 1 in Case 1
Figure 11 shows the distribution of β at the entrance of Stage 1 in Case 2. It is observed that the efficiency becomes maximum from t=32s onwards as presented in Fig. 6, because it has the closest angle, β, to the blade angle as observed in Fig. 11. Even though the flow angle varies by the circumferential angle, the averaged flow angle agrees well with the blade inlet angle and thus the efficiency of Case 2 is higher than the other cases.
Distribution of β at the entrance of Stage 1 in Case 2
4.4. Distributions of water volume fraction in the runner at the maximum efficiency point
Figure 6 shows that in Cases 1 to 5, the efficiency firstly increases to a maximum point and then decreases. Detailed examination is carried out and it is found that the distributions of water volume fraction in the runner are quite similar. As shown in Fig. 12, the runner passage is filled with water from circumferential position of 60 degree. By the end of Stage 2, however, the water volume fraction transforms from 1 to 0. And the runner passage at Region 1 is filled with air. Considering the efficiency curve in Fig. 6, the effect of air layer on the turbine efficiency can be deduced. That is, when the air layer area is small, the increasing of air suction can improve turbine efficiency and when Region 1 is filled with air, it reaches maximum efficiency. When air layer area is larger than that of best efficiency point, further increasing air suction leads to the decrease in turbine efficiency.
Water distributions in the runner passage versus circumferential location at maximum efficiency point
4.5. Impact of air suction
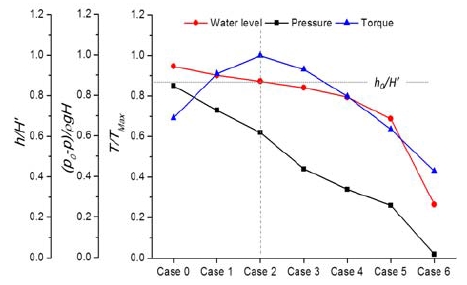
In order to identify the influence of air suction, the interrelationships among water level, pressure and torque distributions are compared as shown in Fig. 13. Here the change in pressure is demonstrated as
| (3) |
Water level, pressure and torque distributions by air suction
where ΔH is the head of the potential energy generated from the draft tube, p0 is the atmospheric pressure and p is the local pressure of the low pressure region in the runner.
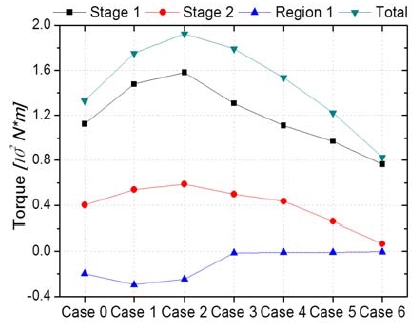
Figure 13 shows that the pressure is proportional to the water level as they present similar falling tendency when the air suction increases from Cases 1 to 5. However, the torque at the runner first increases and then decreases with different air suctions. In Case 2, where air suction ratio is 0.09, water level is close to hBEP, and the torque reaches its maximum point. In other words, when air suction increases, the power obtained from the potential energy in the draft tube decreases. However, the power generated from the runner remains larger while the water level in the draft tube is higher Fig. 12 Water distributions in the runner passage versus circumferential location at maximum efficiency point than hBEP. In this situation, torque at Stages 1 and 2 increases evidently as shown in Fig. 14 and the total power generated from the water increases. It is worth mentioning that Stage 1 is more sensitive to the air suction. In Case 2, β is closest to the angle of blade inlet and its efficiency is the highest. However, when the water level is below hBEP, the situation is reversed. The increase of air suction leads to the increase of β, which deviates the flow from the pressure side of runner blade. As a result, the flow in the runner passage is no longer uniform, so the torque at the runner decreases. On the other hand, increase of air suction leads to the potential energy loss at the draft tube. These two factors cause the decrease in turbine efficiency.
Torque distributions at three parts of runner
4.6 Torque distribution versus circumferential position
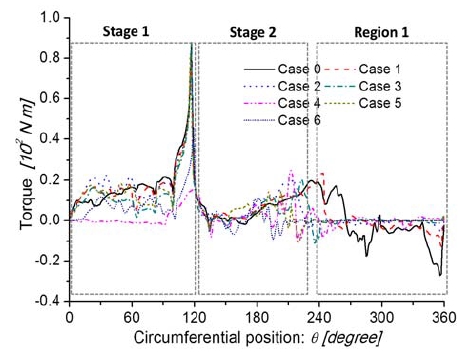
The torque distribution curve of the runner in the circumferential direction is presented in Fig. 15. At Stages 1 and 2, the magnitude of the blade torque is positive to produce output power but at Region 1 it is negative. The curve reaches the crest near the border between Stages 1 and 2. Similarly, this curve presents to have another crest near the border between Stage 2 and Region 1.
Local blade torque versus circumferential position
At Region 1 in Case 0, two torque wave troughs occur, which means there is some power loss. With air suction, torque increases at Stages 1 and 2 from Cases 1 to 3 while Case 2 presents the best performance, but it decreases from Cases 4 to 6. At Stage 2, the torque distribution curve of Case 6 presents the trend that goes to zero from the tangential angle of 180°. From Region 1, the torque curve tends to remain at zero.
5. Conclusions
A newly suggested air suction method is applied to an open ducted cross flow turbine for the first time. Though with very low head, the performance of the cross flow turbine can be significantly improved by this method.
Velocity at the runner inlet is influenced by the air suction. With suitable air suction through air suction pipe, the angle β can get close to blade inlet angle and the generated torque increases significantly.
A maximum efficiency about 0.7 is obtained at the air suction ratio of 0.09. The efficiency of the turbine reaches its maximum point when water level is near the bottom of the runner, the torque at Stages 1 and 2 increases significantly. In other words, for maximum efficiency, the air suction ratio should equal to the air discharge rate in the draft tube when the water level is equal to hBEP. The air flow rate ratio which is sucked naturally is larger than that of other case, which means that a valve in the air suction pipe can be used to decrease the air flow rate to the optimal point.
References
- Haimerl, L. A., (1960), The Cross-Flow Turbine, Water Power Engineering Magazine.
-
Andrade, J. D., Curiel, C., Kenyery, F., Aguillón, O., Vásquez, A., and Asuaje, M., (2011), “Numerical Investigation of the Internal Flow in a Banki Turbine”, International Journal of Rotating Machinery, 2011, p1-12.
[https://doi.org/10.1155/2011/841214]
- Mockmore., C. A., and Merryfield, F., (1949), “The Banki Water Turbine”, Bulletin Series, (25).
- Chandran, A. T., Anil, G., and Chandapillai, J., (2010), “Development and Testing of a Cross Flow Turbine”, International Group for Hydraulic Efficiency Measurement.
- Nasir, B. A., (2013), “Design of High Efficiency Cross-Flow Turbine for Hydro-Power Plant”, International Journal of Engineering and Advanced Technology, 2(3), p308-311.
-
Khosrowpanah, S., Fiuzat, A., and Albertson, M., (1988), “Experimental Study of Cross-Flow Turbine”, Journal of Hydraulic Engineering, 114(3), p299-314.
[https://doi.org/10.1061/(ASCE)0733-9429(1988)114:3(299)]
- Durgin, W. W., and Fay, W. K., (1984), “Some Fluid Flow Characteristics of a Cross Flow Type Hydraulic Turbine”, Small Hydro Power Machinery.
-
Costa Pereira, N. H., and Borges, J. E., (1996), “Study of the Nozzle Flow in a Cross-Flow Turbine”, International Journal of Mechanical Sciences, 38(3), p283-302.
[https://doi.org/10.1016/0020-7403(95)00055-0]
-
Choi, Y. D., Shin, B. R., and Lee, Y. H., (2010), “Air Layer Effect on the Performance Improvement of a Cross-Flow Hydro Turbine”, Journal of Fluid Machinery, 13(4), p37-43.
[https://doi.org/10.5293/KFMA.2010.13.4.037]
- ANSYS Inc, ANSYS CFX Documentation,ver. 13, (2012), http://www.ansys.com.
- Ariff, M., Salim, S. M., and Cheah, S. C., (2009), “Wall Y+ Approach for Dealing with Turbulent Flow Over a Surface Mounted Cube: Part 1 . Low Reynolds Number”, Proceeding of Seventh International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia.
- Ariff, M., Salim, S. M., and Cheah, S. C., (2009), “Wall Y+ Approach for Dealing with Turbulent Flow Over a Surface Mounted Cube: Part 2 . High Reynolds Number”, Proceeding of Seventh International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia.
- Verhaart, P., (1983), Blade Calculations for Water Turbines of the Banki Type, Eindhoven University of Technology.