3D CFD를 활용한 관통 래버린스 실의 회전체 동역학적 해석
Abstract
Labyrinth seals are commonly used in various kinds of turbomachinery to reduce leakage flow. In the present 3D CFD analysis of see-through-type labyrinth air seal, the methodology of determining leakage and rotordynamic coefficients is suggested with the relative coordinate system for steady-state simulation. The leakage flow and rotordynamic forces predicted by using different solvers and turbulent models of FLUENT are compared with the results of the existing bulk-flow analysis code LABYSEAL.FOR and experiment. The present CFD result of direct stiffness(K) shows only improvement in prediction. The results of leakage and rotordynamic coefficients as well as computing time are sensitive against the used solver and turbulent model.
Keywords:
Leakage, Rotordynamic coefficient, See-through-type labyrinth seal, Bulk-flow model, CFD, Fluent키워드:
누설량, 동특성계수, 관통래버린스 실, 벌크흐름 모델1. 서 론
래버린스(labyrinth) 실은 압축기나 스팀터빈 및 가스터빈과 같은 고성능 유체기계의 회전부(rotor)와 비회전부(stator) 사이 틈새를 이루는 아이패킹(eye packing) 실, 인터스테이지(inter stage) 또는 축(shaft) 실 및 밸런스 드럼(balance drum) 실에 가장 보편적으로 적용되고 있는 실이다. 이 실은 작동유체의 누설을 최소화함으로써 터보기계의 효율 향상을 추구하며, 또한 실 틈새로부터 발생되는 유체 가진력에 기인된 진동 불안정성을 최소화하기 위해 설계되는 기계요소이다.
래버린스 실은 누설유량을 최소화하기 위하여 관통 래버린스(see-through labyrinth), 계단식 래버린스(stepped labyrinth), 및 엇갈린 래버린스(staggered labyrinth)의 다양한 형태로 설계되어 사용되고 있다. 최근에는 스팀터빈의 인터스테이지 실에 사용되고 있는 엇갈린 래버린스 실 중간부에 로터에 접촉시킨 브러쉬를 삽입한 브러쉬 실(brush seal)이 개발되는 등 래버린스 실의 형상이 보다 복잡해져 래버린스 실을 통한 누설량 및 동특성계수의 정확한 이론적인 예측을 위해 많은 노력이 이루어져 왔다.
래버린스 실의 이론적 해석을 위해 가장 보편적으로 사용된 방법은 Bulk-flow 모델이다. Hirs(1)의 윤활 이론에 근거하여 단순화된 지배 방정식과 짧은 계산시간 등의 장점으로 초기에 많은 연구자들이 다양한 래버린스 실에 적용해 왔다. 가장 단순한 형태의 래버린스 실인 관통 래버린스 실의 유체력 해석을 위한이론적 연구는 Alford(2)에 의해 처음 시도된 이후, Iwatsubo(3)는 one-control-volume model 해석법을 제시하였고 Scharrer(4)와 하 등(5)은 two-control-volume model 해석법을 통한 개선된 결과를 발표하였다. 계단식 래버린스 실에 대하여, Scharrer(6)의 Blasius 마찰계수 식을 사용한 해석결과와 Ha(7)의 Moody 마찰계수 식을 사용한 개선된 해석 결과가 발표되었다. Ha(8)는 계단식 래버린스 실의 해석법을 확장하여 엇갈린 래버린스 실의 누설량과 동특성계수 예측법을 제시하였다.
Bulk-flow 모델 해석법의 여러 장점에도 불구하고 해석 코드를 개발하는 데 걸리는 시간이 길고, 더욱 복잡해지는 래버린스 형상의 실에 대한 적용의 한계성 때문에 요즈음에는 CFD 해석법이 더욱 선호되고 있다. 하(9-10)는 래버린스 실의 누설량 예측을 위해 상용 소프트웨어(Fluent)를 사용한 2D 및 3D CFD 해석법을 제시하고, Bulk flow 모델 해석 보다 개선된 결과를 발표하였다.
최근에는 CFD 해석법을 사용한 실의 진동 안정성과 관계되는 동특성 계수 예측을 위해서, Rao 등(11)과 하 등(12)은 펌프의 평실을 대상으로 상대좌표계를 사용한 정상상태 해석법을 제안하고 강성계수와 감쇠계수 예측 결과를 발표하였다. 스팀터빈의 래버린스 실에 대한 동특성 계수 예측을 위해 Kirk 등(13)은 상대좌표계를 사용한 정상상태 해석법과 k-ε 난류모델을 적용한 CFX-TASCflow CFD 예측 결과를 발표하였다. 그러나 예측결과는 실험결과와 차이를 보여 압축성 유체를 사용하는 복잡한 형상의 래버린스 실에 대한 정확한 유동 해석 및 동특성 계수 예측에 어려움이 있음을 보였다.
본 연구에서는 다양한 형상의 래버린스 실의 CFD 해석법을 개발하기 위한 기본 단계로, 형상이 가장 단순한 래버린스 실인 관통 래버린스 실에 대한 CFD 해석법을 기 발표된 압축성 작동유체를 사용하는 압축기용 평실의 정상상태 해석법(14)을 기초로 제안하고자 한다. 본 연구의 Fluent를 사용한 CFD 해석 결과를 검증하기 위해서 하(5)의 Bulk-flow 해석 코드(LABYSEAL.FOR)의 결과 및 Pelletti(15)의 실험결과와 비교하여 분석하고자 한다.
2. 해석 대상 래버린스 실의 형상 및 운전조건
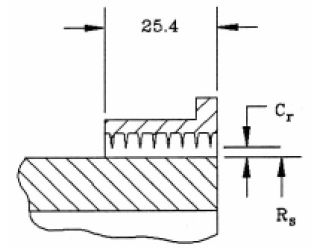
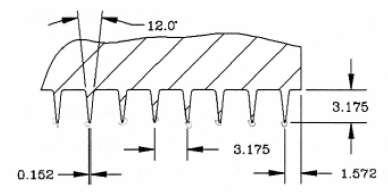
본 연구에서 수행된 CFD 해석법을 검증하기 위해 기 발표된 실험적 연구 결과의 대상 래버린스 실을 해석 대상으로 선정하였다. 기 발표된 관통 래버린스 실의 실험적 연구 결과는 많지 않으나, Pelletti(15)가 Texas A&M University의 Air seal test rig 를 사용하여 발표한 누설량 및 동특성계수 결과와 Ha(5)의 Moody 마찰계수식을 사용한 Bulk-flow 모델 해석 결과가 본 연구의 대상으로서 가장 적합한 것으로 판단되었다. Fig. 1과 Fig. 2는 Pelletti(15)의 Seal No. 1 형상과 Teeth-on-stator type 관통 래버린스 실의 제원을 나타내고 있다. Table. 1은 대상 실의 형상조건과 운전조건을 나타내고 있는데 작동유체는 공기를 사용하였으며, 실 입구에서의 선회류는 없는 것으로 가정하였다.
3. 래버린스 실의 누설량 및 동특성계수 해석
3.1 정상상태 해석을 위한 상대좌표계 설정
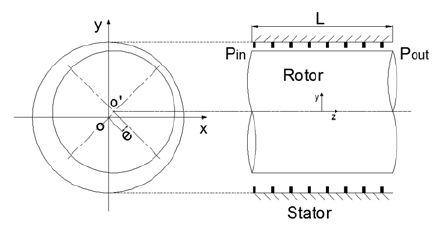
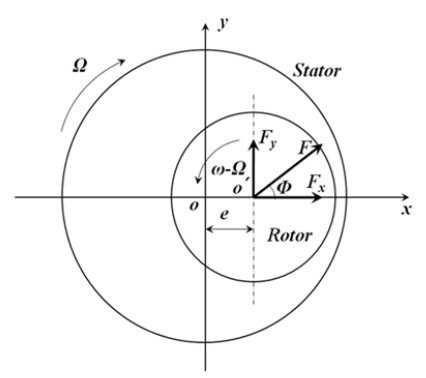
Fig. 3은 본 연구의 대상인 관통 래버린스 실의 형상을 보여주고 있다. Ha(14)의 압축기용 평실의 정상상태 해석법을 따라서 관통 래버린스 실의 정상상태 해석법을 상대좌표계를 사용하여 제시하고자 한다. 로터는 o’을 중심으로 회전각속도 ω로 회전하며 동시에 스테이터의 중심 o에 대하여 휘돌림 진폭 e와 휘돌림 각속도 Ω를 갖는 원궤적의 휘돌림운동을 하고 있는 것으로 가정한다. 관통 래버린스 실의 누설량 및 유체가진력에 기인한 동특성계수를 정확히 예측하기 위해서는 CFD 해석을 통해서 실 간극내의 원주방향과 축방향 유속분포와 정압 및 동압분포를 정확히 해석하여야 한다. 그런데 계산 영역인 실 간극이 주기적으로 변화하는 비정상상태로 해석에 많은 어려움이 있다. 따라서 계산영역이 정상상태가 되도록 Fig. 4와 같이 상대좌표계로 정의하면 계산영역은 로터의 상대 각속도가 ω-Ω, 스테이터의 상대 각속도가 -Ω인 정상상태가 된다.
3.2 래버린스 실의 동특성 계수 및 누설량
로터의 원궤적 휘돌림 운동에 기인된 실 간극내의 압력 예측 결과로부터 원주방향과 축방향 길이에 대해 적분하여 x축 유체력 성분(Fx)과 y축 유체력 성분(Fy)으로 분리하면 Eq. (1)과 같이 나타낼 수 있다. 이 유체력은 Eq. (2)와 같이 동특성계수인 강성계수(direct stiffness coefficient) K, 연성강성계수(cross-coupled stiffness coefficient) k, 감쇠계수(direct damping coefficient) C, 연성감쇠계수(cross- coupled damping coefficient) c로 나타낼 수 있다. 이 때, 작동 유체가 밀도가 작은 공기임으로 부가질량(M, m) 항을 무시하였다. x와 y는 휘돌림 각속도 Ω의 함수인 로터의 중심 위치를 나타내며,
Ω=0인 경우에 대한 실 간극내의 속도 분포 예측 결과로부터 실 입구 또는 출구 단면에 대한 적분을 통해 누설량을 구할 수 있다.
| (1) |
| (2) |
| (3) |
4. 래버린스 실의 CFD 해석
Fig. 3에 나타낸 래버린스 실의 유동장 및 압력분포를 예측하기 위해서 상용소프트웨어인 FLUENT(16)를 사용하여 3D CFD 해석을 수행하였다. 전처리장치인 ANSYS workbench(17)를 사용하여 격자를 생성하였으며, Intel i7-3930K CPU와 64GB DDR3 RAM으로 제작된 PC가 해석에 사용되었다.
4.1 3D 격자 생성
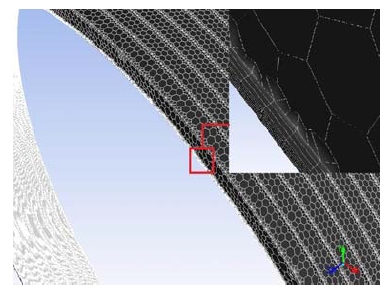
래버린스 핀은 Fig. 2에 나타낸 것처럼 끝단이 0.152mm 이며 12도 각을 갖는 사다리꼴 모양으로 설계되었다. 하지만 격자생성의 어려움과 12도 각을 갖는 핀의 주된 유동에 미치는 영향이 크지 않을 것으로 판단되어 0.152mm 두께의 사각형 핀으로 가정하였다. 계산 영역이 넓기 때문에 가능한 격자 수를 줄이는 방법으로 3D 격자를 생성하였다. 주 흐름부인 래버린스 핀 틈새부에는 육면체(hexa) 격자를 생성하였고, 공동부에는 사면체(tetra) 격자를 생성하였다. 해석 시간을 단축하기 위해서 공동부는 Fig. 5와 같이 다면체(polyhedra) 격자로 변환하였다.
벽면 근처에서의 점성 영향이 충분히 고려되도록 Eq.(4)에 정의된 y+ 값이 19∼27 범위가 되도록 벽면 근처의 격자를 중앙부의 격자 보다 더 조밀하게 생성하였다. 여기서 yp 는 벽면과 첫 번째 격자 중심까지의 거리를 나타낸다.
| (4) |
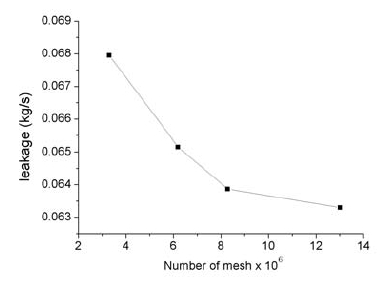
격자수에 따른 누설량, Fx/e 및 Fy/e 값의 수렴성을 체크하기 위하여 격자수 3,300,000∼13,020,000 범위에서 k-ε Standard 난류 모델을 사용한 해석 결과를 Table 2에 나타내었다. 격자수를 증가시킴에 따라서 누설량, Fx/e 및 Fy/e 값이 수렴함을 보였으며, 본 연구에서는 해석 시간을 고려하여 13,020,000개의 격자를 사용한 해석 결과와 비교할 때 3.3 % 이내의 결과를 얻을 수 있는 8,290,000개(래버린스 핀과 로터 틈새부에 6개, 공동부에 35개, 원주둘레부에 1300개)의 격자를 사용하였다. Fig. 6은 누설량에 대한 격자 수렴성을 보여주고 있다.
4.2 3D CFD 해석
본 연구에 사용된 대상 래버린스 실은 8개의 래버린스 핀으로 설계되어, 유동 영역은 8개의 래버린스 핀과 로터 사이의 제트 유동과 7개 래버린스 공동부에서의 회전유동이 있는, 매우 복잡하고 계산영역이 넓은 점이 특징이다. 따라서 해석을 위한 격자 생성 및 해석을 위한 적절한 난류 모델의 선정이 중요한 문제이다. 본 연구에서는 3D CFD 해석을 위한 기초 연구로 우선 2D CFD 해석을 통해 주어진 운전 조건에 대한 래버린스 실 내의 유동장을 검토하였다. 1,200,000개의 사각형 격자를 사용하고, k-ε Standard 난류 모델을 사용한 2D 해석 결과로부터 래버린스 핀과 로터 사이의 제트흐름이 주된 축방향 흐름을 형성하고 래버린스 공동부에 분명한 recirculation 유동이 발생됨을 확인하였다. 실 입구와 출구 부의 압력차가 2.6 bar로 비교적 크지 않아서 유속은 최대 Mach 수가 0.372 정도로 압축성의 영향이 그리 크지는 않은 비압축성 유동과 압축성 유동의 경계에 있는 것으로 판단되었다.
3D 해석시 지배방정식으로 압축성 Reynolds Averaged Navier Stokes Equations, 에너지 방정식, 이상기체방정식을 사용하였다. 적절한 난류 모델을 찾기 위해서 standard wall function을 사용한 k-ε standard(STD)모델과 Realizable k-ε 모델을 선택하고, 각 난류 모델에 대하여 pressure based solver(PBS)와 density based solver(DBS)를 사용한 해석을 수행하여 하(5)의 Bulk-flow 해석 코드(LABYSEAL.FOR) 결과와 Pelletti(15)의 실험결과와 비교 분석을 하고자 하였다.
3.2절에서 설명한 것처럼, 동특성계수를 예측하기 위해서 래버린스 실의 운전조건에 대하여 6가지의 휘돌림 각속도(Ω=0, Ω=1000, Ω=2000, Ω=3000, Ω=4000, 및 Ω=5030 rpm)에 대한 해석을 수행하였다. 수렴 기준으로는 실 입구부와 출구부에서의 질량유량이 동일하고, Fx/e와 Fy/e의 잔류항 값이 10-5 이하가 되는 시점으로 하였다. density based solver를 사용했을 경우 실제 계산시간은 약 15일이 소요되었고, pressure based solver를 사용했을 경우는 약 5일이 소요되어 수렴된 해를 얻는데 많은 시간이 필요하였다.
5. 3D CFD 해석 결과 및 비교 분석
본 절에서는 Table. 1에 제시된 test case에 대하여 본 연구의 3D CFD 해석 결과를 하(5)의 Bulk-flow 모델 해석 결과와 Pelletti(15)의 실험 결과와 비교하여 난류 모델 및 solver에 따른 영향을 분석해 보고자 한다.
Fig. 7은 3D CFD 해석 결과로 Pin=7.9 bar, Pout=5.3 bar, ω=5030 rpm, Ω=0인 경우에 대하여 DBS STD k-ε 모델을 사용한 정압력분포 결과이다. 실 입구에서 유로 단면적의 급격한 축소에 따른 압력강하를 보이고 출구 압력까지 점차적으로 감소함을 보여주고 있다.
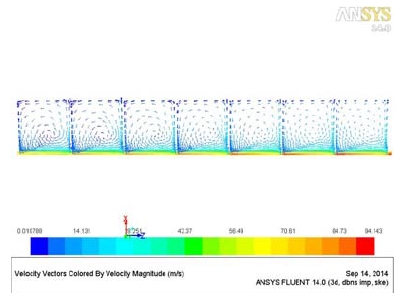
Fig. 8은 3D CFD 해석 결과로 Pin=7.9 bar, Pout=5.3 bar, ω=5030 rpm, Ω=0인 경우에 대하여 DBS STD k-ε 모델을 사용한 실 길이방향 단면에서의 유동장을 나타내고 있다. 래버린스 핀과 로터 틈새에서의 제트 흐름과 공동부에서의 recirculation 흐름이 잘 발달됨을 볼 수 있다. 누설량은 실의 입구 또는 출구 단면에서 축방향 유속을 적분함에 의해 구할 수 있다.
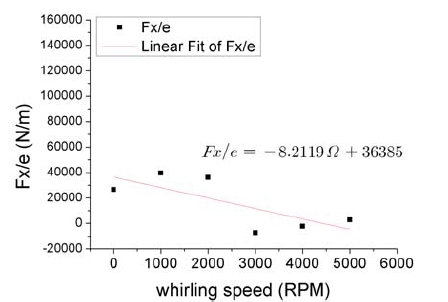
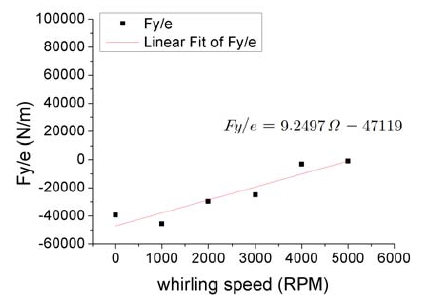
Fig. 9는 3D CFD 해석 결과로 Pin=7.9 bar, Pout=5.3 bar, ω=5030 rpm, Ω=0인 경우에 대하여 DBS STD k-ε 모델을 사용한 z=19.69mm 실 단면에 대한 압력(Pi) 분포 결과를 보여주고 있다. 평실(plain seal)에서와는 달리 래버린스 공동부가 있어서 최소 틈새부에서 최대의 압력이 발생하는 명확한 경향을 보이고 있지 않다. 이 압력을 Eq. (1)에 따라 적분하면 Fx/e 와 Fy/e이 얻어지고, Fig. 10과 Fig. 11에 나타낸 것처럼 여러 Ω에 대하여 해석한 후 Eq. (3)에 따라 curve fitting을 하면 동특성계수인 K, k, C, c를 구할 수 있다.
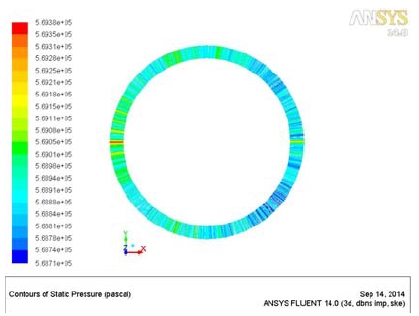
강성계수 K는 터보기계의 위험속도를 결정하는 중요한 동특성계수이며, 연성강성계수 k는 터보기계의 불안정화 영향을 주는 요소이고 감쇠계수 C는 안정화 영향을 주는 요소로 터보기계의 진동 안정성 해석에 중요한 동특성계수들이다. Table 3은 본 연구에서 수행한 해석 결과와 Bulk flow 모델 및 실험결과의 비교를 나타내고 있다.
누설량 예측에 대하여 Bulk flow 모델 해석의 경우는 실헙값에 비하여 6.18 % 크게 예측됨을 보였으나 3D CFD 해석의 경우에는 난류모델 및 solver에 따라서 16.12 %∼49.5 % 크게 예측됨을 보였다. DBS STD k-ε 모델을 사용할 경우가 실험값에 가장 근접된 결과를 보였다.
강성계수 K의 예측에 대하여 Bulk flow 모델 해석의 경우는 실헙값에 비하여 74.47 % 작게 예측됨을 보였으나 3D CFD 해석의 경우에는 난류모델 및 solver에 따라서 7.13 % ∼55.89 % 작게 예측됨을 나타내 개선된 결과를 보였다. DBS STD k-ε 모델을 사용할 경우가 실험값에 가장 근접한 결과를 보였다.
연성강성계수 k의 예측에 대하여 Bulk flow 모델 해석의 경우는 실헙값에 비하여 236.8 % 작게 예측됨을 보였으나 3D CFD 해석의 경우에는 난류모델 및 solver에 따라서 334.2 %∼729.7 % 작게 예측됨을 나타내 더 큰 오차 결과를 보였다. PBS Realizable k-ε 모델을 사용할 경우가 실험값에 가장 근접한 결과를 보였다.
감쇠계수 C의 예측에 대하여 Bulk flow 모델 해석의 경우는 실헙값에 비하여 77.93 % 작게 예측됨을 보였으나 PBS Realizable k-ε 모델을 사용한 3D CFD 해석의 경우는 98.19 % 작게 예측됨을 보였고 STD k-ε 모델을 사용한 해석에서는 부호가 반대인 음의 감쇠계수를 예측하고 있어 개선됨을 보이지 못하고 있다.
6. 결 론
본 연구에서는 압축성 유체를 작동유체로 사용하는 터보기계의 관통 래버린스 실에 대한 누설량 및 동특성계수 예측을 위해 상용소프트웨어를 사용한 3D CFD 해석방법을 제안하고, solver와 난류 모델에 따른 영향을 분석하였다. CFD 해석 결과를 Bulk-flow 모델 해석 및 실험 결과와 비교하면 다음과 같다.
(1) Pressure based solver를 사용할 경우가 수렴된 해를 얻기까지 걸리는 실제 계산시간이 density based solver를 사용했을 경우의 약 1/3로 빠른 해를 얻을 수 있었다.
(2) 누설량의 경우 3D CFD 해석 결과는 실험결과와 Bulk-flow 모델 결과 보다 크게 예측되는 경향을 보였으며, DBS STD k-ε 모델을 사용할 경우가 실험값에 가장 근접된 결과를 보였다.
(3)강성계수(K)의 경우 3D CFD 해석 결과는 Bulk-flow 모델 해석 결과보다 개선됨을 보여 DBS STD k-ε 모델을 사용할 경우는 실험결과와 7.13% 이내의 오차를 나타내었다.
(4)연성강성계수(k)와 감쇠계수(C)의 경우 3D CFD 해석 결과는 대체적으로 Bulk-flow 모델 해석 결과보다 큰 오차를 보여 개선됨을 보여주지 못하였다.
(5)본 연구 대상의 관통래버린스 실에 대하여, 동특성계수 예측에는 PBS Realizable k-ε 모델 해석 결과가 대체적으로 실험 결과와 일치하는 경향을 보였다.
본 연구는 점점 복잡한 형상으로 설계되고 있는 래버린스 실의 해석에 Bulk-flow 모델 해석의 한계성을 극복해 보고자 3D CFD 해석법을 제시한 것으로, 일부 동특성계수의 예측만이 개선된 결과를 보여주었다. 이는 계산영역이 넓어 생성된 격자수가 많고, 압축성 유동으로 적절한 난류 모델 선정과 수렴된 해를 얻기까지 긴 시간이 소요되는 등 여러가지 어려운 점이 많아 향후 격자 생성법 및 해석법에 개선의 여지가 남아 있다. 그렇지만 향후 다양한 형상의 래버린스 실 해석에 3D CFD 해석의 적용 가능성을 보여주었다고 사료된다.
Acknowledgments
본 연구는 2014년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20131010101770)
References
-
Hirs, G. G., (1973), "A Bulk-flow Theory for Turbulence in Lubricating Films", ASME Journal of Lubrication Technology, 105, p137-146.
[https://doi.org/10.1115/1.3451752]

-
Alford, J. S., (1965), “Protecting Turbomachinery from Self-Excited Rotor Whirl", ASME Trans. Journal of Engineering for Power, October, p333-344.
[https://doi.org/10.1115/1.3678270]

- Iwatsubo, T., (1980), “Evaluation of Instability Forces of Labyrinth Seals in Turbines or Compressors", NASA CP 2133 Proceedings of a workshop at Texas A&M University 12-14 May Entitled Rotordynamic Instability Problems in High Performance Turbomachinery, p139-167.
- Scharrer, J., (1987), "A Comparison of Experimental and Theoretical Results for Labyrinth Gas Seals", Ph. D. Dissertation, Texas A&M University.
- 하태웅, (1999), “Moody 마찰계수식을 사용한 래버린스 실의 회전체 동역학적 해석,”, 유체기계저널, 2(3), p52-58.
- Scharrer, J. K., (1988), "Rotordynamic Coefficients for Stepped Labyrinth Gas Seals", ASME/ASLE Tribology Conference, Paper No. 88-Trib-42.
- Ha, T. W., (2001), "Rotordynamic Analysis for Stepped-Labyrinth Gas Seal Using Moody's Friction-Factor Model", KSME International Journal, 15(9), p1079-1089.
- 하태웅, (2002), “엇갈린 래버린스 실의 누설량 및 동특성 해석,”, 윤활학회지, 18(1), p24-33.
- 하태웅, (2006), “CFD를 사용한 복잡한 형상을 갖는 래버린스 실의 누설량 예측,”, 윤활학회지, 22(2), p66-72.
- 하태웅, (2006), “CFD를 사용한 터보기계 비접촉식 실의 누설량 예측”, 유체기계저널, 9(3), p14-21.
- Rao, J. S., and Saravanakumar, M., (2006), "Numerical Simulation of Seal Flow and Determination of Stiffness and Damping Coefficient", IFToMM-Conference on Rotor Dynamics, p25-28.
- Ha, T. W., and Choe, B. S., (2012), “Numerical simulation of rotordynamic coefficients for eccentric annulartype- plain-pump seal using CFD analysis”, Journal of mechanical science and technology, 26(4), p1043-1048.
-
Kirk, G., and Gao, R., (2012), “Influence of pre-swirl on rotordynamic characteristics of labyrinth seals”, Tribology transactions, 55(3), p357-364.
[https://doi.org/10.1080/10402004.2012.656880]

- Ha, T. W., and Choe, B. S., (2014), “Numerical prediction of rotordynamic coefficients for an annular-typeplain-gas seal using 3D CFD analysis”, Journal of mechanical science and technology, 28(2), p505-511.
- Pelletti, J. M., (1990), “A comparison of experimental results and theoretical predictions for the rotordynamic coefficient of short(L/D=1/6) labyrinth seals”, Texas A&M University, TL-SEAL-1-90.
- FLUENT User's Guide Ver. 14.0.
- ANSYS workbench User's Guide Ver. 14.0.