A Comparison of Performance of Six and Twelve-Blade Vane Tidal Turbines between Single and Double Blade-row Types
Abstract
This paper presents a study on Vane Tidal Turbine (VTT) focusing on analysis of two types of blade arrangement originated from the previous studies where the original design was examined and performance-tested for different numbers of blades (six, eight and twelve). Compared to conventional tidal turbines, VTT has several special features and potential advantages which have been being thoroughly developed. The purpose of this study is to analyze VTT’s capability of extracting and converting the hydrokinetic energy of tidal currents into electricity at given arrangement of blades (single and double rows, six and twelve blades) using CFD. From the calculation results, the six-blade single row turbine shows the best performance, in which the highest power and torque coefficients reach up to about 34 % and 36 %, respectively, at TSR=0.94. However, despite of lower power coefficient, by adding more blades, the torque’s extraction of twelve-blade turbine, especially the double row type, is less fluctuate than that of the six-blade setups.
Keywords:
Vane tidal turbine (VTT), CFD, Power coefficient, Blade-row, Torque coefficient키워드:
베인형 조류터빈, 전산유체역학, 동력계수, 블레이드 열, 토크계수1. Introduction
One of the greatest challenges in this century is to produce sufficient energy. The increase in world population and the continuous economic growth in many countries require more access to energy. The U.S.A department of energy projects predicted that global energy demands will increase by 20 % by 2025. The decrease in coal and oil resources and the global warming problem created an increasing need for sustainable alternative energy resources.
The oceans, which cover more than two-thirds of our planet, offer an incredible store of energy. One of the forms of energy within the oceans is that resulting from the gravitational effects of the planetary motions of the Earth, the Moon and the Sun, which produce the tides that drive strong marine currents. Tides possess both potential and kinetic energy. Tidal energy can be utilized by capturing potential energy i.e., by means of tidal barrage and tidal fence, or by capturing kinetic energy i.e., by means of tidal current turbines. The research on tidal energy is underway around the globe (Setoguchi et al., 1993; Setoguchi et al., 2001; Vijayakrishna et al., 2004), and the technology has been tested in many countries (Korde, 1991; Osawa et al., 2002; Clement et al., 2002). At present, there are many kinds of tidal current energy conversion devices which have been being powerfully developed by researchers from many countries all over the world, such as propeller type turbines, Darrieus types turbines, and so on.
A research on water wheel turbines using Computational Fluid Dynamics (CFD) simulation(1), which was done for two kinds of blade’s shape (triangle and rectangle) including the effect of number of blades (four and six), indicated that the triangular blade design shows weak performance compared to rectangular one (about 30 % reduction in efficiency). Therefore, derived from the design of water wheels that are used to harness the energy available in natural water source like rivers and waterfalls, we have been developing new type of horizontal axis tidal turbine that is similar to water wheels structure but is optimized for tidal applications. This turbine is named Vane Tidal Turbine (VTT) as its structure featured and is planned to be installed to areas with a high potential of tidal energy, such as banks, estuaries and so on. From the simulation results in previous study on single VTT with different blade numbers (six, eight and twelve)(2), the six-blade type showed its impressive performance in which the highest power coefficient reaches up to 34 % comparing to the others.
The aim of this study is to evaluate VTT’s performance for various rotor-blade arrangements using CFD. The rotor can be either single row or double rows and the number of blade can be six or twelve. Each setup is calculated at various tip-speed ratios (TSR). By analyzing the power coefficient and torque coefficient values, an optimum arrangement can be found.
2. Turbine Design
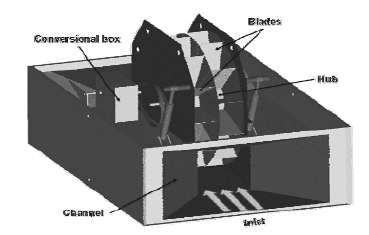
According to water turbine classifications(3,4), VTT can be classified in the group of in-plane turbines which are generally drag based devices (the blade speed is less than water speed) and said to be less efficient than their lift-based counterparts (the blade is faster than the water)(5). Figure 1 shows the experimental model in test bed. VTT has just one moving part (it can be called by “wheel” or “rotor”) which rotates around a horizontal axis. The wheel has two major components:
Model of VTT
-The central hub:This is a horizontal cylinder which is connected to the driven shaft of the current conversion equipment.
-Rotor blades:The blades are the surfaces on which the water’s energy is extracted. These thin rectangular blades are placed in radial position from the hub. There are two types of blade’s arrangement: single row and double rows in which blades are put in staggered formation.
Stationary part is equipped with auxiliary and supporting machineries, including:
-Conversional equipment:This is connected to the shaft located in the central hub through a belt transmission and a gear box. It is used to convert the hydrokinetic energy of the tidal streams into electricity.
-Channel:It provides a mounting for wheel bearings and other parts. The inlet of the channel is narrowed to increase inflow velocity based on De Laval’s law. The outlet of the channel also has the same geometry as the inlet.
The design parameters for modeling in computational simulation are summarized as shown in Table 1.
Design parameters
3. Theory and Numerical Method
3.1 Theory
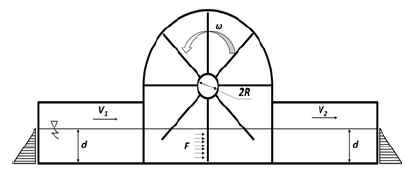
At a depth of water, d with density, ρ of water, under the influence of gravity, g, the pressure P can be defined as follows(6):
| (1) |
Referring to Fig. 2, consider a simple vertical plate which is submerged in water with the depth, d. The triangles represent the hydrostatic pressure. The forces acting on either sides of this plate (its width, w) are F(6):
| (2) |
Operating principle of VTT
If it is now imagined that the plate moves laterally with velocity, V, the power at the plate available from water flow, Pa, is:
| (3) |
Where A is the cross section area of the plates submerged in water under consideration (m2):
| (4) |
The water wheel converts a part of this power to the shaft’s power, Pshaft(1):
| (5) |
Where CP is the power coefficient of the wheel and represents the ratio between the power output from the wheel and power available in the water. Not all of the available power is converted into the shaft power by the wheel. Leaving water should have sufficient kinetic energy to continue its way outside the wheel. The above equations show that the power output from the wheel depends on the power available in the water and the efficiency of the wheel.
In order to analyze the turbine’s performance at different rotational speeds, the runner’s velocity is normalized by the incoming water velocity and a non-dimensional parameter, called “tip-speed ratio” (λ), is used and defined as follows(7):
| (6) |
Where R is rotor’s radius (mm), ω is rotational speed (rad/s), Vin is inflow velocity (m/s). Tip speed ratio is related to the efficiency, and in this paper, the study is carried out with a range of TSRs by varying the cut-in velocity, as shown in Table 2.
Testing Range
3.2 Modeling and Meshing
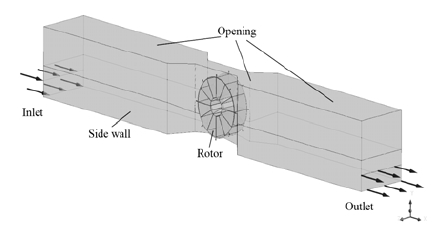
A three-dimensional model of this turbine and its flow field are generated and numerically discretized in computational simulation. Power performance and characteristics of VTT are calculated using CFD commercial code, ANSYS 14. Meshing is done using ICEM CFD. Hexahedral grids are used and the mesh contains 313,000 nodes for the stator part (inlet, outlet, bedplate, side walls). In all cases, the device’s sizing is maintained. For double row rotor setup, both blade rows are equally divided and have the same width.
Totally, there are four options available for blade arrangement, the same mesh strategy is applied for all cases resulted in relatively similar total number of nodes, about 830,000. Figure 3 illustrates the mesh formation for the stationary frame of the calculation domain. Figures 4 and 5 show the mesh formation for six and twelve-blade turbines, respectively, with two types of blade arrangement (single and double rows).
Mesh formation for stator
Mesh formation for rotor of 6-blade turbine
3.3 Calculation Domain and Boundary Conditions
The computational domain is shown in Fig. 5. Two ends of the channel (inlet and outlet) are lengthened ten times as many as the runner’s width. This is sufficient for computational simulation and capable of capturing the wake characteristics. Inlet boundary is set to “Cartesian velocity components”, outlet boundary is average static pressure, and opening boundary condition is “Opening pressure and direction”. The blades, hub, channel, bedplate and side walls are all no-slip wall boundaries. The mesh connection between the rotating and stationary frames is general connection interface boundaries, and is set to “Transient rotor stator”. The working fluid are defined as sea water and air at 25 oC. Turbulence model is shear stress transport (SST), with turbulence intensity set to 5% for the whole flow-field. Simulation is done in transient by ANSYS CFX Solver. Time step is set depending on the rotational speed to effectively get convergency.
Mesh formation for rotor of 12-blade turbine
Computational domain
4. Results and Discussions
4.1 Flow Patterns Analysis
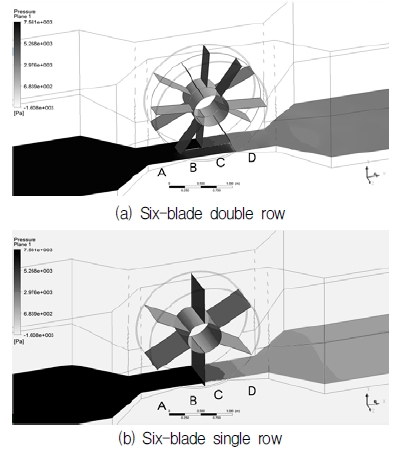
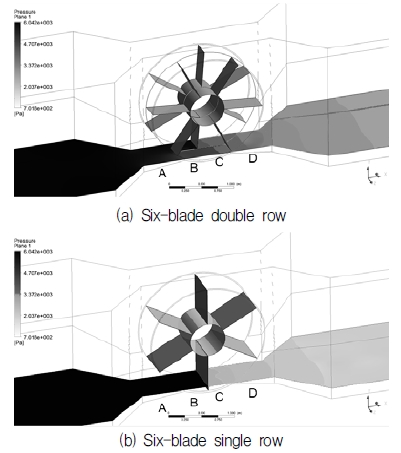
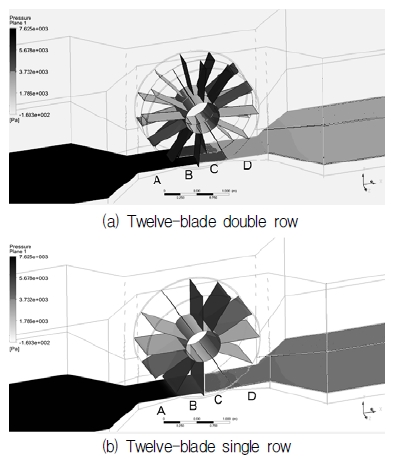
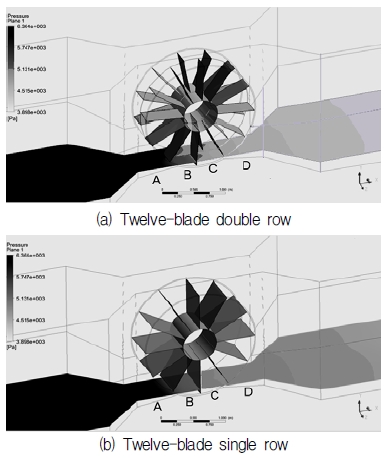
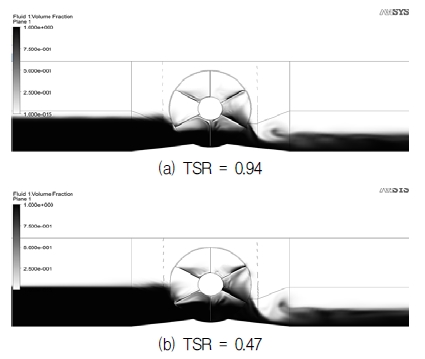
The visualizations of averaged pressure distribution for the six and twelve-blade VTTs with two kinds of blade arrangement at different TSRs are shown in Figs. 7 to 10. These figures present the surfaces of pressure contours which are distributed over the length of the channel from inlet to outlet. In all cases, the view of averaged pressure distribution is oriented from the left (high pressure side, darker color) to the right (low pressure side, lighter color), the area in grey scale illustrates the variance of fluid pressure within the range. The pressure contours plane is marked as four regions: A, B, C, D. Region A illustrates the averaged pressure value distributed from the inlet of the channel to the entrance of rotor, where water is about to contact with the blades. Regions B and C show the averaged pressure distribution of water stream in the spaces between two adjacent blades. And the last one, region D, is where water flows out of rotor and keep flowing to the outlet.
Averaged pressure distribution of six-blade at TSR=0.47
Averaged pressure distribution of six-blade at TSR=0.94
Averaged pressure distribution of twelve-blade at TSR=0.47
Averaged pressure distribution of twelve-blade at TSR=0.94
Figures 7 and 8 show averaged pressure distribution for six-blade type at TSR=0.47 and TSR=0.94, respectively. As shown in Fig. 8, at TSR=0.94 (lowest cut-in speed), it is obvious that the difference in pressure color for single row type between region A and region D is relatively more distinguished than that of the double row type. It means that there is more considerable amount of available energy in outflow water passing through the double row type VTT. In the other words, the water current energy is absorbed effectively by the single row turbine in comparison with the double row type for the same number of blades. At the lowest TSR (highest cut-in speed) as depicted in Fig. 7, the color of pressure from region A to region D in either double or single row rotors does not change as much as at TSR=0.94..
Figures 9 and 10 illustrate averaged pressure distribution for twelve-blade turbines at various TSRs. On the contrary to the six-blade arrangements as analyzed above, the twelve-blade single row turbine has a lower capacity of water flow energy than the twelve-blade double row one. Besides that, in all cases of TSR for twelve-blade turbine, the difference in pressure color of the single and double row types between the region A and the rest, especially at TSR = 0.47, is not as clear as that of the six-blade designs at the same TSR.
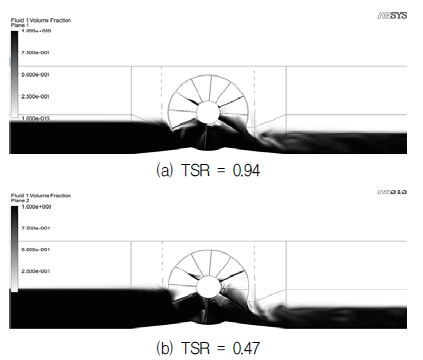
Figures 11 and 12 show the comparison of water volume fraction, which also discovers the behavior of water flow for six and twelve-blade single row turbines. In these figures, it can be clearly seen that at TSR=0.94 (1 m/s and 10 rpm), the water elevation at all types of VTT has the same rate. However, at TSR=0.47 (2 m/s and 10 rpm), water flow has a tendency to ascend and accumulate abnormally, right in front of the entrance of rotor, consequently the water level rise slightly higher than that to be seen at higher TSRs. It can be explained that due to low revolution of the rotor and is kept constant at 10rpm, at higher TSR (lower inflow velocity) the amount of water running throughout the rotor is more regular and it will reduce the formations of some profitless phenomena, such as back flows, local vortexes, etc. These phenomena will increase the energy losses, prevent the incoming flows from approaching the turbine’s blades, and reduce the power efficiency of the device. For six and twelve-blade double row types, the abnormal surge of water level occurs similarly to the six and twelve-blade single row cases.
Water volume fraction for six-blade single row type
Water volume fraction for twelve-blade single row type
4.2 Turbine Efficiency
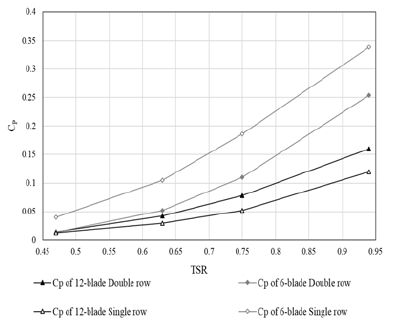
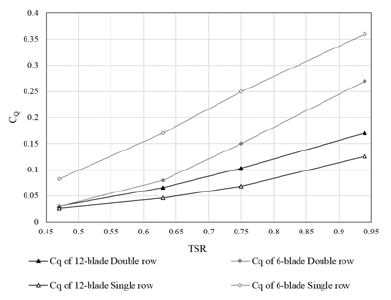
Power performances of VTT are evaluated by power coefficient Cp and torque coefficient Cq which were calculated and expressed in Figs. 13 and 14, respectively. The figures express Cp and Cq as a function of inflow velocity, and show the performances of two configurations of VTT with different blade arrangement (single and staggered blade rows). The study is carried out with a various TSRs by varying the inflow velocity from 1 to 2 m/s within sufficiently long revolutions of the wheel.
Power coefficient as a function of TSR
Torque coefficient as a function of TSR
Both graphs of Cp and Cq show the same patterns which are inclined to rise up from the lowest to the highest TSRs. According to the results depicted in Fig. 13, the power coefficient of six-blade single row type achieves the highest value than that of six-blade double row one. At TSR=0.94 (the biggest cut-in speed), this type reaches up to 33.8% Cp which is about eight and a half times as high as the value at TSR=0.47. Conversely, for twelve-blade turbine, the double row type generates the highest of Cp in comparison with the single one. The highest power coefficient absorbed from this turbine obtains 16% at TSR=0.94, meanwhile, the single row type just attains 12 %. In addition, it is obvious that at lower TSRs (higher cut-in speeds), all kinds of VTT show their worst performance since the power extracted from the blades is extremely low as well as the power coefficient. Similar to the power coefficient chart, as shown in Fig. 14 of torque coefficient that is a similar non-dimensional analysis for the torque(8), the six- blade single row turbine keeps showing its predominant performance comparing to the others at various TSRs. It means that the torque extracted from the rotor’s shaft of this turbine always gets greater than the other kinds of VTT. On the contrary, the tidal current energy conversion capability of the twelve-blade single row type is the smallest compared to the others at the same TSR, as the generated torque coefficient of this kind only achieves 12.6 % which is three times as low as the six-blade single row type, at the greatest cut-in speed (TSR=0.94).
These results in turbine efficiency are reasonable to characteristics of flow patterns (including pressure contours and water volume fractions) analyzed above, where high efficiency is found at the cases with obvious change in pressure of water flow before and after the wheel, and lower water level at higher TSR (lower inflow velocities).
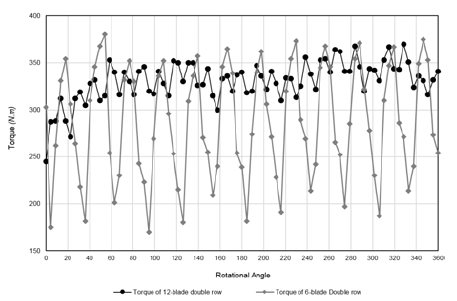
As shown in Fig. 15, it illustrates the variation of torque extracted at the rotor’s shaft due to the water flow acting on the blades at TSR=0.94 for six and twelve-blade double row turbines. The results of six- blade Double row turbine show that when submerged in the water, one blade needs to be inclined with at least 4.5 degrees angle to start contributing to the torque’s generation. The blade contributes by producing torque until 18 degrees; after that, the contribution becomes negative. That means the blade will be active for 13.5 degrees of the 36 degrees inside the water. By adding more blades, more torque generated from the turbine will be improved by contributing to the positive torque(1). The torque’s extraction in one revolution of the wheel (360 degrees rotational angle) for twelve- blade double row type is more continuous and the number of blades takes part into generating torque is more than the other types of VTT.
Torque generation in one revolution
5. Conclusions
This paper introduces a computational evaluation of a tidal current conversion device with two kinds of blade numbers (six and twelve blades) and two blade arrangements. To sum up, the following conclusions are given.
1) Torque and power extractions of the twelve-blade double row turbine are greater than the twelve- blade single row one at higher TSRs, especially at TSR=1.89.
2) The six-blade single row turbine shows its predominant performance comparing to the other types of VTT in this study. At various TSRs, the six-bladed type obtains the highest power coefficient and torque coefficient, especially reaching up to 33.8% power coefficient and 36% torque coefficient at TSR=0.94.
3) Despite of lower power coefficient than six-blade turbines, by adding more blades, the torque’s extraction of twelve-blade turbine, especially the twelve-blade double row type, is more continuous, since the number of blades takes part into generating torque is more than the other types of VTT.
Notes
References
- Ali, A. S., (2010), “Water Wheel CFD Simulations”, Division of Fluid Mechanics, Lund University, p12-40.
- Nguyen, M. H., Hoang, A. D., and Yang, C. J., (2014), “Evaluation of Vane Tidal Turbine’s Performance and Comparison of Efficiency among Six-blade, Eight-blade and Twelve-blade Types”, The Korean Society of Marine Engineering.
- Sornes, K., (2010), "Small-scale Water Current Turbines for River Applications”, Zero Emission Resource Organization, p6-7.
-
Khan, M. J., Bhuyan, G., and Iqbal, M. T., (2009), “Hydrokinetic Energy Conversion Systems and Assessment of Horizontal and Vertical Axis Turbines for River and Tidal Applications”, Appl. Ener., 86, p1823-1835.
[https://doi.org/10.1016/j.apenergy.2009.02.017]
- Khan, M. J., (2006), “In-stream Hydrokinetic Turbines”, Hydro volts institute Power. Tech. Labs, p3-4.
- James, S., Patrick, W., and Gerald, M., (2008), “The Rotary Hydraulic Pressure Machine for Very Low Head Hydropower Sites”, University of Southampton, p2-4.
- Nasir, M., Zhang, L., and Khan, J., (2012), “Diffuser Augmented Horizontal Axis Tidal Current Turbines”, p4-5.
- Mason-Jones, A., O’Doherty, D. M., Morris, C. E., O’Doherty, T., Byrne, C. B., Prickett, P. W., Grosvenor, R. I., Owenb, I., Tedds, S., and Poole, R. J., (2012), “Nondimensional Scaling of Tidal Stream Turbines”, UK, p1-3.