[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 18, No. 1, pp.65-71

ISSN: 2287-9706 (Print)

Print publication date Feb 2015

Received 29 Sep 2014 Accepted 04 Nov 2014

DOI: https://doi.org/10.5293/kfma.2015.18.1.065

Cavitating Flow Analysis of Multistage Centrifugal Pump

Rakibuzzaman^* ; Sang-Ho Suh^*^{, †} ; Hyoung-Ho Kim^* ; Min-Tae Cho^** ; Byeong-Rog Shin^***

*Department of Mechanical Engineering, Soongsil University, 156-743, Korea
**Dooch Co. 295 Sagok-ri, Gyeonggi-do, 445-942
***Institute of Flow Informatics, Korea

다단 원심펌프의 공동현상 유동해석

라키부자만^* ; 서상호^*^{, †} ; 김형호^* ; 조민태^** ; 신병록^***

Correspondence to: ^† suhsh@ssu.ac.kr

Abstract

The purpose of this study is to investigate cavitating flow of the multistage centrifugal pump. Cavitation is observed in the impeller leading edge and trailing edge of the suction area. Head coefficients are measured under different flow operating conditions. The Rayleigh-Plesset cavitation model is adapted to predict the occurrence of cavitation in the pump. The two-phase gas-liquid homogeneous CFD method is used to analyze the centrifugal pump performances with two equation transport turbulence model. The simulations are carried out with three different flow coefficients such as 0.103, 0.128 and 0.154. The occurrence of cavitation described according to water vapor volume fraction. The head versus NPSH (Net Positive Suction Head) also measured using different flow coefficients. Development of cavitation in the centrifugal pump impellerI is discussed. It is showed that the simulation represents the head drop about 3%.

Keywords:

Cavitating flow analysis, CFD, Homogeneous model, NPSH, Vapor volume fraction

키워드:

공동현상 유동해석, 전산유체역학, 균질모델, 유효흡입수두, 증기체적분율

1. Introduction

Cavitation generally occurs if the pressure in a certain region of liquid flow drops below the vapor pressure and, consequently, the liquid is vaporized and filled with cavity⁽¹⁾. The cavitating flow is usually observed in various propulsion systems and high-speed underwater objects, such as marine propellers, impellers of turbomachinery, hydrofoils, nozzles, torpedoes, etc. This phenomenon usually causes severe noise, vibration and erosion^(2-3). Therefore, in order to reduce these unfavorable effects, technology for accurate prediction and estimation of cavitation are very important in the development of high-speed fluid devices⁽⁴⁾. Due to the importance of the cavitation phenomenon and the great process in the cavitation and turbulence models, numerical simulations have been widely used to investigate the cavitation flow field in the pumps^{(5 ~ 9)}. In order to clarify and understand the behavior of cavity flow, cavity flow models and analytical methods for numerical simulations have been proposed^{(10 ~ 13)}. Potential flow methods have been employed for decades to model large cavities in a variety of liquid flow systems including pumps^(5,14).

The CFD plays an important role in the flow field analysis; the advanced commercial CFD software can be used for a wide range of flows, including the cavitating flows^{(15 ~ 17)}. Over the last decade, due to the advancement of the physical modelling and the computational capabilities for cavitating problems, the methods based on the Navier-Stokes equations in computing cavitating flows have received increasingly more attention. These

methods are divided into the following three main categories: the interface tracking method⁽¹⁸⁾, the barotropic equation method^(19,23), and the two equations transport method (TEM)^{(20 ~ 22)}. Among them, the two equations TEM is most widely used strategy, where the flow is treated as a two-phase system with mass transfer between the vapor and liquid phases. In these models, either the simplified Rayleigh-Plesset (R-P) equation^{(20 ~ 22)}, or the empirical formula⁽²¹⁾ are used to establish the interphase mass transfer rates. The mechanisms for cavitation have been extensively investigated^{(23 ~ 24)}, and noticeable efforts have been made on the cavitaion and turbulence models for the simulation of cavitating flow⁽⁸⁾. However, it is difficult to predict accurately cavitation flow simulation in the complex geometry centrifugal pumps. The present study of this paper is focused on the cavitation performance in the centrifugal pump impeller, the development of the cavitation at the suction leading edge of the impeller. In the numerical prediction, the Singhal⁽²⁰⁾ proposed R-P cavitation model, and a two-phase homogeneous gas-liquid CFD method are used. The simulations are carried out with three different flow coefficients such as 0.103, 0.128, and 0.154. The head drop curves are calculated to predict the cavitating performance under cavitation model. In addition, a detailed analysis is accomplished in the vapor volume fraction.

2. Mathematical Model and Numerical Method

The fluid in the cavitating flow field for the pump is considered as a homogeneous, compressible mixed medium of vapor and liquid. The governing differential equations are given as Eq.(1),(2);

∂ ρ m ∂ t + ∂ (ρ m u j) ∂ x j = 0

(1)

∂ (ρ m u i) ∂ t + (∂ ρ m u i u j ∂ x j) = - ∂ p ∂ x i + ∂ ∂ x j [μ + μ t (∂ u i ∂ x j + ∂ u j ∂ x i - 23 ∂ k i ∂ x k δ i j)]

(2)

Where ρ_m and μ are the mixture density and dynamic viscosity, calculated by the weighted average of each phase volume fraction, u is the velocity, p is the pressure, and μ_t is the turbulent viscosity respectively and subscripts i, j, k denotes the axes directions. Mixture density and turbulence viscosity are defined by Eq.(3):

ρ m = ρ l α l + ρ υ (1 - α l), μ t = ρ m C μ k 2 ɛ

(3)

The fluid density is a function of vapor mass fraction f_v, which is computed by solving a transport equation coupled with the mass and momentum conservation equations. Here, the cavitation model proposed by Singhal et al.⁽²⁰⁾. The mixture density is as

1 ρ m = f υ ρ m + f g ρ g + f l ρ l = f υ ρ m + f g ρ g + 1 - f υ - f g ρ l

(4)

f υ = α υ ρ υ ρ m, f g = α g ρ g ρ m, f l = α l ρ l ρ m = 1 - f υ - f g

(5)

Where f_v, f_g, f_l are the component mass fraction of the vapor, gas, and liquid; ρ_v, ρ_g, ρ_l are the component densities, and α_v, α_g, α_l are the volume fractions. The vapor mass fraction f, is governed by a transport equation

∂ ∂ t (ρ m f υ) + ∇ ⋅ (ρ υ f m u i) = ∇ ⋅ (Γ ∇ f m) + R e - R c

(6)

The source term Γ is the diffusion rate, R_e and R_c represents evaporation and condensation respectively and can be functions of flow parameters (pressure, flow velocity) and fluid properties (liquid and vapor phase densities, saturation pressure, and liquid-vapor surface tension). The formation and collapse of a cavity is modeled as a phase transformation. Mass transfer is modeled as finite rate interfacial processes as Eq.(7):

R e = C e k σ ρ l ρ υ [23 p υ - p ρ l] 12 (1 - f υ - f g) R c = C c k σ ρ l ρ υ [23 p υ - p ρ l] 12 f υ

(7)

The recommended values of the empirical factor constants C_e and C_c for 0.02 and 0.01 the gas mass fraction f_g=1.5x10-5, the surface tension coefficient σ=0.0717 N/m, p_v denote vaporization pressure, and k is the turbulent kinetic energy. if p<p_v evaporation occurs and if p>p_v condensation occurs. The k-ω based SST model accounts for the transport of the turbulent shear stress and highly accurate predictions of the onset and the amount of flow separation under adverse pressure gradients^{(16 ~ 17)}. The unknown turbulent viscosity μ_t is determined by solving two additional transport equations for the turbulent energy k, and for the turbulence frequency ω. These two equations can be written as Eq. (8, and 9)

k-equation:

∂ (p k) ∂ t + ∂ ∂ x j (∂ k u i) = ∂ ∂ x j [(μ + μ t σ k)] ∂ k ∂ x j + P k - β ′ ρ k ω + P k b

(8)

ω-equation:

∂ (ρ ω) ∂ t + ∂ ∂ x j (∂ ω u i) = ∂ ∂ x j [(μ + μ t σ ω)] ∂ ω ∂ x j + α ω k P k - β ρ k ω 2 + P ω b

(9)

Where, P_k is the production rate of turbulence, μt is the turbulent viscosity, α, β, β', σ_k and σ_ω are constants.

3. Computational Methodology

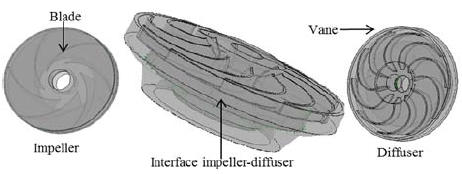
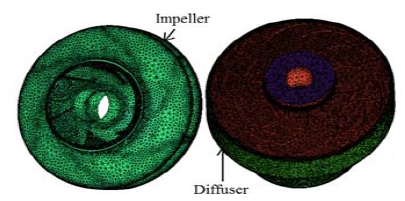
The model pump of impeller and diffuser were meshed using ANSYS ICEM-CFX (Ansys Inc., 2012, USA) based on the control volume-based finite element method (FEM). The strategy in the ANSYS-CFX is very robust and efficient in predicting the changing flows in the turbomachinery. The pump model impeller-diffuser domain, inlet, and outlet casing which were performed on the unconstructed prism tetrahedral cells generated by ICEM-CFD which is shown in Fig. 1. Impeller domain was as rotating part with y-axis and the rotational speed was 3600 rpm, and diffuser was considered as stationary domain. A frozen rotor was applied to couple the rotation and stationary domains. The impeller-diffuser domain is shown in Fig. 2. A commercial CFD code CFX with SST model was used ^{(25 ~ 27)}. The boundary conditions of pump model considered as static frame total pressure at inlet and mass flow rate at outlet under cavitation condition. Generally the boundary of inlet and outlet is same as under non cavitation condition. As the wall boundary condition, no slip condition is on the wall surface. The volume fraction of the vapor and the water are assumed to be 0 and 1 respectively. A steady state analysis is performed in the pump simulation with the given rotational speed at 3600 rpm and the given mass flow rate.

Fig. 1

Impeller-diffuser domain interface

Fig. 2

Meshing of impeller and diffuser of pump

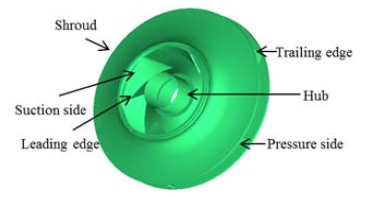
Fig. 3 shows the front view of the impeller and name of various sections, used in the analysis of the cavitation simulation results. Table 1 shows the geometry specification of the centrifugal pump for simulation.

Fig. 3

Front view of the impeller and name of various sections

Table 1

Pump important design specification

4. Results and discussion

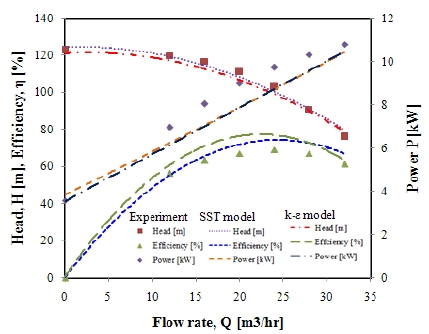
The single-phase experimental and computational performances curves are shown in Fig. 4. The computational simulation is done by SST turbulence model. The SST model can be given the more accurate results than the other turbulence model such as k-ɛ shown in Fig. 4. So, in the cavitation analysis we used k-ω based SST turbulence model. The average deviation for the head is only 5.34%. The efficiency is only 8.22%, respectively. So the numerical simulation results follow the trend to experimental results. For the cavitation conditions, the static pressure is imposed upstream and flow rate downstream. The different NPSH values are obtained by vapor pressure Pv involved in the definition of net positive suction head while the upstream pressure is kept constant. NPSH is the total head of the fluid at the center line of impeller-above the vapor pressure of the fluid, and can be regarded as a measure for the margin against vaporization of the fluid entering the pump ⁽²⁸⁾. The NPSH is defined as Eq.(10)

Fig. 4

Comparison of experiment and computational head, efficiency and power versus flow rate

N P S H = P i n - P υ ρ g

(10)

Where p_in is the static pressure at the pump inlet, pv is the vapor pressure depends on the liquid temperature. Pump head H is the difference in total energies at pump inlet and outlet, and it is formulated as Eq. (11)

H = p 2 - p 1 ρ g + V 22 - V 12 2 g + (z 2 - z 1)

(11)

Where p₁ and p₂ are the pressure of suction and discharge of the pump; v₁ and v₂ are the velocities of the inlet and outlet of the pump; and z₁ and z₂ are the elevation of the pump system. In what follows, three dimensionless parameters are used to define the pump operating points and performance of the curve, namely, flow coefficient ϕ, head coefficient ψ, and cavitation number σ, ⁽²⁹⁾ defined as Eq. (12)

ϕ = Q π D 2 b 2 U t i p, ψ = H U t i p 2 2 g, σ = p i n - p υ 0.5 ρ l U t i p 2

(12)

Where p_in is the static pressure at the pump upstream, H is the pump head, U_tip is the impeller peripheral speed.

4.1. Effect of NPSH

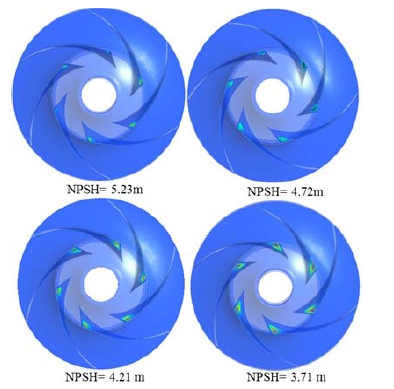
Fig. 5 shows a qualitative comparison of the NPSH value under different NPSH values (5.23m, 4.27m, 4.21m, and 3.71m). The simulated ones are predicted using SST turbulence model in combination with cavitation model and depicted as different net positive suction head. When the NPSH decreases means that head also becomes drop in that region as a result cavitation bubble grows on the impeller blade. At first the cavitation begins the impeller suction leading edge and then the vapor bubble increases gradually; their length increasing with the decreasing NPSH values. The cavitation increases on the impeller blade from leading edge to trailing edge.

Fig. 5

Cavity volume fraction in pump impeller for NPSH

4.1.1 Cavitation performance

Water and vapor are in equilibrium at the equilibrium vapor pressure pv. When the pressure is lowered the tension will increase and at some pressure vaporization will start. The pressure at which this presents is the inception pressure. Actually, the inception pressure depends on the size of the largest nuclei in the fluid. But it is difficult to predict the inception pressure. So, 3% head drop is accounts for cavitation. Fig. 6 shows the computed results under different operating conditions. Fig. 6 (a) represents the head vs. NPSH and Fig. 6 (b) shows the head coefficient vs. cavitation number inception lines. The cavitation is occurred due to gradually decreasing the NPSH or cavitation number. The cavitating behavior obtained at design flow rate Q_n shows the cavitaties on the suction side of the impeller blades. Head begins to approximately drop when the cavitation reaches on the suction impeller by two adjacent blades and rapidly decreases by more than 10% of its non-cavitating conditions. Three flow rates considered 0.8Q_n, 1.2Q_n and Q_n for NPSH values, respectively, of about 18.581m, 15.67m, and 17.24 m.

Fig. 6

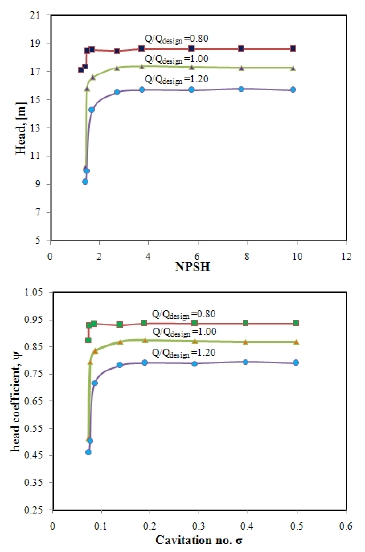
Head drop predicted by numerical simulation (a) Head vs. NPSH (b) Head coefficient vs. Cavitation number

Fig. 6 (a) and (b) shows the same tendency at given different flow rates. In this figure head drop curve initially decreases of the cavitation number has no effect on the energy characteristics of the pump, and the head coefficient remains unchanged. When the value of NPSH as well as the cavitation value continues to decrease, the cavitation is gradually increases resulting the head as well as head coefficient is decreased. Also changing the flow rate of 1.2Q_n the head coefficient is lower than the design flow rate. The different critical cavitation numbers are used in the pump simulations; cavitation number is corresponding to the reduction of 3% of the head coefficient.

4.1.2 Water vapor volume fraction

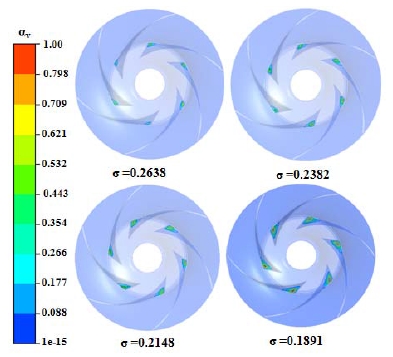
To influence cavitation development on the pump performance, the contours of the water vapor volume fraction distribution is on the plane. The cavitation vapor volume fractions are shown in Fig. 7 which the contours define from 0 to 1. Fig. 7 presents the four cavitation number water volume vapor fraction. The cavitation in the developed model pump is clearly observed by numerical simulations. The cavity bubble at first occurs on the suction side near the blade leading edge, in this case the pressure in that region near the shroud is smaller than of the hub due to the impeller rotational force. so the cavitation bubbles grows becomes larger from hub to shroud as shown in Fig. 7. For the σ = 0.2638, the cavitation can be is clearly on the suction side, at the leading edge of the impeller blades, when the value decreases, the length of cavities grows a significant extent on the impeller blades. Here the pump head begins to drop. For σ = 0.1891 the cavity almost interacts with the blades at the trailing edge of the neighboring blade, at this stage the flow channel is almost remarkably obstructed by the cavities, which is formed a large blockage in the internal flow and thereafter the pump head completely dropped. The distribution of the cavitation on the blade is asymmetrical because of the presence of the pump volute.

Fig. 7

Volume fraction on the plane

5. Conclusion

The improved computation model of shear stress transport (SST) turbulence is used to calculate the cavitating performance flow in the centrifugal pump at a design flow coefficient from 0.077 to 0.154. The effects of the compressibility of mixture fluid were applied of two-phase homogeneous method with Rayleigh- Plesset cavitation model under developed cavitating conditions. The development of the cavitating condition on the impeller blade was observed. In the suction side, the leading edge of the impeller blades, cavitation occurs at first and when the value of cavitation number decreases, the length of cavities grows a significant extent. The development of cavitation also causes the head drop of the pump performance.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant number by the Korea government through the Korea institute of Energy Technology Evaluation and Planning (KETEP). The grant number is 20132010101870 for the Promotion of Science.

Notes

2014 한국유체기계학회학술대회발표논문, 2014년11월26-28일, 부산

References

Kim, D. H., and Park, W. G. et al, (2012), "Numerical simulation of cavitating flow past axisymmetric body", Int. J. Naval Architect Ocean Engineering, 4, p256-266. [https://doi.org/10.3744/JNAOE.2012.4.3.256]
Knapp, R. T., Daily, J. W., and Hammitt, F. G., (1970), Cavitation, McGraw-Hill, New York, p5-8.
Pumping Station Engineering Hand Book, (1991), Japan Association of Agriculture Engineering Enterprises, Tokyo, p50-90.
Shin, B. R. et al, (2004), "Application of preconditioning method to gas-liquid two-phase flow computations", Journal of Fluids Engineering, ASME, 126, p605-612. [https://doi.org/10.1115/1.1777230]
Medvitz, R. B., Kunz, R. F., Boger, D. A. et al, (2002), "Performance analysis of cavitating flow in centrifugal pumps using multiphase CFD", J. of Fluids Eng., 124, p377-383. [https://doi.org/10.1115/1.1457453]
Pierrat, D., Gros, L. et al, (2008), "Experimental and numerical investigations of leading edge cavitation in a helico-centrifugal pump", 12th Int. Symp. on Transport Phenomena and Dynamic of Rotating Machinery, p1-19.
Pouffary, B., Patella, R. F., Reboud, J. L. et al, (2008), "Numerical simulation of 3D cavitating flows analysis of cavitation head drop in turbomachinery", J. of Fluids Eng, 130, p301-310. [https://doi.org/10.1115/1.2917420]
Coutier, D. O., Fortes, P. R., Reboud, J. et al, (2003), "Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation", J. of Fluids Eng, 125, p38-45. [https://doi.org/10.1115/1.1524584]
Katz, J., and Acosta, A., (1982), "Observations of nuclei in cavitating flows", Applied Scientific Reasearch, 38, p123-132. [https://doi.org/10.1007/BF00385943]
LIU, H., REN, Y., WANG, K. et al, (2013), "Experimental investigation and numerical analysis of unsteady attached sheet cavitating flows in a centrifugal pump", Journal of Hydrodynamics, 25(3), p370-378. [https://doi.org/10.1016/S1001-6058(11)60375-3]
Baradaran, F., and Nikseresht, A. H., (2012), “Numerical simualation of unsteady 3D cavitating flows over axisymmetric cavitators”, Journal of Scientia Iranica, 19(5), p1258-1264. [https://doi.org/10.1016/j.scient.2012.07.013]
Fard, M. P., and Roohi, E., (2008), ‘‘Transient simulations of cavitating flows using a modified volume of fluid(VOF) technique", Int. J. Computational Fluid Dynamics, 22(1 ~ 2), p97-114. [https://doi.org/10.1080/10618560701733657]
Senocak, I., and Shyy, W., (2001), "Numerical simulation of turbulent flows with sheet cavitation", Int. Symp. on Cavitation, A7, p2-8.
Funada, T., and Joseph, D. D., (2001), "Viscous potential flow analysis of Kelvin–Helmholtz instability in a channel", Journal of Fluid Mechanics, 445, p263-283. [https://doi.org/10.1017/S0022112001005572]
Saito, Y., Nakamori, I. et al, (2003), "Numerical analysis of unsteady vaporous cavitating flow around a hydrofoil", 5th Int. Symp. on Cavitation, p1-06.
Huang, B., Wang, G. Y. et al, (2010), "A cavitation model for cavitating flow simulations", J. of Hydrodynamics, 22(5), p798-804. [https://doi.org/10.1016/S1001-6058(10)60033-9]
Peng, Y. C., and Chen, X. Y., (2010), "Numerical study of cavitation on the surface of the guide vane in three gorges hydropower unit", J. of Hydrodynamics, 22(5), p703-708. [https://doi.org/10.1016/S1001-6058(09)60106-2]
Lijun, L., Jun, L. et al, (2006), "A numerical method for simulation of attached cavitation flows", Int. J. for Numerical Methods in Fluids, 52, p639-658. [https://doi.org/10.1002/fld.1192]
Delgosha, O. C., Petella, R. F. et al, (2005), "Stability of preconditioned Navier-Stokes equations associated with a cavitation model", J. of Computers and Fluids, 34(3), p319-349. [https://doi.org/10.1016/j.compfluid.2004.05.007]
Sinnghal, A. K., Atavale, M. M., LI, H. et al, (2002), "Mathematical basis and validation of the full cavitation model", Journal of Fluids Engineering, 124(3), p617-624. [https://doi.org/10.1115/1.1486223]
Kunz, R. F., Boger, D. A., Stinebring, D. R. et al, (2000), "A preconditioned Navier-Stokes method for two phase flows with application to cavitation prediction", J. of Computers and Fluids, 29(8), p849-875. [https://doi.org/10.1016/S0045-7930(99)00039-0]
Senocak, I., and Shyy, W., (2002), "A pressure based method for turbulent cavitating flow components", J. of Computational Physics, 179, p363-383. [https://doi.org/10.1006/jcph.2002.6992]
Coutier, D. O., Stutz, B., Vabre, A. et al, (2007), "Analysis of cavitating flow structure by experimental and numerical investigations", J. of Fluid Mechanics, 578, p171-222. [https://doi.org/10.1017/S0022112007004934]
Coutier, D. O., Fortes, P. R., Reboud, J. et al, (2003), "Experimental and numerical studies in a centrifugal pump with two-dimensional curved blades in cavitating condition", J. of Fluids Eng., 125, p970-978. [https://doi.org/10.1115/1.1596238]
Ansys Inc., (2013), ANSYS-CFX (CFX Introduction, CFX Reference guide, CFX Tutorials, CFX-Pre User's Guide, CFX-Solver Manager User's Guide, Theory Guide), release 14.5, USA.
Menter, F. R., (1994), "Two-equation eddy-viscosity turbulence models for engineering applications", AIAA J., 32(8), p1598-1605. [https://doi.org/10.2514/3.12149]
Nicholas, J. G., and Dennis, A. Y,., (2006), "Evaluation of modified two-equation turbulence models for jet flow predictions", 44th AIAA J, p1-12.
Bruno, S., and Frank, C. V., (2009), ‘‘Pump cavitation-various NPSHR criteria, NPSHA margins, and impeller expectancy”, Proceedings of the twenty fifth international pump users symposium, p113-144.
Fox, R. et al, (2012), Fluid Mechanics, John Wiley and Sons Inc., p494-588.