확산접합으로 제작된 냉각판 내부 채널의 변형에 의한 압력손실 및 열전달 성능 영향 연구
Abstract
In channels with small hydraulic diameters, even slight geometric deformations can significantly affect thermal performance. This study investigates the impact of deformation due to diffusion bonding on heat transfer characteristics in the internal channel shape of a liquid cooling cold plate with various pin-fin structures. Deformation amounts were measured and predicted using a generalized formula, and three-dimensional numerical simulations were conducted to analyze heat transfer performance. Results showed that heat transfer performance varied depending on the pin-fin structure, with straight fins decreasing and multi pins improving after deformation. The study suggests that thermal flow analysis can predict changes in heat transfer coefficient, facilitating the design of more efficient cold plates with optimized channel section shapes.
Keywords:
Heat Transfer Coefficient, Pressure Drop, Diffusion Bonding, Channel Deformation키워드:
열전달계수, 압력손실, 확산접합, 채널변형1. 서 론
최근 전자부품의 소형화와 집적화, 시스템의 고출력, 고성능화로 많은 연구자들이 냉각 솔루션의 한계 및 도전에 직면하고 있다. 전자기술의 발전과 함께 전자제품을 냉각하는데 필요한 냉각 구성품의 소형화와 고효율화와 더불어 냉각구조의 열전도도와 열전달계수를 극대화하기 위한 다양한 연구가 수행되고 있다.(1) 고열유속 시스템의 증가로 최근 현열을 이용하는 단상냉각(single phase) 방식뿐만 아니라 상대적으로 높은 열전달계수를 얻을 수 있는 잠열을 이용한 다상유동(multi-phase) 냉각방식(immersion cooling, two phase multi-cooling plate, spray cooling, jet impingement cooling 등)에 관한 연구도 증가하고 있다. 하지만 다상 유동 냉각 방식은 단상 유동 냉각방식보다 유동 특성에 대한 예측이 어렵고, 냉각 루프 구성이 복잡하며, 탑재 플랫폼의 운용 및 기동 환경에 대한 성능 검증의 어려움 등 실 시스템에 적용하기 위해서는 많은 연구와 실험을 필요로 한다.(2) 이러한 점으로 인하여 다상 유동 냉각이 냉각성능 측면에서 많은 이점이 있음에도 불구하고, 아직 산업 전반에 걸쳐 단상 유동 냉각 방식이 많이 적용되고 있다. 대표적인 단상 유동 냉각방식에는 팬을 이용한 강제 공냉 방식, 멀티채널 또는 싱글 채널로 구성된 냉각판을 이용한 수냉 방식이 있는데, 이 중 냉각판을 이용한 수냉 방식은 공냉에 비하여 상대적으로 높은 열전달계수를 얻을 수 있어 자동차, 레이다, 레이저, 전자광학, 항공전자 등 다양한 산업 및 제품에 널리 적용되고 있다.(3,4) 냉각판의 열적 성능은 냉각판의 기하학적 치수 및 형상, 재질, 냉각액의 열 물리적 특성 및 공급조건 등과 밀접하게 연관되어 있으므로 냉각설계를 최적화하기 위해서는 여러 가지 기여 변수를 고려한 트레이드 오프 연구(trade-off study)가 필요하다. 설계 시 냉각판의 형상 최적화와 냉각 성능 분석을 위한 방법으로 상관식을 이용한 모델링이나 전산유체해석(computational fluid dynamics, CFD)에 기반한 수치적 해석을 수행한다(5).
R. W. Knight 및 H. H. Bau 등은 채널 수, 두께 및 단면 비율을 최적화하거나(6,7), 길이에 따라 채널 폭을 변화시키는 등의 연구를 진행하였고(8), A. Jarrett 등은 채널의 폭과 위치를 다양하게 변경하며 냉각판의 최적화 설계를 진행하였다(9). A. F. Al-Neama 등 및 L.W. Jin 등은 채널 내부의 오블리크 휜(Oblique fin), 쉐브론 휜(Chevron fin) 등 다양한 휜 구조를 연구하였으며(10,11), N. Tsuzuki 등은 CFD를 사용하여 물결 모양(waby), 지그재그 및 S자형 휜 등의 형상을 최적화하였다(12). 하지만 냉각판 채널에 대한 대부분의 연구는 열전달 성능을 향상시키기위한 채널 및 휜 구조에 대한 연구가 대부분이며 채널 제작간 발생하는 변형과 이에 따른 열적 성능의 변화에 대한 연구는 부족한 실정이다. 냉각판 제작시 일반적으로 사용되는 브레이징이나 확산접합, 열처리 공정 과정에서 냉각 채널의 수축 변형, 필러의 비산 등과 같은 현상은 채널내 비드 형성, 열변형에 의한 뒤틀림 등을 유발할 수 있다. 냉각판 채널 내부 변형은 X-ray, CT 등과 같은 비파괴 검사로 측정할 수 있으나, 미니/마이크로 채널의 경우 채널의 크기가 작은 특징으로 인하여 정확한 측정이 어렵다. 이 때문에 제작 공정상에서 냉각판 시료를 제작하여 절단 후 검사를 수행하기도 하는데, 이 방법은 다수 채널 형상에 관한 트레이드 오프 연구를 수행하는 경우 많은 시험 시료가 필요할 수 있으므로, 이에 따른 상당한 비용과 시간을 수반하게 된다. 본 연구에서는 이미 셋업된 확산접합과 열처리 공정을 통해 제작된 냉각판에 대해 채널 변형을 측정하고, 공정간 제작 변형이 다양한 냉각 채널 단면 형상에 미칠 수 있는 열전달 성능 영향을 시뮬레이션하여 예측하고자 하였다. 이를 통하여 추후 다양한 냉각 채널 단면 형상으로 제작 시 단면 검사 시료의 수량을 최소화하면서 채널 단면에 따른 냉각성능 변화 및 시스템에 미치는 영향을 예측하고자 하였다.
2. 본 론
2.1 연구 대상 및 방법
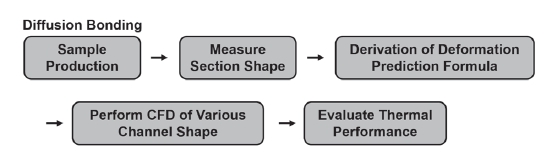
본 연구는 먼저 실 제작간 채널의 변형 양상을 도출하기 위하여 확산접합과 열처리 공정을 적용하여 제작된 16 개 시료에 대한 채널 형상을 측정하였으며, 접합 시 눌림량과 변형된 채널의 관계 분석을 통해 채널 변형량을 예측할 수 있는 관계식을 도출하였다. 이를 활용하여 다양한 채널 단면 형상에 대한 예측된 변형 형상에 대하여 전산유체해석을 수행하여 열전달 성능 분석 및 채널의 변형이 열적 성능에 미치는 영향을 평가하였다. Fig. 1은 본 연구의 방법을 순서도(flow chart)로 간략하게 도식화한 것이다.
2.2 채널의 변형 측정과 변형량 예측
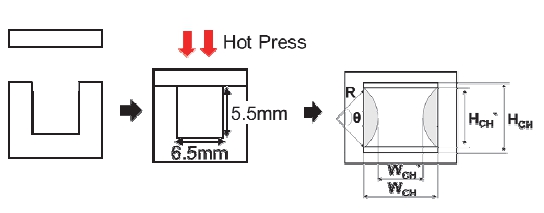
채널 변형 측정에 적용된 냉각판은 보편적으로 널리 사용되고 있는 사각 단면을 가진 멀티채널 냉각판으로, 평판 형태의 상부 알루미늄판과 냉각 채널 그루브 구조를 가지는 하부 알루미늄판을 눌림량 0.11 mm으로 접합하였다. 제작된 냉각판을 와이어 커팅기를 사용하여 단면을 절단하고, 16 개의 채널 각 단면에 대한 변형 형상 및 변형 값을 광학현미경(Rational 社 VMS Plus 4030G)을 이용하여 측정하였다. Fig. 2는 냉각 채널을 수직으로 절단한 단면 형상으로, 변형 전 채널 단면은 채널 폭과 높이가 각각 6.5 mm, 5.5 mm인 직사각형 구조를 가진다. 접합 이전 원 소재는 AL6061-T6이지만, 확산접합 및 열처리 공정간 소재의 물리적 특성이 변하므로, 제작 후 별도 시편 시험을 통해 열전도도를 측정하였다. 측정된 시편의 평균 열전도도는 수직 방향 178 W/m-K, 수평 방향 155 W/m-K이며, 이 값을 CFD 수행 시 냉각판 열전도도 값으로 사용하였다.
제작된 16 개 채널은 Fig. 3과 같이 접합 간 고온 상태에서 위, 아래 프레스에 의해 가해진 상하 방향의 압력에 의하여 냉각 채널 측면 벽이 내부로 볼록하게 돌출되는 호와 같은 형태의 변형이 동일하게 관찰되었다.
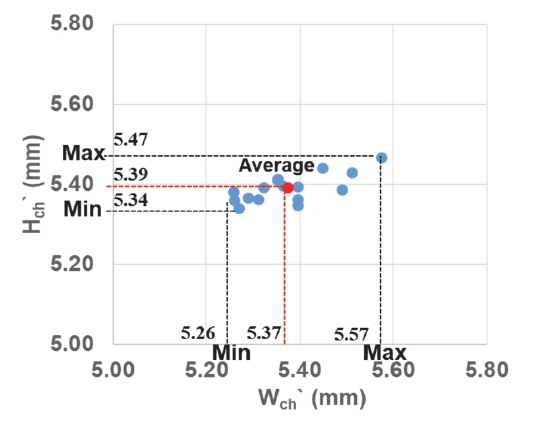
Fig. 4는 실제 측정된 16 개 채널의 폭과 높이 측정값을 나타낸 것이다. Fig. 4의 Wch’, Hch’ 는 제작후 변형된 채널의 최소폭과 높이를 표현한 것이다. Wch’, Hch’ 모두 설계 치수 대비 감소하여 Wch’는 5.26∼5.57 mm, Hch’ 는 5.34∼5.47 mm 범위 내 분포를 보였다. 높이 방향 변형 대비 폭 방향 변형이 상대적으로 넓은 범위의 산포도를 가지는 특성을 보였으며, 변형된 채널의 단면 치수 평균값은 Wch’×Hch’ = 5.37 mm × 5.39 mm으로 분석되었다.
설계 치수 대비 채널의 폭과 높이 방향의 변형량을 δW, δH 로 정의하면, δW, δH 는 각각 식 (1), (2)로 표현할 수 있다.
| (1) |
| (2) |
여기서 Wch, Hch는 각각 설계 기준 폭과 높이가 된다. 계산된 평균 δH는 2 %(평균 변형량 0.11 mm)로, 공정간 눌림량과 동일 하였으며, 계산된 평균 δW는 17.3 %(평균 변형량 1.13 mm)로 δH에 비하여 상대적으로 크게 변형되었다. 제작 공정 동안 냉각판의 질량은 보존된다고 할 수 있으므로, 접합간 눌림량 0.11 mm에 의해 수직 방향으로 감소되는 질량에 해당하는 체적은 수평 방향 채널 폭을 변형시키는데 사용된 체적량과 동일하다고 가정할 수 있다. 그러므로 냉각판 제작 시 공정상의 눌림량이 결정된다면, 변형되는 부피량과 변형으로 나타나는 측면 호의 형상으로부터 제작 후 예상되는 변형의 기하학적 형상 치수를 예측할 수 있다. 식 (3), (4), (5)는 채널과 채널 사이 벽두께(Ws), 채널 폭(Wch), 높이(Hch), 채널 폭 변형량(δW), 채널 높이 변형량(δH) 관계로부터 채널 변형량을 예측하기 위한 관계식을 도출한 것이다.
| (3) |
| (4) |
| (5) |
여기서 A는 변형된 채널의 단면적[mm2], R은 호의 반지름[mm], θ는 호의 각도[rad]가 된다(Fig. 3 참조).
2.3 채널의 기하학적 형상 검토 조건
본 연구에서 제작 공정간 채널 외벽 변형에 의한 열적 성능 및 압력강하 영향을 분석하기 위하여 Hch 및 Wch가 6.0 mm인 조건에 대한 전산유체해석을 수행하였다. 제작 후 변형된 채널 단면 외벽의 평균 치수는 식 (3)으로부터 Table 1과 같이 예측할 수 있다.
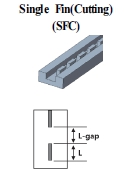
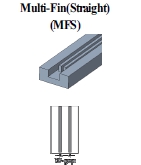
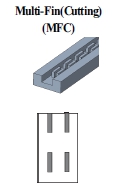
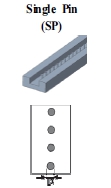
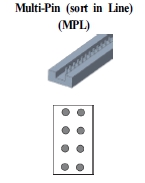
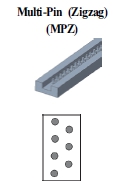
냉각 채널의 내부 형상에 따라 채널 변형으로 인한 열적 영향성의 차이가 발생할 수 있으므로, 그 영향성을 분석하기 위하여 서로 다른 8개의 채널 형상을 선정하고 비교/분석하였다. 비교에 사용된 채널 형상은 Table 2에 나타낸 것과 같이 가장 기본적인 플레인(plane) 채널, 휜 또는 핀(pin) 형상이 단일 배열 또는 이중 배열 구조를 가진 형태이며, 냉각 채널 길이는 200.0 mm, 높이는 11.5 mm, 너비는 15.0 mm로 동일한 외곽 형상을 가진다.
2.4 해석 모델 및 조건
채널에 대한 수치적 모델링은 Siemens사의 FloEFD(ver 2205)를 이용하여 수행되었다. Fig. 5는 각 채널의 열적 성능을 분석하기 위해 수행된 CFD의 대표적인 해석 모델(multi-fin(cutting), plane) 및 경계조건을 나타낸 것이다.
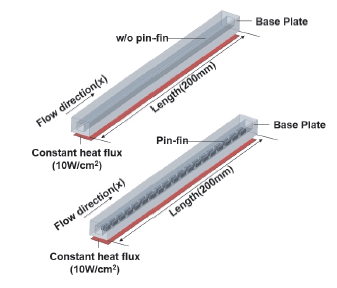
Computational domain of plane model(top) and multi-fin(cutting) model(bottom) and their boundary conditions
해석 시 채널 내 유동은 단상 비압축성 층류 유동이며, 채널 바닥의 열유속은 일정하고, 채널 외부는 단열구조로 되어 있어 외부와의 열교환은 무시할 수 있으며, 모세관 힘에 의한 유동 효과는 무시할 수 있다는 가정을 적용하였다. 모세관 힘을 이용하는 경우 채널 벽과 유체 사이의 계면 장력에 의해 유동이 발생하며, 이를 위해서는 채널 표면이 친수성이어야 한다.(13) 채널 표면을 친수성으로 만들기 위해 일반적으로 별도의 표면처리를 하거나 계면활성제를 첨가하는 방식을 사용하는데,(14,15) 본 연구에서는 표면을 친수성으로 만드는 별도의 공정을 적용하지 않은 일반적인 알루미늄 소재의 냉각판 채널을 대상으로 수행하였으므로 모세관 힘에 의한 유동 효과는 무시할 수 있다.
복합 열전달에 대한 지배 방정식은 식(6)-(12)와 같이 연속방정식, 운동량방정식, 에너지방정식이 적용된다.
연속방정식 :
| (6) |
운동량 방정식 :
| (7) |
| (8) |
| (9) |
냉각액에 대한 에너지 방정식 :
| (10) |
고체에 대한 에너지 방정식 :
| (11) |
냉각액이 입구에서 출구로 흐르면서 채널에서 냉각액으로 유입된 총 열량은 식 (12)로 표현되는데,
| (12) |
이때 ṁ은 질량유량[kg/s], Cp.f는 비열[J/kg-K], Tin, Tout은 각각 유체의 입구, 출구 온도[K]가 된다. 대수평균온도차(The log mean temperature difference, LMTD)는 식 (13)으로 계산되며,
| (13) |
이때 Tb는 냉각 채널의 바닥 면 온도[K]가 된다. 열전달계수 h는 식 (14)로부터 식 (15)로 표현되며,
| (14) |
| (15) |
이때 At는 전산 영역의 전체 열전달영역[m2]이 된다.
누셀수(Nusselt number, Nu)는 식 (16)으로 정의되며,
| (16) |
이때, kf는 유체의 열전도도[W/m-K], Dh는 식 (17)로 표현되는 수력학적 직경[m]이 된다.
| (17) |
이때, Ac는 유동 흐름에 수직인 단면적[m2], L은 채널의 전체 길이[m]를 의미한다.
압력 손실량[Pa]은 식 (18)로 구할 수 있으며,
| (18) |
Pin, Pout은 각각 유체의 입구 압력, 출구 압력[Pa]으로 정의된다.
열유속은 10 W/cm2로 균일하게 바닥에 인가하였으며, 채널 입구의 레이놀즈 값(Re)은 500으로 모든 조건에 대해 동일하게 설정하여 유속을 결정하였다. 냉각액은 EG(Ethylene glycol)와 물이 50:50으로 혼합된 상태로 냉각액 공급온도는 20 ℃이며, 적용된 물성값은 Table 3과 같다.
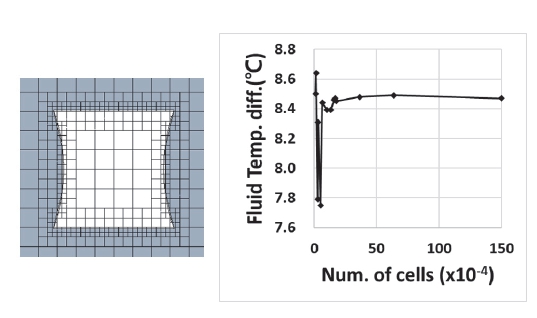
해석영역의 크기는 15.0 mm x 11.5 mm x 202.0 mm이며, 수치해석 시 난류 모델로 κ-ε 모델을 적용하였다. 격자 수에 따른 해석의 민감도 분석을 위해 채널 변형을 고려한 PL 모델을 기준으로 격자수를 1만 개부터 150만 개까지 변경하며 유체의 입출구온도차를 비교하였으며, 격자수가 363,984 개 이상일 때, 유체의 입출구온도차가 수렴하는 것을 확인하였다.(Fig. 6 참조) 이때 격자의 최소 크기는 유체와 고체의 경계면에서 약 0.1 mm이며, 동일한 크기의 격자를 이용하여 나머지 조건에 대해 CFD를 수행하였다.
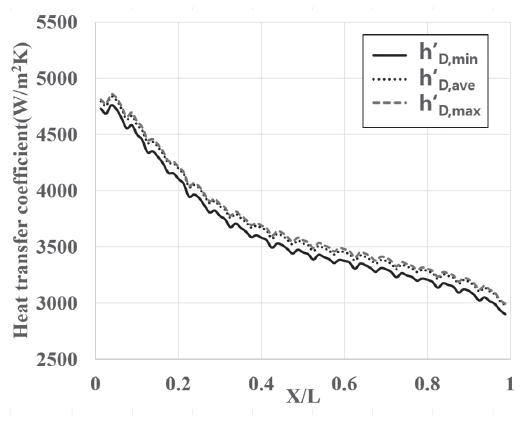
Fig. 7은 변형된 채널의 수력학적 직경 크기에 따른 열전달계수에 미치는 영향을 평가하기 위하여 Fig. 5 형상에 대해 측정된 수력학적 직경이 평균, 최소, 최대(참조 Fig. 4)조건일 때, 열전달계수(순서대로 h′D,ave, h′D,min, h′D,max)해석 값을 비교한 것이다. X/L은 채널 길이 방향을 무차원수로 나타낸 것이다. 채널 길이 방향으로의 국부열전달계수는 컷팅 휜(cutting fin) 형상에 의한 유동 흐름에 의하여 위아래로 변동하면서 출구로 갈수록 점차 감소하는 경향을 보여주었으며, 수력학적 직경의 크기 차이에 관계없이 동일한 패턴 형태로 나타났다. h′D,ave에 대한 h′D,min, h′D,max 값의 편차는 최대 2.7 % 로 계산되었다. 그러므로, 본 연구에서는 실제 제작 시 열전달계수 편차가 플레인(plane) 채널형상 기준으로 최대 2.7 %의 차이가 발생할 수 있음을 고려하고, 수력학적 직경의 평균값을 제작 후 대표적인 변형 값으로 정의하였다.
2.5 해석 결과
Fig. 8은 채널 변형을 고려하지 않은 모델과 채널 변형을 반영한 모델에 대해 냉각판 바닥 표면 및 내부 냉각 채널 벽의 표면 온도를 나타낸 것이다. 냉각액이 채널 길이 방향으로 흐르면서 채널 벽과의 열교환이 일어나며, 냉각액과 채널의 벽 온도는 상승한다. 변형을 고려하지 않은 모델에서, 핀 또는 휜이 있는 냉각 채널(SFS, SFC, MFS, MFC, SP, MPL, MPZ) 7 개의 평균 벽 온도는 55.4 ℃, 핀이 없는 채널(PL)의 평균 벽 온도는 90.4 ℃로 계산되었다. 냉각액 공급온도와 각 채널의 평균 벽 온도의 차이를 비교하면, 핀 및 휜이 있는 7 개 채널의 온도 차는 PL의 온도 차 대비 49.6 % 낮게 나타났다. 변형을 반영한 모델을 보면, 핀 및 휜이 있는 7 개 채널의 평균 벽 온도는 55.5 ℃, PL의 평균 벽 온도는 91.3 ℃로 계산되었으며, 냉각액 공급온도와 각 채널의 평균 벽 온도의 차이를 비교하면, 핀 및 휜이 있는 7 개 채널의 온도 차는 PL의 온도 차 대비 50.2 % 낮게 나타났다.
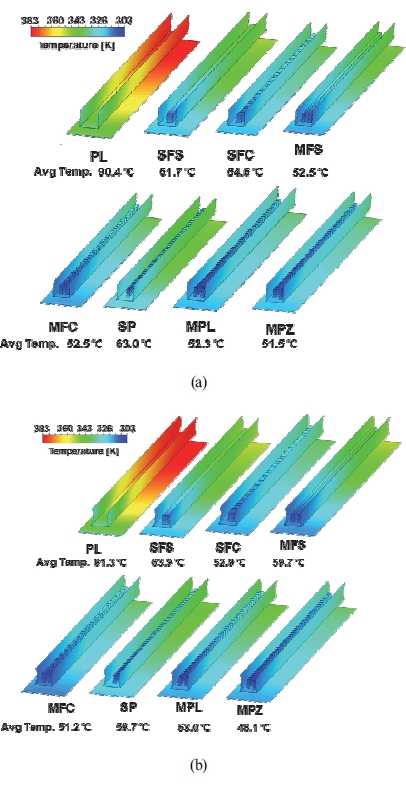
Temperature contours of the base and interface surfaces of channels with different pin-fin structures without deformation(a) and with deformation(b)
이는 핀 또는 휜이 있는 구조는 전열면적 및 열전달계수의 증가로 대류 열전달 성능이 증가하였음을 보여준다. 더 자세히 기술하면 단일 배열로 된 채널(SFS, SFC, SP)보다 복수 배열로 된 채널(MFS, MFC, MPL, MPZ)에서 더 높은 냉각성능을 보여주었으며, 이를 통해 휜의 컷팅 형상 및 핀의 배열 형상에 따라 냉각성능이 크게 변한다는 것을 보여주었다. 앞에서 언급한 본 연구 목표에 따라 본 연구논문에서는 채널 형상의 상대적인 냉각성능 비교보다 채널 단면의 변형으로 인한 각 채널 형상별 영향성 평가에 더 집중하여 해석 결과를 분석 및 고찰하였다.
Fig. 9는 냉각 채널 길이 중앙위치에서 채널 변형을 반영하지 않은 모델과 채널 변형을 고려한 모델의 형상 및 단면 속도 구배를 나타낸 것이다. PL 채널의 경우 채널의 수력학적 직경 감소로 인하여 변형을 반영하지 않은 모델 대비 변형을 고려한 모델에서 채널 중심의 유속은 증가하였다. 다중 휜(multi-fin) 및 핀 구조(MFS, MFC, MPL, MPZ)에서는 변형을 고려한 모델에서 핀 및 휜과 채널 벽면 간의 간격이 상대적으로 감소하면서 해당 위치에서의 냉각액 흐름 속도는 변형을 반영하지 않은 모델 대비 급격히 감소하였지만, 핀 및 휜 윗 부분(채널 상단부)의 유속은 증가하였다. 이러한 단면 유속 변화 현상은 SFS, SFC, SP 구조보다 핀 또는 휜이 다중으로 배열되는 MFS, MFC, MPL, MPZ에서 핀/휜과 벽면과의 좁은 간격으로 인해 상대적으로 크게 나타났으며, 휜이 직선으로 배열되는 MFS에서 가장 크게 나타났다. 이러한 유동 패턴의 변화로 인하여 채널 변형에 따른 열전달계수의 영향은 채널 형상에 따라 달리 관찰되었다.
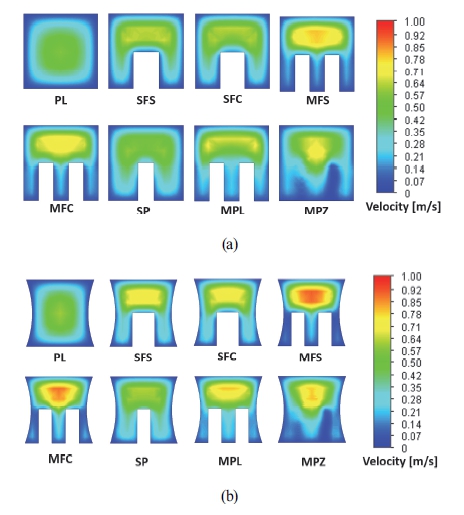
Velocity contour of cross-sectional area of channels with different pin-fin structures without deformation(a) and with deformation(b)
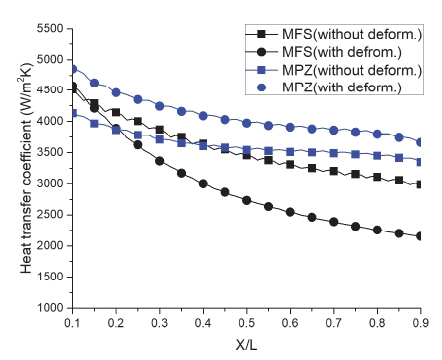
Fig. 10은 채널 형상에 대한 채널 길이 방향 위치별 국부 열전달계수 평균값을 나타낸 것이다. 입구 및 출구에 근접한 영역의 효과를 제거하기 위해 입구/출구 근처의 10% 길이 영역은 제외하고 중간영역만 분석하였다. 채널 입구에서 채널 출구로 갈수록 위치에 따른 국부 열전달계수는 감소한다. 채널 변형을 반영한 모델의 경우, 채널 변형을 고려하지 않은 모델보다 채널의 수력학적 직경이 작기때문에, 채널 입구의 열전달계수가 변형을 고려하지 않았을 때보다 더 큰 값을 갖는다. MFS 채널은 변형 반영 후 길이 방향의 국부 열전달계수가 상대적으로 급격하게 감소하는 특성을 보여주었다. 반면에 MPZ 채널은 변형 반영 전보다 위치에 따라 국부 열전달계수가 전반적으로 개선되었다.(Fig. 11 참조)
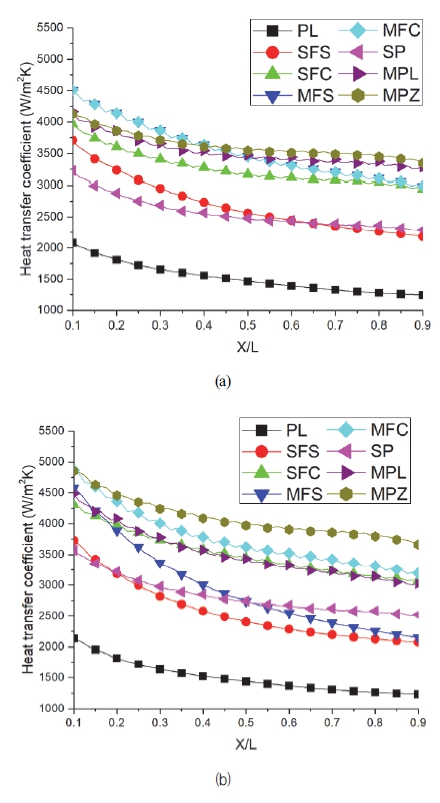
Heat transfer coefficient versus non-dimensional distance(X/L) of channels without deformation(a) and with deformation(b)
Table 4는 채널 전체의 평균 열전달계수를 나타낸 것이다. 앞서 언급한 바와 같이 채널 변형에 의해 직선 휜(SFS, MFS) 조건에서는 휜과 채널 벽 간의 간격이 매우 감소한 효과로 채널 길이 방향 열전달계수는 채널 변형을 반영하지 않은 모델 대비 변형을 고려한 모델에서 각각 4.5 %, 17.0 %로 감소하였다. 채널 내부 핀이나 휜이 없는 PL형상과 핀 구조를 가진 채널(SP, MPL, MPZ)의 평균 열전달계수는 MPL 조건을 제외하고 변형을 고려하였을 때 증가하는 특성을 보였으며, 특히 휜 구조보다 핀 구조 형상의 채널에서는 채널 길이 방향의 국부 열전달계수가 완만하게 감소하는 특성을 보여주었다. 같은 전열면적을 가지는 MPL과 MPZ을 비교하면, 변형된 조건에서 지그재그로 배열된 MPZ의 평균 열전달계수가 MPL보다 상대적으로 16.5 % 크게 나타났다. 이는 핀의 배열 형상에 따라 채널 변형 시 열전달계수가 상이하게 변한다는 것을 보여준다.
또한 채널 변형은 채널 내부의 열전달계수뿐만 아니라, 압력손실량에도 영향을 미치게 된다. Table 5는 채널 변형에 따른 채널 전체의 평균 압력손실량을 비교한 것이다. 모든 채널 형상에서 채널 변형 후 수력학적 직경은 감소하게 되므로, 변형을 반영한 냉각 채널의 압력손실량은 최소 26.9 %(PL 채널)이상 증가하였다. 특히 SFS와 MFS 채널의 경우에는 열전달계수가 감소함에도 압력손실량이 증가하였으며, 변형을 고려하지 않았을 때 가장 높은 평균 열전달계수를 갖는 MPZ 채널의 경우, 평균 열전달계수가 12.7 % 개선되었으나, 채널의 압력손실량은 71.3 % 증가하여 가장 높은 압력손실량의 증가량을 보였다.
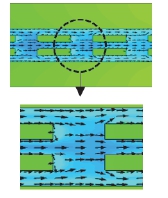
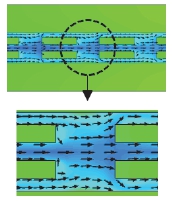
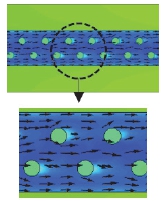
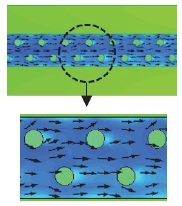
Table 6은 MFS, MFC, MPZ 채널 내 온도와 냉각액 속도 벡터 분포를 나타낸 것이다. MFS 채널은 채널 변형 후 휜과 채널 벽면 사이의 간격 감소로 인하여 채널 중심의 속도는 빨라졌지만, 휜과 채널 벽면 사이에 지나가는 냉각액은 급격히 감소하였다. 채널 변형을 반영한 MFC 및 MPZ 채널은 휜/핀과 채널 벽면과의 간격이 감소하면서 휜/핀에 부딪혀 채널 벽면으로 진행한 냉각액이 벽면에서도 다시 튕겨 나오는 유동 흐름을 관찰할 수 있는데, MPZ 구조에서는 상대적으로 유동 흐름이 더욱 복잡하고, 와류가 더 많이 발생하면서 열전달계수의 증가와 동시에 압력손실 또한 크게 증가하였다.
효율적인 냉각판은 동일한 열유속과 제원 조건에서 냉각장치에 요구되는 펌프 능력(pumping power)은 적고 냉각판의 온도는 최소화되어야 하는데, 이는 냉각 채널에서 압력손실은 최소화하고, 열전달계수는 극대화되어야 한다는 점을 의미한다. 따라서 설계시 냉각장치가 공급할 수 있는 최대 펌프 능력을 고려하여 최대 허용 가능한 압력손실량 이하의 범위에서 가장 높은 평균 열전달계수를 갖는 채널을 선정하여야 한다. 예를 들어 요구 압력손실량이 1,200 Pa 이하인 시스템이 있다고 가정하면, 변형을 고려하지 않고 설계하였을 때 요구 압력손실량을 만족하고 가장 높은 평균 열전달계수를 갖는 모델은 MPZ 모델이지만, 제작 변형을 반영하면 MPZ 모델은 요구 압력손실량을 초과하기 때문에 가장 적절한 모델은 SFC 모델이 된다. 제작간 채널 변형은 일부 채널 형상에서는 열전달계수를 증가시키는 장점이 있으나 압력손실 또한 증가하므로 설계 및 분석 단계에서 그 변형량을 예측하고 열적 성능 및 시스템의 영향성을 반드시 검토해야 한다. 본 연구에서는 단일 채널에 관한 채널 변형의 영향성 및 성능 평가를 하였지만, 동일 형상으로 구성되는 다채널 히트싱크에도 같은 방법으로 성능 변화를 예측할 수 있다.
3. 결 론
본 연구는 다양한 핀 구조를 가진 냉각 채널 제작 시 내부 채널 형상의 변형이 열적 성능 영향에 미치는 영향을 분석하기 위해 접합 눌림량과 채널 변형량에 관한 일반화된 예측 수식을 도출하고, 3차원 수치해석을 통하여 성능 예측을 수행하였다. 본 연구에서 수행한 8개의 냉각 채널 형상 및 냉각액 공급 조건에 대한 채널 변형시 열적 성능 영향을 요약하면 다음과 같다.
1) 변형 전, 후 MPZ 구조의 냉각 채널의 평균 열전달계수가 가장 높게 나타났으며, SFS 및 MFS 구조의 냉각 채널의 변형 후 평균 열전달계수는 변형 전 대비 각각 4.5 %, 17.0 % 감소하였다.
2) 모든 채널 형상 구조에서 변형 후의 압력손실량이 변형 전 압력손실량 대비 증가하였으며, MPZ 구조의 경우 변형 반영 후 압력손실량이 변형 반영 전 대비 71.3 % 증가하였다.
3) 본 연구에서 수행한 열유동 분석 결과를 통해 냉각판 제작간 내부 채널의 변형에 의한 열전달 성능 변화 및 필요한 압력량을 예측할 수 있고, 냉각판 접합 후 필요한 펌프 능력이 냉각시스템의 한계를 초과하지 않는지 사전에 확인할 수 있다.
4) 본 연구논문에서 제시한 방법론을 활용하면 동일한 공정으로 제작되는 냉각판의 접합 간 눌림량이 변경되더라도 변형량 예측을 통하여 냉각판 성능을 예측할 수 있다.
5) 본 연구에서는 채널 입구 레이놀즈 수가 고정된 층류 유동에 대하여 수행되었지만, 향후 난류 유동을 포함한 다양한 레이놀즈 수에 대한 추가적인 계산 및 분석을 수행할 예정이다.
References
-
McGlen, R. J., Jachuck, R. and Lin, S., 2004, “Integrated thermal management techniques for high power electronic devices”, Applied Thermal Engineering, Vol. 24, No. 8∼9, pp. 1143-1156.
[https://doi.org/10.1016/j.applthermaleng.2003.12.029]

-
Mudawar, I., 2011, “Two-Phase Microchannel Heat Sinks: Theory, Applications, and Limitations”, Journal of Electronic Packaging, Vol. 133, No. 4, 41002.
[https://doi.org/10.1115/1.4005300]

-
Bhowmik, H., Tso, C.P., Tou, K.W. and Tan, F. L., 2005, “Convection heat transfer from discrete heat sources in a liquid cooled rectangular channel”, Applied Thermal Engineering, Vol. 25, No. 16, pp. 2532-2542.
[https://doi.org/10.1016/j.applthermaleng.2004.11.022]

-
Kandlikar, S. G. and Hayner II, C. N., 2009, “Liquid Cooled Cold Plates for Industrial High-Power Electronic Devices—Thermal Design and Manufacturing Considerations”, Heat Transfer Engineering, Vol. 30, No. 12, pp. 918-930.
[https://doi.org/10.1080/01457630902837343]

-
Wang, N., Li, C., Li, W. Chen, X., Li, Y. and Qi, D., 2021, “Heat dissipation optimization for a serpentine liquid cooling battery thermal management system: An application of surrogate assisted approach”, Journal of Energy Storage, Vol. 40, 102771.
[https://doi.org/10.1016/j.est.2021.102771]

-
Knight, R. W., Goodling, J. S. and Hall, D. J., 1991, “Optimal Thermal Design of Forced Convection Heat Sinks-Analytical”, Journal of Electronic Packaging, Vol. 113 No. 3, pp. 313-321.
[https://doi.org/10.1115/1.2905412]

-
Knight, R. W., Hal, D. J., Goodling, J. S. and Jaeger, R. C., 1992, “Heat sink optimization with application to microchannels”, IEEE Transactions on Components, Hybrids, and Manufacturing Technology, Vol. 15, No. 5, pp. 832-842.
[https://doi.org/10.1109/33.180049]

-
Bau, H. H., 1998, “Optimization of conduits’ shape in micro heat exchangers”, International Journal of Heat and Mass Transfer, Vol. 41 No. 18, pp. 2717-2723.
[https://doi.org/10.1016/S0017-9310(98)00003-9]

-
Jarrett, A. and Kim, I. Y., 2011, “Design optimization of electric vehicle battery cooling plates for thermal performance”, Journal of Power Sources, Vol 196, No 23, pp. 10359-10368.
[https://doi.org/10.1016/j.jpowsour.2011.06.090]

-
Al-neama, A. F., Khatir, Z., Kapur, N., Summers, J. and Thompson, H. M., 2018, “An experimental and numerical investigation of chevron fin structures in serpentine minichannel heat sinks”, International Journal of Heat and Mass Transfer., Vol. 120, pp. 1213-1228.
[https://doi.org/10.1016/j.ijheatmasstransfer.2017.12.092]

-
Jin, L. W., Lee, P. S., Kong, X. X., Fan, Y. and Chou, S. K., 2014, “Ultra-thin minichannel LCP for EV battery thermal management”, Applied Energy, Vol 113, pp. 1786-1794.
[https://doi.org/10.1016/j.apenergy.2013.07.013]

-
Tsuzuki, N., Kato, Y. and Ishizuka, T., 2007, “High performance printed circuit heat exchanger”, Applied Thermal Engineering, Vol. 30, pp. 1702-1707.
[https://doi.org/10.1016/j.applthermaleng.2006.07.007]

-
Yang, D., Krasowska, M., Priest, C., Popescu, M. N. and Ralston, J., 2011, “Dynamics of Capillary-Driven Flow in Open Microchannels”, The Journal of Physical Chemistry C, Vol. 115, No. 38, pp. 18761-18769.
[https://doi.org/10.1021/jp2065826]

-
Tan, S. H., Nguyen, N.-T., Chua, Y. C. and Kang, T. G., 2010, “Oxygen plasma treatment for reducing hydrophobicity of a sealed polydimethylsiloxane microchannel”, Biomicrofluidics, Vol. 4, No. 3, 032204.
[https://doi.org/10.1063/1.3466882]

-
Makamba, H., Kim, J. H., Lim, K., Park, N. and Hahn, J. H., 2003, “Surface modification of poly(dimethylsiloxane) microchannels”, Electrophoresis, Vol. 24, No. 21, pp. 3607-3619.
[https://doi.org/10.1002/elps.200305627]