높은 표면 거칠기가 적층 제조 압축기 블레이드의 공력 성능에 미치는 영향
Abstract
Additive manufacturing frequently yields components with relatively high surface roughness when compared to their subtractive manufacturing counterparts. This elevated surface roughness can have a profound impact on compressor performance by perturbing the boundary layer. Consequently, a comprehensive investigation into the influence of surface roughness on the aerodynamic performance of additively manufactured compressor blades becomes imperative. In this study, a linear cascade experiment is conducted to examine the effects of elevated surface roughness within a fully rough regime on compressor blades produced through additive manufacturing. Sandpaper is employed as a surrogate for surface roughness. Deviations and total pressure loss are assessed at the midspan using a 5-hole probe. Furthermore, numerical analysis is conducted using two models to simulate the ramifications of surface roughness via the commercial software, ANSYS CFX. In the linear cascade experiments, surface roughness on compressor blades results in a 27.9% increase in mass-averaged deviation at midspan and a 98.2% increase in mass-averaged total pressure loss at midspan. Numerical analysis results exhibit reasonable agreement regarding the increase in pressure loss coefficient due to surface roughness, albeit with a larger deviation than the experimental result. The results from both the experiment and numerical analysis conclusively establish that high surface roughness on additively manufactured compressor blades substantially elevates deviations and pressure loss.
Keywords:
Additive Manufacturing, Surface Roughness, Compressor, Fully Rough Regime, Linear Cascade, Computational Fluid Dynamics키워드:
적층 제조, 표면 거칠기, 압축기, 완전히 거친 상태, 선형 캐스케이드, 전산 유체 역학1. 서 론
PBF(Powder Bed Fusion)를 이용한 적층 제조는 주로 분말 형태의 금속을 녹이고 적층하여 제품의 형상을 만드는 제조 방식이다. PBF를 이용한 적층 제조 방식은 전통적인 제조 방식인 제거 가공(Subtractive manufacturing)에 비해서 적은 재료를 이용해 금속 제품을 만들 수 있고 복잡한 형상을 쉽게 만들 수 있다는 장점이 있다. 이러한 이점 때문에 PBF를 이용한 적층 제조 방식은 항공 우주 산업 및 가스터빈 산업 등 다양한 분야의 터보 기계의 부품을 만드는 데 사용된다(1). 하지만 PBF를 이용한 적층 제조 방식은 제작하는 부품의 형상이 적층 방향과 이루는 각이 큰 경우나, 재료가 부분적으로 덜 녹게 되는 등의 경우에 제거 가공 방식으로 제작된 부품에 비해 상대적으로 높은 표면 거칠기를 가진다(2). 이러한 표면 거칠기는 유동의 경계층을 변화시켜 터보 기계의 성능에 영향을 준다.
흐르는 유동은 벽면을 만나게 되면 점성으로 인한 점착 조건(No-slip condition)에 의해 벽면 근처에서 경계층을 형성한다. 경계층은 난류 유동에서 크게 외층(Outer layer)과 내층(Inner layer)으로 나누어지고 내층은 점성 하부층(Viscous sublayer), 버퍼층(Buffer layer), 로그층(Log layer)으로 나누어진다. 벽면에 존재하는 표면 거칠기는 벽면 근처에서 강한 난류 혼합(Turbulent mixing)을 만들어 점성 하부층을 변화시키거나 파괴한다(3). 이러한 점성 하부층의 변화는 경계층의 평균 속도 분포(Mean velocity profile)를 변화시키고 벽면 전단 응력(Wall shear stress)을 증가시켜 마찰 손실(Friction loss)과 압력 손실(Pressure loss)을 증가시킨다(3,4).
경계층의 평균 속도 분포는 무차원 변수를 통해서 나타낼 수 있다. 점성 하부층의 평균 속도 분포는 식 (1)를 통해 표현되고 로그층의 평균 속도 분포는 식 (2)를 통해 표현된다.
| (1) |
| (2) |
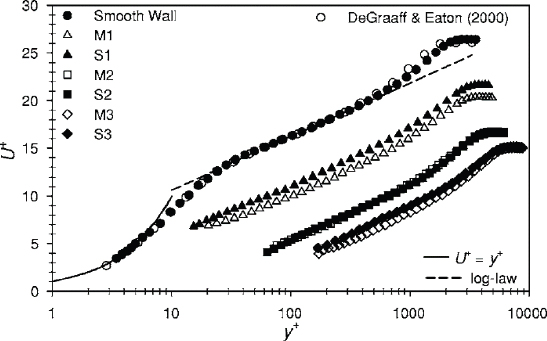
U+는 무차원 평균 속도(Dimensionless Mean Velocity)이고 y+는 무차원 벽 거리(Dimensionless Wall-Normal Distance)이다. 표면 거칠기가 경계층 속도 분포에 주는 영향은 Clauser, F. H. 등(5)의 연구에서 확인할 수 있다. Clauser, F. H. 등은 실험을 통해 경계층의 속도 분포가 표면 거칠기에 의해 형상을 유지한 채 아래로 이동하는 것을 확인했고 표면 거칠기에 의해 나타나는 속도 분포의 이동(∆U+)을 식 (3)을 통해서 나타냈다. 이러한 표면 거칠기에 의한 경계층 속도 분포의 이동은 Flack, K. A.와 Schultz, M. P.의 실험(6)을 통해서도 확인할 수 있다. 이 실험에서 나타난 평균 속도 분포의 이동은 Fig. 1을 통해 확인할 수 있다. κ는 본 카르만 상수(von -Karman Constant, κ=0.41)이고 B는 매끈한 벽면의 절편(B=5.2)이다.
| (3) |
표면 거칠기에 의해 발생하는 압력 손실의 증가는 Nikuradse, J.(7)의 연구를 통해 확인할 수 있다. Nikuradse, J.는 표면 거칠기가 유동에 미치는 영향을 확인하기 위해 실험을 진행했다. 이 실험에서는 균일한 크기의 모래 알갱이(Sand grain)를 이용해 파이프의 표면 거칠기를 모사했고 다양한 레이놀즈수와 표면 거칠기에서 파이프 유동의 압력 손실을 측정했다. Nikuradse, J.는 실험에 사용한 모래 알갱이 크기(KS)를 이용하여 무차원 거칠기 인자인 거칠기 레이놀즈수()를 정의하고 거칠기 레이놀즈수에 따라 유동을 매끄러운 상태(Hydraulically smooth regime, ≤5)와 과도기의 거친 상태(Transitionally rough regime, 5<≤70), 완전히 거친 상태(Fully rough regime, 70<)의 3개의 영역으로 구분했다. 거칠기 레이놀즈수의 정의는 식 (4)를 통해서 확인할 수 있다. KS는 모래 알갱이의 크기이고, uτ는 마찰 속도(Friction Velocity), ν는 유체의 동점도(Kinematic Viscosity)이다.
| (4) |
이후 Schlichting(8)은 다양한 형상의 표면 거칠기에 대한 실험을 진행하면서 등가 모래 거칠기(Equivalent Sandgrain Roughness)를 정의했다. 등가 모래 거칠기는 Nikuradse, J.(7)의 실험 데이터를 바탕으로 균일하지 않은 표면 거칠기를 동일한 표면 마찰 손실(Skin Friction Loss)을 가지는 균일한 모래 알갱이의 크기로 표현하는 것을 의미한다. 이러한 등가 모래 거칠기는 실험을 통해 정확하게 확인할 수 있다.
다양한 연구에서 확인된 표면 거칠기의 영향은 터보 기계의 성능에도 영향을 준다. 터보 기계에 사용되는 블레이드에 표면 거칠기가 존재하면 블레이드 주변 경계층이 영향을 받아 경계층이 더 빠르게 층류에서 난류로 천이되거나 경계층의 박리가 더 빨리 일어나게 되어 터보 기계의 성능이 저하된다(9). 특히 압축기는 역압력구배(Adverse pressure gradient)로 인해 경계층의 박리나 유동의 천이가 더 잘 일어나기 때문에 표면 거칠기가 압축기의 성능에 미치는 영향에 관한 면밀한 연구가 필요하다.
블레이드의 표면 거칠기가 압축기의 성능에 미치는 영향은 Leipold, R. 등(10)의 연구에서 확인할 수 있다. Leipold, R. 등은 표면 거칠기(RZ/c=4×10-4)를 가진 압축기 블레이드를 이용해 다양한 레이놀즈수에서(3×105<Rec<1×106) 캐스케이드 실험을 진행했다. 이 연구에서는 실제 압축기 블레이드의 표면 거칠기를 모사한 압축기 블레이드 이용했다. 실험을 통해 표면 거칠기가 없는 블레이드에서는 레이놀즈수가 높아질수록 블레이드의 미드스팬(Mid span)에서 측정한 전압 손실이 감소하는 것을 확인했고 표면 거칠기를 가진 블레이드는 레이놀즈수가 커질수록 흡입면(Suction side)에서 발생하는 난류 경계층의 박리 때문에 전압 손실이 크게 증가하는 것을 확인했다. 이러한 표면 거칠기로 인한 압축기의 성능 저하하는 표면 거칠기가 높아질수록 더 커지게 된다. Bammert와 Milsch(11)는 저속 압축기 캐스케이드 실험을 통해 표면 거칠기가 증가할수록 압축기 블레이드의 형상 손실(Profile loss)이 커지는 것을 확인했다. 이 연구에서는 5개의 표면 거칠기를 가진 사포를 이용해(2.3×10-4<KS/c<5.6×10-3) 표면 거칠기를 모사했고 블레이드의 형상 손실이 압축기 블레이드 후단 부분에서 발생하는 경계층 박리로 인해 표면 거칠기가 없는 기존 모델보다 2%에서 10%까지 증가하는 것을 확인했다. 위 연구를 통해 압축기 블레이드의 표면 거칠기는 압축기의 성능 저하를 가져오고 표면 거칠기가 높을수록 더 큰 성능 저하를 가져온다는 것을 확인할 수 있다.
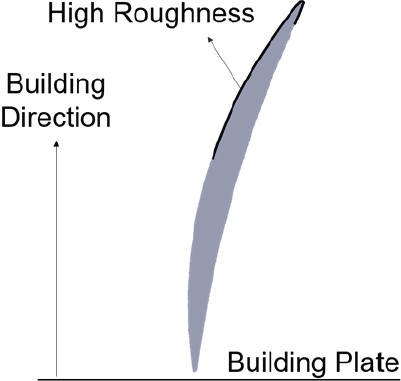
PBF를 이용한 적층 제조를 통해 제작된 압축기 블레이드의 경우 압축기 블레이드가 가지고 있는 캠버각(Camber angle)으로 인해 블레이드 표면이 적층의 방향과 이루는 각도가 위치별로 달라진다. 적층 제조 부품의 표면 거칠기는 제품의 형상이 적층의 방향과 이루는 각도가 커질수록 증가하기 때문에(12) Fig. 2와 같이 제품의 형상이 적층의 방향과 이루는 각도가 큰 부분에서 상대적으로 높은 표면 거칠기가 발생한다. 하지만 기존 연구의 경우 터보 기계 운전 시 블레이드 표면에 발생하는 표면 거칠기를 참고하여 표면 거칠기의 영향성을 평가하였기 때문에 적층 제조 시 발생하는 특정 부분의 표면 거칠기가 공력 성능에 미치는 영향에 대한 실험적, 수치해석적 연구 결과가 부족하다. 따라서 본 연구에서는 적층 제조를 이용해 압축기 블레이드를 제작할 때 선단 흡입면에 주로 발생하는 상대적으로 높은 표면 거칠기가 압축기 블레이드의 공력 성능에 미치는 영향을 선형 캐스케이드 실험을 통해서 확인했다. 또한 표면 거칠기 효과를 모사하는 다양한 수치해석 모델을 이용한 수치해석을 통해 표면 거칠기의 영향을 예측했다.
2. 실험방법
2.1 실험 장치 및 측정 방법
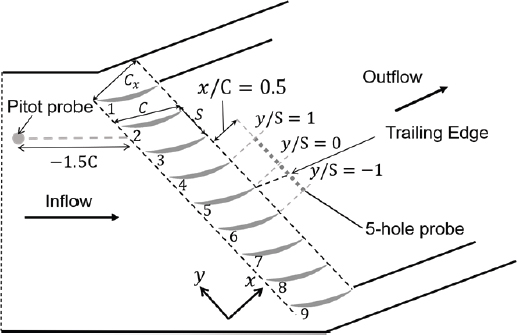
본 연구에서는 저속 선형 압축기 캐스케이드 실험을 통해 적층 제조 시 발생하는 압축기 블레이드의 표면 거칠기가 공력 성능에 미치는 영향을 상온, 상압 환경에서 평가했다. 주 유동은 블로워 (Blower)에서부터 시작하여 디퓨저 (Diffuser), 정체실 (Settling Chamber), 컨트랙션 (Contraction)을 지나 시험 부(Test Section)로 흐른다. 코드 길이 레이놀즈수(Rec)는 연구의 대상이 되는 가스터빈의 압축기 유동을 상사할 수 있도록 해당 압축기의 레이놀즈수를 참고하여 입구 유속을 기준으로 2.9×105로 설정했다. 선형 압축기 캐스케이드 장비는 9개의 압축기 블레이드로 구성되어 있으며 표면 거칠기의 영향을 실험하기 위해 가운데 3개 블레이드는 교체할 수 있게 설계했다. 선형 캐스케이드 장비의 도식적인 모습은 Fig. 3을 통해서 확인할 수 있다.
실험은 22°C의 공기를 이용해 진행하였으며 입구 유동의 속도와 정압(Static Pressure), 전압(Total pressure)은 피토 프로브(Pitot probe)를 이용해 블레이드 1.5C 앞에서 측정했다. 피토 프로브를 이용해 측정한 입구 정압 및 전압은 각각 –271 Pa, 970 Pa이다. 압축기 블레이드의 전압 손실계수(Total pressure loss Coefficient,YP)와 유출 편차각(Deviation angle)은 5공 프로브(5-hole probe)를 이용해 측정했으며 선형 이송 장치를 이용해 블레이드 뒤쪽(x/C=0.5)에서 1개의 피치(-0.5<y/S<0.5)를 측정했다. 전압 손실계수는 식 (5)와 같이 계산했다. 실험에 사용된 블레이드 형상은 축류 압축기 정익(Stator)의 미드스팬이고 형상에 대한 정보는 Table 1을 통해 확인할 수 있다.
| (5) |
2.2 블레이드의 표면 거칠기
본 연구에서는 사포를 이용해 적층 제조 블레이드에서 발생하는 표면 거칠기가 완전히 거친 상태(Fully rough regime)에 있을 때를 실험했다. 적층 제조 시 발생하는 높은 표면 거칠기를 모사하기 위해 80방(80-grit) 사포를 사용했다. 적층 제조 시 발생하는 표면 거칠기는 제작하는 형상에 따라 3 μm∼49 μm의 산술 평균 조도(Arithmetic average roughness, Ra)를 가진다(12). 본 연구에 사용한 80방 사포는 54 μm의 산술 평균 조도를 가지고 있어 적층 제조 시 발생하는 높은 표면 거칠기를 모사한다. 사포의 등가 모래 거칠기는 Flack, K. A. 등(6)의 실험을 통해 얻은 값을 이용했다. 80방 사포의 거칠기 레이놀즈수()는 식 (6)과 식 (7)을 통해서 구했다. 식 (6)은 코드 길이 레이놀즈수를 이용해 거칠기 레이놀즈수를 구할 수 있도록 변형한 식이고 식 (7)은 등가 모래 거칠기를 이용해 마찰 계수를 구하는 식이다(13). 이 실험에서 사용한 80방 사포의 산술 평균 조도와 표면 거칠기 높이, 등가 모래 거칠기, 거칠기 레이놀즈수는 Table 2를 통해 확인할 수 있다.
| (6) |
| (7) |
적층 제조 압축기 블레이드의 표면 거칠기의 위치는 실제 적층 제조 압축기 블레이드를 제작할 때 상대적으로 높은 표면 거칠기가 발생하는 위치로 설정했다. Wildgoose, A. J. 등(12)의 연구에 따르면 적층 제조로 만드는 형상이 적층의 방향과 이루는 각이 커질수록 높은 표면 거칠기를 가진다. 적층 제조로 압축기 블레이드를 제작하는 경우 압축기 블레이드의 캠버각으로 인해 블레이드 표면이 적층의 방향과 이루는 각이 위치마다 달라지고 표면 거칠기 또한 위치마다 달라진다. 따라서 본 연구에서는 실제 적층 제조를 이용해 블레이드를 제작할 때 상대적으로 높은 표면 거칠기가 발생하는 위치를 참고하여 전단으로부터 흡입면의 45%, 압력면의 5%에 표면 거칠기를 부여했다. 표면 거칠기가 발생하는 위치는 Fig. 4를 통해, 실제 사포가 부착된 블레이드는 Fig. 5를 통해 확인할 수 있다. 사포가 부착되는 부분은 사포 두께를 고려하여 실제 블레이드 형상보다 0.3 mm의 단차를 두어 제작했다.
3. 수치해석
3.1 수치해석 모델
본 연구에서는 상용 CFD 프로그램인 ANSYS CFX를 이용해 표면 거칠기 효과를 예측하기 위한 RANS(Reynold –Averaged Navier-Stokes Equation) 수치해석을 진행했다. 수치해석을 위해서 1개의 블레이드 주변 영역을 모사했고 선형 주기조건을 부여했다. 난류 모델은 경계층이 층류에서 난류로 천이되는 것을 확인하기 위해 SST(Shear Stress Model)과 함께 천이 모델인 Gamma-Theta Model(γ-Reθ Model)을 이용했다. 또한 블레이드에 있는 표면 거칠기를 모사하기 위해서 ANSYS CFX내에 있는 White의 표면 거칠기 모델(14)과 Aupiox의 표면 거칠기 모델(15)을 이용했다.
수치해석의 경계 조건은 선형 캐스케이드 실험을 통해 얻은 값을 사용했으며 난류 강도는 5%로 설정하였다. 수치해석을 위한 격자는 육면체 정렬 격자를 사용했다. 격자 요소(Element) 개수 독립성은 개수가 가장 많은 격자를 이용한 수치해석을 통해 얻은 미드스팬에서 질량 평균한 전압 손실 값과 비교(Yp/Yp,finest)하여 확인했다 (Fig. 6). 요소 개수가 5.11×106개일 때 비교 값이 1에 수렴하여 해당 격자 요소 수를 수치해석에 사용했다. 격자의 모습은 Fig. 7을 통해서 확인할 수 있다. 격자는 블레이드의 경계층을 정확히 모사하기 위해서 블레이드 주변에서 y+가 1 이하가 되도록 했다.
3.2 표면 거칠기 모델
F.M. White와 Majdalani, J.(14)는 식 (3)에서 나타나는 로그층 속도 분포의 이동(∆U+)을 거칠기 레이놀즈수를 통해 식 (8)과 같이 표현했다. 이 식은 균일한 모래 알갱이로 인한 표면 거칠기가 있을 때 로그층의 속도 분포의 이동을 표현하기 때문에 정확한 예측을 위해서는 표면 거칠기의 등가 모래 거칠기를 알아야 한다. White 표면 거칠기 모델은 이 식을 이용해 표면 거칠기의 거칠기 레이놀즈수로부터 경계층의 평균 속도 분포를 변화시켜 표면 거칠기에 의한 효과를 모사한다.
| (8) |
또한, White 표면 거칠기 모델에서는 실제 표면 거칠기에 의해 발생하는 유로 차단 효과(Blockage Effect)를 모사하기 위해서 표면 거칠기가 있는 벽면의 위치를 등가 표면 거칠기 높이의 50%만큼을 이동하여 수치해석에 이용한다(16).
B. Aupoix는(15) 벽 주변의 난류 운동 에너지(Turbulent kinetic energy, )와 고유 소산율(Specific Dissipation, )의 분포가 변화하면 경계층의 속도 분포 또한 변화한다는 사실을 이용해 표면 거칠기에 의한 로그층의 속도 분포 이동(∆U+)을 모사했다. B. Aupoix는 식 (9)와 식 (10)을 이용해 표면 거칠기가 난류 운동 에너지에 미치는 영향을 모사했으며, 식 (11)을 통해 표면 거칠기가 고유 소산율에 미치는 영향을 모사했다.
| (9) |
| (10) |
| (11) |
Aupoix 표면 거칠기 모델은 White 표면 거칠기 모델과 달리 표면 거칠기로 인한 벽면의 이동을 모사하지 않아서 벽면 근처의 격자보다 표면 거칠기가 상대적으로 큰 경우에도 벽면 근처에의 경계층을 정확하게 모사할 수 있다는 장점이 있다(16).
4. 결과 및 고찰
4.1 유출 편차각
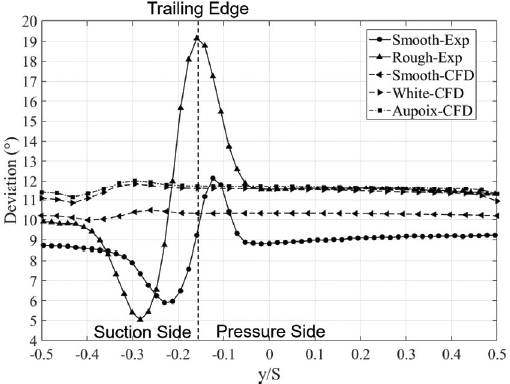
실험과 수치해석의 미드스팬 유출 편차각은 Fig. 8을 통해 확인할 수 있다. 실험에서는 표면 거칠기에 의해 주유동의 유출 편차각이 표면 거칠기가 없는 경우보다 증가하였고 수치해석에서도 표면 거칠기에 의한 주유동 유출 편차각의 증가가 나타났다. 표면 거칠기는 압축기 블레이드를 통과하는 후류에도 영향을 미쳤다. 실험에서는 표면 거칠기가 존재하는 경우 압력면의 후류의 두께는 동일했지만 흡입면의 후류의 두께가 두꺼워졌다. 주유동의 유출 편차각과 후류(Wake)에서 유출 편차각을 비교하였을 때 표면 거칠기가 존재하는 경우 표면 거칠기가 없는 블레이드보다 후류에서 더 큰 최대 유출 편차각을 보였고 또한 더 작은 최소 유출 편차각을 보였다. 하지만, 수치해석의 경우 후류에서 유출 편차각과 주유동의 유출 편차각을 비교하였을 때 표면 거칠기가 있는 경우와 없는 경우 모두 큰 차이를 보이지 않았다.
미드스팬에서 질량 평균 유출 편차각은 Fig. 9를 통해 확인할 수 있다. 실험에서는 미드스팬의 질량 평균 유출 편차각이 표면 거칠기가 없는 압축기 블레이드의 경우 8.6°이고 표면 거칠기가 존재하는 압축기 블레이드의 경우 11.0°로 표면 거칠기가 없는 압축기 블레이드 보다 27.9% 증가했다. 수치해석에서는 미드스팬의 질량 평균 유출 편차각이 표면 거칠기가 없는 경우 10.3°이고 White의 표면 거칠기 모델을 이용한 압축기 블레이드의 경우 11.4°, Aupoix의 표면 거칠기 모델을 이용한 압축기 블레이드의 경우 11.7°로 각각 표면 거칠기가 없는 수치해석과 비교하여 10.7%와 13.6%가 증가했다. 수치해석 결과를 실험 결과와 비교했을 때 수치해석은 유출 편차각을 표면 거칠기의 유무와 상관없이 크게 예측했지만, 표면 거칠기에 의한 유출 편차각의 증가 경향은 잘 예측했다.
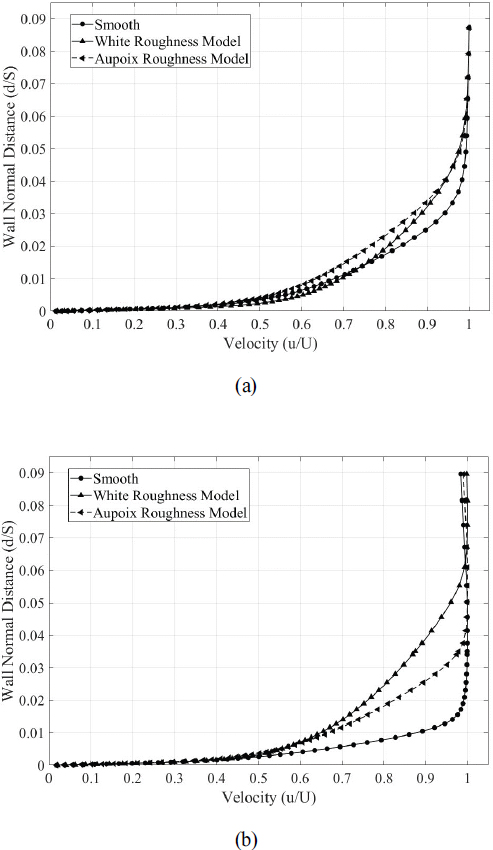
이러한 유출 편차각의 증가는 표면 거칠기로 인한 흡입면과 압력면의 비대칭적인 경계층 두께의 증가에 의한 영향으로 사료된다. Gilge, P(17) 등의 연구에 따르면 표면 거칠기가 흡입면에 미치는 영향이 압력면에 미치는 영향보다 큰 것을 확인할 수 있다. 또한, 본 연구의 실험에서 사용한 압축기 블레이드의 표면 거칠기는 블레이드 전단으로부터 흡입면의 45%, 압력면의 5%에 위치하기 때문에 표면 거칠기에 영향을 받는 흡입면 경계층의 구간이 표면 거칠기에 영향을 받는 압력면 경계층 구간보다 길다. 따라서 표면 거칠기로 인한 흡입면 경계층의 두께 증가가 압력면 경계층의 두께 증가보다 더 커지게 된다. 이러한 경계층 두께의 비대칭적인 변화는 블레이드 표면의 경계층 속도 분포에서 확인할 수 있다. Fig. 10는 수치해석을 통해 x/Cx=0.7에서 얻은 압력면과 흡입면의 경계층의 속도 분포를 보여준다. 블레이드의 경계층에 의해 발생하는 형상 손실은 후단(Trailing edge)의 경계층에 큰 영향을 받기 때문에(18) 블레이드에 부착된 사포가 블레이드 후단 경계층에 미치는 영향을 확인하기 위해 흡입면 유동 박리가 일어나지 않는 위치의 가장 후단인 x/Cx=0.7에서 수치해석을 통해 경계층 속도 분포를 확인하였다. 두 면의 경계층 두께 변화를 비교해보면, 표면 거칠기 모델 적용으로 인한 경계층 두께 증가 효과가 흡입면에서 더욱 크게 나타난다. 압력면과 흡입면의 경계층 두께(δ)와 배제 경계층 두께(Displacement Boundary Layer Thickness, δ*), 운동량 경계층 두께(Momentum Boundary Layer Thickness, θ)는 Table 3을 통해서 확인할 수 있다. 압력면의 경우 배제 경계층 두께가 최대 28.6%가 증가하였지만, 흡입면의 경우 배제 경계층 두께가 최대 159.1%가 증가하였다. 이러한 배제 경계층 두께의 비대칭적인 증가는 주유동의 유효 단면적(Effective area)을 감소시킨다 (Fig. 11). 이러한 효과로 인해 출구 유동각(α2,rough)과 유출 편차각이 증가한다.
4.2 전압 손실계수
실험과 수치해석의 전압 손실계수는 Fig. 12을 통해서 확인할 수 있다. 실험에서는 유출 편차각의 후류 두께 증가 경향성과 동일한 후류 두께 증가가 나타났다. 수치해석에서는 표면 거칠기로 인한 후류 두께 증가 경향성은 유사하였지만, 수치해석의 경우 유출 편차각이 실험값보다 큰 값을 가져 후류의 위치가 실험의 위치보다 흡입면 쪽으로 이동하였다. 실험과 수치해석에서 나타나는 후류 두께의 증가는 표면 거칠기로 인한 경계층 두께의 증가 때문으로 사료된다. 표면 거칠기는 Fig. 10에서 확인할 수 있듯이 경계층 두께를 증가시켰고 이러한 경계층 두께의 증가가 후류 두께 증가를 일으키는 것으로 보인다. 또한, 표면 거칠기는 후류의 전압 손실계수의 최댓값을 증가시켰다. 실험에서는 후류의 전압 손실계수 최댓값이 표면 거칠기가 없는 경우 0.238이고 표면 거칠기가 있는 경우 0.428로 표면 거칠기가 없는 경우와 비교했을 때 79.8% 증가했다. 수치해석에서도 표면 거칠기에 의해 후류의 최대 전압 손실계수가 증가했고 white 표면 거칠기 모델이 실험과 더 비슷한 최대 전압 손실계수의 증가를 보였다. 이러한 최대 전압 손실계수의 증가는 표면 거칠기에 의한 혼합 손실(Mixing loss)의 증가 때문으로 사료된다. 표면 거칠기는 표면 근처에서 강한 난류 혼합을 발생시켜 경계층 내의 난류 강도를 증가시키고 이러한 난류 강도의 증가는 더 큰 혼합 손실을 발생시킨다. 이러한 혼합 손실의 증가로 인해 후류에서 최대 전압 손실계수가 증가하는 것으로 보인다.
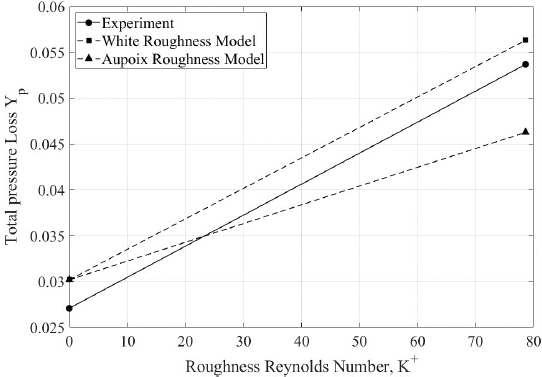
미드스팬에서 질량 평균 전압 손실계수는 Fig. 13을 통해 확인할 수 있다. 실험에서는 표면 거칠기가 없는 압축기 블레이드의 경우 0.0271이고 표면 거칠기가 존재하는 압축기 블레이드의 경우 0.0537로 표면 거칠기가 없는 압축기 블레이드 보다 98.2% 증가했다. 수치해석에서는 미드스팬에서 질량 평균 전압 손실계수는 표면 거칠기가 없는 압축기 블레이드의 경우 0.0302이고 표면 거칠기가 있는 경우는 White 표면 거칠기 모델의 경우 0.0563, Aupoix의 표면 거칠기 모델의 경우 0.0463으로 각각 표면 거칠기가 없는 수치해석의 경우에 비해 86.5%, 53.2%가 증가했다. 표면 거칠기에 의한 미드스팬에서 질량 평균 전압 손실계수 증가의 경우 White의 표면 거칠기 모델이 Aupoix의 표면 거칠기 모델보다 실험과 더 유사한 증가 경향성을 보였다. 이러한 경향성은 White 표면 거칠기 모델의 유로 차단 효과 모사에 의한 것으로 사료된다. 본 연구에서는 블레이드 일부에만 사포를 부착해 표면 거칠기를 부여하였기 때문에 표면 거칠기가 있는 면과 표면 거칠기가 없는 면은 사포의 모래 알갱이 높이로 인해 블레이드 표면의 높이 차이가 발생한다. Aupoix 표면 거칠기 모델은 표면 거칠기가 있는 벽면의 벽면을 이동시키지 않아 표면 거칠기에 의한 높이차에서 발생하는 유동구조를 모사하지 못하였지만, White 표면 거칠기 모델은 표면 거칠기가 있는 벽면을 이동시켜 표면 거칠기가 있는 면과 없는 면의 높이차에서 발생하는 유동 구조를 잘 모사하여 실험과 더 유사한 결과를 보였다.
5. 결 론
본 연구에서는 적층 제조 압축기 블레이드에서 발생하는 표면 거칠기가 압축기 블레이드의 공력 성능에 미치는 영향을 선형 캐스케이드 실험과 두 가지 표면 거칠기 모델을 사용한 수치해석을 통해 분석했다. 본 연구의 결과를 요약하면 다음과 같다.
- 1) 실험과 수치해석 모두 적층 제조 압축기 블레이드에서 발생하는 표면 거칠기에 의해 압력면의 후류 두께는 동일했으나 흡입면의 후류 두께가 증가했고 후류에 발생하는 최대 전압 손실계수 또한 증가했다. 수치해석에서는 적층 제조 압축기 블레이드에서 발생하는 표면 거칠기에 의해 압력면과 흡입면의 경계층 두께가 비대칭적으로 증가했다.
- 2) White의 표면 거칠기 모델과 Aupoix의 표면 거칠기 모델을 이용하여 수치해석을 진행한 결과, 표면 거칠기가 있는 압축기 블레이드의 경우의 유출 편차각은 표면 거칠기가 없는 경우와 비교했을 때 각각 10.7%와 13.6%가 증가했고 실험과 비교하면 표면 거칠기가 있는 경우와 없는 경우 모두 실험보다 큰 유출 편차각을 보였다. 전압 손실은 표면 거칠기가 없는 경우와 비교했을 때 각각 86.5%와 53.2%가 증가했고 실험과 비교하였을 때 White 표면 거칠기 모델이 Aupoix의 표면 거칠기 모델보다 실험에서 측정한 전압 손실의 증가와 더 유사한 경향성을 보였다.
- 3)선형 캐스케이드 실험 결과 적층 제조 압축기 블레이드에서 발생하는 표면 거칠기가 완전히 거친 영역에 있는 경우 표면 거칠기가 없는 경우와 비교했을 때 미드스팬에서 질량 평균한 유출 편차각은 27.9%가 증가했고 전압 손실계수는 98.2%가 증가했다.
Acknowledgments
이 논문은 2022년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UI220023JD).
References
-
Blakey-Milner, B., Gradl, P., Snedden, G., Brooks, M., Pitot, J., Lopez, E., Leary, M., Berto, F., and Du Plessis, A., 2021, “Metal Additive Manufacturing in Aerospace: A Review,” Materials & Design, Vol. 209, 110008.
[https://doi.org/10.1016/j.matdes.2021.110008]

-
Dahotre, N. B., Pantawane, M. V., and Sharma, S., 2022, Laser-Based Additive Manufacturing: Modeling, Simulation and Experiments, Wiley-VCH, Weinheim.
[https://doi.org/10.1002/9783527828814]

-
Kadivar, M., Tormey, D., and McGranaghan, G., 2021, “A review on turbulent flow over rough surfaces: Fundamentals and theories.”, International Journal of Thermofluids, Vol. 10, pp. 100077.
[https://doi.org/10.1016/j.ijft.2021.100077]

-
Schlichting, H., & Gersten, K., 2016, Boundary-layer theory, Springer, Germany.
[https://doi.org/10.1007/978-3-662-52919-5]

-
Clauser, F. H., 1954, “Turbulent boundary layers in adverse pressure gradients,” Journal of the Aeronautical Sciences, Vol. 21, No. 2, pp. 91-108.
[https://doi.org/10.2514/8.2938]

-
Flack, K. A., Schultz, M. P., and Connelly, J. S., 2007, “Examination of a critical roughness height for outer layer similarity,” Physics of Fluids, Vol. 19, No. 9.
[https://doi.org/10.1063/1.2757708]

- Nikuradse, J., 1933, “Laws of flow in rough pipes,” VDI-Forchungsheft 361, Series B, Vol. 4 (English translation NACA TM 1292, 1950).
-
Schlichting, H., 1936, “Experimentelle untersuchun- gen zum rauhigkeitsproblem,” Ingenieur-Archiv, Vol. 7, No. 1, pp. 1-34.
[https://doi.org/10.1007/BF02084166]

-
Bons, Jeffrey P., 2010, “A Review of Surface Roughness Effects in Gas Turbines,” ASME Journal of Turbomachinery, Vol. 132, No. 2, 021004.
[https://doi.org/10.1115/1.3066315]

-
Leipold, R., Boese, M., and Fottner, L., 2000, “The influence of technical surface roughness caused by precision forging on the flow around a highly loaded compressor cascade,” J. Turbomach, Vol. 122, No. 3, pp. 416-424.
[https://doi.org/10.1115/1.1302286]

-
Bammert, K., and Milsch, R., 1972, “Boundary layers on rough compressor blades,” ASME, Turbo Expo: Power for Land, Sea, and Air, Vol. 79818, pp. V001T01A047.
[https://doi.org/10.1115/72-GT-48]

-
Wildgoose, A. J., Thole, K. A., Subramanian, R., Kersting, L., and Kulkarni, A., 2022, “Impacts of the Additive Manufacturing Process on the Roughness of Engine Scale Vanes and Cooling Channels,” Turbo Expo: Power for Land, Sea, and Air, Vol. 86045, pp. V06BT13A025.
[https://doi.org/10.1115/GT2022-84063]

- Gollos, W. W., 1953, Boundary layer drag for non-smooth surfaces, Rand Corporation, USA.
- White, F. M., and Majdalani, J., 2006, Viscous fluid flow, McGraw-Hill, New York.
-
Aupoix, B., 2015, “Roughness corrections for the k-ω shear stress transport model: Status and proposals.” Journal of Fluids Engineering, Vol. 137, No. 2, pp. 021202.
[https://doi.org/10.1115/1.4028122]

- Ansys, C. F. X., 2020, “ANSYS CFX-Solver Theory Guide,” Ansys CFX Release, pp. 157-161.
-
Gilge, P., Seume, J. R., and Mulleners, K., 2018, “Analysis of local roughness combinations on the aerodynamic properties of a compressor blade,” AIAA, Aerospace Sciences Meeting, pp. 0345.
[https://doi.org/10.2514/6.2018-0345]

- Denton, John D., 1993, “Loss mechanisms in turbomachines,” American Society of Mechanical Engineers, Vol. 78897, pp. V002T14A001.