수소 다이어프램 압축기 유동-구조 연성해석 방법론 개발
Abstract
The diaphragm compressors used in hydrogen fuel cell vehicle charging stations undergo repetitive structural deformation of the metal diaphragm in both upward and downward directions. Due to this characteristic, the capacity and lifespan of the compressor must be designed considering the stress distribution acting on the metal diaphragm. In this study, a 2–way fluid-structure interaction analysis methodology was introduced to derive the stress distribution acting on the metal diaphragm. The analysis was conducted for a single cycle with the suction and exhaust valves. In the fluid analysis results, the pressure changes of oil and hydrogen due to the piston motion of the oil piston wall, as well as the deformation of the metallic diaphragm, were observed. Moreover, based on these findings, it was possible to calculate the mass flow rates at the intake and exhaust valves. In the structural analysis results, the maximum stress was observed at the edge of the diaphragm. When the oil piston was positioned at Top Dead Center (TDC), the diaphragm experienced its highest levels of deformation and stress. The stress at this maximum stress point was approximately three times the average stress. Therefore, when designing the diaphragm, it is imperative to consider the concentration of stress in this specific region.
Keywords:
Hydrogen diaphragm compressor, Fluid-solid interaction analysis, Stress키워드:
수소 다이어프램 압축기, 유동-구조 연성 해석, 응력1. 서 론
수소 연료전지 자동차의 충전 스테이션에서는 수소를 일정 압력 이상으로 압축할 것이 요구되는데, 이를 위해서 주로 다이어프램 압축기가 사용되고 있다. 다이어프램 압축기는 왕복동식 압축기보다 작은 압축 용량을 가지고 있지만, 수소를 고압으로 압축할 수 있고 순도를 99.9 % 수준 이상으로 유지할 수 있다. 현재 대형 상용차인 수소 버스 등의 수소 연료전지 자동차의 수가 증가하고 있음을 고려할 때, 차량용 수소 충전 스테이션에서 사용되는 수소 압축기의 압축 용량을 증대할 필요성이 있다.
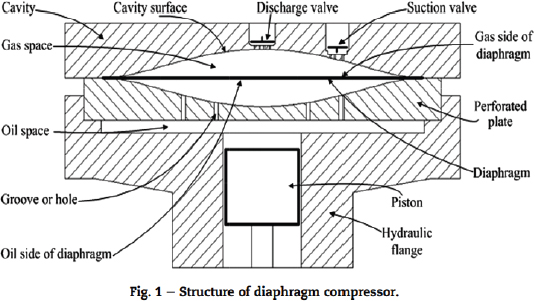
다이어프램 압축기는 Fig. 1과 같이 크게 가스 압축부(Gas Space), 금속 다이어프램, 유압 구동부(Oil Space)로 구성된다. 다이어프램 압축기의 한 행정은 흡입과정과 압축과정으로 진행된다. 수소가스가 흡입 밸브(Suction Valve)로 흡입되는 흡입과정에서는 피스톤이 BDC(Bottom Dead Center)로 이동하면서 금속 다이어프램은 아래 방향으로 변형된다. 이후 수소가스가 압축되어 배기 밸브(Discharge Valve)로 배기되는 배기과정에서는 피스톤이 TDC(Top Dead Center)로 이동하면서 금속 다이어프램은 유압으로 인해 위 방향으로 변형되며, 수소를 배기 압력까지 압축한다. 즉, 압축 과정에서 금속 다이어프램은 위, 아래로 변형을 반복하게 되고, 이는 다이어프램의 피로 파괴를 초래한다. 따라서, 다이어프램 압축기의 캐비티 용량 증대를 위해서는 수소의 흡입과정과 압축과정 중 금속 다이어프램에 작용하는 응력에 대한 분석이 반드시 선행되어야 한다. 특히, Li et al.은 금속 다이어프램의 균열의 경우 압축기에서 발생하는 대표적인 고장 모드로서 주로 다이어프램의 중앙 부분, 가장자리 부분, 그리고 perforated plate의 그루브와 접하는 부분에서 주로 균열이 발생한다고 밝혔다(1).
그 중, 중앙 부분과 가장자리 부분의 균열은 캐비티 형상에 영향을 받아 발생하는데, 이와 관련하여 Chen et al.은 다이어프램이 캐비티 면에 접할 때, generatrix 알고리즘을 사용함으로써 다이어프램의 응력을 감소시키기 위한 캐비티 형상을 제안하였다(2).
또한, Jia et al.은 오일 공급량이 미달될 때 다이어프램이 perforated plate의 그루브에 달라붙으며 응력이 발생하여 파단이 발생하는 것을 보였고, 그루브를 따라 국소적으로 발생하는 radial 응력이 다이어프램이 굽혀지며 생기는 응력과 비등함을 보였다(3).
위의 선행 연구들은 구조 해석만을 사용하여 최적 캐비티 형상 및 다이어프램 내 응력 분포를 산출하였으며, 해당 연구에서 다이어프램에 가해지는 압력과 같은 경계 조건들은 균일하다고 가정되었다.
이러한 점을 반영하여 Choi et al.은 체크밸브를 모델링하는 방안을 탐색하고, 이를 수소 다이어프램 압축기에 반영한 유동-구조 연성 해석을 수행하여 금속 다이어프램의 변형과 가스부의 압력 상승을 확인하였으나(4), 금속 다이어프램에 작용하는 구조 응력과 변형 정도에 대해서는 분석이 이루어지지 않았다.
따라서, 본 논문에서는 2–way FSI (Fluid Solid Interaction, 이하 FSI) 유동 해석 기법을 활용하여 수소, 오일 등의 유체와 금속 다이어프램 간의 유동-구조 상호작용을 고려한 유동 해석 방법론을 정립하였으며, 압축사이클 한 행정에 대한 해석을 수행함으로써 금속 다이어프램에 작용하는 응력 분포 데이터를 도출하고, 나아가 구조적 취약점을 분석하였다.
2. 수치해석 기법
2.1 FSI 해석 기법
본 연구에서는 해석 영역을 Fig. 2와 같이 수소 (가스 압축부), 금속 다이어프램, 오일 (유압 구동부) 세 부분으로 구분하였고 유체 물질은 유동해석을, 고체 물질은 구조해석을 수행하였다. 오일 피스톤 하부벽에 부착되어 있는 크랭크의 피스톤 운동으로 인한 변위를 경계 조건으로 설정하였으며, 이러한 운동은 오일압력을 변화시켜 금속 다이어프램의 변형을 야기한다. 또한, 변형된 금속 다이어프램은 오일챔버 반대편에 위치한 수소를 압축하거나 팽창시킨다. 위와 같은 상호작용을 모델링하기 위해 본 연구에서는 유동-구조 연성 해석(FSI) 기법을 사용하였다.
FSI 기법은 정보 교환의 iteration 여부에 따라 1–way와 2–way로 구분할 수 있다. 1–way FSI 방법은 유동해석의 결과를 유동의 경계에 위치한 구조물로 전달하여 구조물의 변형을 계산하는 방식으로, 변형된 구조물이 다시 유동에 영향을 미치지 않은 채로 다음 time step을 계산하게 된다. 반면, 2–way FSI 방법은 유동 및 구조의 변형을 iterative 하게 계산하며, 잔차가 원하는 수준 이하로 도달하면 다음 time step으로 넘어가 계산을 수행한다. 2-way FSI 방법은 각 time step에서 추가적인 iteration 계산을 수행하므로 계산 시간이 더 오래 걸리지만, 변형된 구조물이 유동에 미치는 영향이 큰 경우에 적합하고 정확도가 높다는 장점이 있다.
본 연구에서는 금속 다이어프램으로 인해 수소가 압축되거나 팽창되는 물리 현상을 모사하기 위해 1-way 및 2–way FSI 해석을 수행하였다. Fluid Solver로는 ANSYS Fluent을, Structure Solver로는 ANSYS Mechanical APDL을 사용하였고, Workbench와 System Coupling 프로그램을 활용하여 두 Solver 간 정보 교환과 FSI 해석을 수행하였다.
2.2 형상 모델링 설정
본 수치해석에서는 계산 시간을 단축하기 위해 축대칭을 가정하여 모델링을 수행하였다. 가스 압축부, 유압 구동부, 금속 다이어프램은 Fig. 2 (b)와 같이 15 ° 회전체 형상으로 모델링하였다.
격자의 종횡비는 CFD 해석 정확도에 큰 영향을 미치므로 격자 생성 시 종횡비를 일정 범위 내로 유지해주어야 한다. 한편, 다이어프램 압축기에서는 금속 다이어프램의 파단이 발생하였을 때 가스와 오일이 직접적으로 혼합되는 것을 방지하기 위해 여러 층의 다이어프램을 겹쳐서 사용한다. 본 연구에서 금속 다이어프램은 반경/두께가 300 배 이상인 원판이 세 겹으로 쌓여 있는 구조이며, 원판 세 겹의 격자를 종횡비를 고려하여 생성한다면 격자의 개수가 많아져 구조해석 계산 시간이 많이 소요된다.
구조해석에서 활용되는 2D shell method는 이차원 표면에 격자를 생성한 후에 가상의 두께를 부여하여 3차원 격자로 모델링하는 기법으로 주로 길이 대비 두께가 얇은 판의 구조해석에서 사용된다. 2D shell method를 사용한 경우 3차원 격자에 비해 자유도가 줄어들기 때문에 계산이 효율적이다. 따라서 본 해석에서는 Fig. 3과 같이 2D shell method를 적용하여 두께가 동일한 세 겹의 격자를 생성하였고, 세 겹의 다이어프램에 대한 변위 및 응력을 계산하였다. 이들 간의 접촉 방식(connection)은 “Bonded” 조건을 부여하였다.
2.3 해석 조건 설정
본 수치해석은 오일 피스톤 하부벽의 피스톤 운동에 따른 수소, 오일, 금속 다이어프램의 거동을 분석하기 위해 비정상 해석을 수행하게 된다. 해석의 초기조건은 수소의 흡입과정 중 금속 다이어프램이 변형되지 않고 유동이 정지한 상태(크랭크 각 90 °)로 설정하였다. 이때 수소, 오일의 압력과 온도는 수소의 흡입 압력(Psuction), 흡입 온도(Tsuction)와 동일한 값을 부여하였다.
오일 피스톤의 하부벽은 Dynamic Mesh 기능을 활용하여 피스톤 운동에 따라 위아래로 진동하도록 모사하였다. 가스 압축부에서의 흡입밸브와 배기밸브는 각각 pressure inlet(Psuction), pressure outlet(Pexhaust) 조건을 부여하였고, “Prevent Reverse Flow” 기능을 활용하여 유체가 설정 압력에 도달하였을 때 한쪽 방향의 흐름만 가능하도록 모사하였다. 가스 압축부 및 유압 구동부 영역에서 다이어프램과 접하는 벽은 deforming wall 조건을 부여하여 구조해석 결과로부터 변형된 변위량을 전달받을 수 있도록 하였고, 축대칭 결과를 얻기 위해 양쪽 대칭면에는 symmetry 경계조건을 추가하였다.
본 연구의 해석 영역은 가스 압축부, 유압 구동부, 금속 다이어프램의 세 영역으로 구분된다. 먼저 가스 압축부의 경우 ANSYS Fluent Database에서 제공하는 “Hydrogen(H2)”의 물성치를 사용하였으며 “Ideal Gas” 조건을 부여하였다. 유압 구동부의 경우, ANSYS Fluent Database에서 제공하는 “Engine Oil”의 물성치를 사용하였다. 피스톤 운동으로 인한 압력 변화를 모사하기 위해 “Compressible – Liquid” 조건을 부여하였다. 금속 다이어프램의 경우, Mechanical APDL의 Engineering Data에서 제공하는 stainless steel을 사용하였으며 밀도, 영률은 각각 7850 kg/m3, 200 GPa이다.
구조해석에서는 금속 다이어프램 중 유체와 접촉하고 있어 압력 정보를 교환하는 안쪽 영역은 “Fluid–Solid Interface” 조건을 부여하였고, 나머지 영역은 “Fixed Support” 조건을 부여하였다. 이 때 다이어프램의 형상은 반경에 비해 두께가 얇으므로 구조해석 시 기하비선형을 고려하였다. 또한 구조해석의 초기조건은 다이어프램의 변형이 발생하지 않은 상태로 설정하였다.
2.4 격자 적용 방식 설정
격자의 크기와 형상은 수치해석 계산의 정확도와 소요 시간에 영향을 미치기 때문에 적절한 격자 생성은 수치해석에서 필수적이다. 해석 소요 시간은 노드의 개수에 따라 결정되며, 일반적으로 같은 크기의 형상에 대하여 육면체(hexa) 격자를 사용한 경우 사면체(tetra) 격자에 비해 노드 수가 적어 계산 시간이 적게 소요된다. 하지만 형상이 복잡하여 육면체 격자로 구성하기 어려운 경우 사면체 격자를 사용해야 한다. 본 연구에서는 복잡한 형상의 격자를 생성하기 위해 사면체 격자를 사용하였다. 앞서 언급된 본 연구의 수치 해석 조건 및 격자 적용 방식은 Table 1에 정리되어 있다.
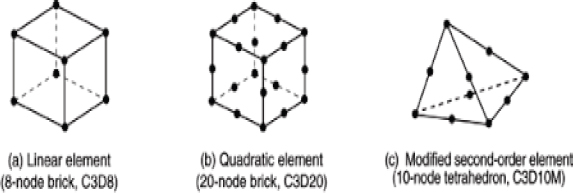
Fig. 4는 격자 요소 내 노드를 배치하는 두 가지 방법을 보여준다. 1차원 linear 방법은 각 요소의 꼭짓점에 노드를 배치시키는 방식이며, 2차원 quadratic 방법은 꼭짓점에 위치한 노드들을 잇는 모서리의 중심에 노드를 추가하는 방식이다. 굽힘 변형이 발생한 구조물 형상을 모사하는 경우 2차원 quadratic 방식의 성능이 더 좋은 것으로 알려져 있다. 따라서 본 해석에서 금속 다이어프램의 격자 생성 시에는 2차원 quadratic 방법을 사용하였다.
2.5 Dynamic Mesh
ANSYS Fluent 프로그램의 Dynamic Mesh 기능은 경계조건이 시간에 따라 변하거나(boundary zone), 그로 인해 주위의 격자가 변형될 때(cell zone) 활용할 수 있는 기능이다.
경계조건이 시간에 따라 변하는 움직임은 선형운동, 회전운동과 같은 강체운동 혹은 외력에 의한 변형 두 가지로 구분할 수 있다. 본 유동해석에서는 크랭크가 부착된 오일 피스톤 하부벽만이 강체 움직임에 해당되며, 오일 피스톤 하부벽과 접촉하는 옆면, 다이어프램과 접촉하는 가스 압축부 및 유압 구동부의 벽면은 변형 움직임에 해당된다. 이러한 경계조건의 움직임으로 인해 유동 영역 내부의 격자는 변형되므로 “deforming” 격자 조건을 부여하였다.
Dynamic Mesh 기법으로는 크게 layering, smoothing, remeshing이 있다. Layering 기법은 경계면에서 cell이 생성되거나 소멸되면서 해석 영역을 변형시키는 방법으로, 직선운동이나 회전운동을 모사하는데 주로 사용된다. Smoothing 기법은 격자를 압축하거나 늘리면서 해석 영역을 변형시키는 방법으로, 새로운 격자가 생성되거나 기존 격자가 소멸되지 않기 때문에 총 격자수는 보존된다. Remeshing 기법은 상대적으로 큰 움직임이나 회전/직선운동을 병행하는 움직임을 모사해야 하는 경우에 적합한 방법으로, 설정한 cell의 제한 범위를 벗어나는 경우 cell/face의 격자가 재생성된다. 본 유동해석에서는 세 가지 기법을 모두 활용하였고, 크랭크가 부착된 오일 피스톤 하부벽의 강체 움직임을 모사하기 위해서 “In-Cylinder” 기능을 사용하였다. Fig. 5는 크랭크 각에 따른 유체 영역의 격자 변화를 보여준다.
3. 수치해석 결과
3.1 해석 시간 간격 dt 탐색
Fig. 6는 2–way FSI 해석의 해를 도출하는 과정을 보여준다. 각 time step(tn)에서 수행하는 계산 과정은 다음과 같다.
- (1) 구조물의 변형량을 업데이트한다.
- (2) 유동해석, 구조해석의 계산을 수행한다.
- (3) 경계면에서 압력 정보와 변위 정보를 비교한다. 유동해석, 구조해석, System Coupling 총 3가지 계산 결과의 잔차가 설정값보다 큰 경우 (1)(2)을 반복하며, 3가지의 잔차 모두 설정값보다 작거나 최대 System Coupling 횟수에 도달한 경우 다음 time step (tn+1=tn+dt) 계산을 수행한다.
주어진 총시간에 대하여 시간 간격 dt를 크게 설정할수록 (1)∼(3) 계산을 반복하는 총 step number가 감소하지만 각 time step에서 피스톤 운동 변위가 커지기 때문에 그에 따른 유동해석, system coupling의 수렴에 필요한 시간이 길어지게 된다. 따라서 구조해석, 유동해석, system coupling 이 모두 수렴하고 총 계산 시간을 최소화하는 최적의 시간 간격을 탐색하기 위한 해석을 수행하였다. 총 시간은 피스톤 행정의 1 주기(0.2 초)의 1 %에 해당하는 0.002 초로 선정하였으며, 세 가지 시간 간격 10, 20, 100 μsec 에 대해 해의 수렴성 및 계산소요 시간을 비교하였다.
각 시간 간격에 대해 유동해석 및 system coupling 수렴에 필요한 iteration 횟수를 Table 2에 정리하였다. 유동해석의 경우 질량, 모멘텀, 에너지 보존식에 대한 잔차 기준을 각각 10-6, 10-3, 10-3으로 설정하였다. system coupling의 경우 오일, 수소부 압력값과 수소 접촉면의 변위, 오일 접촉면의 변위 등 총 4가지 물성치의 rms 변화량이 10-2 이하가 되는 것을 수렴 기준으로 설정하였다.
시간 간격 dt가 100 μsec인 경우 오일 압력이 급격하게 변화하여 유동해석 자체가 수렴하지 않았다. 시간 간격 dt가 20 μsec인 경우 유동해석은 iteration 100회 이내에서 수렴하였지만, 구조해석 변위와 유동해석 압력을 비교하는 system coupling 계산 과정에서 해가 수렴하지 않았다. 시간 간격 dt가 10 μsec인 경우 유동해석 결과와 system coupling이 모두 수렴하였다. 이때 대부분의 time step에서 system coupling은 10 회 이내로 수렴하여 다음 time step 계산이 진행되었다. 따라서 본 연구에서는 dt를 10 μsec으로 설정하여 해석을 진행하였다.
3.2 격자 독립성 검증 (Mesh Independence Test)
격자 독립성 검증은 동일해석 조건 하에서 다양한 노드 개수를 사용하여 격자의 크기가 계산 결과에 영향을 미치지 않는 것을 검증하는 것이다. 해석 수행 시 주요 물리량이 허용된 오차 내에서 수렴하는 지점을 파악하여, 과도한 노드 개수로 인해 계산 시간이 불필요하게 늘어나는 것을 방지한다.
본 연구에서는 격자 독립성 검증을 통해 격자 크기 및 노드 개수를 결정하였다. 검증에 사용된 case의 수는 총 3가지로, 각각의 노드 개수 및 해석 결과를 Table 3에 정리하였다. 3가지 경우에 대하여 배기밸브가 작동되기 직전(크랭크 각 292 °) 세 겹의 금속 다이어프램 금속판이 받는 평균 응력을 비교하였다. 이때 금속 다이어프램은 세 겹으로 구성되어 있기 때문에 각각을 “수소”, “가운데”, “오일”로 표기하였으며, 평균 응력의 오차는 노드 개수가 가장 많은 case 1을 기준으로 계산하였다.
노드 개수가 감소함에 따라 다이어프램 금속판 응력에 대한 평균 오차가 각각 0.54 %, 1.19 %로 증가함을 알 수 있다. 이를 바탕으로 case 1, 2는 노드 개수와 독립적으로 계산 결과가 유사하게 수렴하였다고 판단하였고 case 2를 사용하여 해석을 수행하였다.
3.3 유동 해석 결과
먼저 한 행정 과정에 대하여 1-way FSI를 적용하여 해석한 결과, 압축 행정 과정에서 다이어프램의 변형으로 인한 수소의 압력 상승이 충분히 발생하지 않았으며, TDC (배기)에 도달하기 전 에러가 발생하였다. 이는 1-way FSI 의 경우 구조의 변형이 유동에 영향을 미치지 않기 때문에 다이어프램의 상승으로 인한 수소 영역의 부피 및 압력 변화를 잘 모사하지 못하였기 때문이라고 생각된다.
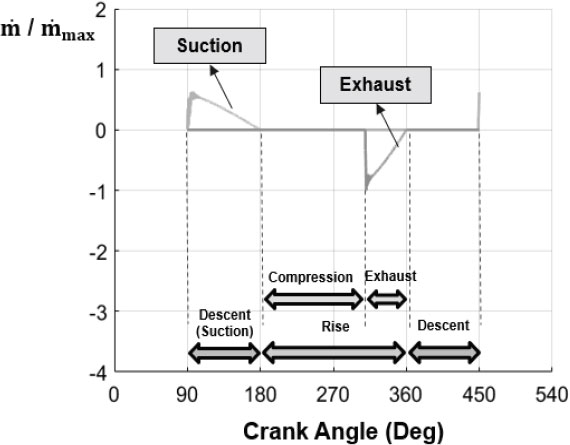
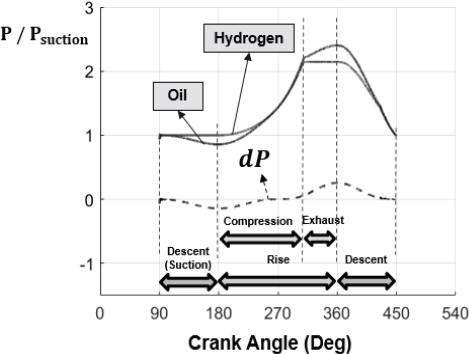
한 행정 과정에 대하여 2-way FSI를 적용한 유동해석 결과는 Figs. 7, 8, 9와 같다. Fig. 7은 한 행정 과정 중 오일 피스톤 하부벽과 다이어프램의 위치 변화를, Fig. 8은 흡배기 밸브의 질량유량 변화를, Fig. 9는 수소와 오일의 압력 변화를 보여준다. 밸브 질량유량을 기준으로 한 행정을 흡입, 압축, 배기, 하강 네 가지 과정으로 구분하였다.
수소가 흡입되는 90 °∼180 ° 구간에서 수소의 압력은 초기압력(Psuction)으로 유지되며 흡입밸브를 통해 흡입과정이 진행된다. 이때 오일의 압력은 감소하고, 두 유체의 압력 차이로 인해 다이어프램이 아래로 변형된다.
이후, 피스톤이 TDC까지 상승하면서 오일의 압력이 상승하여 다이어프램을 변형시킨다. 이로 인해 수소 영역의 부피는 감소하고 수소의 배기압력에 도달하기 전까지 압력이 증가한다. 만약 수소의 압력이 배기압력에 도달하게 되면 수소의 압력은 유지되며 배기밸브를 통해 배기과정이 진행된다. 이때 두 유체의 압력 차이로 인해 다이어프램은 위 방향으로 변형이 발생한다.
피스톤이 TDC를 지난 후 360 °∼ 450 ° 구간에서는 피스톤이 하강함에 따라 수소와 오일의 압력이 점점 감소하여 초기 압력인 Psuction에 도달한다.
3.4 구조해석 결과
Fig. 7은 오일 피스톤 하부벽이 한 행정 과정 중 움직이는 이동거리를 보여준다. 초기조건을 기준으로 BDC와 TDC까지의 이동 거리는 각각 크랭크 반경의 0.89배, 1.11배이다.
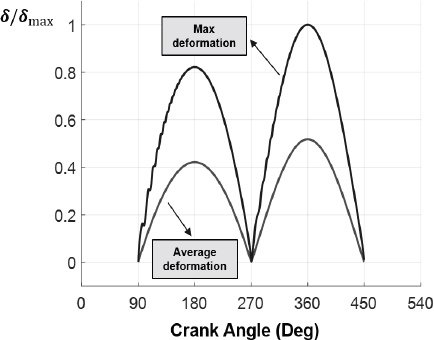
크랭크 각도에 따라 변형된 다이어프램의 평균 변위와 최대 변위(중심 변위)를 측정하여 Fig. 10과 같이 나타내었다. 다이어프램의 평균 변위는 변형이 발생한 원판 영역에 대하여 다이어프램 세 겹의 평균 변위를 계산하였고, 최대 변위는 다이어프램 중심부 변위값으로 도출하였다.
금속 다이어프램과 오일 피스톤 하부벽의 반경을 고려하였을 때 가스 압축부의 부피 변화량과 유압 구동부 피스톤 영역의 부피 변화량은 0.2 % 오차 이내로 유지되었다. 또한 다이어프램은 한 행정 과정 중 중심부에서 최대 변형이 발생하였고, 피스톤이 BDC와 TDC에 위치할 때 최대 변위는 각각 평균 변위의 1.97배, 1.95배로 측정되었다.
Fig. 11은 피스톤이 TDC에 위치하였을 때 다이어프램에 작용하는 응력 분포를 보여준다. 수소와 오일에 의해 힘을 받는 부분과 고정된 부분의 경계가 되는 가장자리(edge) 영역에서 최대 응력이 발생하였고. 피스톤이 BDC에 위치하였을 때에도 가장자리 영역에서 최대 응력이 발생하였다.
Fig. 12는 한 행정 과정 중 다이어프램의 응력변화를 보여준다. 각 time step에서 세 겹의 다이어프램에 작용하는 평균 응력 및 최대 응력을 계산하였다. 피스톤이 BDC와 TDC에 위치하고 있을 때 평균응력 및 가장자리 응력은 극댓값을 가지며, TDC에서 행정 최댓값을 가진다. 본 형상의 다이어프램 모델에서는 가장자리 영역이 가장 큰 구조적 취약점이며, 향후 수소 다이어프램 압축기 설계 시 이를 반드시 고려해야 함을 알 수 있다.
4. 결 론
본 연구의 결과를 요약하면 다음과 같다.
- 1) ANSYS Workbench의 system coupling을 활용하여 수소 다이어프램 압축기에서 발생하는 물리적 현상에 대한 2–way FSI 해석 방법론을 정립하였다. 본 해석의 domain은 2 가지 유체(수소, 오일)와 1 가지 고체 영역(금속)을 포함하며, 가스 압축부, 유압 구동부, 다이어프램 영역은 축대칭을 가정하여 15 ° 회전체 형상으로 모델링하였다. ANSYS Fluent의 Dynamic Mesh 기능을 사용하여 오일 피스톤 하부벽의 피스톤 운동과 다이어프램 경계면 주위에서의 격자의 변형을 모사하였다.
- 2) 유동해석 결과, 오일 피스톤 하부벽의 피스톤 운동으로 인한 오일, 수소의 압력 변화와 금속 다이어프램의 변형을 확인하였다. 또한, 이를 바탕으로 흡입밸브 및 배기밸브에서의 질량 유량을 계산할 수 있었다.
- 3) 구조해석 결과, 최대 응력 지점은 다이어프램의 가장자리임을 확인하였고, 특히 오일 피스톤이 TDC에 위치하였을 때 다이어프램의 변위와 응력이 최댓값을 가졌다. 최대 응력 지점에서의 응력은 다이어프램 평균 응력의 약 3배 가량으로, 다이어프램 설계 시 해당 부분의 응력 집중을 반드시 고려해야 한다.
Acknowledgments
본 연구는 한화파워시스템이 지원하는 공동연구센터 과제의 일환으로 수행되었습니다. 이에 깊이 감사드립니다.
References
-
Li, J., Jia, X., Wu, Z., and Peng, X., 2014, “The cavity profile of a diaphragm compressor for a hydrogen refueling station,” International Journal of Hydrogen Energy, Vol 39, No. 8, pp. 3926-3935.
[https://doi.org/10.1016/j.ijhydene.2013.12.152]

- Chen, J., Jia, X., Xue, C, and Peng, X., 2015, “Design and Validation of new cavity profiles for diaphragm stress reduction in a diaphragm compressor,” International Conference on Compressors and their Systems, London, UK.
-
Jia, X., Chen, J., Wu, H., and Peng, X., 2016, “Study on the diaphragm fracture in a diaphragm compressor for a hydrogen refueling Station,” International Journal of Hydrogen Energy, Vol. 41, No. 15, pp. 6412-6421.
[https://doi.org/10.1016/j.ijhydene.2016.02.106]

- Choi, B.S., Yoon, H.G., Yoo, I.S., and Park, M.R., 2010, “Two-way FSI Simulation of the diaphragm compressor and non-return check valve,” Korean Society for Computational Fluids Engineering, Jeju, South Korea.