발전용 가스터빈의 성능 해석 모델에 따른 부분부하 운전 모사 정확도 비교

1. 서 론

최근 2030 국가 온실가스 감축목표 및 세계적으로 탄소중립에 대한 논의가 확산됨^(1,2)에 따라 재생에너지를 이용한 발전이 증가⁽³⁾하고 있다. 하지만 재생에너지는 간헐적으로 전력을 생산하는 변동성과 불확실성의 문제가 있기에 유연하게 부하추종이 가능한 가스터빈을 활용하여 변동성 문제에 대응하고 있다⁽⁴⁾. 재생에너지의 발전량이 계획 발전량에 대하여 하향 변동성을 나타내면 가스터빈의 발전량을 증가시킴으로써 부족한 전력수요를 해결할 수 있고, 반면 재생에너지의 발전량이 상향 변동성을 나타내어 계획 발전량을 초과할 경우 가스터빈의 발전량을 감소시킴으로써 이를 제한할 수 있다⁽⁵⁾. 즉, 가스터빈은 전력수요의 잦은 변동⁽⁶⁾에 대응하기 용이하고 많은 시간 동안 부분부하 운전을 수행하고 있다. 따라서 가스터빈의 부분부하 성능을 분석하는 것은 중요한 요소이다.

가스터빈은 부분부하 운전 과정에서 연료유량을 조절하여 출력을 제어한다. 또한 복합화력발전의 효율을 향상시키기 위하여 압축기의 가변 입구 안내깃(Variable inlet guide vane, VIGV) 각도를 조절하여 공기유량을 제어한다^(7,8). 연료유량과 공기유량이 변화하면 터빈 출구 온도(Turbine exhaust temperature, TET), 압축기 출구 온도(Compressor discharge temperature, CDT), 압력비(Pressure ratio, PR) 등 가스터빈의 주요 성능 변수들에도 변화가 발생한다. 즉, 터빈 해석 모델이나 냉각공기 추기 모델과 같은 성능 해석 모델에 따라 출력과 효율 등 예측된 부분부하 성능에 영향을 미치게 된다. 따라서 탈설계 해석 모델링 또는 냉각 모델링을 적용함에 있어 주의가 필요하다.

터빈 운전에 대한 정보가 없을 경우에 단순화를 위해서 터빈이 초킹(Choking)되어 운전하고 터빈 효율도 일정하다고 가정하기도 한다^(9-11). 이 단순화 모델은 가스터빈이 높은 압력비의 운전상태 즉, 대체로 부하가 높은 상태에서 운전할 경우 큰 오차 없이 높은 정확도를 보인다. 하지만 낮은 압력비의 부분부하 운전에서는 실제로 터빈이 초킹되지 않을 뿐더러 효율 역시 감소할 것이다.

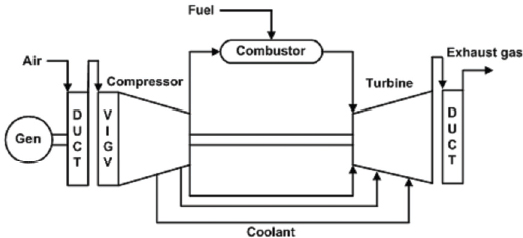
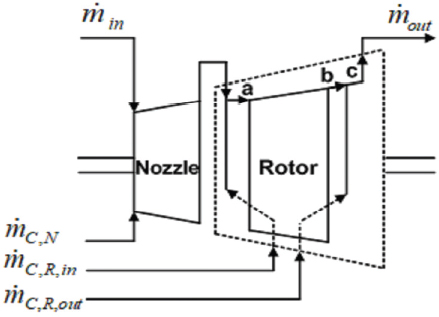
터빈 냉각공기 추기를 고려함에 있어서도 충분한 설계 정보가 없을 경우에 Fig. 1과 같이 압축기의 끝단에서만 냉각공기를 추기하는 간소화된 추기 모델을 이용한다. 이러한 단순화된 모델링은 출력이 충분히 높은 운전 구간에서는 성공적으로 사용되기도 한다^(12-14). 그러나 저부하 구간에서는 가스터빈이 낮은 유량으로 운전하기 때문에 열 균형(Heat balance)을 맞추기 위해 냉각공기의 물성치가 상대적으로 더 중요해진다⁽¹⁵⁾. 따라서 Fig. 2에 예시한 바와 같이 냉각공기를 압축기의 끝단만이 아닌 중간단에서도 추기하는 구체화된 추기 모델링의 필요성이 높다.

Fig. 1

Simplified cooling air extraction gas turbine model

Fig. 2

Detailed cooling air extraction gas turbine model

본 연구에서는 터빈 해석 모델과 냉각공기 추기 모델에 따른 부분부하 성능 모사 정확도를 비교분석하고자 하였다. 터빈 해석 모델 측면에서는 무차원유량과 터빈 효율이 감소하는 현상을 반영할 수 있는 터빈 성능 선도(Performance map)를 사용한 터빈 해석 모델과 단순화된 초킹 가정 해석 모델을 비교하였다. 냉각공기 추기 모델 측면에서는 Fig. 2와 같은 구체화된 냉각공기 추기 모델과 Fig. 1과 같은 간소화된 추기 모델을 이용한 해석 결과를 비교하였다. 그 후 종합적으로 어떠한 성능 해석 모델이 가스터빈의 부분부하 운전을 더 상세하게 모사할 수 있는지 제안하였다.

2. 시스템 모델링

2.1 개요

가스터빈 부분부하 운전 모사 정확도를 비교하기 위해 두 가지의 터빈 해석 모델과 두 가지의 냉각공기 추기 모델을 이용하였다. Table 1에는 가스터빈 성능 해석 모델에 대하여 총 4가지의 Case로 분류하여 나타내었다.

Table 1

Cases of the gas turbine performance analysis model

각 Case에 대한 설계 모델링과 탈설계 모델링에 사용한 프로그램은 MATLAB⁽¹⁶⁾을 이용하여 개발한 In-house program이다. 구성부 해석에는 질량보존법칙 및 에너지보존법칙을 적용하였고, 공기, 연료 및 연소가스와 같은 작동유체는 이상 기체 혼합물로 가정하였다. 연료는 저위발열량이 49,299 kJ/kg인 천연가스(메탄 91.33%, 에탄 5.36%, 프로판 2.14%, 부탄 0.95%, 질소 0.22%)를 사용하였으며, 연료는 연소기에서 완전 연소되는 것으로 가정하였다.

2.2 터빈 모델

2.2.1 터빈 설계 모델링

가스터빈의 고온부품인 터빈은 압축기에서 추기한 냉각공기가 터빈의 노즐과 로터에 주입되도록 문헌⁽¹⁷⁾을 참고하여 Fig. 3과 같이 모델링하였다. Case 1∼4에 사용된 터빈 모델링은 하나의 단으로 이루어져 있고 그 합리성은 다양한 연구들^(18-20)을 통해 검증되었다. Case 1, 2의 간소화된 추기 모델의 경우, 터빈의 노즐과 로터 냉각을 위해 압축기의 끝단에서만 추기된 냉각공기가 사용되었다. 반면, Case 3, 4의 구체화된 추기 모델의 경우에는 압축기 끝단과 중간단에서 추기한 냉각공기가 각각 터빈의 노즐과 로터 냉각으로 사용되었다.

Fig. 3

Schematic of coolant flow at single-stage turbine

로터에서는 터빈이 팽창하며, 연소기 출구로부터 주입된 주 유로의 혼합가스와 냉각에 사용된 노즐 냉각공기가 팽창과정에 관여한다. 또한 로터 냉각공기 중 로터 입구(a) 위치에 주입된 유량도 터빈 팽창 일에 관여한다. 로터 출구(b) 위치에 주입된 로터 냉각공기는 팽창 일에 관여하지 않는다. 이때 터빈의 로터 입구와 출구에 주입된 유량은 동일하다고 가정하였다. 터빈의 출력은 식 (1)로 정의되며, 터빈의 등엔트로피효율은 냉각의 영향을 받지 않는 로터 팽창 과정에 대하여 식 (2)와 같이 적용하였다.

$\[ {\dot{W}}_{Turb }=\left({\dot{m}}_{in}+{\dot{m}}_{C,N}+{\dot{m}}_{C,R, in }\right)\cdot \left(h_a-h_b\right) \]$

(1)

$\[ {\eta }_{Turb,isen }=\frac{h_a-h_b}{h_a-h_{b,s}} \]$

(2)

2.2.2 초킹 가정을 이용한 터빈 해석 모델

초킹 가정을 이용한 해석 모델은 터빈이 전체 압력비에 대하여 초킹되어 운전하는 것으로 가정하였다. 터빈의 탈설계해석 시, 전체 압력비에 대하여 준무차원유량이 일정하도록 계산하는 식 (3)과 초기 설계점의 터빈 효율로 유지되는 식 (4)를 사용하였다.

$\[ {\left(\dot{m}\sqrt{RT}/P\right)}_{Turb,inlet}=constant \]$

(3)

$\[ {\eta }_{Turb,off-design}={\eta }_{Turb,design} \]$

(4)

2.2.3 성능 선도를 이용한 터빈 해석 모델

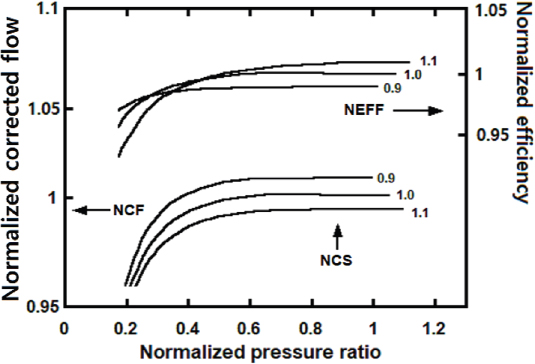
터빈 성능 선도를 이용한 해석 모델은 Fig. 4와 같이 무차원 파라미터로 구성된 선도를 사용하였다. 성능 선도에 사용된 무차원 파라미터들은 식 (5)∼(8)과 같이 무차원화된 회전속도(Normalized corrected speed, NCS), 유량(Normalized corrected flow, NCF), 압력비(Normalized pressure ratio, NPR) 및 효율(Normalized efficiency, NEFF)로 구성된다. 탈설계 과정에서 작동점은 터빈 성능 선도와 압축기 성능 선도의 매칭(Matching)과정⁽²¹⁾에 의해 결정된다.

Fig. 4

Performance map of the turbine.

$\[ NCS=\frac{CS}{C{S}_{Design }}, where CS=\frac{N}{\sqrt{T_{in }}} \]$

(5)

$\[ NCF=\frac{M}{M_{Design }}, where M=\frac{\dot{m}\sqrt{R{T}_{in }}}{P_{in }} \]$

(6)

$\[ NPR=\frac{PR-1}{P{R}_{Design}-1}, where PR=\frac{P_{in }}{P_{out }} \]$

(7)

$\[ NEFF=\frac{\eta }{{\eta }_{Design }} \]$

(8)

2.3 압축기와 냉각공기 추기 모델

2.3.1 간소화된 추기 모델

간소화된 추기 모델은 흡입된 공기가 모두 압축기에서 압축되는 것으로 해석한다. 또한 냉각공기는 압축기의 끝단에서만 추기하며, 추기된 냉각공기의 물성치는 압축기 출구의 물성치와 동일하다. 추기된 냉각공기는 터빈 노즐과 로터 입출구에 나누어 주입된다. 설계점에서 터빈 냉각을 위해 사용되는 냉각공기의 유량은 터빈 입구 온도(Turbine inlet temperature, TIT)와 터빈 로터 입구 온도(Turbine rotor inlet temperature)를 이용하여 계산하였다. 터빈 노즐 냉각에는 TIT 정보를 이용하여 압축기 입구 유량의 7.0%가 사용되었고, 터빈의 로터 입구 냉각에는 TRIT 정보를 이용하여 6.2%의 유량이 사용되었다. 또한 터빈의 로터 출구 냉각은 로터 입구 냉각에 사용된 유량과 동일한 6.2%의 비율을 적용하였다. 압축기의 소모 동력은 식 (9)를 사용하였고 등엔트로피효율은 식 (10)을 이용하여 계산하였다.

$\[ {\dot{W}}_{Comp }=\dot{m}\left(h_{out }-h_{in }\right) \]$

(9)

$\[ {\eta }_{Comp ,isen}=\frac{h_{out ,s}-h_{in }}{h_{out}-h_{in}} \]$

(10)

2.3.2 구체화된 추기 모델

구체화된 추기 모델은 냉각공기의 추기 위치에 따라 물성치를 다르게 모델링한다. 분석한 대상 가스터빈의 압축기는 18단으로 구성되며 추기 위치는 중간단인 13단, 17단, 그리고 끝단인 18단이다. 끝단에서 추기되는 냉각공기의 물성치는 압축기 출구의 압력과 온도와 동일하다. 중간단에서 추기되는 냉각공기의 압력과 온도는 단의 압력비를 동일하게 가정한 식 (11)과 폴리트로픽 효율을 이용한 식 (12)를 통해 계산하였다. 터빈의 노즐 냉각은 간소화된 추기 모델과 동일하게 압축기의 끝단에서 추기된 냉각공기가 사용된다. 반면 로터 냉각의 경우 17단에서 추기된 냉각공기는 로터 입구 냉각으로 사용되고 13단에서 추기된 냉각공기는 로터 출구 냉각으로 사용된다. 터빈 냉각에 사용되는 냉각공기의 유량은 간소화된 추기 모델과 동일한 TIT와 TRIT의 정보를 이용하였다. 터빈의 노즐 냉각에는 압축기 입구 유량의 7.0%, 로터 입출구 냉각에는 각각 6.2%의 유량이 사용되었다. 구체화된 추기 모델에서 압축기 소모 동력은 식 (13)과 같이 중간단에서 추기되는 냉각 유량을 고려하여 계산하였다.

$\[ {\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}}={\left(\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\right)}^{1/\mathrm{ }\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}} \]$

(11)

$\[ \frac{T_{out}}{T_{in }}={\left(\frac{P_{out}}{P_{in }}\right)}^{\frac{\gamma -1}{\gamma {\eta }_{\propto c}}} \]$

(12)

$\[ {\dot{W}}_{Comp }=\sum _{n= stage }^{18}\left({\dot{m}}_{in,n}-{\dot{m}}_{coolant ,n}\right)\cdot \left(h_{out ,n}-h_{in ,n}\right) \]$

(13)

2.3.3 압축기 탈설계 모델링

압축기의 탈설계 해석에는 Fig. 5에 나타낸 성능선도가 사용된다. 성능선도는 식(5)~(8)로 표현된 무차원 파라미터들도 구성하였다. 부분부하 운전 시 공기유량을 조절하기 위하여 VIGV를 사용한다. VIGV 각도가 닫히며 압축기 입구 공기유량이 감소하는 물리적 현상을 해석하기 위하여 압축기 성능 선도를 스케일링⁽²²⁾하는 방법을 사용하였다. 식 (14)∼(16)에서 각 스케일링 팩터(Scaling factor)는 유량, 압력비, 효율이 감소하는 것을 반영한다. 각 스케일링 팩터는 VIGV 각도에 따라 비례하여 변화하도록 설정하였다.

Fig. 5

Performance map of the compressor

$\[ {\dot{m}}_{scaled}={\dot{m}}_{original}\times S{f}_{IGV, flowrate } \]$

(14)

$\[ P{R}_{scaled}=P{R}_{original}\times S{f}_{IGV,PR} \]$

(15)

$\[ {\eta }_{scaled}={\eta }_{original}\times s{f}_{IGV, efficiency} \]$

(16)

2.3.4 냉각 유량 탈설계 해석

탈설계 해석 시 압축기 입구 공기유량 대비 터빈의 노즐 및 로터 냉각에 사용된 유량의 비율은 식(17)과 같이 설계점에서의 비율과 동일하다고 가정하였다.

$\[ {\left.{\left.\frac{{\dot{m}}_{coolant }}{{\dot{m}}_{comp,air }}\right)}_{off-design}=\frac{{\dot{m}}_{coolant }}{{\dot{m}}_{comp,air }}\right)}_{design} \]$

(17)

2.4 대상 가스터빈 및 설계점 모사

대상 가스터빈은 ISO 외기조건(15℃, 101.325kPa, 60% R.H.) 및 정격회전속도 3600rpm에서 최대 출력이 164.6MW인 F급 가스터빈이다. 가스터빈의 설계점은 실제 운전데이터를 참고하여 모사하였다. Table 2에는 운전데이터의 설계점과 함께 In-house program을 이용하여 모사한 구체화된 추기 모델과 간소화된 추기 모델의 설계점을 나타내었으며, 시스템 출력과 효율은 식 (18), (19)를 이용하여 계산하였다. 추기 모델에 따라 압축에 필요한 동력에 차이가 발생하였고, 이로 인하여 간소화된 추기 모델의 압축기 소모 동력은 구체화된 추기 모델에 비하여 4.4MW 더 높았다. 또한 간소화된 추기 모델은 구체화된 추기 모델보다 30.4kJ/kg 더 높은 엔탈피의 로터 입구 냉각공기가 사용되어 터빈 팽창 직전 온도가 1.5℃ 더 높았다. 이로 인하여 두 추기 모델이 동일한 출력과 효율을 나타낼 때 간소화된 추기 모델은 구체화된 추기 모델보다 터빈 등엔트로피효율에서 1.1%p 더 높은 상태로 계산되었다.

Table 2

Design parameters of F-class gas turbine of field data and simulation model

$\[ {\dot{W}}_{GT}=\left({\dot{W}}_{Turb }-{\dot{W}}_{Comp }/{\eta }_{mech }\right)\cdot {\eta }_{gen} \]$

(18)

$\[ {\eta }_{GT}={\dot{W}}_{GT}/{\left(\dot{m}\cdot LHV\right)}_f \]$

(19)

2.5 부분부하 운전 과정

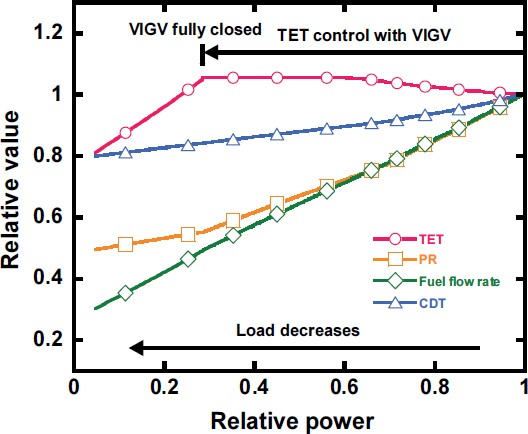
부분부하 운전은 대상 가스터빈의 실제 운전데이터와 문헌⁽²³⁾의 부하 조절 방식을 참고하여 최대 출력인 전부하부터 최소부하까지 부하를 낮추는 운전과정을 모사하였다. Fig. 6은 부분부하 운전 과정에서 터빈 출구 온도, 압축기 출구 온도, 압력비, 연료유량의 변화를 나타내었다. 초기 설계점인 전부하부터 연료유량을 조절하여 부하를 감소시키고 동시에 VIGV 각도를 닫음으로써 TET가 증가한다. TET는 제한 온도인 650℃에 도달할 때까지 증가한다. TET는 부하 약 56%부터 VIGV 각도가 최대한으로 닫히는 부하 약 28%까지 유지된다. 그 후 연료유량만을 조절하여 최소부하인 약 3.8%까지 부하를 낮춘다.

Fig. 6

Partial load operation process of field data

2.6 성능 선도 수정 과정

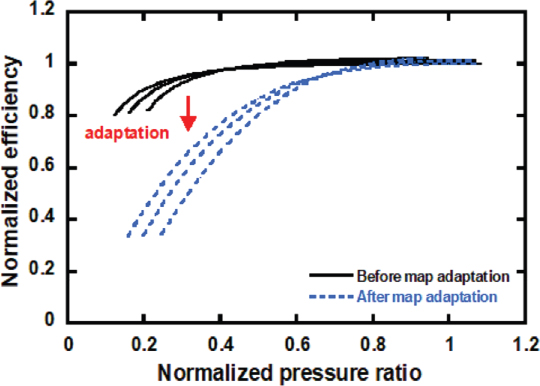
실제 성능 선도는 가스터빈 제조업체로부터 제공되지 않아 기존의 성능 선도를 이용하여 대상 가스터빈에 유효한 성능 선도로 수정(adaptation)⁽²⁴⁾하여야 한다. 압축기의 압력비 성능 선도에서는 VIGV 각도에 따라 유량과 압력비가 유사한 변화를 나타내기에 유량과 압력비에 해당되는 스케일링 팩터가 동일한 비율로 변화하여 선도가 스케일링 되도록 하였다. 효율 성능 선도의 경우, Fig. 7과 같이 VIGV 각도에 따른 스케일링 팩터의 변화율을 조절하여 기존의 압축기 효율보다 더 낮은 효율로 스케일링 되도록 수정하였다. 압축기 성능 선도 상 작동점은 선도가 스케일링되면서 동시에 이동한다. 효율 스케일링 팩터 수정 후, 작동점은 기존의 위치에서 변화하게 되고, 수정된 작동점을 통해 결정된 유량, 압력비, 효율을 통해 성능 변수들을 계산한다. 이는 압축기 성능 선도를 사용하는 Case 1∼4를 대상으로 수행되었다.

Fig. 7

Adaptation process of the compressor efficiency map by scaling factor adjustment

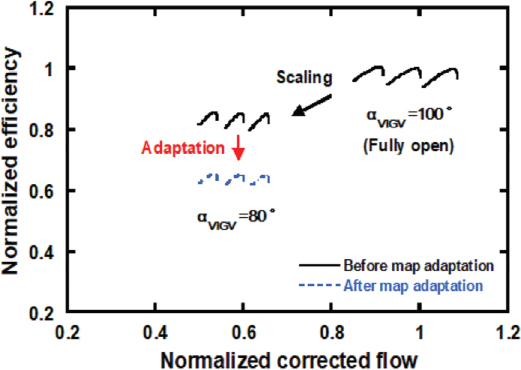
터빈 성능 선도는 탈설계 과정에서 스케일링 되지 않고 작동점이 선도 상에서 이동한다. 따라서 성능 선도의 형상 변화를 통해 작동점 이동에 변화를 주었다. 터빈이 높은 압력비 구간에서는 초킹되어 운전하는 현상을 고려하여 유량 성능 선도에 대한 별도의 수정과정을 거치지 않고, 효율 성능 선도에 대해서만 형상 변화를 수행하였다. 효율 선도는 Fig. 8과 같이 압력비가 감소할수록 기존보다 터빈 효율이 더욱 감소하도록 감소율을 적용하였다. 해당 과정은 터빈 성능 선도를 사용하는 Case 2와 Case 4를 대상으로 수행되었다. 수정된 작동점을 통해 계산된 성능 변수가 운전데이터와 비교하였을 때 1% 이내의 오차를 가지도록 압축기 효율 스케일링 팩터 조절과 터빈 효율 성능 선도의 형상변화를 수행하였다.

Fig. 8

Adaptation process of the turbine efficiency map by changing shape of map

3. 결과 및 논의

3.1 성능 선도 수정 결과

Case 2와 Case 4에 대하여 수정된 성능 선도를 사용하여 가스터빈의 부분부하 운전 모사 결과를 확인하였다. 그리고 성능 선도 수정 전 모사 결과와 함께 각 파라미터의 평균오차를 비교하여 오차 개선 정도를 확인하였다. 평균 오차는 평균절대비오차(MAPE)를 이용하여 계산하였으며, 부하 전체 범위에 대하여 운전데이터를 실제값으로 설정하고 성능 해석 모델을 이용한 결과를 예측값으로 설정하였다. 그 후 평균오차의 크기가 더 작은 모델을 모사 정확도가 우수한 모델로 평가하였다.

Fig. 9에는 구체화된 추기 모델을 사용하는 Case 4에 대하여 성능 선도 수정 전과 수정 후의 TET, CDT, PR, 연료유량의 모사 결과를 운전데이터와 함께 나타내었다. 각 파라미터는 설계점에 대한 상대 값으로 나타내었다. 먼저 Case 4의 경우, VIGV 각도를 조절하여 TET를 제어하는 구간에서는 TET 모사 결과와 운전데이터 사이의 오차는 거의 없었다. 하지만 VIGV가 완전히 닫혀서 TET를 제어하지 않을 때, 수정되지 않은 성능 선도를 사용한 TET　모사 결과는 14.3%의 오차가 발생했다. 반면 수정된 성능 선도를 사용하면 오차는 0.4%로 감소하는 것을 확인할 수 있었다. 수정되지 않은 성능 선도를 사용한 경우, 전체 부하 구간에서 CDT, PR, 연료유량의 평균오차는 각각 1.1%, 4.4%, 6.5%였다. 반면 수정된 성능 선도를 사용하였을 때, CDT, PR, 연료유량의 평균오차는 각각 0.5%, 1.1%, 1.4%로 감소하는 것을 확인하였다. Case 2의 경우, 성능 맵 수정 후 TET, CDT, PR, 연료유량의 평균오차가 각각 1.1%, 0.5%, 1.2%, 1.3%로 감소하였다. 따라서 수정된 성능 선도는 대상 가스터빈의 부분부하 운전을 모사하는데 적합함을 확인하였다.

Fig. 9

Partial load simulation results before and after adaptation to the performance map of case 4

3.2 터빈 해석 모델에 따른 결과 비교

터빈 성능 선도 해석 모델과 초킹 가정 해석 모델의 부분부하 운전 모사 정확도를 비교하였다. 먼저 비교대상인 두 해석 모델은 구체화된 추기 모델을 사용하는 Case 3, 4이다. 전부하부터 최소부하인 3.8%까지의 해석 결과를 운전데이터와 비교하여 주요 성능 변수들의 평균오차를 확인하였다.

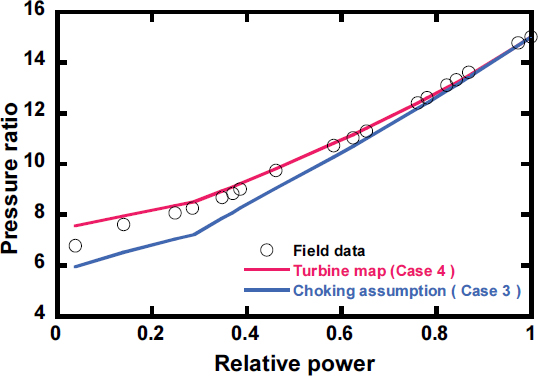
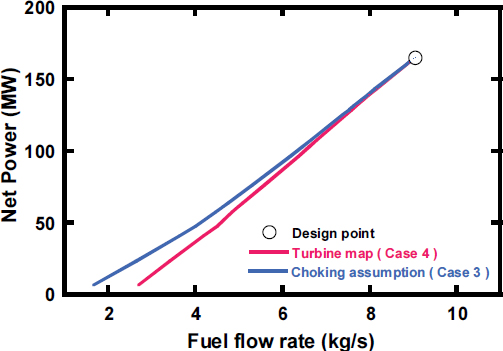
Fig. 10에는 두 해석 모델의 TET 모사 결과를 운전데이터와 함께 나타내었다. VIGV 각도 조절을 통하여 TET를 제어하는 구간에서는 두 해석 모델을 사용한 모사 결과와 운전데이터 간의 오차가 거의 없었다. 하지만 VIGV 각도가 최대한 닫히고 난 이후의 저부하 구간에서는 터빈 해석 모델에 따라 모사 정확도에 차이가 발생하였다. Case 4는 운전데이터와 비교하여 0.4%의 오차가 발생하였지만, Case 3의 경우 14.7%의 평균오차가 발생하였다.

Fig. 10

Results of TET according to turbine analysis model

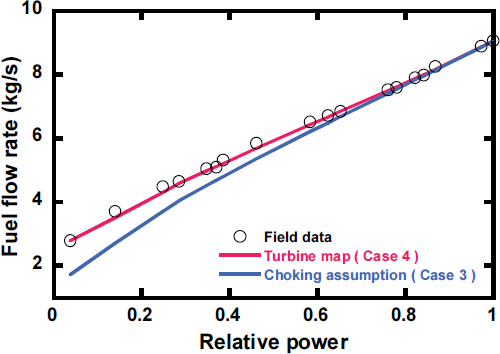
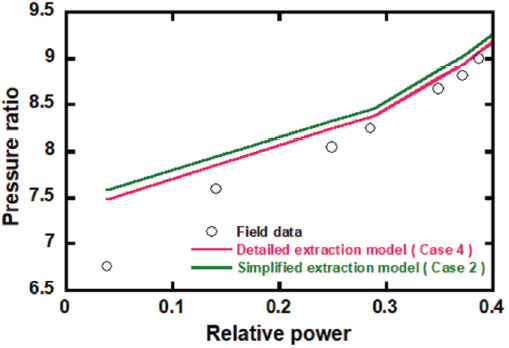
Figs. 11, 12, 그리고 13에는 각각 CDT, PR, 연료유량에 대하여 터빈 해석 모델에 따른 결과를 운전데이터와 함께 나타내었다. Case 3의 경우, CDT는 1.1%, PR은 4.4% 그리고 연료유량은 6.2%의 평균오차가 나타났다. 이는 Case 4의 평균오차인 0.5%, 1.1%, 1.4%에 비해 높은 오차이다.

Fig. 11

Results of CDT according to turbine analysis model

Fig. 12

Results of PR according to turbine analysis model

Fig. 13

Results of fuel flow rate according to turbine analysis model

Figs. 14, 15에는 터빈 해석 모델에 따른 터빈의 무차원유량과 효율에 대한 결과를 나타내었다. 초킹을 가정하는 Case 3의 경우, 전체 부하 범위에서 터빈의 무차원유량과 효율이 설계점의 값을 유지하였다. 반면 터빈 성능 선도를 사용하는 Case 4의 결과에서는 부하가 낮아짐에 따라 해당 값이 설계점으로부터 선도를 따라 감소하였다.

Fig. 14

Results of turbine normalized corrected flow according to turbine analysis model

Fig. 15

Results of turbine normalized efficiency according to turbine analysis model

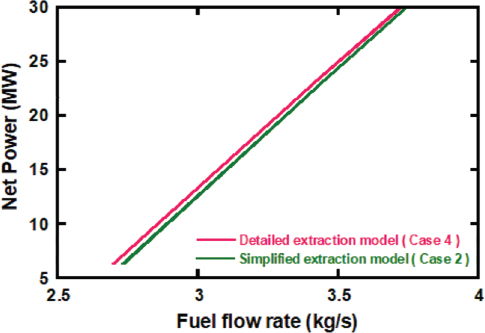
터빈 성능 선도를 사용하는 Case 4는 부분부하 과정에서 낮은 터빈 효율로 인하여 특정 부하의 터빈 출력을 만족시키기 위한 연료유량이 Case 3에 비해 더 요구되었다. 따라서 Figs. 16, 17과 같이 부분부하 과정 중 터빈 성능 선도 모델이 초킹 가정 해석 모델에 비해 동일한 연료유량에서 시스템 출력과 효율이 더 낮았다.

Fig. 16

Results of net power due to fuel flow rate reduction according to turbine analysis model

Fig. 17

Results of net efficiency due to fuel flow rate reduction according to turbine analysis model

추가적으로 Case 1, 2의 간소화된 추기 모델을 사용하였을 때 두 터빈 해석 모델에 따른 모사 정확도를 비교하였다. Case 1의 해석 결과에서 TET, CDT, PR, 연료유량의 평균오차는 각각 14.1%, 1.1%, 4.9%, 6.5%가 발생하였지만, Case 2의 해석 결과에서 1.1%, 0.5%, 1.2%, 1.3%가 확인되었다. 초킹을 가정한 터빈 해석 모델은 부하가 낮아질수록 운전데이터와의 오차가 점차 증가하였고 특히 저부하 구간에서 모사 정확도가 낮았다.

가스터빈의 잦은 부하 변동 구간인 전부하부터 약 80% 부하까지는 두 터빈 해석 모델을 이용한 모사 결과에서 운전데이터와의 큰 오차가 발생하지 않았다. 이는 해당 구간에서 두 해석 모델이 유사한 터빈 효율을 나타내고 초킹 영역과 근접한 운전을 함으로써 높은 모사 정확도를 보였다. 그 후 부하가 낮아짐에 따라 터빈 성능 선도 해석 모델은 터빈 효율과 무차원유량의 감소를 반영하지만, 초킹 가정 해석 모델의 경우 터빈 효율과 무차원유량이 설계점의 값을 유지하면서 실제 운전과의 오차가 점차 증가하였다. 터빈 효율의 감소로 낮은 터빈 비출력을 갖는 터빈 성능 선도 모델은 탈설계 과정에서 더 많은 연료유량 및 터빈 입구 유량이 요구되었다. 이로 인하여 압축기 또한 많은 입구 유량이 요구되었고 초킹을 가정한 해석 모델보다 높은 압력비가 계산되었다. 결과를 통해 높은 부하 구간에서는 Case 1, 3과 같이 초킹을 가정하는 해석 모델을 사용하여도 충분한 성능 모사가 가능하였다. 반면 낮은 부하 구간에 대하여 성능 모사를 할 경우 Case 2, 4의 성능 선도를 사용하는 해석 모델이 더 높은 모사 정확도를 확보할 수 있었다.

3.3 냉각공기 추기 모델에 따른 결과 비교

앞서 수행한 연구에서 터빈 해석 시 성능 선도를 사용한 해석 모델이 더 높은 정확도를 보였다. 따라서 터빈 성능 선도를 사용하는 경우인 Case 2, 4에 대하여 냉각공기 추기 모델에 따른 부분부하 운전 모사 결과를 비교하였다.

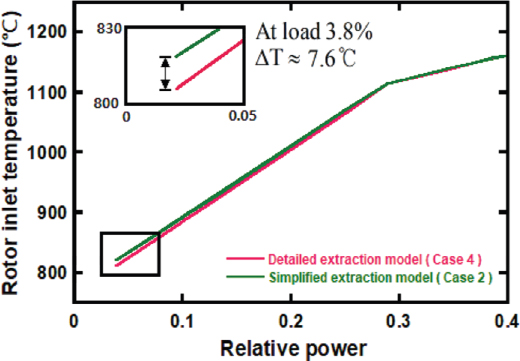
Fig. 18에는 저부하 구간에서 두 추기 모델의 로터 입구 온도에 대한 결과를 나타내었다. 로터 입구 온도의 경우 운전데이터 정보가 없기에 최소부하 3.8%에서 두 추기 모델의 온도를 비교하였다. Case 2의 경우 로터 입구 온도가 819.1℃이고 Case 4는 811.5℃로서 Case 2가 Case 4에 비해 로터 입구 온도가 7.6℃ 더 높았다.

Fig. 18

Results of rotor inlet temperature according to cooling air extraction model at low-load range

Figs. 19, 20에는 TET와 PR에 대한 두 추기 모델의 시뮬레이션 결과를 운전데이터와 함께 나타내었다. VIGV가 최대한 닫히는 약 28% 부하부터 최소부하 3.8%까지의 저부하 구간에서 운전데이터와의 평균오차를 비교하였다. 먼저 TET의 경우, Case 4는 0.4%의 평균오차가 확인되었다. 반면 Case 2는 1.1%가 확인되었다. PR의 경우, Case 2는 5.8%, Case 4는 6.3%의 평균오차가 확인되었다. 또한 최소부하에서 TET를 비교하였을 때, Case 2는 Case 4에 비해 6.0℃ 더 높은 상태가 확인되었다. 저부하 구간에서 CDT의 경우, 간소화된 추기 모델이 비교적 더 높은 것을 확인하였으나 두 모델간의 평균절대오차는 약 0.3℃로서 명확한 차이는 발생하지 않았다.

Fig. 19

Results of TET according to cooling air extraction model at low-load range with field data

Fig. 20

Results of PR according to cooling air extraction model at low-load range with field data

동일한 터빈 해석 모델에서 냉각공기 추기 모델에 따른 부분부하 해석 결과를 비교하였을 때, Case 4의 구체화된 추기 모델이 Case 2의 간소화된 추기 모델에 비해 부분부하 운전 모사 정확도가 높았다. 구체화된 추기 모델은 간소화된 추기 모델에 비해 낮은 엔탈피의 냉각공기가 터빈에 주입되었다. 이는 전체 부하 과정에서 터빈 냉각에 효과적이며 로터 입구 온도와 터빈 출구 온도가 더 높은 경향을 보였다. 반면 압축기에서 흡입된 공기가 모두 압축되는 간소화된 추기 모델의 경우 부분부하 과정에서 압축기 소모 동력이 더욱 큰 수치를 나타낸다. 이에 따라 두 모델의 동일한 부하에서 간소화된 추기 모델의 터빈 입구 유량과 압축기 입구 유량이 상대적으로 더 많이 요구되며, 연료유량과 압력비가 구체화된 추기 모델에 비하여 더 높았다. 이로 인하여 Figs. 21, 22와 같이 저부하 구간에서 동일한 연료유량이 사용될 경우 구체화된 추기 모델의 시스템 출력과 효율이 더 높았다.

Fig. 21

Results of net power due to fuel flow rate reduction according to turbine analysis model

Fig. 22

Results of net efficiency due to fuel flow rate reduction according to turbine analysis model

4. 결 론

발전용 가스터빈의 터빈 해석 모델과 냉각공기 추기 모델에 따른 부분부하 운전 모사 정확도를 비교하였다.

먼저, 터빈 해석 모델에 따른 모사 정확도를 비교하였을 때, 전부하부터 잦은 부하 변동 구간인 부하 80%까지는 터빈 성능 선도 해석 모델과 초킹 가정 해석 모델을 이용한 부분부하 해석 결과가 실제 운전과 유사하였다. 그러나 부하 80%이하 구간에서는 터빈 성능 선도 해석 모델은 부분부하 과정에서 터빈 효율과 무차원유량의 감소를 반영하였다. 이는 터빈 효율과 무차원유량이 설계점의 값을 유지하는 초킹 가정 해석 모델에 비해 높은 정확도를 보였다.

다음으로 냉각공기 추기 모델에 따른 결과를 비교하였다. 구체화된 추기 모델은 간소화된 추기 모델에 비해 더 낮은 엔탈피의 냉각공기가 터빈 냉각에 사용되었다. 또한 간소화된 추기 모델은 동일 부하에서 더 높은 압축기 소모 동력을 갖는다. 이로 인하여 간소화된 추기 모델은 부하가 낮아질수록 터빈 출구 온도, 압력비 등 성능 변수들의 모사 정확도가 구체화된 추기 모델에 비해 낮았다.

실제 가스터빈의 부분부하 운전을 모사할 때, 초킹을 가정하여 해석할 경우 주요 성능 변수들의 평균오차가 최대 14.7%가 발생하였지만, 터빈 성능 선도를 사용할 경우 1% 내외로 오차를 감소시킬 수 있었다. 또한 구체화된 추기 모델을 사용함으로써 저부하 구간에서 주요 성능 변수들의 평균오차가 최대 0.7%p 감소하였으며, 최소부하에서는 로터 입구 온도와 터빈 출구 온도가 각각 7.6℃ 6.0℃ 더 낮아지게 되어 실제 운전에 대한 더욱 상세한 모사가 가능하였다. 모사 정확도가 우수한 터빈 성능 선도 해석 모델과 구체화된 추기 모델을 선정함으로써 낮은 유량으로 운전하는 가스터빈의 시동 및 정지과정이나 하부사이클에 대한 해석이 필요한 경우 더 정확한 성능 정보를 제공할 수 있을 것으로 기대된다.

Acknowledgments

본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No.20193310100050)

References

• Arutyunov, Vladimir S. and Georgiy V. Lisichkin., 2017, “Energy resources of the 21st century: Problems and forecasts. Can renewable energy sources replace fossil fuels,” Russian Chemical Reviews, Vol. 86, No. 8, pp. 777. [https://doi.org/10.1070/RCR4723]
• IEA, 2022, World energy outlook 2022, Paris, France: International Energy Agency.
• P. Roy, He, J., Zhao, T. and Singh, Y. V., 2022, “Recent advances of wind-solar hybrid renewable energy systems for power generation: A review,” IEEE Open Journal of the Industrial Electronics Society, Vol. 3, pp. 81-104. [https://doi.org/10.1109/OJIES.2022.3144093]
• Jia, K., Liu, C. and Li, S. and Jiang, D., 2023, “Modeling and optimization of a hybrid renewable energy system integrated with gas turbine and energy storage,” Energy, Vol. 279, Article 116763. [https://doi.org/10.1016/j.enconman.2023.116763]
• G. Guandalini, S. Campanari and M. C. Romano, 2015, “Power-to-gas plants and gas turbines for improved wind energy dispatchability: Energy and economic assessment,” Applied Energy, Vol. 147, pp. 117-130. [https://doi.org/10.1016/j.apenergy.2015.02.055]
• Lee, J. Y. and Cho, Y. S., 2022, “National-scale electricity peak load forecasting: Traditional, machine learning, or hybrid model?,” Energy, Vol. 239, Article 122366. [https://doi.org/10.1016/j.energy.2021.122366]
• Kim, J. H., Kim, T. S., Sohn, J. L. and Ro, S. T., 2003, “Comparative analysis of off-design performance characteristics of single and two-shaft industrial gas turbines,” Journal of Engineering for Gas Turbines and Power, Vol. 125, No. 4, pp. 954-960. [https://doi.org/10.1115/1.1615252]
• Kim, T. S., 2004, “Comparative analysis on the part load performance of combined cycle plants considering design performance and power control strategy,” Energy, Vol. 29, pp. 71-85. [https://doi.org/10.1016/S0360-5442(03)00157-9]
• Kurzke, J., 2007, “About simplifications in gas turbine performance calculations.”, Turbo Expo: Power for Land, Sea, and Air, Vol. 47926, pp. 493-501. [https://doi.org/10.1115/GT2007-27620]
• Kwon, H. M., Moon, S. W. and Kim, T. S., 2020, “Performance enhancement of the gas turbine combined cycle by simultaneous reheating, recuperation, and coolant inter-cooling,” Energy, Vol. 207, pp. 118271. [https://doi.org/10.1016/j.energy.2020.118271]
• Kim, J. S., Park, Y. K. and Kim, T. S., 2022, “Modeling for thermal performance analysis of power generation gas turbines using 1D simulation programs,” The KSFM Journal of Fluid Machinery, Vol. 25, No. 5, pp. 5-11. [https://doi.org/10.5293/kfma.2022.25.5.05]
• Moon, S. W., Kwon, H. M., Kim, T. S., and Sohn, J. L., 2018, “A novel coolant cooling method for enhancing the performance of the gas turbine combined cycle,” Energy, Vol. 160, pp. 625-634. [https://doi.org/10.1016/j.energy.2018.07.035]
• Stathopoulos, P., 2018, “Comprehensive thermodynamic analysis of the humphrey cycle for gas turbines with pressure gain combustion,” Energies, Vol. 11, No. 12, pp. 3521. [https://doi.org/10.3390/en11123521]
• Moon, S. W. and Kim, T. S., 2021, “Simulation of optimizing the partial load performance of a gas turbine combined cycle using exhaust heat recuperation and inlet bleed heating,” Journal of Engineering for Gas Turbines and Power, Vol. 143, No. 6. [https://doi.org/10.1115/1.4048845]
• Yin, S., Gu, C. W. and Ji, X. X., 2015, “Development and validation of a full-range performance analysis model for a three-spool gas turbine cooling,” Energy, Vol. 89, pp. 545-557. [https://doi.org/10.1016/j.energy.2015.06.015]
• MathWorks Inc. MATLAB R2022a; MathWorks Inc.: Natick, MA, USA, 2022.
• Kim, J. H., Kim, T. S. and Moon, S. J., 2016, “Development of program for transient behavior simulation of heavy-duty gas turbines,” Journal of Mechanical Science and Technology, Vol. 30, No. 12, pp. 5817-5828. [https://doi.org/10.1007/s12206-016-1152-z]
• Yun, Y. I., Park, I. Y. and Song, S. J., 2005, “Performance degradation due to blade surface roughness in a single-stage axial turbine,” Journal of Turbomachinery, Vol. 127, pp. 137-143. [https://doi.org/10.1115/1.1811097]
• Kwon, H. M., Moon, S. W., Kim, T. S., Kang, D. W., Sohn, J. L. and Lee, J., 2019, “A study on 65% potential efficiency of the gas turbine combined cycle”, Journal of Mechanical Science and Technology, Vol. 33, pp. 4535-4543. [https://doi.org/10.1007/s12206-019-0850-8]
• Kim, M. J. and Kim, T. S., 2019, “Integration of compressed air energy storage and gas turbine to improve the ramp rate,” Applied Energy, Vol. 247, pp. 363-373. [https://doi.org/10.1016/j.apenergy.2019.04.046]
• Walsh, P. P. and Fletcher, P., 2004, Gas turbine performance, John Wiley & Sons. [https://doi.org/10.1002/9780470774533]
• Kim, J. H. and Kim, T. S., 2019, “A new approach to generate turbine map data in the sub-idle operation regime of gas turbines,” Energy, Vol. 173, pp. 772-784. [https://doi.org/10.1016/j.energy.2019.02.110]
• Park, Y. K., Moon, S. W. and Kim, T. S., 2021, “Advanced control to improve the ramp-rate of a gas turbine: Optimization of control schedule,” Energies, Vol. 14, No. 23, pp. 8024. [https://doi.org/10.3390/en14238024]
• Kang, D. W. and Kim, T. S., 2018, “Model-based performance diagnostics of heavy-duty gas turbines using compressor map adaptation,” Applied Energy, Vol. 212, pp. 1345-1359. [https://doi.org/10.1016/j.apenergy.2017.12.126]