써모사이폰 열교환기 열설계 프로그램의 개발과 검증

1. 서 론

다양한 산업의 고도화에 따라 인류의 에너지 소비량은 지속적으로 증가하고 있다. 미국 에너지성 산하의 Lawrence Livermore National Laboratory에서 매년 발행하는 미국 내 에너지 소비량 표(1)에 따르면, 미국 내에서만 1년 동안에 총 9.73경 BTU(British Thermal Unit)의 에너지가 소비된다. 하지만 생성된 에너지 중 33%만이 실제로 사용되고, 67%의 에너지는 폐열 등으로 버려지고 있다. 이러한 낮은 에너지 사용 효율은 CO2의 배출을 증대시키며, 결과적으로 지구 온난화를 가속 시킬 수 있다. 따라서, 이와 같이 산업에서의 에너지 효율을 증가시키는 것은 매우 중요하며, 이를 달성하기 위해 다양한 연구들이 이루어지고 있다. 대표적인 연구로 폐열을 열원으로 이용하여 상대적으로 저온을 가지는 유체의 온도를 상승시켜 다양한 활용처에 공급하는 열교환기 연구들이 주목받고 있다. 특히, 기존 열교환기들 대비 장점을 갖는 써모사이폰 열교환기에 대한 관심이 증가하고 있다.⁽²⁾

써모사이폰 열교환기는 Fig. 1과 같이 하우징 내부에 써모사이폰 다발을 배치하고, 분리판을 설치하여 저온부와 고온부를 지나는 개별 유체들의 열교환이 가능하도록 고안된 장치이다. 써모사이폰 열교환기는 작동유체의 상변화를 이용하여 효과적인 열전달이 가능한 써모사이폰의 특성을 동일하게 활용할 수 있다. 아래와 같은 대표적 장점들을 가진다.

Fig. 1

Thermosyphon heat exchanger

첫째, 써모사이폰은 내부 등온성을 가지고 있기 때문에 큰 온도 차이를 경험해야하는 열교환기 환경에 있어, 열변형으로 인한 문제로부터 상대적으로 자유롭다. 둘째, 주입되는 작동유체의 종류에 따라 다양한 온도 조건에서 폐열 회수가 가능하다. 셋째, 구동시 발생하는 압력 손실이 타 열교환기 대비 작으므로 외부 동력에 대한 의존도가 낮다. 이 밖에 기존 열교환기들에서 큰 문제로 야기되는 좁은 유로에 의한 파울링(fouling)이나, 유지보수 등에 대해 상대적으로 우수한 장점을 가지고 있다. 따라서, 최근에는 이러한 다양한 장점들을 바탕으로 써모사이폰 열교환기를 공조 시스템, 제철소, 데이터센터 냉각, 발전소 냉각탑 등 다양한 분야에 활용하는 연구들이 시도되고 있다.⁽³⁾

다양한 장점을 갖는 써모사이폰 열교환기를 보다 효과적으로 개발하기 위해서는 써모사이폰 열교환기 설계 단계에서 열성능을 보다 빠르게 예측하고, 사용처에 따라 다양한 공정 조건을 적용할 수 있도록 하는 열설계 프로그램의 개발이 필수적이다. 하지만 이에 대한 연구들은 기존 써모사이폰 열교환기 연구 대비 미미한 수준이며, 이는 써모사이폰의 작동 과정이 내부에서 상변화를 동반하기 때문에 현열을 이용한 기존 열교환기 설계 프로그램으로는 열설계를 제대로 수행할 수 없기 때문이다.

Delpech et al.⁽⁴⁾은 히트파이프 열교환기를 이용하여 유리 공장의 가마에서 발생하는 고온의 공기로부터 회수할 수 있는 에너지의 양을 이론적으로 계산하였다. 히트파이프의 내부에서 일어나는 열전달에 대한 고찰 대신, 고온 환경에서 가해지는 복사 열전달과 자연 대류의 영향에 대한 비교가 주로 다루어졌다. 그들은 실험과 수치해석 결과를 비교하여 15% 이하의 오차를 보이는 것을 확인하였다. Ramos et al.⁽⁵⁾은 공기-물 써모사이폰 열교환기에 대하여 ANSYS Fluent를 이용하여 229만개 가량의 격자를 이용한 모델의 전산유체해석을 진행하고 실험을 통한 결과와 비교하였다. 이 때, 써모사이폰은 열전도율이 매우 높은 고형 전도체(solid conductor)로 간주하였다. 실험 결과와 해석값은 증발부에서 평균 5%, 응축부에서 평균 7%의 오차를 보였다. Noie⁽⁶⁾는 ε-NTU법을 이용한 해석 모델을 통하여 예측한 공기-공기 써모사이폰 열교환기에서의 열성능과 실험을 통한 결과를 비교하여, 저온부와 고온부의 열용량이 같은 경우에, 열교환기가 최소 성능을 가짐을 확인하였다. 이 연구에서는 써모사이폰 내부의 상변화 열전달에 대해서는 별도로 다루지 않았다. Brough et al.⁽⁷⁾은 실험실 규모의 도자기 가마에서 히트파이프 열교환기를 이용하는 폐열회수에 대해 TRNSYS(TRaNsient SYstems Simulation program)를 통한 계산과 실제 실험의 검증을 진행하였다. 검증에 사용된 툴인 TRNSYS의 내부에서 히트파이프는 유효 열전도도가 일반적 고체에 비하여 큰 값을 갖는 열전도율이 매우 높은 전도체로 간주하였고, 실험 결과와 해석을 통한 결과를 비교하여 15% 이내의 오차를 보였다. Jouhara et al.⁽⁸⁾은 평판 휜을 적용한　써모사이폰 열교환기를 다양한 기울임 각도와 열유속 조건에서 실험과 해석 결과와 비교하였다. 하지만 써모사이폰 내부의 상변화 열전달 현상에 대한 상세한 서술은 없었으며, 열교환기의 기울임 각도는 0°(지면에 대하여 수평)에서 90°(지면에 대하여 수직)까지 22.5° 간격으로 설정하였다. 총 5가지 기울임 각도 조건에서의 실험 결과, 90°에 가까워질수록 열교환기는 더 높은 유용도를 보였고, 이 경향은 열유속이 높아질수록 뚜렷하게 나타났다. 앞서 설명한 선행 연구들은 써모사이폰 내부의 상변화 현상에 의한 열전달에 대하여 고려하지 않았거나, 관 전체를 높은 유효 열전도도를 갖는 열전도율이 매우 높은 고형 전도체로 간주하여 고정된 상수 값으로 가정하여 계산하였다. 또한 열교환기의 작동에 필요한 동력 결정에 큰 영향을 미치는 성능 지표인 압력강하(pressure drop)를 의미있게 고려하지 않았다.

본 연구에서는 써모사이폰 열교환기 설계의 효율성을 높이기 위하여 Fortran 기반 써모사이폰 열교환기 열설계 프로그램을 개발하였다. 프로그램은 기존의 열설계 프로그램 대비 다음과 같은 차별점을 갖는다. 먼저, 써모사이폰 내부 상변화 현상에 대한 경험적 상관식을 적용하여 열교환기 성능 예측의 정확성을 높이고자 하였다. 또한, 열교환기 사용을 위하여 추가적으로 제공해야 할 동력을 계산하기 위하여 압력강하를 계산하였다. 압력강하의 계산을 위하여 관군을 지나는 외부 유동에 대한 경험적 상관식들을 통해 얻을 수 있는 마찰 계수를 이용하였다. 열성능 예측 모델을 기반으로 써모사이폰 열교환기의 성능을 계산할 수 있는 열설계 프로그램을 작성하였다. 다양한 상관식들과 열성능 예측 모델을 통하여 수치해석적인 방법에 비하여 보다 빠르고 간편하게 열설계 결과를 얻을 수 있었다. 마지막으로, 열설계 프로그램을 검증하기 위하여 직접 써모사이폰 열교환기를 제작하여 열성능 시험을 진행하였으며, 열성능 시험 결과와의 비교 및 검증을 통해 열설계 프로그램의 신뢰성을 확보하였다.

2. 이론적 성능 해석 모델

2.1 써모사이폰 열교환기 성능 계산

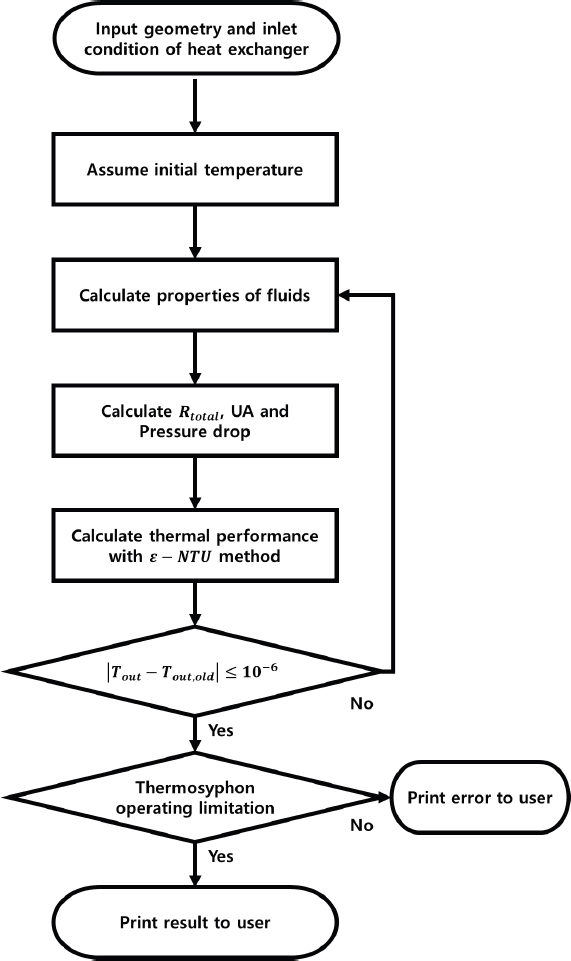
써모사이폰 열교환기 설계 프로그램의 성능 계산 과정을 Fig. 2에 도시하였으며, 다음과 같은 순서로 열교환기의 성능을 계산한다. 먼저, 프로그램에 열교환기의 크기, 내부에 배치된 써모사이폰의 개수 및 배열 등의 초기 필요 정보들을 입력한다. 필요 조건들을 프로그램에 입력하면, 이를 기반으로 열교환 면적, 유체 속도와 같이 열교환기의 형상에 대한 정보가 반영된 인자들을 계산한다. 계산된 형상 기반 인자들은 유체의 입구 조건과 함께 열교환기 내부 초기 평균 온도를 계산하는데 사용되며, 이를 통해 해당 온도에서 유체의 물성치 또한 계산한다. 계산된 유체의 물성치들은 열교환기의 대류 열전달계수, 압력 손실, 써모사이폰의 열저항 등을 예측하는 상관식에 활용되며, 이를 통해 초기 총괄 열전달계수 및 NTU(Number of Thermal Unit)를 계산한다. ε-NTU법에 기반하여 획득된 NTU를 통해 유용도를 계산하고 이를 통하여 열전달률을 구한다. 구해진 열전달률을 통하여 각 입구단의 질량유량 및 비열 조건과 함께 초기 출구 온도를 계산한다. 이러한 일련의 계산과정을 최종 계산된 출구 온도와 이전 계산된 출구 온도간의 차이가 10^-6℃이하가 될 때까지 반복 수행한다. 마지막으로, 수렴된 출구 온도로부터 계산한 열전달률을 기반으로 점성한계(viscous limit)⁽⁹⁾, 음속한계(sonic limit)⁽¹⁰⁾, 유입한계(entrainment limit)⁽¹¹⁾, 비등한계(boiling limit)⁽¹²⁾ 등의 여러 써모사이폰의 작동한계(operation limit)를 넘지 않는지 검증한 후 문제가 없다면 그 결과를 출력한다. 최종적으로 출력되는 정보들은 열교환기 출구온도, 유용도, 열전달률, 그리고 압력강하이다. 본 연구에서 적용된 프로그램 내의 모든 물성치들은 오픈 소스 라이브러리인 CoolProp⁽¹³⁾을 이용하여 취득하였다.

Fig. 2

Design program flow chart

2.2 열저항 분석

본 열설계 프로그램을 통한 열교환기의 열성능 계산은 열저항 분석을 통하여 이루어진다. 개별 써모사이폰의 내부에서 이루어지는 열전달이 Fig. 3에 그려져 있으며, 총 열저항은 식 (1)과 같다.

Fig. 3

Thermal resistances of thermosyphon

$\[ R_{total }=R_{e,h}+R_{e,c}+R_{w,h}+R_{w,c}+R_{PB}+R_{FC} \]$

(1)

R_e,h,R_e,c는 각각 고온부와 저온부에서의 써모사이폰과 열교환기 외부 유체 사이의 대류 열저항, R_w,h,R_w,c는 고온부와 저온부 써모사이폰 벽면에서의 반지름 방향의 전도 열저항, 그리고 R_PB,R_FC는 써모사이폰 내 증발부에서의 풀비등 열저항과 응축부에서의 막응축 열저항이다. R_total은 단일 써모사이폰의 전체 열저항을 의미한다.

각 써모사이폰의 총괄 열전달계수(UA)는 정의에 의해 식 (2)과 같이 표시할 수 있다.

$\[ {\left(UA\right)}_{HP}=\frac{1}{R_{total }} \]$

(2)

이 때 (UA)_HP는 단일 써모사이폰의 열전달 면적을 고려한 총괄 열전달계수(overall heat transfer coefficient)를 의미한다. 열교환기는 복수의 써모사이폰으로 이루어져 있기 때문에, 이에 따른 열교환기 전체의 열전달 면적을 고려한 총괄 열전달계수는 식 (3)과 같이 나타낼 수 있다.

$\[ {\left(UA\right)}_{HX}=N_t{\left(UA\right)}_{HP} \]$

(3)

(UA)_HX는 열교환기의 전체 열전달 면적을 고려한 총괄 열전달계수이고, N_t는 열교환기 내 써모사이폰의 수를 의미한다.

2.3 써모사이폰 관군에 대한 상관식의 적용

써모사이폰 열교환기 내부의 열전달 현상은 Fig. 4와 같이 응축부와 증발부에서 외부 유동이 관군을 지나며 강제 대류가 일어나는 상황으로 간주할 수 있다. 다양한 외부 유체의 상태와 관군의 형상 조건에 따른 선행 연구들^(14-16)이 진행되었다. 본 연구에서는 압력강하와 열전달의 계산을 위하여 선행 연구들 중 매끈한 관군에 대한 상관식들을 적용하였다.

Fig. 4

External flow across tube banks

2.3.1 관군에 대한 압력강하 상관식

매끈한 관군에서의 압력강하에 대한 상관식은 식 (4)의 Gaddis와 Gnielinski⁽¹⁷⁾의 상관식을 사용하였다.

$\[ \begin{array}{l}\mathrm{H}\mathrm{g}=-\frac{1}{\rho }\frac{dp}{dx}\frac{L^3}{{\nu }^2}\\ \mathrm{H}\mathrm{g}=\mathrm{H}{\mathrm{g}}_{\mathrm{l}\mathrm{a}\mathrm{m}}+\mathrm{H}{\mathrm{g}}_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b},\mathrm{s}}\left[1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{\mathrm{R}\mathrm{e}}_{\mathrm{d}}+200}{1000}\right)\right]\\ {\mathrm{H}\mathrm{g}}_{\mathrm{l}\mathrm{a}\mathrm{m}}=140{\mathrm{R}\mathrm{e}}_{\mathrm{d}}\left[{\left(b^{0.5}-0.6\right)}^2+0.75\right]/\left[a^{1.6}\left(4ab/\pi -1\right)\right]\\ {\mathrm{H}\mathrm{g}}_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b},\mathrm{s}}=f_{t,s}{\mathrm{R}\mathrm{e}}_{\mathrm{d}}^{1.75}+f_{n,t}{\mathrm{R}\mathrm{e}}_{\mathrm{d}}^2\\ f_{t,s}=1.25+0.6/{\left(a-0.85\right)}^{1.08}+0.2{\left(b/a-1\right)}^3-0.005{\left(a/b-1\right)}^3\\ f_{n,t}=\left\{\begin{array}{ll}1/{\left(2a\right)}^2\left(1/N_r-1/10\right)& \mathrm{f}\mathrm{o}\mathrm{r} 5\le N_r\le 10\\ 0& \mathrm{f}\mathrm{o}\mathrm{r} N_r>10\end{array}\right.\end{array} \]$

(4)

Hg는 하겐 수로, 압력강하에 대한 무차원수이다. 하첨자 lam, turb는 층류(laminar)와 난류(turbulent) 조건에서의 하겐 수, 하첨자 s는 엇갈림 배열(staggered array)을 의미한다. f_t,s는 관 사이의 간격에 대한 영향을 의미하며, f_n,t는 관의 수에 의한 영향을 의미한다. N_r은 관군의 열 수를 의미한다. a는 유동 방향의 관 사이 간격을 관 직경으로 나눈 값이며, b는 유동 수직 방향의 관 사이 간격을 관 직경으로 나눈 값이다.

압력강하 ∆p는 하겐 수를 통하여 계산할 수 있다.

$\[ \Delta p=\frac{{\mu }^2{N}_r}{\rho d_o^2}\mathrm{H}\mathrm{g} \]$

(5)

이 때 μ는 유체의 점성계수, ρ는 밀도, 그리고 d_o는 관의 외경을 의미한다.

2.3.2 관군에 대한 열전달 상관식

앞 절에서 제시된 상관식을 이용해 구한 하겐 수를 통해 관군과 외부 유동사이의 열전달에 관련된 무차원수인 누셀 수를 구할 수 있다. 열전달에 관한 상관식은 식 (6)의 Martin⁽¹⁸⁾이 제시한 상관식을 사용하였다.

(6)

Lq는 레베크 수이다. Pr은 유체의 프란틀 수이다. c는 관 사이의 대각선 길이를 직경으로 나눈 값이다.

외부 대류에 의한 관군의 열전달 계수인 h_ext는 누셀 수를 통하여 계산할 수 있다.

$\[ h_{ext }=\frac{k}{d_o}{\mathrm{N}\mathrm{u}}_{\mathrm{d}} \]$

(7)

이 때, k는 유체의 열전도도이다.

2.3.3 내부 상변화 열전달 상관식

써모사이폰 내부에서 일어나는 내부 상변화는 크게 증발부에서 일어나는 증발 및 비등과 응축부에서 일어나는 응축의 두 가지로 나눌 수 있다. 선행연구에 따르면 써모사이폰은 작동유체의 충진율(filling ratio, FR)과 가해지는 외부 열유속에 따라 최대 12 kW/mK정도의 유효열전도도를 가진다.⁽¹⁹⁾ 기존의 써모사이폰 열교환기 연구들은 실험이나 해석을 이용하여 얻은 고정된 유효열전도도를 통해 써모사이폰 전체를 열전도율이 매우 높은 전도체로 가정한 후 해석을 수행하였다. 고정된 유효열전도도의 사용을 통하여 써모사이폰 내부의 복잡한 상변화 현상을 간단하게 표현할 수 있지만, 열유속의 조건에 따라 매번 변화하는 써모사이폰 내부의 열전달 성능을 반영하지 못하는 한계가 있다. 본 연구에서는 써모사이폰 내부의 현상을 보다 정확히 반영하기 위하여 상변화 열전달 현상을 모델링한 경험적 상관식들을 이용하여, 관 내부의 열전달 성능을 예측하였다.

써모사이폰의 증발부에서는 풀비등이 지배적인 열전달 현상인 것으로 알려져있다.⁽²⁰⁾ 따라서, 본 연구에서는 핵 비등 열전달에 대한 Cooper⁽²¹⁾의 상관식(h_PB)을 사용하였다.

$\[ h_{PB}=55.0{\left(\frac{p}{p_{cr}}\right)}^{0.12-0.21{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}{R}_P}{\left(-{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\frac{p}{p_{cr}}\right)}^{0.55}{M}^{- 0.5} \]$

(8)

이 식에서 p는 써모사이폰 내부 압력, p_cr는 작동유체의 임계점 압력, R_P는 표면 조도 계수, 그리고 M은 작동유체의 분자량이다.

증발부 내에서 풀비등이 일어나는 영역은 써모사이폰 내부 작동유체의 충진율의 영향을 받는다.

$\[ FR=\frac{V_l}{V_e}\times 100\left(\%\right) \]$

(9)

이 때 V_l는 액체 상태의 작동유체의 부피, V_e는 써모사이폰 내경 기준 증발부의 부피이다. 두 값의 비율인 충진율 FR 은 증발부 내에서 작동유체가 차지하는 부피를 나타낸다.

증발부에서의 풀비등에 의한 열저항(R_PB)은 식 (10)과 같이 나타낼 수 있다.

$\[ R_{PB}=\frac{1}{h_{PB}\pi d_i{L}_e{N}_{t}FR/100} \]$

(10)

이 식에서 d_i는 관의 내경, L_e는 써모사이폰 증발부의 길이이다.

써모사이폰의 응축부에서는 상변화된 증기들이 응축부 벽면에서 주로 막응축에 의해 열을 전달한다.⁽²²⁾ 본 연구에서는 막응축의 열전달을 예측하기 위해 일반적인 막 두께를 계산하는 대신, 무차원수 A를 사용하도록 수정된 층류 영역에 대한 Kutateladze의 상관식과 난류 영역에 대한 Labuntsov⁽²³⁾의 상관식을 사용하였다.

(11)

이 때 k_l, μ_l, v_l는 작동유체의 열전도도, 마찰계수, 그리고 동점성계수이다. L_c는 응축부의 길이, T_sat, T_s는 각각 작동유체의 포화온도와 표면온도이다. g는 중력가속도, $$ h_{fg}^{\text{'}}$$는 현열에 의한 효과를 포함하도록 수정된 잠열을 의미한다.

응축부의 열저항(R_FC)은 식 (12)과 같이 나타낼 수 있다.

$\[ R_{FC}=\frac{1}{h_{FC}\pi d_i{L}_c{N}_t} \]$

(12)

3. 써모사이폰 열교환기 열성능 시험

3.1 열교환기와 성능 시험 장비

본 설계 프로그램은 핀이 없는 매끈한 타입의 구리 관으로 제작된 써모사이폰 열교환기를 대상으로 개발되었으며, 실제 제작된 써모사이폰 열교환기의 실험 결과와 비교, 검증하였다. 본 연구에서 제작된 써모사이폰 열교환기 내부의 파이프는 엇갈림 배열로 구성하였고, 동일 면적에서 더 높은 유용도를 얻기 위하여 고온부에 2개, 저온부에 4개의 배플을 설치하였다. 배플의 설치로 인한 효과 또한 프로그램에 적용되어, 실험값과의 비교를 진행하였다.

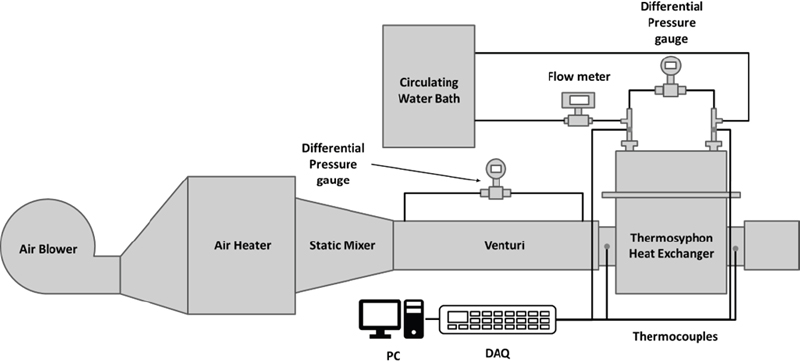
열교환기 성능 시험을 위한 실험 장치는 Fig. 5에 나타나 있다. 써모사이폰 열교환기의 고온부에 일정한 온도와 유량의 공기(air)를 공급하기 위하여 송풍기와 에어 히터를 이용하였으며, 고른 온도 분포의 유동을 얻기 위하여 스태틱 믹서를 사용하였다. 저온부에서도 일정한 온도와 유량의 물(water)을 공급하기 위하여 항온조를 사용하였다. 고온부에서는 벤투리를 통하여 질량 유량을 측정하였고, 저온부에서는 유량계를 이용하여 질량 유량을 측정하였다. 열교환기의 입구와 출구에서의 온도와 압력강하를 측정하여 각각의 평균온도로 표현하였다. 압력강하의 경우 측정 상의 한계로 인하여 열교환기 출입구에서의 확장, 축소부에서의 압력손실이 포함된 값을 기록하였으나, 이러한 부차적 손실에 의한 값도 프로그램에 반영하여 보정할 수 있도록 하였다.

Fig. 5

Thermosyphon heat exchanger performance test rig

3.3 불확도 계산

써모사이폰 열교환기 열성능 시험의 결과의 신뢰도를 평가하기 위하여 불확도 계산을 진행하였다. 국제표준화기구(International Organization for Standardization, ISO)의 측정불확도 표현 지침에 따라 열교환기의 고온부와 저온부에서의 열전달률과 압력강하, 그리고 열교환기의 유용도에 대하여 불확도 계산을 진행하였다.⁽²⁴⁾ 각 불확도 인자에 대해 식 (15-17)를 이용하여 계산하였다.

$\[ \delta q=\sqrt{\sum _{i=1}^n \left(\frac{\partial q}{\partial x_i}\right)\delta x_i^2} \]$

(15)

$\[ \delta \epsilon =\sqrt{\sum _{i=1}^n \left(\frac{\partial \epsilon }{\partial x_i}\right)\delta x_i^2} \]$

(16)

$\[ \delta \Delta p=\sqrt{\sum _{i=1}^n \left(\frac{\partial \Delta p}{\partial x_i}\right)\delta x_i^2} \]$

(17)

모든 측정기기를 통한 측정값의 분포는 사각형 형태의 분포를 갖는 것으로 가정하였으며, 95%의 신뢰 수준에서의 상대 확장 불확도를 계산하였다. 불확도 계산의 결과는 Table 1과 같다.

Table 1

Result of uncertainty analysis

4. 결과 및 검토

4.1 열교환 성능 시험 및 해석 결과

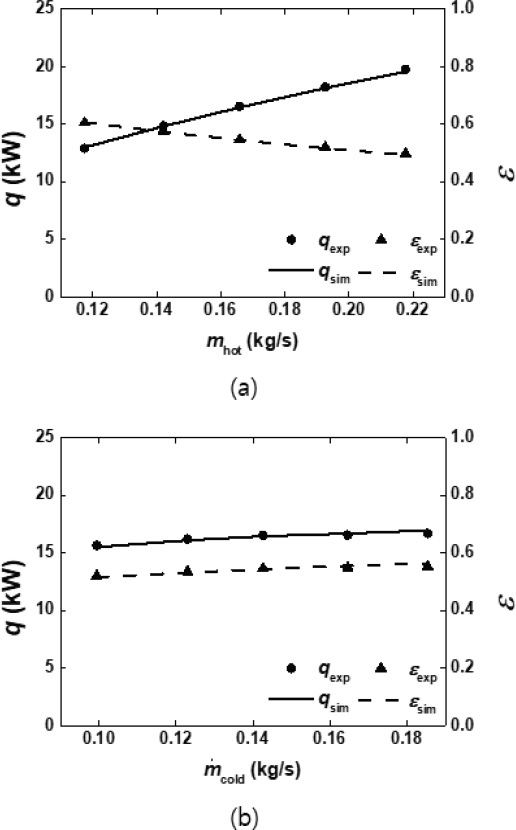
열교환기의 열성능에 관련된 주요 지표인 열전달률과 유용도에 대하여 성능 시험 결과와 해석 프로그램 사이의 비교를 진행하였다. Fig. 6은 저온부와 고온부 중 한 쪽의 질량 유량을 고정한 채로, 다른 한 쪽의 질량 유량을 변화시켜가며 실험한 데이터와 동 조건에서의 해석 결과를 비교한 그래프이다. 저온부의 질량유량을 고정한 채로 고온부의 질량유량을 변화시켰을 때, 열교환기의 열전달률은 지속적으로 증가하고, 유용도는 감소하는 경향을 보였다. 이는 식(13)에서 제시된 유용도의 정의를 고려하였을 때, 두 열교환 유체 중 고온 공기가 상대적으로 작은 열용량을 가지기 때문이다. 고온부의 질량유량을 고정한 채로 저온부의 질량유량을 변화시킨 경우, 열전달률과 유용도가 소폭 상승하는 것을 확인할 수 있다. 열성능 시험 결과와 해석 결과 모두 저온부의 질량유량이 –30%까지 감소하더라도 물의 비열이 공기에 비하여 큰 값을 가지기 때문에 고온부에 비하여 더 높은 열용량을 가짐을 확인할 수 있다.

Fig. 6

Performance comparison (a) fixed cold fluid (b) fixed hot fluid

4.2 압력강하 성능 시험 및 해석 결과

열교환기에서 발생하는 압력강하를 예측하는 것은 유체를 공급하는 펌프 또는 송풍기 등의 스펙을 결정하고, 이로 인해 발생되는 필요 에너지를 파악하는데 매우 중요한 요소이다. 즉, 열교환기의 성능 예측 시 압력강하의 예측을 함께 진행하여 열교환기가 가동하기 위하여 필요한 추가 동력의 크기를 함께 결정할 수 있다.

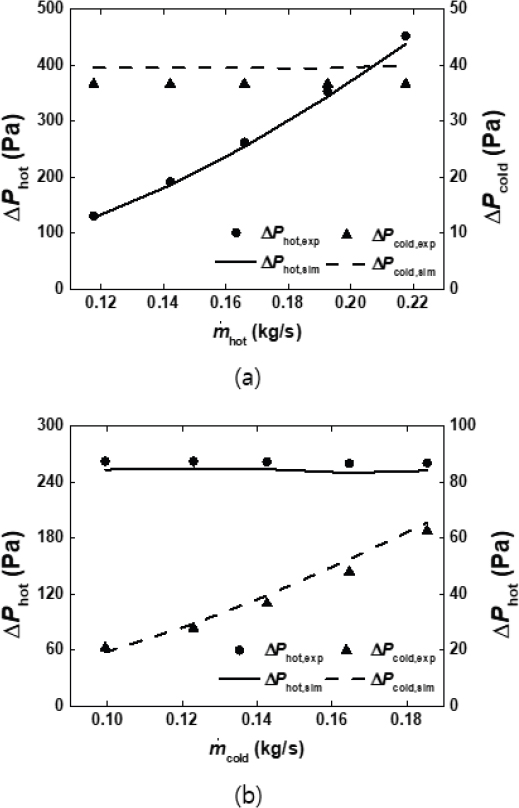
Fig. 7은 각각 고온부의 질량유량 변화에 따른 압력강하와, 저온부의 질량유량 변화에 따른 압력강하 그래프이다. 각 그래프에서 공통적으로 질량 유량이 변하는 부분의 압력강하는 질량 유량과 비례하게 증가하고, 고정된 질량 유량을 갖는 부분은 압력강하가 거의 일정하게 유지되는 모습을 확인할 수 있다. 고온부의 공기의 경우, 질량유량의 변화에 따라 최대 약 470 Pa의 압력강하를 보인 반면, 저온부 냉각수의 경우 최대 60 Pa에 그쳤다. 이를 통해, 비슷한 질량유량이더라도, 상대적으로 작은 밀도를 가지는 공기가 더 큰 유속을 갖는 것을 확인할 수 있다.

Fig. 7

Pressure drop comparison (a) fixed cold fluid (b) fixed hot fluid

5. 결 론

본 연구에서는 기존 연구들에서 제안된 수치해석 방법 대비, 적은 계산 비용으로 써모사이폰 열교환기의 열성능 및 압력강하를 예측하는 설계 프로그램을 개발하였다. 또한 실제 써모사이폰 열교환기를 제작하고 성능 시험을 진행하여 본 연구에서 개발한 열설계 프로그램의 정확성을 검증하였다. 주요한 결론은 다음과 같다.

• 1) 써모사이폰 열교환기의 형상, 입구에서의 유체 온도, 그리고 질량유량을 입력 변수로 받아 열전달률, 유용도, 그리고 압력강하와 같은 성능 지표를 예측하는 프로그램을 제작하였다.
• 2) 써모사이폰 열교환기의 해석을 위하여 열교환기 내부에서 일어나는 상변화 열전달을 비롯한 여러 열전달 현상들에 대한 경험적 상관식들과 ε-NTU법을 사용하였다.
• 3) 제작한 열교환기 설계 프로그램의 검증을 위하여 실제 써모사이폰 열교환기를 제작하고, 열성능 평가를 진행하여 각각의 결과를 비교하였다. 비교 결과 열성능에 대하여 최대 1.6%, 평균 0.8%의 오차를 보였으며, 압력강하에 대하여 최대 9.1%, 평균 5.2%의 오차를 보였다.
• 4) 비교 결과를 통하여 본 연구에서 개발한 열설계 프로그램의 성능 해석 결과가 실제 써모사이폰 열교환기의 성능을 1% 미만의 오차로 정확하게 예측할 수 있음을 확인할 수 있었다.

본 연구 결과를 통해 개발된 써모사이폰 열설계 프로그램이 수치해석적 방법에 비하여 적은 계산 비용으로 여러 형태의 써모사이폰 열교환기의 설계에 적용되어 국내의 히트파이프 열교환기 산업의 경쟁력 향상에 기여할 수 있을 것으로 기대된다.

Acknowledgments

본 연구는 산업통상자원부 에너지수요관리핵심기술개발사업의 일환으로 수행되었으며, 한국에너지기술평가원의 연구비 (과제번호: 20212020800270) 지원으로 이루어졌으며 이에 감사드립니다.

References

• Lawrence Livermore National Laboratory, 2011, “US Energy and Carbon Flow Chart.”
• Jouhara, H., Khordehgah, N., Almahmoud, S., Delpech, B., Chauhan, A. and Tassou, S.A., 2018, “Waste heat recovery technologies and applications”, Thermal Science and Engineering Progress, Vol. 6, pp. 268-289. [https://doi.org/10.1016/j.tsep.2018.04.017]
• Srimuang, W. and Amatachaya, P., 2012, “A review of the applications of heat pipe heat exchangers for heat recovery”, Renewable and Sustainable Energy Reviews, Vol. 16, No. 6, pp. 4303-4315. [https://doi.org/10.1016/j.rser.2012.03.030]
• Delpech, B., Axcell, B. and Jouhara, H., 2019, “Experimental investigation of a radiative heat pipe for waste heat recovery in a ceramics kiln”, Energy, Vol. 170, pp. 636-651. [https://doi.org/10.1016/j.energy.2018.12.133]
• Ramos, J., Chong, A. and Jouhara, H., 2016, “Experimental and numerical investigation of a cross flow air-to-water heat pipe-based heat exchanger used in waste heat recovery”, International Journal of Heat and Mass Transfer, Vol. 102, pp. 1267-1281. [https://doi.org/10.1016/j.ijheatmasstransfer.2016.06.100]
• Noie, S.H., 2006, “Investigation of thermal performance of an air-to-air thermosyphon heat exchanger using ε -NTU method”, Applied Thermal Engineering, Vol. 26, No. 5, pp. 559-567. [https://doi.org/10.1016/j.applthermaleng.2005.07.012]
• Brough, D., Ramos, J., Delpech, B. and Jouhara, H., 2021, “Development and validation of a TRNSYS type to simulate heat pipe heat exchangers in transient applications of waste heat recovery”, International Journal of Thermofluids, Vol. 9, pp. 100056. [https://doi.org/10.1016/j.ijft.2020.100056]
• Jouhara, H. and Merchant, H., 2012, “Experimental investigation of a thermosyphon based heat exchanger used in energy efficient air handling units”, Energy, Vol. 39, No. 1, pp. 82-89. [https://doi.org/10.1016/j.energy.2011.08.054]
• Faghri, A. (1995) Heat pipe science and technology Global Digital Press.
• Groll, M. and Rösler, S., 1992, “Operation principles and performance of heat pipes and closed two-phase thermosyphons”, Journal of Non-Equilibrium Thermodynamics, Vol. 17, No. 2, pp. 91-151.
• Nguyen-Chi, H. and Groll, M., 1981, “Entrainment or flooding limit in a closed two-phase thermosyphon”, Journal of Heat Recovery Systems, Vol. 1, No. 4, pp. 275-286. [https://doi.org/10.1016/0198-7593(81)90038-2]
• Peterson, G.P., 1994, “An introduction to heat pipes. Modeling, testing, and applications”, Wiley Series in Thermal Management of Microelectronic and Electronic Systems.
• Bell, I.H., Wronski, J., Quoilin, S. and Lemort, V., 2014, “Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp”, Industrial & Engineering Chemistry Research, Vol. 53, No. 6, pp. 2498-2508. [https://doi.org/10.1021/ie4033999]
• Žukauskas, A., 1972, “Heat transfer from tubes in crossflow”, Advances in heat transfer, Elsevier, pp. 93-160. [https://doi.org/10.1016/S0065-2717(08)70038-8]
• Kays, W.M. and London, A.L., 1984, “Compact heat exchangers”, McGraw-Hill, New York.
• Giedt, W.H., 1957, Principles of engineering heat transfer, van Nostrand.
• Gaddis, E.S. and Gnielinski, V., 1985, “Pressure drop in cross flow across tube bundles”, Vol. 25, No. 1.
• Martin, H., 2002, “The generalized Lévêque equation and its practical use for the prediction of heat and mass transfer rates from pressure drop”, Chemical Engineering Science, Vol. 57, No. 16, pp. 3217-3223. [https://doi.org/10.1016/S0009-2509(02)00194-X]
• Kim, M. and Moon, J.H., 2021, “Numerical investigation and modeling of thermal resistance and effective thermal conductivity for two-phase thermosyphon”, Case Studies in Thermal Engineering, Vol. 27, pp. 101358. [https://doi.org/10.1016/j.csite.2021.101358]
• Guichet, V., Almahmoud, S. and Jouhara, H., 2019, “Nucleate pool boiling heat transfer in wickless heat pipes (two-phase closed thermosyphons): A critical review of correlations”, Thermal Science and Engineering Progress, Vol. 13, pp. 100384. [https://doi.org/10.1016/j.tsep.2019.100384]
• Cooper, M.G., 1984, “Heat Flow Rates in Saturated Nucleate Pool Boiling-A Wide-Ranging Examination Using Reduced Properties”, Advances in Heat Transfer, Vol. 16, pp. 157-239. [https://doi.org/10.1016/S0065-2717(08)70205-3]
• Guichet, V. and Jouhara, H., 2020, “Condensation, evaporation and boiling of falling films in wickless heat pipes (two-phase closed thermosyphons): A critical review of correlations”, International Journal of Thermofluids, Vol. 1-2, pp. 100001. [https://doi.org/10.1016/j.ijft.2019.100001]
• Incropera F. and DeWitt D., 2018, “Fundamentals of Heat and Mass Transfer,” 8th Edition, J. Wiley & Sons, New York.
• ISO, 1995, “Guide to the Expression of Uncertainty in Measurement”, Geneva, Switzerland, Vol. 122.