전기화학 수소 압축기 성능 및 기계적 특성에 대한 셀 디자인 변수의 영향 조사

1. 서 론

화석 연료의 남용으로 인한 기후 변화에 대응하기 위해 전 세계적으로 많은 연구와 노력이 이루어지고 있다. 수소는 이 위기를 극복하기 위한 대체 에너지로 매우 효율적이며 액체 또는 가스 상태로 쉽게 저장 및 운반할 수 있는 장점을 가지고 있다. 그러나 수소를 액체로 저장할 경우 많은 양의 수소를 최소한의 부피로 저장할 수 있으나, 고순도의 수소로 압축할수록 기계적인 방법보다 비용이 많이 들고 효율이 떨어진다. 현재 가장 일반적으로 사용되는 수소 압축 저장 방법은 기계적인 방법으로 내구성, 소음, 수소의 오염 등의 단점이 있다. 반면에 고분자전해질막을 이용한 전기화학 수소압축기는 더 적은 에너지를 화학적인 방법을 통해 수소 가스를 압축하는 것이 더 효율적이고 선호되는 방법이라고 할 수 있다^[1,2]. 최근에는 전기화학수소압축기에 대한 많은 연구가 수행되고 있으며, 높은 압축 비율과 우수한 성능을 달성하기 위해 다양한 분야에서 전기화학수소압축기 시스템에 괸한 연구 결과가 보고되고 있다.

전기화학수소압축기 셀의 성능을 향상시키기 위해서는 수분 관리가 매우 중요한 요소 중 하나이다. 고분자전해질막 연료전지(PEMFC, Polymer Electrolye Membrane Fuel cell)와 마찬가지로 전해질 막은 수소 이온의 전도도를 높이기 위해 수화되어야 한다^[3]. 그러나 고분자전해질막 연료전지와 달리 전기화학수소압축기 셀에서는 환원 반응으로 인해 물이 생성되지 않기 때문에, 수소가 애노드로 유입되는 물을 통해 막을 수화시키는 것이 중요하다. Zou 등 ^[4]은 충분한 수분이 공급되지 않을 경우, 전류 밀도의 증가가 막의 탈수를 유발하여 옴 손실(ohmic loss)이 증가한다고 분석했다. 해당 논문에서는 다양한 운전 조건에서 막의 탈수를 완화 하여 전기화학수소압축기 셀의 성능을 향상시키는 시도를 하였으며, 입구 수소 압력이 30 kPa일 때 22의 압축 비율을 달성했다. Hao 등 ^[5]은 캐소드에 내부 가습기를 사용하는 설계를 고안했으며, 전기화학수소압축기를 2 MPa까지 작동시키고, 전기화학 임피던스 분광법을 통해 주된 초과전위가 막 저항에 기인함을 보였다.

특히 전기화학수소압축기 셀의 경우 셀 내부에서 큰 압력 경사가 발생하기 때문에 구성 요소의 기계적 특성과 구조적 안정성이 중요한 요소가 된다. 셀을 장기간 고압으로 운전할 때, 카본지 (Carbon paper)와 탄소 섬유에서 전단이 발생하기 때문에 카본 펠트는 구조 강도와 내성 측면에서 안정성 면에서 더 우수한 성능을 가진다^[6]. Rohland 등 ^[7]은 고압 압축 조건에서 막전극접합체 (MEA, Membrane electrode assembly)의 변형을 막기 위해 유연한 특수 그래파이트 시트와 금속 펠트를 각각 캐소드 및 애노드 유로에 사용하는 것을 제안했다. 수소를 0.1-4.3 MPa로 압축하고 0.04∼5.7N⋅m³/h 의 유속을 생성했다. Sdanghi 등 ^[8]은 카본지 대신 두꺼운 다공성 티타늄 층(PTL, Porous titanium layer)을 애노드에 사용하여 전해질 막을 압력 차이로부터 보호했다. 또한, 그들은 실험 연구와 함께 가상 2차원 모델을 개발하여 전기화학수소압축기의 효율성을 향상시키는 물리적 매개변수를 추정했다.

효율적인 전기화학수소압축기 운전을 위해 수소 환원 반응 중에는 물이 생성되지 않기 때문에 전해질 탈수화 방지는 중요한 도전 과제로 부각된다. 게다가, 신뢰성 있고 장기간의 운전을 위해 전기화학수소압축기 셀 및 스택 구조는 애노드와 캐소드 사이의 수소 압력 차이에 견딜 수 있도록 적절하게 설계되어야 한다. 기존의 연구들에서는 전기화학 수소 압축기의 애노드 탈수 문제와 압력 차이로 인한 셀의 구조적인 문제에 대한 구체적인 원인들의 규명이 부족하다. 이번 연구에서는 수치해석을 통해 해당 원인을 규명하고 해결 방안을 위한 설계 최적화에 필요한 여러 셀 디자인 요소들에 따른 셀의 성능 및 구조적인 안정성에 대한 시뮬레이션을 수행하였다. 본 연구에서는 이전 연구에서 개발한 3차원 전기화학수소압축기 모델을 사용하여 전기화학수소압축기의 핵심 구성 요소 설계가 셀 성능과 기계적 거동에 미치는 영향을 조사했다^[9]. 이 모델은 유한요소법(FEM, Finite element method) 기반의 고체역학 모델과 전산유체역학 기반의 유체 모델을 포함하여 전기화학적 및 기계적 행동을 정확하게 포착하여 전기화학적 수소 압축 과정 중 전기화학수소압축기 셀의 성능과 여러 특성들에 대해 해석한다. 매개변수 연구의 초점은 다양한 수소 압축 비율에서 기체확산층(GDL, Gas diffusion layer), 전해질막, 및 유로의 차원적 영향을 분석하는 데에 놓여 있다. 특히, 전류 밀도, 물질 농도, 기계적 응력 및 구성 요소 변형의 다차원 분포는 주요 물리 현상을 이해하고 셀 디자인 및 운전 조건을 최적화하기 위해 사용된다.

2. 수치 모델

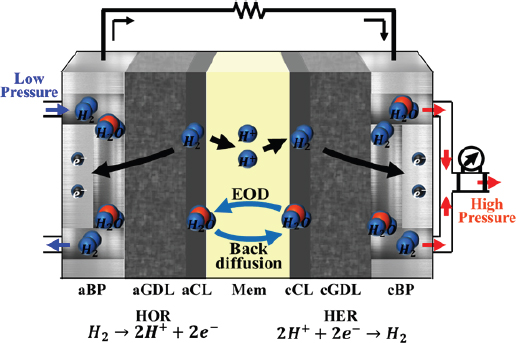
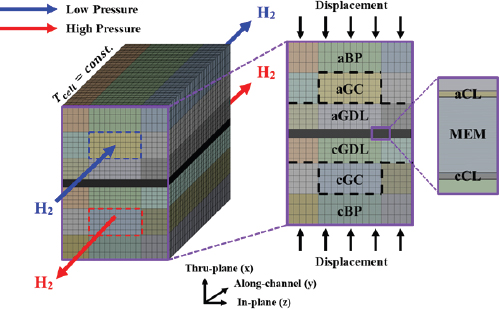
Fig. 1은 전기화학수소압축기 셀 내의 전기화학 반응과 물질 이동의 개략적인 도표를 보여준다. 전체적인 계산 도메인에서 모델은 분리판 (BPs, Bipolar plate), 가스 채널 (GCs, Gas channel), 가스 확산층 (GDLs), 촉매층 (CLs, Catalyst layer) 및 고분자 전해질 막을 고려하며, Fig. 2에 표시된 대로 직선 채널을 가진 단일 셀에 적용된다. 수소 산화 반응 (HOR, Hydrongen oxidation reaction)과 수소 환원 반응 (HER, Hydrogen evolution reaction)을 통해 전기화학 반응 및 물질 이동을 고려하기 위해 기계적 행동과 결합된 전산유체역학 기반 모델을 사용한다. 다음은 모델 개발 시 사용된 가정 사항이며, 2.1 절에서 설명되어 있다.

Fig. 1

Schematic diagram of an EHC cell with major components and key transport processes

Fig. 2

computational domain and mesh configuration of an EHC cell

2.2 전기화학수소압축기 전기화학 반응

전기화학수소압축기 모델은 질량, 운동량, 전하 및 개별 물질의 보존 방정식 네 가지로 구성되었다. 이러한 보존 방정식은 전기화학 반응에 기반한 소스/싱크텀과 결합되었다. 소스/싱크텀은 수소 산화 반응및 수소 환원 반응을 위한 버틀러 볼머 방정식과 관련이 있다. 수소 가스는 애노드 촉매층에서 산화되고 캐소드 촉매층에서 환원되며 다음 전기화학 반응에 따른다.

$\[ \begin{array}{l}\mathrm{A}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ H_2\to 2H^{+}+2e^{-}\left(E_a^0=0V\right)\end{array} \]$

(1)

$\[ \begin{array}{l}\mathrm{A}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ 2H^{+}+2e^{-}\to H_2\left(E_c^0=0V\right)\end{array} \]$

(2)

방정식에서, $$ E_a^0$$와 $$ E_c^0$$는 각각 표준 상태 조건에서 수소 산화 반응과 수소 발생 반응의 열역학적 평형 전위를 나타낸다.

수소 산화 반응과 수소 환원 반응의 전달 전류 밀도인 j의 표현은 버틀러 볼머 방정식에 기반하여 유도된다.

$\[ \begin{array}{l}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ j=a_a{i}_{0,a}\left[\left(\frac{C_{H_2}}{C_{H_2}^{ref }}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{{\alpha }_{a}F{\eta }_a}{RT}\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-{\alpha }_{c}F{\eta }_a}{RT}\right)\right]\end{array} \]$

(3)

$\[ \begin{array}{l}\mathrm{H}\mathrm{E}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ j=a_c{i}_{0,c}\left[\left(\frac{C_{H_2}}{C_{H_2}^{ref }}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{{\alpha }_{a}F{\eta }_c}{RT}\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-{\alpha }_{c}F{\eta }_c}{RT}\right)\right]\end{array} \]$

(4)

식 (3)과 (4)에서, α_a와 α_c는 각각 개별 반쪽 전지 반응(Half-cell reaction)에 대한 애노드 전달 계수를 나타낸다. 또한, a_a와 a_c는 각각 애노드 및 캐소드 촉매층의 실효 활성화 면적(Specific area)을 나타낸다. 실효 활성화 면적은 다음과 같이 표현될 수 있다.

$\[ a=\frac{a_{ECSA}{L}_{Pt}}{{\delta }_{CL}} \]$

(5)

여기서 a_ECSA,L_pt, 그리고 δ_CL은 각각 전기화학적 활성 표면적, 촉매층에서의 Pt의 Loading량, 그리고 촉매층의 두께를 나타낸다. a_ECSA와 δ_CL은 다음과 같이 표현될 수 있다.

$\[ a_{ECSA}=\frac{3}{r_{pt}{\rho }_{Pt}} \]$

(6)

$\[ {\delta }_{CL}=\left[\frac{\left(I/C\right)\left(\frac{{\rho }_c}{{\rho }_e}\right)\left(\frac{1}{{\rho }_{c}wt\%}\right)+\left(\frac{1}{{\rho }_{PT}}+\frac{1}{{\rho }_{c}wt\%}\right)}{1-{\epsilon }_{CL}}\right]L_{Pt} \]$

(7)

식 (3)과 (4)에서의 i_0,a와 i_0,c는 각각 애노드 촉매층에서의 수소 산화 반응과 캐소드 촉매층에서의 수소 환원 반응의 교환 전류 밀도를 나타내며, 수정된 아레니우스 형태로 온도와 압력의 함수로 표현될 수 있다^[10]. 이는 다음과 같다.

$\[ i_0=i_0^{ref}{\left(\frac{P}{P_{ref}}\right)}^{\gamma }\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right] \]$

(8)

Table 1에는 물리화학적, 운동학적 및 운반 특성을 Table 2는 촉매층 사양(L_pt, I/C, wt.% 등)을 나열했다. 위 식에서 E_a는 활성화 에너지이며, 식 (3)과 (4)에서 수소 산화 반응에 대한 표면 과전위인 η_a와 수소 환원 반응에 대한 표면 과전위인 η_c는 다음과 같이 표현될 수 있다.

Table 1

Physiochemical, kinetic, and transport properties

Table 2

Catalyst layer specification, cell dimensions, and operation conditions

$\[ \begin{array}{l}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ {\eta }_a={\varphi }_s-{\varphi }_e-E_a\end{array} \]$

(9)

$\[ \begin{array}{l}\mathrm{H}\mathrm{E}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ {\eta }_c={\varphi }_s-{\varphi }_e-E_c\end{array} \]$

(10)

여기서, ϕ_s와 ϕ_e는 각각 고체상의 전자 전위와 전해질 상의 이온 전위를 나타낸다. E_a와 E_c는 각각 애노드 촉매층에서의 수소 산화 반응과 캐소드 촉매층에서의 수소 환원 반응의 열역학적 평형 전위를 나타내며, 다음과 같이 온도에 대한 함수로 표현될 수 있다.

$\[ \begin{array}{l}\mathrm{H}\mathrm{O}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ E_a=E_a^0+\frac{\Delta s_a}{2F}\left(T-T_0\right)-\frac{RT}{2F}\mathrm{l}\mathrm{n}{P}_a\end{array} \]$

(11)

$\[ \begin{array}{l}\mathrm{H}\mathrm{E}\mathrm{R}\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{L}\\ E_c=E_c^0+\frac{\Delta s_c}{2F}\left(T-T_0\right)-\frac{RT}{2F}\mathrm{l}\mathrm{n}{P}_c\end{array} \]$

(12)

네렌스트(Nernst) 전압은 식 (13)에 의해 계산된다.

$\[ E_{nernst }=E_c-E_a=-\frac{RT}{2F}ln\frac{P_c}{P_a} \]$

(13)

∆S_a와 ∆S_c는 각각 애노드 촉매층에서의 수소 산화 반응과 캐소드 촉매층에서의 수소 환원 반응 반응 동안의 엔트로피 변화를 나타낸다.

3. 결과 및 논의

본 연구에서는 주요 설계 변수가 변형 정도와 수분 관리에 미치는 영향을 조사하였다. 기계적 행동을 고려한 셀 운영 중에 발생하는 수치 시뮬레이션이 수행되었다. 다양한 두께의 나피온(Nafion, Dupont, 미국) 막 (Case 1 및 2)인 N115 (127 μm), NR212 (50.8m) 및 N117 (183 μm)가 사용되었다. 기체확산층의 두께 (Case 3 및 4)는 참조 값 주변의 낮은 값과 높은 값으로 변화되었다.

먼저, Fig. 3a에 표시된 대로 N115, N117 및 NR212와 같은 다양한 나피온 막을 사용하여 시뮬레이션 및 실험적으로 측정된 결과 곡선은 높은 일치율을 보여준다. 작동 전류 밀도 범위 (0 < I < 1.0 A/cm²)에서 막이 더 두꺼워질수록 셀 전압이 증가하는 것을 확인할 수 있다. 특히, N115와 N117에서는 고전류 밀도에서 지수적인 전압 상승이 나타나는데, 이는 수분 탈수로 인한 이온 전도도 감소로 인한 것이다^[8,^14]. 전압의 급격한 상승에 해당하는 전류 밀도 지점은 참조 사례 (N115)에서 약 0.77 A/㎠, Case 2 (N117)에서는 약 0.57 A/㎠로 나타났다. 반면, NR212의 Case 1은 작동 중에 전압이 선형적으로 증가하는데, 이는 프로톤 전도도가 높아져 옴 손실이 낮아지기 때문이다. 높은 전류 밀도 (I > 1.0 A/㎠)에서는 셀 전압의 급격한 상승이 예상된다. Fig. 3b는 기체확산층 두께에 따른 셀 성능 곡선을 비교할 수 있다. 이 곡선들은 0.7A/㎠까지 거의 동일한 성능을 보이지만 고전류 밀도 범위에서 전압 차이가 발생한다. 특히, Case 3은 곡선의 기울기가 가장 작으므로 기체확산층의 낮은 두께로 성능 향상이 이루어진 것으로 결론지을 수 있다.

Fig. 3

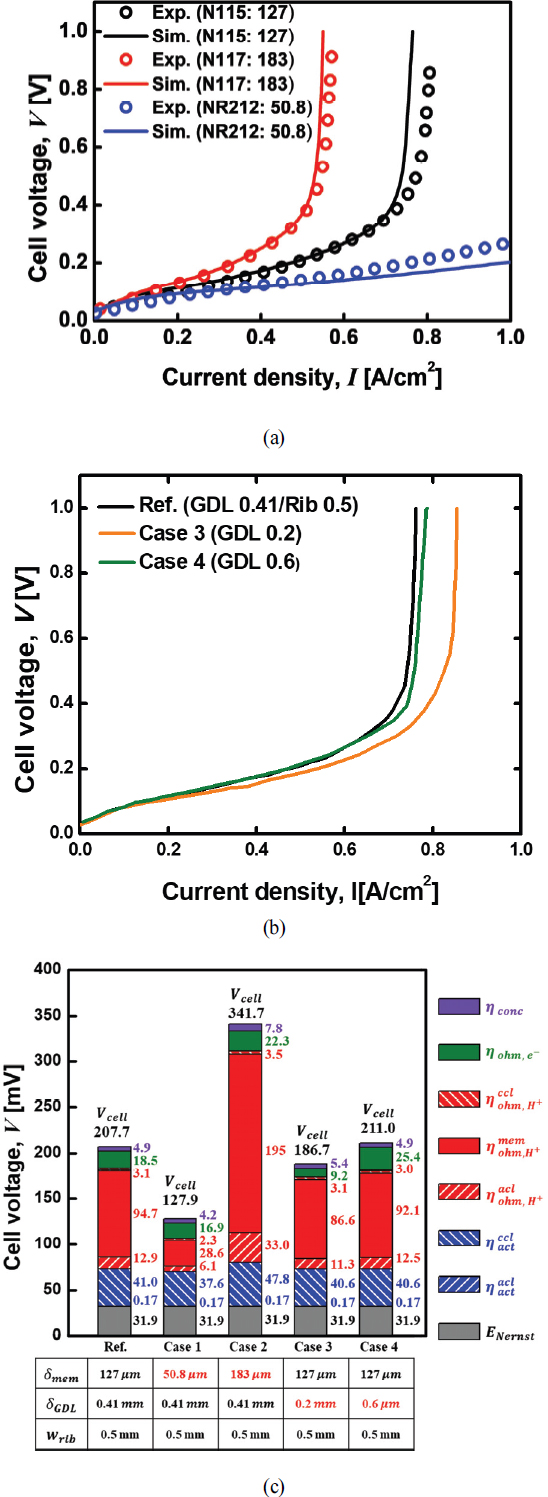
Polarization curves of (a) simulated and measured data for Case. Ref (N115, δmem = 127 μm), Case 1 (NR212, δmem = 50.8 μm) and Case 2 (N117, δmem = 183 μm), (b) Case 3 (δGDL = 0.2 mm), Case 4 (δGDL = 0.6 mm), (c) Comparison of cell voltage losses at constant current density of 0.5 A/cm2

0.5A/㎠의 고정 전류 밀도에서 각 경우의 총 셀 전압과 최소 수분 함량을 Table 3에 나타냈다. 적용된 셀 전압은 열역학적 평형 전위, 활성화 전위(η_act), 옴 전위(η_ohm) 및 농도 초과전위(η_conc)의 합으로 표현될 수 있다. Fig. 3c에 그려진 대로 먼저, 열역학적 평형 전위는 Pc=10 bar 에 해당하는 네렌스트 전압은31.9mV이다(식 (13) 참조). 애노드의 활성화 초과전위는 수소산화 반응이 매우 빠르게 진행되기 때문에 0.17mV로 나타났다. 반면, 캐소드에서는 수소 환원 반응에 의해 37-48 mV의 손실이 측정되었다. 양이온 전달에 따른 옴 전압 손실(η_ohm,H+)은 주로수분 함량에 의존하는 전도도 때문에 발생한다. 따라서 고압에서는 애노드보다 캐소드에서 더 높은 옴 손실이 측정되었다. 또한, 전해질 막을 통한 양이온 전달은 전체적인 셀 전압에 큰 기여를 하며, NR212를 사용한 Case 1은 가장 낮은 옴 전위인 28.6mV를 나타내며, N117를 사용한 Case 2에서는 195mV로 가장 큰 손실을 보였다. 이는 막의 두께를 감소시킴으로써 성능 향상의 정도가 다른 경우보다 더 명확하다는 것을 의미한다. 또한 전자 전달에 의한 옴 전위 손실(η_ohm,e^-)은 9.2 mV에서 25.4 mV로 예측되며 주로 기체확산층 두께에 영향을 받는다.

Table 3

Summary of geometric details of parametetric cases amd calculated results

다양한 막 두께에 따른 변형과 폰 미제스(Von-mises) 응력 분포는 Fig. 4에 나타나있다. 채널의 립 아래의 다공성 기체확산층이 압축되고 생성된 수소가 Pc=10 bar에서 방출되기 때문에 애노드 방향으로 변형된다. 이 변형은 종자 분포에 불균일한 변화를 일으키고 수분 이동에 상당한 영향을 미친다고 알려져 있다^[15]. 또한, 전해질 막 두께가 줄어듬에 따라 변형과 폰 미제스응력이 증가하는 것도 보여진다. 여기서 양극 채널 영역에서 기체확산층의 최대 침투 두께 (∆δ_int,max)는 Ref. 케이스, Case 1 및 2의 침투 비율 (∆δ_int,max/δ_GDL)이 각각 약 31.7 %, 34.1 % 및 26.8 %인 경우 약 0.13 mm, 0.14 mm, 0.11 mm로 측정된다. 결과적으로, 막의 더 얇은 두께는 셀 운행 중에 더 심한 변형과 더 높은 응력 발생을 야기한다.

Fig. 4

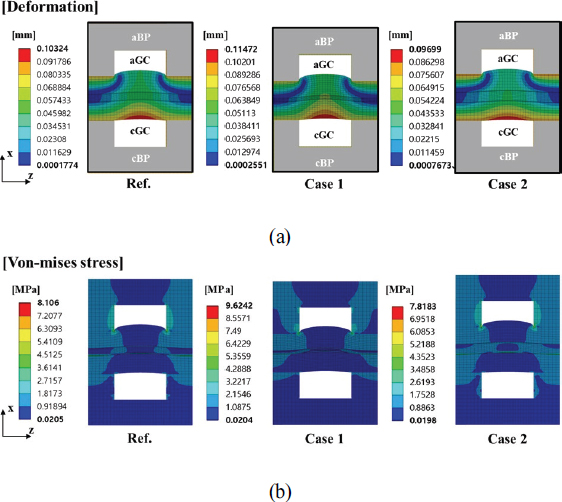
Distribution of (a) deformation (b) Von-mises stress during cell operation for Case. Ref (N115, δmem = 127 μm), Case 1 (NR212, δmem = 50.8 μm) and Case 2 (N117, δmem = 183 μm)

Fig. 5는 다른 기체확산층의 변형과 폰 미제스응력 분포를 보여준다. Fig. 4에서와는 반대로 클램핑 압력이 적용되지만 고강도의 애노드 방전 압력으로 인해 변형이 양극 방향으로 발생한다. 따라서 두꺼운 기체확산층 두께를 가진 Case 4의 애노드에서는 거의 균일한 변형이 예측된다. 이는 셀 조립 및 양극 압력의 복합적인 영향으로 인한 것이다. 또한, 기체확산층의 최대 침투 두께 (∆δ_int,max)는 침투 비율이 각각 31.7 %, 55 % 및 23.3 %인 경우 Ref. 케이스, Case 3 및 4에서 각각 약 0.13 mm, 0.11 mm, 0.14 mm로 측정된다. 최대 응력 값에 대해서는, 기체확산층 두께가 0.41 mm(Ref. 케이스)인 경우 기계적으로 우수함을 보인다. 앞서 언급한 바와 같이 기체확산층은 셀 구성 요소 중에서 영률이 가장 낮은 다공성 매체이다. 셀 적층 방향으로의 변위범위는 기체확산층 두께에 비례하므로, δ_GDL=0.6mm인 Case4가 가장 큰 침투 정도를 가진다. 반면, δ_GDL=0.2mm인 Case3은 더 얇은 두께 때문에 가장 작은 변형을 야기한다. 이는 전기화학수소압축기 셀 운전 중 더 안정적인 기계적 특성을 위해 기체확산층 설계 변수가 최적화되어야 함을 의미한다.

Fig. 5

Distribution of (a) deformation (b) Von-mises stress during cell operation for Case. Ref (δGDL = 0.41 mm), Case 3 (δGDL = 0.2 mm) and Case 4 (δGDL = 0.6 mm)

전산유체역학 기반 시뮬레이션은 다양한 전기화학수소압축기 셀 디자인에서의 수소 및 물의 이동 메커니즘을 분석하기 위해 수행되었다. 주의해야 할 점은 물이 애노드 쪽에서만 공급되며, 셀은 전해질 막에 물의 함유량이 유지되도록 설계되어야 한다는 점이다. Fig. 6a는 전류밀도 0.5 A/cm²의 작동 조건에서 막 두께에 따른 애노드와 캐소드의 중간면에서의 물 농도 분포를 나타낸다. 막의 두께가 더 두꺼운 N117 (Case 2)의 셀에서 최소 물 농도(C_H2O,min)는 1.346 mol/m³으로 확인된다. 이는 막의 두께를 줄임으로써 애노드에서의 수분 고갈 정도가 효과적으로 완화된다는 것을 의미한다. 기계적인 영향을 고려하면, 막의 두께가 낮아지면 (Case 1), 셀의 변형이 가장 크기 때문에 채널에서보다 물의 분포가 불규칙하게 나타난다. Fig. 6b에서 참조 케이스를 포함한 케이스 1 및 2에 대해 전류 밀도에 따른 막을 통한 순수한 물의 플럭스를 비교할 수 있다. 막을 통한 순수한 물의 플럭스는 전기삼투견인과 역확산에 의한 두 개의 물 플럭스를 결합하여 다음과 같이 정의할 수 있다.

Fig. 6

(a) Distributionofwaterconcentrationat in the middle cross-section of anode and cathode (b) net water molar flux from the anode through the membrane to the cathode as a function of operating current density for Case. Ref (N115, δmem = 127 μm), Case 1 (NR212, δmem = 50.8 μm) and Case 2 (N117, δmem = 183 μm)

여기서 λ_mem/cCL와 λ_mem/aCL는 전해질 막과 애노드 촉매층 사이, 전해질 막과 캐소드 촉매층 사이의 접합면에서의 물 함유량을 나타낸다. 먼저, $$ {\ddot{n}}_{net }$$은 작동 전류 밀도 범위 내에서 양수이며 전류 밀도가 증가함에 따라 계속 상승하여 전기삼투견인의 영향이 물의 이동에 지배적인 것을 명확하게 보여준다. 반면 NR212 (Case 1)의 $$ {\ddot{n}}_{net }$$은 Fig. 3a에 나타난 셀 전압의 추세와 동일하게 선형적으로 증가하여 막의 탈수를 방지하기에 충분한 물 확산량을 가지고 있음을 의미한다.

Fig. 7a는 기체확산층 두께에 따른 물의 농도를 보여준다. 더 얇은 기체확산층 두께 (Case 3)에서 최소 물 농도가 3.337 mol/m³으로 관찰되었다. 이는 기체확산층 두께가 감소함에 따라 캐소드의 건조 현상이 완화되는 경향이 있음을 의미한다. 게다가, 기체확산층 두께가 증가함에 따라 비교적 균일한 변형이 발생하므로 양 채널에서 물 농도의 균일성이 증가하는 것을 관찰하였다 (Fig. 5 참조). 또한, Fig. 7b에서는 기체확산층 두께에 대한 물 이동을 나타내며, Fig. 3b의 성능 곡선의 전압 추세를 설명할 수 있다. 기체확산층 두께의 감소는 약간의 물 확산량 증가를 가져오며 (식 (22) 참조), 캐소드에서 애노드로의 확산 경로가 짧아져 막의 수분을 유지하는 데 도움이 됨을 결론으로 도출할 수 있다.

Fig. 7

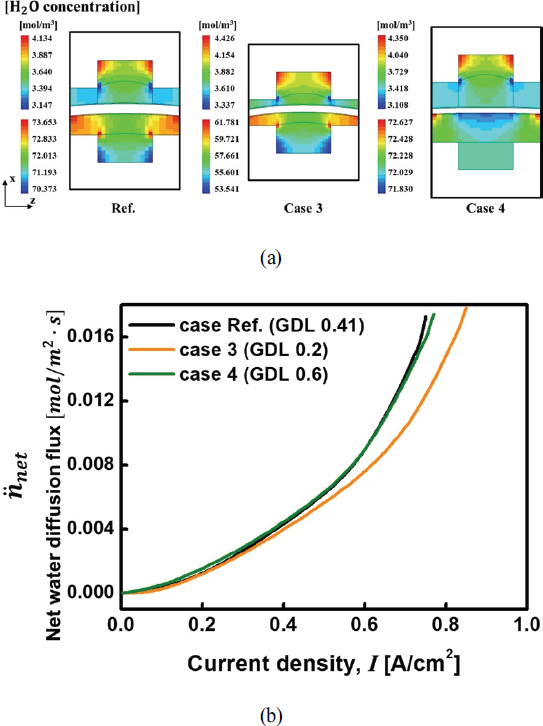
(a) Distribution of water concentration at 0.5 A/cm2 in the middle cross-section of anode and cathode (b) net water molar flux from the anode through the membrane to the cathode as a function of operating current density for Case. Ref (δGDL = 0.41 mm), Case 3 (δGDL = 0.2 mm) and Case 4 (δGDL = 0.6 mm)

수행된 시뮬레이션은 기체확산층 특성에 따라 10 bar와 100 bar의 압력 비율 (P_c / P_a)에서 수행되었다. 이를 통해 성능을 분석하고 기체확산층이 더 높은 수소 압축에 대한 영향을 충분s히 견딜 수 있는지 검증했다. Fig. 8a에서 관찰된 바와 같이, 카본 페이퍼로 제작된 기체확산층은 캐소드 방출 압력이 100 bar로 운전되는 경우에 임계적인 기계적 손상을 보인다. 따라서 기계적 신뢰성이 뛰어난 티타늄 (Ti) 폼으로 기체확산층을 교체하는 것을 필수적으로 고려해야 한다. 이로 인해 전기화학적 성능이 향상될 것으로 예상된다. 카본 페이퍼로 제작된 기체확산층과 티타늄 폼 기체확산층의 영률은 각각 6.3 MPa와 10,400 MPa이므로, 티타늄 폼이 카본 페이퍼 기체확산층보다 변형이 적고 더 높은 응력을 견딜 수 있음을 확인했다.

Fig. 8

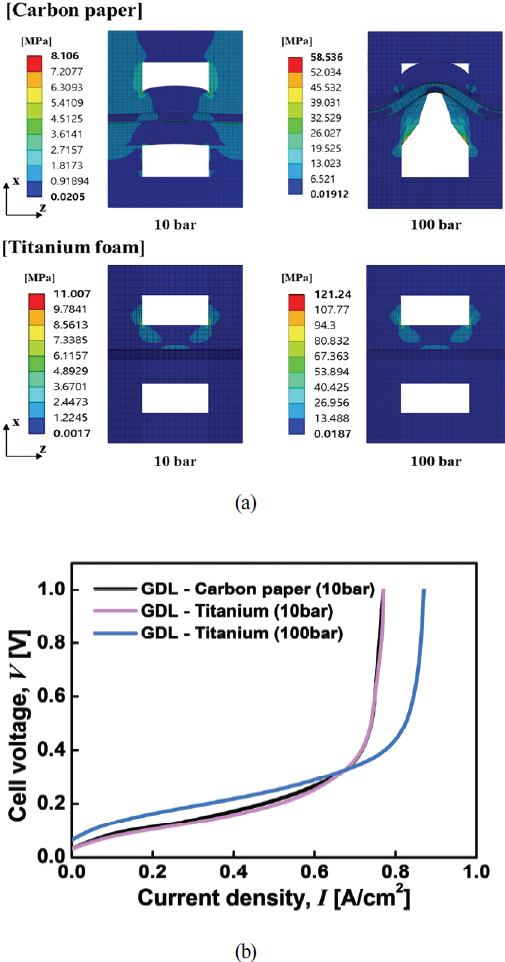
(a)Distribution of Von-mises stress and (b) polarization curves of simulated data of carbon paper GDL and titanium foam GDL at different pressure ratios (Pc / Pa)

Fig. 8b는 10 bar의 동일한 캐소드 방출 운전 압력 하에서 카본 페이퍼 기체확산층과 티타늄 폼 기체확산층의 성능 곡선을 비교한다. 0-1.0 A/㎠의 전류 밀도 범위에서 낮은 전류 밀도 범위인 0.1-0.6 A/㎠에서는 티타늄의 전자 전도도가 증가함에 따라 셀 전압이 50 mV 향상되는 것을 보여준다 또한. 캐소드 방출 압력이 100 bar까지 압축되면, 네렌스트 전압의 기여도가 증가하며 (식 (13) 참조), 전체 셀 전압이 증가한다. 높은 수소 방출 압력은 수분 관리에 효과적이기 때문에 (참고 문헌^[9]), 캐소드 방출 운전 압력이 100 bar인 경우에는 적용된 셀 전압이 급격히 상승하는 지점이 더 높은 전류 밀도로 이동된다. 따라서, 캐소드 방출 압력이 10 bar인 경우는 낮은 전류 밀도에서 성능이 더 우수하며, 캐소드 방출 압력이 100 bar인 경우는 전류 밀도가 증가함에 따라 성능이 향상된다. 그러나 G. Chen 등 ^[16]은 티타늄 재료가 상당히 비싸며 현재는 얇고 가벼우며 다공성을 높이기가 어렵고 본 연구에서는 3차원 유한요소법 및 전산유체역학 기반 모델을 사용하여 전기화학수소압축기(전기화학 수소 압축) 셀 디자인 변수가 기계적 특성과 수분 관리에 미치는 영향을 분석했다. 전해질 막 두께, 가스 확산층(기체확산층) 두께 등 다양한 공정 및 재료 비용이 많이 소요될 것으로 예상된다. 그럼에도 불구하고, 특히 전기화학수소압축기에서는 고압력 운전에서 티타늄 재료를 사용하는 것이 유리하다.

4. 결 론

변수를 단일 전기화학수소압축기 셀에서 조사했다. 이 모델은 셀 조립 절차 및 운전 과정을 고려하여 변형 및 폰 미세응력 분포를 자세히 분석하여 기계적 안정성을 더 잘 이해하기 위한 노력을 기울였다.

또한, 전기화학수소압축기 구성요소에서의 전기화학 및 전달 과정을 시뮬레이션하여 셀 성능과 수분 이동을 예측했다. 이 연구의 주요 결론은 다음과 같다.

• 1. 현재의 전기화학수소압축기 모델은 다른 막 조건에서 실험 데이터와 시뮬레이션 결과 간에 좋은 일치를 보여주었다. 특히, 이 모델은 불충분한 수분을 나타내는 고전류 밀도 영역에서 적용 전압의 급격한 상승을 성공적으로 포착하였다.
• 2. 수소 압축 비율이 10인 경우의 시뮬레이션 결과에서는 전해질막과, 가스확산층의 두께가 두꺼울수록 낮은 내부응력을 보였다. 그러나 기체확산층 두께가 더 두꺼운 경우(δ_GDL = 0.6 mm)에는 채널로 가장 큰 침투 정도를 보여주므로 전기화학수소압축기의 효율적인 운전을 위해 최적화가 필요하다.
• 3. 물의 수송거리가 셀 적층 방향으로 감소함에 따라, 낮은 막 두께는 물의 역확산의 영향으로 인해 애노드 탈수 현상이 완화되는 경향을 보였다. 또한, 얇은 기체확산층은 애노드 채널과 막전극접합체 사이의 확산 거리가 짧아지므로 유리한 조건이다.
• 4. 고압 운전에 견딜 충분한 기계적 특성이 기체확산층에 필요하다. 따라서, 전기화학수소압축기가 높은 압력 비율(P_c / P_a > 100)로 운전될 때, 상업용 카본 페이퍼 기체확산층에 비해 강도가 높은 티타늄 폼을 기체확산층 구성 요소로 사용하는 것이 권장된다.

전기화학수소압축기(전기화학 수소 압축) 셀은 애노드 건조 문제뿐만 아니라 애노드와 캐소드 사이의 높은 압력 차이로 인한 기계적인 결함에도 영향을 받는다. 따라서 전기화학수소압축기 셀은 기계적 신뢰성과 전기화학적 성능을 동시에 고려하여 설계되어야 한다.

Acknowledgments

이 논문은 2023년도 정부(산업부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임. (과제번호:P0021513)

References

• M. Rhandi, M. Trégaro, F. Druart, J. Deseure, M. Chatenet, Electrochemical hydrogen compression and purification versus competing technologies: Part I. Pros and cons, Chinese J. Catal. 41 (2020) 756-769. [https://doi.org/10.1016/S1872-2067(19)63404-2]
• W. Chen, B. Cameron, S. Narayanan, A Cryocooler Driven by Electrochemical Compressors with No Moving Parts. n.d.
• Proceedings of the Symposium on Diaphragms, Separators, and Ion-Exchange Google Kitaplar, n.d
• J. Jou, Y. Jin, Z. Wen, S. Xing, N. Han, K. Yao, Z. Zhao, M. Chen, J. Fan, H. Li, H. Wang, Insights into electrochemical hydrogen compressor operating parameters and membrane electrode assembly degradation mechanisms, J. Power Sources 484 (2021) 229249. [https://doi.org/10.1016/j.jpowsour.2020.229249]
• Y. Hao, H. Nakajima, H. Yoshizumi, A. Inada, K. Sasaki, K. Ito, Characterization of an electrochemical hydrogen pump with internal humidifier and dead-end anode channel, Int. J. Hydrog. Energy 41 (2016) 13879-13887. [https://doi.org/10.1016/j.ijhydene.2016.05.160]
• D. Qiu, H. Janßen, L. Peng, P. Irmscher, X. Lai, W. Lehnert, Electrical resistance and microstructure of typical gas diffusion layers for proton exchange membrane fuel cell under compression, Appl. Energy 231 (2018) 127-137. [https://doi.org/10.1016/j.apenergy.2018.09.117]
• B. Rohland, K. Eberle, R. Ströbel, J. Scholta, J. Garche, Electrochemical hydrogen compressor, Electrochim.Acta43 (1998) 3841-3846. [https://doi.org/10.1016/S0013-4686(98)00144-3]
• B. Rohland, K. Eberle, R. Ströbel, J. Scholta, J. Garche, Electrochemical hydrogen compressor, Electrochim. Acta 43 (1998) 3841-3846. [https://doi.org/10.1016/S0013-4686(98)00144-3]
• J. Lee, S. Yoon, H. Park, M. F. Chinannai, T. T. Phan, S. Kim, H. Ju, Coupled mechanical and electrochemical modeling and simulations for Electrochemical Hydrogen Compressors (EHC), Under review.
• F. Barbir, PEM fuel cells: Theory and practice, Elsevier, 2012.
• R.B. Bird, W.E. Stewart, E.N. Lightfoot, Transport phenomena, Wiley, Newyork, 2006.
• T.F. Fuller, Solid-polymer-electrolyte fuel cells (Ph.D. Thesis), University of California, 1992. [https://doi.org/10.2172/7001224]
• H. Zhang, M.A. Rahman, F. Mojica, P.C. Sui, P.Y.A. Chuang, A comprehensive two-phase proton exchange membrane fuel cell model coupled with anisotropic properties and mechanical deformation of the gas diffusion layer, Electrochim. Acta 382 (2021) 138273. [https://doi.org/10.1016/j.electacta.2021.138273]
• M. Nordio, F. Rizzi, G. Manzolini, M. Mulder, L. Raymakers, M.V.S. Annaland, F. Gallucci, Experimental and modelling study of an electrochemical hydrogen compressor, Chem. Eng. J. 369 (2019) 432-442. [https://doi.org/10.1016/j.cej.2019.03.106]
• D.H. Jeon, H. Kim, Effect of compression on water transport in gas diffusion layer of polymer electrolyte membrane fuel cell using lattice Boltzmann method, J. Power. Sources 294 (2015) 393-405. [https://doi.org/10.1016/j.jpowsour.2015.06.080]
• G. Chen, H. Zhang, H. Zhong, H. Ma, Gas diffusion layer with titanium carbide for a unitized regenerative fuel cell, Electrochim. Acta 55 (2010) 8801-8807. [https://doi.org/10.1016/j.electacta.2010.07.103]
• L. Zhang, Y. Liu, H. Song, S. Wang, Y. Zhou, S.J. Hu, Estimation of contact resistance in proton exchange membrane fuel cells, J. Power Sources 162 (2006) 1165-1171. [https://doi.org/10.1016/j.jpowsour.2006.07.070]
• L. Hao, K. Moriyama, W. Gu, C.Y. Wang, Modeling and experimental validation of Pt loading and electrode composition effects in PEM fuel cells, J. Electrochem. Soc. 162 (2015) F854. [https://doi.org/10.1149/2.0221508jes]
• H. Ju, G. Luo, C.Y. Wang, Probing liquid water saturation in diffusion media of polymer electrolyte fuel cells, J. Electrochem. Soc. 154 (2007) B218-B228. [https://doi.org/10.1149/1.2401034]
• B.M. Stühmeier, M.R. Pietsch, J.N. Schwämmlein, H.A. Gasteiger, Pressure and temperature dependence of the hydrogen oxidation and evolution reaction kinetics on Pt electrocatalysts via PEMFC-based hydrogen-pump measurements, J. Electrochem. Soc. 168 (2021) 064516. [https://doi.org/10.1149/1945-7111/ac099c]
• M.J. Lampinen, M. Fomino, Analysis of free energy and entropy changes for half-cell reactions, J. Electrochem. Soc. 140 (1993) 3537. [https://doi.org/10.1149/1.2221123]
• DuPont, NafionTMNafrion PFSA®PFSAMembranesN-112, NE-1135, N-115, N-117, NE-1110perfluorosulfonicacidpolymer.
• J. Hilsenrath, C.W. Beckett, W.S. Benedict, L. Fano, H.J. Hoge, J.F. Masi, R.L. Nuttal, Y.S. Touloukian, Tables of thermodynamic and transport properties, National bureau of Standrds Circular 564, Government pringing office, Washington 25, D. C., 1955.
• J. Hilsenrath, C.W. Beckett, W.S. Benedict, L. Fano, H.J. Hoge, J.F. Masi, R.L. Nuttal, Y.S. Touloukian, Tables of thermodynamic and transport properties, National bureau of Standrds Circular 564, Government pringing office, Washington 25, D. C., 1955.
• R.B. Bird, W.E. Stewart, E.N. Lightfoot, Transport phenomena, Wiley, Newyork, 2006.
• JNTG, JNTG_2021 Product Catalog.
• R. Singh, P.D. Lee, T.C. Lindley, C. Kohlhauser, C. Hellmich, M. Bram, T. Imwinkelried, R.J. Dashwood, Characteriazation of the deformation behavior of intermediate porosity interconnected Ti foams using micro-computed tomography and direct finite element modeling, Acta Biomater 6 (2010) 2342-2351. [https://doi.org/10.1016/j.actbio.2009.11.032]
• B.S. Mitchell, An introduction to materials engineering and science for chemical and materials engineers, John Wiley & Sons, New Jersey, 2004. [https://doi.org/10.1002/0471473359]
• H.A. Ly, H. Inoue, Y. Irie, Numerical simulation on rapid evaluation of fatigue limit through temperature evolution, J. Solid Mech. Mater. Eng. 5 (2011) 459-475. [https://doi.org/10.1299/jmmp.5.459]
• Z. Zhan, H. Zhao, P.C. Sui, P. Jiang, M. Pan, N. Djilali, Numerical analysis of ice-induced stresses in the membrane electrode assembly of a PEM fuel cell under sub-freezing operating conditions, Int. J. Hydrogen Energy 43 (2018) 4563-4582. [https://doi.org/10.1016/j.ijhydene.2018.01.064]
• O. Tabata, K. Kawahata, S. Sugiyama, I. Igarashi, Mechanical property measurements of thin films using load-deflection of composite rectangular membranes, Sens. Actuators 20 (1989) 135-141. [https://doi.org/10.1016/0250-6874(89)87111-2]
• F.N. Büchi, M. Inaba, T.J. Schmidt, Polymer electrolyte fuel cell durability, Springer, New York, 2009. [https://doi.org/10.1007/978-0-387-85536-3]