반응표면법을 활용한 소형풍력터빈의 유인날개 형상 최적화에 관한 연구

2.1 설계변수

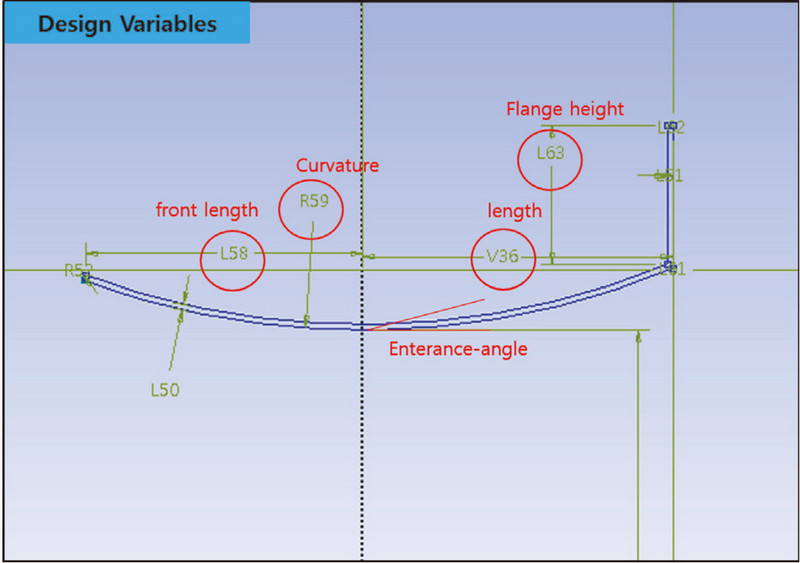
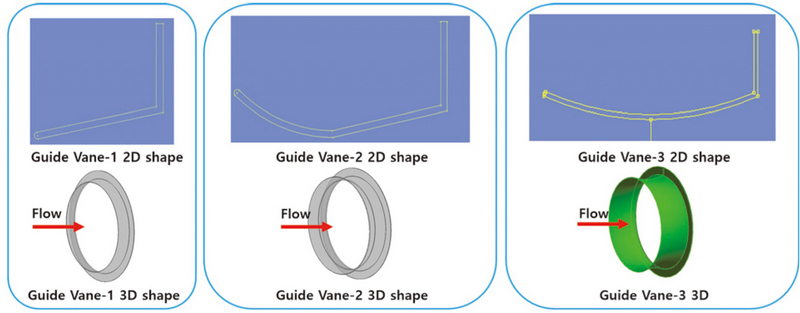
상용코드(ANSYS Workbench 2019)의 반응표면법을 활용하여 3개의 형상에 대한 최적화 설계를 수행하였으며, 기본 형상에 대한 설계는 참고문헌[8, 10, 11]을 참고하여 유인날개 입구의 축소 및 확대관의 형상이 유속증가에 미치는 영향을 보기위해 모델링 하였다. 설계변수는 Fig. 1과 같이 유인날개의 길이, 곡률길이, 플랜지 높이, 입구각이라 명명한 형상값에 대하여 설계변수를 두고, Fig. 2와 같이 총 3개 형상을 모델링하여 설계 및 분석을 수행하였다.

Fig. 1

Design variables

Fig. 2

Geometry of guide vane

유인날개-1 은 설계변수로 입구각, 유인날개의 길이, 플랜지 높이 3개의 변수를 적용하였으며, 유인날개-2는 입구각, 유인날개 전체길이, 유인날개 앞단길이, 플랜지 높이의 4개의 변수를 적용하여 모델링을 진행하였고, 마지막으로 유인날개-3은 곡률길이, 유인날개 길이, 플랜지 높이의 3개의 변수를 적용하였다.

최적화에 대한 형상의 수치는 기존수치에서 ±10% 오차범위 내에 변경을 수행하였으며, 설계변수 설정과 최적화 진행, 마지막으로 형상 최소화에 최대유속이 나올 수 있도록 해석 및 분석을 수행하였다.

2.2 수치해석 격자

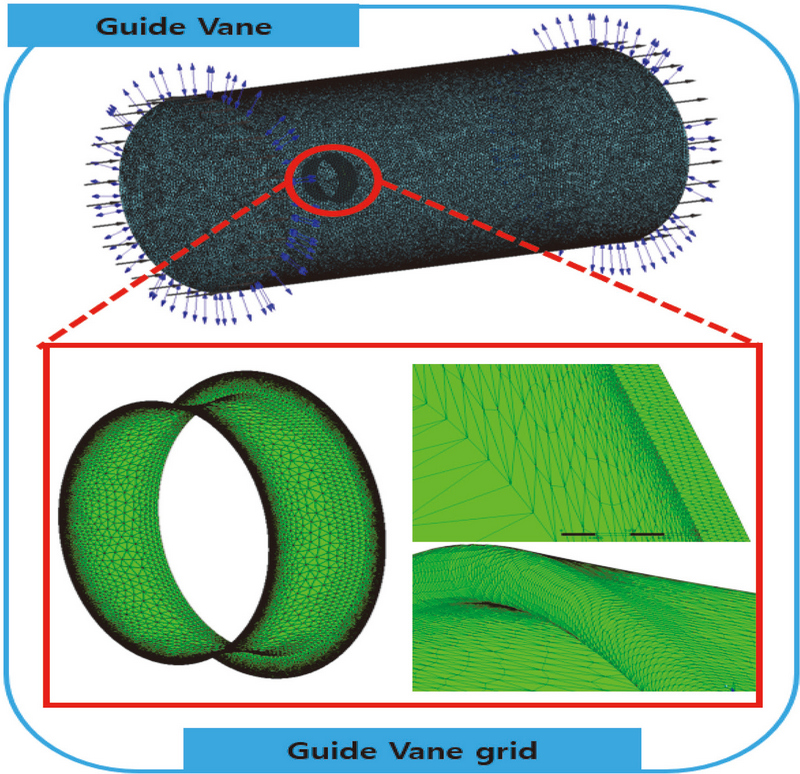
해석에 사용된 격자의 경우 상용코드를 이용하여 격자를 생성하였으며, 격자형식은 테트라-프리즘을 사용하였다. Fig. 3은 본 연구에 적용한 유동장과 유인날개의 형상에 대한 격자 계산을 확인할 수 있다. 격자는 유인날개 부분의 형상을 구현하기 위하여 170만 노드 사용하여 조밀하게 작성하였으며, 벽면에 대한 유동장 구현을 위하여 프리즘 격자를 구성하였다. 또한, 계산의 안정성을 위하여 외부 유동장의 크기는 유인날개 직경의 입구로 3D(D: 유인날개 직경), 출구로 7D, 오픈방향으로 5D만큼 유동장을 형성하였다.

Fig. 3

Numerical grids of flow field

2.3 경계조건 및 해석조건

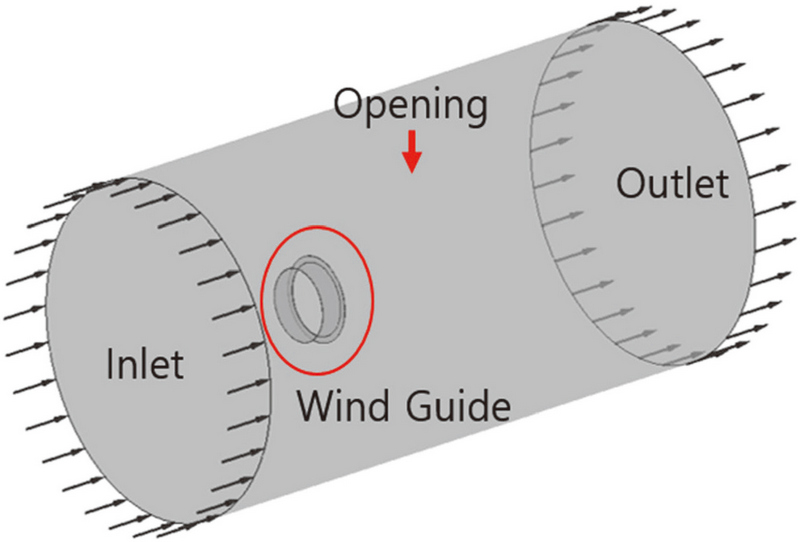
모든 해석에 대한 경계조건은 Fig. 4와 같이 구성되어 있으며, 상부는 개방(opening) 조건을 주었으며, 입구(inlet)와 출구(outlet) 조건으로 해석을 수행하였다.

Fig. 4

Boundary condition

Table 1에서와 같이 모든 계산은 정상상태 계산을 수행하였으며, 계산 수행에 사용된 난류 모델로서는 k-Epsilon 모델을 적용하였다. 유체는 공기를 사용하였으며, 입구 경계조건은 유속조건으로 5m/s로 부여하였고, 출구에는 대기압에 해당하는 압력 조건을 부여하였다.

Table 1

Boundary & analysis condition

최적화 계산 전 플랜지 높이는 0.13m로 고정하였다. 유형별에 따른 날개길이와 각도 등 변수로 하였으며, 이는 Table 2에서 변수값에 대한 수치를 확인할 수 있다. 최적화를 위한 수치의 변화는 현재 수치의 ±10%의 범위를 주고 최대유속이 나오는 형상최적화와 형상크기의 최소화일 때의 최대유속을 얻을 수 있도록 최적화를 수행하였다.

Table 2

Initial design value

3.1 유인날개-1의 수치해석

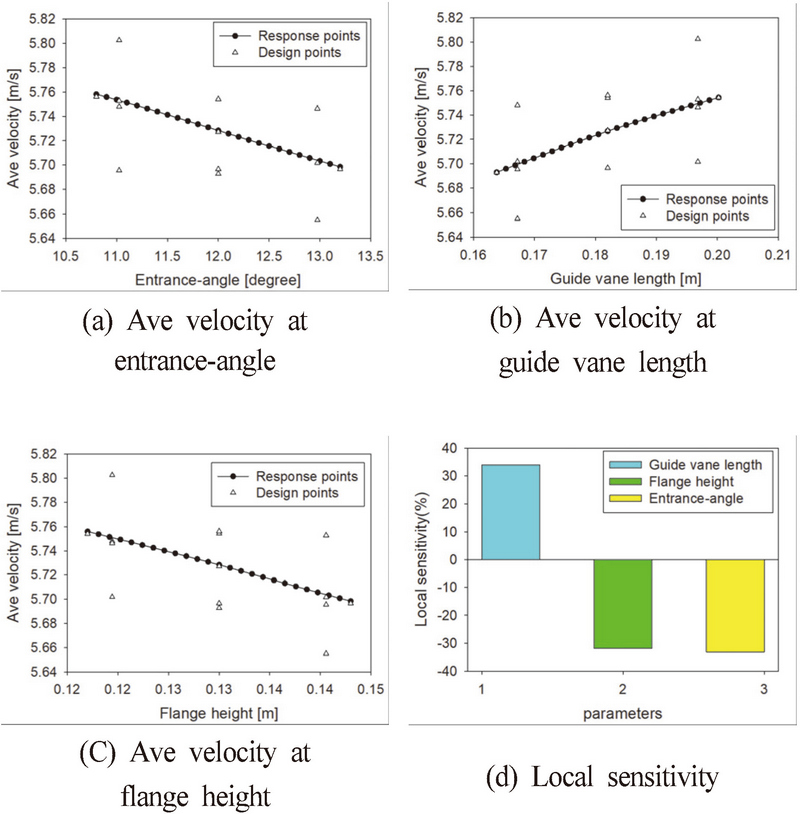
Fig. 5 표면반응법 해석의 결과로써 설계변수의 변화에 따른 평균유속에 대한 경향을 보여주고 있으며, (a)는 입구각도가 증가함에 따라 유속은 감소하며, (b)는 유인날개 길이가 증가함에 따라 유속이 증가하는 것을 확인할 수 있다. (c)는 플랜지 길이가 증가함에 따라 유속이 감소하였고, (d)는 유속변화에 있어 각 변수의 민감도를 보여주고 있다.

Fig. 5

Response chart for guide vane-1

Table 3은 설계값에 대한 유속값을 보여주고 있으며, 설계값 유속은 5.72m/s 최적화에 대한 최대 유속은 5.8m/s 유속으로 확인할 수 있다. 이는 초기 설계값에 비해 유속증가가 0.08m/s 증가한 것을 확인하였다.

Table 3

Results of design point

또한 최적화에 따른 유인날개의 설계변수 수치 변화는 Table 4에서 확인할 수 있으며, 크기를 최소화하며 최대 유속값을 찾기 위한 최적화를 진행한 결과 설계값보다 0.03m/s 증가함을 보여준다.

Table 4

Results of design variables(Guide vane-1)

3.2 유인날개-2의 수치해석

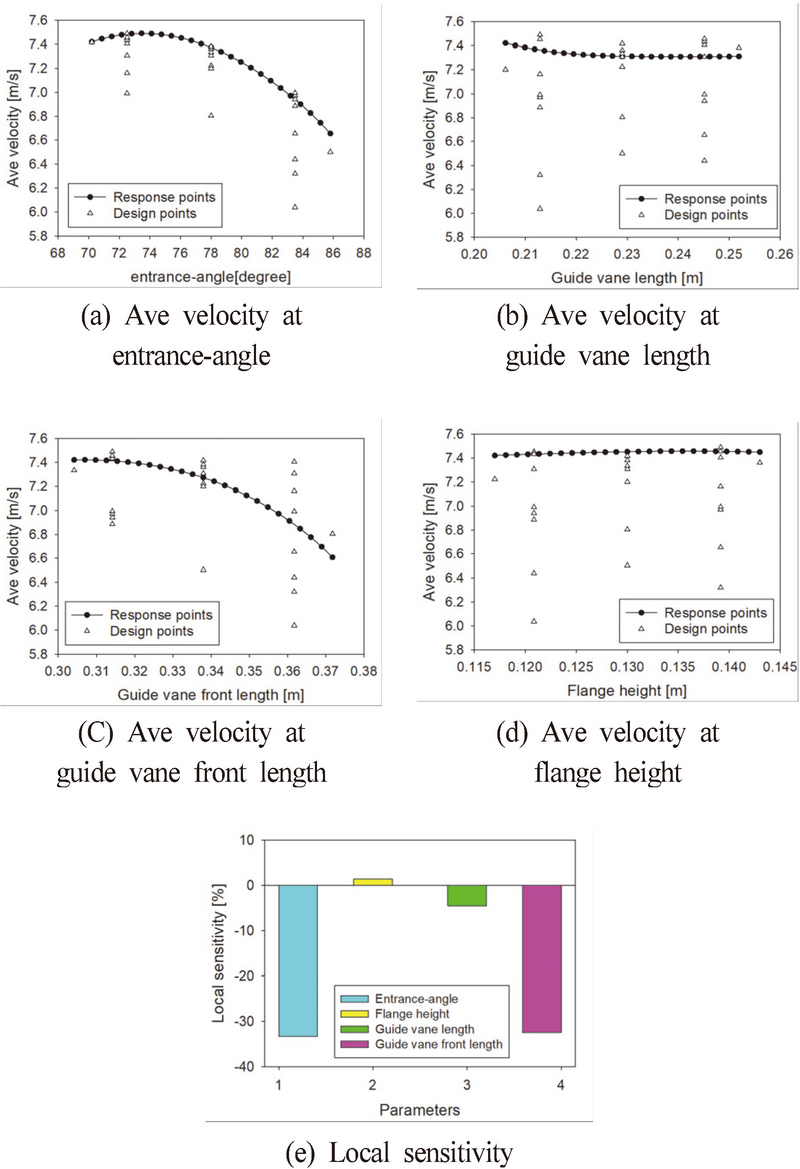
Fig. 6 유인날개-2의 표면반응법 해석의 결과로써 설계변수의 변화에 따른 평균유속에 대한 경향을 보여주고 있으며, (a)는 입구각도가 증가함에 따라 유속이 감소, (b)는 유인날개 길이가 증가함에 따라 유속이 감소하는 것을 확인하였다. (c)는 유인날개 앞단의 길이가 길어지면 유속이 감소하는 것을 볼 수 있으며, (d)는 플랜지 길이가 증가함에 따라 유속이 증가하고, (e)는 유속변화에 있어 각 변수의 민감도를 보여준다.

Fig. 6

Response chart for guide vane-2

Table 5은 디자인 포인트에 대한 유속값을 보여주고 있으며, 설계값 유속은 7.31m/s이며, 최적화에 대한 최대 유속은 7.49m/s로 초기 설계값에 비해 유속이 0.18m/s 증가함을 알 수 있다.

Table 5

Results of Design Point

최적화에 따른 유인날개의 설계변수 수치 변화는 크기의 최소화에 따른 최대 유속을 찾기 위한 최적화 진행결과 설계값보다 0.11m/s 증가함을 확인하였고, 이는 Table 6와 같다.

Table 6

Results of design variables(Guide vane-2)

3.3 유인날개-3의 수치해석

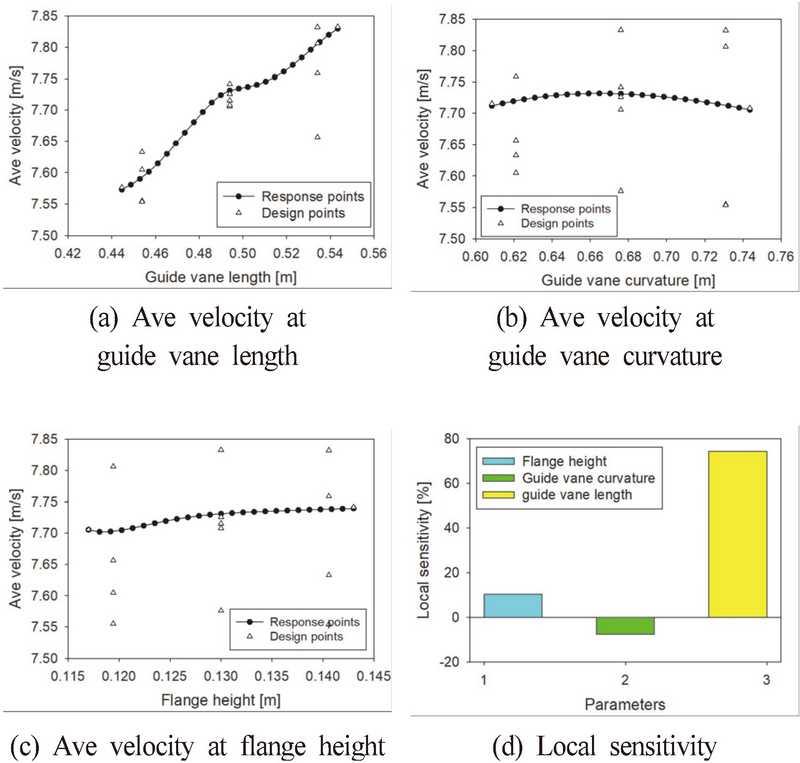
Fig. 7 표면반응법 해석의 결과로써 설계변수의 변화에 따른 평균유속에 대한 경향을 보여주고 있으며, (a)는 유인날개 길이가 증가함에 따라 유속이 증가하며, (b)는 유인날개 곡률길이가 증가함에 따라 유속이 감소하는 것을 알 수 있다. (c)는 플랜지 길이가 증가함에 따라 유속이 증가하며, (d)는 유속변화에 있어 각 변수의 민감도를 보여준다.

Fig. 7

Response chart for guide vane-3

Table 7은 디자인 포인트에 대한 유속값을 보여주고 있으며, 설계값 유속은 7.73m/s이며, 최적화에 대한 최대 유속은 7.83m/s 유속으로 확인할 수 있으며, 초기 설계값에 비해 유속증가가 0.1m/s 증가하였다.

Table 7

Results of Design Point

마지막으로, Table 8은 최적화에 따른 유인날개 설계변수의 수치 변화에 대한 것을 보여주며, 크기를 최소화하여 최대 유속값을 찾기 위한 최적화 진행 결과 설계값보다 0.14m/s 감소함을 확인하였다.

Table 8

Results of design variables(Guide vane-3)

3.4 유동해석 및 고찰

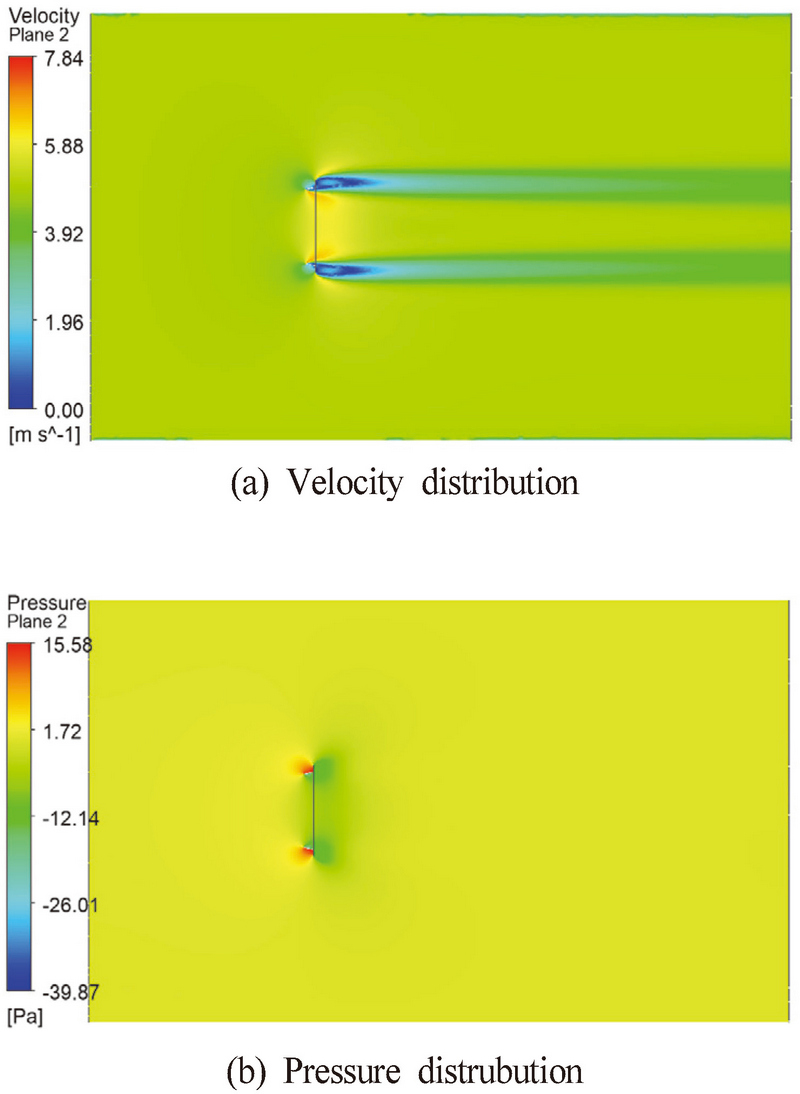
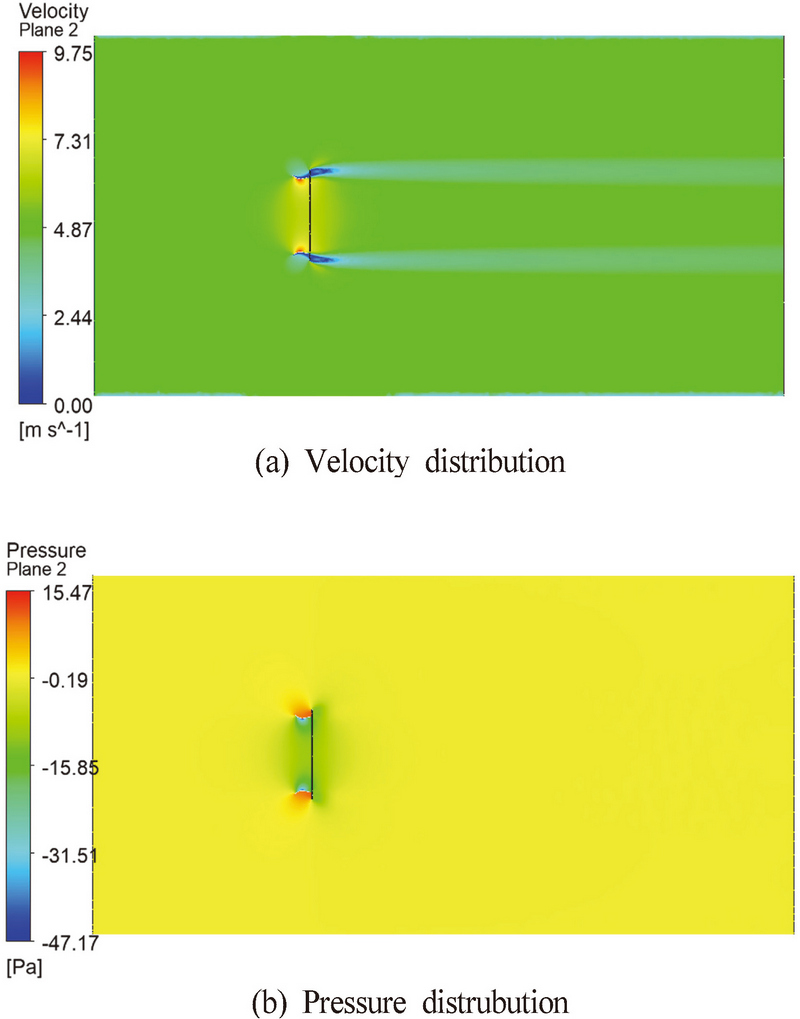
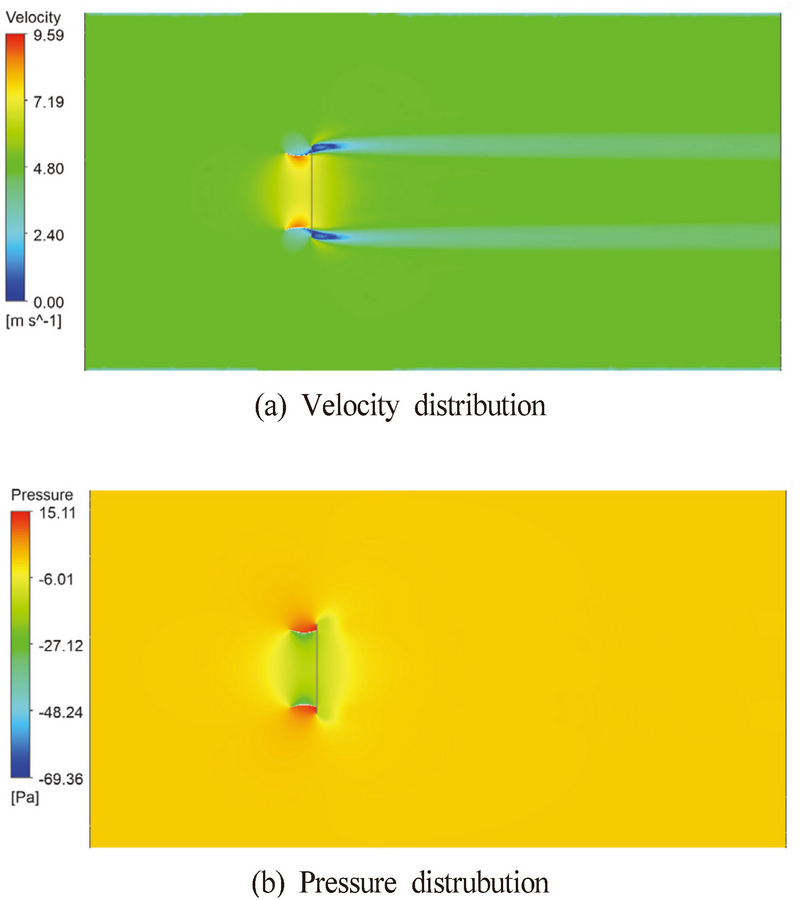
Fig. 8∼10은 유인날개의 중간 위치 단면에서의 유속과 압력 분포를 나타낸다. 본 논문에서 채택한 유인날개의 경우, 플랜지를 활용해 유인날개의 뒤편에 와류를 만들어 압력을 낮추어 유입되는 유속을 증가시켰다.

Fig. 8

Flow field around guide vane-1

Fig. 9

Flow field around guide vane-2

Fig. 10

Flow field around guide vane-3

유인날개를 적용한 풍력발전용 터빈의 경우, 유입되는 유속의 증가 및 압력의 감소에 따라 출력의 증가율은 높아진다. 이는 Fig. 10의 유인날개 부근에서의 유속과 압력 분포와 같이 최적화 분석에 따른 유인날개 3이 유인날개 1, 2 보다 압력이 더 낮아 높은 유속을 얻을 수 있음을 알 수 있다. 따라서, 유인날개 3의 형상이 유속증가에 유리한 것을 확인할 수 있다.

4.1 모델링 및 격자

이 논문에 사용된 소형풍력터빈의 용량은 500W 소형풍력터빈을 설계하여 계산을 수행하였고, 로터의 직경은 1.36m, 설계 정격유속은 11m/s, 주속비는 4로 설계하였으며, 에어포일은 s814를 사용하여 설계하였다.

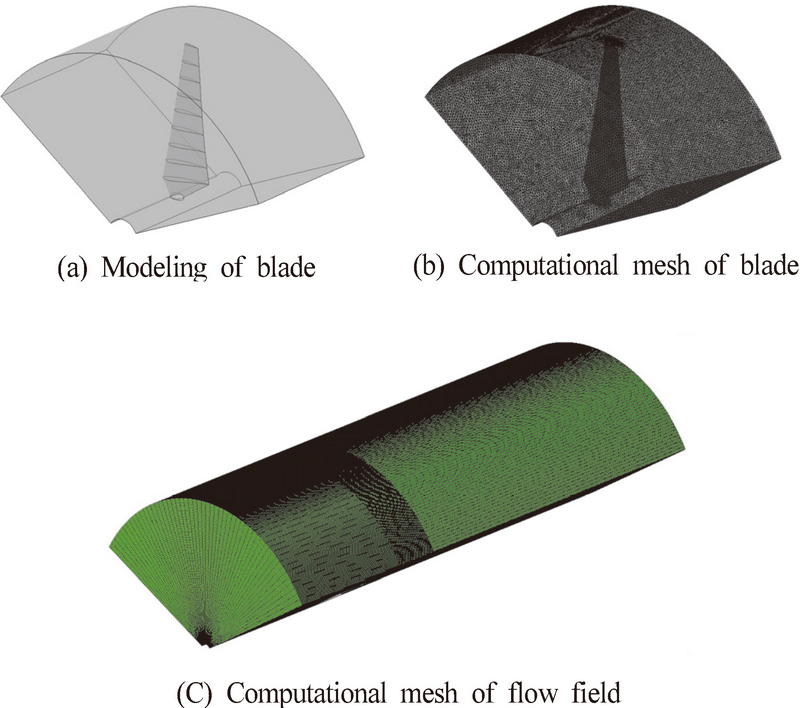
계산격자의 경우, 수치해석에 사용된 상용코드를 이용하였으며, 블레이드 격자형식은 테트라-프리즘과 헥사격자를 활용하였다.

Fig. 11의 (a)는 해석을 위한 블레이드 3D 모델링을 보여주며, (b)는 블레이드의 수치해석 격자를 보여준다. 블레이드의 형상 유지 및 y⁺값을 1이하로 하기 위해 총 486만 노드 격자를 사용하여 구성하였으며, (c)는 전체 유동장 격자로, 총 유동장의 격자수는 914만개 노드 격자를 사용하여 구성하였다.

Fig. 11

Computational domain

계산의 안정성을 위하여 외부 유동장의 크기는 블레이드의 크기의 입구로 5D(D: 터빈직경), 출구로 10D, 오픈방향으로 7D만큼 유동장을 형성하였다.

4.2 경계조건 및 해석조건

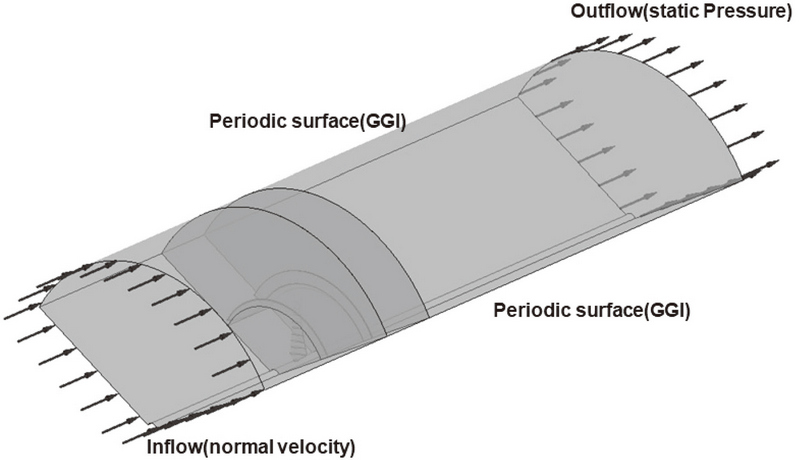
모든 해석에 대하여 경계조건은 Fig. 12와 같이 구성되어 있으며, 상부는 개방(opening) 조건을 주었으며, 입구(inlet)와 출구(outlet) 조건을 주고 해석하였다.

Fig. 12

Boundary conditions for CFD analysis

Table 9와 같이 모든 계산은 정상상태 계산을 수행하였으며, 계산에 사용된 난류 모델로서는 k-Epsilon 모델을 적용하였다. 유체는 공기를 사용하였으며, 입구 경계조건은 유속조건으로 11m/s로 부여하며, 출구는 대기압에 해당하는 압력 조건을 부여하였다.

Table 9

Boundary & analysis condition

해석은 주속비 3∼8까지 총 6개 케이스 계산을 수행하였으며, 최종적으로 설계 주속비 4에서 유인날개의 최적화를 동시에 진행하는 계산을 진행하여 출력에 대하여 결과를 도출하였다.

4.3 수치해석 결과

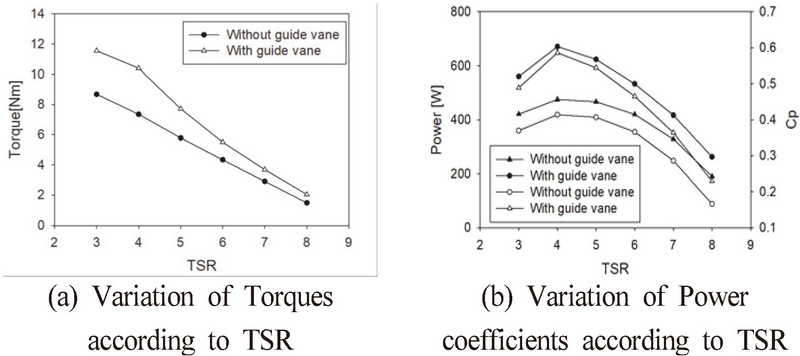
Fig. 13은 유인날개의 유무에 따른 해석 결과를 보여준다. (a)는 유인날개의 유무에 따른 출력토크를 보여주고 있으며, (b)는 풍력터빈의 성능계수를 비교하고 있다. 설계 주속비 4에서 최대 출력을 보여주고 있으며, 각각 474W와 671W의 출력을 나타내는 것을 확인할 수 있다. (b)와 같이 유인날개가 없는 경우 효율은 0.41을 보여주고 있으나, 유인날개를 사용할 때 0.56까지 상승함을 알 수 있다. 여기서, 효율은 식 (1)을 이용하여 산출하였으며, 유인날개 유무와 관계없이 면적(A)은 블레이드 단면적을 동일하게 사용하여 비교분석 하였다.

Fig. 13

Torque and Power coefficient Results

마지막으로, Table 10은 표면반응법을 통해 블레이드를 적용한 최적화 디자인 포인트를 보여준다. 기본 유인날개의 출력은 671W였으며, 최적화를 통해 계산된 최대 출력값은 716.5W로 확인할 수 있다. 또한, Table 11은 기본 형상에서의 최적화에 따른 결과값을 나타내며, 형상 최소화를 통한 최적화를 진행한 결과, 644W의 출력으로 기본 형상보다 출력이 감소하는 현상을 확인할 수 있다. 표면반응법을 활용하여 최적화를 진행할 때, 정확히 얻고자 하는 값을 도출값으로 설정 후 최적화를 진행하여야 한다.

Table 10

Results of Design Point

Table 11

Comparison of results of design variables

본 논문에는 단일 유인날개와 블레이드의 최적화 결과값 경향이 다르다는 것을 확인할 수 있는 것처럼 회전체같이 전체 유동장에 영향을 주는 변수값은 선정 후 계산함으로써, 더욱 정확한 최적화가 가능할 것으로 사료된다.