축류펌프의 설계부하 및 부분부하지점 비정상 유동구조 변화 분석

2.1 수치해석 기반 모델

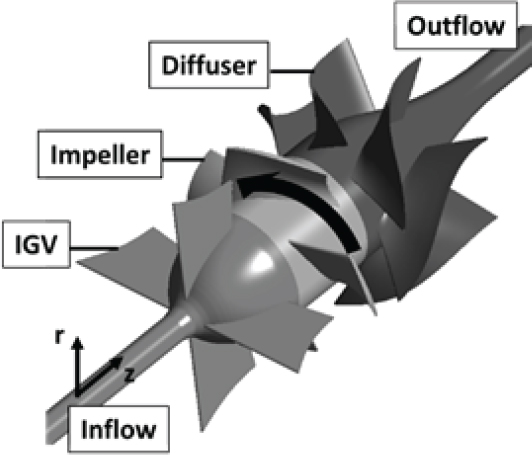
수치해석에 기반이 된 모델은 한국생산기술연구원에서 설계한 빗물처리 펌프로, Fig. 1과 같이 구성된다. 해당 축류펌프는 세 단계로 나누어져 있는데, 각각 입구 가이드 베인(IGV), 임펠러, 그리고 디퓨저로 구성되어 있다. 입구 가이드 베인은 유동 구조가 바뀜에 따라 임펠러 전류 회전속도를 억제하여 입사각의 변화를 최소화하는 역할을 가진다. 축류펌프의 블레이드 개수는 입구 가이드 베인 4개, 임펠러 4개, 그리고 디퓨저 7개의 블레이드를 갖고 있으며, 입구 가이드 베인을 지나면서 내부 반지름이 증가하고 외부 반지름이 감소하면서 통로의 수축이 일어나게 되고, 디퓨저를 통과하면서 내부 반지름이 다시 감소하여 통로의 확장이 일어나게 되는 구조로 되어 있다.

Fig. 1

Axial flow pump numerical simulation base model

2.2 수치해석 격자 설정

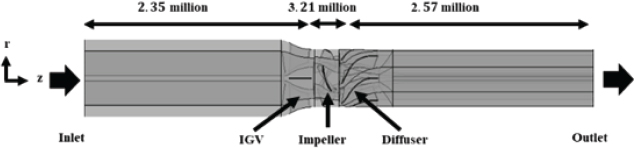
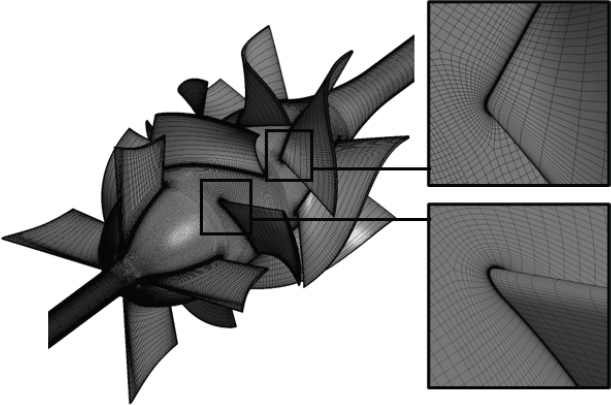
해당 펌프의 유동 구조 분석은 불안정 레이놀즈 평균 나비에-스톡 시뮬레이션(URANS)을 통해서 진행하였으며, 격자 독립성 검증 및 한국기계연구원에서 진행한 실험결과와 비교를 통해서 수치해석 모델의 정확도를 검토하였다. 격자는 Hexahedral 격자로 Turbogrid 격자생성 프로그램을 통해 제작되었다. 수치해석 도메인은 세 부분으로 분리하여 제작하였는데, Fig. 2는 입구부터 입구 가이드 베인까지 포함한 도메인, 회전하는 부분인 임펠러 도메인, 그리고 디퓨저부터 출구까지를 포함한 도메인으로 전체 총합 812만 개로 구성되어 있다. Fig. 3은 임펠러와 디퓨저 블레이드의 격자를 나타내는 그림으로, 두 블레이드 표면 모두 y+ 5 미만을 유지하도록 설정하였으며, 경계층 성장 비율은 1.2로 설정하였다. 경계층에서의 수치해석을 진행하는 과정에서 입구와 출구의 경계조건 모두 임펠러 유동에 영향을 주지 않기 위해 임펠러 지금의 3배 연장하였다. 실제 실험조건과 유사성을 높이기 위해 다상 유동 조건에서 수치해석을 진행하여 임펠러 내 발생하는 캐비테이션을 고려하였고, 증기와 액체 사이 질량 교환 모델로는 Rayleigh-Plesset 모델을 사용하였다. 실제 축류펌프에서는 작동과정에서 온도변화가 크지 않으므로, 해당 수치해석 시 물의 온도는 298K로 고정하였다. 자세한 경계조건에 대한 정보는 Table 1에 기술되어 있다.

Fig. 2

Computational Domain & Mesh element Numbers

Fig. 3

Impeller & diffuser grid element information

Table 1

Mesh information and boundary conditions

2.3 수치해석 모델 신뢰도 검사

수치해석의 신뢰도 평가를 위한 축류펌프의 성능시험은 한국기계연구원에서 수행하였다. Fig. 4는 한국기계연구원에 설치된 축류펌프 성능시험장치의 모습이다. 축류펌프는 펌프의 흡입압력을 조절할 수 있는 10ton 용량의 고압 밀폐 저수조와 펌프의 입구 및 출구를 배관으로 연결하여 폐루프로 구성된 시험설비에 설치되었다. 축류펌프는 수평형으로 제작되었고, 회전축은 커플링으로 전동기 축과 연결하여 구동하였다. 그 사이에 토크미터를 설치하여 펌프 축에 전달되는 토크를 측정하여 축동력을 산출하였다. 펌프의 토출 배관에는 터빈유량계를 설치하여 펌프의 작동유량을 측정하였고, 펌프의 전양정은 입구 및 출구 배관에 설치한 정압계 및 차압계를 설치하여 측정하였다. 펌프의 성능시험은 국내 시험규격인 KS B 6301⁽¹⁴⁾에 준하여 수행되었으며, 펌프의 전양정 및 수력효율 또한 규격에 제시된 수식에 따라 산정하였다. 성능을 측정하는 계측기의 세부 사양은 Table 2에 기술하였다. 규격에 제시된 전양정 및 효율 식은 아래와 같다.

Fig. 4

Axial flow pump test facility at Kora Institute of Machinery & Materials, (A) Overall test rig view (B) Test section section

펌프 전양정 ; $$ H=\frac{\mathrm{\Delta }{p}_{12}}{\rho g}+\frac{v_2^2-v_1^2}{2g}$$

펌프 효율 ; $$ \eta =\frac{\rho gQH}{T\omega }\times 100\left[\mathrm{\%}\right]$$

Table 2

Measurement equipments

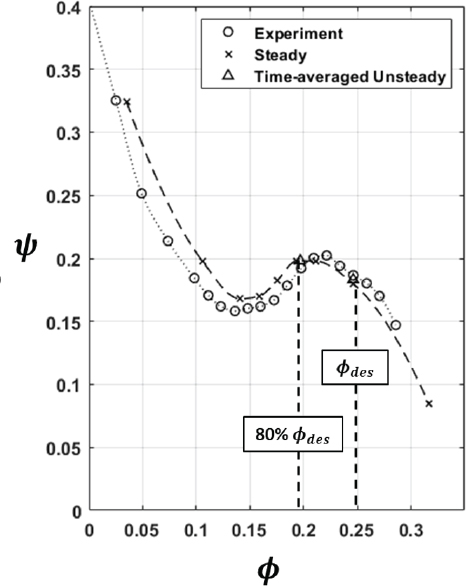
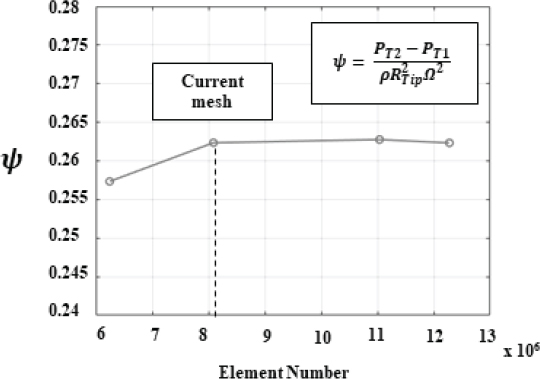
이때 ∆p₁₂는 펌프 입-출구 차압을 나타내며, v₂ 는 펌프 출구에서의 유체 평균 속도, v₁ 은 펌프 입구에서의 유체 평균 속도, T 는 펌프 회전 토크를 나타내며 마지막으로 ω 는 펌프 회전 속도를 나타낸다. Fig. 5는 축류펌프 성능곡선을 각각 실험, 정상수치해석 (RANS), 그리고 비정상수치해석을 통해 얻은 결과를 보여주고 있다. x 축은 무차원화한 유량계수이며, y축은 무차원화한 전양정계수로 설계 유량의 16∼120 % 지점까지의 성능곡선을 보여준다. 수치해석을 통해 얻은 결과는 실험 성능곡선과 유사한 분포를 보인다. 또한, 설계 유량지점과 부분 부하 지점인 80 % 설계 유량지점에서 비정상, 정상 유동의 수치해석 결과와 실험결과는 3 % 이내로 일치하였으므로 비정상 유동 값과 정상 유동 계산 모두 실험결과와 유사한 유동 구조로 되어 있음을 알 수 있다. Fig. 6과 같이 격자 독립성 검사를 통해서 해당 수치해석은 격자 수 812만 개가 넘어가면서 전양정의 차이가 1 % 내고 수렴하는 것을 확인할 수 있었으므로, 해당 연구에서는 효율적인 계산을 위해서 812만 개의 격자를 사용하였다.

Fig. 5

Axial flow pump performance curve

Fig. 6

Grid independence test

3.1 축류펌프 내 유동 특성

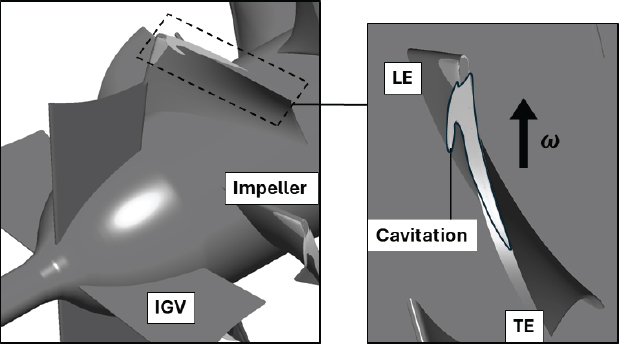
해당 수치해석은 다상 유동 조건을 고려한 수치해석으로 증기압보다 낮은 구간은 캐비테이션이 발생하게 된다. Fig. 7은 임펠러 팁 간극 유동으로 인해 발생한 캐비테이션을 보여주는 그림으로, 수치해석 상에서 캐비테이션이 발생한 구간은 증기 부피의 비율 10 %인 곳을 표시한 등가 곡면으로 설정하였다. 본 임펠러 블레이드에서는 블레이드 전단에 발생하는 sheet 캐비테이션과 블레이드 팁 간극에서 발생하는 팁 누설 유동 캐비테이션이 발생하는 것을 확인할 수 있다. 해당 캐비테이션은 90∼100 % span 부근 임펠러 주위 유동에만 발생하므로, 본 연구에서 진행하는 70 % span에는 캐비테이션으로 인한 영향은 없는 것으로 간주하고 연구를 진행하였다. 축류펌프 임펠러 웨이크는 임펠러 블레이드의 경계층 유동이 후단에서 박리되면서 발생하며, 경계층의 전단으로 인해 주 유동과 비교하여 낮은 상대속도를 갖고 있다. 동시에 주 유동과 임펠러 모두 임펠러의 회전속도를 갖고 있으므로, 절대속도의 방향과 크기 모두 달라진다.

Fig. 7

Cavitating region at axial flow pump impeller tip region

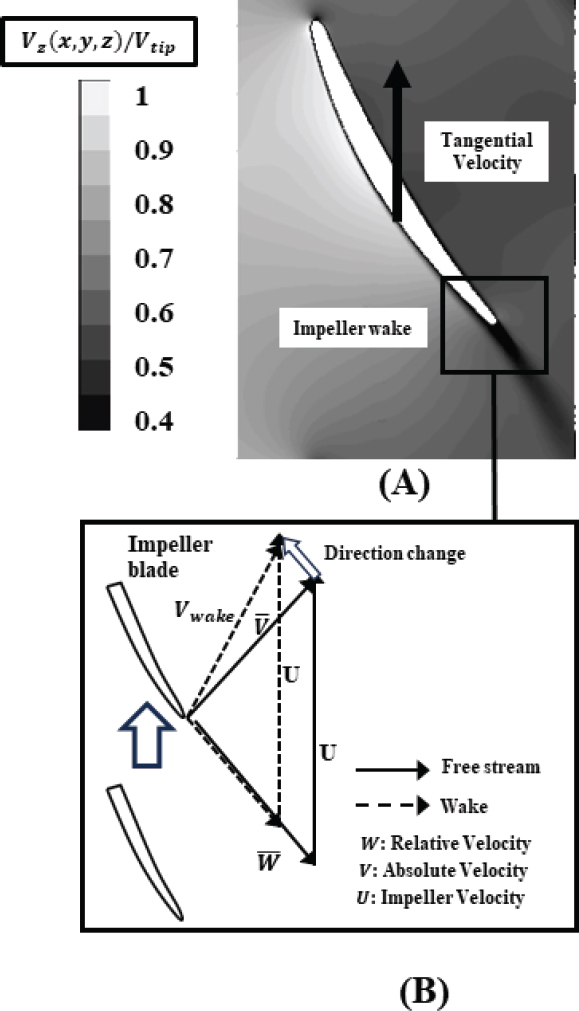
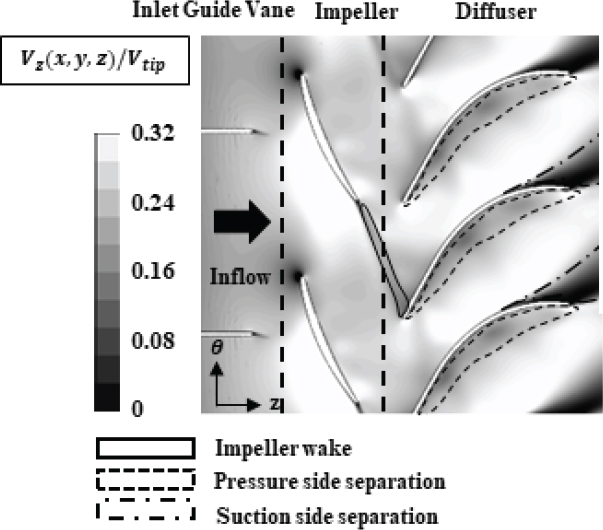
Fig. 8은 축류펌프의 축 방향 속도분포와 임펠러 웨이크와 주 유동의 속도 차이를 속도 삼각형의 구성을 통해 보여주는 그림으로. 웨이크는 주 유동에 비해 높은 입사각을 갖고 있음을 확인할 수 있다. 이로 인해 웨이크는 디퓨저 압력 면에 침체되며 또한, 침체된 웨이크는 압력 면의 양방향으로 분산된다.⁽¹²⁾ 양방향으로 분산된 유동은 주 유동과 혼합화여 디퓨저 통로 내 웨이크를 중심으로 양 방향으로 순환하는 와류를 생성하게 되고 디퓨저 내에서 난류혼합 손실량을 증가시킨다.⁽⁴⁾ 한편, 웨이크는 블레이드의 압력 면과 흡입 면의 속도 차이로 인해서 이와 동시에 웨이크는 디퓨저 블레이드의 압력 면과 흡입 면의 속도차이로 인하여 스트레칭이 발생하여 주 유동과 웨이크 사이의 속도 차를 감소시키는 혼합현상이 발생하게 되는데 해당 현상은 점성효과와 독립적인 효과로, 점성력으로 인해 발생하는 난류혼합의 양을 감소하게 하여 전체 손실의 양을 감소시킨다. Fig. 9는 비정상 수치해석을 통해 계산한 70 % 스팬에서의 축 방향 속도분포를 나타낸 그림으로, 펌프 내부에서 발생하는 세부적인 유동들을 보여주고 있다. 임펠러 후단에 부착되어 디퓨저까지 분포하는 저속구간은 임펠러 경계층으로 인해 형성된 임펠러 웨이크임을 알 수 있다. 해당 웨이크는 임펠러가 회전함에 따라 같이 이동하면서 펌프 유동 구조 내부에 비정상 유동구조를 발생시킨다. 이때, 임펠러 날개 뒷전에서 웨이크가 발생하게 되고, 이 웨이크는 디퓨저 날개 전단에 의해서 절단된다. 절단된 웨이크는 디퓨저 내부 통로를 이동하게 되는데, 이때 다른 저속구간이 존재함을 알 수 있다. 디퓨저 압력 면에 색깔이 어두운 저속구간이 발생함을 알 수 있는데 이는 디퓨저의 전단 날개 각도와 유동 각의 차이로 인해 압력 면에서 박리가 발생하기 때문이다. 또한, 디퓨저의 흡입면 후단 근처에서 저속구간이 발생하여 크게 확장되어 가는 것을 볼 수 있는데, 이는 디퓨저의 허브 코너 박리가 발생하여 형성되는 것이다. 디퓨저의 흡입 면 박리와 압력 면 박리 모두 디퓨저 내부의 유효통로 면적을 줄여 웨이크 스트레칭이 발생하게 되는 정도를 줄이게 된다.

Fig. 8

(A) Axial velocity contour at axial flow pump (B) Velocity triangle of impeller wake and main flow

Fig. 9

Axial velocity distiribution and separated region

3.2 설계 유량지점 비정상 유동 구조 특성

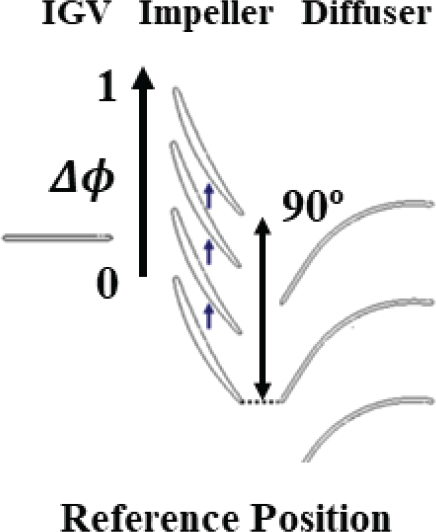
Fig. 10은 시간에 따라 변화하는 비정상 유동장 구조를 묘사할 시 참조 위치를 나타내고 있다. 참조 위치 중 원점으로 설정하는 위치는 임펠러의 뒷전과 디퓨저의 전단이 일치하는 순간을 기준으로 두며, 주기 ∆ϕ 는 임펠러가 90도 회전하였을 때, 즉 후행 임펠러 블레이드가 선행 임펠러 블레이드와 동일한 위치에 있을 때로 설정하여, 한 주기가 지난 후 임펠러와 디퓨저의 상대적 위치가 같도록 설정하였다. 본 연구에서는 주기 ∆ϕ를 4등분하여 각 시간 간격별로 변하는 비정상유동구조를 분석하였다.

Fig. 10

Reference position between impeller and diffuser at unsteady simulation

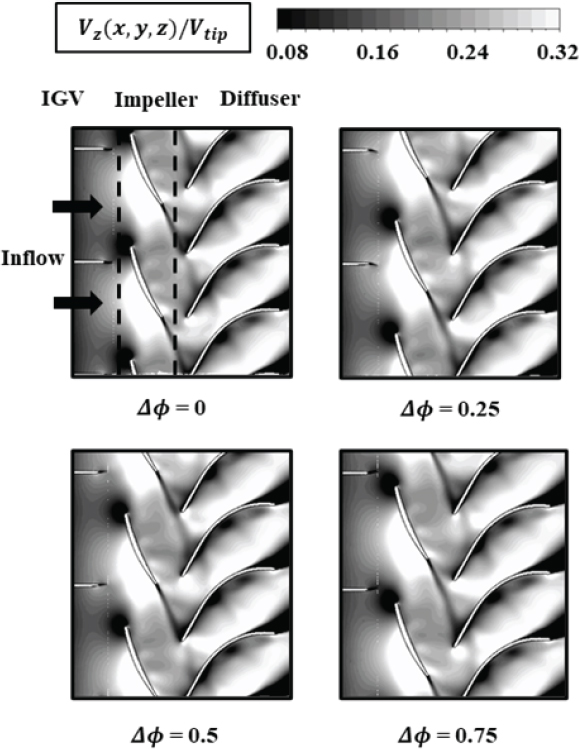
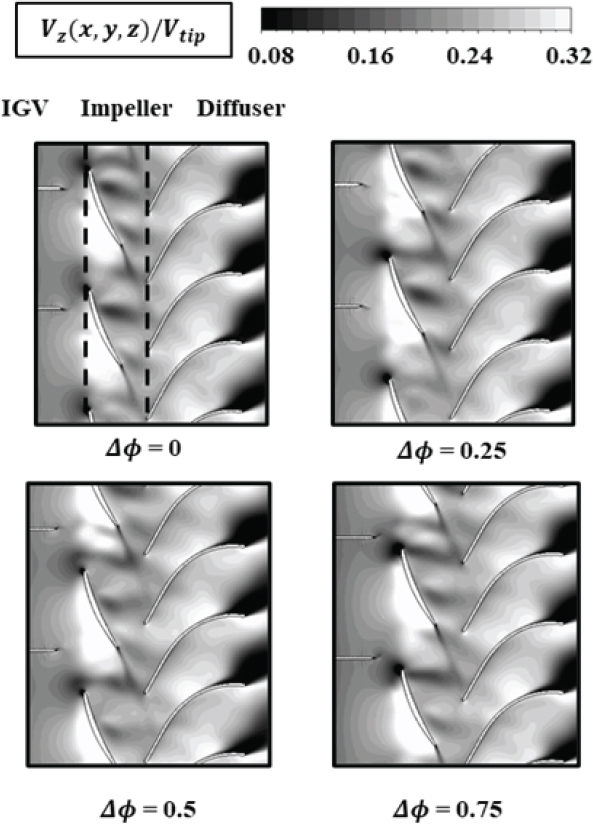
Fig. 11은 70 % span에서 시간에 따른 축 방향 속도분포를 나타낸다. 축 방향 속도는 속도가 느릴수록 어둡게 나타나며, 해당 유동에서는 임펠러 전단 부근, 임펠러 후단과 연결 되어 있는 가느다란 선, 그리고 디퓨저 압력 면과 흡입 면에 저속구간이 관찰되고 있음을 알 수 있다. 한편 입구 가이드 베인 주변에는 후단에는 저속구간이 관찰되지 않아 웨이크가 크게 형성되어 있지 않음을 알 수 있는데, 입구 면적의 감소로 유속이 증가하여 정압이 감소하고, 입구 가이드 베인 블레이드의 두께가 얇아 압력 구배가 발생하지 않아 경계층이 크게 발달하지 않기 때문이다. 이로 인하여 입구 가이드 베인으로 인한 후류 유동 구조에 미치는 영향 역시 거의 없는 것을 알 수 있다. 한편 임펠러 후단에서 발생하는 색깔이 어두운 영역은 낮은 축 방향 속도를 보유하고 있는 웨이크를 나타내는 것임을 알 수 있다. 임펠러 웨이크는 디퓨저를 통과하기 전까지 주 유동과 혼합되면서 굵기가 증가하고, 주 유동과 속도 차가 감소하면서 색깔이 밝아지는 과정을 확인할 수 있다. 디퓨저의 경우 압력 면에 낮은 속도 구간이 발생한 것을 확인할 수 있는데, 이를 통해 음수 입사각으로 인한 유동 박리가 일어나 저속구간이 발생한 것을 알 수 있다. 임펠러 웨이크는 이후 디퓨저 전단에 의해 절단되면서 디퓨저 통로 내부 불안정 유동분포가 발생하게 되는 원인을 제공한다. 디퓨저 후단에서는 흡입 면 측에서 색깔이 어두운 구간이 증가하며 디퓨저 후단에서 확장되는 것은 허브 코너 박리로 인해 유로 단면적이 감소하고 있는 것을 보여준다.

Fig. 11

Periodic axial velocity contour at 70 % span

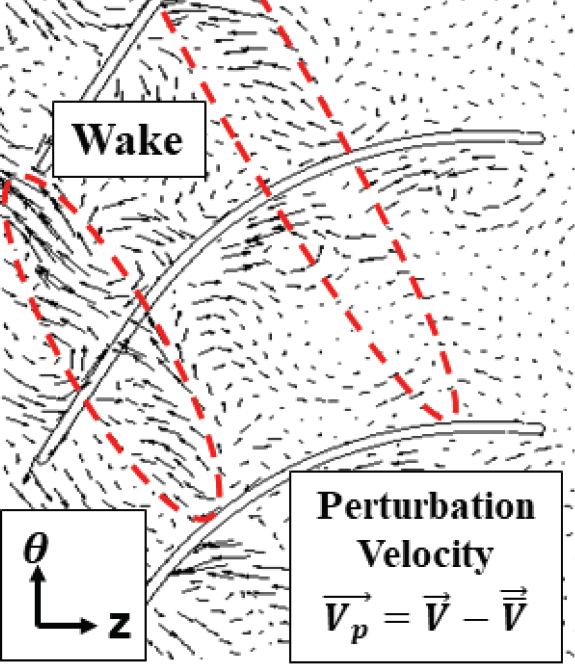
이때 디퓨저 전단에 의해 절단된 임펠러 웨이크는 디퓨저 통로 내에서 비정상 유동분포를 만들어 내는 것 역시 확인할 수 있다. 디퓨저 후류로 운송될수록 임펠러 웨이크로 인한 저속구간이 감소하는 것을 통해 임펠러 웨이크가 주 유동과 혼합되면서 소멸하는 것을 알 수 있다. 정확한 임펠러 웨이크의 변화 양상을 알기 위해 섭동 속도를 정의하여 내부에서 웨이크가 변화하는 양상을 관찰하였다. 섭동 속도는 시간 평균 속도와 현재 속도의 차이를 나타낸 값으로, 식 (1)과 같다.

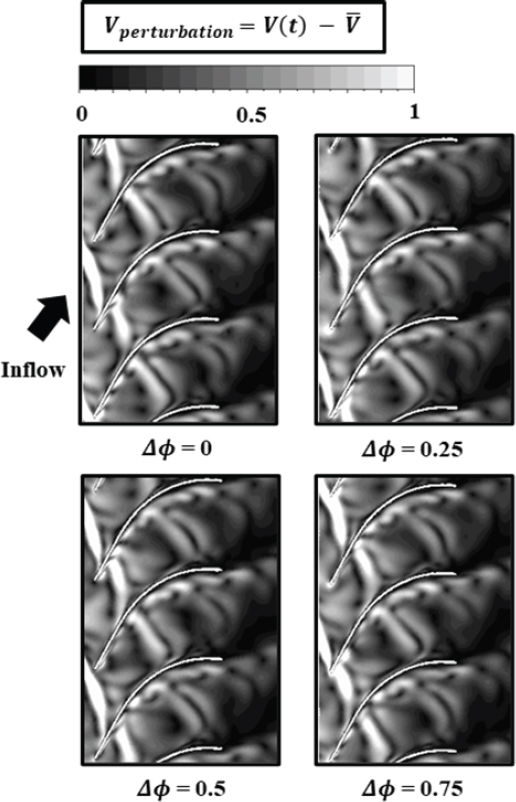
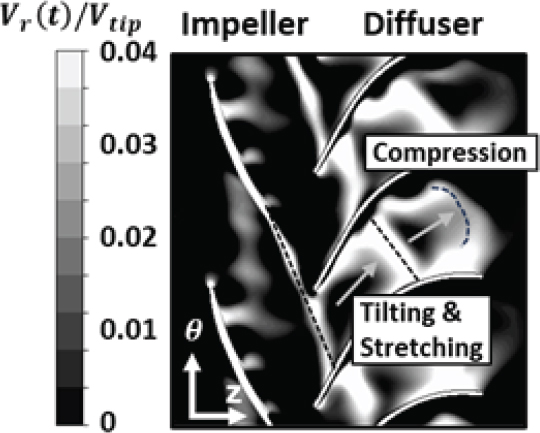
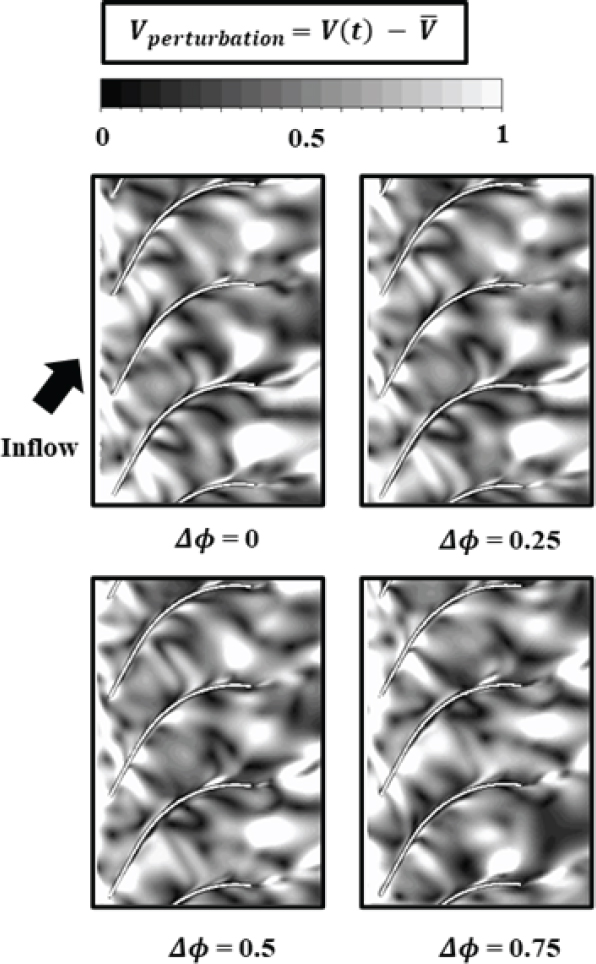
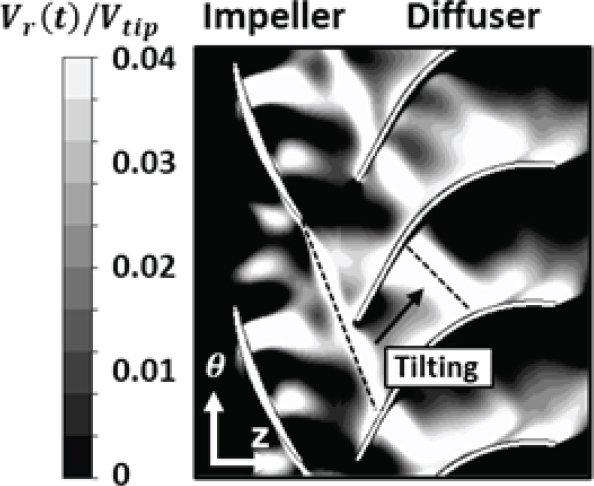
해당 섭동 속도를 Fig. 12와 같이 벡터분포로 나타낼 수 있으며, Fig. 7(B)와 같이 속도 차를 가진 구간을 볼 수 있고, 해당 영역이 웨이크를 대변한다. Fig. 13은 디퓨저 통로 내 섭동 속도분포를 보여주며, 축 방향 속도와 비교하여 더욱 정확한 임펠러 웨이크의 변화 양상을 보여준다. 임펠러 웨이크는 디퓨저 전단에 의해 절단된 후 기울어짐을 확인할 수 있는데, 이는 디퓨저의 압력 면과 흡입 면 사이 속도 차로 발생한다. 이는 압축기에서도 발생하는 현상으로, 웨이크는 이 작용 때문에 늘어나게 되고, 켈빈 순환정리에 따라 주 유동과 속도 차이가 감소하게 되어 가역적 혼합과정이 일어나게 된다. 이는 주 유동과 난류혼합과정을 통한 손실을 줄여주게 된다. 이는 축 방향 속도분포에서 확인 가능한 흡입 면의 허브 코너 유동 박리로 인한 작용이다. 이와 동시에 흡입 면의 허브 코너 유동 박리 역시 저속구간으로 이루어져 있으므로, 임펠러 웨이크는 중간 피치와 블레이드 표면의 저속구간 사이 속도 차로 인해 구부러지게 되는 것을 확인할 수 있다.

Fig. 12

Perturbation velocity contour at 70 % span

Fig. 13

Perturbation velocity contour inside diffuser passage at 70 % span

통로 폭 감소로 인해 웨이크는 다시 압축되게 되므로 주 유동과 속도 차는 가역적으로 증가하게 되고 이는 난류혼합손실의 증가를 불러온다. 즉 허브 코너 유동 박리는 유동 박리로 인한 손실의 증가도 가져오지만, 비정상 유동 구조인 임펠러 웨이크의 혼합 손실 증가도 가져오게 됨을 유추할 수 있다. 임펠러 웨이크가 회전 방향 속도가 더 높은 것은 동일한 압력 구배에 노출되었을 때 유체에 작용하는 원심력이 더 크다는 것을 의미하며, 이는 방사형 속도 값이 더 크다는 것을 의미한다. Fig. 14는 임펠러와 디퓨저에서의 방사형 속도 분포를 나타낸 값으로, 임펠러 뒤에 연결된 하얀 영역은 임펠러 웨이크로 인하여 높은 방사형 속도 값을 갖고 있는 것을 볼 수 있다. 허브 코너 박리구간과 압력 면의 유동 박리 구간을 제외하면 웨이크가 후단으로 갈수록 오히려 길이가 증가하는 것이 아닌, 굽고 길이가 감소하는 것을 볼 수 있다.

Fig. 14

Radial velocity contour inside diffuser passage at 70 % span

3.3 부분 부하 비정상 유동 구조 특성

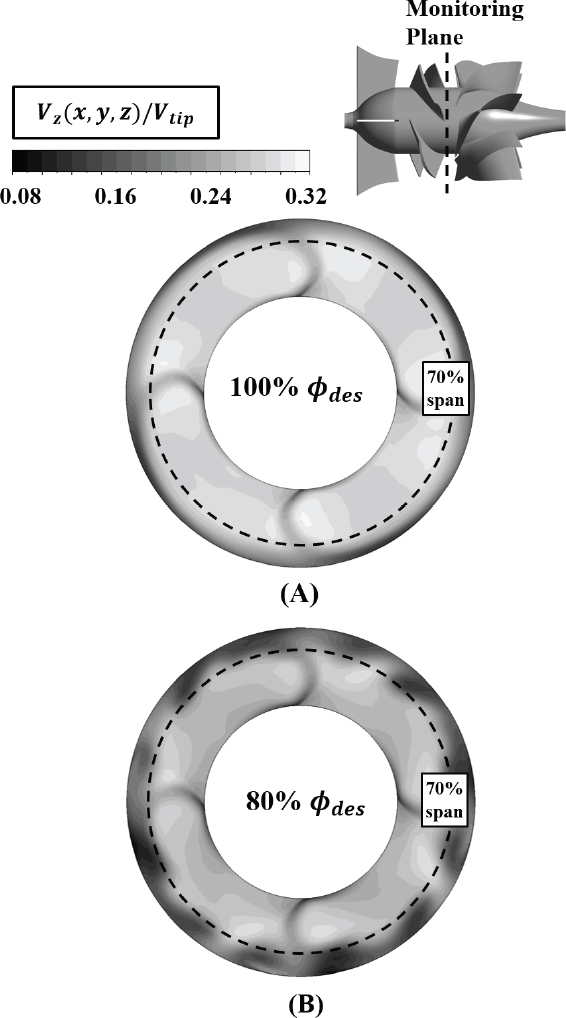
Fig. 15는 80 % 부분 부하 조건에서 비정상 유동해석을 통한 시간에 따른 축 방향 속도분포를 나타낸 그림이다. 부분 부하 조건의 경우, 펌프를 통과하는 유동의 평균 축 방향 속도가 감소하게 되고, 그와 더불어 펌프의 양정이 증가한다. 이로 인해 디퓨저 내 역압 구배를 포함한 압력 구배의 크기가 증가하며 허브 코너 박리가 되는 구간이 설계 유량에서 계산한 허브코너 박리구간보다 일찍 일어나고 디퓨저 유로의 축소가 더 많이 발생했음을 알 수 있다. 따라서 임펠러 웨이크는 스트레칭이 발생하는 구간은 설계 유량에 비해 더 감소하게 된다. 펌프의 양정 증가는 또한 팁 간극 유동의 크기가 증가하게 만들어, 70 % span에서도 임펠러와 임펠러 사이 낮은 속도 구간이 발생하고 있는 것을 알 수 있다. 팁 간극 유동으로 인해서 70 % span의 유동 역시 불안정성이 증가하게 되고, 이는 임펠러 웨이크 주변의 어두운 색깔 구간의 분포로 확인할 수 있다. Fig. 16은 부분 부하 구간에서의 섭동 속도의 분포를 보여주고 있다.

Fig. 15

Axial velocity contour at impeller trailing edge at (A) design flow rate and (B)Partial flow rate

Fig. 15

Partial flow rate periodic axial velocity contour at 70 % span

Fig. 16

Partial flow rate perturbation velocity contour at 70 % span

해당 섭동 속도 분포에서는 팁 간극 유동의 영향으로 인해서 임펠러 웨이크로 인한 섭동 속도분포 구간이 명확히 구분되지 않는다. 디퓨저 내에 유동이 불균형한 영역이 임펠러 웨이크로 인한 영향뿐만 아니라 불안정한 임펠러 내 유동 구조의 영향으로 인해 펌프 내의 불균일도가 설계 유량에 비교하여 증가했음을 알 수 있다. 위 두 결과를 통하여 부분 부하 지점의 축류펌프 유동은 웨이크 스트레칭으로 인한 혼합과정이 축소하고 점성력으로 인한 혼합이 지배적으로 일어나게 되는 것을 알 수 있다. Fig. 17은 디퓨저 내 방사 방향 속도분포를 나타낸 값으로, 설계 유량지점에서 디퓨저 내 방사 방향 속도분포와 다른 양상을 보인다. 임펠러 웨이크는 부분설계지점에서 더 두꺼운 양상을 보이며, 디퓨저 내부에서 동일하게 압력 면과 흡입 면의 속도 차에 의해 기울어짐은 발생하나, 속도 차로 인한 웨이크가 굽는 현상은 관찰되지 않았다. 이는 팁 간극유동으로 인한 영향과 더불어 허브 코너 박리로 인한 높은 방사속도를 가지게 된 디퓨저 블레이드 흡입 면 후단으로 인하여 임펠러 웨이크 성분이 더 높은 스팬으로 이동하여 웨이크 성분이 관찰되지 않은 것으로 보인다.

Fig. 17

Partial flow rate radial velocity contour inside diffuser passage at 70 % span

3.4 유량 변화에 따른 웨이크 성분 정량화

앞서 비정상 유동해석을 통하여 축 방향속도, 섭동 속도 분포, 그리고 방사 속도분포 데이터값을 통해서 설계 유량과 부분 부하 유량에서 웨이크의 소산 양상이 정성적으로 다른 것임을 확인하였다. 웨이크 혼합과 소산되는 양을 계산하기 위하여 내부 유동구조의 불안정성을 정량화하는 지표를 사용하였다. Adamczyk [4]는 주어진 스테이터 행의 유입과 유출 사이의 결정적 불안정성을 보여줌으로써 이 측면에 대한 통찰력을 제공한다. 그는 이러한 불안정성을 나타내는 선형 이론 유도 계수(K)를 도입하여 특정 축 방향 거리에 걸친 웨이크 혼합과의 운동 에너지 변화를 연결하는 수단을 제공하였다[4]. Van Zante [7]는 Adamczyk의 공식을 개선하여 스테이터 중간 피치 위치에서 Disturbance kinetic energy(DKE)를 정의하며 웨이크의 성분을 정량화하고자 하였다. 이는 식 (2)와 같다.

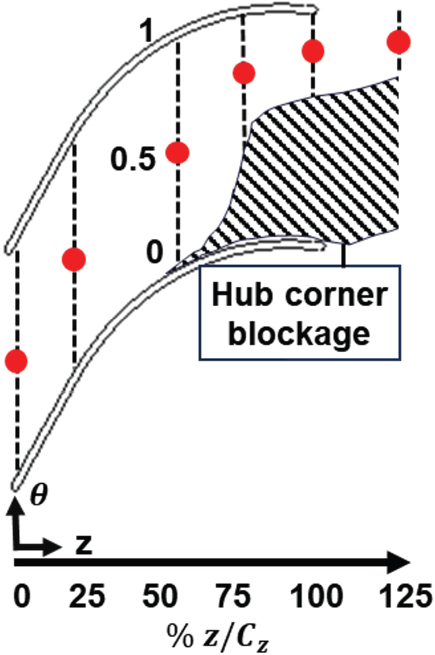
이때, $$ A_t=\frac{1}{\mathrm{\Delta }\sigma }{\int }_0^{\mathrm{\Delta }\sigma } dt$$를 의미하며, $$ V_z^{\text{'}}$$은 시간 평균 축방향 속도와 축방향 순간속도의 차를 의미하고 $$ V_{\mathrm{t}\mathrm{a}\mathrm{n}}^{\text{'}}$$은 시간 평균 원주 방향 속도와 순간 원주 방향 속도의 차를 의미한다. U₀는 임펠러 입구의 평균 축 방향 속도이다. 해당 상수값은 디퓨저 내부 허브코너 유동박리로 인한 유효면적이 줄어드는 구간을 반영하여 미드피치 값을 설정하였다. 유동박리가 이루어진 영역과 주 유동을 구분하는 기준은 축방향속도가 주유동 대비 1 % 이하인 곳으로 설정하였으며, Fig. 18은 부분부하 조건에서 허브 코너 박리로 인한 유효면적이 줄어드는 구간을 반영한 미드피치 구간을 나타낸다. 유효면적은 70 % span 축방향 속도 분포에서 속도가 0인 부분을 제외한 구간으로 설정하였다.

Fig. 18

Mid-pitch line considering hub corner separation blockage

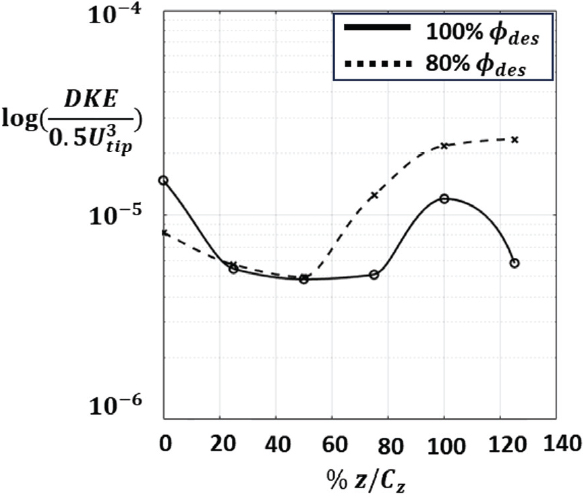
Fig. 19는 설계 유량 및 80 % 설계 유량 지점에서 유선 방향의 DKE를 임펠러 팁 속도의 세제곱으로 무차원화하여 나타낸 그림으로, 디퓨저 입구부터 디퓨저의 125 % 축 방향 길이까지의 분포를 보이고 있다. 설계 유량지점의 경우 디퓨저를 통과하면서 주 유동과 혼합으로 인해서 DKE의 값이 감소하나, 이후 z/C_z = 75 % 지점을 지나면서 허브 코너 박리로 인한 유동면적의 감소로 인하여 오히려 강도가 증가하게 된다. 증가한 강도는 디퓨저를 빠져나온 이후 유동면적이 다시 증가하면서 줄어들게 된다. 한편 설계유량의 80 %지점에서는 DKE의 값이 디퓨저를 통과하면서 감소하다가 z/C_z =50 % 지점에서 증가하는 양상을 보였는데, 이는 디퓨저 흡입 면에서 유동 박리가 설계 유량보다 더 빨리 발생했기 때문이다. 이로 인해 z/C_z = 125 % 지점에서 두 경우의 DKE 값을 비교해보면 설계 유량지점의 경우 DKE의 값이 디퓨저 입구보다 감소했지만, 설계 유량의 80 % 지점의 경우 디퓨저 입구보다 DKE 값이 증가한 것을 알 수 있다.

Fig. 19

Streamwise disturbance kinetic energy distribution at 70 % span

3.5 부분 부하와 설계 유량 유동 구조 변화 고찰

본 연구는 비정상 유동구조 해석을 통해 축류펌프에서 비정상 유동구조 파악 및 웨이크가 수송되는 과정을 분석하였다. 웨이크는 디퓨저 블레이드에 도달할 때까지 코어 흐름 근처에서 혼합되어 운반되고 강도가 감소한다. 디퓨저 블레이드는 웨이크를 두 부분으로 절단하고 절단된 웨이크는 디퓨저를 통과하여 디퓨저 통로 내부에 불안정한 흐름 구조를 생성한다. 웨이크는 디퓨저 내부를 순환하면서 디퓨저 블레이드의 압력 면과 흡입 면의 속도 차, 그리고 유동 박리로 인하여 웨이크가 기울어지고 구부러지며, 이에 따라서 웨이크의 길이가 증가하거나 감소하는 것을 섭동 속도와 방사 방향 속도분포를 통해 확인할 수 있었다. 디퓨저 압력과 흡입 면 측의 유동 박리구간 근처 유동과 디퓨저 미드 피치 유동 사이의 속도 차이는 디퓨저의 80∼100 % 유선 방향에서 웨이크로 하여금 휘어지는 효과를 주게 되며, 감소한 통로 넓이는 디퓨저의 100∼120 % 유선 방향에서 웨이크의 늘어남을 방해한다. 이 경향은 유량이 감소할수록 더욱 증가하며, Disturbance kinetic energy 분포를 통해서 웨이크의 세기는 설계유량의 경우 디퓨저를 통과하면서 감소하지만, 부분설계유량의 경우 디퓨저를 통과하면서 증가한 허브코너 박리구간으로 인하여 웨이크의 세기가 오히려 증가하게 됨을 확인하였다. 이로 인하여 해당 펌프에서 디퓨저의 허브코너 박리는 웨이크 성분이 소산 되는 것이 아니라 증폭시키는 영향을 주어 혼합손실을 증가시키는 경향이 있음을 알 수 있으며, 이 경향은 부분 설계 유량지점에서 유동 박리 영역이 증가함에 따라 웨이크 성분이 증폭되는 것을 관찰함에 따라 같은 경향을 보이는 것 역시 확인할 수 있다.