스프레드시트방법에 따른 선박용 방화문의 온도 상승 수치계산 절차 개발에 관한 연구
Abstract
An analysis methods using commercial software and experimental methods to evaluate the fire resistance of fire doors place an economic burden on customers. Therefore, in this paper, we developed a numerical computation procedure for predicting temperature rise in fire doors using convenient spreadsheet methods and finite difference methods. For the main parameters applied in the numerical calculation, the surface emissivity εm= 0.30∼0.75 of EGI steel plate for fire door finishing materials was applied from a previous paper on emissivity determination. The thermal conductivity of mineral wool insulation was based on information provided by the manufacturer, and linear and exponential thermal conductivities were applied to enable application to high temperatures after 600℃. For the steel plate, the specific heat, density, and thermal conductivity recommended for carbon steel in Eurocode 3 were applied. The numerical calculation procedure of the developed spreadsheet method was verified for reliability and accuracy through comparison with fire test data, and therefore, it is judged that the developed spreadsheet method can be used when designing fire doors.
Keywords:
Fire Door, Spreadsheet, Finite Difference Method, Numerical Calculation키워드:
방화문, 스프레드시트, 유한차분법, 수치계산1. 서 론
선박에서는 화재 확산을 방지하기 위하여 내화성능을 갖는 격벽(Bulkhead) 및 갑판(Deck)에 의하여 방화구획화가 이루어지고 있다. 방화구획의 내화성능은 화재 저항 요구 시간에 따라 A & B, F 등급으로 구분되어 있으며, 방열성(Insulation) 유무에 따라서 해당 등급에 0∼60 수치를 부여하여 방화구획을 구분하고 있다.[1]
또한, 방화구획에는 사람 및 장비출입을 위한 개구(Opening) 설치가 필요하며, 이러한 개구에도 해당 방화구획과 동등한 내화성능을 갖는 방화문(Fire door)을 설치하여야 한다. 방화문은 격벽 및 갑판과 더불어 선박의 화재 예방을 위한 주요 방화기자재에 해당한다.[2]
방화문이 가져야하는 내화성능은 등급에 따라 지정된 시간동안 구조적 보존성(Integrity)에 의하여 화염이 관통하지 않도록 개구부 발생 없이 형상을 유지할 수 있어야 하며, 등급 뒤에 부여된 시간동안 방열성능으로 열의 침투 및 확산을 방지 할 수 있어야 한다, 선박에서는 구조적 보존성 및 방열성을 내화성능이라 정의하고 있다.[3]
방화문의 내화성능 평가는 표준화재 및 탄화수소화재 공칭 시간-온도곡선(Nominal time-temperature curve)에 따라 등급별 요구 시간동안 내화성능 평가 실험을 수행 하거나, 실험 장비에 수용 불가능한 큰 치수 방화문의 경우 실험된 동일 구조의 방화문 실험결과를 토대로 International Maritime Organization (IMO) & International Society of Classification Society (IACS)에서 규정한 절차에 따라 상용 소프트웨어를 활용한 열 해석 및 구조해석 결과를 확인하여 승인 받도록 규정 되어 있다.[4,5]
이러한 내화실험 및 상용 소프트웨어를 활용한 해석은 대부분의 방화문 제조사가 자체적으로 수행하기 어려워 관련 전문 시험기관 또는 연구기관에 의뢰하고 있으며, 결과를 확인하기까지 상당한 기간이 소요되고 있다.
중소기업 입장에서는 실험과 해석방법 모두가 부담이 되기에 상호보완적 관계가 성립될 수 있도록 하는 것이 필요하며, 예로서 방화문 내화실험 전 사전 설계를 통하여 시행착오를 줄일 수 있다면 방화문의 내화성능 확보에 필요한 비용과 기간 단축으로 중소기업의 부담을 덜 수 있을 것이다.
IMO & IACS의 방화문에 관한 열전달 분석 방법은 방화문의 화재 노출면 경계조건만 제공하고 있어 수치적 계산방법으로는 풀 수 없으며, 해석을 위한 대류 및 복사 열 전달 계수에 대한 정보는 제공되어 있지 않아 실질적으로 수치계산 및 해석에 사용되고 있지 못한 실정이다.[6]
따라서, 본 논문은 선박용 방화문 설계를 위한 수치계산 절차 개발을 목적으로 하여, 방화문에 관한 열전달 모델과 경계조건에 따른 유한차분 방정식 및 열전도 수치계산에 필요한 매개변수를 결정 하였으며, 수치계산 솔버는 엑셀 프로그램의 스프레드시트 방법을 적용하여 방화문의 문짝에 대한 1차원 과도 열전도 수치계산을 수행 하였다. 또한 수치계산으로 산출된 온도는 실험 데이터와 비교를 통하여 신뢰성과 정확도를 검증 하였다.
2. 재료의 열적 특성
2.1 방사율
방사율(Emissivity) ε은 표면 마감과 온도에 따라 달라지며, 금속의 경우 온도가 증가함에 따라 증가하고 비금속의 경우 일반적으로 온도가 증가함에 따라 감소하는 것으로 알려져 있다.[7] Eurocode 1(EN 1991-1-2, 2002)과 SBI, Swedish Institute of Steel Construction(Fire Engineering Design of Steel Structures, 1976)에서 강철 온도 예측을 위해 화재와 강철 부재는 비 복사 매체에서 두 개의 평행한 평면으로 취급하고 있다. 따라서 합성 방사율 εres는 화재 노출 기간 전체에 걸쳐 일정하게 유지되며 다음 식 (1)과 같이 제안 하고 있다.[8,9]
| (1) |
여기서, εres는 합성 방사율, εf는 화재의 방사율, εm는 철강 부재의 방사율이다.
εf와 εm값에 대하여 구조물에 대한 조치 Eurocode 1(EN 1991-1-2, 2002)에서는 콘크리트 구조물 설계 Eurocode 2(EN 1992-1-2, 2004), 석조 구조물 설계 Eurocode 6(EN 1996-1-1, 2005), 알루미늄 구조 설계 Eurocode 9(EN 1999-1-1, 2007)에서 재료 관련 화재 설계 부분에서 별도의 정보가 제공되지 않는 한 방사율 εf = 1, εm = 0.8로 사용할 것을 제안 하고 있다. 강구조물 설계 Eurocode 3(EN 1993-1-2, 2005)에서 강철 표면과 관련된 방사율은 탄소강의 경우 0.7, 스테인리스강의 경우 0.4를 사용하는 것을 제안하고 있다.[8,10∼13]
Sadiq, et al.(2013)는 탄소강의 방사율 εm 값이 80∼520℃의 온도 범위에서 0.28∼0.69 사이로 변하는 것으로 나타났다고 보고 하였으며,[14] 최태진 등(2024)은 방화문 표면마감재 3종에 대하여 방사율 측정실험을 수행하였고, 200∼600℃ 온도 범위에서 Electro Galvanized Iron(EGI) steel의 방사율 εm는 0.30∼0.75, Galvanized Iron(GI) steel의 방사율 εm는 0.1∼0.85 사이로 변하며, Stainless steel의 방사율 εm는 0.4∼0.2 사이로 감소하고, 600℃ 이상에서는 온도와 무관하다고 보고 하였다.[6]
2.2 비열
방화문 마감재 EGI steel plate에 대한 비열(Specific heat)은 Eurocode 3에서 제안하고 있는 탄소강에 대한 온도 변화에 따른 비열을 적용 하였다. Ohmura, et al.(2003)은 낙하열량계 방법을 사용하여 미네랄울 단열재의 비열을 측정하였으며, 미네랄울 단열재의 비열이 840∼900J/kg ℃ 범위로 나타났으며, 850J/(kg℃)라고 보고 하였다.[15] TALAT Lecture 2502: Material Aspects of Fire Design에서는 미네랄울 단열재의 비열이 온도 변화에 따라 800∼1600J/(kg℃)로 제안하고 있다.[16] 본 논문에서는 Ohmura, et al.(2003)이 제안한 850J/(kg℃)을 수치계산에 적용 하였다.
2.3 열전도율
방화문 마감재 EGI steel에 대한 열전도율(Thermal conductivity)은 Eurocode 3에 따른 탄소강의 열전도율을 적용하였으며. 온도 변화에 따른 열전도율의 함수에 관한 식은 아래 식 (2)와 같다.[13]
| (2a) |
| (2b) |
여기서, Ts는 철강 부재 온도이다,
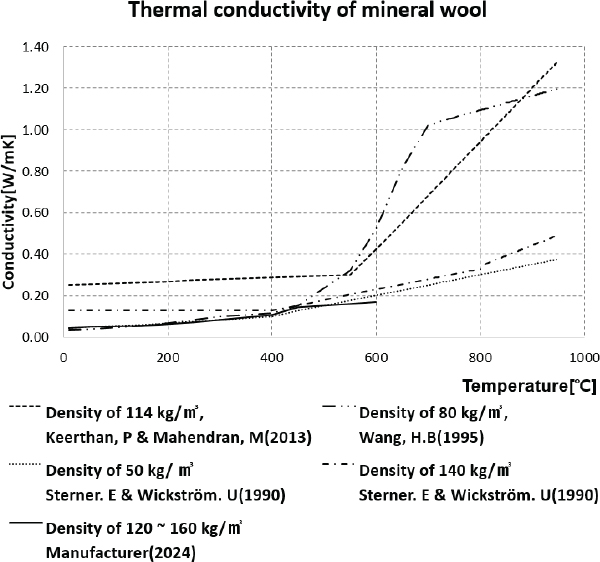
미네랄울 단열재의 열전도율에 관한 정보는 Fig. 1에서와 같이 열전도율 값이 다양하게 나타나 있는 것을 확인 할 수 있다. 이는 서로 다른 제조 원료와 방식 그리고 상이한 밀도, 열전도율 시험방법으로부터 발생한 차이라 볼 수 있으며, 실험에 사용된 밀도 120kg/㎥ 미네랄울 단열재의 열전도율은 제조사로부터 다음과 같이 식(3)으로 주어져 있다.[17∼20]
| (3a) |
| (3b) |
여기서, Ts는 단열재 온도이다,
제조사로부터 제공된 미네랄울 단열재의 열전도율 정보는 –20∼600℃ 범위 까지만 주어져 있으며, 600℃ 이후 고온에서 미네랄울 단열재의 열전도율 정보는 주어져 있지 않다. 방화문이 표준화재 시간-온도곡선에 노출되는 온도 범위는 60min 실험 기준으로 약 950℃ 까지 주어진다. 따라서 위의 열전도율 정보는 Fig. 2에서와 같이 600℃ < k ≤ 950℃ 온도 범위에 대한 열전도율 정보가 필요하며, 식 (4a)와 (4b)는 제조사에서 제공한 열전도율 정보를 바탕으로 가정된 선형 함수 및 지수 함수형 열전도율 이다.
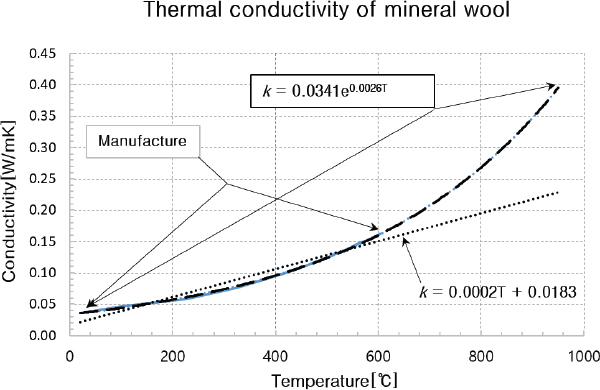
The thermal conductivity of linear and exponential mineral wool assumed based on the mineral wool thermal conductivity information provided by the manufacturer
| (4a) |
| (4b) |
여기서, Ts는 단열재 온도이다.
3. 경계조건
3.1 화재 경계조건
선박용 방화문의 내화성능 평가에 사용되는 대표적인 공칭 시간-온도곡선에는 화재원 특성에 따라 셀룰로오스(Cellulosic)를 연료로 유럽에서 개발되어 주거용 및 일반 산업분야에서 발생할 수 있는 화재 유형을 시뮬레이션한 표준화재 시간-온도곡선으로, 건축용 시험표준 ISO 834-1과 선박용 시험 표준 IMO Res. MSC 307(88) Part 3가 있으며 식(5)에 따른다.[21,3]
| (5) |
여기에서, Tg 는 가열로 내 평균 온도, t 는 시간이다.
3.2 노출면 & 비 노출면 경계조건
Eurocode 1에서는 화재에 노출된 구조 부재의 표면은 대류와 복사에 의해 열이 전달되며, 일반적으로 복사는 화재 초기 단계를 제외 하고 대류보다 지배적이고, 노출면 철강 표면으로 열전달(경계조건)은 다음과 같이 주어진 순 열유속 으로 나타낼 수 있다.[8]
| (6) |
여기서,
F 형상 계수 [-]
εm부재의 표면 방사율 [-]
εf 화재의 방사율 [-]
σ 스테판볼츠만상수 (= 5.67×10-8 W/m2K4)
Tg 가열로 내 유효 복사 온도, 또는 가스 온도 [°C]
Ts 부재의 표면 온도 [°C]
hc 대류 열전달계수 [W/m2K]
노출면에서의 대류 열전달계수 hc는 표준화재 시간-온도곡선의 경우 25W/(m2K)를 사용할 것을 권장하고 있다.[8]
구획부재의 노출되지 않은 면의 표면에서 열 전달 는 Eurocode 1에서 다음 식 (7)과 같이 계산해야한다고 제안하고 있다.[8]
| (7) |
여기서, T∞는 주변 대기 온도이며, 비 노출면의 방사율 εm은 다른 값이 동기 부여 될 수 없는 경우 0.8을 사용하도록 권고하고 있다. 또한 대류 열전달계수는 hc= 4W/(m2K)로 가정하거나 복사에 의한 열전달 효과를 포함한다고 가정할 때 대류 열전달계수 hc= 9W/(m2K) 및 표면 방사율 εm= 0 으로 설정할 것을 권장하고 있다.[8]
4. 열전달 모델 및 유한차분 방정식
4.1 지배방정식
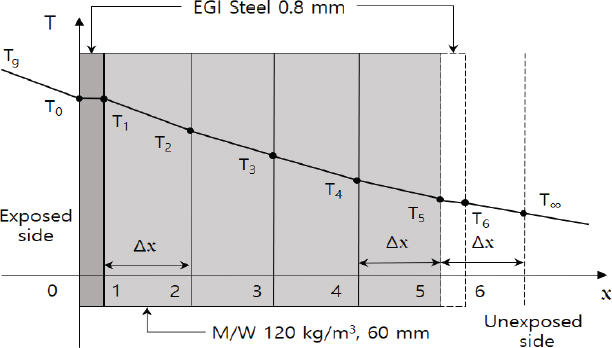
방화문의 문짝 열전도 수치해법 적용에 있어 면적 대비 두께가 작아 열전달은 Fig. 3에서와 같이 문짝의 수직 방향으로 1차원 비정상 열전도를 적용할 수 있으며, 방화문의 문짝 비정상 열전도 유한차분 방정식에서 시간에 대한 전진 차분 형식으로 수치 계산을 수행하였다. 에너지 균형식에서 방화문의 문짝 내부는 물성치가 일정하고 열 발생이 없는 과도조건의 열방정식으로 다음 식 (8)과 같다.[7]
| (8) |
여기서, 0 ≤ x ≤ 6, t > 0.
식 (8)의 우측 항은 방화문의 문짝 에너지 변화율에 대한시간 도함수를 나타내고 있으며, 식 (8)의 유한차분 형태는 식 (9)와 같이 나타낼 수 있다.[7]
| (9) |
여기서, 열확산계수
4.2 노출면 및 비 노출면 경계 절점
위 식 (9)의 좌측항은 일반적으로 방화문의 문짝 내부 절점의 전도항을 나타내지만, 내화시험의 화재노출면에서는 방화문의 문짝 화재노출 조건에 대한 대류, 복사항을 포함하고 있으며, 식 (10)과 같이 나타낼 수 있다.[7,8]
| (10) |
식 (10)은 에 대하여 정리가 필요하므로 양변에 A를 소거하고, 1/k 과 2∆x를 곱해주고, 열확산율 α=k/ρC, 무차원 푸리에수 Fo=α∆t/∆x2 및 Bi=hc∆x/kst로 정의 하고, 노드 m은 절점 번호 0, 1, 2 ...6으로 바꾸어 주게 되면 식 (10)은 식(11)과 같아진다.
| (11) |
식 (11)은 대류와 복사를 포함하는 혼합 경계 절점에 대한 유한차분 방정식으로 접촉면 및 내부 절점의 경우 보다 제한적이고 더 작은 시간 단계가 요구되어 진다. 그러므로 식 (11)에서 의 계수가 최대 허용 시간 단계 ∆t 를 구하는데 사용되어야 모든 절점 m에 대하여 안정성 기준을 만족할 수 있다. 식 (11)의 의 계수로부터 허용 시간 단계 ∆t는 아래 식 (12)를 통하여 계산이 가능하다.
| (12) |
Eurocode 1에서 권장하고 있는 화재에 노출된 철강 부재 표면 및 비 노출면 온도상승 계산은 3.2절의 노출면 & 비 노출면 경계조건에서의 식 (6)과 (7)에 주어져 있으며, 유한차분 방정식은 다음과 같이 나타낼 수 있다.[8,22]
| (13) |
| (14) |
위 식 (13)와 (14)의 전진차분형식에 대한 안전성 기준은 아래 식 (15)와 같이 주어진다.[22]
| (15) |
여기서.
Vst 철강 부재의 부피 [m3]
Cst 철강 부재의 비열 [J/kg℃]
ρst 철강 부재의 밀도 [kg/m3]
Ast 화재에 노출된 면적 [m2]
| (16) |
총 열전달 계수 htot는 방정식 (16)에 따라 크게 증가하므로 시간 상수와 임계 시간 단계가 그에 따라 감소한다. 실제로 시간 증분을 현재 시간 상수의 10 % 미만으로 유지하는 것으로 권장하고 있다.[22]
4.3 Steel & 단열재 접촉면 절점
Steel 방화문의 경우 양면 마감 steel & 내부 단열재의 샌드위치 구조로 되어 있어 Steel & 단열재 접촉면 절점을 가지게 되며 Fig. 3에서 절점 1과 절점 5가 접촉면 절점에 해당한다. 접촉면에 대한 유한차분 방정식은 아래 식 (17)과 같다.[7,19]
| (17) |
위 식 (17)을 에 대하여 정리 하면 노출면의 접촉면 절점에 대한 유한차분 방정식은 다음과 같아진다.
| (18) |
비 노출면의 접촉면 절점의 경우 위 식 (18)에서 절점 번호를 바꾸어주면 식 (19)와 같이 된다.
| (19) |
접촉면 절점의 시간 증분 ∆t 에 대한 제한은 아래 식 (20)과 같다.
| (20) |
4.4 단열재 내부 절점 2, 3, 4 및 절점 5
| (21) |
위 식 (21)은 미네랄울 단열재 내부 절점 2에 관한 유한차분 방정식으로 에 대하여 정리하여 주면 다음 식 (22)와 같아지며, 내부 절점 3, 4도 동일한 내부 절점에 해당하므로 식 (22)에서 절점 번호를 바꾸어 정리하게 되면 식 (23) 및 (24)와 같다.[7]
| (22) |
| (23) |
| (24) |
| (25) |
위 식 (25)는 비 노출면측 미네랄울 단열재의 절점 5에 해당하는 유한차분 방정식으로 여기서, Bi=hc∆x/k 로 정의 하며, 절점 5의 유한차분 방정식에는 Fig. 3에서와 같이 유체 공간의 가상 절점 가 필요하다.[23]
5. 온도 수치계산
5.1 노출면 온도 수치계산
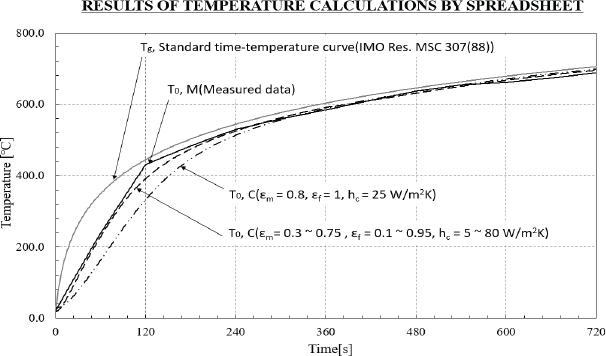
표준화재 노출조건에 따른 방화문 마감 EGI steel plate 의 온도 상승 값을 계산하기 위하여 엑셀 스프레드시트를 이용하는 방법으로 Table 1에서와 같이 노출면 온도 T0,C 계산을 위한 정보들을 순서별로 나열하였다. 노출면 온도 T0,C 계산은 방정식 (13)을 사용하였으며, T0,M 은 실험을 통하여 수집된 방화문의 노출면 온도 데이터이다.

Results of numerical calculation of exposed surface temperature of fire doors using spreadsheet method
방화문 노출면 온도 T0,C 계산을 위한 입력 정보에는 Section factor A/V = 1,250m-1, 밀도 ρ = 7,850kg/m3, 대류열전달계수 hc = 5∼80W/m2K, Stefan–Boltzmann constant σ = 5.67 × 10-8W/m2K4, 온도에 따른 EGI steel plate의 비열 변화는 Eurocode 3에서 carbon steel 권장 값을 사용 하였으며, EGI steel plate의 표면 방사율 εm은 선행 논문[6]에서 제안한 0.30∼0.75를 적용 하였다. 화재의 방사율 εf 는 시험 시작 시 0.95로 가정 하였고, 18min 까지 0.7로 선형적으로 감소하며, 19min 부터 60min 까지 0.15 에서 0.1 까지 선형적으로 감소하는 것으로 하였다.
대류 열전달계수 hc는 시험 시작 후 6min 까지는 80W/m2K, 6min 이후는 5W/m2K 이하가 최적의 값으로 추정된다. 이러한 매개변수를 기반으로 한 수치계산 결과는 Fig. 4에서와 같이 측정된 실험 데이터를 통하여 상관관계를 확인할 수 있다.
대류 열전달계수가 감소하는 이유는 시험 초기 가열로 내부 온도가 상온에서 급격하게 상승하기 때문이며, 이는 버너의 초기 높은 출력 값에 따른 가열로 내부 난류 화재가 지배적이기 때문이다. 이후 가열로 내부 온도 상승이 안정적으로 이루어지게 되면 버너 출력이 낮아지면서 가열로 내부는 복사열이 지배적인 환경으로 변하게 된다.
5.2 비 노출면 온도 수치계산
Table 2는 4.2절 노출면 및 비 노출면 경계 절점에 관한 식 (13)∼(14) 및 4.4절 내부절점에 관한 식 (22)∼(25)를 사용하여 방화문의 비 노출면 온도 T6,C를 산출하기 위한 계산 순서와 결과를 보여주고 있다. 데이터는 분량이 많은 관계로 계산된 일부 만을 나타내었다. 내부 절점 온도 및 비 노출면 온도 계산을 위한 입력 정보에는 미네랄울 밀도 120kg/㎥, 두께 60mm, 비열 850J/kg℃, 선형 및 지수함수 열전도율 k, 마감 EGI steel plate의 정보는 5.1절에서와 동일한 A/V, ρ, σ, εm값을 사용하였다.

Unexposed surface temperature numerical calculation results (linear function thermal conductivity k = 0.0002T + 0.0183 applied)
T1의 온도는 본 논문에서 사용하고 있는 스프레드시트 방법으로 계산을 수행하기 위하여 절점 0의 온도와 절점 1의 온도가 동일하다는 가정에 따라 T0,C=T1 가 된다. 이러한 가정은 방화문 마감 EGI steel plate의 두께가 매우 얇기 때문에 노출면 경계절점에 관한 유한차분 방정식 (11)에 따른 계산에는 매우 짧은 시간 증분 ∆t가 필요하며, 스프레드시트 방법으로 계산을 수행하기에는 어려움이 있다. 이는 노출면 경계절점의 시간 증분에 관한 식 (12)의 계산을 통하여 다음과 같이 확인할 수 있다.
이러한 이유로 상용소프트웨어를 활용한 열 해석에서는 3.1절의 화재 경계조건에 관한 방정식 (5)를 방화문 노출면 온도로 지정(화재온도와 노출면 온도가 동일하다는 가정)하여 해석을 수행하는 경우가 있다. 그러나 이러한 가정은 마감 EGI steel이 두꺼울 경우 보수적인 해석 결과를 도출하게 된다. 따라서 본 논문에서는 대체 방법으로 Eurocode 1에서 제안하고 있는 노출면과 비 노출면에서의 순열유속 결정에 사용되는 상관 식 (13), (14)를 스프레드시트 방법에 적용하여 방화문 노출면 및 비 노출면 경계 절점 온도에 대하여 수치계산을 수행 하였으며, 또한 식 (15)로부터 시간 증분에 대한 계산 결과를 아래와 같이 확인 할 수 있다.
계산된 시간 증분 ∆t의 값은 3.8s 가 된다. 계산된 시간 증분은 스프레드시트 방법으로 수치 계산을 수행하기에 무리가 없으며, 전진차분형의 안정성 기준 확보를 위해 시간 증분 ∆t = 1s 로 적용 하였다.
노출면 경계 절점에 대한 온도 결정 다음으로는 Steel & 단열재 접촉면 절점 온도에 대한 수치 계산이 필요하며, 이에 대한 상관식은 4.3절의 식 (18)과 식 (19)가 해당한다. 또한 Steel & 단열재 접촉면 절점에서의 시간 증분에 대한 제한 식 (20)에 값을 대입하여 계산을 하게 되면 0.01s 의 시간 증분을 얻을 수 있으며, 계산된 시간 증분 ∆t는 앞서 계산된 노출면 경계조건에서의 0.001s 의 시간 증분과 같이 스프레드시트 방법에서 계산이 어려운 상황이다. 따라서 접촉면에서 EGI steel plate와 미네랄울 단열재의 온도는 동일하다는 가정이 필요하다.
T2 ∼ T4 는 미네랄울 단열재의 내부 절점으로 유한차분 방정식 (22)∼(24)에 따라 내부 절점 ∆x 에서의 미네랄울단열재의 수치 계산된 온도에 따른 열전도율 k, 열확산계수 α, 푸리에 수 Fo 가 각각 방정식에 적용되었다.
미네랄울 단열재의 열전도율은 제조사에서 제공하는 20∼600℃ 범위에 해당하는 상관식을 온도 범위 950℃ 까지 확장하여 적용하고자 제 2장 재료의 열적 특성에서 언급한 바와 같이 선형 함수 열전도율(k = 0.0002T + 0.0183) 및 지수 함수 열전도율(k = 0.0341 e0.0026T)로 가정하여 수치 계산에 적용 하였다. 무차원 푸리에 수 Fo 는 0.001 ~ 0.009로 안정성 기준 Fo ≤ 1/2를 만족하고 있음을 확인할 수 있다.
T5 는 Steel & 단열재 접촉면 절점으로 앞에서 언급한 것과 같이 서로 온도가 동일하다는 가정과 더불어 EGI steel plate 마감을 무시하고 단열재인 미네랄울과 대기 온도 간 열전달이 일어나는 것으로 수치계산을 수행하여야 한다. 이와 관련하여 대표적인 사례는 보호된 강철 부재의 온도상승 계산에 관한 Eurocode 3(EN 1993-1-2, 2005) 및 ECCS (European Convention for Constructional Steelwork_ 1983)에서 방화재료의 열용량이 강철 단면의 1/2 미만인 경우 방화재료의 열용량은 무시되며 관련 식에서 없어진다. 방화재료의 상대적 열용량 Φ에 관한 식은 다음과 같다.[13]
| (26) |
위 식 (26)에 따라 미네랄울 단열재의 상대적 열용량을 계산하게 되면
위 계산에서와 같이 방화문의 온도 수치 계산에서는 단열재인 미네랄울의 열용량이 마감 강판인 EGI steel plate 열용량보다 약 2.2배가 크다는 것을 확인할 수 있다. 따라서 비 노출면에서 마감 강판 EGI steel plate의 열용량은 무시 되며, 미네랄울 단열재와 대기 온도 간 열전달이 일어나는 것으로 계산하는 것이 적절하다. 그러지 않을 경우 수치계산 결과는 발산하게 된다. 더불어 주의할 사항은 마감 강판인 EGI steel plate 열용량이 미네랄울 대비 작다고 완전히 없어지는 것은 아니며, 최종적인 방화문의 문짝 표면 온도 T6,C 는 EGI steel plate에 대하여 Eurocode 1에서 제안하고 있는 비 노출면의 순열유속 계산 식 (14)와 대류열전달계수 hc = 5.45W/m2K, 선행 논문에서 제안한 εm = 0.3 를 적용하여 수치계산이 이루어진다. 또한 식 (14)에서 는 로 미네랄울 단열재의 온도를 적용하여 수치계산을 수행한다.
T6,M 은 표준화재 시간-온도 곡선에 따라 실험된 방화문의 비 노출면 측정 데이터이며, T∞ 는 주위 온도, qc 및 qr은 비 노출면에서의 대류 열유속 및 복사 열유속이다.
Fig. 5는 선형 함수 및 지수 함수 열전도율이 적용된 방화문의 비 노출면 온도 T6,C의 수치계산 결과를 나타내고 있다. 선형 함수 열전도율(k=0.0002T+0.0183)이 적용된 수치 계산 결과는 3min에서 54min 까지 실험결과보다 다소 낮은 온도(∆T = -14.2℃)를 나타내고 있으며, 60min 최종 실험결과 215.1℃ 보다 4.8℃ 높은 219.9℃를 산출하였다.
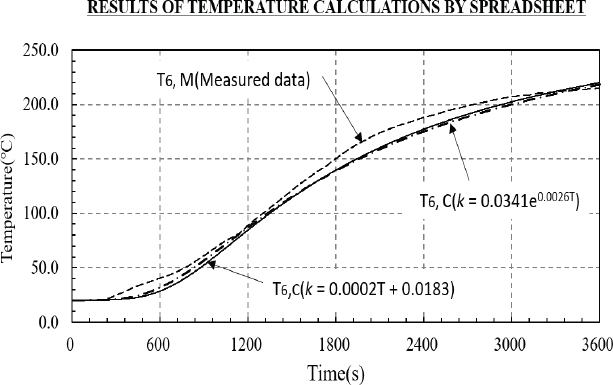
Numerical calculation results for the temperature of the unexposed surface of fire doors with linear function thermal conductivity (k = 0.0002T + 0.0183) and exponential thermal conductivity(k = 0.0341e0.0026T)
지수 함수 열전도율(k = 0.0341e0.0026T) 이 적용된 수치 계산 결과는 3min에서 55min 까지 실험결과보다 다소 낮은 온도(∆T = -15.7 ℃)를 나타내었고, 60min 최종 실험결과 215.1 ℃ 보다 3.0 ℃ 높은 218.1 ℃를 산출하였다.
수치계산 결과와 실험 데이터 간 차이가 발생된 원인으로는 실제 실험에서는 가열로 인하여 마감 Steel과 단열재료의 분리 및 단열재의 체적 감소현상이 발생하게 되고 이는 방화문 문짝 두께의 증가 또는 감소 현상으로 이어지게 된다. 또한 균일하지 못한 재료의 밀도, 충전 상태 등 여러 가지 원인이 있을 수 있다. 수치계산절차에서는 열전달 관련 매개변수에 대하여 가정치 또는 근삿값의 사용, 일정한 상수 값 적용 등이 수치계산 결과와 실험 데이터 간 차이가 발생하게 된 원인으로 추정된다.
6. 결 론
방화문의 온도 상승 예측에 관한 수치계산 절차 개발과 관련하여 본 논문에서는 유한차분법 및 계산 솔버로 스프레트시트 방법을 적용하여 표준화재 시간-온도곡선에 노출된 방화문의 온도 상승에 관한 수치계산을 수행 하였으며, 다음과 같은 결론을 얻을 수 있었다.
- 1) 제조사로부터 제공된 열전도율의 범위는 600℃ 까지 이며, 실제 실험 온도 범위를 충족하지 못하고 있다. 이러한 한계로 인하여 온도 범위를 950℃ 고온 범위로 확장하고자 제조사 제공 정보를 토대로 선형 함수 열전도율(k=0.0002T + 0.0183) 및 지수 함수 열전도율(k=0.0341e0.0026T)을 가정하여 수치계산에 적용 하였다. 가정된 두 가지 열전도율은 5장의 Fig. 5에서와 같이 각각 적합한 수치계산 결과를 도출 하였다. 지수 함수 열전도율이 측정 데이터에 근접한 결과를 나타냈었으며, 방화문 온도 상승 예측을 위한 수치계산 절차에 적용 가능 하다.
- 2) 노출면 경계 절점에서의 유한차분 방정식 (11)은 안정성 기준을 만족하기 위하여 시간 증분 ∆t = 0.001s 간격이 필요하며, 스프레드시트 방법으로는 계산이 불가능하다. 따라서 대체 계산 방법으로 Eurocode 1에서 제안하고 있는 노출면 및 비 노출면 순열유속 계산 방법 식 (13), (14)를 적용하여 방화문의 노출면 및 비 노출면 온도 계산을 수행 하였다. 수치계산 결과는 측정 데이터와 잘 일치 하였으며, 방화문 온도 상승 예측을 위한 수치계산 절차에 적용 가능 하다.
- 3) 미네랄울 단열재의 절점 5에서 유한차분 방정식은 인접하고 있는 마감 EGI steel plate가 아닌 단열재와 대기 온도 상호간 열전달이 이루어지는 것으로 하여야 적합하며, 단열재와 마감 EGI steel간 열전달 모델을 적용하게 되면 수치 계산 결과는 수렴하지 못하고 발산하게 된다. 이는 해당 재질의 상대적 열용량 비율에 따라 열용량이 큰 재질을 열전달 대상으로 결정 하여야 한다.
- 4) 상용 소프트웨어의 사용 부담을 덜기 위해 비교적 사용 및 접근성이 편리한 스프레트시트 방법으로 방화문의 노출면부터 비 노출면까지 유한차분 방정식을 적용하여 수치계산 절차 개발을 진행 하였다. 또한 개발된 스프레드시트 방법의 수치계산 절차는 실험 데이터와 비교 검증을 통하여 방화문 온도 상승 예측 프로그램으로서 타당성을 확인하였다. 따라서 개발된 스프레드시트 방법의 수치계산 절차는 방화문 설계 시 활용 가능한 것으로 판단된다.
References
- International Convention for the Safety of Life at Sea(SOLAS), 1974, IMO.
-
Choi, T. J., Kim, J. S., Lim, Y. S., Lee, K. H., Kang, H. G., Park, S. H., Kim, Y. T., 2014, “An experimental study on the fireproof performance of fire damper according to change of the insulation conditions on the exposed side and unexposed side of the coaming,” Journal of the Korean Society of Marine Engineering, Vol. 38, No. 1, pp. 99-104.
[https://doi.org/10.5916/jkosme.2014.38.1.99]

- MSC/Res. 307(88), 2012, “Adoption of the international Code for application of Fire Test Procedures (2010 FTP code),” IMO.
- MSC.1/Circ.1319, 2009, “Recommendation for the evaluation of fire performance and approval of large fire doors,” IMO.
- UI FTP 3, 2010, “Fire door,” IACS.
-
Choi, T. J. Kim, Y. T., 2024, “Experimental study to determine the emissivity of fire door finishing materials according to calorimetry method,” Journal of Advanced Marine Engineering and Technology, Vol. 48, No. 3, pp. 107-114.
[https://doi.org/10.5916/jamet.2024.48.3.107]

- Y. A. Cengel, A. J. Ghajar, 2020, “Heat and Mass Transfer,” 4th Edition: McGraw-Hill.
- EN 1991-1-2, 2002, Eurocode 1, “Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire,” CEN.
- SBI. 1976. Fire Engineering Design of Steel Structures. Swedish Institute of Steel Construction: Stockholm.
- EN 1992-1-2, 2004, Eurocode 2, “Design of concrete structures - Part 1-2: General rules - Structural fire design,” CEN.
- EN 1996-1-2, 2005, Eurocode 6, “Design of masonry structures - Part 1-2: General rules - Structural fire design,” CEN.
- EN 1999-1-2, 2007, Eurocode 9, “Design of aluminium structures - Part 1-2: Structural fire design,” CEN.
- EN 1993-1-2, 2005, Eurocode 3, “Design of steel structures - Part 1-2: General rules - Structural fire design,” CEN.
-
Sadiq, H., Wong, M. B., Tashan, J., Mahaidi, R. A., Zhao. X. L., 2013, “Determination of steel emissivity for the temperature prediction of structural steel members in fire,” Journal of Materials in Civil Engineering, Vol.25, No 2, pp. 167-173.
[https://doi.org/10.1061/(ASCE)MT.1943-5533.0000607]

-
Ohmura. T., Tsuboi. M., Onodera. M., Tomimura. T., 2003, “Specific heat measurement of high temperature thermal insulations by drop calorimeter method.” Int J Thermophys Vol.24, pp.559–575.
[https://doi.org/10.1023/A:1022936408676]

- Steinar Lundberg, 1997. “Material Aspects of Fire Design. TALAT Lectures 2502 (training in Aluminium Application Technologies, Leonardo da Vinci project TAS/WP (pp. 21). EAA,” European Aluminium Association.
-
Keerthan. P., Mahendran. M., 2013, “Thermal performance of composite panels under fire conditions using numerical studies: Plasterboards, Rockwool, Glass Fibre and Cellulose Insulations. Fire Technol. Vol.49, pp.329–356.
[https://doi.org/10.1007/s10694-012-0269-6]

- Sterner. E., Wickström. U., 1990, “TASEF-Temperature Analysis of Structures Exposed to Fire. User’ s Manual; APPENDIX A8 Materials,” Swedish National Testing Institute: Borås, Sweden.
- Wang, H. B., 1995, “Heat Transfer Analysis of Components of Construction Exposed to Fire-a Theoretical, Numerical, and Experimental Approach,” Ph.D. Thesis, University of Salford, Salford, UK.
- KCC, Thermal conductivity of mineral wool, 120∼160K, https://www.kccworld.co.kr/technical/building–materials/insulation.do
- ISO 834-1, 1999, “Fire Resistance Tests Elements of Building Construction – Part 1: General Requirements”, International Organization for Standardization.
-
Wickström, U., 2016, “Temperature Calculation in Fire Safety Engineering,” Springer International Publishing Switzerland.
[https://doi.org/10.1007/978-3-319-30172-3]

- Jeon, J. H., 2009, “Fire Dynamics for PBD,” Donghwa Technology.