입구 압력 왜곡 형상에 따른 축류 압축기 성능 변화 연구
Abstract
The evolution of modern commercial turbofan engines has led to larger diameters, which enhance efficiency and reduce noise. However, this has also increased the likelihood of inlet pressure distortion, particularly due to crosswinds. Computational fluid dynamics (CFD) was used to examine the effects of inlet pressure distortion on the tip and hub of a NASA rotor 67 model. Performance metrics, including the total pressure ratio, adiabatic efficiency, surge margin, and operating flow range, were evaluated. Metrics declined linearly as the central angle of the tip distortion area increased. A linear decline in total pressure ratio and adiabatic efficiency was observed when the hub distortion angle was increased at a 90° tip distortion angle. Conversely, surge margin and operating flow range exhibited a peak at a hub distortion angle of 180°. In comparison to the absence of inlet distortion, surge margin and operating flow range were reduced to 42.19 % and 52.27 %, respectively, with a 90° tip inlet distortion, and recovered to 95.94 % and 102.49 % with an additional 180° hub inlet distortion. The study also revealed that tip pressure distortion resulted in the generation of a weak shock wave and an increase in entropy due to tip leakage flow. These effects were found to be mitigated by the introduction of additional hub pressure distortion with an appropriate central angle.
Keywords:
Computational fluid dynamics, Axial compressor, Surge margin, Inlet pressure distortion, Flow separation, Tip leakage flow키워드:
전산유체역학, 축류 압축기, 서지 마진, 입구 압력 왜곡, 유동 박리, 익단 누설 유동1. 서 론
축류 압축기는 작동유체에 에너지를 전달하여 압축하는 유체기계로, 항공용 가스터빈 엔진, 발전용 가스터빈 엔진 및 압축공기를 필요로 하는 에너지 플랜트 등의 다양한 산업에 이용되고 있다. 가스터빈 엔진은 공기를 매개로 추력을 생성하는 추진기관의 일종이며, 작동 구조에 따라 터보 제트, 터보 홴, 터보 프롭, 램(ram) 제트 등으로 구분된다. 그 중 현대 항공기에 주로 사용되는 엔진은 터보 홴 엔진이다. 터보 홴 엔진은 기존 터보제트 엔진의 전면에 홴을 부착하여 가스터빈 외부로 지나가는 흐름인 ‘바이패스(bypass)’ 유동을 형성한다. 가스터빈 내부로 흐르는 유동 대비 바이패스 유동의 비를 ‘바이패스비(bypass ratio)’라고 하며, 여객기 등의 저속 항공기는 고 바이패스비 엔진을, 전투기 등의 고속 항공기는 저 바이패스비 엔진을 주로 사용한다.
현대 여객기에 사용되는 바이패스비 8 이상의 고 바이패스비 엔진은 저속 영역에서 효율이 높고 소음이 적은 장점이 있으나, 입구 면적이 증가함에 따라 공기 저항이 커지며 측풍(crosswind) 등 입구 유동의 불안정성에 취약한 단점이 있다. 가스터빈 입구 유동의 압력이 일정하지 않고 왜곡된 현상을 ‘입구 압력 왜곡(inlet pressure distortion)’ 현상이라고 한다. 입구 압력 왜곡 현상은 가스터빈 전방에 있는 압축기 성능 저하를 초래하며, 결과적으로 엔진의 전반적인 성능과 안정성에 악영향을 미칠 수 있다. 이 현상은 측풍 이외에 곡관, 경계층(boundary layer) 등의 요인에 의해 발생한다.
가스터빈에 사용되는 축류 압축기는 회전하며 유체에 에너지를 전달하는 동익(rotor)과 유동을 일정하게 유지시키는 정익(stator)으로 이루어져 있으며, 동익과 정익이 하나의 단(stage)을 이룬다. 가스터빈에는 다단 축류 압축기가 설치되어 공기를 압축시키고, 압축비는 가스터빈의 열역학적 효율에 영향을 미친다.
입구 압력 왜곡 현상에 의해 압축기 성능이 저하되는 것을 여러 연구자들이 확인하였다. Lee 등(1)은 입구 압력 왜곡 모사 시험장치를 제작하고 시험 평가를 진행하였으며, Li 등(2)은 입구 180도 영역의 압력 왜곡 상황에서 압축기의 성능 변화 및 충격파 생성을 확인하였다. Rusu(3)는 입구 압력 왜곡 형상을 스팬(span) 방향 길이, 각도, 혼합 유형으로 분류하고, 다단 압축기에서 왜곡도 변화를 확인하였다. 항공용 가스터빈의 경우, 입구 압력 왜곡의 주 원인은 측풍이며 왜곡 영역은 주로 압축기의 슈라우드(shroud) 및 익단(tip) 부분에 형성된다. Liu 등(4)은 고바이패스비 터보 홴 엔진의 나셀(nacelle)에 측풍이 부는 상황에서 입구 전압력 분포를 모사하여 익단 부분에 왜곡 영역이 형성되는 것을 확인하였으며, Li 등(5)은 3단 축류 압축기에서 익단과 허브(hub) 위치의 방사형 압력 왜곡에 의한 성능 변화를 연구하였고, 익단 방사 압력 왜곡은 익단 누설 유동(tip leakage flow)을 강화하여 압축기의 실속(stall)을 유발함에 반해 허브 방사 압력 왜곡은 실속을 지연시키며 압축기의 안정성을 향상시키는 결과를 제시하였다. Bedke(6)는 입구 압력 왜곡 유무에 따른 실속 발생 원리를 비교하고 성능 저하를 확인하였다.
본 논문에서는 측풍 상황에서 입구 압력 왜곡 형상을 모사하였으며, 왜곡 영역의 각도에 대한 압축기의 성능 변화를 수치해석을 통해 분석하였다. 중심각과 스팬 방향 길이를 모두 고려한 익단 압력 왜곡 영역과 허브 압력 왜곡 영역을 생성하였으며, 영역 중심각을 해석의 변수로 설정하였다. 압축기의 주요 성능 지표로 전압비(total pressure ratio), 단열 효율(adiabatic efficiency), 서지 마진(surge margin), 작동 유량 범위(operating flow range)를 확인하였다.
2. 이론적 배경
2.1 성능 곡선
성능 곡선은 다양한 작동 조건 하에서 유체 기계의 성능을 나타내는 선도이다. 본 연구에서는 동익 회전 속도 100 %를 일정하게 유지하며 압축기 출구의 정압(static pressure) 조건을 조절하여 질량유량에 따른 전압비와 단열 효율을 측정하여 성능 곡선을 작도하였다. 출구 정압이 증가할수록 질량유량이 감소하고 전압비가 증가하며, 단열 효율은 증가하다가 특정 질량유량 값에서 최댓값을 갖고 감소하는 경향을 보인다. 질량유량이 일정 값 이하로 감소할 때 전압비가 급격하게 감소하는 서지(surge) 현상이 일어나며, 성능 지표 계산의 정확도를 높이기 위해 서지 지점 근처까지 반복계산을 수행하였다. 성능 곡선에서 단열 효율이 가장 높은 지점을 최고 효율점(peak efficiency point, PE), 서지 현상이 나타나기 직전의 지점을 서지점(near surge point, NS), 고유량 영역에서 질량유량 증가량이 0.1 % 이하로 나타나는 지점을 초크점(choke point, CP)으로 지정하였다.
3. 수치해석
3.1 축류 압축기 모델
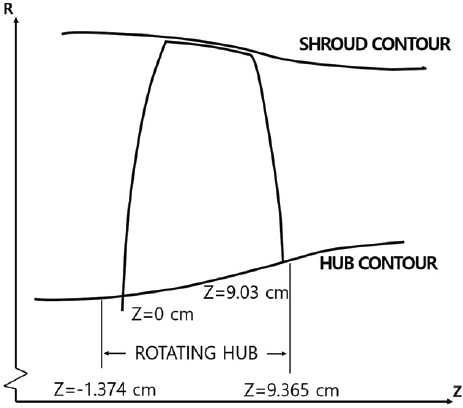
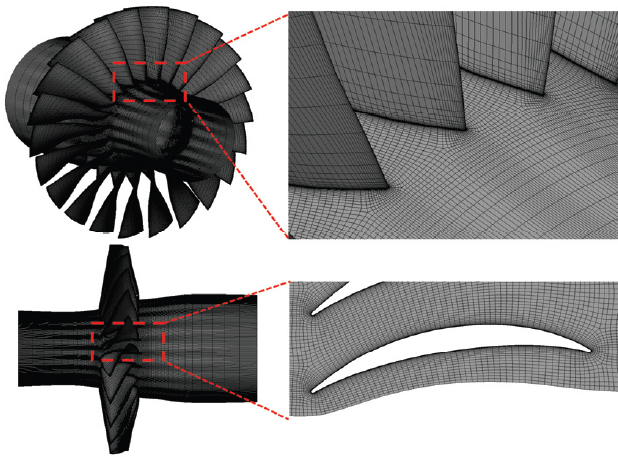
본 연구에서는 NASA에서 설계된 NASA Rotor 67 천음속 축류 압축기 모델(7)을 사용하였다. 해당 모델은 22개의 블레이드를 가진 동익 모델이며 표준 대기 조건에서 실험을 진행하였다. 설계점에서 회전 속도는 16043 rpm, 작동 유량은 33.25 kg/s이고 전압비는 1.63이다. 수치해석에 사용된 압축기 모델의 3차원 형상과 자오면에서 본 단면 형상을 Fig. 1과 Fig. 2에 도시하였으며, Table 1은 해당 모델의 작동 변수이다.
3.2 격자계 구성
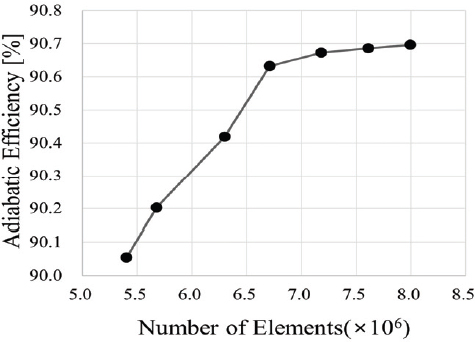
유동해석을 위한 격자계는 터보기계 격자 생성에 특화된 상용 프로그램 ANSYS Turbogrid를 사용하여 생성하였으며, 해석 영역에 대한 육면체 정렬 격자를 형성하였다. Fig. 3은 본 연구에 사용된 격자계를 나타낸 것이다. 벽면 유동을 정확하게 모사하기 위해 유로 격자 생성 방법으로 경계층 조건(boundary layer condition)을 설정하였으며, 익단 누설 유동의 정확도를 높이기 위해 익단과 슈라우드 사이의 격자를 조밀하게 생성하였다. 격자의 수치해석 신뢰성을 확보하기 위해 격자 수에 따른 압축기 단열 효율을 기준으로 격자 의존성 시험(grid dependency test)을 수행하였으며, 수행 결과 격자 요소가 7백만개 이상일 때 단열 효율 변화가 0.05 % 이내로 나타나는 것을 확인하였다. 수치 해석의 정확도와 해석 시간의 경제성을 고려하여 최종적으로 약 7.18백만개의 요소를 가진 격자를 선택하여 해석을 수행하였다. 격자의 블레이드 표면 평균 Y+ 값은 약 2.18이다. 격자 의존성 시험 결과를 Fig. 4에 도시하였다.
3.3 해석 방법
유동해석 상용 프로그램으로 회전 기계 해석에 적합한 ANSYS-CFX를 사용하였다. 작동유체는 이상 기체의 공기로 설정하였으며, 입구 경계조건으로 실험 조건과 동일한 대기 상태의 전압력과 전온도 조건을 설정하였고 출구에는 정압 조건을 설정하였다. 허브와 슈라우드, 블레이드 벽면은 점착(no-slip)과 단열 조건을 설정하였으며 슈라우드 벽면은 역회전 벽면(counter rotating wall) 조건을 설정하였다. 난류모델로 블레이드 벽면 근처의 유동을 잘 모사하는 k—ω SST(shear stress transport) 모델을 사용하였다. 해당 모델은 유동이 경계층 내에서 전이하는 구간에는 k-ω 모델을, 경계층에서 떨어진 곳에서는 k-ε 모델을 사용하는 하이브리드 접근 방식을 사용하여 전이 구간에서 난류를 보다 정확하게 예측할 수 있다. 비대칭 입구 압력 왜곡 형상을 적용하기 위해 22개의 익형에 대한 해석을 진행하였다. 계산 영역 전체를 회전 영역으로 설정하였고, 정상상태(steady-state) 해석을 진행하였다. 해석의 수렴성 및 신뢰성을 확보하기 위해 연속방정식 및 운동량 방정식의 해가 갖는 잔류값(residuals)이 0.0001 이하가 되면서 입⋅출구의 질량유량, 전압비 및 단열 효율의 변화가 없을 때까지 해석을 진행하였다.
3.4 입구 압력 분포 형상
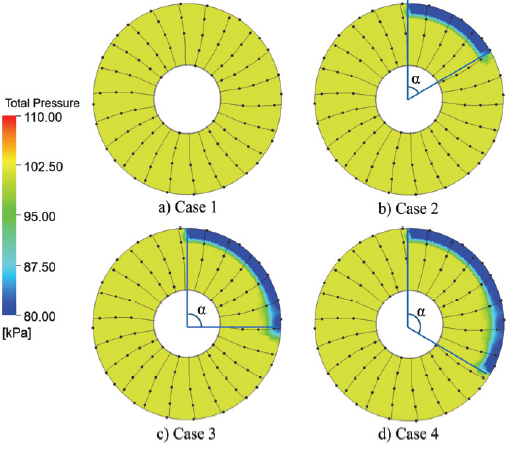
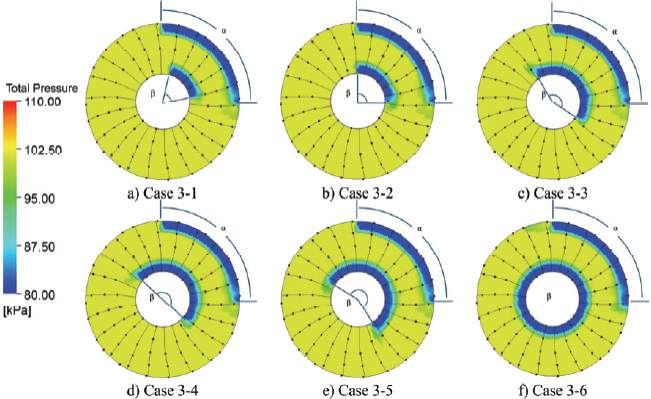
입구 압력 왜곡 현상의 영향을 확인하기 위해 압력 분포 형상을 설정하였다. 입구에 균일한 1기압이 주어진 case 1을 생성하였으며, 측풍에 의한 압력 왜곡에 따른 성능 변화를 확인하기 위해 Liu(3)와 Rusu(3)의 선행 연구를 기반으로 익단에 압력 왜곡 영역을 설정한 case 2, 3, 4를 생성하였다. 각 case에서 스팬 방향 80 %∼100 % 지점에 왜곡 영역의 중심각 α를 60°, 90°, 120°로 설정하였다. 기본 압력은 101.325 kPa이며, 왜곡 영역의 압력은 기본 압력에서 20 % 저하된 81.06 kPa로 설정하였다. 이후 허브 압력 왜곡의 영향을 확인하기 위해 α가 90°인 case 3을 기준으로 case 3-1, 3-2, 3-3, 3-4, 3-5, 3-6를 생성하였다. 각 case에서 스팬 방향 0 %∼20 % 지점에 왜곡 영역의 중심각 β를 60°, 90°, 150°, 180°, 210°, 360°로 형성하였으며, 허브 왜곡 영역 압력은 익단 왜곡 영역과 동일한 81.06 kPa로 설정하였다. 이때 익단 왜곡 영역과 허브 왜곡 영역의 각도 중심을 일치하도록 조정했다. 익단 입구 압력 왜곡 분포 형상은 Fig. 5에 도시하였으며, 익단과 허브 입구 압력 왜곡 분포 형상은 Fig. 6에 도시하였다. 측풍 상황에서 입구 유동각이 압축기 성능에 미치는 영향은 압력 왜곡에 비해 상대적으로 미미하며, 압축기 동익의 고속 회전에 의해 쉽게 상쇄되기 때문에 본 연구에서는 고려하지 않았다.
4. 결과 및 고찰
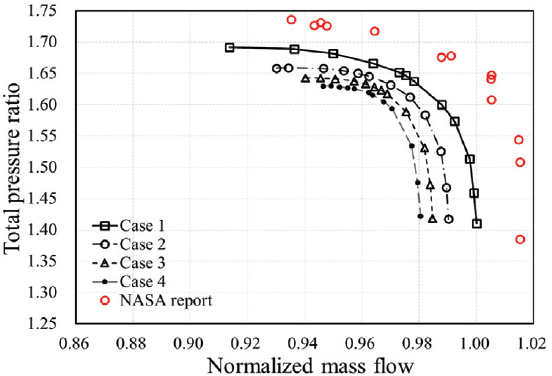
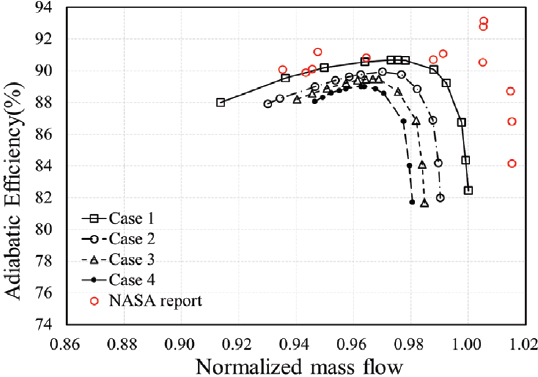
Case 1의 수치 해석 결과 최고 효율점의 질량유량은 33.589 kg/s, 전압비는 1.647, 단열 효율은 90.680 %, 서지 마진은 9.677 %, 작동 유량 범위는 8.632 %로 나타났다. NASA rotor 67 시험 결과(7)와 수치해석 결과의 성능 곡선을 비교하였을 때, 최고 효율점을 기준으로 질량유량은 2.979 %, 전압비는 0.011 %, 단열 효율은 2.652 %의 오차를 보여 실험 결과와 유사한 경향을 보였다. 입구 압력 분포 외 격자 및 경계조건을 통일하여 비교 결과의 신뢰성을 높였다.
4.1 익단 입구 압력 왜곡
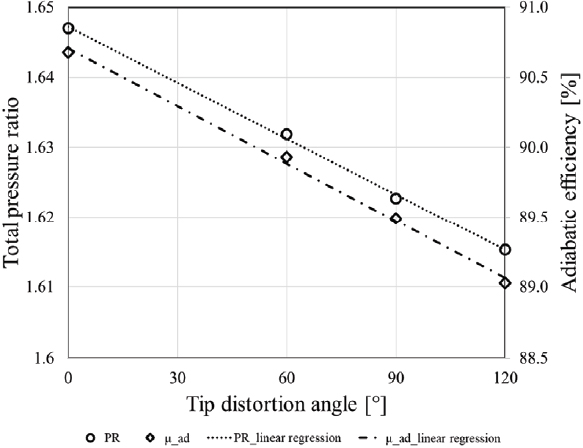
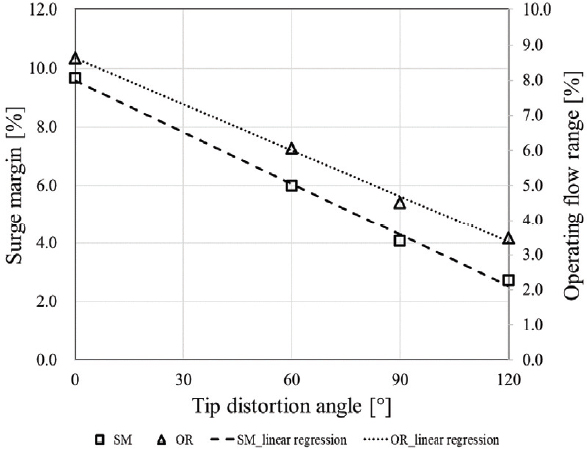
실험과 수치해석의 전압비와 단열 효율 성능 곡선을 비교하고 case 1의 초크점 유량을 기준으로 질량유량을 정규화 하여 각각 Fig. 7과 Fig. 8에 도시하였다. 해석 결과를 선형 회귀 분석하여 결정계수 R2을 확인한 결과 최고 효율점의 전압비, 단열 효율에서 각각 0.9987과 0.997, 서지 마진 및 작동 유량 범위에서 각각 0.9965와 0.997로 나타나 압력 왜곡 영역 중심각 α에 대해 선형 결과를 보이는 것을 확인하였다. 왜곡 영역 중심각 각도 α에 따른 최고 효율점의 전압비와 단열 효율 변화를 Fig. 9에, 서지 마진과 작동 유량 범위 변화를 Fig. 10에 도시하였고, 그 값을 Table 2에 기술하였다. 성능 변화 추세선 식과 R2 값을 Table 3에 기술하였다.
4.2 익단과 허브 입구 압력 왜곡
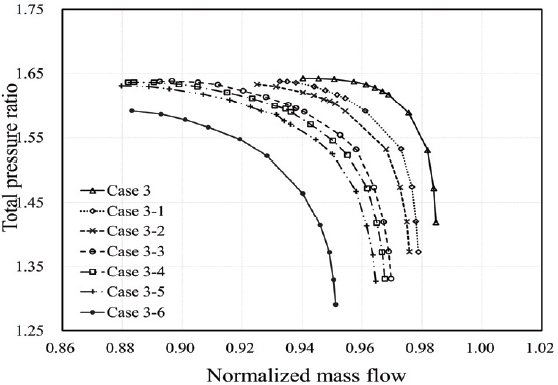
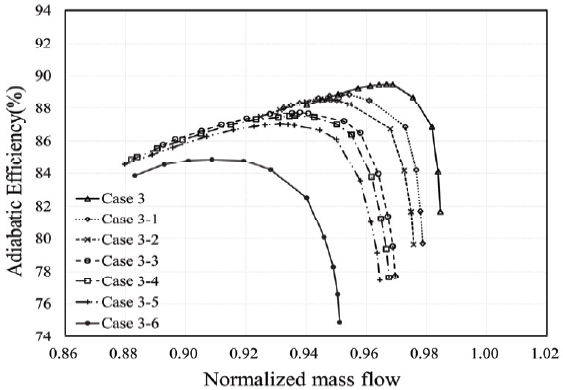
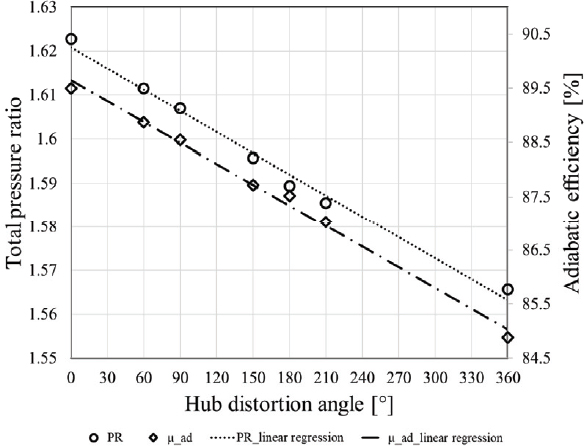
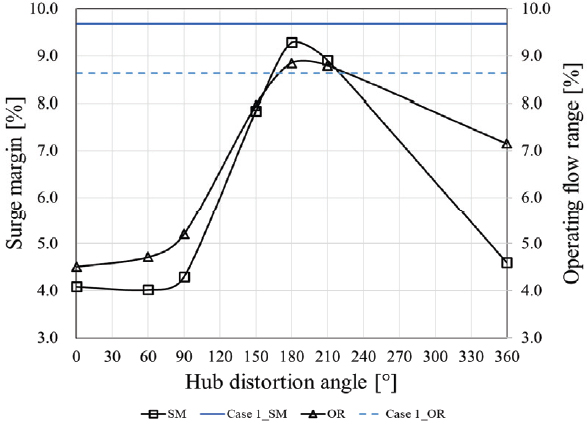
Case 3에서 case 3-6까지의 전압비와 단열 효율 성능 곡선을 각각 Fig. 11와 Fig. 12에 도시하였다. Table 4는 허브 압력 왜곡 영역의 중심각 β에 따른 성능 지표 변화를 나타내며, Fig. 13은 case 1과 case 3∼case 3-6의 최고 효율점 전압비와 단열 효율을, Fig. 14는 서지 마진과 작동 유량 범위를 비교한 그래프이다. 선형 회귀분석 결과 최고 효율점의 전압비와 단열 효율의 R2 값은 각각 0.9904, 0.9937로 β가 증가할수록 선형적으로 감소하였으나, 서지 마진과 작동 유량 영역은 비선형적인 결과를 보였으며 β=180°인 case 3-4에서 최댓값을 보였다. Case 1과 비교하여, case 3의 경우 서지 마진은 42.19 %, 작동 유량 범위는 52.27 %까지 감소하였으나 case 3-4의 경우 서지 마진은 95.94 %, 작동 유량 범위는 102.49 %까지 회복되었다.
4.3 블레이드 흡입면 유선 분포
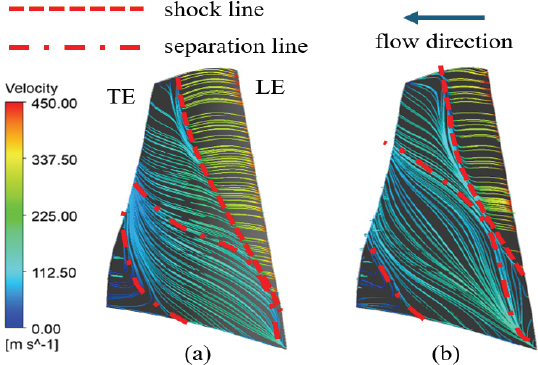
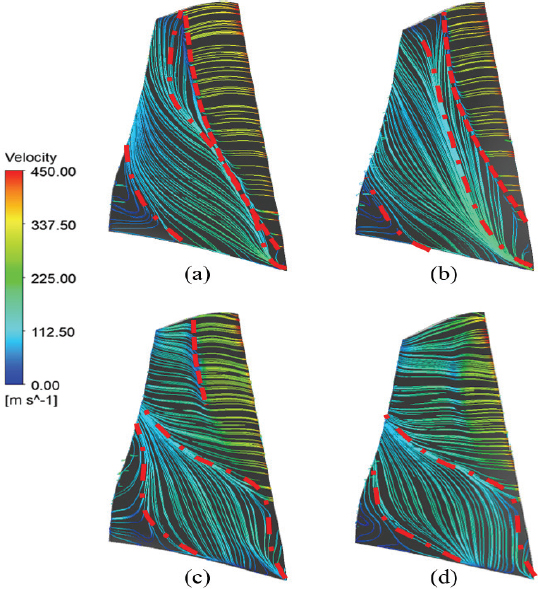
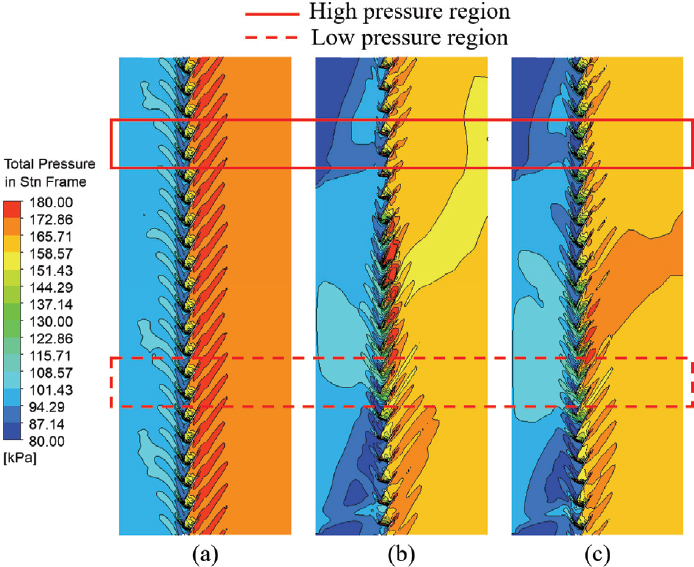
성능 지표 회복의 원인을 확인하기 위해 내부 유동장을 분석하였다. Fig. 15는 case 3과 case 3-4의 최고 효율점에서 축 방향 45 % 지점 평면의 전압력 분포이다. 입구 압력 왜곡의 영향이 압축기 내부 유동 방향을 따라 회전하여 y축 기준 반시계방향으로 110° 부근에 저압 영역을 형성하였다. 익단 입구 압력 왜곡의 영향에 따른 전압력 분포를 확인하여 y축 기준 방위각 290° 부근의 블레이드 영역을 고압 영역(high pressure region, HP)으로, 방위각 110° 부근의 블레이드 영역을 저압 영역(low pressure region, LP)으로 설정하였다. Fig. 16은 case 1의 최고 효율점과 서지점의 블레이드 흡입면(suction side) 유선 분포를 나타낸 것이다. 왜곡이 없기 때문에 모든 방위각에서 유사한 형상의 유선이 나타났으며 블레이드 표면의 유속이 급격하게 낮아지는 지점에서 충격파(shock)가 나타난 것을 확인할 수 있다. 허브 근처 블레이드 앞전(leading edge, LE) 및 뒷전(trailing edge, TE)에서 유동 박리(flow separation)가 일어났으며, 서지점의 경우 최고 효율점에 비해 충격파 선이 블레이드 앞전으로 앞당겨졌으며 블레이드 앞전 허브에서 갈라진 유동 박리 선이 익단 방향으로 이동했다. Fig. 17과 18은 각각 case 3과 case 3-4의 최고 효율점과 서지점의 블레이드 흡입면 유선 분포이다. 운전 지점 및 압력 영역에 따라 case 3과 case 3-4의 4가지 지점에서의 유선을 확인하였으며, (a)와 (b)는 각각 최고 효율점과 서지점의 고압 영역, (c)와 (d)는 각각 최고 효율점과 서지점의 저압 영역에서의 유선 분포를 나타낸다. Case 3의 경우, 최고 효율점과 서지점 모두 고압 영역 블레이드의 흡입면에서 충격파가 발생하였으며 허브 근처에서 강도 높은 유동 박리가 시작되어 익단 방향으로 유선이 형성되었다. 유동 박리는 익단 부근에서 다시 기존 유동 방향으로 돌아가는 재부착(reattachment) 경향을 보였다. 특히 서지점의 경우 충격파 위치가 경미하게 앞전으로 이동하였다. 저압 영역 블레이드 흡입면의 경우, 최고 효율점에서는 익단 근처에 부분적인 충격파가 발생하였으나 서지점에서는 충격파가 발생하지 않았다. 블레이드 앞전에서 유동 박리가 발생하지 않아 유동이 하류까지 진행되었으며 블레이드 뒷전 허브 근처에 서 약한 유동 박리가 발생하였다. Case 3-4의 경우, 고압 영역의 충격파와 유동 박리는 case 3와 유사한 형태를 보였다.저압 영역의 경우 최고 효율점과 서지점의 블레이드 앞전 허브 근처에서 case 1과 유사한 형태의 유동 박리가 발생하였으며, 최고 효율점의 익단 근처에서만 부분적인 충격파가 발생하였다. 이를 통해 허브에 추가적인 압력 왜곡을 부여하여 블레이드 허브 근처 유동을 왜곡이 없는 경우와 유사하게 회복할 수 있다는 것을 확인했다.
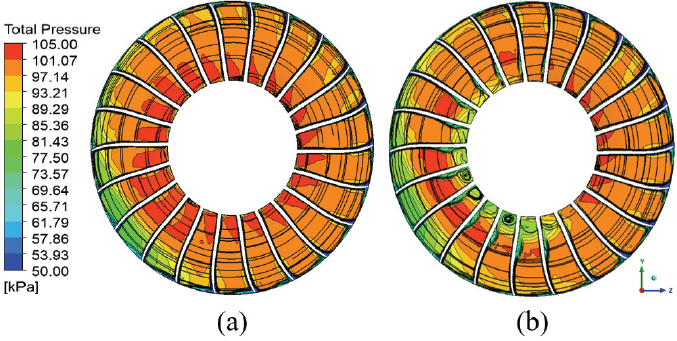
Total pressure contours and streamlines at 45 % axial direction plane from inlet surface of (a) case 3 and (b) case 3-4 at PE
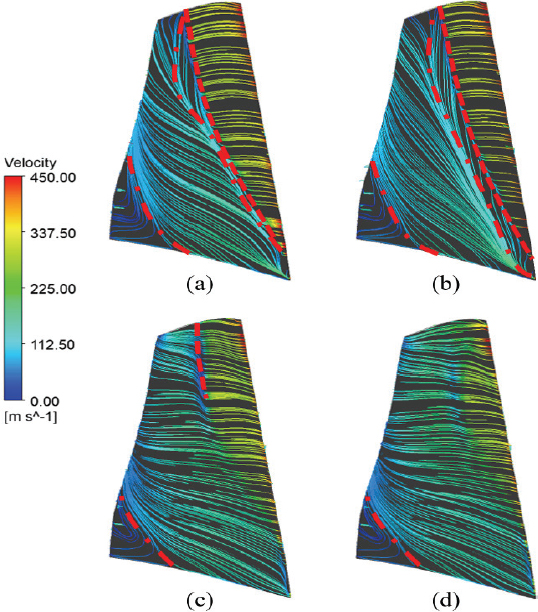
Streamlines of case 3 at (a) high pressure region at PE (b) high pressure region at NS (c) low pressure region at PE (d) low pressure region at NS
4.4 익단 누설 유동
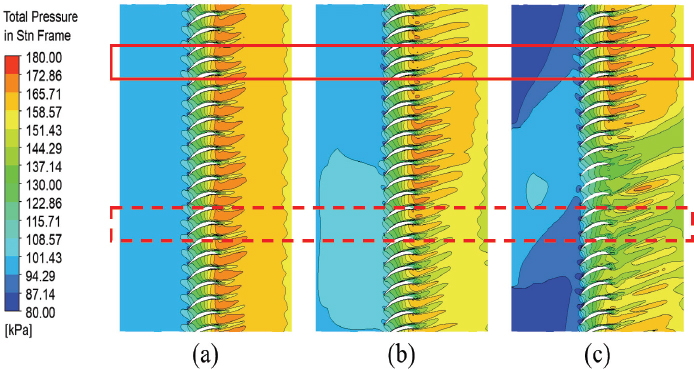
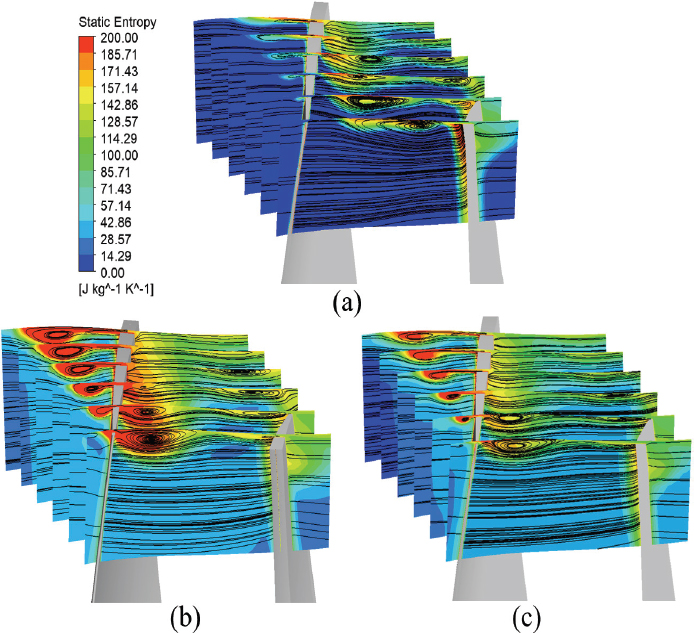
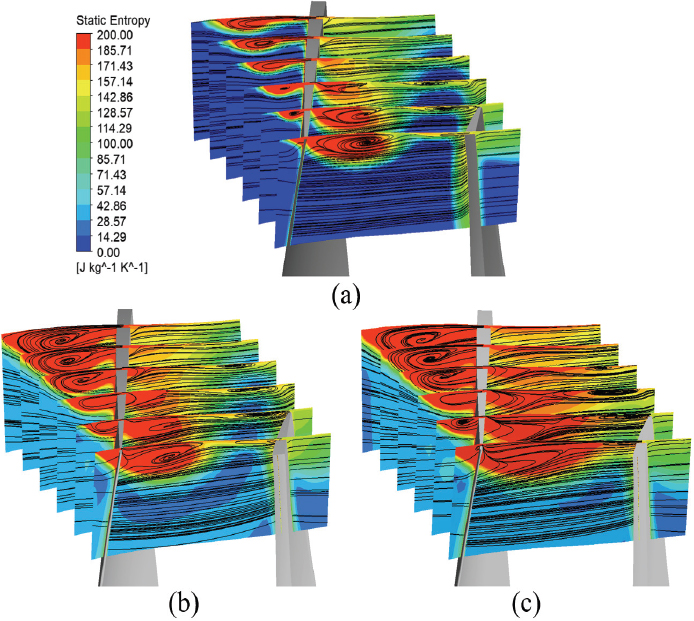
서지 마진 및 작동 유량 범위의 비선형성은 각 case의 서지점 변화에 의한 것이다. 서지점 변화의 원인을 확인하기 위해 서지의 원인 중 하나인 익단 누설 유동을 확인하였다. Fig. 19는 case 1, case 3, case 3-4의 서지점에서 스팬 방향 95 % 지점 익단 근처 영역의 전압력을 나타낸 것이며, Fig. 20은 스팬 방향 5 % 지점 허브 근처 영역의 전압력을 나타낸 것이다. Case 1과 case 3, case 3-4의 블레이드 전방 전압력 분포를 확인했을 때, 입구 압력 왜곡의 영향력이 압축기 내부의 회전 유동장을 따라 축 방향으로 진행하며 방위각이 변하는 저압 영역을 형성하는 것을 확인할 수 있다. 입구 압력 왜곡의 영향을 받는 블레이드 위치를 기준으로 방위각 290° 부근의 고압 영역과 방위각 110° 부근의 저압 영역을 표기하였다. 허브 근처 전압력 분포를 확인했을 때, 익단에만 압력 왜곡이 가해진 case 3에 비해 허브에 추가적인 압력 왜곡이 가해진 case 3-4에서 블레이드 전후로 전압력이 낮은 경향을 보였다. 그러나 익단 근처 전압력 분포의 경우, case 3과 case 3-4의 블레이드 전방 전압력은 유사하나 블레이드 후류에서 case 3은 전압력이 낮은 영역이 나타난 것에 비해 case 3-4에서 전압력이 높은 영역이 나타났다. Fig. 21과 Fig. 22는 각각 case 1, 3, 3-4의 최고 효율점과 서지점에서 블레이드 익단에 입구 압력 왜곡에 의한 저압 영역이 나타나는 방위각 110° 부근의 정 엔트로피(static entropy) 분포 및 익단 누설 유동을 확인한 것이다. 익단 누설 유동에 의해 생성된 익단 누설 와류(tip leakage vortex)와 고 엔트로피 영역을 확인할 수 있다. 최고 효율점에서, 입구 압력 왜곡이 주어진 case 3과 case 3-4의 경우 관찰 영역의 평균 정 엔트로피가 case 1 보다 높게 나타났으며, 와류 영역이 블레이드 앞전 쪽으로 이동하였다. Case 3의 경우 익단 누설 와류의 크기가 확대되었으며, 와류 영역의 정 엔트로피가 크게 증가하였다. 반면 case 3-4의 경우 익단 누설 유동에 의한 엔트로피가 감소하였고, 와류의 크기 또한 왜곡이 없는 경우와 비슷하게 축소되는 것을 확인하였다. 이는 익단 압력 왜곡으로 인해 생성된 저압 영역에 작동유체 흐름이 유도되어 익단 누설 유동이 증가하나, 허브에 추가적인 압력 왜곡이 형성될 경우 유동이 허브 영역으로 동시에 유도되어 익단 누설 유동이 약화되기 때문으로 판단된다. 반면 서지점에서는 모든 case에서 최고 효율점과 비교해 고엔트로피 영역이 크게 증가하였으며 와류 영역 또한 확대되었다. Case 3-4의 경우, 익단 고엔트로피 영역이 확대되었으나 블레이드 앞전 영역에서 익단 누설 와류가 나타나지 않았다. 이는 추가로 부여된 허브 압력 왜곡이 유동을 허브 방향으로 유도하여 익단 누설 유동을 억제하고, 이로 인해 서지 유발 효과가 완화된 것으로 해석된다.
5. 결 론
본 연구에서는 항공기 엔진 나셀에 측풍이 부는 상황을 가정하여 엔진 입구의 전압력 분포를 모사하고, 입구 압력 왜곡 현상이 축류 압축기의 공력성능에 미치는 영향을 분석하였다. NASA rotor 67 모델의 익단과 허브에 중심각에 따른 20 %의 압력 왜곡 영역을 형성하여 수치해석을 진행하였으며, 입구 압력 분포 형상에 따른 압축기의 성능 변화를 확인하고 내부 유동장 검사를 통해 원인을 분석하였다. 유동 해석의 결과를 요약하면 다음과 같다.
- 1) 입구 평면 스팬 방향 80 %∼100 % 지점에 중심각 0°, 60°, 90°, 120°의 압력 왜곡 영역을 형성하였고, 왜곡 영역의 압력은 기준 101.325 kPa 대비 20 %의 왜곡이 주어진 81.06 kPa로 설정하였다. 성능 지표로 최고 효율점의 전압비 및 단열 효율, 서지 마진, 작동 유량 범위를 확인하였으며, 해석 결과 입구 압력 왜곡 영역의 각도가 증가함에 따라 모든 성능 지표가 선형으로 감소하는 것을 확인하였다.
- 2) 익단 압력 왜곡 영역의 각도가 90°인 case 3을 기준으로 스팬 방향 0 %∼20 % 지점에 중심각 60°, 90°, 150°, 180°, 210°, 360°의 추가적인 압력 왜곡 영역을 형성하였다. 해석 결과 전압비, 단열 효율은 허브 압력 왜곡 영역 증가에 따라 선형으로 감소하였으나, 서지 마진 및 작동 유량 영역은 허브 압력 왜곡 영역의 중심각이 180°일 때 최댓값을 보이는 비선형 결과를 보였다. 입구 압력 왜곡이 없는 case 1과 비교하여 서지 마진은 약 96 %, 작동 유량 범위는 약 102 %까지 회복되었다.
- 3) 성능 지표 회복의 원인을 파악하기 위해 압축기 내부 유동장을 고찰하였다. Case 1, case 3, case 3-4의 블레이드 흡입면에서의 유선을 비교하였다. 각 경우 최고 효율점과 서지점에서 입구 압력 왜곡의 영향에 따른 고압 영역과 저압 영역을 확인하였다. 그 결과 모든 경우에서 최고 효율점에 비해 서지점에서 충격파가 블레이드 상류로 앞당겨지는 현상이 관찰되었으며, 고압 영역의 블레이드 앞전 허브 근처에서 유동 박리가 발생하였다. Case 3의 경우 유동 박리가 크게 발생하고 유동 재부착이 확인되었으며, 저압 영역에서 충격파 강도가 약해져 작동유체 흐름이 유지되었다. Case 3-4의 경우 고압 영역의 유동은 case 3과 유사한 형태를 보였으나 저압 영역의 블레이드 앞전 허브 근처에서 case 1과 같은 유동 박리가 발생하였다.
- 4) 블레이드가 회전함에 따라 회전 유동장이 형성되었으며 압력 왜곡 영역 또한 압축기 축방향으로 진행하면서 회전하는 모습을 보였다. 전압력 분포를 통해 왜곡 영역을 확인하고 최고 효율점과 서지점에서 각 case의 해당 영역 익단 누설 유동과 정 엔트로피를 고찰하였다. 그 결과 허브에 추가적인 압력 왜곡이 주어졌을 때 최고 효율점의 경우 익단 누설 유동에 의한 정 엔트로피가 감소하였으며, 서지점의 경우 정 엔트로피 영역이 증가하였으나 블레이드 앞전의 익단 누설 와류가 억제되는 것을 확인하였다. 이는 익단 압력 왜곡이 부여된 경우 유동이 익단으로 유도되어 익단 누설 유동을 유발하나, 추가적인 허브 압력 왜곡이 유동을 허브 방향으로 유도하여 익단 누설 유동의 효과를 감소시켰기 때문으로 판단된다.
- 5) 입구 평면 스팬 방향 80 %∼100 % 지점에 중심각 90°의 압력 왜곡이 주어진 경우, 스팬 방향 0 %∼20 % 지점에 중심각 180°의 추가적인 압력 왜곡 영역을 부여했을 때 서지 마진 및 작동 유량 범위 회복이 최대로 나타나는 것일 확인하였다. 추후 다양한 익단 및 허브 압력 분포에 따른 성능 지표 변화를 확인하여 익단 압력 왜곡에 따른 성능 지표 감소를 완화할 수 있는 최적의 허브 압력 형상을 찾는 연구가 필요할 것으로 보인다.
Acknowledgments
본 연구는 국토교통부의 재원으로 국토교통과학기술진흥원의 지원을 받아 수행되었음. (No. RS-2022-00142936)
References
- Lee, J., Lee, K., Kho, S., Kwak, J., 2007, “Inlet Distortion Test of Gas Turbine Engine,” Journal of Aerospace System Engineering, Vol. 1, No. 1, pp. 53∼59
-
Li, Z., Zhu, X., Yan, Z., and Pan, T., 2022, “Numerical Investigation on the Performance of a Transonic Axial Compressor with Inlet Distortion and Low Reynolds Number,” Energies, Vol. 15, No. 10: 3612
[https://doi.org/10.3390/en15103612]

- Rusu, R., 2017, “Experimental Investigation of Inlet Distortion in a Multistage Axial Compressor,” Master Thesis, Dept. Aero. Astro., Purdue University, USA
- Liu, K., Sun, Y., Zhong, Y., Zhang, H., Zhang, K., and Yang, H., 2014, “Numerical investigation on engine inlet distortion under crosswind for a commercial transport aircraft,” 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia; September 7-12, 2014
-
Li, J., Du, J., Liu, Y., Zhang, H., and Nie, C., 2020, “Effect of inlet radial distortion on aerodynamic stability in a multi-stage axial flow compressor,” Aerospace Science and Technology, Vol. 105, No. 105886
[https://doi.org/10.1016/j.ast.2020.105886]

- Bedke, A. M., 2022, “The Effects of Various Inlet Distortion Profiles on Transonic Fan Performance,” Master Thesis, Dept. Mech. Eng., Brigham Young University, USA
- Strazisar, A. J., Wood, J. R., Hathaway, M. D., and Suder, K. L., 1989, “Laser anemometer measurements in a transonic axial-flow fan rotor,” NASA Technical Paper 2879