초발수표면 적용 난류 채널 유동의 저항 저감 효과를 예측하기 위한 Effective Slip Length 모델링
Abstract
Research on the flow characteristics and drag reduction effects of superhydrophobic surfaces(SHS) has been vigorously conducted. In particular, studies utilizing Direct Numerical Simulation (DNS), known for its high accuracy in computational fluid dynamics, have been prevalent. However, the high computational cost of DNS limits the scale of computational domain that can be studied. In this research, we present a model that uses the k-epsilon turbulence model combined with the effective slip length of superhydrophobic surfaces. This model can predict drag reduction effects without the direct implementation of superhydrophobic structures in actual-scale geometry. Initially, to validate our model, we focused on turbulent channel flows and limited our study to ridge-type superhydrophobic structures. The simulations were conducted under various conditions, and the results demonstrated that our model effectively predicts the drag reduction effects of superhydrophobic surfaces in areas where P+ is below 100. Further research aimed at expanding this model to accommodate various superhydrophobic structures and external flow conditions is expected to provide a powerful tool for effectively predicting the drag reduction effects under conditions that are challenging to handle with DNS.
Keywords:
Superhydrophobic surface, Drag reduction, Slip length, Wall function키워드:
초발수표면, 저항 저감, 미끄럼 길이, 벽함수1. 서 론
초발수표면의 유동 특성 및 저항 저감 효과를 분석하기 위한 연구는 과거부터 활발히 이루어져왔다. 그 중에서 DNS를 활용한 연구의 경우 높은 정확도를 가지고 있지만, DNS의 높은 계산 비용으로 인해서 실제 스케일에서 미세 구조들을 직접 구현하는 것이 아닌 매우 작은 규모의 유동장내에서 초발수표면의 공기층은 No-shear, 벽면은 No-slip 조건을 부여하는 방식으로 계산 비용을 낮추어 진행되어왔다.(1∼4) 따라서 큰 규모의 실형상 운동체에 대한 유동해석에는 DNS에 비해 정확도는 조금 낮지만 비교적 계산비용이 저렴한 Reynolds Averaged Navier Stokes(RANS) 난류 모델들을 사용하는 것이 적절하다. 하지만 아직까지 RANS를 활용해 초발수표면의 저항 저감 효과를 분석하는 연구는 부족한 실정이다. 이에 본 연구에서는 상술한 DNS의 한계를 극복하며 계산비용이 낮은 k-ε 난류모델과 초발수표면에 대한 effective slip length를 활용하여 실제 규모의 유동장에 적용할 수 있으며, 초발수표면 구조의 직접적인 구현 없이 저항 저감 효과를 예측할 수 있는 모델을 제시하고자 한다.
2. 배경 이론
2.1 벽함수(Wall function)
난류 경계층에서 벽 근처의 유동은 매우 급격하게 변화한다. 이러한 변화를 정확하게 모사하기 위해서는 매우 세밀한 격자가 필요하지만, 이는 계산 비용을 크게 증가시킨다. 따라서 계산비용의 증가 없이 벽근처의 유동을 모사하기 위해 벽함수를 사용하게 된다. 벽함수는 주로 RANS 난류 모델과 함께 사용되며 크게 viscous sublayer와 log-law region으로 나뉘는 두 영역에서 사용된다. Viscous sublayer는 벽 근처에서 유체의 점성력이 지배적으로 나타나는 영역으로 일반적으로 벽으로부터의 무차원 거리인 y+가 0이상 5 이하인 영역을 의미한다. 이 영역에서 유체의 속도 분포는 선형적으로 변하게 되며 이를 식으로 나타내면 다음과 같다.
| (1) |
여기서 U+와 y+는 각각 무차원 속도, 무차원 거리를 나타내며, 두 무차원수는 아래와 같은 식으로 계산된다.
| (2) |
| (3) |
U와 y는 각각 속도, 벽으로부터의 거리를 나타내며, friction velocity Uτ는 다음과 같다. 여기서 τw는 벽면 전단 응력(wall shear stress)을 뜻한다.
| (4) |
난류 경계층 내의 또 다른 영역인 log-law region은 난류가 지배적으로 나타나는 영역으로, 일반적으로 y+가 30 이상인 영역을 의미한다. log-law region의 상한선은 레이놀즈 수의 영향을 크게 받으며, 해석하고자 하는 케이스에 따라 그 상한선의 y+ 값이 작게는 100에서 크게는 수천까지 정의될 수 있다. 이 영역에서 유체의 속도는 다음과 같이 계산된다.
| (5) |
여기서 κ는 von kàrmàn 상수, E는 실험적으로 결정되는 상수로 일반적으로 κ≈0.41, E≈9.8을 사용한다.
앞서 언급된 viscous sublayer와 log-law region 사이의 5<y+<30인 영역을 buffer layer라고 부르는데, 이 영역에서는 앞서 언급된 두 모델 모두 적용이 불가능하다. 이런 문제를 해결하기 위한 방법으로 식 (1)과 식(5)를 합쳐 아래의 식 (6)과 같이 정의하고, buffer layer에 최대한 격자를 배치하지 않도록 하는 방법을 사용할 수 있다.
| (6) |
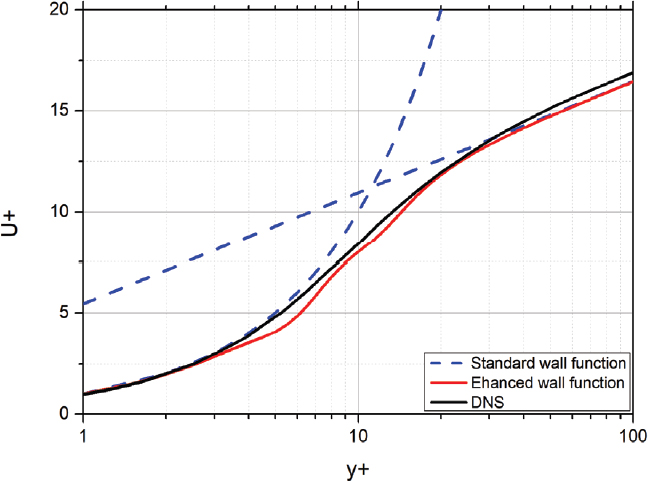
식 (6)의 경우 대표적으로 사용되는 벽함수 모델 중 하나이며, 이 식을 standard wall function이라고 부르게 된다. 하지만 Fig. 1에서 볼 수 있듯이 standard wall function의 경우, 실제 유동 및 DNS 데이터와 비교하였을 때 buffer layer 내에서 큰 오차를 가진다. 이러한 오차를 줄이면서 벽함수를 y+에 대한 하나의 식으로 나타내기 위해 Kader의 연구(5)에서 제시된 식 (7)을 이용할 수 있다.
| (7) |
식 (7)을 통해 viscous sublayer에 대한 식 (1)과 log-law region에 대한 식 (5)의 blending을 진행하면, 아래의 식 (8)과 같은 새로운 벽함수를 정의할 수 있다.
| (8) |
식 (8)을 enhanced wall function이라고 부르며, Fig. 1을 통해 enhanced wall function을 사용할 경우 standard wall function에 비해서 buffer layer의 오차가 많이 개선되는 것을 확인할 수 있다.
2.2 미끄럼 조건(Slip condition)
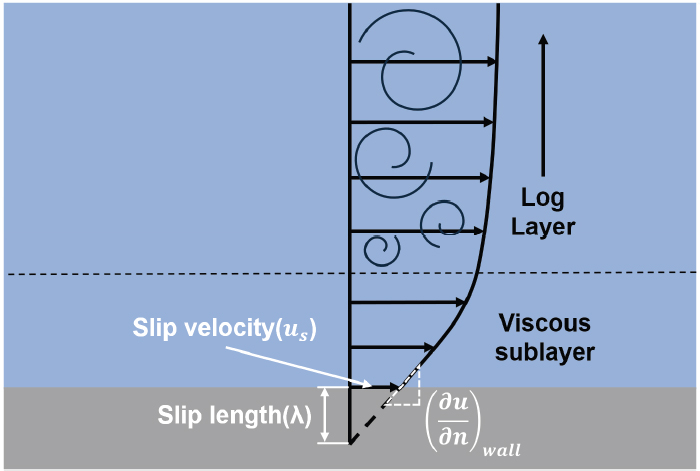
유체와 벽 혹은 유체와 유체 사이의 경계면에서 유체의 속도가 0이 되어 움직이지 않는 경우를 no-slip 조건이라고 부른다. 만일 유체가 경계면에서 완전히 정지하지 않고 어떠한 속도를 가지고 움직이는 경우, 이를 미끄럼 조건(slip condition)이라고 부르며, 이러한 미끄럼 조건을 설명하기 위해 여러 가지 경계 조건을 사용할 수 있다. 그 중 초발수표면에 대한 수치해석적 연구에서 자주 언급되며 가장 대표적으로 사용되는 조건이 바로 Navier slip 경계 조건이다. Navier slip 경계조건은 다양한 이론적, 수치적, 실험적 연구(6,7,8,9)에서 활용되어 왔으며, 이를 통해 미끄럼 길이(λ, slip length)와 미끄럼 속도(us, slip velocity) 사이의 관계를 식 (9)와 같이 나타낼 수 있다. Navier slip 경계 조건에 대한 모식도는 Fig. 2에 나타내었다.
| (9) |
여기서 은 벽면에 수직인 방향으로의 속도 구배를 나타낸다.
3. 초발수표면 모델링
3.1 초발수표면 형상
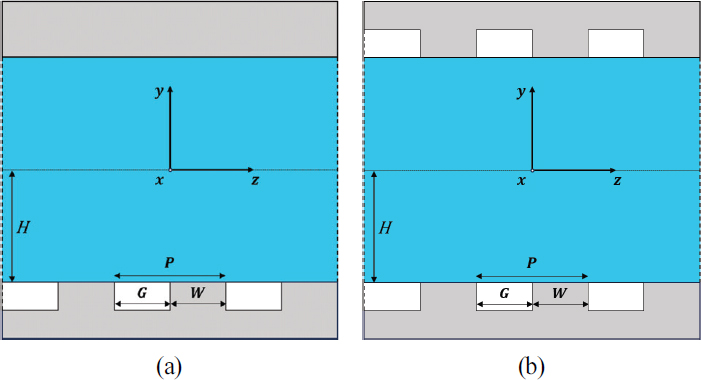
본 연구에서는 +x를 유동방향(streamwise), +y를 벽면에 수직인 방향(wall normal), +z를 횡방향(spanwise)로 정의하였다. 초발수표면의 여러 가지 다양한 구조들 중에서 형상이 유동방향(streamwise)으로 일정한 “Ridge type” 형상을 사용하였고 초발수표면의 공기층 너비를 G, 벽면의 너비를 W로 정의하였고 횡방향(spanwise)으로 반복되는 초발수구조의 길이를 P=G+W 로 정의하였다. 그 외에 초발수표면의 공기층 비율(Gas fraction)을 Φ=G/P로 정의하였다.
사용된 좌표축과 초발수표면 형상 그리고 주요 변수들은 Fig. 3에 나타내었다.
3.2 초발수표면 Effective Slip Length 및 벽함수 모델링
Philip, Peaudecerf, Temprano-Coleto의 선행 연구(10,11,12)에 따르면 초발수표면의 유동방향(streamwise) 및 횡방향(spanwise) effective slip length λx, λz는 각각 아래의 식과 같이 나타낼 수 있다.
| (10) |
| (11) |
Effective slip length는 δτ=ν/Uτ를 사용해 로 나타낼 수 있다. 또한 Fukagata의 연구(13)에 따르면 초발수표면의 벽함수는 아래와 같이 나타낼 수 있다.
| (12) |
식 (12)은 log-law region에 적용되는 벽함수인 식 (5)와 비교했을 때 추가적인 항 ∆U+(,)가 더해지는 것을 확인할 수 있는데, 이는 추가된 항이 초발수표면의 효과로 인해 발생한 slip velocity를 나타내는 것으로 생각할 수 있다.
Busse의 연구(14)에 따르면, ∆U+(,)는 무차원 미끄럼 길이 λx와λz의 함수로 아래 식과 같이 계산된다.
| (13) |
여기서 는 유동방향(streamwise) 미끄럼 길이 λx에 의해 증가하는 속도, 는 횡방향(spanwise) 미끄럼 길이 λz의 영향으로 감소하는 속도를 의미한다. 즉, 기존의 log-law region에 대한 벽함수를 U+방향으로 ∆U+(,)만큼 평행이동 시킨 것이다.
Tomlinson의 연구(15)에서 이러한 방법을 통해 초발수표면의 저항 저감에 대한 이론적인 연구를 진행하였지만, log-law region에 대한 식만 제시되었다. 따라서 본 연구에서는 viscous sublayer에도 유사한 방법을 적용하여 아래와 같은 새로운 벽함수를 도입하였다.
| (14) |
4. 전산 해석 절차 및 해석 모델 검증
4.1 전산 해석 절차
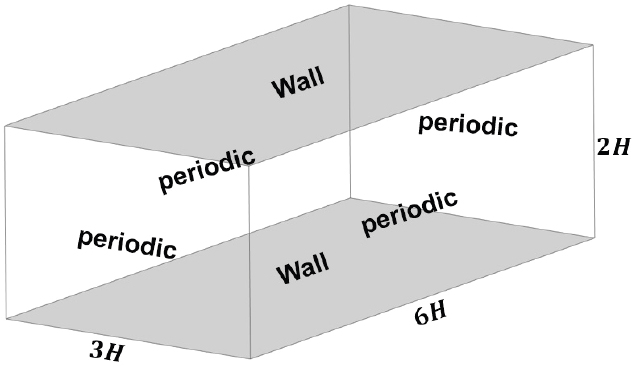
본 연구는 상용 소프트웨어인 ANSYS Fluent를 이용하였으며, Realizable k-ε 난류 모델을 사용해 해석을 진행하였다. 유동장의 형상이나 경계 조건과 같은 여러 해석 조건들의 경우 DNS를 활용한 선행 연구(1,4,16,17)들을 참고하였다. 6H×2H×3H의 직육면체 형상을 가진 유동장을 선택하였으며, 유동방향(streamwise) 및 횡방향(spanwise)으로 모두 주기 조건(periodic condition)을 부여하였다. 또한 유동장의 윗면과 아랫면은 벽으로 정의하였으며 해석에 사용된 유동장과 경계 조건은 Fig. 4에 자세히 나타내었다.
No-slip 벽면과 초발수표면의 2가지 케이스에 대한 검증 절차가 진행되었다. No-slip 케이스는 유동장의 윗면과 아랫면 모두 No-slip 조건을 사용하였으며, 초발수표면 케이스의 경우 Fig. 3 (a)와 같이 유동장의 아랫면에는 초발수표면, 윗면에는 No-slip 조건을 적용하였다. 초발수표면은 앞서 언급된 effective slip length를 이용해 구현하였으며, P/H=0.375, Φ=0.5인 조건을 사용하였다. 경계조건으로 사용된 주기 조건의 경우 일정한 질량 유량을 부여하였으며, No-slip 벽면에 대한 검증을 마친 후에 이와 동일한 질량 유량을 초발수표면 케이스에도 적용하여 해석을 진행하였다. 여기서 계산된 No-slip 케이스의 friction reynolds number를 Reτ0로 정의하였다. 유동을 나타내기 위한 변수로 Reτ, 초발수표면을 나타내기 위한 변수로 P/H, Φ의 총 3가지 무차원 변수를 이용하였으며 Reτ의 정의는 아래와 같다.
| (15) |
여기서 Uτ는 friction velocity를 나타내며, ν는 동점성계수로 유체의 점성계수 μ를 밀도 ρ로 나눈 값이다. 또한 H는 두 평판 사이 거리의 절반을 나타낸다. 검증을 위한 해석의 경우 Reτ0=180인 조건에서 진행되었다. 또한 작동 유체로 액체 상태의 물(water liquid)을 선정하였으며, 물의 밀도는 ρ=998.2kg/m3, 점성 계수는 μ=0.001003kg/m∙s 를 사용하였다. 각 케이스에 대한 자세한 해석 조건은 Table 1 에 나타내었다.
본 연구와 같이 채널 유동 조건인 경우 총 항력 대비 압력 항력이 차지하는 비중이 매우 낮아 그 영향이 없는 것으로 간주할 수 있다. 이와 반대로 마찰 항력은 총 항력의 대부분을 차지하기 때문에 마찰 항력을 비교하여 저항 저감 효과를 계산할 수 있다. 또한 마찰 항력은 벽면 전단 응력과 면적의 곱으로 나타낼 수 있으므로 아래의 식을 통해 저항 저감 효과를 계산하였다.
| (16) |
여기서 τ0는 No-slip 케이스의 벽면 전단 응력을 나타내며 τ는 초발수표면이 적용된 케이스의 벽면 전단 응력을 나타낸다.
4.2 전산 해석 모델 선정 및 검증
우선 본 연구에서 사용된 realizable k-ε 난류 모델의 적합성을 검증하기 위해 Patel의 연구[18]를 참고하였다. Patel의 연구에 따르면 bulk velocity Ub를 이용한 레이놀즈 수를 라고 정의할 때 Reb<1,350인 경우 laminar flow, Reb>1,800인 경우 fully turbulent flow라고 할 수 있으며 Reb=3,000인 영역까지는 transitional effects가 나타난다고 정의하고 있다. 본 연구에서 레이놀즈 수가 가장 낮은 조건은 Reτ0=180으로, 이 조건에서 Reb는 Table 2에 나타난 것과 같다. 이는 transitional effect가 나타난다고 알려진 Reb=3,000보다 큰 레이놀즈 수 영역이기 때문에 transitional effect를 무시할 수 있는 fully turbulent flow라고 할 수 있다. 또한, Reτ0=180인 조건에서 진행된 시뮬레이션의 결과를 DNS 데이터와 비교하여 Fig. 5 및 Table 2에 자세히 나타내었다. 이러한 과정을 통해 본 연구에서 realizable k-ε 난류 모델을 사용한 해석 조건이 타당하다는 결론을 얻을 수 있었다.
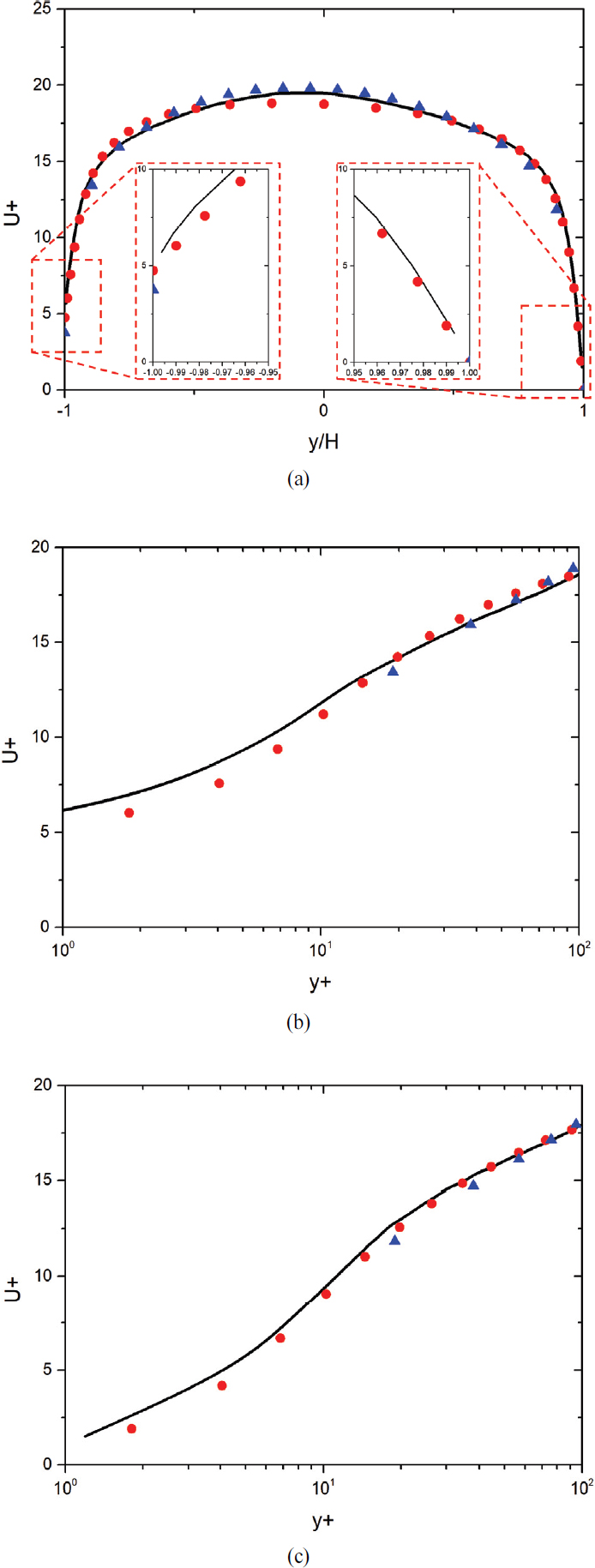
Velocity comparison between our simulations and DNS data; ― Martell et al(1), ● enhanced wall function, ▲ standard wall function (a) velocity profile comparison (b) velocity profile close to SHS (c) velocity profile close to no-slip wall
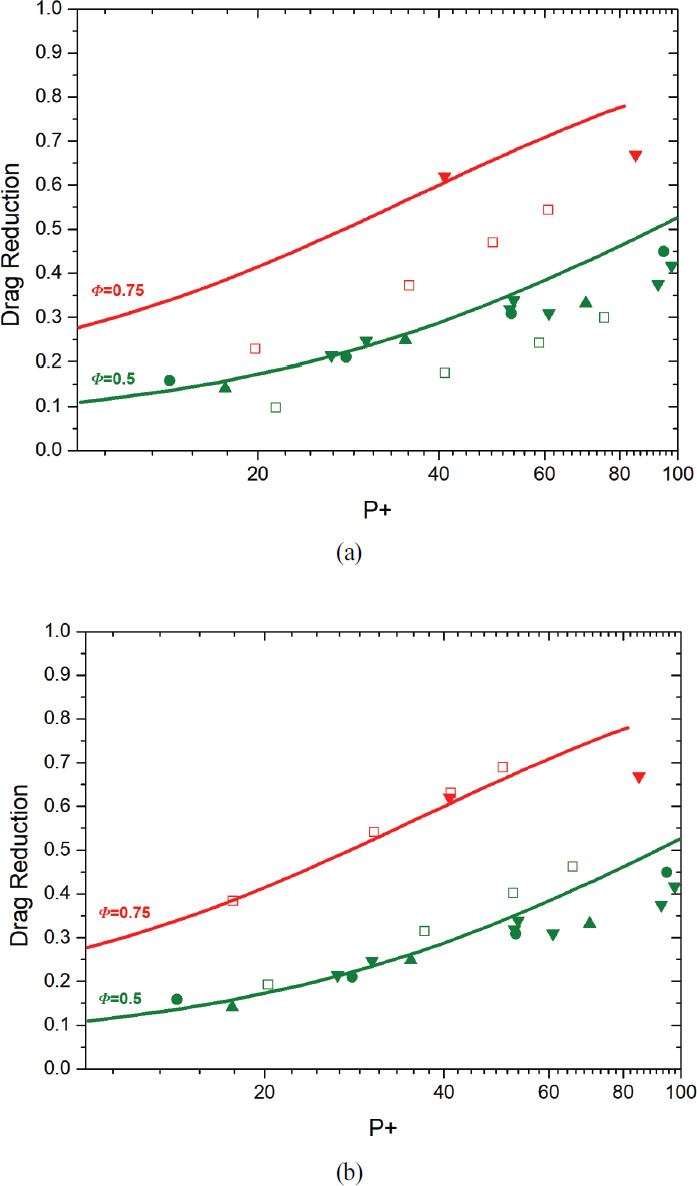
또한 보다 정확한 해석을 위해 다양한 벽 근처 모사(near wall treatment)가 고려되었다. 여러 가지 벽 근처 모사 방법 중에서 선행 연구(1∼4,15,16)와 비교해 가장 높은 정확도를 보였던 standard wall function과 enhanced wall function을 비교한 모습을 Table 2와 Fig. 5, Fig. 6에 나타내었다. Table 2는 No-slip 케이스에서 계산된 여러 레이놀즈 수 및 마찰계수를 나타낸 것으로, 선행 연구와 비교하였을 때 standard wall function이 enhanced wall function에 비해 조금 더 정확하게 예측한 것을 알 수 있다. 또한 Fig. 5는 유동장의 아래쪽 벽면에 초발수표면이 적용된 케이스의 속도 분포를 선행 연구와 비교한 것으로 벽 근처 영역에서는 enhanced wall function이, 유동장의 중심 부근에서는 standard wall function이 각각 높은 정확도를 보였다. 하지만 저항 저감 효과를 비교해보았을 때, 두 모사 방법 사이에 큰 차이를 확인할 수 있었다. Fig. 6은 초발수표면의 저항 저감 효과를 P+=P/δτ와 비교해 나타낸 것으로, 선행 연구들과 비교하였을 때, enhanced wall function이 standard wall function보다 저항 저감 효과를 훨씬 더 정확하게 예측하는 모습을 확인할 수 있었다. 따라서 본 연구에서는 저항 저감 효과를 효율적으로 예측할 수 있는 enhanced wall function을 사용하였다.
5. 초발수표면 적용 난류 채널 유동 해석
5.1 전산 해석 격자 및 해석 조건 설정
난류 채널 유동 해석에서는 앞선 4장에서 언급된 것과 동일한 유동장이 사용되었으며, 이에 대한 자세한 설명은 Fig. 4 에 나타나있다. 또한 Fig. 3 (b)와 같이 유동장의 윗면과 아랫면 모두 초발수표면을 적용하여 해석을 진행하였다. 동일한 3가지 무차원 변수 Reτ, P/H, Φ가 사용되었으며, 여기서 사용된 각 변수들의 수치는 Table 3에 나타내었다. 또한 Realizable k-ε 난류 모델 및 enhanced wall function을 사용하였으며, 주기 조건으로 일정한 질량 유량을 부여하였다. 그 외의 여러 해석 조건들은 모두 Table 4에 나타내었다.
전산 해석을 위한 유동장은 앞서 언급되었던 Fig. 4와 동일한 6H×2H×3H의 유동장을 사용하였다. 본격적인 해석을 진행하기에 앞서 해석에 사용할 격자의 수준을 결정하기 위해 총 N개의 격자를 이용하여 격자 의존성 테스트(grid independence test)를 진행하였다. 격자 의존성 테스트의 경우, Reτ에 따라 달라지는 유동 조건과 무관하게 벽면에서 첫 번째 격자의 무차원 거리 y+를 1 내외로 유지할 수 있도록 유동조건에 따라 총 3가지 조건에 대한 테스트를 진행하였다. 격자 의존성을 확인하기 위해서 벽면 전단 응력과 y+를 이용해 비교를 진행하였고, 진행된 격자 의존성 테스트의 결과는 Table 5와 Table 6에 나타내었다.
해석에 사용할 격자를 선정하기 위해서 가장 조밀한 격자 대비 벽면 전단 응력에서 오차가 0.1% 내외, 그리고 y+가 1 내외라는 두 가지 조건을 선정 기준으로 제시하였으며, 각 케이스별로 두 조건을 모두 만족시킬 수 있는 격자를 사용하였다.
최종적으로 Reτ0=180인 경우 54,000개, Reτ0=395인 경우 72,000개, Reτ0=590인 경우 90,000개의 사각형 격자를 유동장 내에 구성하여 해석을 진행하였으며 격자에 대한 자세한 정보는 Fig. 7과 Table 7에 나타내었다.
5.2 초발수표면 적용 난류 채널 유동 해석 결과
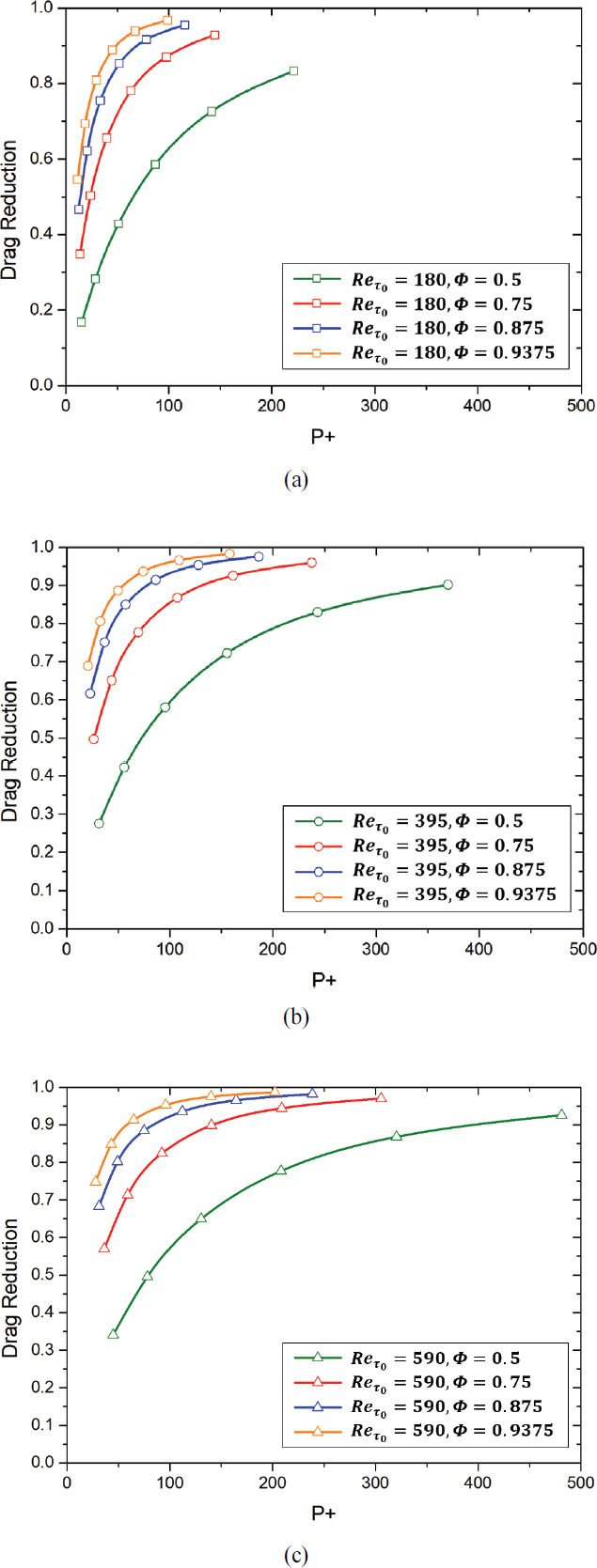
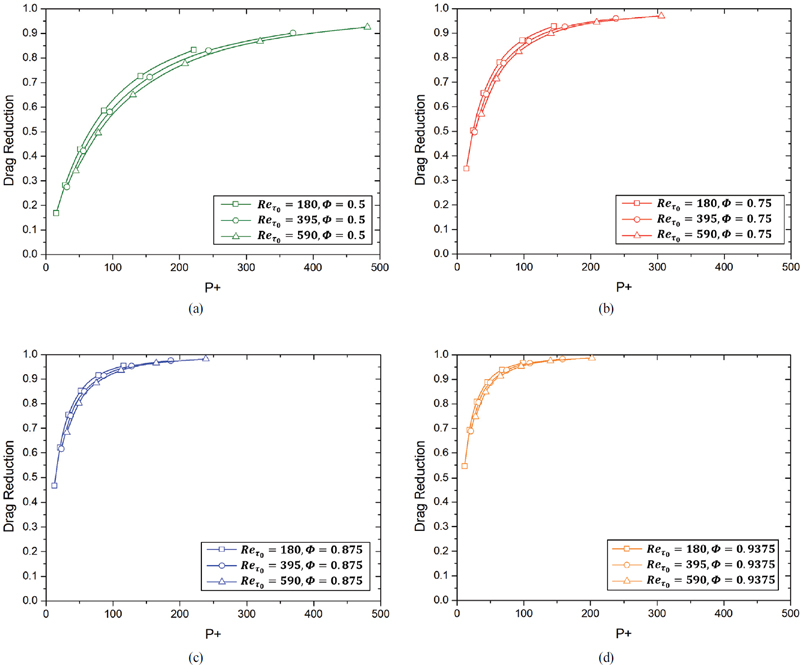
Table 3에 나타난 3가지 무차원 변수의 수치에 따라 총 72개의 케이스에 대한 해석을 수행하였으며 그 결과들을 다양한 관점에서 분석하고, 여러 선행 연구 결과(2∼4, 15)들과 비교해보았다. 우선 해석 결과들을 동일한 Reτ 및 동일한 Φ에 대해 비교해 Fig. 8과 Fig. 9에 나타내었다. Fig. 8은 동일한 유동 조건 아래에서 공기층 비율 Φ의 영향을 알아보기 위한 것으로, Φ가 증가함에 따라 Reτ와 무관하게 저항 저감 효과가 증가하는 모습을 볼 수 있었다. 이와 반대로 Fig. 9에서는 공기층의 비율이 일정할 때 Reτ가 저항 저감 효과에 미치는 영향을 알아보았으며, 그 결과 동일한 Φ가 주어진다면 Reτ와 무관하게 저항 저감 효과가 특정한 곡선을 나타내며 그 위에 집중적으로 분포되어 있음을 확인할 수 있었다.
또한 Fig. 8과 Fig. 9에서 동일하게 확인할 수 있었던 점은 바로 P/H의 영향으로, Reτ와 Φ가 일정하다면 P/H가 증가함에 따라 저항 저감 효과가 커지는 모습을 볼 수 있었다. 또한 P/H가 증가할수록 저항 저감 효과의 증가폭이 줄어들며 특정 값에 수렴하는 모습을 확인할 수 있었다.
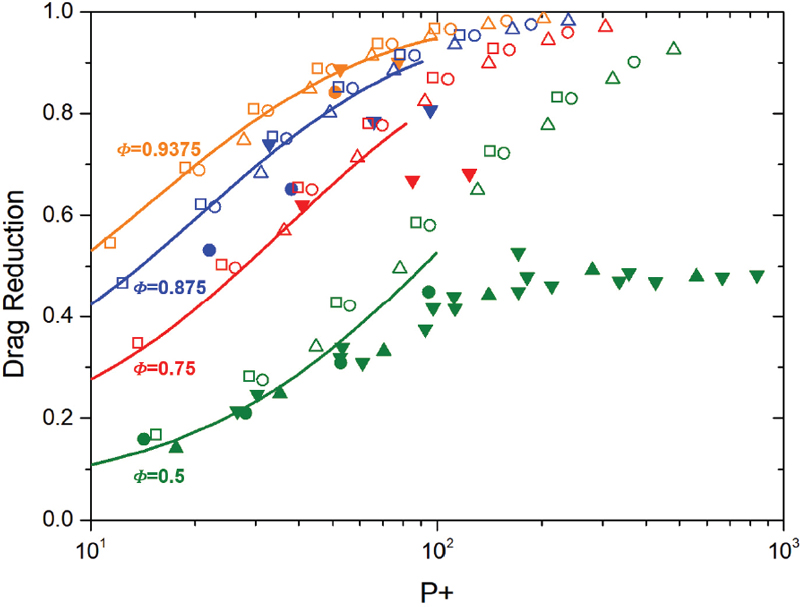
추가적으로 해석 결과들을 선행 연구 논문의 이론적인 예측 결과(15) 및 DNS 데이터(2,3,4)들과 비교해보았으며 그 결과를 Fig. 10에 나타내었다. P+가 100 이하인 영역에서는 초발수표면의 저항 저감 효과를 높은 정확도로 예측하였지만, P+가 100 이상인 영역에서는 DNS 데이터와 비교해 저항 저감을 큰 폭으로 과대평가 하는 것으로 나타났다.
6. 결 론
본 연구에서는 초발수표면의 격자 구조를 직접 구현하는 것이 아닌, 모델링을 활용해 RANS 시뮬레이션을 직접 수행하고 그 결과를 자세히 분석하였다. 이와 관련된 선행연구가 존재하는지에 대한 문헌조사를 실시하였으나, 관련 연구를 찾을 수 없었으며, 따라서 본 연구는 RANS 난류 모델을 이용해 초발수표면의 저항 저감 효과를 예측할 수 있는지에 대한 가능성을 보여준 첫 번째 연구이다.
Effective slip length 모델링 및 이를 활용한 벽함수 모델링을 적용한 k-ε 난류 모델을 바탕으로 난류 채널 유동 조건에서 시뮬레이션을 진행하였으며, 초발수표면 저항 저감 효과 예측의 정확도를 알아보았다. 그 결과 이론적인 수치 및 DNS 데이터들과 비교해 P+가 100 이하인 영역에서는 저항 저감을 효과적으로 예측하는 모습을 볼 수 있었다. 하지만 P+가 100 이상인 영역에서는 큰 오차가 발생하는 모습을 보였는데, 이러한 오차는 본 연구에서 사용된 식 (10)과 식 (11)에서 기인한 것으로 생각된다. 식 (10)과 식 (11)을 살펴보았을 때 공기층 비율 Φ가 정해진다면 effective slip length λx, λz와 P+가 선형적인 관계를 형성한다는 사실을 알 수 있는데, 이를 선행 연구 논문(4)과 비교하여 나타내면 Fig.11과 같다. Fig. 11의 DNS 데이터들은 모두 공기층 비율 Φ가 0.5인 상황이며, 다양한 Reτ 조건 하에서 계산된 effective slip length를 나타낸 것이다. Fig. 11을 보았을 때 P+가 100인 지점을 기준으로 100 이하인 경우 DNS 데이터와 비교해 큰 오차를 보이지 않지만, 100 이상인 영역으로 가면서 매우 큰 오차가 발생하는 것을 관찰할 수 있다. 따라서 이러한 부분을 보완한다면 P+가 100 이상인 영역에서 발생하는 오차를 줄일 수 있을 것으로 생각된다. 결과적으로, 저항 저감 예측의 정확도가 P+에 따라 크게 변화하는 모습을 보였지만 이를 통해 본 연구에서 제시된 방법론을 적절히 활용하면 초발수표면의 저항 저감을 효과적으로 예측할 수 있을 것이라는 가능성을 엿볼 수 있었다.
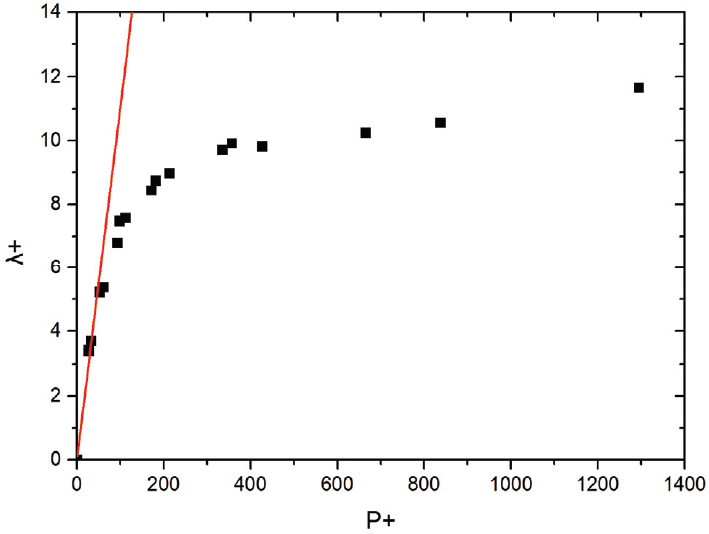
Comparison of effective slip length model against DNS data; ― effective slip length model(Φ =0.5), ■ Park et al(4)
또한 본 연구의 경우 “Ridge type” 초발수표면 구조 및 난류 채널 유동에 대해 진행된 연구로, 그 상황이 매우 제한되어 있다. 따라서 향후 추가적인 연구를 통해 정확도를 높이고 더 나아가 Ridge type이 아닌 다양한 초발수표면 구조에 대한 모델링, Blunt body 혹은 실형상 수중운동체와 같은 외부 유동 조건으로 확장시켜 적용 가능한 형태로 발전시킨다면 초발수표면의 저항 저감을 효과적으로 예측하는 고속, 고효율, 고정밀 RANS 난류 모델을 개발하는 데에 큰 도움이 될 것으로 기대된다.
Acknowledgments
이 논문은 2024년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UD230502DD)
References
-
Martell, M. B., Perot, J. B., &Rothstein, J. P., 2009, “Direct numerical simulations of turbulent flows over superhydrophobic surfaces,” Journal of Fluid Mechanics, 620, pp. 31∼41.
[https://doi.org/10.1017/S0022112008004916]

-
Rastegari, A., & Akhavan, R., 2015, “On the mechanism of turbulent drag reduction with super-hydrophobic surfaces,” Journal of Fluid Mechanics, 773, R4.
[https://doi.org/10.1017/jfm.2015.266]

-
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y., & Frohnapfel, B., 2014, “Turbulent flow over superhydrophobic surfaces with streamwise grooves,” Journal of Fluid Mechanics, 747, pp. 186-217.
[https://doi.org/10.1017/jfm.2014.137]

-
Park. H., Park. H., & Kim. J., 2013, “A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow,” Physics of Fluids, 25(11).
[https://doi.org/10.1063/1.4819144]

-
Kader, B. A., 1981, “Temperature and concentration profiles in fully turbulent boundary layers,” International Journal of Heat and Mass Transfer, 24(9), 1541-1544.
[https://doi.org/10.1016/0017-9310(81)90220-9]

-
Min, T., & Kim, J., 2004, “Effects of hydrophobic surface on skin-friction drag,” Physics of Fluids 16(7), L55-L58.
[https://doi.org/10.1063/1.1755723]

-
Voronov, R. S., Papavassiliou, D. V., & Lee, L. L., 2008, “Review of fluid slip over superhydrophobic surfaces and its dependence on the contact angle,” Industrial & Engineering Chemistry Research, 47(8), 2455-2477.
[https://doi.org/10.1021/ie0712941]

-
Vinogradova, O. I., 1999, “Slippage of water over hydrophobic surfaces,” International Journal of Mineral Processing, 56(1-4), 31-60.
[https://doi.org/10.1016/S0301-7516(98)00041-6]

-
Nouri, N. M., Sekhavat, S., & Mofidi, A., 2009, “Drag reduction in a turbulent channel flow with hydrophobic wall,” Journal of Hydrodynamics, Ser. B, 24(3)m 458-466.
[https://doi.org/10.1016/S1001-6058(11)60267-9]

-
Philip, J. R., 1972, “Flows satisfying mixed no-slip and no-shear conditions,” Zeitschrift für angewandte Mathematik und Physik ZAMP, 23, pp. 353-372.
[https://doi.org/10.1007/BF01595477]

-
Peaudecerf, F. J., Landel, J. R., Glodstein, R. E., & Luzzatto-Fegiz, P., 2017, “Traces of surfactants can secerely limit the drag reduction of superhydrophobic surfaces,” Proceedings of the National Academy of Sciences, 114(28), 7254-7259.
[https://doi.org/10.1073/pnas.1702469114]

-
Temprano-Coleto, F., Smith, S. M., Peaudecerf, F. J., Landel, J. R., Gibou, F., Luzzatto, P., 2023, “A single parameter can predict surfactant impairment of superhydrophobic drag reduction,” Proceedings of the National Academy of Sciences, 120(3), d.
[https://doi.org/10.1073/pnas.2211092120]

-
Fukagata, K., Kasagi, N., & Koumoutsakos, P., 2006, “A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces,” Physics of Fluids, 18(5).
[https://doi.org/10.1063/1.2205307]

-
Busse, A., & Sandham, N. D., 2012, “Influence of an anisotropic slip-length boundary condition on turbulent channel flow,” Physics of Fluids, 24, 055111.
[https://doi.org/10.1063/1.4719780]

-
Tomlinson, S. D., Peaudecdecerf, F. J., Temprano-Coleto, F., Luzzatto-Fegiz, P., Jensen, O. E., & Landel, J. R., 2023, “A model for slip and drag in turbulent flows over superhydrophobic surfaces with surfactant,” International Journal of Heat and Fluid Flow, 103, 109171.
[https://doi.org/10.1016/j.ijheatfluidflow.2023.109171]

- Martell, M. B., 2009, “Simulations of turbulence over superhydrophobic surfaces,” Masters Theses, Mechanical and Industrial Engineering, University of Massachusetts Amherst.
-
Jiménez, J., & Moin, P., 1991, “The minimal flow unit in near-wall turbulence,” Journal of Fluid Mechanics, 225, 213-240.
[https://doi.org/10.1017/S0022112091002033]

-
Patel, V. C., & Head, M. R. 1969, “Some observations on skin friction and velocity profiles in fully developed pipe and channel flows,” Journal of Fluid Mechanics, 38(1), 181-201.
[https://doi.org/10.1017/S0022112069000115]