천음속 축류 압축기의 블레이드 H2C 변형이 공력 성능 및 구조적 건전성에 미치는 영향

2.1 축류 압축기 모델

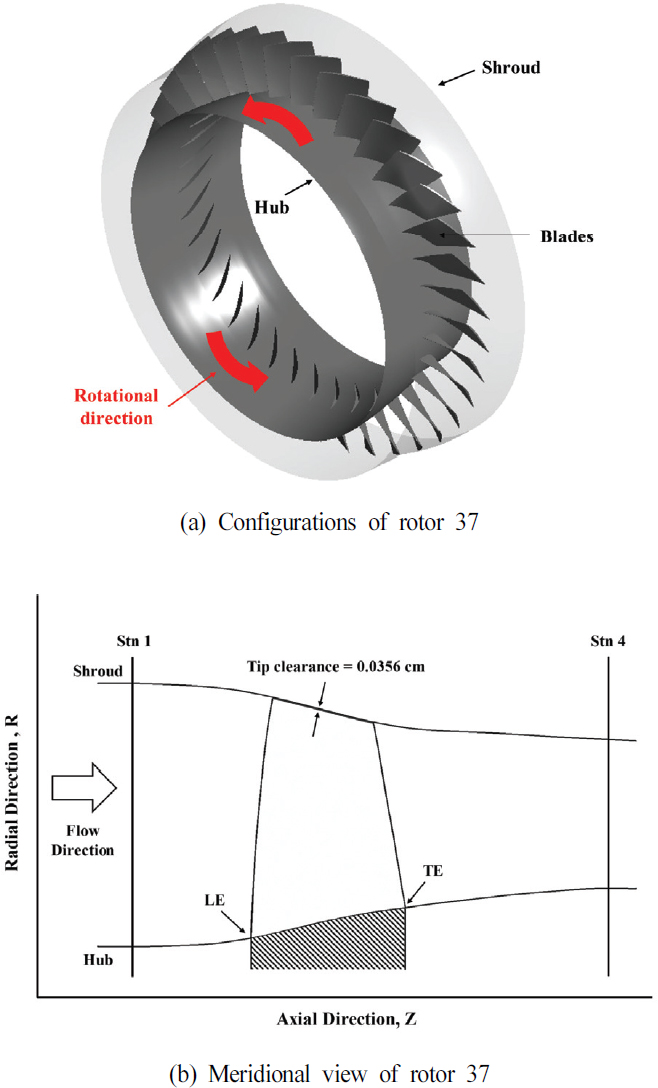
본 연구에서는 NASA의 천음속 축류 압축기 rotor 37을 연구모델로 선정하였다. 이 모델은 선행 논문 및 보고서⁽⁸⁾를 바탕으로 설계되었으며, 상세 제원은 Table 1에 기술하였다. 설계된 3차원 형상을 Fig. 1(a), 자오면(meridional plane) 기준에서의 형상 단면을 Fig. 1(b)에 나타내었다. 이 형상은 100 % 회전 속도에서 작동할 때의 hot 블레이드이며, 이를 초기 hot 블레이드로 가정하였다.

Table 1

Results of numerical analysis at the design point of NASA rotor 37

Fig. 1

Representation of NASA rotor 37

2.2 H2C(hot-to-cold) 기법

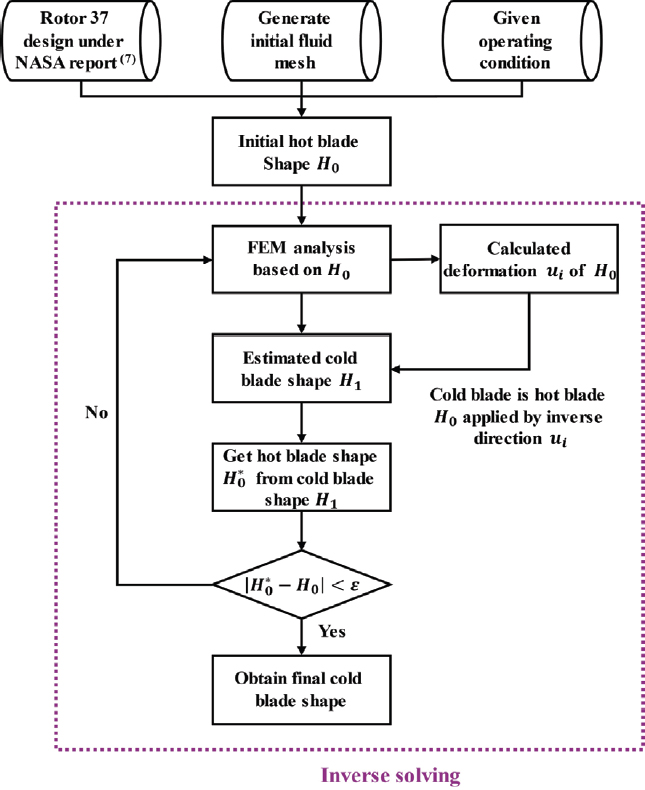
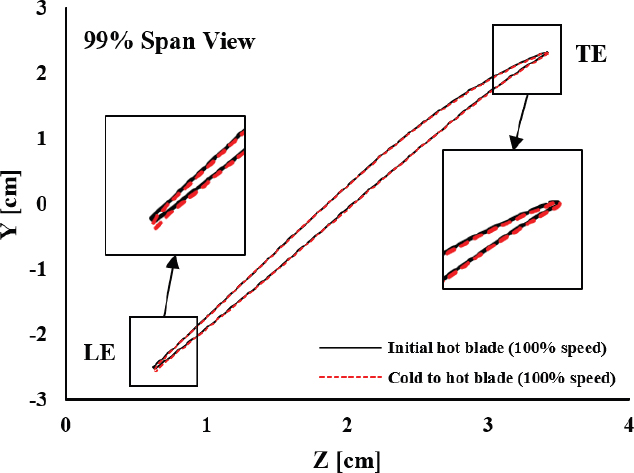
H2C(hot-to-cold)는 hot 블레이드를 cold 블레이드로 변환하는 과정을 의미한다. 본 연구에서는 초기 hot 블레이드를 cold 블레이드로 변환하기 위해 역해석 기반의 정적 구조 해석을 수행하였으며, ANSYS Mechanical R23.1을 사용하였다. 여기서 역해석은 변위 기반의 역방향 해석을 의미한다. 역해석은 5단계로 이루어지며, Fig. 2에 단계를 도시하였다. 먼저, 초기 hot 블레이드에 외부 하중을 적용하여 변형량을 계산한다. 이때 발생한 변형은 u_i로 정의한다. 그 후, 초기 hot 블레이드에 역방향으로 u_i만큼 변형시킨 형상이 cold 블레이드와 유사하다고 가정한다. 이 가정을 바탕으로 초기 cold 블레이드를 도출한다. 도출한 초기 cold 블레이드의 검증을 위해 초기 cold 블레이드로부터 hot 블레이드를 재도출하고, 재도출된 hot 블레이드와 초기 hot 블레이드를 비교하여 오차를 계산한다. 여기서, 오차는 상대 오차를 의미한다. 상대 오차가 허용 범위인 0.2 % 내에 있으면 반복 결과에 따른 최종 cold 블레이드가 도출되고, 허용 범위인 0.2 % 범위에 벗어나면 cold 블레이드를 다시 가정하는 과정부터 반복된다. H2C와는 반대로, C2H(cold-to-hot)는 cold 블레이드를 hot 블레이드로 변환하는 과정을 의미하며, 이 과정을 위해 정해석 기반의 정적 구조 해석을 수행하였다. 여기서 정해석은 변위 기반의 정방향 해석을 의미한다. 초기 hot 블레이드와 cold 블레이드로부터 얻은 hot 블레이드를 99 % 스팬 방향에서 비교한 결과를 Fig. 3에 도시하였다. 두 형상 간의 차이는 해석 과정에서 발생할 수 있는 오차이거나 ANSYS Mechanical R23.1의 역해석 기능의 한계로 발생한 것으로 보인다.

Fig. 2

Flow chart of H2C process by inverse solving

Fig. 3

Comparison of initial hot blade and cold-to-hot blade

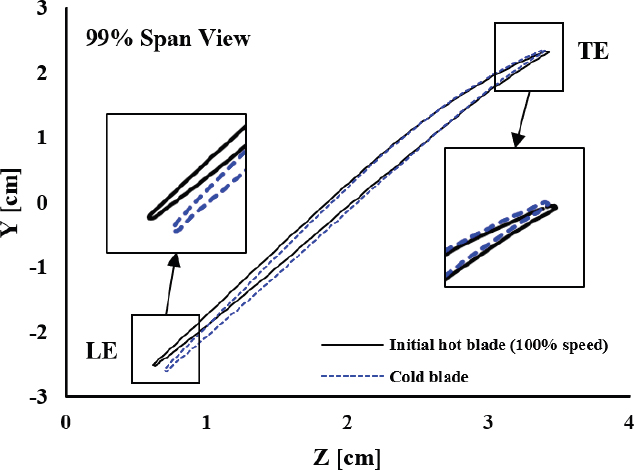
그러나, 전연(leading edge)과 후연(trailng edge)에서의 차이는 각각 0.127mm, 0.021mm로 계산되었으며, 이는 블레이드 길이를 고려할 때 전연에서는 0.18 %, 후연에서는 0.042 %에 해당한다. 이러한 수준의 오차는 블레이드 간의 변환 기법이 검증되었다고 판단할 수 있다. 초기 hot 블레이드와 cold 블레이드를 99 % 스팬 방향에서 비교한 결과는 Fig. 4와 같으며, hot 블레이드와 cold 블레이드의 변형 차이를 확인할 수 있다.

Fig. 4

Comparison of initial hot blade and cold blade

2.3 단방향 유체-구조 연성 해석

작동 조건에 따른 hot 블레이드를 도출하기 위해서는 외부 하중(공력, 열부하, 원심력)을 고려해야 하므로 유체-구조 연성 해석을 수행해야 한다. 유체-구조 연성 해석은 단방향과 양방향으로 나뉜다. 단방향은 구조 모델의 변위가 유동장에 미미한 영향을 미칠 때 사용하며, 양방향은 반대로 구조 모델의 변위가 유동장에 미치는 영향이 클 때 적용한다. 본 연구에 사용된 NASA Rotor 37의 재질은 200-maraging steel⁽⁹⁾로 큰 밀도와 강성을 가지면서 구조 모델의 변형이 크지 않으므로 선형으로 가정할 수 있다. 이에 따라 유동 해석으로부터 얻은 압력과 열을 구조 모델 표면에 전달하여 열 유동 및 원심력에 의해 변형되는 단방향 유체-구조 연성 해석을 수행하였다.

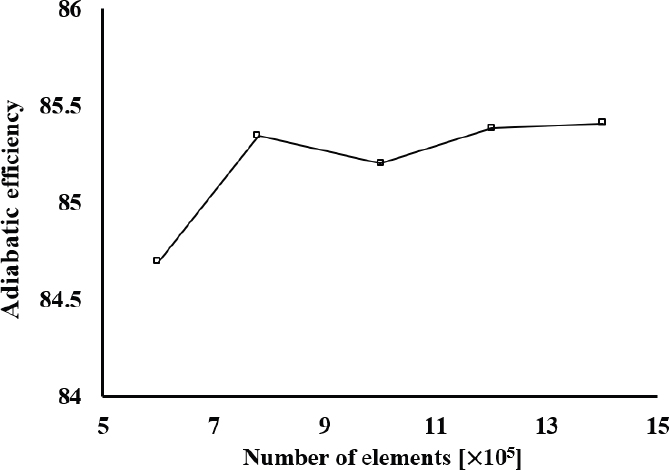
유동 해석을 위한 격자 생성은 ANSYS TurboGrid 23 R1을 활용하였다. 블레이드 표면을 제외한 영역은 H형 격자로 형성하였고, 허브, 슈라우드와 블레이드 벽면에서의 y+ 값이 1을 넘지 않도록 격자를 설정하였다. 격자 개수에 따른 수치해석의 신뢰성을 평가하기 위해 압축기 주요 성능 지표인 단열 효율(η) 기준으로 격자 의존성을 검토하였다.

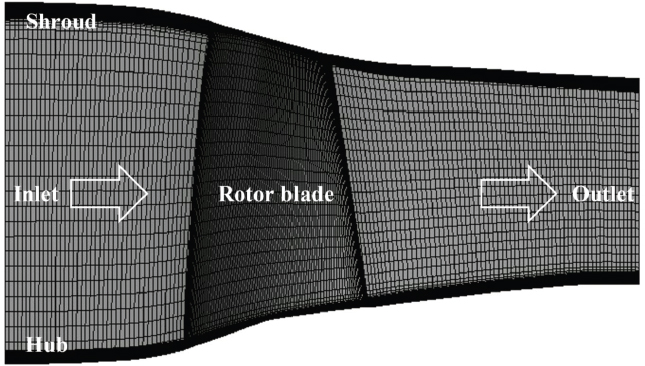
여기서 p_o,4는 출구 압력, p_i,1는 입구 압력, γ는 비열비, T_o,4은 출구 온도, T_i,1은 입구 온도를 의미한다. 검토 결과는 Fig. 5와 같으며, 수렴성이 보이는 약 120만 개 격자를 수치해석을 위한 격자로 선정하였다. 선정된 격자의 통로 영역의 스팬 방향 격자 층 개수는 50개이며, 슈라우드 간극 영역의 격자 층 개수는 20개이다. 선정된 격자가 구성된 모델은 Fig. 6에 나타내었다. 유동 해석은 ANSYS CFX 23 R1을 활용하였다. 작동유체는 이상 기체인 공기를 사용하였고, 정상상태로 가정하였다. 지배 방정식은 3차원 나비에-스토크스 방정식과 에너지 방정식이 사용되었고, 난류 모델은 압력 구배 흐름에 대해 정확하게 예측하는 것으로 알려진 k–ω SST를 사용하였다⁽¹⁰⁾. 블레이드 입구 경계면에는 전온도 288.15K와 전압력 101.325kPa을 설정하였다. 블레이드 출구 경계면에는 정압 조건을 부여하여 초킹 영역부터 서지 영역까지 정압을 상승시키며 계산을 수행하였다. 그 외 벽면은 점착 조건을 적용하였고, 상세한 경계조건은 Table 2에 도시하였다.

Fig. 5

Results of grid dependency test

Fig. 6

Grid systems for numerical analysis of CFD

Table 2

Boundary conditions applied in this study

구조 해석을 위한 격자 생성은 ANSYS Meshing을 이용하였으며, 생성된 격자는 Fig. 7에 도시하였다. 경계조건으로 블레이드의 기하 중심 기준으로 외부 점을 생성하고, 이 점에 대해 회전 및 축 방향을 구속하여 중심에서 회전하는 블레이드를 모사하였다.

Fig. 7

Grid systems for numerical analysis of static structure

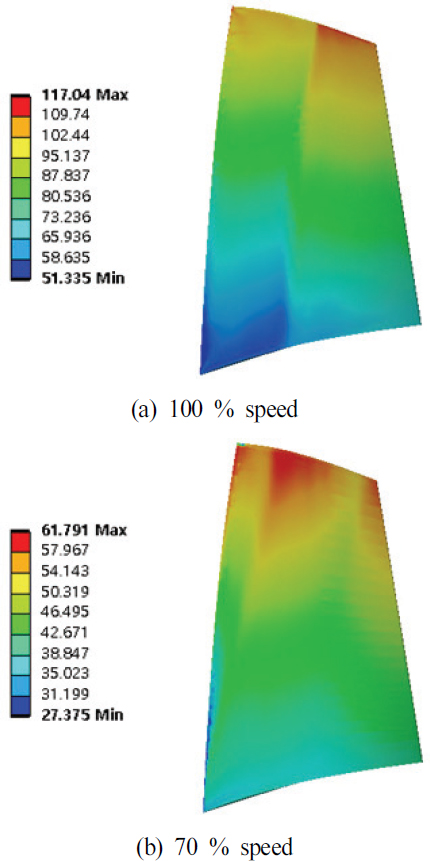
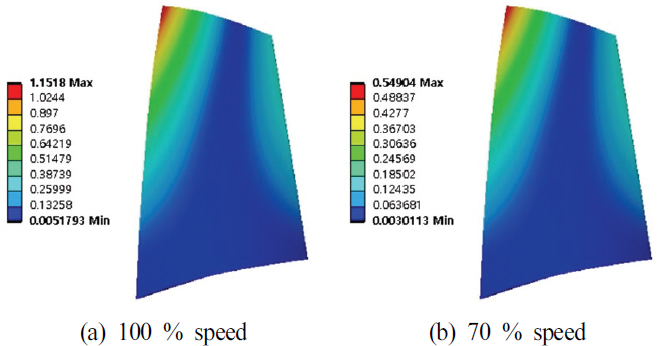
또한, 정상상태 유동 해석 결과인 표면 온도 분포를 활용해 열전도 해석을 수행하여 블레이드의 전체 온도 분포를 계산하였다. 블레이드의 전체 온도 분포는 Fig. 8에 나타내었다. 100 % 회전 속도 조건에서 블레이드의 최대 온도는 블레이드 팁의 전연에서 117.04℃, 70 % 회전 속도 조건에서 블레이드의 최대 온도는 블레이드 팁의 전연에서 61.791℃로 계산되었다. 구조 해석의 외부 하중 조건으로 블레이드의 전체 온도 분포, 표면 압력 분포와 원심력을 고려하였다. 연구에 사용된 블레이드의 재질은 200-maraging steel로 Piollet 등⁽⁹⁾의 평균 물성값을 사용하였다. 사용된 값은 탄성계수 180GPa, 푸아송비 0.3, 밀도 8,000kg/m³, 항복 강도 1.38GPa이다. 열전도계수는 19.6W/m⋅K를 적용하였으며, Table 3에 나타내었다. 이와 같은 조건으로 cold 블레이드에 70 % 회전 속도 조건에 대한 단방향 유체-구조 연성 해석을 수행하여 70 % 회전 속도에 따른 hot 블레이드를 도출하였다.

Fig. 8

Blade surface temperature distribution

Table 3

Material properties of NASA rotor 37

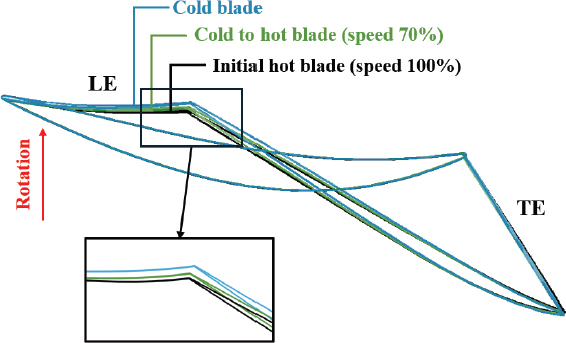
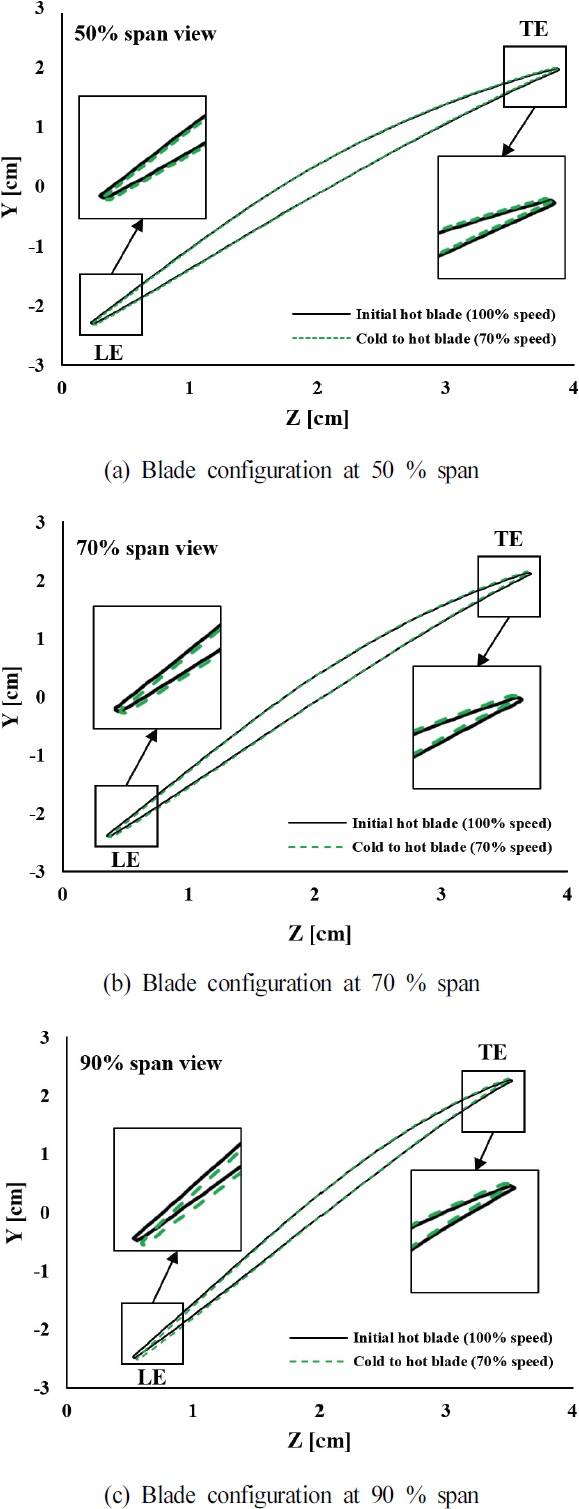
변형은 주로 블레이드 팁에서 발생하며, 이러한 변형은 블레이드의 속도에 따라 다르게 나타난다. Cold 블레이드를 기준으로 할 때, 100 % 회전 속도에서 hot 블레이드 팁의 전연은 약 1.11mm, 블레이드 팁의 후연은 0.35mm가 변형되었다. 70 % 회전 속도에서는 hot 블레이드 팁의 전연은 약 0.52mm, 블레이드 팁의 후연은 약 0.17mm가 변형되었다(Fig. 9 참조). 전연은 회전할 때 유동이 처음 접하는 부분으로 공기 흐름이 급격하게 바뀜에 따라 높은 압력 구배와 공기역학적 힘으로 후연에 비해 큰 하중을 받게 된다. 또한, 전연은 후연에 비해 회전 중심에서 떨어져 있으므로 원심력에 의한 영향도 크게 받으므로 변형이 크게 발생한다.

Fig. 9

Comparison of three different blade shapes

반면, 후연은 상대적으로 낮은 압력의 힘을 받으므로 적은 변형이 발생하게 된다. 70 % 회전 속도의 hot 블레이드와 100 % 회전 속도에서의 초기 hot 블레이드를 스팬 방향으로 비교한 결과를 Fig. 10에 나타내었다. 특히, 후연의 변형은 50 %, 70 %, 90 % 스팬에서 점차 증가하고, 전연의 변형은 상대적으로 적지만, 50 % 스팬 이후 점차 증가하는 경향을 보였다.

Fig. 10

Comparison of blades based on rotational speed

3.1 유동 해석 결과

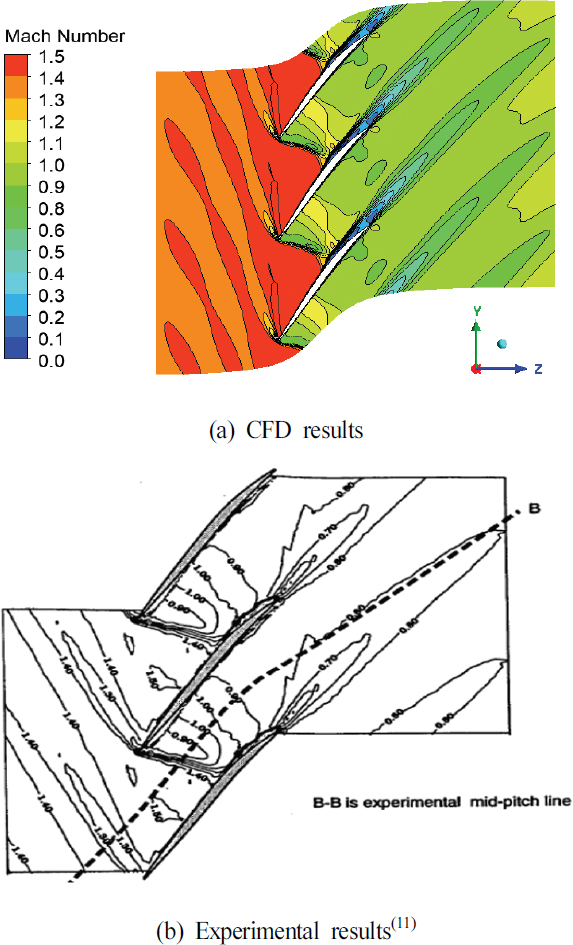
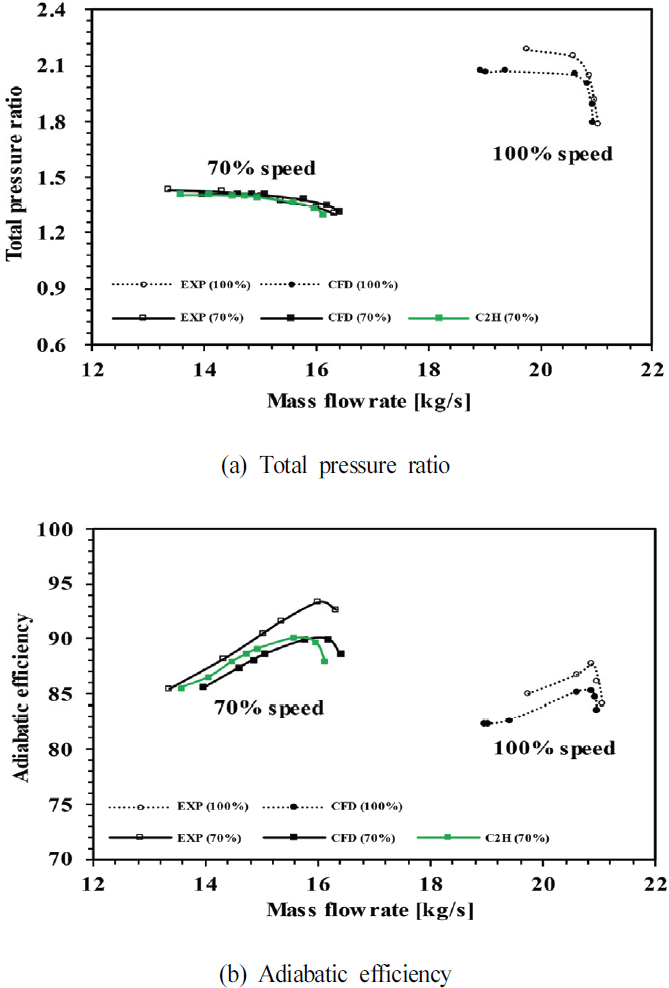
초기 hot 블레이드를 검증하기 위해 최고 단열 효율 조건에서의 마하수를 70 % 스팬에서 해석 및 실험 결과⁽¹¹⁾를 비교하였다. 비교한 결과는 Fig. 11에 도시하였으며, 실험 결과의 마하수와 유사한 것을 확인할 수 있다. 또한, 100 % 회전 속도에서 질량 유량에 따른 성능 곡선을 나타내어 실험 결과와 비교하여 검증하였다. 압축기 성능 지표로 전압력비와 단열 효율을 선정하였으며, 질량 유량에 따른 각 성능 지표 곡선을 Fig. 12에 나타내었다. 초기 hot 블레이드는 최대 단열 효율이 85.4 %이며, 최대 단열 효율 조건에서 전압력비는 2로 계산되었다. 이는 각 실험 결과인 87.6 %와 2.056에 근접한 결과를 보였다. 이 검증을 바탕으로 70 % 회전 속도에서 초기 hot 블레이드와 작동 조건에 따른 hot 블레이드의 유동 해석을 통해 공력 성능을 비교하였다. 70 % 회전 속도에서의 초기 hot 블레이드의 최대 단열 효율은 90 %이며, 전압력비는 1.35로 계산되었다. 반면, 같은 회전 속도에서 작동 조건에 따른 hot 블레이드의 최대 단열 효율은 90.1 %, 전압력비는 1.37로 초기 형상 대비 높은 공력 성능을 나타냈다.

Fig. 11

Comparison of blade Mach number contours at 70 % span

Fig. 12

Comparison of the measured data(8) and numerical reults

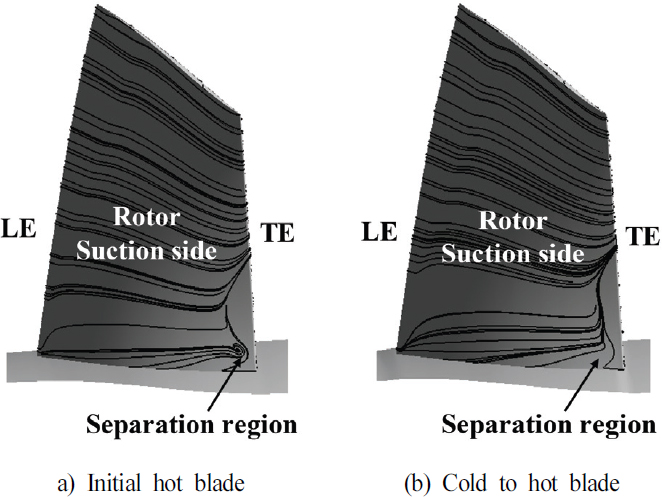
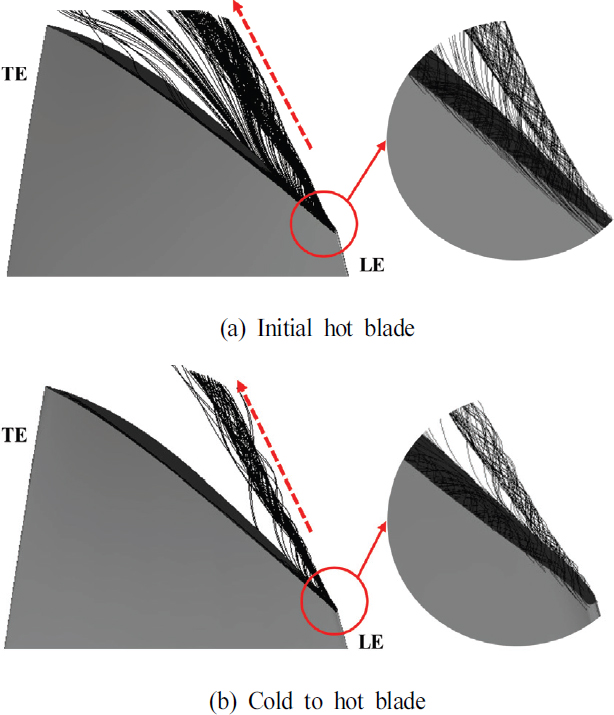
또한, 작동 조건에서의 hot 블레이드가 실험 결과와 더 일치하는 결과를 보였다(Fig. 12 참조). 형상에 따른 단열 효율 차이는 유동 손실로 인해 발생한다. 이러한 손실의 영향을 분석하기 위해 고압 영역에서 흡입면과 허브 사이에 발생하는 코너 박리(corner separation)와 팁과 슈라우드 사이로 유동이 새어 나가는 현상인 팁 간극 누설 유동(tip clarence leakage flow)을 확인하였다. 코너 박리는 통로를 막아 손실을 발생시키는 현상으로 형상에 따라 발생하는 코너 박리를 Fig. 13과 같이 블레이드 표면의 유선으로 나타내었다. 초기 hot 블레이드에서 발생한 코너 박리가 작동 조건에 따른 hot 블레이드에서 완화되는 것을 확인할 수 있다.

Fig. 13

Comparison of streamline distributions at 70 % rotational speed

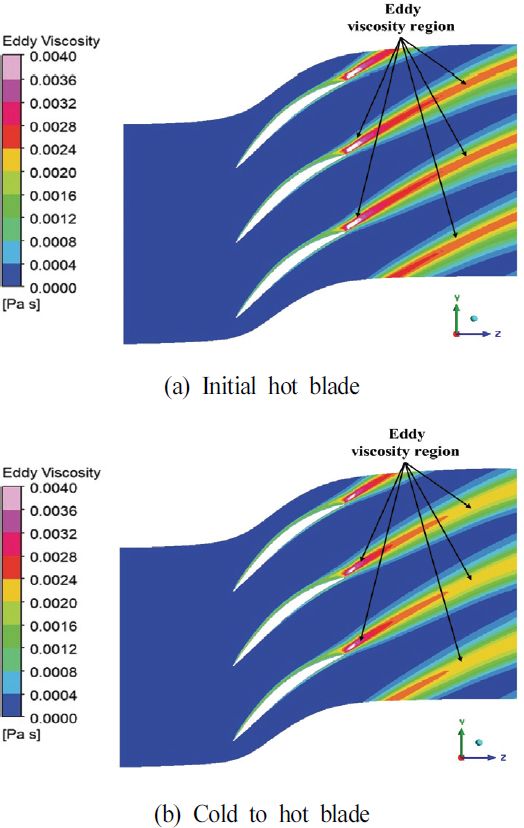
또한, 코너 박리가 발생한 10 % span 방향에서의 와류 점성 계수를 비교하였다. 여기서 와류 점성 계수는 유동의 불안정성과 관련된 인자로 와류 점성 계수가 작을수록 유동이 안정하다고 판단한다. 와류 점성 계수의 비교 결과는 Fig. 14에 나타내었다. 결과와 같이 초기 hot 블레이드에서 높은 와류 점성 계수를 보였던 영역이 작동 조건에 따른 hot 블레이드에서 낮아진 것을 확인할 수 있다. 팁 간극 누설 유동은 좁은 틈을 통과하면서 블레이드의 회전 방향의 반대로 와류가 형성되는 현상으로 형상에 따른 간극 누설 흐름은 Fig. 15에 도시하였다. 초기 hot 블레이드는 블레이드 팁 근처에서 복잡하고 불안정한 흐름을 보였으며, 표면에서 명확한 흐름 분리 패턴을 나타낸다. 반면, 작동 조건에 따른 hot 블레이드에서는 블레이드 팁 근처에서의 흐름이 비교적 안정화되는 것을 보여준다.

Fig. 14

Comparison of eddy viscosity contours at 10 % span with 70 % rotational speed

Fig. 15

Comparison of tip leakage flow results at the blade tip

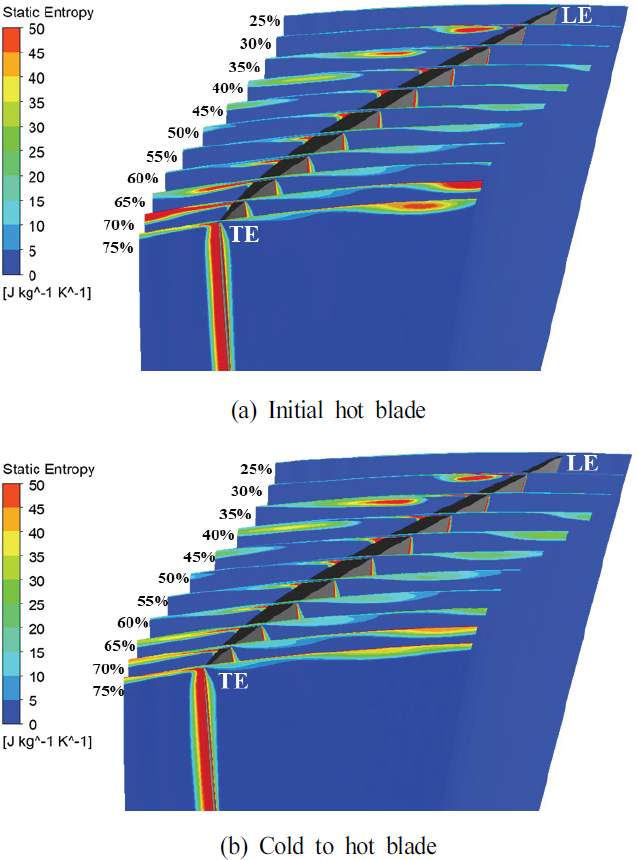
블레이드 팁 근처의 복잡한 패턴은 공기 누설이 발생함을 나타내며, 이는 초기 hot 블레이드가 더 많은 공기 누설을 발생함을 알 수 있다. 즉, 초기 형상과 작동 조건에 따른 형상의 유동각 차이로 인해 팁 간극 누설 유동에 영향을 미치는 것을 확인하였다. 이러한 누설에 의한 유동 손실은 정적 엔트로피와 관련이 있다. 블레이드의 경계층에서 난류 강도의 차이로 인하여 에너지가 손실되며, 그 결과로 엔트로피가 증가하게 된다. Fig. 16에서 초기 형상의 블레이드 팁 근처에서 정적 엔트로피가 더 큰 것을 확인할 수 있으며, 이는 에너지 손실이 더 발생함을 의미한다. 이러한 결과에 따라 블레이드의 형상 변화는 유동 안정성 및 손실에 영향을 미치므로 정확한 공력 성능의 평가를 위해서는 작동 조건에 따른 형상을 고려해야 함을 알 수 있다.

Fig. 16

Comparison of static entropy results at the blade

3.2 구조 해석 결과

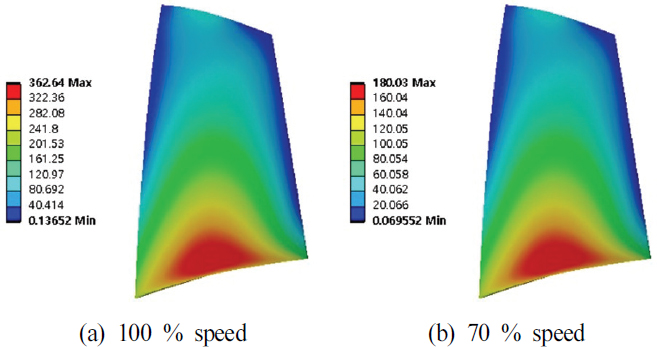
구조 건전성 평가를 위해 cold 블레이드를 기준으로 작동 조건(100 %, 70 % 회전 속도)에 따라 단방향 유체-구조 연성 해석을 수행하였다. 이 과정에서 3.1절에서 언급한 최대 단열 효율 조건에 해당하는 유동 해석으로부터 얻은 표면 온도 분포를 활용해 열전도 해석을 수행하고, 계산된 블레이드의 전체 온도 분포를 열부하 조건으로 적용하였다. 또한, 유동 해석 결과의 압력장과 원심력에 의한 강성 효과도 함께 고려하였다. 정적 구조 해석 결과는 Figs. 17, 18에 나타냈다. 최대 등가 응력은 von Mises 응력을 분석한 결과 블레이드-허브 접합부와 블레이드 흡입면과 허브 경계층이 만나는 코너에서 발생하였고, 최대 변위는 블레이드 팁에서 발생하였다. 100 % 회전 속도에 따른 블레이드의 최대 등가 응력은 블레이드-허브 접합부에서 약 362.64MPa, 코너에서 약 361.71MPa였으며, 최대 변위는 블레이드 팁에서 약 1.15mm이다.

Fig. 17

Static structural analysis results of total deformation

Fig. 18

Static structural analysis results of von Mises stress

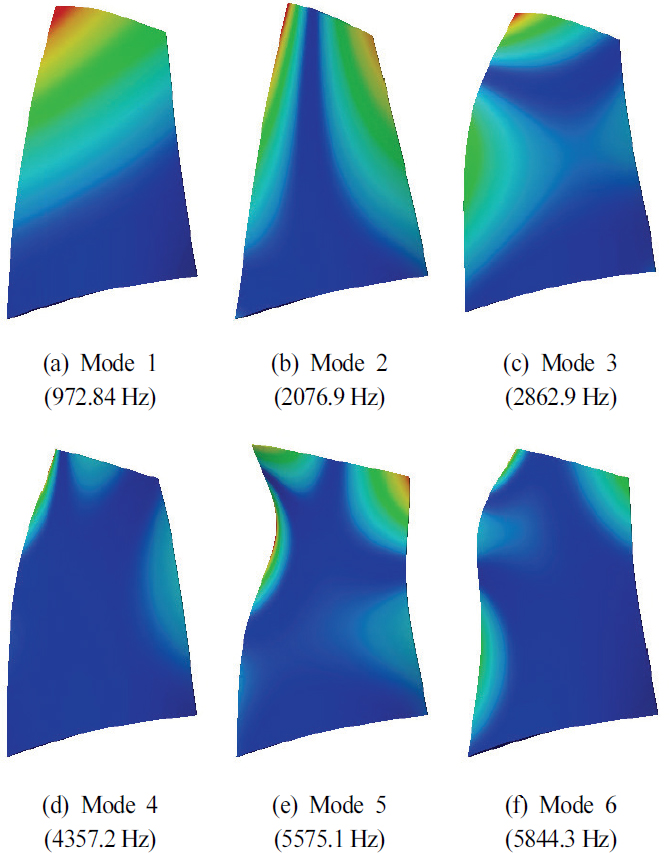
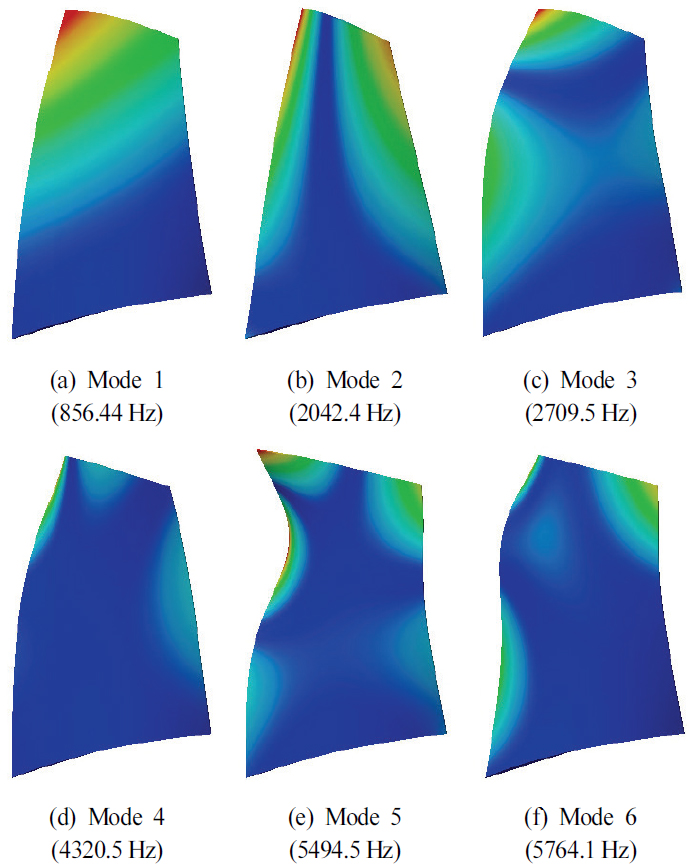
반면에, 70 % 회전 속도에 따른 블레이드의 최대 등가 응력은 블레이드-허브 접합부에서 약 180.03MPa, 코너에서 약 177.59MPa였으며, 최대 변위는 블레이드 팁에서 약 0.55mm로 나타났다. 회전 속도 증가에 따라 원심력이 증가하므로 70 % 회전 속도보다 100 % 회전 속도에서 약 0.6mm의 변형이 더 발생하였다. 이에 따라 블레이드-허브 접합부와 코너에서 응력이 약 2배 집중되는 결과를 보였다. 이러한 결과는 응력 집중 부위와 변위 특성을 파악하여 구조적으로 취약한 부분을 판단할 수 있으며, 회전 속도가 증가할수록 구조적으로 취약함을 알 수 있다. 작동 조건에 따라 고유진동수가 바뀌므로 공진 발생 가능성에 대해 평가를 수행해야 한다. 여기서, 공진은 엔진 차수(engine order, EO)인 회전주파수의 정수배 성분과 고유진동수와 교차할 때 발생한다. 이러한 공진을 평가하기 위해 캠벨 선도(campbell diagram)가 사용되며, 이 선도의 x축은 회전 속도를, y축은 고유주파수를 나타낸다. 회전 속도에 대한 고유진동수의 변화를 파악하기 위해 전하중 모드(pre-stressed modal) 해석을 통해 작동 조건에 따른 1∼6차의 진동 모드 형상을 나타내고, 블레이드의 고유진동수를 추출하였다. 1∼6차의 모드 형상은 Figs. 19, 20에 나타내었다. 1차 진동 모드는 회전축의 접선 방향의 굽힘(bending) 모드에 해당하며, 2차 진동 모드는 비틀림(torsion) 모드에 해당한다. 이러한 1차와 2차 진동 모드는 블레이드의 기본적인 모드 형상을 나타내며, 3차 진동 모드부터 여러 번의 굽힘 혹은 비틀림이나, 굽힘과 비틀림이 동시에 나타나는 복잡한 모드 형상이 나타난다. 작동 조건에 따른 진동 모드 형상은 상당히 유사한 결과를 나타냈다.

Fig. 19

Cold blade mode shapes at 100 % speed

Fig. 20

Cold blade mode shapes at 70 % speed

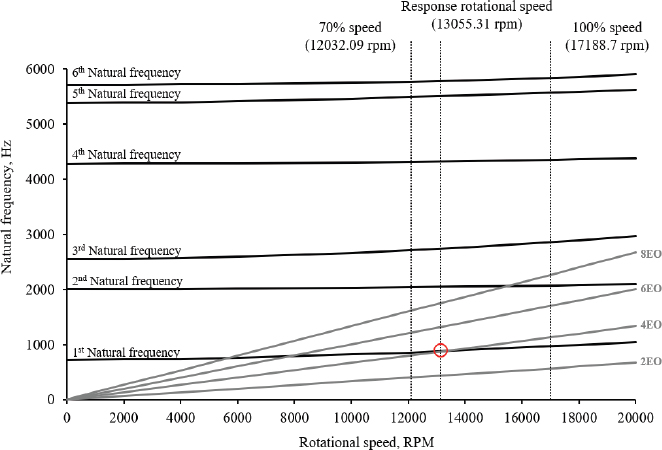
원심력에 의한 차이는 고유진동수에 영향을 미치므로 고유진동수를 계산해야 한다. 계산된 고유진동수는 Table 4에 나타내었고, 블레이드의 고유진동수는 회전 속도에 따라 증가하는 결과를 확인할 수 있다. 고유진동수의 증가는 회전으로 인해 블레이드에 가해지는 하중이 증가함에 따라 강성이 높아지는 응력의 강성 보강 효과(stress stiffening)가 발생했기 때문이다. 또한, 비틀림의 영향이 큰 2차, 4차 진동 모드에서 고유진동수의 증가율이 높은 것을 확인할 수 있으며, 복잡한 진동이 발생하는 5차와 6차 진동 모드에서는 2차, 4차 진동 모드 대비 고유진동수의 증가율이 낮아지는 것을 확인할 수 있다. 이러한 고유진동수의 차이는 회전수와 관련하여 공진에 영향을 주므로 캠벨 선도를 이용하여 영향성을 평가하였다. 도출된 캠벨 선도는 Fig. 21에 나타내었다. 여기서 x축 방향의 수평선은 블레이드의 고유진동수를 나타내며, 대각선은 엔진 차수로 회전주파수의 정수배 성분을 의미한다. 캠벨 선도 내 작동 조건인 회전 속도를 점선으로 표시하였고, NASA Rotor 37 블레이드에서 발생하는 엔진 차수⁽⁸⁾를 고려하여 공진을 평가하였다. 평가한 결과, 70 % 회전 속도에서 1차 모드의 고유진동수와 4EO에서 공진 발생 가능성이 확인되었다. 그러나, 1차 모드의 고유진동수와 4EO가 교차하여 공진이 발생하는 회전 속도는 약 13,055.31rpm이며, 70 % 회전 속도를 기준으로 ±8 %의 마진을 고려하였을 때 공진이 발생하지 않음을 확인하였다.

Table 4

6 mode frequencies with cold blade according to rotational speeds

Fig. 21

Campbell diagram of the cold blade