정수장 관내 직조 금속 여과망의 손실 특성에 관한 연구
Abstract
This study aims to analyze the flow characteristics of filter mesh assemblies used in advanced water treatment plants. In these facilities, filter meshes are essential for removing suspended solids and organic matter that are not filtered out during sedimentation. Various installation methods and types of metal screens exist; however, pressure losses from the design and operation of these meshes significantly impact water treatment efficiency. Existing research primarily focuses on pressure drop equations and modifications to friction factors for porous media, but variability in testing conditions and flow characteristics limits their applicability. This study utilizes Computational Fluid Dynamics (CFD) to simulate the flow through filter mesh assemblies and conducts experimental validation using empirical velocity profiles within the conduits. It is through this research that pressure drop models based on filter mesh assemblies and porosity are proposed, providing foundational data for optimized design in water treatment facilities.
Keywords:
Filter mesh, Pressure drop, Porous media, Woven metal screen, Conduit flow, Water treatment plant키워드:
여과망, 압력 손실, 다공성 매질, 직조 금속 스크린, 관로 유동, 정수장1. 서 론
정수장 내 여과망(Filter mesh)은 고도정수처리장의 마지막 여과 단계에 설치되어 침전지에서 걸러주지 못한 현탁물질, 유충, 일부 유기물과 무기물을 제거하는 역할을 한다.(1) 정수장에 사용되는 여과망 시스템은 설치 방식에 따라 배관 설치형, 큐브박스형(Cube-box type), 필터 플랜지형(Flange type) 등이 있으며 그중 관리가 편리하고 별도의 수로 공사가 필요 없는 배관 설치형이 많이 사용된다.
직조 금속 스크린(Woven metal screen)은 정수장에 사용되는 대표적인 여과망으로, 화학적, 열적, 기계적 내구성이 뛰어나고 배치가 쉬우며, 공극률(Porosity)에 비해 높은 투과성(Permiability)을 특징으로 한다.(2) 직조 금속 스크린은 직조 패턴에 따라 평직(Plain weaves), 능직(Twill weaves), 포드리니어(Fourdrinier), 더치(Dutch) 등으로 분류된다.(3)
직조 금속 스크린 여과망은 정수 과정에서 수송 관로에 수직으로 설치되어 침전지에서 거르지 못한 부유물을 제거하는 역할을 하지만, 관로 내 구조물로써 난류, 단면적 축소, 압력 차이 등의 현상을 동반하여 유체 에너지 손실을 일으킨다. 이러한 손실은 여과망의 설계 변수에 따라 크게 달라지며, 사용 시간에 따른 단면 폐색 현상으로 가중되어 심각할 경우 여과망의 파손, 정수지 수위의 급격한 변화를 발생시킨다.(4)
따라서, 여과망의 압력 손실 특성은 정수 과정에서 매우 중요하며 관련된 실험적 연구는 다음과 같다. Ergun(5)은 다공성 매질(Porous media)을 튜브 다발로 가정하여 차압을 점성항과 관성항의 합으로 나타내었다. Armour(3) 등은 5가지 패턴의 직조 금속 스크린에 대한 실험을 진행하였으며, 공극률과 유속, 설계 변수(Design parameter)에 따른 차압(Pressure drop) 방정식을 도출하였다. 이외에 Sodre(6) 등은 벽효과(Wall effect)를 고려하기 위한 수정된 레이놀즈수(Reynolds number, Re)를 제안하였으며, Wu(2) 등은 Ergun 방정식의 관성항을 수정하여 높은 Re에서 정확성을 확인하였다.
위 연구들은 직조 스크린의 실험을 통한 마찰계수(Friction factor) 수정에 집중되었다. 그러나 위 연구 방법은 조건별 시험이 동반되어 많은 시간이 필요하며, 스크린의 복잡한 형상을 나타내는 데 한계가 있다.
따라서, CFD(Computational fluid dynamics)를 이용한 근사 모델 개발과 최적화 연구가 진행되었다.
Teitel(7)은 스케일 차이가 큰 모델에서 직조 스크린을 다공성 매질로 가정하여 유동 특성을 나타낼 수 있음을 증명하였다. 또한, 공극률에 따라 투과성과 관성 계수(Inertial factor)를 수정하는 방법을 제시하였다. Sun(8) 등은 세 가지 매개변수(와이어 직경, 메시 간격, 메시 공극)에 따른 수정된 Re를 제안하였으며, 상사 법칙을 적용하여 직조 스크린으로 단순화할 수 있음을 확인하였다. Iwaniszyn(9) 등은 서로 다른 와이어 직경과 공극률 모델에 대한 시험을 진행하여 단일 패턴 CFD를 통해 검증하였다.
위와 같이 직조 스크린에 대한 실험 및 수치해석 연구가 많이 진행되었지만, 정수장 내 유동을 모사하는 데는 몇 가지 문제가 존재한다. 첫째, 작동 유체, 가압 방식, 관로 직경에 따라 연구 결과가 다르다. 둘째, 관로 내 유동과 벽면 마찰을 고려하지 않았다. 셋째, 현재까지 대상 여과망 조립체에 관한 연구 결과가 부족하다.
정수장 내 여과망은 기존 연구된 직조 스크린과 설계 변수가 매우 다르며, 정수장 환경에 따라 유동 특성이 달라지기 때문에, 시험과 수치해석이 필요하다.
본 연구는 고도정수처리장에서 사용되는 여과망 조립체의 유동 특성에 관한 수치 모델 연구를 목표로 하며 여과망 조립체의 CFD 해석이 수행된다. 또한, 관로 내 환경은 속도 프로파일 경험식을 응용하며, 축소 관로 시험을 진행하여 수치해석 모델과 비교 검증한다. 최종적으로 정수장 환경에서 여과망 조립체 및 공극률에 따른 차압 모델을 도출한다.
2. 여과망 차압 모델
2.1 모델 정의
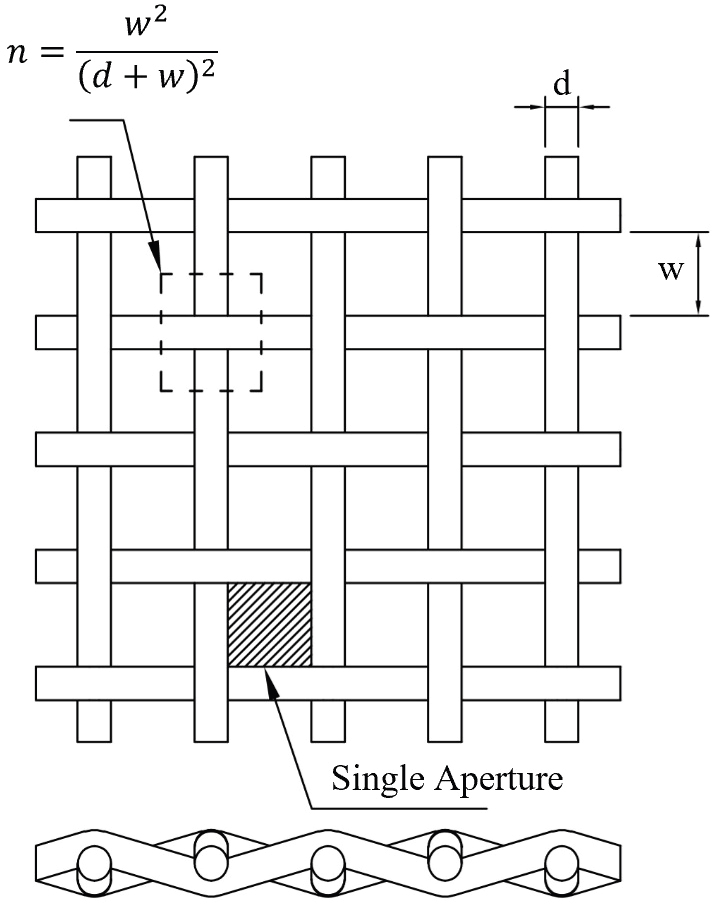
본 연구에서는 여과망으로 스테인리스 선재 계열의 정사각 평직 스크린을 사용한다. Fig. 1은 여과망의 형상을 나타낸 것으로 설계 변수는 와이어 직경(d)과 공극 너비(w)로 구성된다. 여과망은 단일 공극(Single aperture)의 패턴 형상으로 이루어져 있으며, 그에 따른 공극률(Porosity, n)을 계산하면 다음과 같다.
| (1) |
Fig. 2는 정수장에 사용되는 여과망 조립체의 사진으로, 정수용 여과망(Filter mesh)을 중심으로 형상 유지 및 강성을 높이기 위한 구조용 망(Reinforcement net)이 전/후에 있다. 해석 모델은 그림과 같지만, 두 망의 척도 차이로 전체 모델을 해석하기에 어려움이 있다. 따라서, 모델 정의를 위해 Re에 대한 상사성 해석이 필요하다.
| (2) |
| (3) |
식(2)와 식(3)은 각각 관로 유동과 여과망 유동에 대한 Rep, Res를 나타낸다. 여기서, 관로 평균 유속(Average velocity of conduit, ), 여과망 평균 유속(Average velocity of filter mesh, ), 작동 유체의 밀도(Density, ρ), 점도(Viscosity, μ), 관로의 수력학적 직경(Hydraulic diameter of conduit, dp), 여과망의 수력학적 직경(Hydraulic diameter of filter mesh, ds)를 나타낸다. 작동 유체가 비압축성이라 가정하면 여과망을 지나는 평균 유속은 다음과 같다.
| (4) |
식(4)를 식(3)에 대입하여 Res를 수정하면 식(5)와 같다.
| (5) |
상사성 해석 결과, Res는 여과망 공극률과 관로 평균 유속, 여과망의 와이어 직경에 관한 함수임을 확인하였다. 따라서, 본 연구에서는 구조용 망의 단일 공극을 모델로 설정하여 해석을 진행한다.
2.2 차압 특성 분석
여과망은 배관 내 설치되었을 때, 점성 손실(Viscous loss)과 단면 축소, 유속 변화에 따른 부가적인 동적 손실(Dynamic loss)을 일으킨다. 이러한 손실 특성은 기존 다공성 매질과 유사한 부분이 존재하며 관련된 연구가 진행되었다. Miguel(10) 등은 정적 상태의 비압축성 유동을 Forchheimer 방정식으로 나타냈다.
| (6) |
식(6)은 다공성 매질의 차압 방정식 중 1차원 유동일 때 일반적으로 사용된다. 여기서 K는 투과성 계수(Permiability factor)로 물질 전달 정도를 나타내며, Y는 관성 계수, u는 유동 속도를 나타낸다. 직조 스크린은 와이어 직경, 직조 방식, 공극 크기 등 설계 매개변수에 따라 유동 특성이 달라진다. 따라서, K와 Y는 위 변수들을 포함할 수 있는 공극률에 대한 지수함수로 연구되었다.(7),(10),(11),(12)
| (7) |
여기서 계수 A, B와 지수 α, β는 스크린 고유 특성으로 CFD 해석 결과를 회귀 분석하여 도출한다.
2.3 관내 유동을 고려한 차압 모델
여과망이 설치되는 관로는 정수장 환경에 따라 유동 조건이 다르므로 관로 내 벽 마찰(Wall friction)을 고려해야 한다. 본 연구에서는 관내 유동을 모사할 수 있는 경험식을 사용하여 수정된 차압 방정식을 제시한다.
Nikuradse(13)는 난류 유동에서 거친 파이프의 마찰계수(Friction factor, λ)를 정의하였다. 난류 유동에서 마찰계수는 Re에 독립적이며 시험을 통해 식(8)과 같이 제안하였다.
| (8) |
여기서 d는 파이프의 직경, e는 사립 조도(Sand grain roughness)로 마찰계수는 직경에 대한 상대 조도(Relative roughness, d/e) 값으로 정해진다. 벽면 속도 분포를 나타내기 위한 마찰 속도(Friction velocity, u*)는 벽 법칙(Law of the wall) 따라 식(9)와 같다.
| (9) |
식(8)을 식(9)에 대입하여 속도 프로파일 식을 도출할 수 있으며 시험 결과를 토대로 각 상수를 결정한 경험식은 식(10)과 같다.
| (10) |
여기서 u는 벽면에서의 거리 y에서 유동 방향 속도를 나타낸다. 식(6)을 y에 관한 함수로 변경하여 속도 프로파일에 따른 여과망 차압은 다음과 같이 도출할 수 있다.
| (11) |
식(11)에서 여과망 직전 유속이 속도 프로파일과 같다고 가정하고 에너지 보존법칙에 따라 나타내면 다음과 같다.
| (12) |
3. CFD 해석 방법
본 연구에서 여과망 손실 특성 분석과 시험 검증은 CFD 해석을 기반으로 하며 해석 코드는 상용 프로그램인 ANSYS Fluent 24R1을 사용한다.
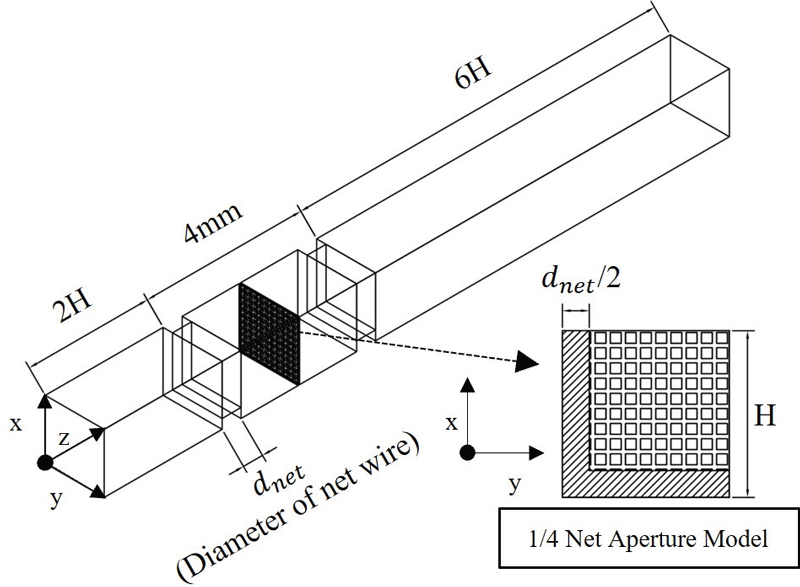
2.3의 정의에 따른 여과망 조립체 모델은 Fig. 3과 같다. 여과망 조립체 모델은 3개의 망을 동일 간격으로 배치하였으며, 전체 간격은 여과망 시제품 기준인 4mm로 설정하였다. 해석 도메인은 구조용 망의 한 공극을 기준으로 하였으며 해석 시간을 고려해 1/4 대칭 모델로 축소하여 진행하였다.
여과망의 너비인 4mm 간극은 정수용 여과망, 전/후 구조용 망의 와이어 직경이 포함되며 구조용 여과망은 전체 모델의 연속된 육면체 격자(Hexahedron mesh)를 생성하기 위해 유동 방향으로 평행하게 배치하였다.
경계조건은 마찰이 있는 와이어 부분을 제외하고 대칭으로 설정하였으며 해석의 수렴성을 고려하여 입구는 2H, 출구는 6H를 연장하였다. 난류 모델은 Shklyar(14)의 연구 결과를 참고하여 벽면과 자유 전단층 유동을 잘 나타낼 수 있는 k-ω SST를 사용한다.
4. 시험장치
CFD를 이용한 모델 검증을 위해 축소 배관의 여과망 차압 시험을 진행하였다. 사용되는 여과망은 Fig. 2의 여과망 조립체로 설계 변수는 CFD 모델과 같다.
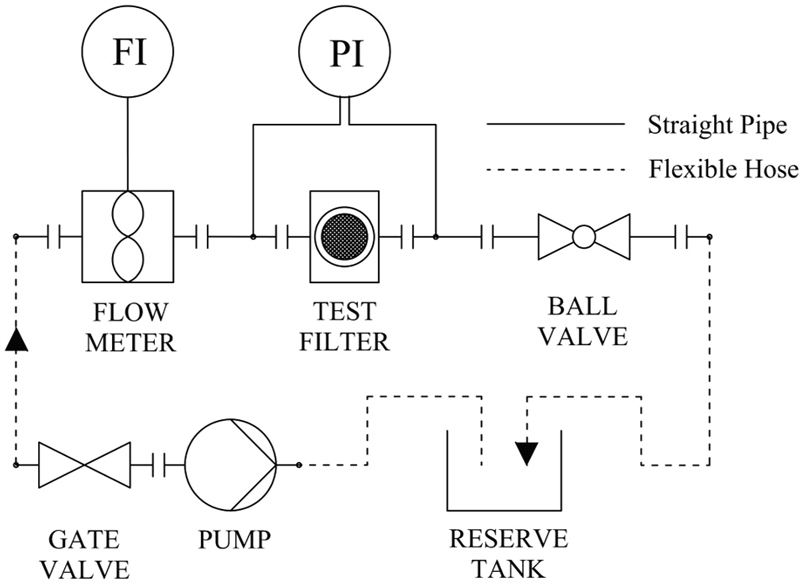
시험장치는 상온의 정수장 물(22℃) 환경에서 일정 압력을 유지할 수 있는 펌프를 사용하여 1∼2.5m/s 사이의 유속 조건에서 진행하였다. Fig. 4의 개략도와 같이 관로 내 유량을 조절할 수 있는 밸브를 여과망 뒤 단에 배치한다. 관내 유속은 터빈 유량계를 통해 측정되며, 별도의 정류기를 설치하지 않고, 유량계 앞 파이프를 연장하여 계측 정확도를 높였다. 여과망 전/후에는 압력 손실을 측정할 수 있도록 차압계가 설치되며 여과망 통과 후 국부적으로 낮아진 압력이 충분히 회복된 후 계측하기 위해 여과망에서 6D 이상 거리로 이격하여 배관 니플을 설치하였다.
시험에 사용될 파이프는 물에 의한 부식을 방지하기 위해 스테인리스 강관(50A)을 사용하며 플랜지와 용접으로 제작한다. Fig. 2의 여과망 시료는 고압에서의 누설을 방지하기 위한 고무 패킹과 함께 결합 되며, 두 플랜지 사이 공간에 고정된다.
5. 결과 및 분석
5.1 여과망 조립체의 유동 특성
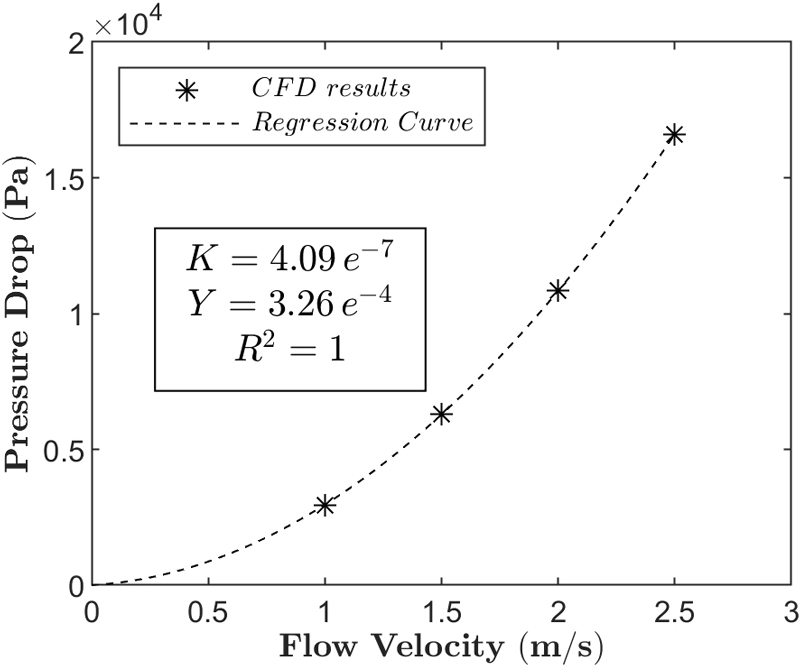
차압 모델의 투과성 계수와 관성 계수를 구하기 위해 여과망 조립체의 CFD 해석을 진행하였다. 해석은 시험 조건과 같은 직경 50mm 파이프의 1∼2.5m/s 유속 조건에서 수행되었으며 해석 결과는 Fig. 5와 같다.
유동 속도에 따른 CFD 해석 결과가 일정한 경향이 나타나기에, RANS 방정식 및 사용된 k-ω난류 모델의 특성에 따라 비압축성 완전 난류 유동임을 유추할 수 있다.
본 연구에 사용되는 Darcy 법칙과 연관하여 분석했을 때, 여과망 조립체의 손실 특성은 유동 속도의 2차 항임을 알 수 있다. 식(11)과 같이 회귀 곡선을 나타내었을 때, CFD 결과를 잘 나타내며, 도출된 투과성 계수와 관성 계수, R-square(R2) 값을 Fig. 5에 나타내었다.
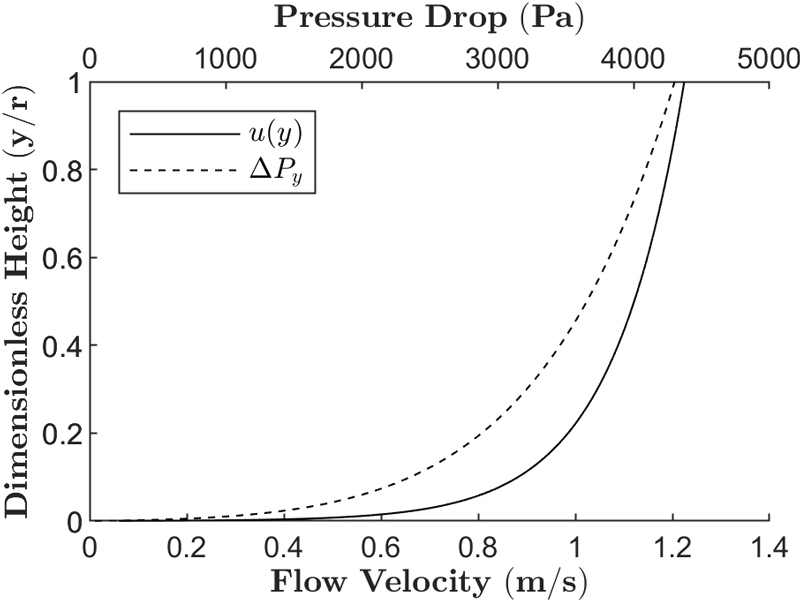
Fig. 6은 관로 벽면에서 거리비(y/r)에 따른 속도와 차압을 나타낸 그래프이다. 식(10)에 따라 속도 프로파일을 나타냈을 때, 평균 유속에 비례하여 관로 중심에서 최대 1.22배 이상의 속도차가 발생함을 알 수 있다. 위 속도차는 벽면 마찰에 의한 결과로, 차압 모델에 대입했을 때 평균 유속에서 차압 대비 1.44배의 손실을 발생시킨다.
식(12)에 위 결과를 대입하여 전체 관로의 평균 차압을 도출하였으며, 단일 공극의 CFD 해석과 비교하여 1.30배 이상의 차압 결과를 확인하였다. 이는 각 지점에서 속도에 의한 손실이 크게 차이 나며, 지점을 통과하는 유량이 속도에 비례하기 때문으로, 관로 내 유동을 고려하였을 경우 평균 관내 유속 결과보다 높은 차압이 발생함을 의미한다.
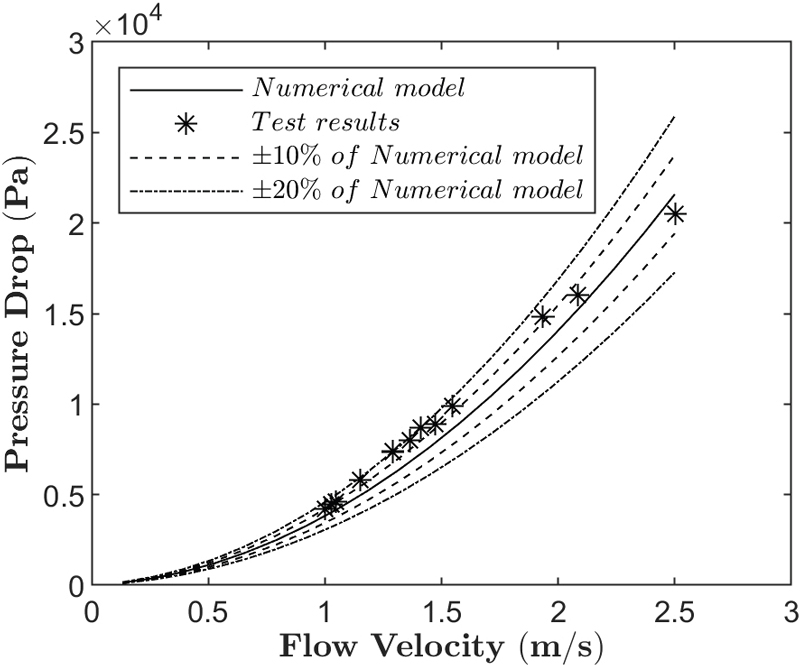
차압 모델을 검증하기 위해 진행한 축소 배관 시험의 결과는 위 해석 결과와 함께 Fig. 7에 나타내었다. 시험 결과, 비교적 저속(1∼2m/s)에서 10 % 이상의 오차값이 발생하며 고속(>2m/s)에서 수치 모델에 수렴하는 경향이 나타났다. 정상 상태 유동에서 진행한 CFD 해석과 다르게 펌프의 맥동, 여과망의 형상 변화, 속도 프로파일 모델과 실제 유동의 차이 등의 변수로 인해 발생한 오차임을 유추할 수 있다.
5.2 공극률에 따른 여과망 투과율과 관성 계수
투과율과 관성 계수를 도출하기 위해 5.1의 모델에서 정수용 여과망의 공극률을 변경하여 해석을 진행하였으며 각 망의 설계 변수는 Table 1에 나타내었다.
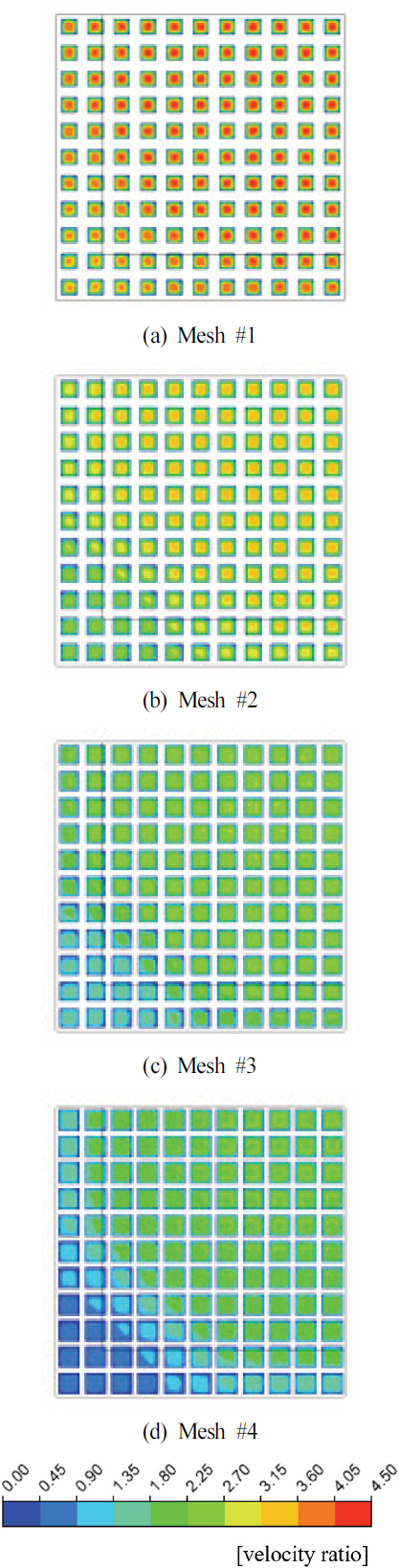
Fig. 8은 관로 유속 1m/s에서 각 망의 중심부 속도비(u/)를 나타낸 컨투어(Contour) 결과이다. 분석 결과, 공극률이 낮을수록 공극을 통과하는 속도가 높아짐을 알 수 있다. 1m/s 유속 조건에서 공극률이 가장 높은 Mesh #4와 가장 낮은 Mesh #1을 비교했을 때, Mesh #4에 대한 Mesh #1의 단면적비는 0.53으로 여과망을 지나는 평균 유속은 단면비의 역수인 1.89배 이상 증가한다. 해석 결과, 차압 모델 식(6)에 따라 유속비의 제곱인 3.57과 근사한 3.66배 이상의 압력 손실을 확인하였다. 위 결과는 여과망을 통과하는 평균 유속이 압력 손실에 지배적임을 보여주며 이는 선행된 직조 스크린 연구 결과와 일치한다.
여과망의 속도 분포를 분석했을 때, 구조용 망에 의한 유동 방해로 중심부에서 멀어질수록 낮은 속도비를 나타낸다. Fig. 9는 중심부에서 거리에 따른 속도비 그래프로 모든 망에서 비슷한 경향을 보이나, 공극률이 낮을수록 속도 편차가 비교적 적음을 알 수 있다. 이는 공극 면적이 줄어들수록 저항이 높아지기 때문으로, Mesh #1의 경우 속도비가 4.24∼3.64, Mesh #4의 경우 2.23∼0.73 범위로 분포하여 공극률에 따른 편차가 매우 큰 것을 알 수 있다.
공극률에 따른 투과율과 관성 계수를 도출하기 위한 4가지 여과망의 관로 유속 1∼2.5m/s 해석 결과를 Fig. 10에 도시하였다. 투과율과 관성 계수를 식(7)의 지수함수로 회귀분석을 하였으며 결과는 Table 1에 나타내었다.
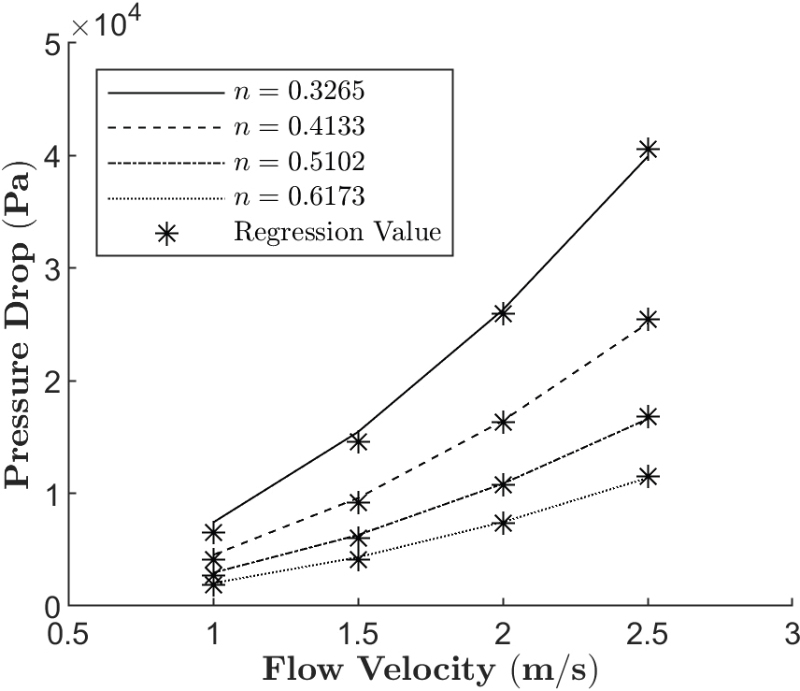
Pressure drop as a function of flow velocity for different porosities with regression curves from a mesh filter pressure drop model
| (13) |
Fig. 5에 도시된 Mesh #3의 K, Y 값은 Table 1의 값과 큰 차이를 보인다. 속도 2차 항 비례계수인 Y/K1/2의 결과는 Fig. 5에서 0.51, Fig. 10에서는 1.85로 3배 이상의 차이가 존재한다. Fig. 10의 기울기 차이를 분석했을 때, 공극률이 낮아질수록 Y/K1/2가 차압에 지배적임을 알 수 있다. 따라서, 낮은 공극률 모델을 고려한 회귀분석 결과는 비교적 선형의 성질을 가지는 Mesh #3의 단일 회귀 결과와 큰 차이가 발생한다. 공극률에 따른 K, Y의 증가 폭은 지수 α, β 제곱에 비례하며 해석 결과, 투과율 지수 α는 β에 비해 약 5배 높게 나타났다. 이는 여과망 차압 모델에서 투과율이 가장 핵심 변수로 작용하며 공극률에 의해 결정됨을 의미한다.
위 결과에 따라 R2 검증하였을 때, 0.9982로 CFD 해석 결과를 매우 잘 나타냄을 알 수 있다.
6. 결 론
본 연구에서는 정수장 여과망의 손실 특성을 확인하기 위해 CFD 해석을 진행하였다. 위 결과를 기반으로 관내 유동을 고려한 수정된 차압식을 제시하였다. 또한, 정수장 환경에서 축소 관로 시험을 진행하여 차압 모델을 검증하였다. 해석 결과를 토대로 여과망 조립체의 손실 특성과 관내 유동 및 각 지점에서 압력 손실을 분석하였다. 또한, 서로 다른 공극률을 가진 4가지 여과망 모델에 대해 CFD 해석을 진행하였으며, 그에 따른 속도 분포 및 압력 손실을 분석하였다. 최종적으로 여과망 설계 변수를 모두 포함할 수 있는 투과율과 관성 계수 회귀식을 도출하여 신뢰성을 검증하였다. 본 연구의 결과를 요약하면 다음과 같다.
- 1) 여과망 조립체의 CFD 해석 결과, 차압은 유동 속도 2차 항의 경향이 보이며 Forchheimer 식으로 회귀분석 했을 때, R2=1로 여과망 특성을 잘 나타냈다.
- 2) 관로 내 유동을 고려한 수정된 차압식은 CFD 해석보다 1.30배 높은 결과를 도출하였고 축소 관로 시험과 비교했을 때, 저속 영역(1∼2m/s)에서 9.4∼17.3 %, 고속 영역(>2m/s)에서 4.9∼5.6 % 오차를 나타냈다.
- 3) 공극률에 따른 정수용 여과망의 해석 결과를 분석하였을 때, 공극률에 따라 속도 분포 및 차압의 차이가 발생하며 공극을 통과하는 평균 유속과 차압 관계를 분석했을 때, 여과망 차압은 평균 유속에 지배적임을 알 수 있다.
- 4) 공극률(0.3265∼0.6173)과 관로 유속(1∼2.5m/s)에 따른 CFD 해석 결과를 토대로 투과율과 관성 계수를 도출하였으며, 지수함수로 회귀분석 하였을 때, R2=0.9982로 여과망 특성을 매우 잘 나타낼 수 있다.
Acknowledgments
본 연구는 K-water 와부정수장의 시험 지원과 (주)현대밸브의 기업 수탁 연구과제로 수행되었음.
References
- Jung, Yong-Jun., and Min, Kyung-Sok., 2004, “Evaluation of a Rapid Sand Filter with Surface Wash and Backwash Conditions,” Journal of Korean Society on Water Environment, Vol. 20, No. 6, pp. 652∼656.
-
Wu, W. T., Liu, J. F., Li, W. J., and Hsieh, W. H., 2005, “Measurement and Correlation of Hydraulic Resistance of Flow through Woven Metal Screens,” International Journal of Heat and Mass Transfer, Vol. 48, No. 14, pp. 3008∼ 3017.
[https://doi.org/10.1016/j.ijheatmasstransfer.2005.01.038]

-
Armour, J. C., and Cannon, J. N., 1968, “Fluid Flow through Woven Screens,” AIChE Journal, Vol. 14, No. 3, pp. 415∼420.
[https://doi.org/10.1002/aic.690140315]

- Shin, 2017, “An Experimental Study on the Design, Production and Performance Test of C-Type Strainer for the Improvement of Flow Characteristics : With a Focus on the Comparison with Y-Type Strainer,” Ph.D. Thesis, Department of U-City IT Convergence and Urban Policy, Hansei University, Gyeonggi-do.
- Ergun, S., 1952, “Fluid Flow Through Packed Columns,” Journal of Physical Chemistry, Vol. 48, No. 2, pp. 89∼94.
-
Sodre, J., and Parise, J., 1997, “Friction Factor Determination for Flow through Finite Wire-Mesh Woven-Screen Matrices,” ASME Journal of Fluids Engineering, Vol. 119, No. 4, pp. 847∼851.
[https://doi.org/10.1115/1.2819507]

-
Teitel, M., 2010, “Using Computational Fluid Dynamics Simulations to Determine Pressure Drops on Woven Screens,” Biosystems Engineering, Vol. 105, No. 2, pp. 172 ∼179.
[https://doi.org/10.1016/j.biosystemseng.2009.10.005]

-
Sun, H., Bu, S., and Luan, Y., 2015, “A High-Precision Method for Calculating the Pressure Drop Across Wire Mesh Filters,” Chemical Engineering Science, Vol. 127, pp. 143∼150.
[https://doi.org/10.1016/j.ces.2015.01.023]

-
Iwaniszyn, M., Sindera, K., Gancarczyk, A., Korpyś, M., Jędrzejczyk, R. J., Kołodziej, A., and Jodłowski, P. J., 2021, “Experimental and CFD Investigation of Heat Transfer and Flow Resistance in Woven Wire Gauzes,” Chemical Engineering and Processing-Process Intensification, Vol. 163, p. 108364.
[https://doi.org/10.1016/j.cep.2021.108364]

-
Miguel, A., Van de Braak, N., and Bot, G., 1997, “Analysis of the Airflow Characteristics of Greenhouse Screening Materials,” Journal of Agricultural Engineering Research, Vol. 67, No. 2, pp. 105∼112.
[https://doi.org/10.1006/jaer.1997.0157]

-
Huang, H., and Ayoub, J., 2008, “Applicability of the Forchheimer Equation for Non-Darcy Flow in Porous Media,” SPE Journal, Vol. 13, No. 01, pp. 112∼122.
[https://doi.org/10.2118/102715-PA]

-
Flores-Velazquez, J., and Montero, J., 2008, “Computational Fluid Dynamics (CFD) Study of Large Scale Screenhouses,” Acta Horticulturae, Vol. 1, No. 797, pp. 117∼122.
[https://doi.org/10.17660/ActaHortic.2008.797.14]

- Nikuradse, J., 1950, “Laws of flow in rough pipes,” NACA TM 1292.
-
Shklyar, A., and Arbel, A., 2007, “Numerical Simulations of Turbulent Flow through Screen Mesh,” Acta Horticulturae, Vol. 2, No. 801, pp. 995∼1003.
[https://doi.org/10.17660/ActaHortic.2008.801.118]