수치해석을 이용한 리튬 이온 배터리 입구와 출구 위치의 최적화 연구

1. 서 론

국제적인 환경 규제의 증가와 환경오염에 대한 우려로 인해 화석 연료의 대체 에너지로 친환경 에너지에 대한 수요가 증가하고 있다. 그에 따라서 기존의 자동차 또한 내연기관에서 전기자동차, 하이브리드 자동차 등에 대한 수요가 증가하고 있다. 이에 따라 전기자동차의 시장이 증가하는 추세를 보이고 있다.^(1-2)

전기자동차는 동력을 위해 모터를 사용하고, 모터 구동을 위한 전원 장치로 다량의 배터리를 사용한다.⁽³⁾ 전기 자동차에 주로 사용되는 배터리는 리튬-이온 배터리로, 높은 에너지 밀도, 긴 수명의 장점을 갖고 있다. 리튬-이온 배터리는 첨가하는 전해질의 물질에 따라 Lithium Cobalt Oxide(LCO), Lithium Manganese Oxide(LMO), Nickel Manganese Cobalt(NMC) 등으로 분류할 수 있다. 리튬-이온 배터리는 기존의 Nickel Cadmuim (NiCd), Nickel-Metal(NiMH) 배터리에 비해 높은 에너지 밀도와 우수한 수명 주기를 갖는다. 또한 NMC 배터리는 다른 리튬-이온 배터리보다 경제적이며 수명 주기가 길고 에너지 밀도가 높다. EV 산업에서 이러한 이유로 NMC 배터리의 사용을 적극적으로 개발 중이다.

전기자동차의 비용과 수명은 주로 배터리의 가격과 수명이 주요한 부분을 차지하고 있다. 배터리는 전기자동차 비용의 40 %를 차지하며 배터리의 가격을 낮추고 수명을 늘리는 등의 연구는 국제적인 환경 규제에 대응해 전기자동차가 내연기관 자동차를 대체하기 위해 중요하다.

리튬-이온 배터리의 성능과 수명은 작동 온도에 영향을 받는다. 리튬-이온 배터리는 작동 가능한 온도 범위를 벗어나 동작한다면 배터리의 성능과 수명이 급격히 저하될 수 있다. 배터리의 최적의 작동 온도 범위는 25∼40℃로, 해당 온도에서 우수한 성능과 수명을 유지할 수 있다⁽⁴⁾. 허용 가능한 작동 온도 범위는 –20∼60℃로, 해당 온도 범위를 넘어선다면 배터리의 성능과 수명이 급격하게 저하될 수 있다. 따라서 이를 위해 배터리의 온도를 작동 온도 범위 내로 유지해야한다. 하지만 주행 상황에 따라 배터리의 온도는 장기간 동안 60℃ 이상으로 상승할 수 있으며, 이는 배터리의 성능과 수명이 급격하게 저하될 뿐 아니라 열 폭주로 인해 화재, 폭발과 같은 치명적인 위험을 야기할 수 있다⁽⁵⁾. 이에 따라 배터리 열 관리 시스템(Battery Thermal Management System, BTMS)이 중요한 역할을 한다. 배터리 열 관리 시스템은 배터리의 온도를 작동 온도 범위 내로 유지하여 배터리의 수명과 성능을 유지한다. 배터리 열 관리 시스템은 Active BTMS와 배터리 팩 주변으로 공기를 순환시키는 Passive BTMS로 나눌 수 있다.⁽⁶⁾ Active BTMS는 냉각 액체가 고온의 배터리 팩을 통과하여 온도를 낮춰 적절한 작동 온도를 유지시켜 배터리 수명을 유지한다. 열 발생량이 많은 고밀도 배터리에서는 냉각 액체를 사용하는 열관리 시스템이 가장 효율적인 열관리 방법이다.⁽⁷⁾

본 연구에서는 기존의 유랭식 배터리 냉각 시스템에서 입구와 출구의 위치에 따른 냉각의 효과를 확인하기 위해 CFD를 활용하여 냉각 성능을 분석하였다. 배터리 팩의 최고 온도가 60℃에 도달하는 유량을 선정하고 경향을 확인하였다. 또한 동일한 조건에서 배터리 팩의 입구와 출구의 위치를 변화시켜 배터리 팩 내의 최고 온도를 낮출 수 있도록 Surrogate Management Framework(SMF) 최적화 기법을 이용하여 배터리 팩의 입구와 출구의 최적 위치를 산정하였다.

2. 시뮬레이션 설정

2.1 배터리 팩 모델링

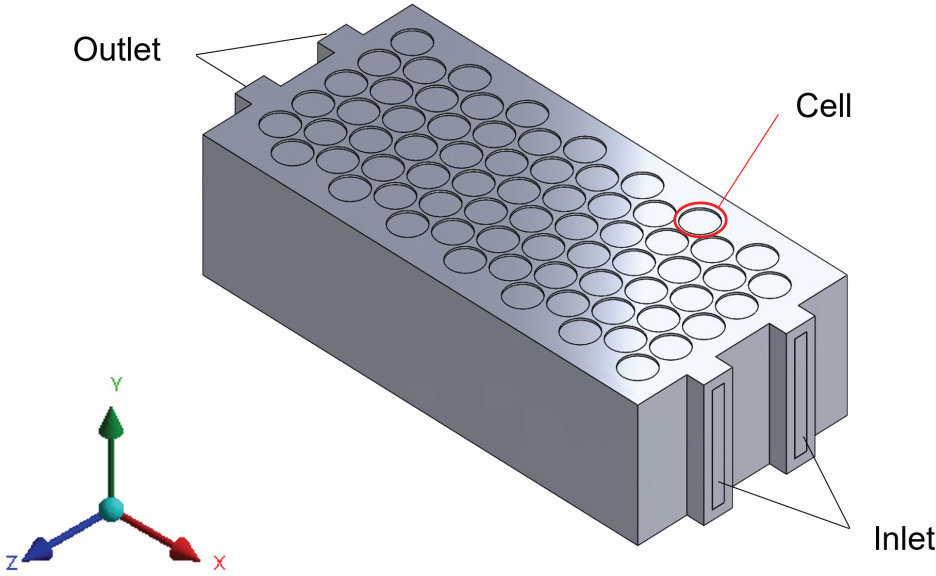
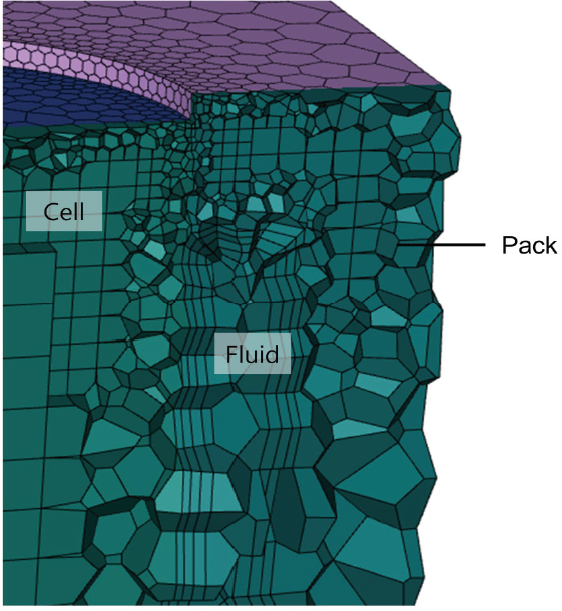
본 연구에서는 Jindal 등⁽⁸⁾이 연구한 Nickel Manganese Cobalt(NMC) 리튬 이온 배터리 팩에 대한 해석을 진행하였다. 배터리 팩을 구성하기 위해 사용한 단일 배터리 셀과 배터리 팩의 특성들은 각각 Table 1과 Table 2에 나타내었다. Fig. 1은 배터리 팩의 전체적인 형상 및 입⋅출구의 위치를 보여준다. 배터리 팩은 277 × 66.7 × 123.75mm의 크기로, 70개의 배터리 셀이 x방향으로 14개, z방향 5개씩 각각 배열되어 있으며, 각 배터리 셀의 간격은 셀 중심으로부터 각각 x방향 17mm, z방향 19.5mm으로 배열되어 있다. 이 형상은 Jindal 등⁽⁸⁾이 연구한 형태로서, 본 논문에서는 reference case로 지칭된다. Fig. 2에서 보여주듯이, 본 연구에서는 Poly-hexcore 격자 구조를 사용하였으며, 배터리 셀과 팩 사이 유동을 정확히 모사하도록 격자를 구성하였다.

Table 1

Specifications for NMC cells

Table 2

Specifications for battery pack

Fig. 1

3D model of battery pack

Fig. 2

Mesh configuration near battery cell

Jindal 등⁽⁸⁾에 비해 격자수(약 160만개)를 증가시켰으며, 이를 통해 아래와 같이 reference case에 대한 결과가 Jindal 등⁽⁸⁾과 비슷하게 도출되어 현재 연구결과에 대한 신뢰성을 확보하였다. Jindal 등⁽⁸⁾이 수행한 연구에서 배터리 팩의 최고 온도는 59.816 ℃로 나타났으며 본 논문의 해석 결과는 60.048 ℃으로 나타났다.

배터리 팩의 냉매는 높은 열전달 특성으로 인해 배터리 냉각에 주로 사용되는 에틸렌글리콜과 물의 5:5 혼합물을 모델링하였다⁽⁹⁾. Table 3은 해석에 사용한 냉매의 물성치를 나타내었다⁽¹⁰⁾.

Table 3

Temperature-dependent physical properties of 50/50 EG/water used for cooling of the battery module

2.3 최적화 알고리즘

본 연구에서는 배터리 팩 입구와 출구의 위치가 배터리 팩의 냉각 성능에 미치는 영향을 분석하기 위해 입⋅출구의 위치를 변경하여 냉각 성능을 비교하였다. 또한 Surrogate Management Framework(SMF) 최적화 기법을 통해 입⋅출구 위치에 따른 배터리 팩의 최고 온도를 도식화하여 경향성을 분석하였다. SMF 최적화 기법은 매개변수 공간에서 목적함수를 추정하고 최적 지점을 예측하는 기법으로서, 기존의 데이터를 기반으로 대체 함수를 구축하여 목적 함수를 예측한다.^(11-12) 이를 통해 전체 공간을 추정하고 수렴까지 이를 반복하여 추정한 전체 공간을 통해 최적 위치를 산출한다.

매개변수 공간에 대한 SMF 기법의 효과적인 적용을 위해 Latin Hypercube Sampling(LHS)을 통해 초반부 표본들을 추출하였다. LHS는 표본 추출 방법 중 하나로, 각 매개변수 축을 샘플링 개수로 나누어 각 공간에서 데이터를 추출해 데이터가 매개변수 공간에서 고르게 분포될 수 있도록 추출하는 방법이다. 배터리 팩의 두 입구는 대칭으로, 동일한 거리에 위치하므로 중심선으로부터 떨어진 거리를 정규화하여 매개변수 x₁을 나타내었다. 동일한 방법으로 출구의 매개변수를 x₂로 나타내었으며, 배터리 팩의 최고 온도를 목적 함수로 하여 전체 공간을 추정하여 최적화를 진행하였다. 매개변수를 구하는 식은 아래와 같다.

$\[ x_i=\frac{l_i}{L-W}\left(i=\mathrm{1,2}\right) \]$

(2)

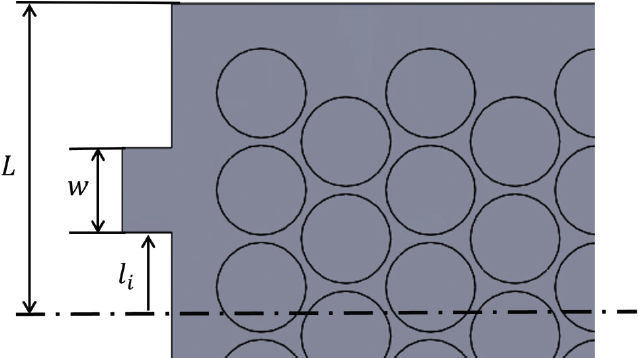
Fig. 3은 배터리 팩의 xz평면인 일부 표면으로서, 식(2)에서 매개변수 계산에 사용한 변수를 보여주고 있다. 배터리 팩은 두 개의 입구가 중심선으로부터 대칭으로, 동일한 거리에 위치해있다. 위 식에서 L과 W는 고정된 값으로, L은 중심선으로부터 배터리 팩의 끝까지의 거리를 가리키며, W는 입⋅출구의 너비를 가리킨다. l₁은 중심선으로부터 입구영역이 떨어진 거리를 나타내며, l₂는 출구영역이 떨어진 거리를 나타낸다. 본 연구는 이러한 SMF 기법을 활용하여, 목적함수인 배터리 셀 최고온도를 최소화하는 x₁과 x₂을 최적화하였다.

Fig. 3

Parameter description near outlet region

3. 결 과

3.1 해석 결과

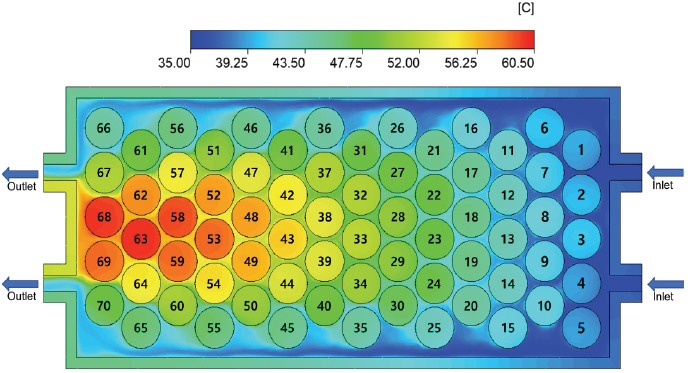
Fig. 4는 reference case에 대한 수치해석의 결과로, Jindal 등⁽⁸⁾이 수행한 리튬 이온 배터리팩의 해석에 대한 검증을 수행하였다. 바닥으로부터 y = 25mm의 위치에서 배터리 팩 단면의 온도 분포를 나타낸다. 입구영역에 위치한 배터리 셀은 열 방출이 이루어져 약 40℃의 온도를 형성하지만 출구 영역으로 갈수록 배터리 셀의 온도가 증가하는 것을 알 수 있다. 또한 가장자리의 배터리 셀보다 배터리 팩의 중심에 위치한 배터리 셀의 온도가 높은 것을 알 수 있다. 출구 영역 중앙에 위치한 63번 배터리 셀은 팩 내의 가장 고온의 배터리 셀이며, 온도는 60.048℃로, 리튬-이온 배터리의 허용 가능한 작동 온도인 60℃까지 도달하였음을 확인할 수 있다. 근처의 58번, 68번 셀 또한 60℃까지 도달하였으며 해당 영역의 열 방출이 활발하지 않다는 것을 확인할 수 있다.

Fig. 4

Temperature contour of reference case at y = 25 mm

3.2 최적화 결과

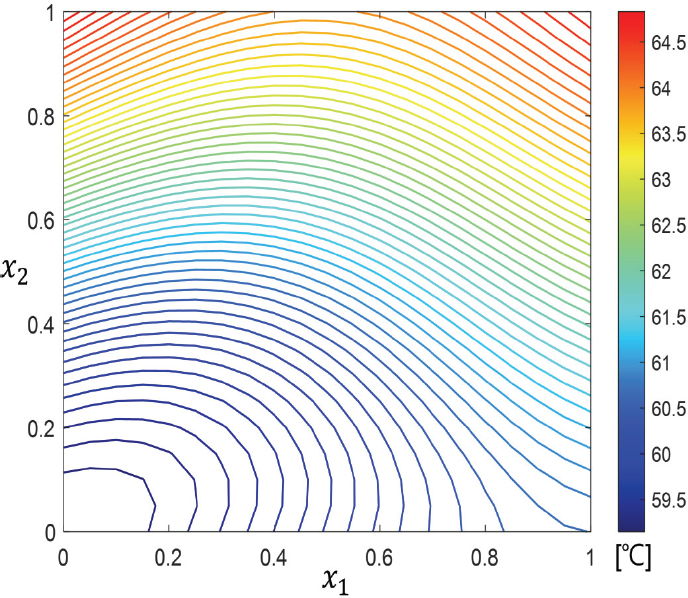
Table 4는 SMF 최적화 기법을 적용하며 최적의 입⋅출구의 위치를 탐색한 결과이다. Case 1은 reference case로, SMF 최적화를 위한 표본으로 사용되었다. Case 2-5는 LHS를 통해 추출한 추가 표본으로서, 이를 이용하여 SMF 최적화를 진행해 최고 온도의 분포를 산출하였다. SMF 기법은 기존 데이터들을 기반으로 예측한 최적화 지점(minimum point)과 전체적인 예측을 개선하기 위한 추가 지점(space-filling point)을 생성한다. SMF를 통해 얻어진 최적화 지점이 수렴될 때까지 이 과정들은 반복하였고, 2번의 과정을 거친 후 최종 수렴하였다. Table 4에서 case 6 과 7은 각각 5개의 case로부터 도출된 최적화 지점과 추가 지점이며, case 8 과 9는 7개의 case로부터 도출된 지점들이다. 결과적으로 minimum point 1 이 2보다 우수하기 때문에 알고리즘이 종료되었다. 이 표본들은 Case 6-9로 나타내었다. LHS 샘플링 및 SMF 기법을 통해 예측된 배터리 셀 최고온도는 Fig. 5에 나타내었다. Fig. 5는 전체 매개 변수 공간에 대해 목적 함수를 예측한 것으로, 수렴된 SMF 결과를 보여준다. 이를 통해 입구와 출구의 위치에 따른 최고 온도의 분포를 확인할 수 있다.

Table 4

Optimal parameters and the resulting value in two-parameter optimization

Fig. 5

Maximum-temperature contour predicted by SMF technique

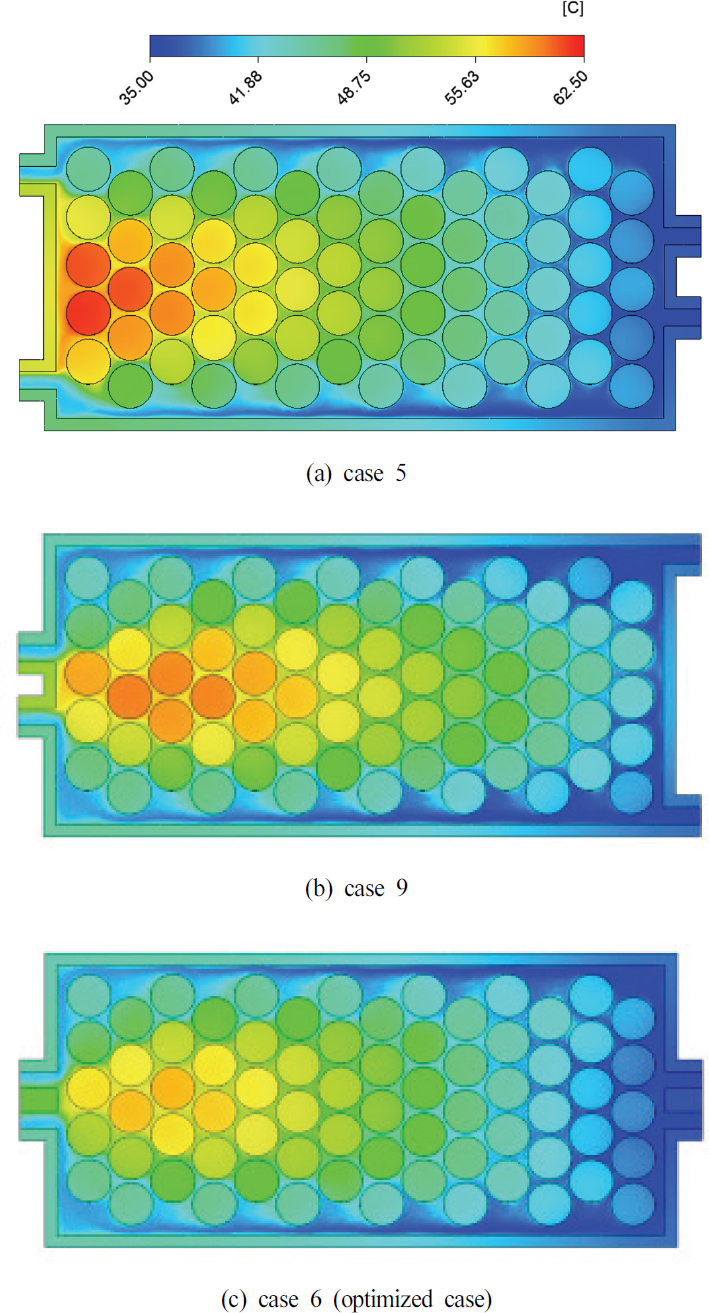
SMF 기법을 통해 예측된 결과를 토대로 특이점이 있는 케이스들과 최적화된 결과를 Fig. 6에 나타내었다. Fig. 6는 동일한 위치에서의 온도 분포를 나타낸다. Fig. 6(a)는 case 5의 온도 분포로, 입구의 위치가 중앙에 위치한 모델의 온도 분포이다. 기존의 팩과 달리 69번 셀의 온도가 가장 높으며 두 출구 사이의 온도가 가장 높은 것을 알 수 있다. Fig. 6(b)는 case 9으로, 출구의 위치가 중앙에 위치한 모델의 온도 분포이다. 기존의 배터리 팩과 동일하게 출구와 인접한 중앙 영역이 가장 고온의 영역이며 58번 배터리 셀의 온도가 가장 높다. Fig. 6(c)는 case 6의 결과로서, SMF 기법으로 예측된 최적의 결과이다. 입구와 출구가 모두 중앙에 위치할 때 최고 온도가 가장 낮은 것을 보인다. 기존의 팩과 동일하게 58번 셀 인근의 영역이 가장 높은 온도를 나타내지만, 출구와 인접한 68번 셀의 온도가 감소한 것을 확인할 수 있다.

Fig. 6

Top view of temperature contour at y = 25 mm

즉, 입구와 출구 위치에 따라 가장 고온인 배터리 셀은 변하지만, 고온의 영역은 일정하게 출구 사이의 배터리 중앙 부분이며 해당 영역의 온도를 낮추는 것이 중요함을 알 수 있다. 이러한 결과는 2개의 입구 및 출구들이 각각 배터리 중앙에 위치할 때 냉각 성능이 가장 뛰어나다는 것을 의미하며, SMF 기법으로 도출된 case 6가 이에 부합한다.

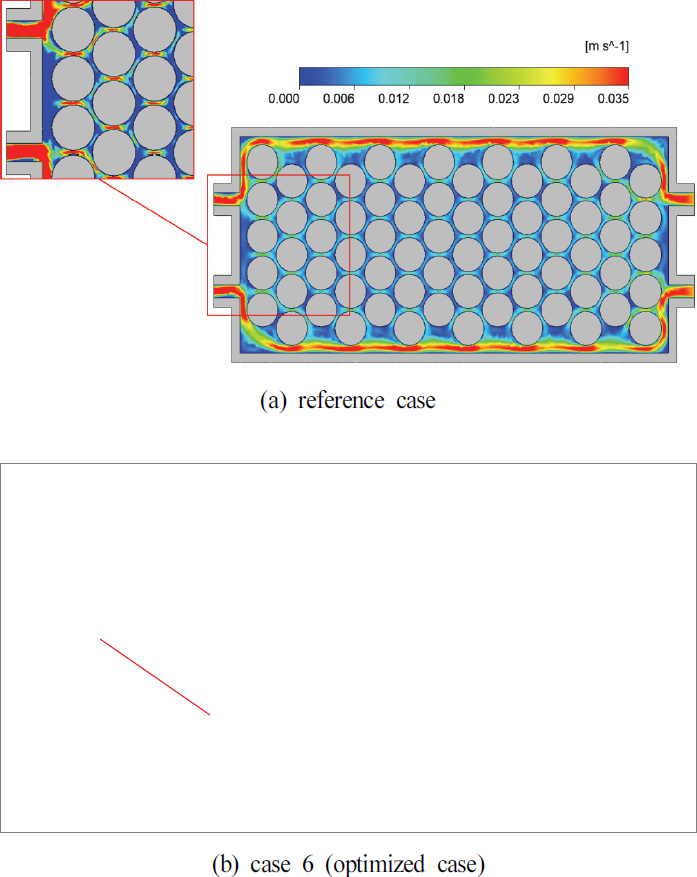
이러한 입구 및 출구의 위치에 따른 최고 온도에 대한 영향은 배터리 셀 주변의 유동을 통해 확인할 수 있다. Fig. 7은 동일한 위치에서 속도의 분포를 보여준다. Fig 7(a)와 (b)는 각각 reference case와 SMF 기법을 통해 산출한 최적의 case이다. 기존의 배터리 팩에 비해 최적화된 배터리 팩이 중앙부 배터리 셀 사이 유동의 속도가 증가한 것을 확인할 수 있다. 이는 기존의 배터리 팩에서 중앙부의 유동이 원활하지 못해 열 배출이 활발하지 못한 반면 입⋅출구가 중앙에 위치한 최적의 case가 중앙부로의 유동이 개선되어 배터리 셀 표면의 열전달을 증가시켜 효과적으로 배터리 최고온도를 감소시킨 것으로 분석된다.

Fig. 7

Top view of velocity contour at y = 25 mm

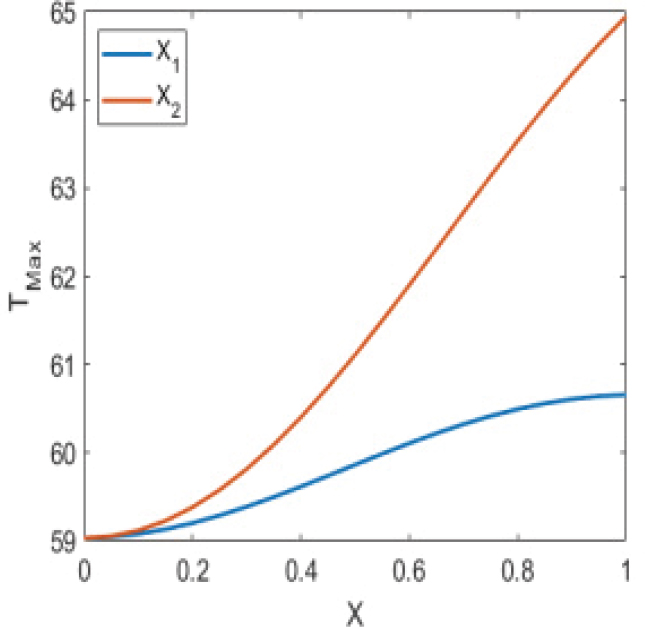
배터리 셀의 최고 온도에 대한 입구와 출구의 매개변수 x₁, x₂의 민감도는 Fig. 8에 나타내었다. Fig. 8은 x₁과 x₂가 각각 0일 때, x₂과 x₁에 따른 최고 온도 변화를 보여준다. 이 그림에서는 x₁과 x₂ 값이 모두 증가할수록 최고 온도가 증가하는 경향이 관찰되었다. 그러나 x₂의 기울기가 x₁보다 전체적으로 가파른 것을 확인할 수 있었고, 이는 입구의 위치보다 출구의 위치가 최고 온도를 결정하는데 주요한 요소임을 의미한다.

Fig. 8

Relationship between optimal parameter x and maximum temperature Tmax

4. 결 론

본 연구에서는 리튬-이온 배터리의 입구와 출구 위치에 따른 냉각 성능을 비교하고 최적의 입구와 출구의 위치를 산출하였다. SMF 최적화 기법을 통해 입구와 출구의 위치에 따른 최고 온도의 분포를 예측하였으며, 입구와 출구의 위치를 최적화하였다. 최적화 결과 배터리 팩의 입구와 출구의 위치가 중앙에 몰려있을 때 냉각 성능이 가장 우수하였다. 이는 열이 집중되는 배터리 팩 중앙부의 셀 사이를 지나는 유동이 개선되어 열전달을 증가시켜 배터리 온도가 감소한 것으로 판단된다. 또한 SMF 최적화 기법을 통해 입⋅출구 위치와 최고 온도의 민감도 분석을 수행하였다. 이를 통해 배터리 팩의 출구의 위치가 입구의 위치보다 배터리 팩의 냉각 성능을 결정하는데 주요한 요인임을 확인하였다.

본 연구에서 입⋅출구의 위치가 배터리 냉각에 미치는 영향을 확인하였으며, 이를 통해 최적의 입⋅출구 위치를 예측하였다. 향후 연구로서 입⋅출구 위치의 변화에 따른 열전달량의 변화를 확인해 상관관계를 분석하고자 한다. 또한 배터리 셀 간격에 대한 영향성을 분석하고자 하며 이는 배터리 팩의 냉각 성능을 더욱 개선시킬 수 있을 것으로 기대된다.

Acknowledgments

본 성과는 2024년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다(2021RIS-004). 또한, 이 성과는 “정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다(RS-2023-00281635).”

References

• Sanguesa, J.A., Torres-Sanz, V., Garrido, P., Martinez, F.J., Marquez-Barja, J. M., 2021, “A review on electric vehicles: technologies and challenges,” Smart Cities, Vol. 4., No. 1, pp. 372-404. [https://doi.org/10.3390/smartcities4010022]
• Pelegov, Dmitry V., and José Pontes, 2028 “Main drivers of battery industry changes: Electric vehicles—A market overview,” Batteries Vol. 4, No.4, pp. 65. [https://doi.org/10.3390/batteries4040065]
• Sharma, S., Panwar, A. K., & Tripathi, M. M., 2020, “Storage technologies for electric vehicles,” Journal of traffic and transportation engineering (english edition), Vol. 7, No. 3, pp. 340-361. [https://doi.org/10.1016/j.jtte.2020.04.004]
• Pesaran, A. A., 2002, “Battery thermal models for hybrid vehicle simulations,” Journal of power sources, Vol. 110, No.2, pp. 377-382. [https://doi.org/10.1016/S0378-7753(02)00200-8]
• Ma, S., Jiang, M., Tao, P., Song, C., Wu, J., Wang, J., Deng, T., Shang, W., 2018, “Temperature effect and thermal impact in lithium-ion batteries: A review,” Progress in Natural Science: Materials International, Vol. 28, No. 6, pp. 653-666. [https://doi.org/10.1016/j.pnsc.2018.11.002]
• Rao, Z., Wang, S., 2011, “A review of power battery thermal energy management,” Renewable and Sustainable Energy Reviews, Vol. 15, No. 9, 4554-4571. [https://doi.org/10.1016/j.rser.2011.07.096]
• Jarrett, A., and Kim, I. Y, 2011, “Design optimization of electric vehicle battery cooling plates for thermal performance” Journal of Power Sources, Vol. 196, No. 23, pp. 10359-10368. [https://doi.org/10.1016/j.jpowsour.2011.06.090]
• Jindal, P., Sharma, P., Kundu, M., Singh, S., Shukla, D. K., Pawar, V. J., Wei, Y., and Breedon, P., 2022, “Computational Fluid Dynamics (CFD) analysis of Graphene Nanoplatelets for the cooling of a multiple tier Li-ion battery pack,” Thermal Science and Engineering Progress, Vol. 31, 101282. [https://doi.org/10.1016/j.tsep.2022.101282]
• Sekrani, G., and Poncet, S., 2018, “Ethylene-and propylene-glycol based nanofluids: a litterature review on their thermophysical properties and thermal performances,” Applied Sciences, Vol.8, No. 11, 2311. [https://doi.org/10.3390/app8112311]
• Islam, M. R., Shabani, B., and Rosengarten, G., 2017, “Electrical and thermal conductivities of 50/50 water-ethylene glycol based TiO2 nanofluids to be used as coolants in PEM fuel cells,” Energy Procedia, Vol. 110, pp. 101-108. [https://doi.org/10.1016/j.egypro.2017.03.113]
• Marsden, A. L., Wang, M., Dennis, J. E., and Moin, P., 2004, “Optimal aeroacoustic shape design using the surrogate management framework,” Optimization and Engineering, Vol. 5, pp. 235-262. [https://doi.org/10.1023/B:OPTE.0000033376.89159.65]
• You, J., Lee, J., Hong, S. and You, D., 2019. “Optimization of Biomimetic Propulsive Kinematics of a Flexible Foil Using Integrated Computational Fluid Dynamics–Computational Structural Dynamics Simulations,” Journal of Fluids Engineering, 141(6), p.061106. [https://doi.org/10.1115/1.4041879]