[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 18, No. 3, pp.26-32

ISSN: 2287-9706 (Print)

Print publication date Jun 2015

Received 31 Oct 2014 Accepted 13 Feb 2015

DOI: https://doi.org/10.5293/kfma.2015.18.3.026

부유체-균형추 파력발전장치의 전력에 대한 이론적 연구

이성범^* ; 이승건^** ; 문병영^***^{, †}

*부산대학교 조선해양공학과
**군산대학교 조선공학과

Theatrical Research an Generated Power of Float-Counterweight Wave Converters

Sung-Bum Lee^* ; Seung-Keon Lee^** ; Byung-Young Moon^***^{, †}

*Pusan National University Naval Architecture & Ocean Engineering
**Kunsan National University Department of Naval Architecture

Correspondence to: ^† moonby20@gmail.com

Abstract

The authors are developing a motion of floater body type wave energy converter of the float-counterweight system. This consists of the driving pulley, wire, float and counterweight suspended from idler pulleys and rachet mechanism. Though it has succeeded in solving the major structural strength problem in which the floats would slam against adjacent structure(s) by wave load acting horizontally. In order to overcome this problem. We propose a new system in which the wire transmitting the power is wound around the pulleys and the float receiving the wave power is pulled by the wire from both its upper and lower ends to avoid the occurrence of slackening during the wave cycle. In the paper, we developed the dynamics model for the proposed system. Energy gain has been calculated for realistic wave conditions and compared with the original float-counterweight device. The important differences from the float-counterweight system are that (1) both upward and downward motions of water surface can be utilized without problem. (2) slackening of energy gain and wire tension are effectively suppressed, and (4) for the same time averaged energy gain, the maximum wire tension is fairly lowered.

Keywords:

Wave Converter, Floating body Motion, Ocean Energy

키워드:

파력발전장치, 부유체 운동, 해양에너지

1. 서 론

화석 연료의 고갈과 환경문제에 관한 규제가 강화됨에 따라 신재생에너지에 대한 관심이 날로 높아지고 있다. 이 중 해양에너지는 태양광이나 풍력발전과 비교해 예측 가능성이 높고 안정적이며, 에너지 밀도는 공기의 약 800배로 가능성이 풍부하다. 이러한 해양에너지를 이용하는 발전으로는 파력, 조석, 해류, 조류, 온도차. 염분의 농도차 등이 있으며, 그 중에서도 파력에너지의 세계적인 부존 량은 약 2 TW(Tera Watt)로 추정되고 있다.^1)~4)

한국은 광역 파랑에너지 밀도는 계절별 및 해역별 차이가 크며, 겨울철이 상대적으로 큰 편이다. 전체적으로 북서계절풍에 의한 풍파가 지배적이며 동해 근해는 크지 않다. 한국 연안을 따라 근해는 3 kw/m, 그 외해는 5 kw/m 정도의 단위길이 당 파랑에너지 밀도를 보이고 있으며, 제주 서서남해역이 가장 커서 11 kw/m정도의 에너지밀도가 분포하고 있는 것으로 나타나고 있다. 파력발전의 경우 아직 본격적인 상용화는 이루어지지 않고 있으나, 가까운 장래에 기술개발과 함께 상용화에 이를 것으로 기대된다.

또한 한국 연안에서 20 km이내, 수심 200 m이내 해역의 면적(약 46,725 km²)에 4 MW/km²의 파력 발전기를 설치할 경우 파랑에너지 부존잠재령은 약 187 GWh이며, 이 해역의 5%를 파력발전에 이용할 경우 가용잠재량은 9.3GWh로 추정되었다. 가용잠재량에 파력발전 가동률(20%)을 적용한 기술적 잠재량은 약 2.3 GWh이며, 이는 연간 발전량과 석유환산톤으로 환산할 경우 약 16.4 TWh, 3.5백만 toe인 것으로 나타났다.

국내의 파력발전 기술수준은 2008년 말 기준으로 선진국 대비 78.0% 수준으로, 진동수주형 파력발전 기술은 실증단계에 진입하고 있으며, 월파형 파력발전은 설계기반 기술을 확보하고 있다. 또한 최근에는 가동물체형 파력발전에 대한 연구도 시작되고 있다. 국내에서 최초로 개발된 파력발전장치는 60 kw급 부유식 진동수주형 파력발전기인 주전 A호와 등부표용 부유식 소형 파력발전기인 BBDB(Backward Bent Duct Buoy)로 실해 역에 설치되어 실증시험이 수행된 바 있다.⁵⁾⁶⁾ 그 밖에도 유력한 장치들은 많이 개발하였지만, 이상이 현재의 주된 장치가 되고 있다.

본 연구팀에서도 파력발전장치를 개발 중이며, 현재 개량을 꾀하고 있다. 그렇지만 이상으로 말한 장치와 비교해서, 개발된 부유체-균형추식 파력발전장치⁷⁾는 많은 문제를 떠안고 있다. 본 논문에서는 부유체-균형추식 파력발전장치를 개량한 장치에 대해 연구하였다.

2. 부유체-균형추식 파력발전장치와 상시 긴장식 파력발전장치의 역학

2.1 부유체-균형추식 파력발전장치와 상시 긴장식 파력발전장치의 구조

2.1.1 부유체-균형추식 파력발전장치의 구조

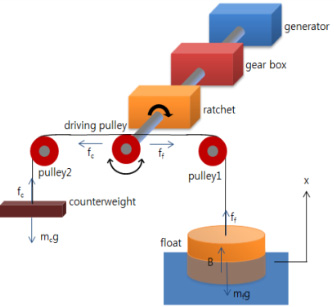
본 연구실의 부유체-균형추식 파력발전장치는 수면의 상하운동을 이용하는 파력발전장치이다. 풀리. 와이어, 부유체, 균형추, 증속기, 발전기로부터 구성되어 유체의 움직임을 와이어를 개입시켜 풀리에게 전해 회전운동으로 변환해 발전한다. 통상, 파에 의한 유체의 운동은 상하운동이기 때문에, 구동 풀리의 회전방향은 한 방향으로 움직이지 않기 때문에, 라쳇 기구를 도입하는 것으로써, 구동 풀리의 회전을 형편상, 유체의 하강 시에만 한 방향으로 해서 발전을 해서 전력을 발생시킨다.⁸⁾

이 장치의 의미가 있는 점은 첫 번째로, 와이어를 사용하는 것으로써, 복잡한 파의 거동에도 대응 가능하고, 구조 강도상의 문제를 해결하고 있는 것이다. 두 번째로, 중량물을 부유체와 균형추만으로 해서, 장치 부품에 의한 에너지의 손실을 줄이고 이론상의 에너지 변환효율을 30%로 높게 유지하고 있는 것이다. 세 번째로 장치를 수중에 넣은 가동부분과 동력을 변환하는 기계 부분으로 분리시켜, 설치·유지보수를 용이하게 해서 경제적으로 뛰어난 것이다. 그렇지만 파랑이나 장치의 조건에 따라서는 부유체 상승 시에 와이어가 느슨해져. 그 장력이 부가되어, 하강 시에 돌발적인 큰 인장력이 발생하는 것과 발생전력이 적은 것 등에 개선할 필요성을 느낀다. 그 때문에 현재는 텐션 풀리을 마련하고 와이어의 급격한 인장을 억제하는 것이나, 수조실을 마련⁹⁾하고 파의 연직방향의 변위만을 발생시켜 파고를 증폭시키는 것, 장치를 복수 연결시키는 것으로 발생전력의 증가¹⁰⁾와 안정화를 높여서 장치의 성능 향상을 꾀하고 있다.

2.1.2 상시 긴장식 파력발전장치의 구조

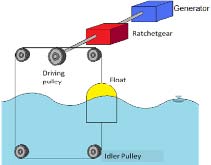
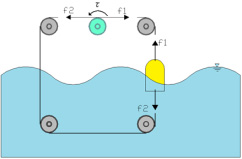
본 연구실에서 개발 중인 상시 긴장식 파력발전장치이다. 고정 발판, 구동 풀리, 라쳇기구, 홈붙이 풀리, 와이어, 부유체, 발전기로 구성된다. 종래의 부유체-균형추식 파력발전 장치와 같이, 수면의 상항운동을 와이어를 개입시켜 구동 풀리를 회전시켜 발전시키는 방식이다. 이 장치가 종래의 장치에 대해서 뛰어난 점은 부유체를 와이어에 의해 상하운동으로부터 인장 구속해, 와이어 장력이 부가되는 것을 회피하고 있는 점과 수면의 상승 시에도 발전을 가능하게 한 점이다.

이 장치를 구성하는데 필요한 것은 첫 번째로, 와이어 장력이 부가되는 것을 회피하기 위해서, 수면에 떠있는 부유체를 상하운동으로부터 와이어에 의해 인장 구속하는 것이다. 두 번째로, 장치로서 와이어에 항상 인장력을 붙인 상태로 구동 풀리에 동력을 전달하기 때문에 수면 위쪽에 있는 구동 풀리에 동력을 전달하기 때문에 수면 위쪽에 있는 구동 풀리의 양측이 고정부에 2개 그리고 수중의 고정부에 2개의 아이들 풀리를 배치하는 것이다. 세 번째로, 큰 와이어 장력을 견디기 위해서 풀리를 고정하는 지지 구조체를 라멘구조와 동등의 구조역학 특성을 가지는 것으로 하는 것이다. 네 번째로, 수중의 아이들 풀리는 어떠한 경우도 수면 상에 있는 것은 용납되지 않고, 그 위치를 (음력의 초하루와 보름 평균 간조면)-(1/2×최대파고)-(여유장)의 위치로 하는 것이다. 다섯 번째로, 라쳇기구를 다는 회전축에 하중이 직접 작용하는 것은 피할 필요가 있기 때문에, 상부의 2개의 아이들 풀리의 중간에 구동 풀리를 배치한 구성으로 하였다.

유체의 형상에 대해서는 수면의 상하운동의 동력을 효율적으로 획득할 수 있어 파의 수평력의 영향을 받기 어렵고, 여러 가지의 방향의 파에 대해서 치우치지 않게 동작하는 것이 바람직하다. 그 때문에 ｢유체 수평치수 < 0.1×(대표적인 파의 파장)｣가 이상이며, 또 유체 상부가 월파를 효율적으로 흘리는 구조가 좋다. Fig. 2과 같은 형상을 제안하였다.

Fig. 1

Sketch of the float-counterweight device

Fig. 2

Sketch of the new device

2.2 여러 가지의 장치의 역학 방정식

2.2.1 부유체-균형추식 파력발전장치의 역학

부유체-균형추식 파력발전장치의 역학 모델은 무부하 정지상태에서의 부유체와 카운터웨이트의 균형식, 가동상태에서의 부유체의 운동방정식, 회전체의 운동방정식, 발전기 관련의 역학의 4개로부터 구성된다.

(1) 부유체의 무부하 정지상태에서의 균형식

부유체의 무부하 정지상태에서의 균형식은 식 (1)으로서 주어진다. M_f는 부유체의 질량, D_f 는 부유체의 직경, h는 부유체의 흘수, M_c 는 카운터웨이트의 질량, ρ_w 는 해수의 밀도, g는 중력가속도이다. 이 식은 연직방향의 균형에 대해 세울 수 있어 또 부유체·카운터웨이트에 연결한 와이어의 장력은 서로 동일하다고 하는 관계로부터 성립되고 있다.

M f g = 14 π ρ ω g D f 2 h + M c g

(1)

(2) 가동상태에서의 부유체 운동방정식

본 장치에서는 부유체와 수면의 위치 관계에 의해, 부유체가 일부 몰수, 전체 몰수, 공중에 매달린 경우가 존재한다. 거기서 각각의 상태에서의 운동방정식은 다음과 같이 주어진다. 여기서, x_f, x_w 는 각각 무부하·정지상태로부터의 부유체 수면 변위량, f_f 는 부유체에 연결한 와이어 장력, C_D 는 항력계수, C_M 는 가상질량계수이다.

① 부유체가 일부 몰수 시(0 ≤ h + X_ω - X_f ≤ H_f)

M f ∙ d 2 x f d t 2 = f f + 14 π ρ ω D f 2 g h + x ω - x f - M f g + 18 C D ρ ω ∙ d x ω d t - d x f d t d x ω d t - d x f d t π D f 2 - 14 C M D f 2 ρ ω h + x ω - x f d 2 x f d t 2

(2)

식 (2)의 우변 제1항은 와이어 장력, 제2항은 부유체에 작용하는 부력, 제3항은 부유체에 작용하는 중력, 제4항은 물과 부유체의 상대운동에 의해 부유체가 받는 형상 저항, 제5항은 부유체가 유체 중에서 가속하는데 필요한 부가적인 힘, 부가질량을 나타낸다. 발전을 시켰을 때 부유체가 일부 몰수상태인 것이 적절하다.

② 부유체의 전체 몰수 시(h + X_ω - X_f > H_f)

M f ∙ d 2 x f d t 2 = f f + 14 π ρ ω D f 2 g H f - M f g + 18 C D ρ ω ∙ d x ω d t - d x f d t d x ω d t - d x f d t π D f 2 - 14 C M D f 2 ρ ω H f d 2 x f d t 2

(3)

식 (3)의 우변의 의미는 식 (1)의 경우와 같다.

③ 부유체가 공중에 매달렸을 시(h + X_ω - X_f < 0)

M f ∙ d 2 x f d t 2 = f f - M f g

(4)

Fig. 3

Tensile forces and the angle of rotation of the driving pulley

(3) 회전체의 운동방정식

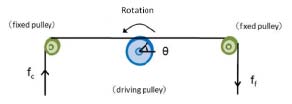
회전체의 운동방정식은 식 (5)으로서 주어진다. θ는 회전체의 무부하 ·정지상태로부터의 반시게방향의 회전각, I 는 회전체 전체의 관성모멘트, C는 기계 전체의 점성감쇠계수, τ는 발전기에 의해 구동 풀리가 받는 반시계방향의 토오크, f_c는 카운터웨이트에 의한 장력, R_m 는 구동 풀리의 반경이다. 좌변 제1, 2항은 각각의 운동량 미분, 기계 전체의 점성에 의한 감쇠를 나타낸다. 또 부유체 하강시만 구동 풀리는 회전하기 때문에, 식 (5)의 τ는 항상 +가 된다.

I d 2 θ d t 2 + C d θ d t = τ + f c - f f R m

(5)

또 카운터웨이트의 상승량을 x_c로 하면, 카운터웨이트의 운동방정식은 식 (6)으로서 주어진다.

M c d 2 x c d t 2 = f c - M c g

(6)

(4) 발전기 관련 역학

발전기 관련 역학으로서 토오크 τ, 발생전압 e, 발생전력 P_G 는 식 (7)~(9)로서 표현한다. i는 발생전류, G 는 기어비, k_τ는 토오크계수, $k ϵ$ 는 유도발전계수, r는 부하저항이다. 부유체 하강 시에만 τ는 +, e 는 식 (8)이 되어 상승 시에는 τ = 0, e = 0이 된다.

τ = - G k τ i

(7)

e = G k ϵ d θ d t

(8)

P G = r ∙ i 2 = r - G k ϵ r ∙ d θ d t 2

(9)

또 부유체 변위 x_f 와 카운터웨이트 변위 x_c , 풀리의 회전각 θ 에는 다음과 같은 관계가 있다.

x f = R m θ

(10)

x c = - R m θ

(11)

(5) 계산 조건

파의 조건으로서는 정현파를 가정한다. 파고를 H , ω을 파의 진동수로 하면, 수면 변위는 식 (12), 초기조건은 식 (13)으로서 주어진다.

x ω = H 2 c o s ⁡ (ω t)

(12)

θ 0 = H 2 R m, θ ˙ 0 = 0

(13)

여기서, 식 (12)는 초기시간을 수면이 최고일 때로 나타난다. 이러한 이유는 최저 수위나 파고가 0일 때를 초기조건으로 하면, 수면이 하강을 시작할 때까지 발전량이 0이 계속된다. 또, C_D , C_M 을 정의해 왔지만, 이 장치는 부유체가 물표면 근처에서 일부 몰수 상태 혹은 조금의 머리로 수몰한 상태로 운동하기 때문에, 기왕의 연구의 문제 설정이 다르다. 그 때문에 물과 부유체의 상대운동에 의한 상호 작용력을 무시해 계산한다.

기계 점성감쇠 계수 C는 계산을 실시한 후에 산출하기 때문에, 초기의 시점에서는 임의의 값으로 해서 계산을 실시하였다. 수치해석의 수법으로서는 4차의 Runge-Kutta method를 이용하였다.

2.2.2 상시 긴장식 파력발전장치의 역학

상시 긴장식 파력발전장치의 역학 모델은 무부하 정지상태에서의 부유체와 카운터웨이트의 균형식, 가동상태에서의 부유체의 운동 방정식, 회전체의 운동방정식, 발전기 관련 역하으로부터 주로 구성된다.

Fig. 4

Sketch showing wire tensions in the new system

(1) 부유체의 무부하 정지상태에서의 균형식

부유체의 무부하 정지상태에서의 균형식은 다음과 같이 주어진다. 식 (14)의 M_c는 카운터웨이터의 질량, M_f 는 부유체의 질량, D_f 는 부유체의 직경, ρ_w 는 해수의 밀도, g는 중력가속도, h는 부유체의 흘수이다. 이 식은 연직방향의 균형에 대해 세울 수 있으며, 부유체와 카운터웨이트에 연결한 와이어의 장력은 서로 동일하다는 관계로부터 성립되고 있다.

M f g = 14 π ρ ω D f 2 h g

(14)

(2) 부유체의 가동상태에서의 운동방정식

부유체가 일부 몰수, 전체 몰수, 공중에 매달린 경우에 대해서 다음과 같이 주어진다. 여기서, f₁ , f₂ 는 각각 부유체 상부, 하부에 접속된 와이어의 장력이다. 여기에서는 구 방식에서 고려하고 있던 부가 질량력과 형상 저항을 고려하지 않았다.

① 부유체가 일부 몰수 시(0 ≤ h + X_w - X_f ≤ H_f)

M f d 2 x f d t 2 = 14 π ρ ω D f 2 g x ω - x f + f 1 - f 2

(15)

② 부유체가 전체 몰수 시(h + X_w - X_f > H_f)

M f d 2 x f d t 2 = 14 π ρ ω D f 2 g H f + f 1 - f 2 - M f g

(16)

③ 부유체가 공중에 마달렸을 시(h + X_w - X_f < 0)

M f d 2 x f d t 2 = f 1 - f 2 - M f g

(17)

(3) 회전체의 운동방정식

회전체의 운동방정식은 식 (18)이 된다.

I d 2 θ d t 2 + C d θ d t = τ + f 2 - f 1 R m

(18)

(4) 발전기 관련 역학

발전기 관련 역학은 다음과 같다.

τ = - G k i

(19)

e = G k ϵ d θ d t

(20)

P G = r ∙ i 2 = r - G k ϵ r ∙ d θ d t 2

(21)

또, 부유체와 구동 풀리의 회전각의 관계는 식 (22)으로서 주어진다.

x f = R m θ

(22)

(5) 계산조건

이론식에게 주는 파의 조건으로서는 식 (23)로 가정한다. 초기조건으로서는 식 (24)으로 해서, 조파장치에 의해 조파를 시작하였을 때 각을 초기 시간으로 하고 있다. 또 식 (14)의 쌍곡선 탄젠트 함수 tanh는 장치에 의한 조파의 첫 시작을 표현하고 있다.

x ω = H 2 t a n h t s i n 2 π T t

(23)

θ 0 = 0, θ ˙ 0 = 0

(24)

(6) 와이어의 장력

부유체의 상부, 하부에 접속된 와이어의 장력은 식 (26)으로서 주어진다. 조건식으로서 식 (25)을 이용했다. 식 (26)은 발생하는 와이어 장력의 작은 부분을 와이어가 느슨해지지 않게 미리 작용시킨 와이어 장력의 기적치와 근사하는 것을 나타내고 있다.

M i n f 1, f 2 = 기적치

(25)

① 부유체가 상승하고 있는 경우(f₂ > f₁)

f 2 = f 1 + 14 ρ ω π D f 2 g x ω - x f - R m M f d 2 θ d t 2

(26)

② 부유체가 하강하고 있는 경우(f₁ > f₂)

f 1 = f 2 - 14 ρ ω π D f 2 g x ω - x f + R m M f d 2 θ d t 2

(27)

3. 파랑 조건 및 장치 제원에서의 전력 평가

3.1 계산에 이용하는 장치 제원

복수 연결 시의 발생전력의 평가를 실시하기 전에 안정된 발생전력의 상태를 살펴보기 위해서 Table 1은 수치해석에 이용한 장치 제원이다. 이 장치는 일본의 미츠비시중공업 (주) 나가사키 연구소에서 실시한 실험의 제원을 그대로 사용해, 상시 긴장식에 관해서는 그 제원의 부유체 질량만 변경하고 있다. 계산조건의 파는 상시 긴장식에서 제안한 것을 사용했다.

Table 1.

Parameters of equipment

3.2 부유체와 수면의 변위

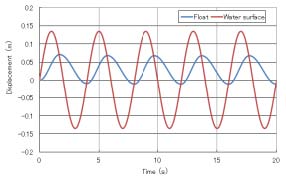
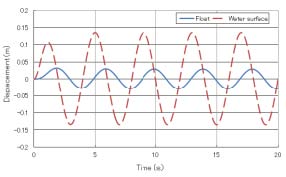
계산결과, 부유체-균형추식, 상시 긴장식의 부유체와 수면의 변위는 각각 Fig. 5, 6이 되었다. 부유체의 변위에 대해, 부유체-균형추식에서는 부유체가 평균 해수면에서 보다 위쪽을 중심으로 해서 운동해서, 상시 긴장식에서는 평균 해수면을 중심으로서 운동하고 있는 결과가 되었다. 또 양 방식에서, 수면의 변위에 대해서 부유체의 변위는 작아졌다. 부유체-균형추식이 평균 해수면의 위쪽을 중심으로 해서 운동하는 이유는 발전을 하강 시에만 실시하기 때문에, 충분히 하강을 다할 수 없기 때문이다. 또 양 방향에 대해 수면의 변위에 비해 부유체 변위가 작아진 이유는 에너지 변환에 비해 부유체 변위가 작아진 이유는 에너지 변환에 동력을 사용해 수면의 상승에 의한 에너지가 모두 부유체의 상하운동으로 변환되지 않기 때문이다.

또 양식에 대해서 초기조건을 변화시키고 계산을 실시했는데, 초기조건에 다른 조건을 부가했을 경우에서도, 시간이 경과하면 같은 변위를 나타내는 것을 알 수 있다. 이것은 일반적인 초기조건의 영향은 시간이 경과하는 것에 따라 약해지는 사실에 기인하고 있다.

이상의 결과, 상시 긴장식은 평균 해수면을 중심으로 해변위해, 부유체-균형추식에 비해 그 거동이 안정되어 있는 결과를 얻었다. 이 때문에 부유체의 변위가 예상하기 쉽고, 장치를 설계하는데 있어서 뛰어난 결과를 얻었다.

Fig. 5

Temporal variation of water level and float displacement of the float-counterweight device

Fig. 6

Temporal variation of water level and float displacement of the new system

Fig. 7

Temporal variation of the water tension of float-counterweight device

Fig. 8

Temporal variation of the wire tension of the new system

Fig. 9

Temporal variation of electric power of float-counterweight device

Fig. 10

Temporal variation of electric power of new system

3.3 와이어 장력

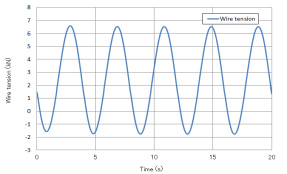
Fig. 7, 8에서 보면 상시 긴장식을 보면, 최저치 부근에서 갑자기 와이어 장력이 변화하고 있는 것을 알 수 있다. 이 때문에 충격적인 힘이 발생할 우려가 있지만, 이것은 그림의 외관상이며, 실제로는 상하의 와이어 장력은 매끄럽게 변화해, 충격적인 힘은 발생하지 않는다.

또 부유체-균형추식을 보면, 와이어 장력의 초기치가 제로가 아니다. 이것은 실험의 제원을 이용했기 때문에, 실험의 제원에서는 부유체의 균형이 실현되지 않기 때문이다.

이상의 결과, 상시 긴장식은 부유체-균형추식과 비교해 강도상 뛰어난 것을 알 수 있다.

3.4 발생전력

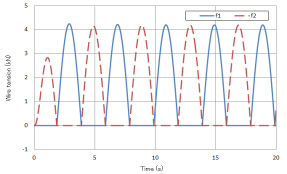
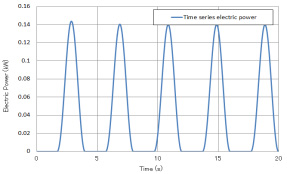
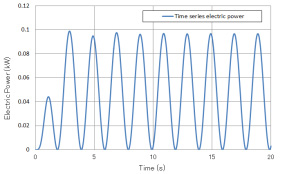
발생전력은 Fig. 9, 10에서 보면 부유체-균형추식은 하강시만 발전해서, 상시 발전이 가능하지 않지만, 발생전력의 최대치가 상시 긴장식에 비해 큰 결과가 나왔다. 상시 긴장식에서는 발생 전력의 피크는 작아졌지만 상시 발전이 가능해져, 발생 전력의 파형이 안정되는 결과를 얻었다. 부유체-균형추식, 상시 긴장식의 발생전력은 각각 0.039 kW, 0.049 kW이다.

또 그림은 생략하지만, 부유체-균형추식, 상시 긴장식의 양 방식에 있어서 전체 몰수, 공중에 매달린 상태가 발생하는 경우, 발생전력이 안정되지 않는 것을 알았다.

4. 결 론

부유체-균형추식 파력발전장치와 상시 긴장식 파력발전장치의 비교를 실시했다. 비교한 결과를 정리하면 다음과 같이 요약할 수 있다.

1) 종래 본 연구실이 제안하고 있던 부유체-균형추식 파력발전장치에 대해, 그 개량한 상시 긴장식 파력발전장치를 제안했다.
2) 상시 긴장식은 부유체-균형추식의 문제점인 와이어 장력이 부가되는 현상을 해소하고, 충격적인 힘의 발생을 없게 했다. 그 때문에 구조 강도가 뛰어나다.
3) 상시 긴장식은 일부 몰수 상태의 경우, 부유체-균형추식에 비해 와이어 장력이 작다. 그러나 전체 몰수 상태 또한 파고가 높고, 주기가 짧은 경우, 부유체-균형추식에 비해 와이어 장력은 커진다.
4) 상시 긴장식은 상시 발전이 가능하고, 일부 몰수 상태가 실현되고 있는 경우 발생전력이 안정적이기 때문에, 움직임을 상정하기 쉽고, 설계에 유리하다.

Acknowledgments

본 연구는 교육부와 한국연구재단의 지역혁신인력양성사업으로 수행된 연구결과 (No. 2013H1B8A2023237)의 지원으로 연구되었습니다.

References

“BP Statistical Review of World Energy”, BP, (2009).
Evans, D. V., “Wave Power Absorption within a Resonant Harbor”, Proc 2nd IntSymp On Wave Energy Utilization, Trendheim, p371-378, (1982).
Folley, M., Whittaker, T., and Osterried, M., “The Oscillating Wave Surge Converter”, Proc 14th Int Offshore and Polar Eng. Conf, Toulon, CD-ROM, p189-193, (2004).
Cruz, J., “Ocean Wave Energy”, Springer, (2008). [https://doi.org/10.1007/978-3-540-74895-3]
Korean energy Management Corporation, “New & Renewable energy white paper", (2010).
Hadano, K., Hashida, M., and Sato, M., “An Attempt to Make High Performance Wave Energy System”, Proc 12th Int Offshore and Polar EngConf, Kitakyshu, p556-561, (2002).
Hadano, K., Taneura, K., Watanabe, M., Nakano, K., Saito, T., and Matsuura, M., “On the Dynamics of the Float Type Wave Energy Conversion”, JSCE Journal B, 62(3), p270-383, (2006). [https://doi.org/10.2208/jscejb.62.270]
Hadano, K., Lee, S. B., and Moon, B. Y., Dynamics model of the float-type wave energy converter considering tension force of the float cable, Journal of the Korean Society of Marine Engineering, 38(2), p217-224, (2014). [https://doi.org/10.5916/jkosme.2014.38.2.217]
Hadano, K., Moon, B. Y., Lee, S. B., and Kim, K. J., "The Experimental Study about Kinetic Change of Water Surface in the Chambers for Wave Energy Converter", Jouranl of Korean Society for Fluid machinery, 17(2), p41-47, (2014). [https://doi.org/10.5293/kfma.2014.17.2.041]
Lee, S. B., Hadano, K., and Moon, B. Y., "A study for electric power of float-counterweight wave energy converter", Journal of the Korean Society of Marine Engineering, 38(7), p936-942, (2014). [https://doi.org/10.5916/jkosme.2014.38.7.936]

제 원	명 칭	기호와 단위	F-C Type	WGSW
부유체	질 량	M_f(kg)	1680	1288
	높 이	H_f(m)	2	2
	직 경	D_f(m)	0.7	0.7
	홀수양	r_s	0.5714	0.5714
구 동 풀 리	반 경	R_m(m)	0.18	0.18
구 동 풀 리	관성모멘트	I(kg·m²)	1.2348	1.2348
증속기	기어비	G	41.36	41.36
발전기	유 도 발전계수	k_e(V/rpm)	0.08	0.08
	토오크 계 수	k_τ(N·m/A)	1.2838	1.2838
	부하저항	r(Ω)	0.666	0.666
동 력 전달부분	점 성 감쇠계수	C(N·m·s)	1470	1470
파	주 기	T(s)	4	4
파	파 고	H(m)	0.27	0.27
중력가속도		g(m/s²)	9.8	9.8
해수밀도		ρ_ω(kg/m³)	1025	1025
균형추	질 량	M_c(kg)	150