내부냉각노즐의 열차폐코팅을 위한 복합열전달 해석기법 연구

1. 서 론

가스터빈의 고압터빈 영역은 연소기에서 나오는 고온 고압의 작동유체에 노출되며. 이러한 고온 고압 환경은 터빈 요소들에 크리프를 발생시키거나 심하면 파손이 일어나게 한다. 따라서 터빈 요소들을 보호하기 위해 대류냉각(convection cooling), 충돌냉각(impingement cooling), 막냉각(film cooling), 열차폐코팅(thermal barrier coating, TBC) 등의 다양한 냉각기법이 적용된다.⁽¹⁾

그중에서 TBC는 열전도도가 낮은 재료를 금속 표면에 코팅해서 열차폐 층을 형성시키는 냉각기법이다. TBC는 터빈과 연소기의 부품들을 절연시켜 엔진의 내구성을 높일 뿐만 아니라 효율 향상에도 영향을 미친다.⁽²⁾

다양한 냉각기법이 적용된 터빈은 초기 설계 단계에서 실험을 수행하기에 어려움이 있다. 따라서 많은 연구자들이 복합열전달(conjugate heat transfer, CHT) 전산해석을 통한 설계를 진행하고 있으며, 그 일환으로 TBC가 적용된 터빈 요소에 대한 전산해석을 수행했다.

Hylton 등⁽³⁾은 내부냉각이 적용되는 NASA의 Mark II 베인과 C3X 베인을 이용하여 실험과 2차원 전산해석을 수행하였다. 주 유동과 냉각 유동의 작동 조건을 변화시키면서 열/유동 특성을 확인하였다.

Gupta⁽⁴⁾는 NASA의 C3X 베인을 모델로 사용하여 복합열전달 해석기법을 통한 3차원 열/유동 전산해석을 수행하였다. 난류 모델을 바꿔가면서 Hylton 등⁽³⁾의 결과와 비교하였다. 또한, TBC를 적용한 베인 표면 온도의 변화를 확인하였다.

Mensch 등⁽⁵⁾은 블레이드 끝벽(end wall)에 충돌냉각과 막냉각이 적용된 형상을 통한 TBC의 영향성을 확인하기 위해 복합열전달 전산해석을 수행하였다.

Boyle⁽⁶⁾은 TBC와 막냉각 기법의 교차적용 연구를 수행하였다. TBC가 적용된 경우에는 막냉각 없이 내부냉각만 작용하는 경우에 동일한 블레이드 표면 온도를 얻는데 필요한 냉각유체의 양이 감소한다고 하였다.

이처럼 TBC를 적용한 터빈 요소에 대한 전산해석 연구가 이루어져 왔으나, TBC 적용을 위한 전산해석 기법 정립은 미비한 상황이다.

본 연구에서는 TBC 적용 연구 시의 효과적인 복합 열/유동 해석기법 검토를 위하여 두 가지 해석기법을 수행, 비교 분석을 하였다. 첫 번째 기법은 실제 TBC 형상을 물리적으로 모델링하는 기법이고, 두 번째 기법은 베인 표면과 주 유동 사이에 수치적인 열저항만 모델링하는 기법이다.

2. 열차폐코팅(TBC)

TBC는 가스터빈 냉각기법의 하나로, 열전도도가 낮은 재료로 금속의 표면을 코팅하여 주 유동의 뜨거운 공기로부터의 열전달을 억제하는 열차폐 역할을 한다.

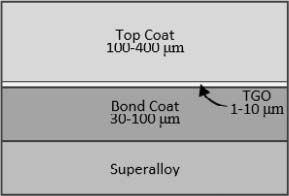
Fig. 1은 TBC 시스템의 도식을 나타낸 것이다. TBC는 세가지 층으로 구성된다. 상단은 탑코트(top coat, TC) 층으로서 열전도도가 1~2 W/m·K로 낮은 yttria stabilized zirconia(YSZ)와 같은 재료를 사용해 열차폐 역할을 한다. 하단은 본드코트(bond coat, BC) 층으로서 TC 층을 초내열합금(superalloy)에 붙여주는 역할을 한다. 중간층은 열성장산화물(thermally grown oxide, TGO) 층으로서 BC 층의 산화작용으로 생성된다.

본 연구의 TBC는 열차폐에 영향이 미미한 BC 층과 TGO 층을 제외한 TC 층만 고려하였다.

2.1 열전달 과정

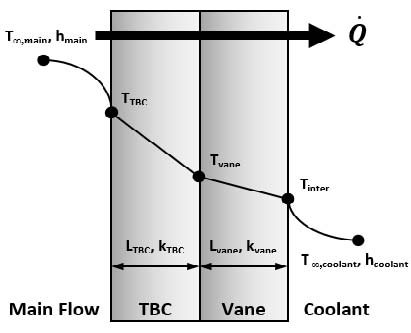
TBC 두께는 매우 얇아서 1차원 열전달 과정으로 가정할 수 있다. Fig. 2는 TBC가 적용된 베인의 열전달 과정을 1차원으로 가정한 경우를 도식한 그림이다. 이때 열전달률($$ \dot{Q}$$)은 식 (1)과 같으며, 총열저항(R_total)은 식 (2)와 같이 나타낼 수 있으며 모든 열저항의 합과 같다.⁽⁷⁾

$\[ \dot{Q}=\frac{T_{\infty , main}-T_{\infty , coolant}}{R_{total}} \]$

(1)

$\[ R_{total}=\frac{1}{h_{main}A}+\frac{L_{TBC}}{k_{TBC}A}+\frac{L_{vane}}{k_{vane}A}+\frac{1}{h_{coolant}A} \]$

(2)

여기서 T_∞, h, L, k는 각각 유체 온도, 대류열전달계수, 전도 길이, 열전도도이며, a 는 단면적으로 모두 같다고 가정한다. 아래 첨자 중 “main”, “TBC”, “vane”, “coolant”는 각각 주 유동 영역, TBC 영역, 베인 영역, 냉각 유동 영역을 나타낸다.

Fig. 1

Schematic of the thermal barrier coating system(7)

Fig. 2

Heat transfer diagram of the TBC applied vane

2.2 열차폐코팅 적용기법

2.2.1 물리적 형상 모델링 기법

실제 TBC를 모사하기 위해 베인 표면 위에 TBC 형상에 해당하는 해석 영역을 만들었다. 그리고 만들어진 TBC 형상에 TBC 재료의 물성치를 적용하였다. 본 연구에서는 이러한 TBC 적용기법을 물리적 TBC(physical TBC) 기법이라고 명하였다.

물리적 TBC 기법은 실제 TBC를 모사하기 때문에 베인 형상의 변화가 발생한다. 이로 인해 야기되는 압력, 속도, 질량 유량 등의 유동 특성 변화를 관찰할 수 있다는 장점이 있다. 하지만 TBC에 해당하는 해석 영역 추가로 인해 전산해석에 소요되는 자원과 시간이 증가하게 되어 해석 비용이 증가하게 된다. 또한, TBC 두께를 변화시키면 형상을 수정하고 격자를 새로 만들어야 하는 어려움도 있다.

Fig. 3

C3X vane geometry domain

2.2.2 수치적 모델링 기법

ANSYS CFX의 경계면 처리기법인 thin material 기법은 경계면 사이에 열저항을 추가하는 모델링 기법이다. 앞서 설명한 물리적 형상 모델링 기법과 달리 실제 형상을 모사하지 않고 주 유동과 베인의 경계면에 수치적으로 TBC의 열저항만 모델링하기 때문에 베인 형상의 변화가 없다. 본 연구에서는 이러한 TBC 적용기법을 수치적 TBC(numerical TBC) 기법이라고 명하였다.

수치적 TBC 기법은 형상 수정 및 격자 재생성을 하지 않아도 되기에 격자 생성의 어려움이 해소되고, 격자수가 증가하지 않아 해석 비용을 절감할 수 있다. 하지만 실제 TBC 형상이 없으므로 TBC 표면 온도를 구할 수 없고, 베인 표면 온도만 알 수 있다. 또한, TBC 형상으로 인한 유로 면적 변화가 야기하는 유동 특성 변화를 모사할 수 없고, 막냉각이 적용된 경우에는 냉각홀의 출구 인접 영역의 유동 현상을 정확히 모사할 수 없다.

3. 전산해석 전처리 과정

3.1 전산해석 모델 형상

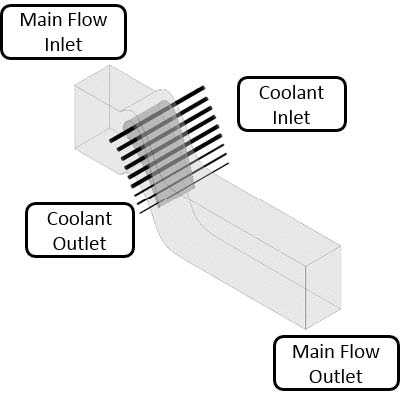
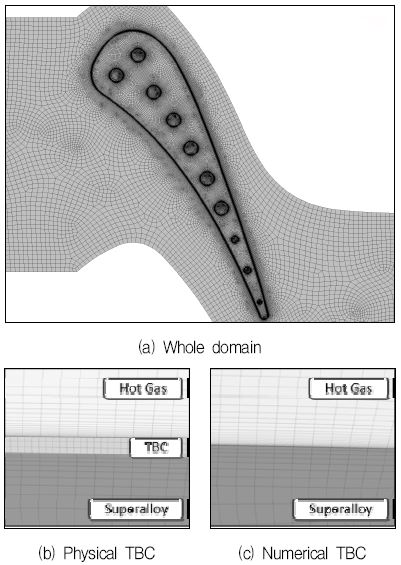
본 연구에서는 Hylton 등⁽³⁾이 사용한 NASA의 C3X 베인 형상을 사용하였다. C3X 베인은 주 유동(main flow) 영역 1개, 베인(vane) 영역 1개, 냉각 유동(coolant) 영역 10개, 총 12개의 영역으로 구성되고, 자세한 형상은 Fig. 3에 나타내었다.

물리적 TBC 기법은 베인 표면 위에 TBC 영역을 추가해서 총 13개의 영역으로 해석을 진행하였다. 수치적 TBC 기법은 기존 C3X 베인과 같은 12개의 영역으로 해석을 진행하였다.

Table 1.

Main flow boundary conditions

Table 2.

Coolant boundary conditions

Table 3.

Material properties of ASTM 310 stainless steel

3.3 전산해석 툴

본 연구에서는 ANSYS CFX 15.0을 사용하였고, 복합열전달 해석기법을 사용하여 3차원 열/유동 전산해석을 수행하였다. 유동의 수렴성을 위해 모든 변수의 root mean square(RMS) residual이 5×10^-5 이하가 되도록 하였다.

Fig. 4

Thermal conductivity of YSZ ceramic(9)

Fig. 5

C3X vane grids

3.4 경계 조건

본 연구에서는 Hylton 등⁽³⁾의 Run 158(4321) 실험의 경계 조건을 사용하였다. 주 유동 영역의 경계 조건은 Table 1에 나타내었다. 냉각 유동 영역의 경계 조건은 실험 데이터를 바탕으로 Table 2와 같이 설정하였다.

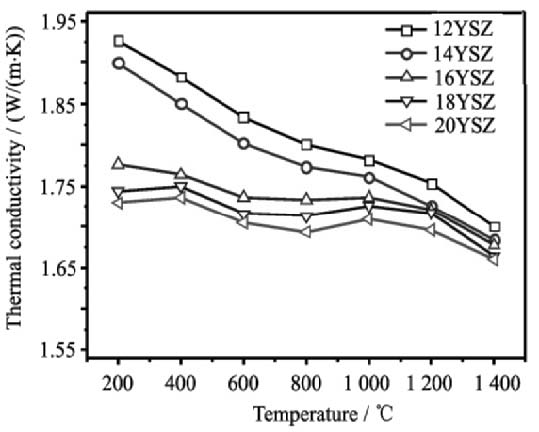
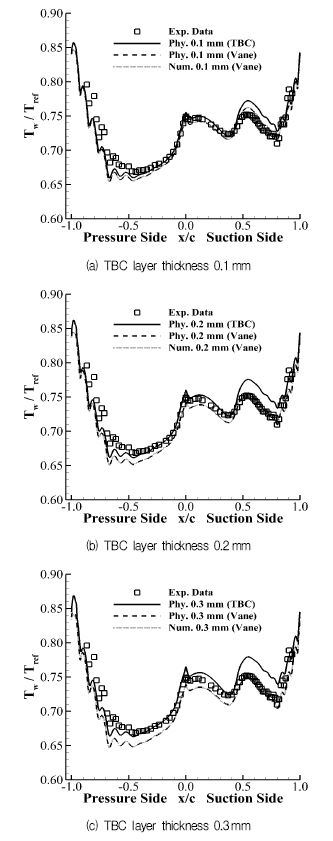
작동유체는 이상기체로 정압비열, 점성계수, 열전도도를 온도의 함수로 보정하여 사용하였다. 베인의 소재는 ASTM 310 stainless steel을 사용했으며, 물성치는 Table 3에 나타내었다. TBC는 Song 등⁽⁹⁾에서 연구한 20 mol.% YSZ를 사용했으며, 온도에 따른 열전도도는 Fig. 4에 나타내었다. TBC 두께는 0.1 mm, 0.2 mm, 0.3 mm를 적용하였다.

Table 4.

Number of elements of the computational domain

Fig. 6

Normalized static pressure distributions at midspan

4. 전산해석 결과

4.1 압력 분포

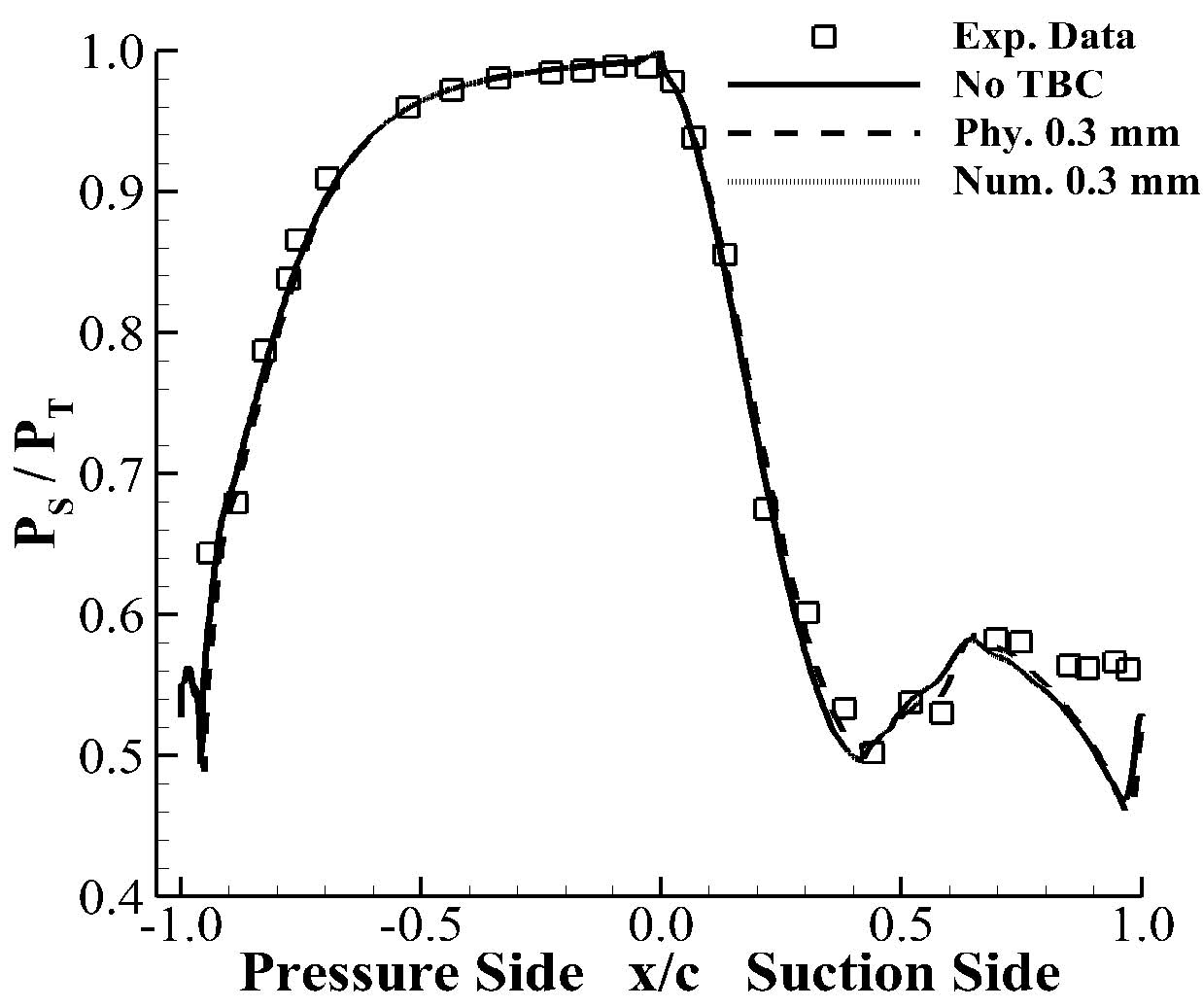
베인 span 방향 50% 위치에서의 표면 압력 분포를 Fig. 6에 나타내었다. 압력은 고체 표면의 정압력(P_S)을 주 유동 입구에서의 평균 전압력(P_T)으로 나눈 무차원화 값을 사용하였다. TBC가 없는 경우와 수치적 TBC 기법을 적용한 경우에는 베인 표면 압력을 사용하였으며, 물리적 TBC 기법을 적용한 경우에는 TBC 표면 압력을 사용하였다.

Fig. 7

Mass flow rate and throat area

모든 해석 결과는 실험값과 비슷한 경향을 보였다. 흡입면(suction side) 0.7≤x/c≤0.9 부근에서 실험결과와 최대 10%의 오차를 보였다. 이는 김진욱 등⁽⁸⁾의 연구결과에서 알 수 있듯이, 유동의 강한 비정상성 때문에 발생하는 현상이다.

수치적 TBC 기법을 적용한 경우의 표면 압력 분포는 TBC가 없는 경우와 일치하였다. 이는 수치적 TBC 기법을 적용할 경우, 베인 형상이 변하지 않기 때문이다. 물리적 TBC 기법을 적용한 경우의 표면 압력 분포는 TBC가 없는 경우와 x/c=0.6 부근에서 최대 2%의 차이를 보이지만, 전체적으로 비슷한 경향을 보였다. 이는 TBC에 의한 베인의 두께 변화가 5% 미만으로 매우 작기 때문이다.

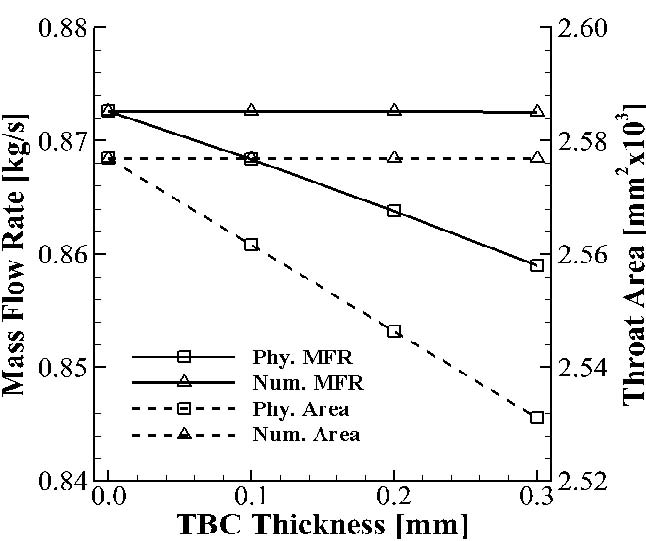
TBC 두께에 따른 질량유량과 노즐 목(throat) 면적 변화를 Fig. 7에 나타냈다. 수치적 TBC 기법을 적용한 경우는 형상 변화가 없으므로 노즐 목 면적이 TBC가 없는 경우와 같다. 따라서 질량유량, 압력, 속도 분포 등이 동일하게 나타난다. 물리적 TBC 기법을 적용한 경우는 TBC에 의해 노즐 목 면적이 발생한다. TBC 두께가 0.3 mm일 때 노즐 목면적이 1.7% 감소하였으며, 이때 질량유량은 1.5% 감소하고 압력과 속도 분포는 비슷하게 나타났다. 만약 TBC 두께가 더 증가하면 노즐 목 면적이 줄어들게 되어 초크 상태가 되거나 충격파(shock)가 발생하는 등 유동 특성 변화가 증가할 것으로 예상한다.

TBC에 의한 압력이나 질량유량과 같은 유동 특성을 알고자 할 경우에는 물리적 TBC 기법을 사용하는 것이 적합하다. 하지만 TBC 두께가 얇아 TBC에 의한 유동 특성 변화가 크지 않은 경우에는 수치적 TBC 기법을 사용하여 비슷한 결과를 얻을 수 있다.

Fig. 8

Normalized temperature distributions at midspan

4.2 온도 분포

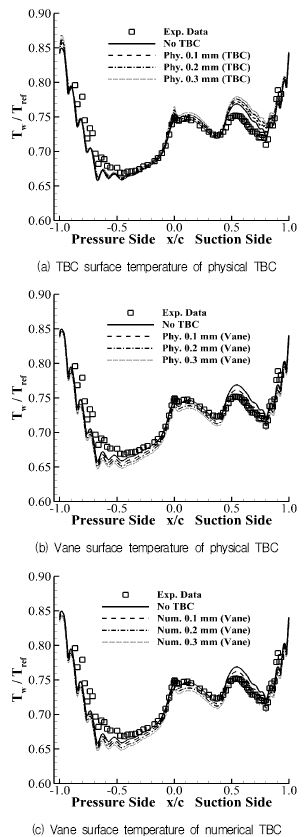
베인 span 방향 50% 위치에서의 표면 온도 분포를 Fig. 8과 Fig. 9에 나타내었다. 온도는 표면 온도(T_w)를 작동유체 온도(T_ref=811 K)로 나눈 무차원화 값을 사용하였다. 여기서 “Vane”은 베인 표면 온도를, “TBC”는 TBC 표면 온도를 나타낸 것이다. 모든 해석 결과의 표면 온도 분포는 실험값과 비슷한 경향을 보였다.

Fig. 8은 TBC 두께 변화에 따른 표면 온도 분포를 나타낸 것이다. 물리적 TBC 기법을 적용한 경우의 TBC 표면 온도는 Fig. 8a에 나타내었고, 베인 표면 온도는 Fig. 8b에 나타내었다. TBC 두께가 증가할수록 베인 표면 온도는 감소하고, TBC 표면 온도는 증가하는 경향을 보였다. Fig. 8c에는 수치적 TBC 기법을 적용한 경우의 베인 표면 온도를 나타내었다. 물리적 TBC 기법을 적용한 경우 마찬가지로 TBC 두께가 증가할수록 베인 표면 온도가 감소하는 경향을 보였다.

Fig. 9은 TBC 적용기법에 따른 표면 온도 분포를 나타내었다. 물리적 TBC 기법을 적용한 경우와 수치적 TBC 기법을 적용한 경우의 베인 표면 온도는 동일한 분포를 보였다. TBC두께가 증가할수록 베인 표면 온도는 감소하고 TBC 표면 온도는 증가하여 TBC 내 온도 차이가 증가하는 경향을 보였다.

Fig. 9

Comparison of the TBC layer application methodology

Fig. 10

Overall cooling effectiveness

Mensch 등⁽⁵⁾과 Davidson 등⁽¹⁰⁾은 베인의 냉각 성능을 알고자 베인 표면 온도를 무차원화한 냉각 유효성(overall effectiveness)과 TBC 표면 온도를 무차원화한 TBC 유효성(TBC effectiveness)을 사용하였다. 냉각 유효성과 TBC 유효성은 각각 식 (3)과 식 (4)와 같다.

$\[ \mathrm{\varnothing }=\frac{T_{\infty , main}-T_{\omega , vane}}{T_{\infty , main}-T_{coolant, inlet}} \]$

(3)

$\[ \tau =\frac{T_{\infty , main}-T_{\omega , TBC}}{T_{\infty , main}-T_{coolant, inlet}} \]$

(4)

여기서 T_∞,main 은 주 유동의 온도, T_{coolant,inlet}은 냉각 유동의 입구 온도, T_w,vane 은 베인 표면 온도, T_w,TBC 는 TBC 표면 온도를 나타낸다.

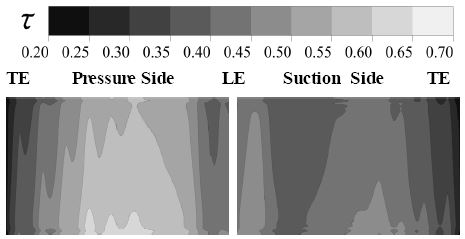
베인과 TBC의 표면 전체에 대한 냉각 유효성과 TBC 유효성은 Fig. 10과 Fig. 11에 나타내었다. 물리적 TBC 기법을 적용한 경우와 수치적 TBC 기법을 적용한 경우의 냉각 유효성은 비슷한 분포를 보였다. 베인 표면과 TBC 표면 모두 압력면이 흡입면보다 냉각이 잘되는 것을 알 수 있다. 냉각 유동이 베인을 지나면서 온도가 상승하기 때문에 냉각 유동의 출구 주변이 입구보다 냉각 성능이 떨어진다. 냉각 유동 경계면과 베인 표면의 거리가 가장 먼 3번과 4번 냉각홀 사이와 후연부(trailing edge)의 냉각 성능이 가장 낮게 나타났다. TBC 적용 시 베인 표면 전체의 냉각 성능이 향상되고 TBC 표면은 떨어진다.

냉각 유효성과 TBC 유효성의 평균값을 Table 5에 나타내었다. 수치적 TBC 기법을 적용한 경우와 물리적 TBC 기법을 적용한 경우의 냉각 유효성이 동일한 값을 나타냈다. TBC 두께가 증가할수록 냉각 유효성은 증가하고 TBC 유효성은 감소한다. 하지만 단위 두께 당 냉각 유효성과 TBC 유효성의 차이가 감소하는 경향을 보이는데, 이는 TBC 두께 증가로 총 열저항이 증가하고 열전달률이 감소하기 때문으로 보인다.

위 결과들을 통해서 물리적 TBC 기법과 수치적 TBC 기법 모두 동일한 온도 분포와 냉각 성능을 보여주는 것을 알 수 있었다. TBC 두께를 변화시키면서 냉각 성능 경향성을 확인하고자 하는 경우 격자를 재생성하지 않아도 되는 수치적 TBC 기법을 사용하면 해석비용을 절감할 수 있다.

4.3 전산해석 소요시간

TBC가 없는 경우와 수치적 TBC 기법을 적용한 경우의 전산해석 소요시간은 비슷하게 나타났다. 이는 격자 구성이 동일하기 때문으로 보이며, 유동 영역과 고체 영역 사이에 모델링된 열저항은 전산해석 소요시간에 영향이 거의 없음을 알 수 있다. 반면 물리적 TBC 기법을 적용한 경우는 전산해석 소요시간이 최대 10% 증가하였다. 이는 TBC이 해당하는 해석영역이 추가되고 이로 인해 격자수가 증가하기 때문으로 보인다. 따라서 해석시간이 오래 걸리는 복잡한 형상은 수치적 TBC 기법을 적용했을 경우 해석 비용을 절감할 수 있을 것으로 예상한다.

Fig. 11

TBC effectiveness of physical TBC 0.3 mm

Table 5.

Average surface effectiveness

5. 결 론

본 연구에서는 TBC 적용을 위한 전산해석기법 연구를 진행하였다. 검증 모델로는 NASA의 C3X 베인을 이용하였으며, 복합열전달 해석기법을 사용하여 3차원 열/유동 전산해석을 수행하였다. 실제 TBC 형상을 모사한 물리적 TBC 기법과 베인 표면에 수치적으로 TBC의 열저항만 모델링한 수치적 TBC 기법을 비교하였으며, 연구 결과를 요약하면 다음과 같다.

1) 물리적 TBC 기법은 실제 TBC에 의한 유동 특성을 모사할 수 있지만, TBC 두께 변화 시 형상 수정 및 격자 재생성과 해석 비용 증가와 같은 어려움이 있다.
2) 수치적 TBC 기법은 TBC에 의한 형상 수정 및 격자 재생성의 어려움이 해소되지만, TBC에 의한 유동 특성 변화를 모사할 수 없다.
3) 수치적 TBC 기법은 형상 변화가 없어 TBC가 없는 경우와 압력과 질량유량이 동일하게 나타났고, 물리적 TBC 기법은 두께 변화가 작아 압력과 질량유량에 미치는 영향이 미미하게 나타났다. TBC에 의한 유동 특성을 모사하기 위해서는 물리적 TBC 기법이 적합하다.
4) 물리적 TBC 기법과 수치적 TBC 기법을 적용한 경우의 베인 표면 온도 분포와 냉각 유효성은 동일하게 나타났다. TBC 두께가 증가할수록 베인 표면 온도는 감소하고 TBC 표면 온도는 증가하여 TBC 두께 변화에 따른 냉각 성능을 잘 나타냈다. TBC에 의한 냉각 성능만 알고자 할 경우 수치적 TBC 기법을 사용해도 무방하다.
5) 전산해석 소요시간은 물리적 TBC 기법을 적용한 경우가 수치적 TBC 기법을 적용한 경우에 비해 최대 10% 증가하였다.

수치적 TBC 기법을 이용하여 TBC 두께 변화에 따른 온도 특성을 분석하고, 적합한 TBC 두께를 선정하여 물리적 TBC기법을 이용하여 유동 특성을 확인하면 TBC 적용 연구를 더 효과적으로 진행할 수 있을 것으로 생각한다.

Acknowledgments

본 연구는 산업통상자원부 항공우주부품기술개발사업 (KA000157)의 지원을 받아 수행되었습니다.

References

• Saravanamuttoo, H. I. H., Rogers, G. F. C., Cohen, H., and Straznicky, P. V., (2009), Gas Turbine Theory, 6th Edition, Prentice Hall, London, p366-376.
• Padture, N. P., Gell, M., and Jordan, E. H., (2002), “Thermal Barrier Coatings for Gas-Turbine Engine Applications”, Science, 296, p280-284. [https://doi.org/10.1126/science.1068609]
• Hylton, L. D., Mihelc, M. S., Turner, E. R., Nealy, D. A., and York, R. E., (1983), “Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes”, NASA CR-168015.
• Gupta, J., (2009), “Application of Conjugate Heat Transfer(CHT) Methodology for Computation of Heat Transfer on a Turbine Blade”, Masters Thesis, The Ohio State University.
• Mensch, A., Thole, K. A., and Craven, B. A., (2014), “Conjugate Heat Transfer Measurements and Predictions of a Blade Endwall With a Thermal Barrier Coating”, Journal of Turbomachinery, 136(12), p121003. [https://doi.org/10.1115/1.4028233]
• Boyle, R. J., (2006), “Effects of Thermal Barrier Coating on Approaches to Turbine Blade Cooling”, ASME Turbo Expo 2006, GT2006-91202. [https://doi.org/10.1115/gt2006-91202]
• Cengel, Y. A., (2002), Heat Transfer: A Practical Approach, 2nd Edition, McGraw-Hill, Singapore, p128-137.
• Kim, J., Bak, J., Lee, S., Kang, Y., Cho, L., and Cho, J., (2014), “A Study on the Numerical Analysis Methodology for Thermal and Flow Characteristics of High Pressure Turbine in Aircraft Gas Turbine Engine”, KSFM Journal of Fluid Machinery, 17(3), p46-51. [https://doi.org/10.5293/kfma.2014.17.3.046]
• Song, X., Xie, M., Zhou, F., Jia, G., Hao, X., and An, S., (2011), “High-Temperature Thermal Properties of Yttria Fully Stabilized Zirconia Ceramics”, Journal of Rare Earth, 29(2), p155-159. [https://doi.org/10.1016/S1002-0721(10)60422-X]
• Davidson, F. T., KistenMacher, D. A., Bogard, D. G., (2014), “Film Cooling With a Thermal Barrier Coating: Round Holes, Craters, and Trenches”, Journal of Turbomachinery, 136(4), p041007. [https://doi.org/10.1115/1.4024883]