신발형 리브의 형상변화가 열전달 및 압력 강하에 미치는 영향

1. 서 론

화석연료의 고갈 및 가격 상승, 환경문제 등 세계적으로 에너지 문제가 대두됨에 따라 이에 대한 대응책으로 고효율의 가스터빈이 많은 조명을 받고 있다. 가스터빈의 경우 높은 열효율을 얻기 위해 고온 및 고압의 터빈 입구조건이 요구되는데 이러한 작동환경에서는 블레이드의 수명 및 성능을 보호하기 위한 냉각기술이 필수적이다. 터빈 블레이드의 냉각은 크게 내부냉각과 외부냉각으로 구분할 수 있으며 대표적인 내부냉각기법으로는 리브(rib), 딤플(dimple), 핀휜(pin-fin) 등의 난류촉진장치를 이용해 열전달을 증가시키는 방법이 있다.

이들 중 본 연구에서 다루고자 하는 냉각기법인 리브에 대해서는 이미 다양한 실험 및 수치해석적 연구가 수행되었다. Chandra 등⁽¹⁾은 정사각형 내부냉각유로에서 리브들이 설치된 면의 수를 변화시켜가며 표면 열전달 및 마찰계수를 측정하였다. 그 결과 면의 수가 늘어남에 따라 열전달계수 및 마찰계수가 증가한다는 것을 확인하였다. Islam 등⁽²⁾은 PIV(Particle image velocimetry)를 이용해 한 면에 리브들이 설치된 사각형 유로에서 리브 간 거리를 달리하며 난류유동 구조를 분석하였다. 그 결과 이 거리와 리브에 의해 박리된 유동의 재부착 길이(Reattatchment length)는 레이놀즈수(Reynolds number)가 15,000을 넘는 경우 서로 독립적인 것으로 나타났다. Graham 등⁽³⁾은 리브에 의한 폐쇄율(Blockage ratio)이 유동에 미치는 영향을 파악하기 위한 실험을 실시하였다. 그 결과, 리브의 바로 앞과 뒤에서 상당한 재순환유동이 발생하는 것을 확인하였다. 작은 리브의 경우 후류에서 재부착이 발생하는 반면 큰 리브의 경우 리브와 리브 사이 전체 영역에서 박리유동이 발생함을 알 수 있었다. Wang과 Sunden⁽⁴⁾은 실험을 통해 연속적으로 설치된 리브와 불연속적으로 설치된 리브에 대해 난류 유동을 관찰하였다. 그 결과 불연속의 리브에서는 말발굽 형태의 와류가 나타났으며 연속으로 설치된 리브에 비해 핫스팟(Hotspot)이 많이 나타나는 것을 확인하였다.

Fig. 1

Geometry of ribbed cooling channel.

Fig. 2

An example of grid system

위에 언급한 연구들과 함께 다양한 단면 형상을 갖는 리브의 열전달 성능에 대해 여러 연구가 이루어졌다. Liou와 Whang⁽⁵⁾은 실시간 홀로그래픽 간섭법(Real-time holographic interferometry)을 이용해 정사각형, 반원 및 이등변 삼각형 등 세 가지 단면형상의 리브가 각각 설치된 직사각형 유로에 대한 열전달 및 압력강하 성능을 조사하였다. 그 결과 정사각형, 반원 및 삼각형 리브가 설치된 유로에서 면적평균 열전달계수가 리브가 설치되지 않은 유로에 비해 각각 1.9-2.7, 1.6-2.1, 그리고 1.7-2.2 배로 증가한 것을 확인하였으며, 반원형과 삼각형의 리브가 정사각형의 경우에 비해 핫스팟이 적게 발생하는 것을 확인하였다. Manca 등⁽⁶⁾은 수치해석을 이용하여 정사각형, 직사각형, 이등변삼각형, 직각사다리꼴, 등변사다리꼴 등 여러 가지 단면의 리브가 부착된 냉각유로에 대해 연구를 수행하였다. 이를 통해 종횡비가 2인 삼각형 리브가 열전달 성능이 가장 높다고 보고하였다. Moon 등⁽⁷⁾은 수치해석을 통해 냉각유로에 부착된 12가지 리브단면 형상에 대해 수치해석적 연구를 수행하여 그 성능을 평가한 결과 신발형 단면을 갖는 리브가 열전달과 압력강하 측면에서 우수한 성능을 나타낸다고 보고하였다. 그러나, 이 연구에서는 신발형 리브의 단면형상 변화가열전달 성능 및 압력강하에 얼마만큼 영향을 미치는 지에 대한 연구는 수행되지 않았다.

본 연구에서는 신발형 리브의 기하학적 형상이 열전달 및 압력강하 특성에 미치는 영향을 분석하기 위해 신발형 리브들이 부착된 사각형 유로내 난류열전달 현상을 수치적으로 해석하고 열전달과 압력강하에 대한 파라메터 연구를 네 가지 형상변수를 사용하여 수행하였다.

2. 유동해석방법

본 연구에서는 삼차원 유동 및 열전달 해석을 위해 상용 전산유체역학 소프트웨어인 ANSYS CFX 15.0⁽⁸⁾을 이용하였다. 정상상태 압축성 Reynolds-averaged Navier-Stokes(RANS)방정식을 수치적으로 계산하여 유동 및 열전달 해석을 수행하였으며, 난류모델로는 Spezial-Sakar-Gatski(SSG)의 pressure-strain model을 사용한난류응력모델(Reynolds stress model)을 사용하였다. SSG모델은 유선의 굴곡이 강한 경우의 유동에 대해 비교적 정확한 예측을 보이는 것으로 알려져 있다.

Shui 등⁽⁹⁾은 리브가 설치된 유로에 대해 SSG 모델과 2-방정식 모델들인 SST와 k-e모델의 예측성을 검증하여 SSG모델이 유동구조 및 열전달을 가장 잘 예측한다고 보고하였다. 유동해석을 위해 고려된 계산영역은 Fig. 1과 같이 종횡비가 2이고 수력직경이 34 mm인 직사각형 냉각유로이며, 신발형 리브가 총 10개가 설치되어 있다. 유로의 높이 및 길이는 각각 25.5 mm와 268 mm이고 유로의 첫 번째 리브는 x/L=0.0896에 위치하고 있다. 그리고, 리브 사이의 거리와 유로 길이의 비 (P/L)는 0.0896, 리브 사이의 거리와 리브 너비의 비(P/e)는 10으로 하는 등 Moon 등⁽⁶⁾의 선행연구와 동일한 유로를 사용하였다. 수력직경을 기준으로 한 레이놀즈수는 10,000이다. 경계조건으로는 입구와 출구에 각각 속도와 정압력 조건을 사용하였다. 열전달면인 리브표면과 리브가 설치된 면에는 2,000W/m² 의 일정한 열유속 조건을 사용하였고 이를 제외한 나머지 면에는 단열조건(Adiabatic condition)을 적용하였다. 모든 벽면에는 점착조건(No-slip condition)이 적용되었다.

Fig. 3

Geometric parameters of a boot-shaped rib

Fig. 2에서와 같이 격자계는 육면체 정렬 격자계를 사용하였다. 리브 후방부에서 생성되는 복잡한 유동구조를 정확하게 해석하고 벽 근처의 높은 속도구배를 계산하기 위해 리브 주변 및 벽근처 격자를 조밀하게 구성하였으며, 벽에서 가까운 첫 번째 격자점에서의 y⁺ 값을 2.0 이하로 유지하였다. 계산에사용된 격자수로는 Moon 등⁽⁷⁾의 선행연구에서 수행한 격자의존성 시험의 결과를 바탕으로 약 360만개를 최적격자수로 사용하였다.

수치해석을 위하여 Intel i7 3.41GHz PC를 사용하였으며 한 형상을 계산하는데 약 4시간의 계산시간과 약 200번의 반복계산이 소요되었다. 수렴 여부는 RMS잉여값(Root mean square residual)이 10^-5 이하일 경우 수렴하였다고 판단하였다.

3. 형상변수 및 목적함수

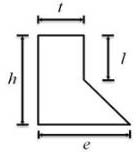
Fig. 3에 나타낸 리브 단면의 형상변화가 열전달 성능 및 압력강하에 미치는 영향을 살펴보기 위하여 4개의 무차원화된 형상변수로 리브 상단의 너비와 하단 너비의 비(t/e), 리브 상단의 높이와 리브 높이의 비(l/h), 리브의 높이와 유로 높이의 비(h/H), 리브 하단의 너비와 리브 높이의 비(e/h)를 각각 선정하였으며 Table 1에 각 형상변수들의 변화 범위를 나타내었다.

신발형 리브의 열전달 성능 및 압력강하를 확인하기 위하여 두 개의 성능함수를 정의하였다. 열전달과 관련한 성능함수는 다음과 같이 정의된다.

Table 1

Ranges of geometric parameters

여기서,

T_ω 와 T_b 는 각각 열전달이 일어나는 표면의 온도와 주 유동의 평균온도를 의미한다. k는 냉각유체로 사용된 공기의 열전도도, q₀는 열전달면에서의 열유속, D_h은 유로의 수력직경, Re는 수력직경을 사용한 레이놀즈수, Pr은 프란틀 수 (Prandtl number)를 의미한다. Nu는 각 면에서의 면적평균 누셀트 수(Nusselt number)이며 Nu₀ 는 회전하지 않는 매끈한 관에서 완전 발달된 유동에 의한 누셀트 수로서 Dittus-Boelter 관계식으로부터 계산된다. 열전달 성능은 난류유동이 완전 발달한 2번째 리브부터 10번째 리브 사이의 면에 대해 평가되었다.

압력강하와 관련된 성능함수의 정의는 다음과 같다.

여기서,

f₀ 는 매끈한 관에서 완전 발달된 유동에 대한 마찰계수로서 Petukhov 실험적 관계식에서 계산되며, Δp는 유동장에서의 압력강하를 나타낸다. ρ는 냉각유체(공기)의 밀도, U_IN은 입구에서 유동의 평균속도, P 는 피치를 의미한다.

4. 결과 및 검토

신발형 리브단면의 형상변화가 열전달 성능 및 압력강하의 변화에 미치는 영향을 알아보기 위해 4개의 형상변수, t/e, l/h, h/H그리고 e/h를 각각 변화시켜가며 수치해석을 실시하였다. 이 경우 변화하지 않는 변수들은 Table 1에 주어진 기준치로 고정된다. 본 연구의 수치해는 Moon 등⁽⁷⁾의 선행 연구에서 타당성이 검증된 바 있다.

Fig. 4

Variation of FNu with tip width-to-rib width ratio

Fig. 5

Variation of Ff with tip width-to-rib width ratio

4.1 리브 상단의 너비와 하단 너비의 비(t/e)

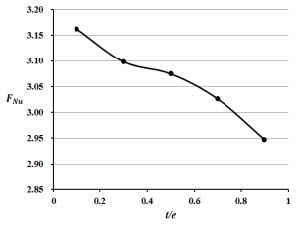
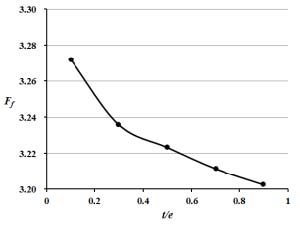
Fig. 4와 5는 고정된 리브 하단 너비 e에 대하여 0.1≤ t/e ≤ 0.9 의 범위에서 리브 상단의 너비를 변화시킨 경우에 대해 각각 면적평균 누셀트 수와 마찰계수 변화를 나타내고 있다. t/e가 감소할수록 면적 평균된 누셀트 수가 증가하는 경향을 볼 수 있다. 압력강하의 경우 t/e가 증가할수록 감소하는 경향이 나타났다. 그러므로 t/e가 감소할수록 열전달 성능은 향상되지만 압력강하 성능은 나빠지는 것을 알 수있다.

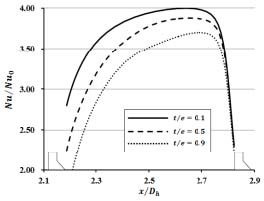
Fig. 6에서는 3번째와 4번째 리브 사이의 x-z평면(y=0)에서 t/e변화에 따른 유선분포를 나타낸다. t/e가 감소할수록 리브후류에서 생성되는 유동박리 영역의 크기가 감소하고 재부착 길이가 짧아지는 것을 확인할 수 있으며 이로 인해 열전달 성능이 증가되는 것을 알 수 있다. Fig. 7에서는 세 번째와 네 번째 리브 사이 열전달면의 중앙선(y=0)에서의 누셀트 수의 분포를 나타내었다. 재부착이 상대적으로 빠르게 일어지는 t/e = 0.1인 경우가 t/e = 0.5 와 0.9인 경우보다 최대 누셀트 수 및 전반적인 누셀트 수의 크기가 상당히 큰 것을 확인할 수 있다.

Fig. 6

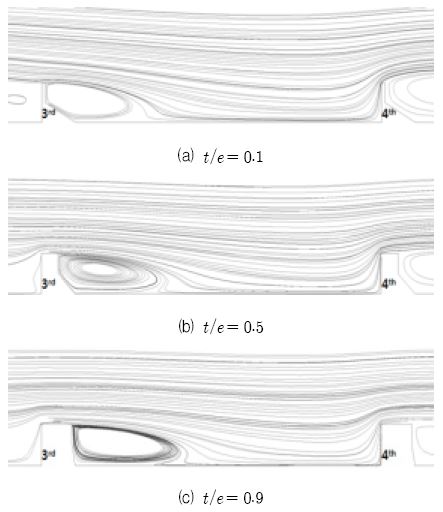
Streamlines between third and fourth ribs on x-z plane for ribs for different tip width-to-rib width ratio

Fig. 7

Distributions of Nusselt number distribution along the centerline of heated surface between third and fourth ribs

4.2 리브 상단의 높이와 리브 높이의 비(l/h)

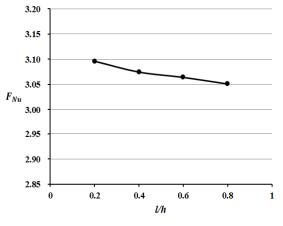
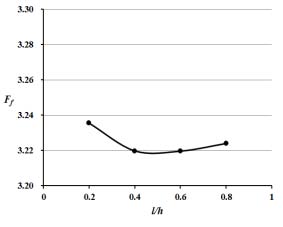
리브 상단의 높이와 리브 높이의 비에 따른 면적평균 누셀트 수의 변화가 0.2 ≤ l/h ≤ 0.8 범위에서 Fig. 8에 나타나 있다. l/h가 감소할수록 열전달 성능은 완만하게 증가하는 것으로 나타났지만 그 변화의 폭은 주어진 범위에서 t/e의 경우 (Fig. 4) 보다 1/4 정도로 작음을 알 수 있다. Fig. 9는 l/h 변화에 따른 압력강하와 관련한 성능함수의 변화를 나타낸 것이다. l/h=0.4와 0.6 사이에서 압력강하의 최소치가 존재함을 알 수 있다. 그리고, l/h가 이 범위 보다 작은 경우가 큰 경우 보다 압력강하가 크게 나타난다.

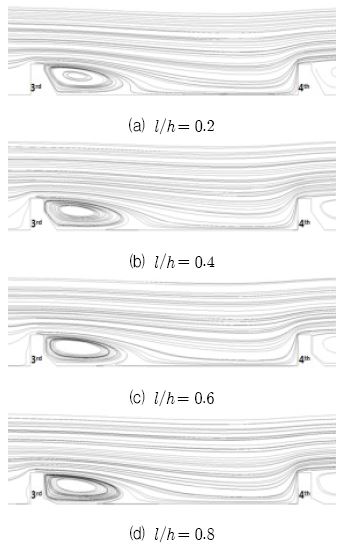
Fig. 10은 3번째와 4번째 리브사이의 x-z평면(y=0)에서 l/h변화에 따른 유선분포를 나타낸 것이다. 유선분포를 확인한 결과 l/h가 작은 경우 유선의재부착이 상대적으로 빨리 일어나고 있으나 이 변수에 따른 재부착거리의 변화가 크지 않은 것을 확인할 수 있어 l/h가 열전달 성능에 큰 영향을 미치지 않는 이유를 알 수 있다.

Fig. 8

Variation of FNu with tip height-to-rib height ratio.

Fig. 9

Variations in Ff with different tip height-to-rib height ratio

4.3 리브의 높이와 유로 높이의 비(h/H)

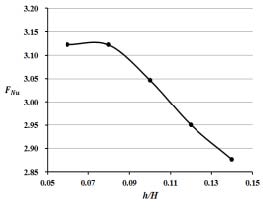
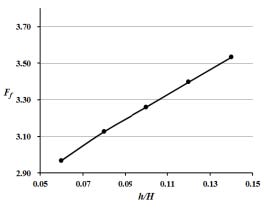
리브의 높이와 유로 높이의 비 h/H 를 0.06에서 0.14까지 변화시켜가며 면적평균 누셀트 수와 마찰계수의 변화를 각각 나타낸 것이 Fig. 11과 12에 보여진다. 앞서 리브 상단의 너비를 변화시킨 경우와는 다르게 h/H 가 감소할수록 면적평균된 누셀트 수가 전체적으로 증가하고 마찰계수도 감소하는 경향을 볼 수 있다. 따라서, h/H 가 감소하는 것이 열전달 성능 및 압력강하에 공히 긍정적인 영향을 미치는 것을 확인할 수 있다. 특히 압력강하의 변화의 폭이 18%에 가깝게 큰 것이 주목할 만하다. 리브의 높이가 상대적으로 낮은 h/H=0.06인 경우와 h/H =0.08인 경우와 비슷한 열전달 성능을 보이는 반면, 압력강하는 h/H =0.06에서 더 낮은 것을 볼 수 있다. 그러나, Fig. 13에 나타난 열전달면의 국부 누셀트 수분포에서는 두 경우가 차이가 나는 것을 확인할 수 있다. h/H 가 0.06인 경우 두 번째와 세 번째 리브사이에서는 높은 누셀트 수 분포를 보이지만 유동이 하류로 갈수록 h/H 가 0.08인 경우에 비해 누셀트 수의 감소폭이 큰 것을 알 수 있다. 동일한 열전달면에서의 온도분포를 나타낸 Fig. 14에서도 두 경우의 온도분포 상의 차이를 확인할 수 있다.

Fig. 10

Streamlines between third and fourth ribs on x-z plane for different l/h

Fig. 11

Variation of FNu with rib height-to-channel height ratio

Fig. 12

Variation of Ff with rib height-to-channel height ratio

Fig. 13

Nusselt number distributions on the heated surface for different rib height-to-channel height ratios.

Fig. 14

Temperature distributions on the heated surface for different rib height-to-channel height ratios

Fig. 15는 y=0에서 3번째와 4번째 리브 사이의 유선분포를 나타낸 것이다. Fig. 15(a)나 (b)와 같이 리브의 높이가 상대적으로 작은 경우 유선의 재부착 거리가 짧아 재부착 이후에 새롭게 발달하는 열경계층으로 인해 높은 누셀트 수 분포를 나타냄을 알 수 있다. 이와 같은 결과는 Zahra 등⁽¹⁰⁾이 실험을 통해 유로 높이에 대한 리브 높이의 비인 폐쇄율이 감소할수록 열전달 성능이 증가한다고 보고한 연구 결과와 동일한 경향을 나타내는 것을 알 수 있다.

Fig. 15

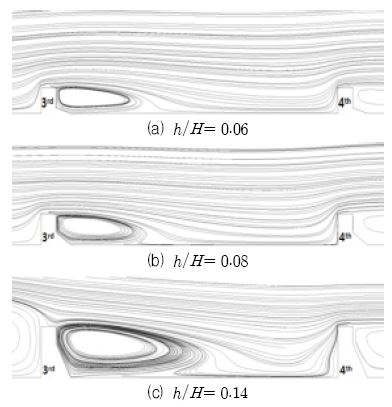
Streamlines between third and fourth ribs on x-z plane for different rib height-to-channel height ratios

Fig. 16

Variation of FNu with rib width-to-height ratio

4.4 리브 하단의 너비와 리브 높이의 비(e/h)

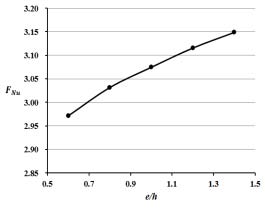
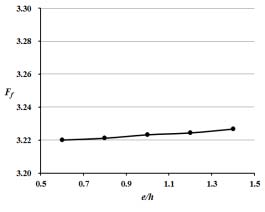
리브 하단의 너비를 변화시켜 0.6 ≤ e/h ≤ 1.4 범위에서의 면적평균 누셀트 수와 마찰계수의 변화를 Fig. 16과 17에 나타내었다. Fig. 16은 e/h가 커질수록 열전달 성능이 증가하는 경향이 보였으며 그 변화의 폭은 그림 4에 나타난 t/e의 경우와 유사하다. e/h = 1.4인 경우 Moon 등⁽⁷⁾이 해석한 기존 형상(e/h = 1.0)보다 평균 누셀트 수가 2.4 % 증가한 값을 나타낸다. e/h가 증가함에 따라 압력강하도 증가하는 것으로 나타났지만 그 변화가 무시할 정도로 작은 것이 주목할 만하다.

Fig. 18은 3번째와 4번째 리브사이의 열전달면에 대한 누셀트 수 분포를 나타낸 것이다. 리브 하단이 넓어지면서 누셀트 수가 낮은 어두운 부분의 면적이 상대적으로 감소하는 것을 확인하였다.

Fig. 17

Variation of Ff with rib width-to-height ratio

Fig. 18

Nusselt distributions on the heated surface between third and fourth ribs for different e/h

5. 결 론

본 연구에서는 종횡비가 2.0인 직사각형 냉각유로에서 신발형 리브의 4가지 형상변수가 열전달 및 압력강하에 미치는 영향을 확인하기 위해 삼차원 RANS해석을 수행하였다. 계산결과는 리브 상단의 너비와 하단 너비의 비, t/e가 감소함에 따라 유선의 재부착이 빠르게 유발되어 열전달이 향상됨과 동시에 압력강하도 증가하는 상반된 경향을 보였다. 시험된 t/e 범위에서 평균누셀트 수와 마찰계수의 변화폭은 각각 약 7%와 2%이다. 리브 상단의 높이와 리브 높이의 비, l/h가 증가할수록 열전달 성능은 감소하나 그 변화의 폭은 t/e의 경우에 비해 1/4에 불과하여 그 영향이 크지 않았으며 압력 강하의 경우 시험된 범위 내에서 최소치가 존재하였으나 역시 l/h에 대한 민감도는 t/e에 비해 2/7 정도로 낮았다. 평균 누셀트 수의 리브의 높이와 유로 높이의 비, h/H 에 따른 변화폭은 약 8% 정도로 나타났으며 이 변수가 감소할수록 열전달은 증진되었으나 h/H 가 시험된 범위의 하한치인 0.6과 0.8에서 유사한 누셀트 수를 보였다. 압력강하 성능도 h/H 가 감소함에 따라 매우 크게 감소하여 그 변화의 폭이 18%에 달했다. 따라서 h/H 의 감소는 시험된 범위 즉 0.06에서 0.14사이에서 열전달과 압력강하에 공히 긍정적이고 민감한 영향을 미쳤다. 유동장 분석을 통해 리브 높이가 낮아짐에 따라 유선의 재부착거리가 짧아져 열전달이 향상됨을 확인할 수 있었다. 리브 하단의 너비와 리브 높이의 비, e/h가 증가하는 경우 열전달 성능이 향상되는 경향을 보였고 그 변화의 폭은 약 6% 정도였으며 압력강하의 경우도 e/h가 증가함에 따라 높아졌지만 그 변화는 무시할 수 있을 정도로 작았다.

Acknowledgments

이 논문은 2014년도 정부(미래창조과학부)의 재원으로 한국 연구재단의 지원을 받아 수행된 연구임(No. 2009-0083510).

References

• Chandra, P.　R., Alexander, C. R., and Han, J. C., (2003), “Heat transfer and friction behaviors in rectangular channels with varying number of ribbed walls”, International Journal of Heat and Mass Transfer, 46, p481-495. [https://doi.org/10.1016/S0017-9310(02)00297-1]
• Islam, M. S., Kaminaga, M., Hino, R., Monde, M., (2009), “Prediction of turbulent flow structure in a fully developed rib-roughened narrow rectangular channel”, Journal of Thermal Science, 18(2), p126-136. [https://doi.org/10.1007/s11630-009-0126-1]
• Graham, A., Sewall, E., and Thole, K. A., (2004), “Flowfield Measurements in a Ribbed Channel Relevant To Internal Turbine Blade Cooling”, Proceeding of ASME Turbo Expo 2004. [https://doi.org/10.1115/gt2004-53361]
• Wang, L., and Sunden, B., (2007), “Experimental investigation of local heat transfer in a square duct with various-shaped ribs”, International Journal of Heat Mass Transfer, 43, p759-766. [https://doi.org/10.1007/s00231-006-0190-y]
• Liou, T. M., and Hwang, J. J., (1993), Effect of ridge shapes on turbulent heat transfer and friction in a rectangular channel, International Journal of Heat Mass Transfer, 36(4), p931-940. [https://doi.org/10.1016/S0017-9310(05)80277-7]
• Manca, O., Nardini, S., Ricci, D., (2011), “Numerical analysis of water forced convection in channels with differently shaped transverse ribs”, Journal of Applied Mathematics, 2011, p25. [https://doi.org/10.1155/2011/323485]
• Moon, M. A., Park, M. J., and Kim, K. Y., (2014), “Evaluation of heat transfer performances of various rib shapes”, International Journal of Heat and Mass Transfer, 71, p275-284. [https://doi.org/10.1016/j.ijheatmasstransfer.2013.12.026]
• Ansys CFX-15.0, (2013), Ansys Inc.
• Shui, L., Gao, J. M., Xu, L., Wang, X. J., (2010), “Numerical investigation of heat transfer and flow characteristics in a steam-cooled square ribbed duct”, Proceedings of ASME Trubo Expo 2010:Power for Land, Sea and Air. [https://doi.org/10.1115/gt2010-22407]
• Zahra, G. T., Wang, L., Sunden, B., (2013), Effect of Blockage-ratio on Developing Heat Transfer for a Rectangular Duct with Transverse Ribs, Proceedings of ASME Turbo Expo 2013 : Turbine Technical conference and exposition.