[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 28, No. 1, pp.16-22

ISSN: 2287-9706 (Print)

Print publication date 01 Feb 2025

Received 19 Aug 2024 Revised 26 Dec 2024 Accepted 27 Dec 2024

DOI: https://doi.org/10.5293/kfma.2025.28.1.016

평균유선 해석법의 손실 모델 계수 보정을 통한 원심펌프의 성능 예측 정확도 개선

심현석^*^{, †}

*국립창원대학교 기계공학부

Improvement in Accuracy of Performance Prediction for Centrifugal Pumps by Loss Model Calibration of Meanline Analysis

Hyeon-Seok Shim^*^{, †}

*Department of Mechanical Engineering, Changwon National University

Correspondence to: ^†E-mail : hsshim@changwon.ac.kr

Abstract

This study presents an improved one-dimensional meanline analysis for predicting the hydraulic performance of a single-stage centrifugal pump. The basic model for the meanline analysis is derived from the Euler equation, defined by the velocity triangle and the Wiesner slip factor. Empirical coefficients from the loss models proposed in previous studies are listed and selected as variables for calibration. Latin hypercube sampling is employed to generate multiple sampling points to calibrate the coefficients in the loss models. Three centrifugal pumps with different specific speeds are selected, and the relative errors of the head and efficiency values obtained from experiments and the meanline analysis are calculated to quantify the prediction model's accuracy. The optimal combination of loss model coefficients that minimizes the mean square error between the experimental values and the meanline analysis is determined from the sampling points. The reliability of the methodology is demonstrated by showing that the predicted values for head and efficiency are within 5% and 10% error ranges, respectively.

Keywords:

Meanline analysis, 평균유선 해석법, 원심펌프, 비속도, 손실 모델, 실험계획법

키워드:

평균유선 해석법, 원심펌프, 비속도, 손실 모델, 실험계획법

1. 서 론

전산해석 자원의 고속화와 대용량화, 그리고 전산유체역학(CFD) 해석 신뢰성의 향상에 따라, 이를 활용한 펌프 설계 기술이 발전하고 있다. 3차원 유동 현상을 모사하여 그 특성을 형상 설계에 직접 반영하는 CFD 기반 펌프 설계 기술은 30여 년의 짧은 역사에도 불구하고, 경험적 노하우에 의존한 기존 설계 방식을 빠르게 대체하고 있다⁽¹⁾. 한편, CFD 기반 3차원 펌프 형상 설계 기술은 충분히 매력적이지만, 격자계, 난류 모델, 고정-회전자 처리 기법 등 수치 해석 기법에 따른 오차가 발생할 수 있어, 펌프 성능과 유동을 정확하게 모사하는 데 여전히 한계가 있다. 더욱이, 케이스 당 수 시간 이상이 소요되는 이 기술은 형상 변수의 차원을 확장하여 많은 수의 인자를 평가해야 할 경우, 해석 시간이 과도하게 길어지는 단점이 있다. 이러한 관점에서 3차원 CFD 기반 펌프 설계 기술은 여전히 완벽한 기술이라고 할 수 없다. 설계자 입장에서 펌프 설계 시간을 단축하는 것은 중요한 문제이므로, 수 초 내에 성능을 효과적으로 예측할 수 있는 낮은 차수의 성능 예측 기법을 지속적으로 발전시키는 필요성이 있다.

평균유선 해석법(meanline analysis)은 1차원 평균 유선에서의 오일러 방정식과 경험적인 손실 모델을 사용하여 탈 설계점에서의 성능을 예측하는 방법으로, 초기 설계 단계에서 주요 형상 정보와 사양을 기반으로 빠르고 간단하게 성능 곡선을 예측할 수 있다는 장점이 있다. 원심형 터보기계의 평균반경 해석법과 그에 따른 경험적 손실 모델은 대부분 원심압축기를 대상으로 연구되어 왔다. Japikse⁽²⁾는 원심압축기 임펠러의 유동을 제트-후류(jet-wake) 영역으로 구분하고, 임펠러 출구에서 두 영역이 혼합된다는 가정 하에 속도 성분을 계산하는 TEIS(Two Elements In Series) 모델을 제안하였다. Aungier⁽³⁾는 베인 디퓨저, 베인리스 디퓨저, 리턴 채널 등 다양한 구성 요소로 이루어진 원심압축기의 탈 설계점 성능을 예측할 수 있는 평균유선 해석법을 정립하였으며, 유량계수가 0.009에서 0.15까지, 압력비가 최대 3.5에 이르는 산업용 원심압축기의 성능 데이터베이스를 활용해 예측 정확도를 검증함으로써 해석의 신뢰성을 확보하였다. Oh 등⁽⁴⁾은 문헌에 공개된 원심압축기의 실험식 기반 손실 모델을 정리하고, 성능 예측에 적합한 최적의 조합을 찾기 위한 연구를 수행하였다. 이들은 Eckardt 임펠러⁽⁵⁾의 성능 곡선 데이터를 활용하여 오차가 최소화되는 손실 모델 조합을 찾아 연구 방법의 타당성을 검증하였다.

Fig. 1

Definition of geometric parameters

CFD 기반 설계 기술의 발전으로 인해, 평균유선 해석법과 관련된 연구는 과거 10여 년간 상당히 제한적으로 이루어졌다. 그러나 최근 데이터 기반 인공지능 기술이 발전하면서 평균유선 해석법의 정확도를 개선하려는 연구가 활발히 진행되고 있다. Benini와 Cenzon⁽⁶⁾은 Veres⁽⁷⁾가 확립한 탈 설계점에서의 척도(scaling)를 활용한 평균유선 해석법을 기반으로 예측 정확도를 개선하기 위한 연구를 수행하였다. 이들은 성능 척도를 위한 상관식의 상수를 최적화 인자로 선정하고, 유전자 알고리즘(genetic algorithm)을 사용하여 실험값과의 오차를 최소화함으로써 탈 설계점에서의 예측 정확도를 향상시켰다. Huang 등⁽⁸⁾은 인공신경망 기법(artificial neural network)을 이용해 원심펌프 평균유선 해석법에 포함된 양정 손실 항과 동력 손실 항을 보정하여 성능 예측 정확도를 크게 향상시켰다.

물을 작동 매개로 사용하는 원심펌프는 원심압축기와 작동 원리는 유사하지만, 작동 운전 범위와 무차원수 범위뿐만 아니라 임펠러 형상 및 누설로 인해 발생하는 내부 유동 특성에서 많은 차이가 있다⁽⁹⁾. 그럼에도 불구하고, 원심펌프의 손실 모델은 주로 원심압축기를 대상으로 개발된 모델을 사용하기 때문에 성능 예측의 정확도를 확보하는 데 많은 한계가 있다. 이러한 문제를 개선하기 위한 연구가 필요하다. 이에 본 연구에서는 임펠러와 벌류트로 구성된 단단(single-stage) 원심펌프를 대상으로 수력 성능을 예측하기 위한 1차원 평균유선 해석법을 구축하였다. 기존 문헌에서 제안된 손실 모델의 경험적 계수를 나열하고, 각 손실 모델을 보정하기 위한 변수로 정의하였다. 서로 다른 비속도를 가지는 3개의 원심펌프에 대해 성능 시험 데이터를 이용하여 평균유선 해석법으로 도출된 양정과 효율을 비교하고, 이를 통해 오차를 정량화하였다. 손실 모델에 포함된 계수를 보정하기 위해 실험계획법을 활용하여 다양한 계수 조합에 대한 실험점을 구성하였으며, 실험값과 평균유선 해석 예측값 간의 오차를 최소화하는 최적의 경험적 계수 조합을 도출하였다.

Fig. 2

Example of velocity triangle

2. 평균유선 해석법

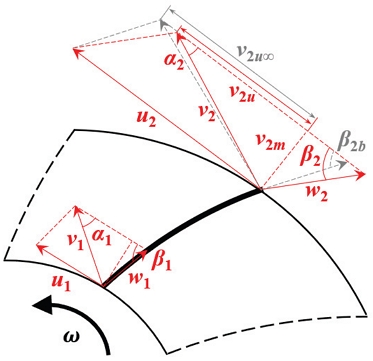
원심펌프의 양정과 효율을 예측하기 위해 Oh 등⁽⁴⁾이 제시한 평균유선 해석 절차를 참조하여 다음과 같은 과정을 수행하였다. 먼저, 펌프의 기본적인 형상 정보를 바탕으로 임펠러 입구와 출구에서의 유동 속도 삼각형을 이용한 오일러 방정식을 계산하여 이론 양정을 도출한다. 입구 유동은 90°로 유입된다고 가정하며, 미끄럼 계수는 널리 알려진 Wiesner 식⁽¹⁰⁾을 다음과 같이 적용한다.

H t h = 1 g u 2 v 2 u

(1)

σ = 1 - v 2 u ∞ - v 2 u u 2 = 1 - sin β 2 b Z 0.7

(2)

경험적으로 계산된 임펠러와 벌류트에서 발생하는 내부 손실 수두를 이론 양정에서 제외하여 실제 양정을 다음과 같이 계산한다.

H = H t h - Δ h i n t

(3)

축동력은 오일러 이론 양정에 외부 손실 수두를 더한 값으로 계산된다.

P = ρ g Q H t h + Δ P l k + Δ P r c + Δ P d f

(4)

최종적으로, 실제 양정으로부터 계산된 수동력과 외부 손실을 고려한 축동력의 비를 통해 펌프의 효율을 산출한다.

η = ρ g Q H t h - Δ h i n t ρ g Q H t h + Δ P l k + Δ P r c + Δ P d f

(5)

Table 1은 본 연구에서 사용된 손실 모델의 목록을 보여준다. 본 연구에서는 기존의 널리 알려진 연구 결과들을 바탕으로 문헌 조사를 수행하여, 4개의 임펠러 손실 모델과 4개의 벌류트 손실 모델을 펌프 내부에서 발생하는 유동 특성에 따른 내부 손실 모델로 정의하였다. 외부 손실은 펌프 양정의 변화에는 기여하지 않으면서 동력의 증가를 유발하는 손실로, 본 연구에서는 대표적인 요인으로 알려진 누설 손실, 원판 마찰 손실, 그리고 재순환 손실 3가지만을 고려하였다.

Table 1

Selected loss models and coefficients

3. 손실 모델 경험적 계수 보정

앞서 Table 1에서 나타난 바와 같이, 임펠러 손실, 벌류트 손실, 그리고 외부 손실 모델은 경험적 계수를 포함한다. 이들 손실 모델은 특정 실험 결과를 통해 정량화되었으며, 압축기의 형상과 운전 특성에 맞게 정의되었다. 다시 말해, 이들 손실 계수는 일반적인 펌프의 손실 특성을 완전히 반영하지 못한다는 것을 의미한다. 따라서 펌프 손실 특성에 맞게 경험적 계수를 수정하는 작업이 필요하다. 본 연구에서는 주어진 성능 곡선 데이터를 기반으로 원심펌프의 성능 예측에 적합한 경험적 계수를 찾기 위한 절차를 수립하였다.

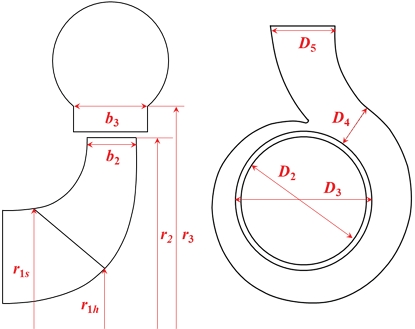
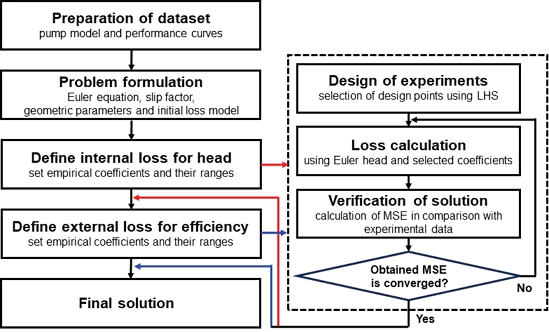
Fig. 3은 본 연구에서 사용된 평균유선 해석법의 경험적 계수 보정을 통한 예측 정확도 보정 절차를 보여준다. 우선, 원심펌프의 운전 조건과 직경, 날개 입구/출구 각도 등 Fig. 1에서 정의된 주요 형상 변수를 설정한다. 이후, 펌프의 성능곡선 예측을 위해 아래의 2단계의 해석 절차를 수행한다.

Fig. 3

Calibration procedure of empirical coefficients in loss models

1단계에서는 펌프 양정 예측을 위해 Table 1에 나열된 내부 손실과 관련된 8개의 경험적 계수의 범위를 설정한다. 설정된 범위 내에서 정의된 변수의 조합을 평가하기 위해 실험 계획법으로 라틴 하이퍼큐브 샘플링(Latin hypercube sampling, LHS)⁽¹⁸⁾을 선택하여 실험점을 구성한다. 각 실험점에서 조합된 계수를 대입하여 평균유선 해석으로 얻은 양정 예측 값과 실험값의 평균 제곱 오차(mean square error, MSE)를 계산하고, 이 값이 최소가 되는 경우를 양정 예측을 위한 경험적 계수들의 최적 조합으로 정의한다.

2단계에서는 펌프의 효율을 정의하는 단계로, 식 (5)에서 나타난 바와 같이 펌프의 정의는 양정과 축동력이 모두 포함되므로, 1단계에서 도출한 내부 손실 계수의 최적 조합을 초깃값으로 설정한다. Table 1에서 나타난 바와 같이 외부 손실과 관련된 5개의 경험적 계수에 대한 범위를 설정하였으며, 1단계와 마찬가지로 LHS를 사용하여 변수 범위 내 실험점을 구성한다. 각 실험점에서 계산된 효율값과 실험값의 MSE를 계산하고, 이 값이 최소가 되는 경우를 효율 예측을 위한 경험적 계수의 최적 조합으로 정의한다.

4. 결과 및 검토

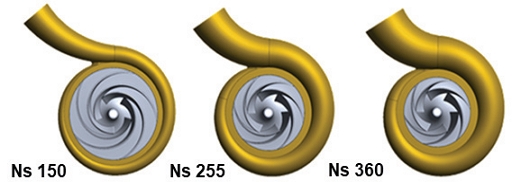
본 연구는 평균유선 해석법의 평가를 위해 Fig. 4에 도시된 바와 같이 다양한 비속도를 가지는 총 3종의 밀폐형 임펠러와 벌류트로 구성된 단단 원심펌프를 선정하였다. Table 2는 본 연구에서 사용된 펌프들의 양정, 동력, 비속도를 포함한 주요 사양을 나타낸 것이다. 이들의 비속도는 일반적으로 사용되는 원심펌프의 범위를 대표하며, 넓은 비속도 범위의 원심펌프에 대한 범용적인 평균유선 해석 모델을 개발하기 위해 기준 형상으로 선정되었다. 해당 펌프들은 성능시험 설비의 사양에 맞게 설계되었으며, 유량은 2∼4 m³/min, 양정은 21∼43 m의 범위에서 정의되었다⁽¹⁹⁾.

Fig. 4

Tested centrifugal pumps

Table 2

Specifications of centrifugal pumps

Fig. 5는 원심펌프에 대한 실험값, 기존 계수 조합의 평균유선 해석 예측 값, 그리고 보정된 계수 조합으로 예측한 성능곡선을 비교한 것이다. 공통적으로, 양정의 경우 보정된 계수 조합으로 도출한 예측 값이 실험값과 정량적, 정성적으로 모두 잘 일치하는 것을 볼 수 있다. 특히, 기존 계수 조합은 모든 비속도에서 저 유량 영역에서 양정을 과대 예측하는 반면, 고 유량 영역에서는 과소 예측하는 경향이 있다. 반면, 보정된 계수 조합은 이러한 경향을 잘 수정하여 반영한 것으로 보인다. 효율은 더 극적인 차이를 보여주는데, 기존 계수 조합은 저 유량 영역에서 효율값을 매우 낮게 예측하여 편차가 크지만, 보정된 계수 조합은 해당 영역에서도 효율값과 실험값의 경향을 상당히 유사하게 예측한다.

Fig. 5

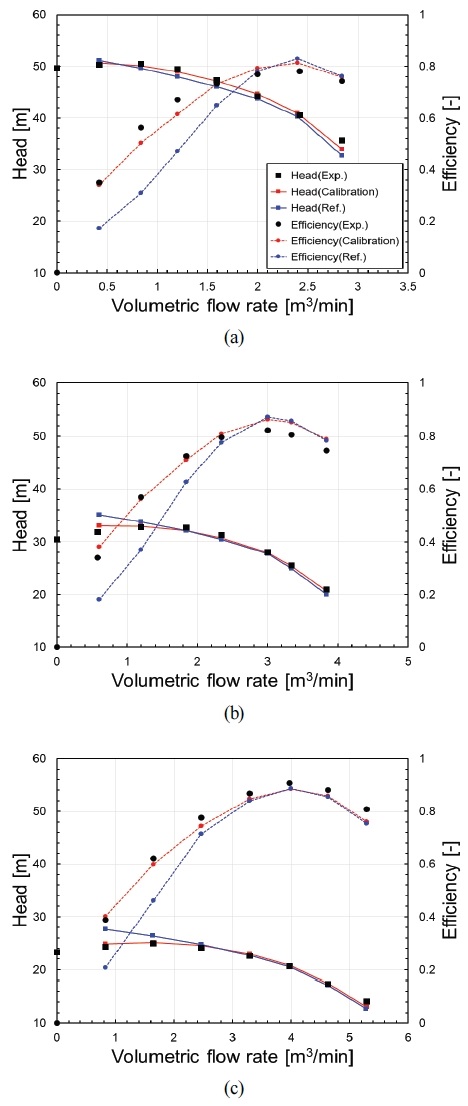
Comparison of predicted performance curves with experimental data: (a) Model A, (b) Model B, (c) Model C

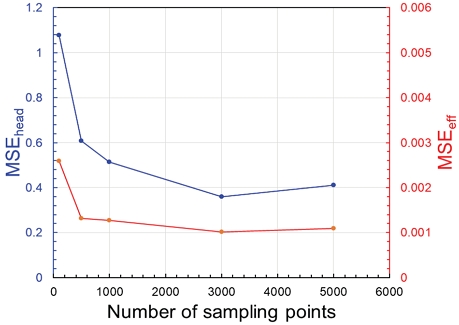
Fig. 6은 LHS 실험점의 개수에 따른 손실 모델의 MSE 값 변화를 보여준다. 그림에서 확인할 수 있듯이, 양정의 경우 3,000개 이후에는 MSE 값이 약 0.36으로 일정하며, 효율 역시 500개 이후로는 약 0.0013 수준에서 큰 변동 없이 비교적 일정한 값을 유지하는 것을 확인할 수 있다. 이는 변수 범위 내 탐색을 위한 적정 실험점 개수와 관련이 있다. 예를 들어, 대표적인 실험계획법인 3수준 완전요인설계(full factorial design)를 사용하여 5개와 8개의 설계변수를 평가하려면 각각 243개(=3⁵)와 6,561개(=3⁸)의 실험점이 필요하다. LHS는 다른 실험계획법에 비해 효과적인 공간 분포를 구성할 수 있다는 점을 고려하면⁽¹⁸⁾, 본 연구에서 얻은 MSE 값에 영향을 미치지 않는 실험점 개수는 합리적이라고 할 수 있다.

Fig. 6

Variations of MSE with number of sampling points

Table 3은 본 연구에서 평가된 경험적 계수의 범위와 최종 선택된 계수 값을 각각 나타낸 것이다. 여기서 보정된 계수의 조합은 앞서 언급한 바와 같이 실험계획법을 통해 얻은 실험점에서 계산한 결과 중, 실험값과 해석값의 MSE가 가장 낮은 조합이다. 또한 표에서 확인할 수 있듯이, 보정된 계수들은 최솟값 또는 최댓값의 경계에 해당하지 않으며, 모두 평가된 범위 내에서 정의되었다. 이는 기존 문헌에서 제시된 수치 범위에서 크게 벗어나지 않으며, 적절한 수정을 통해 실험값과의 상대 오차를 성공적으로 감소시킨 것으로 평가할 수 있다.

Table 3

Ranges of loss model coefficients and calibrated values

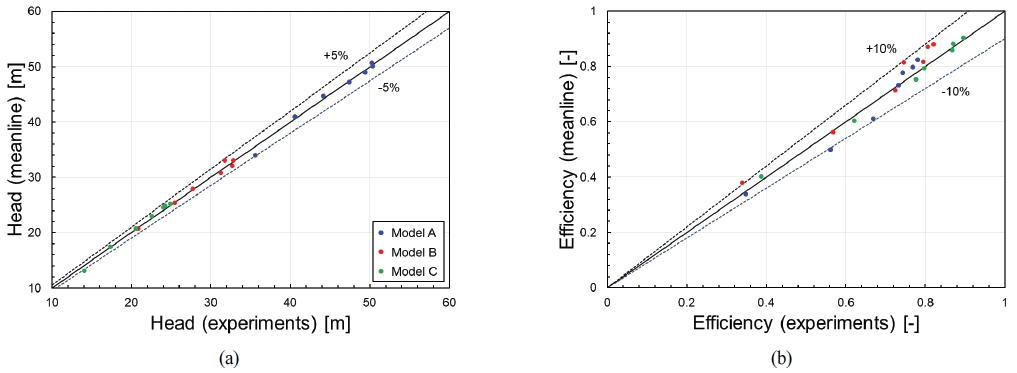
Fig. 7은 보정된 계수 조합으로 도출된 성능 함수들의 실험값과의 오차 분포를 나타낸 것이다. 양정의 경우, 개선된 계수 조합은 평가된 운전 영역에서 ±5% 내외의 우수한 예측 결과를 보여준다. 한편, 효율은 양정보다는 낮은 ±10% 범위의 예측 정확도를 나타내는데, 이는 펌프 효율의 정의상 축동력과 양정의 오차를 함께 포함하기 때문으로 보인다. 또한, 외부 손실은 유체역학적 손실 이외에도 기타 기계적 손실 등을 포함하므로 정확한 값을 도출하기에는 제한이 있다. 그럼에도 불구하고, 초기 설계 단계에서 빠르게 성능을 예측하기 위한 용도인 평균유선 해석법의 특성을 고려하면, 해당 수치는 납득할 만한 것으로 보인다.

Fig. 7

Comparison of experimental data with calibrated prediction values: (a) head, and (b) efficiency

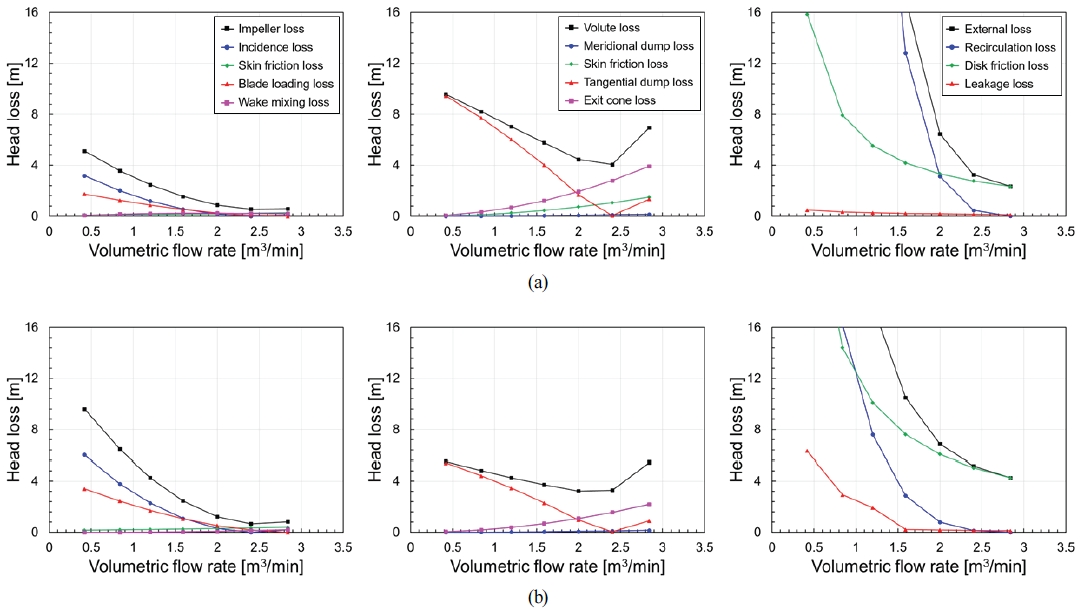
Fig. 8은 Model A의 손실 모델 보정 전후의 손실 값 변화를 보여준다. 우선, 임펠러 손실의 변화를 보면, 보정된 임펠러 손실 값은 기존 조합에 비해 저 유량 영역에서 증가한 것을 확인할 수 있다. 이러한 결과는 그림에서 나타난 바와 같이 주로 입사각 손실과 날개 부하 손실의 증가에 의한 것이다. 반면, 보정된 벌류트 손실 값은 기존 조합에 비해 탈 설계 영역에서 감소한 것을 확인할 수 있는데, 이는 주로 접선 속도 손실과 출구 확산 손실의 감소에 의한 것이다. 펌프의 양정은 임펠러 손실과 벌류트 손실의 합에 의해 결정됨을 고려할 때, 이들 손실 계수의 적절한 보정이 펌프 양정 예측 정확도를 향상하는 데 기여한 것으로 판단된다.

Fig. 8

Contributions of internal and external losses for Model A: (a) reference, and (b) calibration

보정된 조합으로 얻은 외부 손실은 저 유량 영역에서 기존 조합에 비해 값을 작게 예측하였다. 주목할 점은, 보정된 계수 조합이 원판 마찰 손실과 누설 손실을 크게 예측함에도 불구하고, 재순환 손실이 급격히 증가하는 시점이 저 유량 영역으로 이동하여 전체 외부 손실 값을 작게 예측한다는 것이다. 이는 재순환 손실이 외부 손실에 미치는 기여도가 상대적으로 크기 때문으로 볼 수 있다. 실제로 Oh 등⁽⁴⁾은 재순환 손실이 전 운전 영역에 걸쳐 원판 마찰 손실과 누설 손실에 비해 더 큰 영향을 미쳐 효율에 지대한 영향을 준다고 보고하였다. 결국, Fig. 8에서 나타난 바와 같이 재순환 손실 경험적 계수의 적절한 보정을 통해 원심펌프 성능 예측에 적합한 결과를 도출한 것으로 이해할 수 있다.

5. 결 론

본 연구에서는 서로 다른 비속도를 가지는 임펠러와 벌류트로 구성된 단단 원심펌프를 대상으로 1차원 평균유선 해석법의 손실 모델의 경험적 계수 보정을 수행하였다. 보정을 위한 경험적 계수로는 내부 손실 모델에 포함된 8개 계수와 외부 손실 모델에 포함된 5개 계수, 총 13개의 계수를 정의하고, 실험계획법을 통해 데이터 세트를 확보하였다. 예측값과 실험값의 MSE가 가장 작은 조합을 최적의 계수 조합으로 정의하였다. 양정과 효율에 대한 손실 경험적 계수 보정 결과, 전 유량 범위에서 각각 ±5%, ±10%의 오차 범위 내에서 예측 정확도를 달성하였으며, 이를 통해 넓은 비속도 범위에서 신뢰할 수 있는 정확도를 가지는 평균유선 해석법을 도출하였다.

Acknowledgments

이 논문은 2023∼2024년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과임.

References

Kim, K. Y., Samad, A., and Benini, E., 2019, Design Optimization of Fluid Machinery: Applying Computational Fluid Dynamics and Numerical Optimization, Wiley-Black well, Singapore. [https://doi.org/10.1002/9781119188377]
Japikse, D., 1985, March. Assessment of single-and two-zone modeling of centrifugal compressors, studies in component performance: Part 3. In Turbo Expo: Power for Land, Sea, and Air (Vol. 79382, p. V001T03A023). American Society of Mechanical Engineers. [https://doi.org/10.1115/85-GT-73]
Aungier, R. H., 1995, “Mean streamline aerodynamic performance analysis of centrifugal compressors,” ASME Journal of Turbomachinery, Vol. 117, pp. 360–366. [https://doi.org/10.1115/1.2835669]
Oh, H. W., Yoon, E. S., and Chung, M., 1997, “An optimum set of loss models for performance prediction of centrifugal compressors,” Proc. Inst. Mech. Eng. A, J. Power Energy, Vol. 211, pp. 331–338. [https://doi.org/10.1243/0957650971537231]
Eckardt, D. Flow field analysis of radial and backswept centrifugal compressor impellers. Part I: flow measurements using a laser velocimeter. In ASME 25th Annual International Gas Turbine Conference and Twenty-second Annual Fluids Engineering Conference, New Orleans, Louisiana, March 1980, pp. 77–86.
Benini E, Cenzon M. Calibration of a meanline centrifugal pump model using evolutionary algorithms. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy. 2009;223(7):835-847. [https://doi.org/10.1243/09576509JPE742]
Veres, J., 2009, January. Axial and centrifugal compressor mean line flow analysis method. In 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition (p. 1641). [https://doi.org/10.2514/6.2009-1641]
Huang, R., Zhang, Z., Zhang, W., Mou, J., Zhou, P. and Wang, Y., 2020. Energy performance prediction of the centrifugal pumps by using a hybrid neural network. Energy, 213, p.119005. [https://doi.org/10.1016/j.energy.2020.119005]
Japikse, D., Marscher, W. D., and Furst, R. B., 1997, Centrifugal Pump Design and Performance, Concepts ETI, Vermont.
Wiesner, F. J. A review of slip factors for centrifugal impellers. Trans. ASME, J. Engng for Power, 1967, 89, 558–572. [https://doi.org/10.1115/1.3616734]
Conrad, O., Raif, K. and Wessels, M. The calculation of performance maps for centrifugal compressors with vane-island diffusers. In ASME Twenty-fifth Annual International Gas Turbine Conference and Twenty-second Annual Fluids Engineering Conference, New Orleans, Louisiana, March 1980, pp. 135–147
Zhang, Y.L. and Li, W.G., 2023. A precisive calculation method of volumetric and hydraulic efficiency of centrifugal pumps. Physics of Fluids, 35(7). [https://doi.org/10.1063/5.0155675]
Coppage, J. E., Dallenbach, F.,Eichenberger, H. P., Hlavaka, G. E., Knoernschild, E. M. and Van Lee, N. Study of supersonic radial compressors for refrigeration and pressurization systems. WADC report 55-257, 1956.
Johnston, J. P. and Dean Jr, R. C. Losses in vaneless diffusers of centrifugal compressors and pumps. Analysis, experiment, and design. Trans. ASME, J. Engng for Power, 1966, 88, 49–62 [https://doi.org/10.1115/1.3678477]
Ayder, E., and Van den Braembussche, R., 1994, “Numerical Analysis of the Three-Dimensional Swirling Flow in Centrifugal Compressor,” ASME J. Turbomachinery, 116(3), pp. 462–468. [https://doi.org/10.1115/1.2929435]
Liu, M., Tan, L. and Cao, S., 2019. Theoretical model of energy performance prediction and BEP determination for centrifugal pump as turbine. Energy, 172, pp.712-732. [https://doi.org/10.1016/j.energy.2019.01.162]
Gülich, J.F., 2003. Disk friction losses of closed turbomachine impellers. Forschung im Ingenieurwesen, 68(2), pp.87-95. [https://doi.org/10.1007/s10010-003-0111-x]
McKay, M. D., Beckman, R. J., and Conover, W. J., 1979, “Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code,” Technometrics, 21(2), pp. 239–245 [https://doi.org/10.1080/00401706.1979.10489755]
Choi, Y.-S., Kim, K.-Y., Yoo, I.-S., and Lee, Y.-K., 2018, “Development of Design Program for Centrifugal and Mixed-Flow Pump,” Korea Ministry of Trade, Industry and Energy, Sejong-si, South Korea, Report No.10044860.

Table 1

Selected loss models and coefficients

		Loss model	Equation	Coefficient
Internal loss	Impeller loss	Incidence loss (Conrad et al.⁽¹¹⁾)	$Δ h i n c = c i n c w 1 u i 2 2 g$	*c_inc*
		Skin friction loss (Zhang and Li⁽¹²⁾)	$Δ h s f = λ L i D h i w 2 2 g where λ = c s f R e 0.25 D h i = D 1 b Z b 1 + π D 1 + D 2 b 2 Z b 2 + π D 2$	*c_sf*
		Blade loading loss (Coppage et al.⁽¹³⁾)	$Δ h b l = c b l D f 2 u 22 g where D f = 1 - w 2 w 1 t + 0.75 g H t h / u 22 w 1 t / w 2 Z r / π 1 - D 1 t / D 2 + 2 D 1 t / D 2$	*c_bl*
		Wake mixing loss (Jonston and Dean⁽¹⁴⁾)	$Δ h w m = 1 1 + tan 2 α 2 1 - ϵ w a k e - b * ϵ w a k e 2 v 22 2 g$	*ε_wake*
	Volute loss	Meridional dump loss (Aungier⁽³⁾)	$Δ h m d = c m d ρ v 3 m 2$	*c_md*
		Tangential dump loss (Aungier⁽³⁾)	$Δ h t d = c t d 1 ρ r 3 v 3 u 2 r 4 1 - 1 S P 2; S P > 1 Δ h t d = c t d 2 ρ r 3 v 3 u 2 r 4 1 - 1 S P 2; S P < 1 where S P = r 3 v 3 u r 4 v 4 u$	c_td₁ & c_td₂
		Skin friction loss (Aungier⁽³⁾)	$Δ h s k, v = λ L ρ v 3 + v 4 / 2 2 2 d H$	*c_sf*
		Exit cone loss (Ayder et al.⁽¹⁵⁾)	$Δ h e c = c e c v 4 u - v 5 u 2$	*c_ec*
External loss		Leakage loss (Liu et al.⁽¹⁶⁾)	$Δ P l k = ρ g Δ Q l k H t h where Δ Q l k = c l k 1 π D 0 Y c l k 2 u 22 - u 12 c l k 1 = 1 1 + 0.5 η l k + λ l k X 2 Y$	η_lk& c_lk₂
		Disk friction loss (Guelich⁽¹⁷⁾)	$Δ P d f = k R R cos ⁡ δ ρ ω 3 r 25 1 - r i r 2 5 where k R R = c d f R e 0.2 s a r 2 0.1$	*c_df*
		Recirculation loss (Oh et al.⁽⁴⁾)	$Δ P r c = ρ g Q c r c 1 sinh ⁡ c r c 2 π / 2 - α 2 3 D f 2 u 22 g$	c_rc₁ & c_rc₂

	Model A	Model B	Model C
Volumetric flow rate [m³/min]	2	3	4
Head [m]	43	27.8	21.2
Power [kW]	20	17	14
Rot. Speed [RPM]	1,780	1,780	1,780
Specific speed	150	255	360

		model	Ref.	Upper bound	Calibration
Internal loss	Impell er Loss	ε_wake	1.4	2.8	0.28
		c_sf	0.32	0.63	0.46
		c_inc	0.6	1.2	1.1
		c_bl	0.050	0.10	0.098
	Volute Loss	c_md	0.5	1.0	0.95
		c_td₁	0.25	0.50	0.14
		c_td₂	0.50	1.0	0.33
		c_ec	0.40	0.80	0.22
External Loss		c_rc₁	0.00008	0.00016	0.00013
		c_rc₂	3.5	7.0	2.6
		c_df	0.0255	0.0510	0.0463
		η_lk	0.75	1.5	0.46
		c_lk₂	0.70	1.4	0.51