입구 온도 및 압력 조건에 따른 초임계 이산화탄소 원심압축기 내액화 정량적 예측에 관한 수치적 연구

2.1 실기체 효과

초임계 이산화탄소 압축기 해석을 위해선 이산화탄소의 물성치 및 상변화가 고려되어야 한다. 임계점 근처의 이산화탄소는 미세한 온도 변화에도 물성치가 매우 심하게 바뀐다. 따라서 임계점 근처에서는 널리 쓰이는 삼차 상태방정식들은 열역학적 상태를 정확히 예측할 수 없다⁶. 현재 알려진 상태방정식 중 SW-EoS가 임계점 근처 이산화탄소의 물성치를 가장 정확하게 구할 수 있다고 알려져 있다⁷. SW-EoS는 수백 개의 항이 포함된 경험식으로, 유동 해석 시 해당 상태방정식으로 열역학 성질을 계산하면 계산량이 많아지기 때문에 많은 선행 연구들과 같이 사전에 계산된 물성치 테이블을 활용한다. 이산화탄소의 물성치 테이블은 NIST의 REFPROP 프로그램을 통해 구할 수 있는데, REFPROP은 SW-EoS를 풀어 주어진 온도 및 압력에서의 필요한 물성치들을 제공한다. 물성치 테이블은 온도-압력 도메인 내에 그리드 형태로 정의되며 각 온도-압력 점에서 밀도, 엔탈피, 비열 등의 열역학 성질과 포화 선도에 대한 정보를 포함한다.

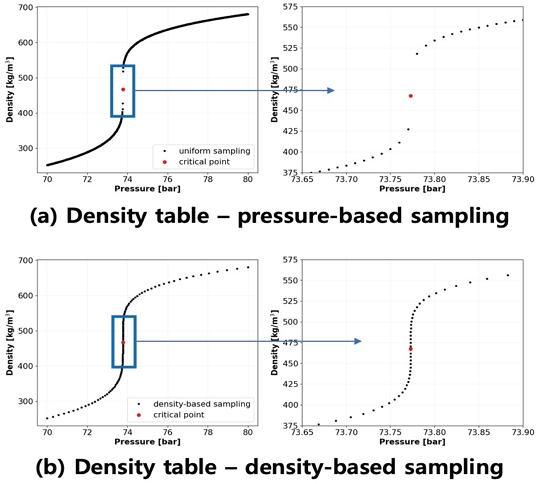
본 연구에서는 REFPROP API를 사용할 수 있는 Python 라이브러리를 이용하여 온도-압력 도메인 범위와 해상도를 조절할 수 있는 물성치 테이블 생성 코드를 작성한다⁸. 본 연구에서 사용한 유동 해석 프로그램에서는 물성치 테이블을 온도와 압력 도메인 내에서 그리드 형태로 정의된다. 이러한 물성치 테이블 방식에서는 임계점 근처에서 급격한 물성치 변화가 나타나고, 이를 잡기 위해서 임계점 근처에서 많은 샘플링이 필요하다. 온도와 압력을 등간격으로 균일하게 샘플링하게 되면 임계점 부근에서 적은 샘플링이 이루어지므로 밀도 기반 샘플링을 통해 물성치 테이블을 작성하였다. 균일 샘플링은 온도-압력 도메인에서 그리드를 균일하게 나누어 등간격의 압력과 온도를 갖는 각 점에서의 물성치를 구하는 방식이다. 밀도 기반 샘플링은 등간격의 밀도를 갖도록 하는 온도-압력 그리드를 구하고 그때의 각 지점에서 물성치를 구하는 방식이다. 밀도는 임계점 부근에서 빠르게 변하므로, 밀도 기반 샘플링은 임계점 근처에서 많은 점을 샘플링한다. Fig. 1에서 동일한 온도-압력 구간에서 같은 수의 점을 샘플링하였을 때, 샘플링 방식에 따라 임계점 근처에서 물성치 정확도 차이를 볼 수 있다.

Fig. 1

CO2 density table near the critical point by (a) pressure-based sampling (b) density-based sampling

2.2 상변화 모델링

초임계 상태로 압축기로 들어오는 이산화탄소는 임펠러 선단 부근에서 국부적인 가속에 의해 온도와 압력이 떨어지게 되고 이로 인해 액화가 발생할 수 있다. 이러한 다상유동을 해석하기 위해선 기체-액체 사이 상변화를 모델링해야 한다. 본 연구에서는 Homogeneous Binary Mixture (HBM)모델을 사용하여 기체와 액체 사이 상변화를 모델링한다. HBM 모델은 해석 도메인 내에 정의된 셀 안의 유체가 액체와 기체가 균일하게 섞인 하나의 혼합 물질과 같다고 가정한다. 이때 기체와 액체는 온도, 압력, 속도 등의 물리량이 동일하다고 가정한다. 준안정 상태(meta-stable state)를 고려하지 않는다면 포화 선도를 제외한 온도-압력 지점에서 유체는 하나의 상을 갖게 된다. 만약 온도와 압력이 포화 선도에 놓인다면 엔탈피를 기준으로 유체의 건도를 계산하고, 계산된 건도를 바탕으로 기체 상과 액체 상의 물성치를 선형 보간하여 상변화 중인 유체의 물성치들을 계산한다. HBM 모델은 액체와 기체의 유동장이 동일하다는 가정을 통해 변수의 개수를 줄이고, 둘 사이의 운동량 및 에너지 교환을 고려하지 않는다. 그로 인해 상대적으로 적은 계산량이 요구된다.

3.1 초임계 노즐 실험

2장에서 구축한 해석 방법론을 검증하기 위해 데이터가 공개된 초임계 이산화탄소 노즐을 해석한다. 해당 노즐 실험에서는 초임계 상태로 들어온 이산화탄소가 CD(수렴-발산) 노즐을 지나며 목 부근에서 급격한 팽창을 하고, 그로 인해 압력과 온도가 감소하여 액화가 진행된다⁹. 임계점 근처 이산화탄소의 상변화가 발생한다는 점이 초임계 이산화탄소 압축기와 비슷하다. 따라서 많은 선행 연구들은 자신들의 압축기 해석 기법을 해당 노즐 실험에서의 공개된 데이터와 비교를 통해 간접적으로 검증한다.

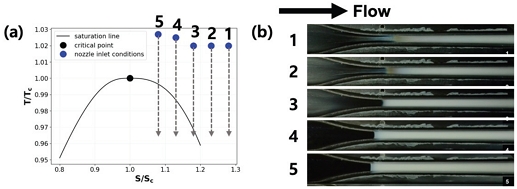
노즐 실험 선행 연구는 5개의 초임계 입구 조건의 이산화탄소를 노즐에 통과시켜 가며 흐름 방향의 압력 분포를 실험적으로 측정하고 액적 발생을 가시화하였다. Table 1에서 각 입구 조건을 볼 수 있다. Fig. 2-(a)는 실험된 5개의 초임계 입구 조건을 T-S 다이어그램에 표시한다. 1번에서 5번으로 갈수록 입구 온도는 비슷한 수준을 유지하지만, 입구 엔트로피 감소하는데, 이는 입구 조건이 액체 상에 가까워짐을 의미한다. 노즐 내부에서 유동이 빠르게 팽창하기 때문에 열교환이 거의 없어 흐름 방향으로 엔트로피가 증가하지 않고 유지된다. 따라서 T-S 다이어그램에서 나타나듯, 입구에서부터 흐름이 진행됨에 따라 엔트로피는 유지된 채로 온도가 감소하며 목 부근에서 포화곡선을 만나 상변화가 진행된다. Fig. 2-(b)는 입구 조건에 따른 액화 발생 위치를 카메라를 통해 시각화한 것이다, 입구 조건이 임계점과 가까워질수록 포화곡선을 더 일찍 지나기 때문에 초임계 이산화탄소의 상변화가 더 일찍 시작함을 볼 수 있다.

Table 1

Temperature, pressure, and entropy of the critial point of CO2 and the inlet conditions of 5 nozzle cases

Fig. 2

Nozzle experiment with sCO2. (a) T-S diagram of five inlet temperature and pressure conditions, (b) condensation visualization.

3.2 노즐 형상 및 해석 방법론

공개된 노즐 형상 정보를 바탕으로 해석을 위한 격자가 생성되었다. ICEMCFD 프로그램을 사용하여 다중 블록 기반의 정렬형 격자를 생성하였다. Fig. 3은 해석에 사용된 노즐 격자를 보여준다. 노즐은 수평면을 기준으로 상하 대칭의 형상을 갖고 있어, 효율적인 계산을 위해 대칭면을 기준으로 절반 부분만 계산되었다. 또한 Lettieri는 노즐 실험의 유동은 평면 유동의 특징을 갖는다고 보고했다. 하지만 본 연구에서 사용하는 유동 해석 프로그램은 3D 격자에 대한 해석만을 지원하기 때문에 깊이 방향으로 단 한 개의 셀을 배치하여 깊이 방향으로의 방향성을 무시한다. Hosangadi가 언급하였듯, 목 부근에서는 유동의 속도가 빠르고 상변화가 일어나기 때문에 흐름 방향으로 충분한 격자 해상도가 요구된다¹⁰. 본 해석에서는 격자 의존성 조사를 통해 목 부근에서의 격자 크기를 선정하였다. 또한 벽면 근처 난류 모델링을 위해 Y⁺ 값은 1과 비슷한 값을 갖도록 하였다.

Fig. 3

Nozzle geometry and mesh refinement near the throat.

노즐 해석을 위해 상용 3D RANS 솔버 프로그램인 ANSYS CFX 2020 R2을 사용한다. k-ω SST 모델을 이용하여 벽면 근처 난류 특성을 모델링한다. 노즐의 대칭면은 대칭 경계 조건이 적용되고, 깊이 방향으로의 단면은 주기적 경계 조건이 적용되어 2D 유동을 모사한다. 입구 경계 조건은 실험에서 측정된 전압력 및 전온도로 설정되고, 출구 경계 조건은 출구에서 초음속을 갖도록 충분히 낮은 정압이 설정된다.

노즐 내 작동 유체는 이산화탄소이며, 해석 영역 내에서 임계점 근처의 이산화탄소는 이상 기체와는 다른 거동을 보인다. 압축인자 $$ Z\equiv \frac{P}{\rho RT}$$는 어떤 기체가 이상 기체와 다른 정도를 수치화한 것으로, 1에 가까울수록 해당 기체는 이상 기체와 비슷한 거동을 갖는다는 의미를 가진다. 노즐 내 이산화탄소의 압축인자는 0.4-0.6의 범위를 보여주며, 이상 기체 가정이 타당하지 못함을 나타낸다. 따라서 앞선 절에서 언급하였듯, REFPROP으로부터 얻은 이산화탄소의 물성치 테이블을 바탕으로 유체의 열역학적 특성을 계산한다.

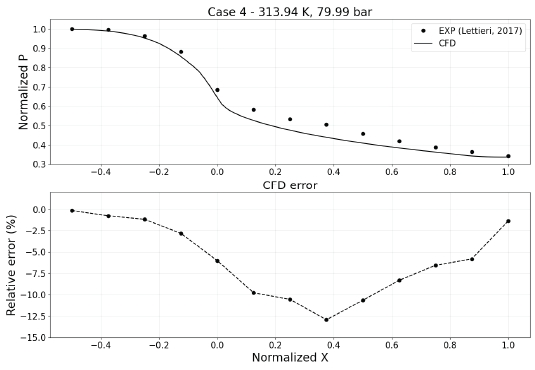
Fig. 4은 Case 4에 대해서 공개된 실험 데이터와 본 연구에서 진행한 해석 결과의 흐름 방향 압력 분포를 비교한다. x축은 흐름 방향의 위치를, y축은 압력값과 오차를 나타낸다. x=0은 CD 노즐의 목 위치를 의미한다. 해석된 5개 경우 모두 흐름 방향의 압력 오차가 Case 4와 비슷하며, Table 2는 각 경우의 압력 최대 오차를 보여준다. CFD 결과는 상변화가 발생하기 전인 x<0 영역에서 5% 수준의 압력 차이를 보인다. 하지만 목 부근에서 상변화가 발생하고부터 이 오차는 15% 정도까지 커진다. 상변화 발생 이후의 오차 증가는 HBM모델을 사용한 Hosangadi의 선행 연구와 정량적으로 일치함을 보인다¹⁰. 하지만 이산화탄소의 과냉각 상태를 모델링하여 수치해석을 진행한 Lettieri의 선행 연구에서는 상변화 이후에도 실험과 일치하는 결과를 보인다⁹. 따라서 상변화 이후에 발생하는 오차는 상변화 모델링에서 기인하는 것임을 알 수 있다. 구체적으로 HBM 모델은 유체의 준안정 상태(본 연구에서는 과냉각)를 고려하지 않기 때문이다. 해당 노즐 실험에서 초임계 상태로 들어온 이산화탄소는 CD 노즐을 지나 초음속 상태로 빠져나가게 되는데, 이 과정에서 팽창률 $$ \dot{p}\equiv -wdp/dx$$의 값이 1.25×10⁴s^-1정도로 커지게 된다. 급격한 팽창은 기체 상태의 이산화탄소가 포화곡선을 지날 때 바로 액화되지 않고 과냉각되는 상황을 야기한다.

Fig. 4

CFD validation with the previous experimental pressure measurement for the case 4.

Table 2

Maximum pressure errors for 5 nozzle cases.

하지만 본 연구에서 다루는 원심압축기의 마하수는 0.8 정도로 천음속 구간에서 운용이 된다. 따라서 팽창률이 초음속 노즐의 경우보다 작고, 그로 인해 이산화탄소의 과냉각이 상대적으로 덜 이루어지기 때문에 상변화 모델링에서 오는 오차는 노즐의 경우보다 더 적을 것으로 판단한다.

4.1 압축기 해석 형상

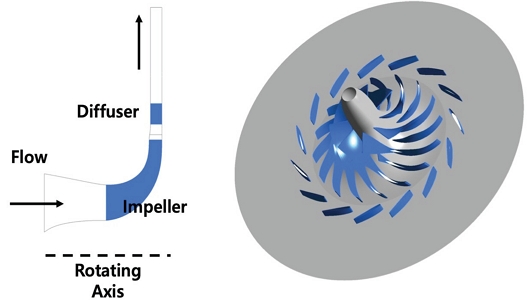
본 연구에서는 한화파워시스템 사에서 개발한 10MWe 급 원심압축기를 대상으로 수치해석을 진행한다. 원심압축기는 임펠러와 디퓨저 1단으로 구성되어 있다. 원주 방향으로 임펠러는 8개의 메인 블레이드와 8개의 스플리터를 가지고 있으며, 디퓨저는 15개의 블레이드를 가지고 있다. 본 연구에서 대상으로 하는 압축기는 임펠러의 쉬라우드 구조가 있는데, 본 해석에서는 단순화된 형태로 임펠러 팁 간극이 없는 형상으로 해석한다. 해석 영역은 임펠러 상류부터 디퓨저 하류까지로, 하류의 볼루트나 상류의 입구 구조 등 다른 형상은 해석에 반영되지 않는다. 본 압축기의 임펠러는 적층제조(DMLS : Direct Metal Laser sintering)으로 제작되는데, 실제 제작된 압축기의 표면 거칠기를 측정하여 해석에 반영한다. Fig. 5는 해석에 사용된 압축기의 자오면 형상과 360도 3차원 형상을 보여준다.

Fig. 5

Geometry of the centrifugal compressor for the numerical study. (left) meridional view (right) full annulus view.

4.2 압축기 해석 수렴성 증가

이번 절에서는 압축기 해석 수렴을 위한 구체적인 해석 방법을 소개한다. 임계점 근처에서 이산화탄소는 0.1℃의 온도 변화에도 밀도가 10% 이상 변할 만큼 급격한 물성치 변화를 가진다. 또한 임계점에서는 정압 비열이 무한에 가까울 정도로 커지는데, 이러한 임계점 근처에서의 이산화탄소 물성치 특성은 유동 해석의 수렴을 저해한다. 해석의 수렴성을 증가시키기 위해 2가지 방법들(충분히 짧은 시간 간격 및 초기 해석 조건 개선)을 적용한다.

CFX 솔버는 유동의 속도, 형상의 크기 및 격자의 크기 등을 기준으로 적절한 시간 간격을 계산한다. 본 연구의 경우, 시간 간격은 10^-4 초로 계산되는데, 이 시간 간격은 너무 커서 계산을 수렴시키지 못한다. 초기 계산에서는 5×10^-6초, 상세 계산에서는 5×10^-7 초로, 계산된 기본 시간 간격의 수백분의 일 수준으로 줄여야 압축기 계산이 수렴한다.

시간 간격이 줄었기 때문에 해석이 수렴하기까지 물리적 계산 시간이 늘어난다. 이를 단축하기 위해 계산을 초기 계산과 상세 계산 두 단계로 나눈다. 초기 계산에서는 계산 초반의 계산 안정성 향상과 계산 시간 단축을 목표로 한다. 계산 초반의 계산 안정성을 위해 압축기의 회전 속도와 입구 유량을 50%로 설정하여 계산한다. 추후 계산 진행에 따라 압축기 회전 속도와 입구 유량을 점진적으로 증가시켜, 최종적으로 설계 속도와 설계 유량에 도달하도록 한다. 또한 계산 정밀도는 낮지만 수렴성이 좋은 upwind scheme을 사용하여 수치 해석을 진행한다. 계산 시간을 줄이기 위해서 상대적으로 큰 시간 간격, 낮은 물성치 테이블의 해상도, 그리고 32bit 단일 정밀도로 계산한다.

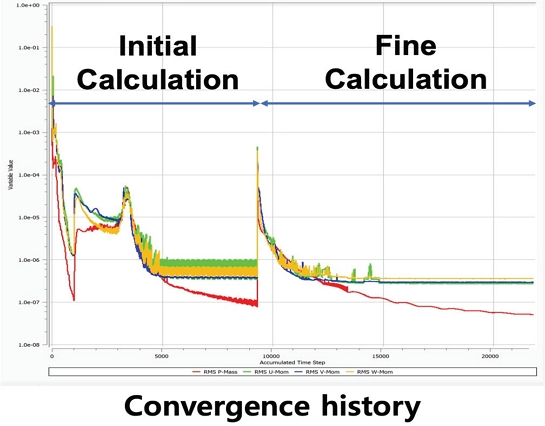
초기 계산이 수렴하면, 해당 결과를 초기 조건으로 하는 상세 계산을 진행한다. 정밀한 계산 결과를 목표로 하는 상세 계산은 초기 계산 단계에 비해 짧은 시간 간격 및 높은 물성치 테이블 해상도를 가지고, 고차 이산화를 통한 수치 해석을 진행한다. 또한 물성치 테이블 해상도가 높아짐에 따라 임계점 근처의 물성치들과 그들이 포함된 항들이 절단 오차에 의해 계산이 중단되는 경우가 발생하기도 한다. 따라서 상세 계산에서는 단일 정밀도가 아닌 64bit 이중 정밀도로 계산한다. Fig. 6는 두 계산 과정이 진행되는 동안 지배방정식의 잔차 기록을 보여준다. 상세 계산 이후에는 연속 방정식과 운동량 방정식 잔차의 제곱평균제곱근 모두 10^-6 이하로 떨어지며 수렴함을 볼 수 있다.

Fig. 6

Convergence history of the two sub-calculations.

4.3 압축기 해석 방법 및 조건

압축기 해석 방법은 노즐 해석의 경우와 같이 상용 3D RANS 솔버 프로그램인 ANSYS CFX 2020 R2를 사용하고, k-ω SST 모델을 이용하여 벽면 근처 난류 특성을 모델링한다. 압축기 내 모든 벽면에는 측정된 표면 거칠기(19 μm)가 적용된다. CFX의 표면 거칠기 처리 방식에 의해 벽면으로부터 거칠기 크기의 반보다 가까운 곳에서 경계층 속도를 구하지 못한다¹¹. 따라서 첫 번째 셀의 높이는 거칠기 크기의 절반으로 설정되고, 이때 Y+ 값은 2,000 정도의 값을 갖는다. 입구 경계 조건은 온도 및 압력 조건이 부과되고, 출구 경계 조건은 질량 유량으로 설정된다. 본 연구에서는 압축기의 입구의 온도 및 압력 조건을 제외하고 임펠러 입구에서의 속도 삼각형을 고정하기 위해 모든 해석 경우들은 동일한 입구 체적 유량 $$ {\dot{Q}}_{des}$$을 설정한다. 이를 통해 질량 유량을 역으로 계산한다. 입구 온도와 압력을 알기 때문에 REFPROP 프로그램을 통해 입구 밀도를 계산할 수 있고, 설계 체적 유량에 입구 밀도를 구하면 입구 유량 $$ {\dot{m}}_{des }$$을 구할 수 있다. 질량 유량은 전 도메인에서 일정하게 유지되므로 입구 유량은 곧 출구 유량과 같고, 이를 출구 경계 조건으로 설정한다.

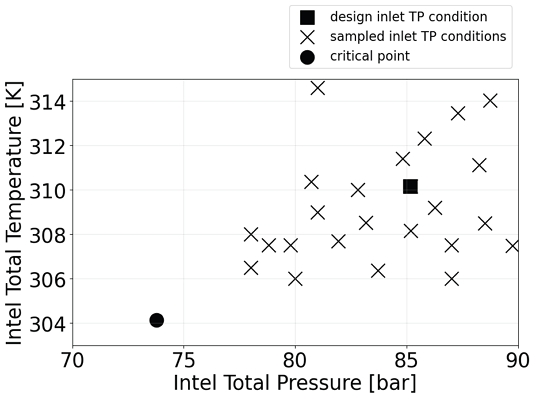
설계 운용 조건에서의 입구 전온도와 전압력은 각각 310.15 K, 85.17 bar이다. 입구 온도 및 압력 조건에 따라 압축기 내 액화 정도를 조사하기 위해 설계 입구 조건 근방에서 추가적으로 해석 입구 조건을 샘플링한다. 우선 라틴 하이퍼큐브 샘플링(LHS)의 방식으로 일부 입구 조건을 샘플링하고, 추가적인 인위 샘플링을 통해 총 24개의 해석 입구 조건을 선별한다. 샘플링은 초임계 이산화탄소 압축기의 통상적인 입구 조건 (압력: 80-90 bar, 온도: 305-315 K) 내에서 진행된다. Fig. 7은 해석된 24개의 입구 조건을 온도-압력 도메인에 표시한 그림을 보여주고, Table 3는 각 경우의 입구 온도-압력 조건을 보여준다. 여기서 Case 1은 설계 입구 온도-압력 조건이다.

Fig. 7

24 Samples of tested inlet temperature and pressure conditions.

Table 3

24 tested inlet temperature and pressure conditions.

4.4 압축기 해석 결과

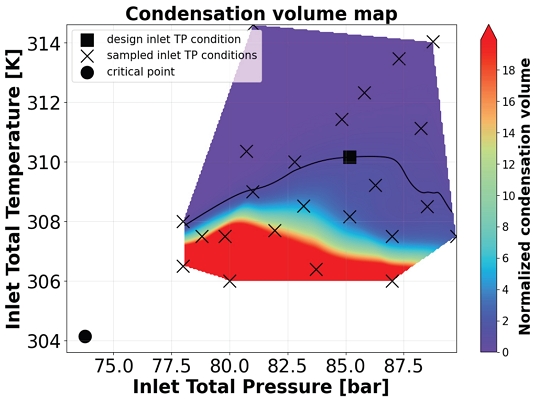
Fig. 8은 입구 온도 및 압력 조건에 따라 압축기 내에서 액화가 발생한 상대적인 부피를 보여준다. 상변화하는 셀 안에는 액체 상태와 기체 상태가 공존하는데, 액체 상태의 비율이 0 %보다 큰 경우, 액화가 발생한다고 판단한다. 액화 발생 영역은 설계 입구 조건에서의 그것으로 나눈 상대값을 의미한다. 액화 발생 영역은 입구 온도에 민감한 모습을 보인다. 입구 전온도가 311 K이 넘으면 입구 압력에 무관하게 액화가 거의 발생하지 않지만, 308 K 이하로 떨어지면 액화 발생이 많이 일어나는 것을 볼 수 있다. 또한 동일한 입구 온도 조건에서 입구 압력에 따라 압축기 내 응축 영역이 달라진다. 그 이유는 온도-엔트로피 다이어그램에서 찾아볼 수 있다.

Fig. 8

Condensation Volume Map.

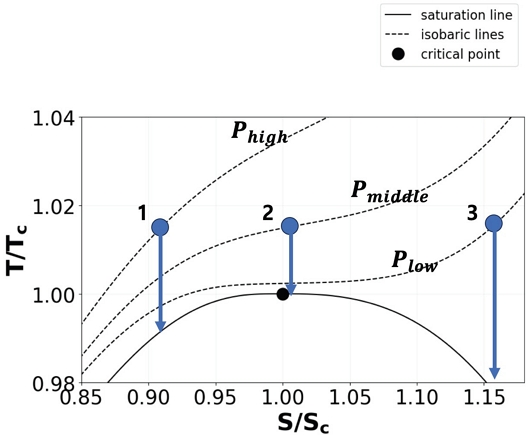
Fig. 9는 임계점 근처에서 온도-엔트로피 다이어그램을 보여준다. 검은 실선은 포화선도를 의미하며, 세 점선은 서로 다른 압력에 대한 등압선을 의미한다. 같은 입구 온도에서 각기 다른 입구 압력을 갖는 3개의 입구 조건을 생각해보자. 초임계 이산화탄소 압축기는 임펠러 선단에서 등엔트로피 과정에 가까운 팽창 과정을 갖는다. 상황을 단순화하여 압축기 입구에서부터 상변화가 발생할 때까지 등엔트로피 팽창 과정을 거친다 가정하자. 등엔트로피 과정이므로 Fig. 9에서 열역학적 과정은 수직으로 진행되며, 입구 엔트로피가 임계 엔트로피와 가까울수록 상변화가 더 쉽게 발생할 수 있다. 따라서 주어진 입구 온도에 대해서 입구 압력에 따라 응축 영역이 변하는 이유는 입구 압력에 따라 입구 조건과 포화 선도와의 거리가 변하기 때문이다.

Fig. 9

T-S Diagram and isobarlic lines.

Fig. 8에서 조사된 24개의 입구 조건 중 액화 발생이 가장 많이 발생한 경우에서, 압축기 내 액화 발생 영역이 Fig. 10에 표시되어 있다. 임펠러 블레이드 선단 주변에 회색으로 표시된 부분이 액화 발생 부분이다. 메인 임펠러 선단에 액화가 많이 발생하며, 특히 팁 쪽으로 갈수록 블레이드 속도가 빨라지기 때문에 더 넓은 영역에서 액화가 발생한다. 또한 스플리터 블레이드의 선단 팁 부근에서도 소량의 액화 발생 영역을 발견할 수 있다.

Fig. 10

Condensation near the impeller leading edge.

본 해석에서의 상변화 모델은 이산화탄소의 준안정 상태, 블레이드 선단에서는 과냉각 상태를 고려하지 못하고, 포화 선도에 도달하자마자 상변화가 발생한다고 예측한다. 하지만 빠른 속도로 팽창하는 이산화탄소는 포화 선도를 지나 과냉각되어 기체 상태를 오래 유지할 수 있다. 따라서 실체 압축기 내부에서는 본 해석에서 예측한 영역보다 더 적은 영역에서 액화가 발생할 것으로 판단한다.