[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 18, No. 4, pp.43-48

ISSN: 2287-9706 (Print)

Print publication date Aug 2015

Received 31 Oct 2014 Revised 13 Feb 2015 Accepted 05 Mar 2015

DOI: https://doi.org/10.5293/kfma.2015.18.4.043

반응표면법을 이용한 원심압축기 임펠러 쉬라우드 형상최적설계

강현수^* ; 황인주^** ; 김윤제^***^{, †}

*성균관대학교 대학원 기계공학과
**한국건설기술연구원 환경 · 플랜트연구소
***성균관대학교 기계공학부

Optimal Design of Impeller Shroud for Centrifugal Compressor Using Response Surface Method

Hyun-Su Kang^* ; In-Ju Hwang^** ; Youn-Jea Kim^***^{, †}

*Graduate School of Mechanical Engineering, Sungkyunkwan University
**Environment and Plant Research Division, Korea Institute of Civil Engineering and Building Technology
***School of Mechanical Engineering, Sungkyunkwan University

Correspondence to: ^† yjkim@skku.edu

Abstract

In this study, a method for optimal design of impeller shroud for centrifugal compressor using response surface method (RSM) and multi-objective genetic algorithm (MOGA) was studied. Numerical simulation was conducted using ANSYS CFX with various configurations of shroud. Each of the design parameters was divided into 3 levels. Total 15 design points were planned by central composite design (CCD) method, which is one of the design of experiment (DOE) techniques. Response surfaces based on the results of DOE were used to find the optimal shape of impeller shroud for high aerodynamic performance. The whole process of optimization was conducted using ANSYS Design Xplorer (DX). Results showed that the isentropic efficiency, which is the main performance parameter of the centrifugal compressor, was increased 0.4% through the optimization.

Keywords:

Centrifugal Compressor, Response Surface Method, Shape Optimization, Design of Experiment

키워드:

원심 압축기, 반응표면법, 형상최적설계, 실험계획법

1. 서 론

원심압축기는 고속으로 회전하여 유체에 압력에너지와 속도에너지를 전달하는 대표적인 유체기계이다. 일반적으로 원심압축기는 인듀서, 임펠러, 디퓨져, 그리고 볼류트로 구성되어 있다. 특히, 임펠러는 원심압축기 공력성능에 큰 영향을 미치는 요소이다. 그러나 원심압축기 임펠러는 매우 복잡한 3차원 형상을 가지고 있으며, 설계를 위한 다양한 변수들이 존재한다. 따라서 설계 변수들과 원심압축기 공력 성능간의 복잡한 상관관계를 분석하고 최적형상 도출을 위해 최적화에 대한 연구가 다양하게 이루어지고 있다.

최근, 최적설계 방법 중 실질적인 해석이 아닌 근사모델기반의 반응표면 최적설계가 많이 사용되고 있다.

Kim 등⁽¹⁾은 압축기 효율 향상을 위해 반응표면법을 이용하여 임펠러 자오면 형상과 디퓨져 깃수를 최적설계 하였다. Kim 등⁽²⁾은 반응표면법 중 하나인 신경회로망기법과 다목적 최적화 방법을 사용하여 임펠러 자오면 형상을 최적설계하여 원심압축기 효율과 압력비를 각각 향상 시켰다.

Wang 등⁽³⁾은 반응표면법 중 크리깅(kriging)기법을 이용하여 임펠러의 다양한 설계각을 최적화 하여 원심압축기의 효율을 향상 시켰다. 최형준 등⁽⁴⁾은 인공지능망과 유전자 알고리즘을 이용하여 임펠러 자오면 형상을 최적설계 하였고 CFD결과와 1% 미만의 오차를 갖는 근사모델을 제시하였다.

그 외 많은 연구자들에 의해 원심압축기 최적설계가 진행되고 있다^(5,6). 하지만 다단 원심압축기에 대한 최적설계 연구는 상대적으로 부족하며, 특히 임펠러의 다양한 설계변수 중 쉬라우드 커브(shroud curve)에 대한 최적설계는 많은 진행이 이루어지지 않았다.

본 연구에서는 15,000 HP급 다단 원심압축기의 2단 압축기 임펠러의 쉬라우드 커브 형상에 대한 최적설계를 수행하였다. 먼저 기본모델의 CFD결과와 실험값과의 결과를 비교하여 타당성을 입증하였고, 실험계획법과 반응표면법을 이용하여 임펠러 쉬라우드 커브 최적설계를 수행하였다. 최종적으로 기본모델보다 높은 공력성능을 갖는 임펠러 형상을 도출하였다.

2. 수치해석

2.1 기본모델

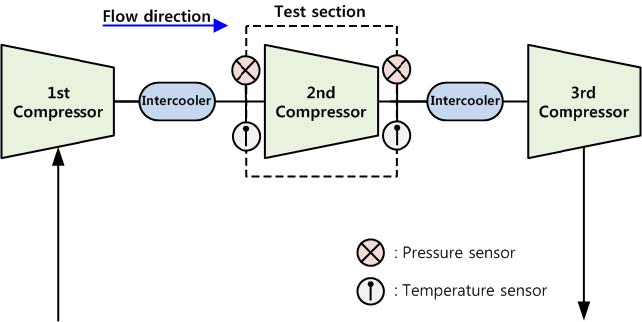
본 연구에 사용된 기본 모델은 총 3단 원심압축기의 2단압축기이며(Fig. 1 참고) 조립된 3차원 모델을 Fig. 2 에 나타내었다.

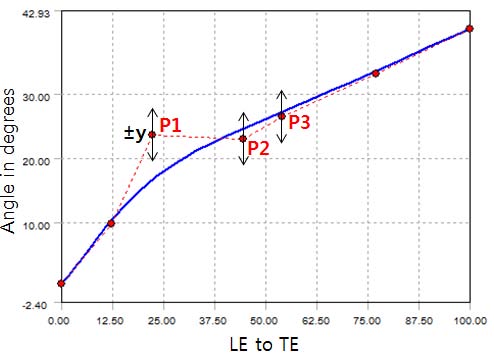
원심압축기의 직경은 약 800 mm이며, 임펠러와 디퓨져의 블레이드는 각각 14개, 11개로 구성되어있다. 3차원 형상은 ANSYS Blade editor를 이용하여 설계하였다. 임펠러와 디퓨져의 최적화 과정과 형상 치수의 설계 변수화는 매우 중요한 과정인데, Table 1에는 Fig. 3에서 선정된 각각의 설계변수들에 대한 변수화를 나타내었다. 해석에 사용된 원심압축기의 작동유체는 공기이며, 출구 유량은 29.7 kg/s, 회전 속도는 약 12,000 rpm이다.

Fig. 1

Schematic of the multi-stage compressor

Fig. 2

Configuration of the multi-stage compressor

Table 1

Design parameters on the modeled compressor

Fig. 3

Control points of the shroud blade angle

2.2 격자계 구성 및 경계조건

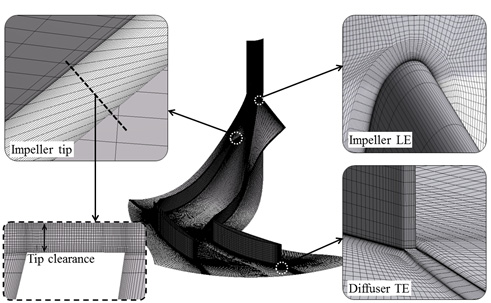
수치해석에 사용된 격자계는 ANSYS Turbogrid를 사용하여 블레이드 주변에는 O-형, 그 외의 영역에는 H-형 격자를 사용하였으며, 임펠러와 케이싱의 팁 간극에서 15겹의 격자를 생성하였다. Fig. 4은 격자계를 나타내고 있으며, 격자개수는 임펠러 904,000개, 디퓨져 354,000개 이다.

수치해석은 ANSYS CFX 14.5를 이용하였으며, 해석영역은 임펠러 입구부터 디퓨져 출구까지 설정하였다. 작동유체는 이상기체를 사용하여 정상상태해석(steady-state analysis)을 수행하였으며, 난류모델은 유체기계 해석에서 비교적 정확히 예측하는 k-ω기반의 SST(shear stress transport)모델을 사용하였다⁽⁷⁾. 경계조건으로 입구에는 전압력을 설정하였고, 출구에는 전온도와 질량유량 조건을 적용하였다. 그 외의 벽면에는 점착조건(no-slip condition)을 적용하였고, 임펠러와 디퓨져 경계에는 frozen rotor 조건를 사용하였다. 자세한 경계조건은 Table 2에 나타내었다. 원심압축기 전체 성능을 평가하기 위해서 다음식을 이용하여 등엔트로피 효율, 압력비, 그리고 일계수를 분석하였다.

Isentropic efficiency, η = h 2 s - h 1 h 2 - h 1

(1)

Pressure ratio, p R = P o u t l e t P i n l e t

(2)

Work coefficient, μ = h 02 - h 02 s U T 2

(3)

원심압축기 유로내 손실을 나타내기 위해 전엔탈피 손실계수를 사용하였다.

Total enthalpy loss coefficient, q = h 02 - h 02 s U T 2

(4)

기본모델에 대한 수치해석 결과를 검증하기 위해 2단 압축기의 출구 온도와 압력비를 실제 데이터와 비교하였으며 높은 적합도를 보였다 (Table 3 참고).

Fig. 4

Grid systems

Table 2

Boundary conditions applied in this study

Table 3

Comparison results

3. 최적설계

3.1 실험계획법

실험계획법은 정해진 설계점을 바탕으로 설계영역을 선택하고 세밀히 고찰할 수 있어 성능변수 분석을 용이하게 한다. 본 연구에서는 전산 수치 실험에서 많이 사용되고 있는 중심합성계획법(central composite design, CCD)을 사용하였는데, 이 방법은 최소의 수치해석 결과로 최대의 정보를 얻을 수 있는 장점이 있다. 중심합성계획의 실험점 추출(sampling)은 다음과 같은 식으로 구성되어 있다.

y = 2 k + 2 k + 1

(5)

여기서 y는 실험의 개수, k는 설계변수의 수 이다. 설계변수는 3개 이므로 15개의 실험개수가 도출되며, 실험값과 수치해석의 결과를 Table 4에 나타내었다.

Table 4

Parameters of DOE

3.2 반응표면법

반응표면법은 실험계획법에 의해 계산된 점들을 바탕으로 근사적으로 반응면 함수를 구하는 기법이다. 반응표면 함수는 일반적으로 다음과 같은 2차 다항식으로 나타낼 수 있다.

z = β 0 + ∑ i = 1 n β i x i + ∑ i = 1 n β i i x i 2 + ∑ i < j n β i j x i x j

(6)

여기서 z는 반응표면 함수이며, xi, xj는 설계변수, β₀ ,β_i , β_ii , β_ij는 미정계수들이다. 위 식을 기반으로 생성된 반응표면 함수는 비선형성이 강한 공력설계 문제에서 비교적 낮은 적합도를 보였다. 이와 같은 단점을 보완하기 위해 본 연구에서는 크리깅(kriging)기법을 시용하였다. 크리깅 기법은 공력 형상 설계에서 널리 사용되고 있으며 다항식 모형보다 설계점의 위치를 정확히 통과하므로 비선형성이 강한 공력 설계 문제를 보다 유연하게 모델링 할 수 있다.

크리깅 모델은 다음식과 같이 두 개의 항으로 구성된다.

F x = f x + Z x

(7)

여기서 F(x)는 미지의 함수이고, f(x)는 x의 알려진 함수로 전역의 설계공간을 나타내며, Z(x)는 전역 모형으로부터 생성된 국소적 편차(local deviation)를 나타낸다⁽⁸⁾.

본 논문에서 사용한 반응표면의 적합도 평가는 실제 추출점에서의 값과 반응표면에서 계산한 값의 오차에 대한 평균값인 RMSE(root mean square error)를 사용하였다.

3.3 최적설계

최적설계 방법으로는 다목적 유전 알고리즘(multi-objective genetic algorithm, MOGA)을 사용하였는데, 유전 알고리즘(genetic algorithm)은 변이(mutation), 교차(cross) 등 생물학적 유전을 모방한 연산 알고리즘이다. 기본적으로 비구배율(gradient-free)법에 기반 하나, 주어진 변수 영역 내의 전역(global)을 탐색하여 전역 최적점(global optimum)을 찾을 확률이 매우 높다. 다목적 유전 알고리즘은 목적함수가 2개 이상인 유전 알고리즘을 의미하며 다목적(multi- objective) 최적화에 특히 적합하다. 전역에서 최적 조건을 찾아내는 한편 불연속 함수에도 대처할 수 있는 장점이 있기 때문에 비선형성이 강한 유체기계 설계에 적합하다^(9),(10).

먼저, 목적함수로 원심압축기 전체 성능지표인 등엔트로피 효율(isentropic efficiency)과 손실지표인 전엔탈피 손실계수(total enthalpy loss coefficient)를 최적설계의 2가지 목적 함수로 정의 하였다.

목적함수가 선정된 다음 과정으로 제한조건을 선정하였는데, 현재 수준의 압력비와 일계수를 갖도록 하였다. 위의 목적 함수와 제한조건을 적용한 최적화의 정식화는 다음과 같다.

Find x i i=1, 2, 3 To maximize Isentropic efficiency, η To minimize Total enthalpy loss coefficient, q Subject to 2.2012 ≥ Total pressure ratio, p R 0.6580 ≥ Work coefficient, μ 18.8 ≤ x 1 ≤ 28.2 18.4 ≤ x 2 ≤ 27.6 21.2 ≤ x 3 ≤ 31.8

(8)

4. 결과 및 고찰

4.1 기본모델

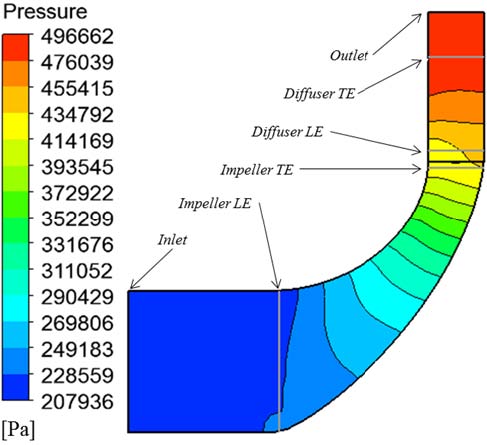
먼저, 원심압축기 성능변수를 계산하였는데, 등엔트로피 효율은 86.7%, 압력비는 2.201를 얻었다. 그 외 전엔탈피 손실계수는 0.0871, 일계수는 0.658을 얻었다. Fig. 5에 2단 원심압축기 자오면에서의 압력 분포를 나타내었다. 임펠러 입구에서 디퓨져 출구까지 압력이 점차 상승하는 것을 확인 할 수 있으며, 임펠러 고속회전에 의한 공기 압축이 잘 일어나고 있는 것을 확인할 수 있다.

Fig. 5

Pressure distribution on the meridional plane

Fig. 6 (a)

Results of sensitivity with various design parameters – Isentropic efficiency

Fig. 6 (b)

Results of sensitivity with various design parameters – Total enthalpy loss coefficient

Fig. 6 (c)

Results of sensitivity with various design parameters – Pressure ratio

Fig. 6 (d)

Results of sensitivity with various design parameters – Work coefficient

Table 5

Comparison results between RSM and CFD analyses

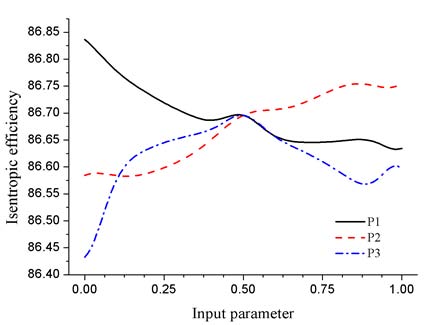
4.2 민감도 분석

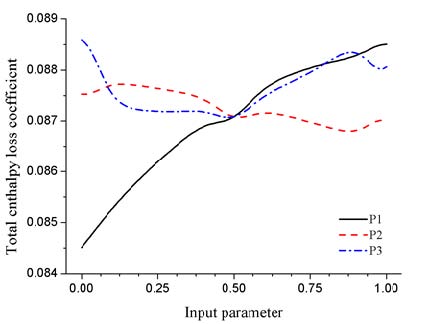
Fig. 6 (a)~(d)는 크리깅 방법의 설계변수 변화에 따른 응답변수의 민감도를 나타낸다. x축은 입력변수로 그 범위를 0에서 1까지 무차원화 하였으며, 기본모델의 설계변수 값은 0.5를 의미한다. 첫 번째 등엔트로피 효율에 대한 반응표면 결과를 보면 P1의 경우 설계변수 값이 커질수록 출력변수가 감소하는 음의 관계, P2의 경우 양의 관계를 보였으며, P3는 x축 0.5에서 가장 높은 값을 보였다. 두 번째 전엔탈피 손실계수에 관한 반응표면결과에서 P1은 양의 관계를 보였으며 P2는 음의 관계, P3는 x축 0.5에서 최소값을 가졌다.

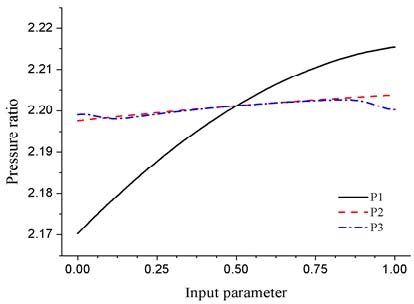
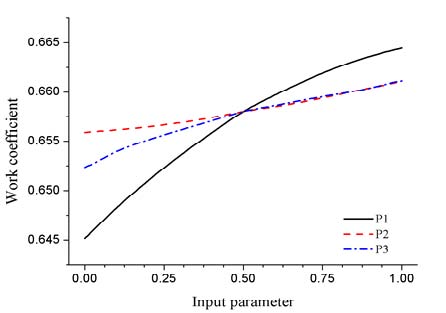
반면에 압력비와 일계수 반응표면 결과에서는 3가지 설계변수 모두 양의 관계를 나타내었다. 이를 통해 본 연구에서 설정한 쉬라우드 블레이드 상단부의 각도는 압력비와 일계수에 긍정적인 영향을 미친다는 것을 유추할 수 있다. 또한 민감도 분석에서 기울기(gradient)가 큰 변수들은 블레이드 형상 설계에서 중요한 요소임을 알 수 있다.

4.3 최적화 결과

반응표면법과 수치해석의 최적화 결과를 Table 5에 나타내었다. 등엔트로피 효율에 관한 근사모델과 CFD 결과의 상대오차는 0.07% 발생하였고, 전엔탈피 손실계수는 0.7%, 그리고 압력비와 일계수는 각각 0.1%, 0.3%의 상대오차가 발생하였다. 특히, 등엔트로피 효율의 근사모델은 다른 출력변수에 비해 정확히 예측되었다. 이 결과를 통해 등엔트로피 효율의 근사모델 적합도가 높다는 것을 알 수 있다.

Table 6에는 기본모델과 최적모델의 결과를 비교하였다. 최적설계 결과로 첫번째 목적함수인 등엔트로피 효율은 0.4% 증가하였고 두번째 목적함수인 전엔탈피 손실계수는 2.3% 감소하였다. 제한조건인 압력비와 일계수는 현재의 수준을 유지하였다.

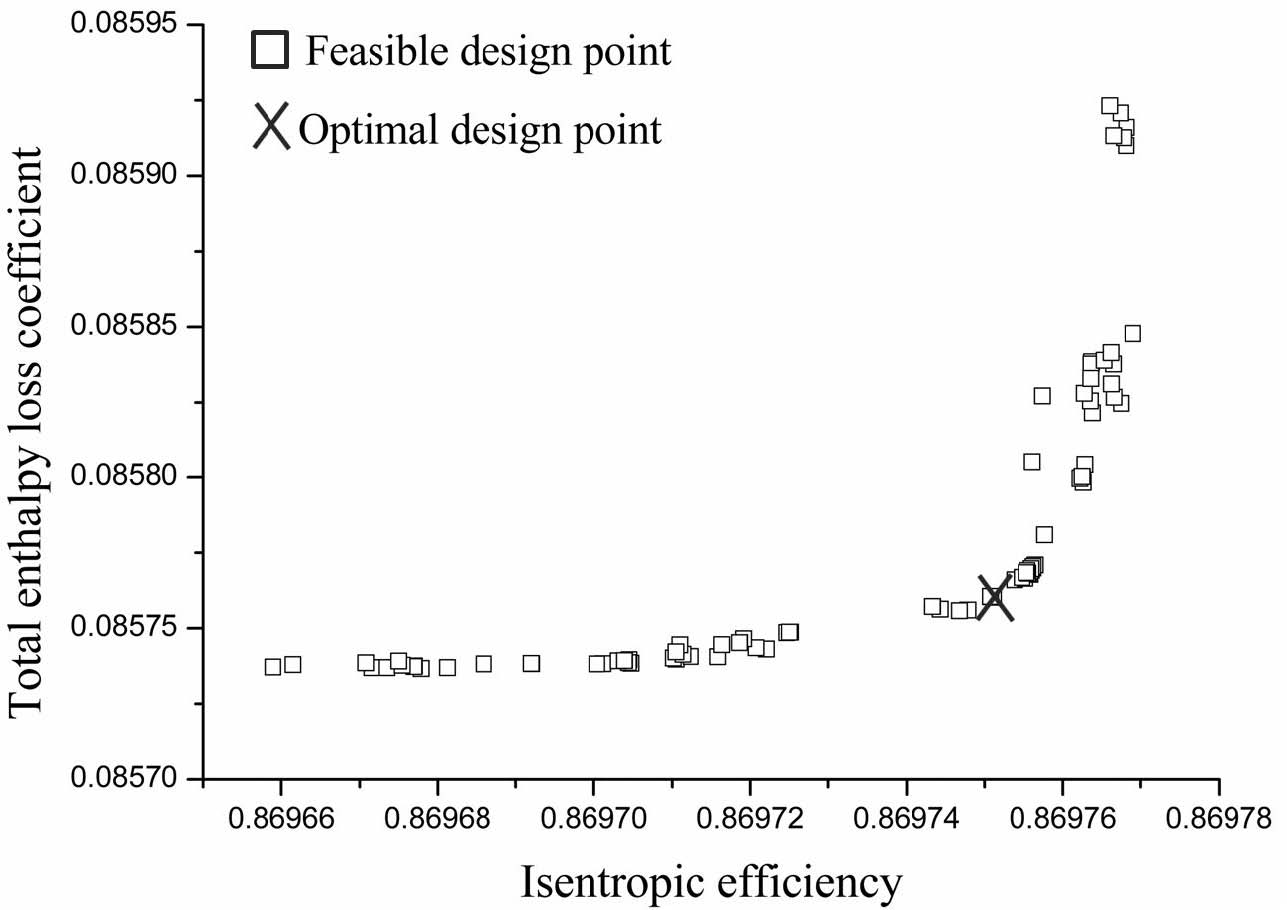
다목적 최적설계는 파레토 프론트(Pareto front) 라고 하는 점군형태의 최적점들이 존재한다. Fig. 7에는 설계공간에 존재하는 파레토 최적해에 대해 두 개의 목적함수 관계를 나타낸 것이다. 이 그래프를 통해서 두 목적함수 등엔트로피 효율과 엔탈피 손실계수의 관계(비례)를 알 수 있다. 또한, 그래프에서 검정색 실선은 변경 가능한 최적군을 의미하고, X표시는 최종 최적점이다. 여기서, 최적점은 등엔트로피 효율이 86.975% 이상 만족하면서, 엔탈피 손실계수를 0.08575이하로 갖는 지점을 의미하며 본 연구에서의 최종 최적 모델로 적용하였다.

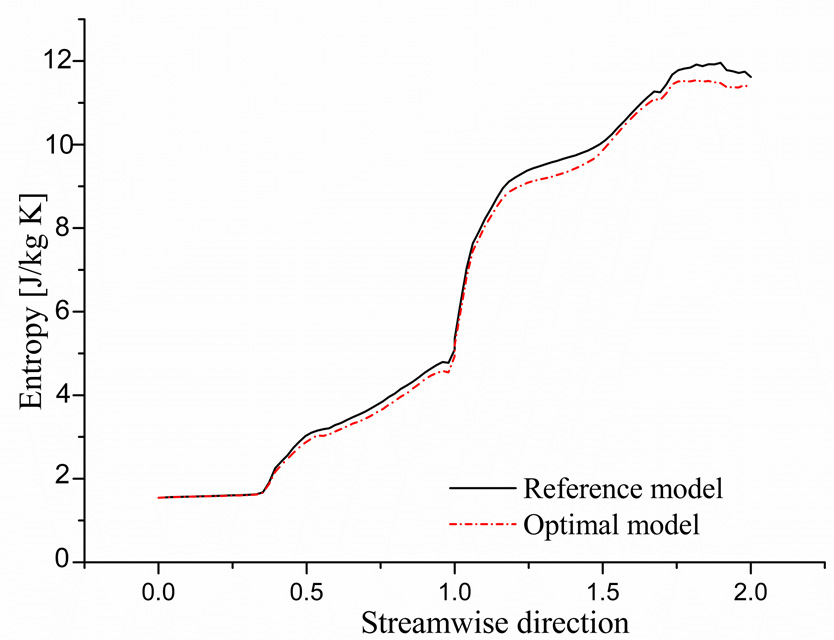
Fig. 8에는 원심압축기 유로 내 엔트로피 분포를 나타내었다. 그래프 X축의 0은 임펠러 입구, 1은 임펠러와 디퓨져 경계, 2는 디퓨져 출구를 각각 의미한다. 전체적으로 최적모델의 엔트로피 분포가 기본모델에 비해 낮았다. 출구에서의 엔트로피 값은 유로내에서 축적된 손실을 나타내므로 초기모델 보다 최적모델의 효율상승과 전엔탈피 손실계수의 감소 이유를 도식적으로 알 수 있다.

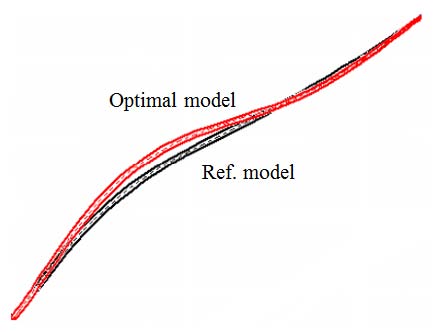
Fig. 9에 초기모델과 최적모델의 임펠러 쉬라우드 형상을 비교하였다.

Table 6

Comparison results between Ref. model and optimal model

Fig. 7

Trade-off analysis for Pareto front

Fig. 8

Comparison results of entropy distribution between the Ref. model and optimal model

Fig. 9

Comparison results of Shroud shape

5. 결 론

본 연구에서는 원심압축기 임펠러 블레이드에 대한 형상 최적설계를 수행하였다. 최적설계 과정에서 실험계획법과 반응표면법의 사용으로 다수의 설계변수와 성능변수들 간의 상관관계를 분석하였다.

형상 최적설계의 결과로 최적 모델은 초기모델과 같은 수준의 압력비와 일계수를 가지며 등엔트로피 효율은 0.4% 증가, 전엔탈피 손실계수는 2.3% 감소하는 임펠러 쉬라우드 최적 형상을 도출하였다.

Acknowledgments

본 연구는 국토교통부 플랜트연구사업 LNG플랜트사업단의 연구비 지원에 의해 수행되었습니다.

References

Kim, S. M., Park, J. Y., Ahn, K. Y., and Baek, J. H., (2009), “Numerical investigation and validation of the optimization of a centrifugal compressor using a response surface method”, J. Power and Energy, 224, p251-259. [https://doi.org/10.1243/09576509JPE842]
Kim, J. H., Choi, J. H., and Kim, K. Y., (2009), “Design optimization of a centrifugal compressor impeller using radial basis neural network method”, Proceeding of ASME Turbo Expo, 7, p443-451. [https://doi.org/10.1115/gt2009-59666]
Wang, X. F., Xi, G., and Wang, Z. H., (2006), “Aerodynamic optimization design of centrifugal compressor’s impeller with Kriging model”, J. Power and Energy, 220, p589-597. [https://doi.org/10.1243/09576509JPE201]
Choi, H. J., Park, Y. H., Ahn, H. Y., and Cho, S. Y., (2011), “Optimization of a centrifugal compressor impeller(I): artificial neural network and genetic algorithm”, Journal of Korea Society for Aeronautical & Space Sciences, 39(5), p433-441, (in korean). [https://doi.org/10.5139/JKSAS.2011.39.5.433]
Benni, E., and Pediroda, V., (2001), “Aerodynamic optimization of an industrial centrifugal compressor impeller using genetic algorithm”, Proceedings of Eurogen, Athens, p467-472.
Benni, E., and Tourlidakis, A., (2001), “Design optimization of vaned diffusers for centrifugal compressors using genetic algorithms”, American Institute Aeronautics and Astronautics Paper, p2001-2583.
Bardina, J. E., Huang, P. G., and Coakley, T., (1997), “Turbulence modeling validation”, 28th AIAA.
Ju, B. H., Cho, T. M., Jung, D. H., and Lee, B. C., (2006), “An error assessment of the Kriging based approximation model using a mean square error”, Trans. Korean Soc. Mech. Eng. A, 30(8), p923-930, (in Korean). [https://doi.org/10.3795/KSME-A.2006.30.8.923]
Joo, H. J., Lee, J. H., Jun, H. D., and Kim, H. S., (2012), “A study on optimal stage gauge network using multi objective genetic algorithm”, Proceeding of Korean Society of Civil Engineers, p923-930.
Jo, Y. M., and Choi, S. I., (2012), “Shape Optimization of UCAV for aerodynamic performance improvement and radar cross section reduction”, Proceeding of Korean Society for Computational Fluids Engineering, p98-113.

Design Parameters	Description	Level 1	Level 2*	Level 3
X₁	P1 [°]	18.8	23.5	28.2
X₂	P2 [°]	18.4	23.0	27.6
X₃	P3 [°]	21.2	26.5	31.8