상반각 정익이 천음속 축류 압축기 손실에 미치는 영향에 관한 연구
*포항공과대학교 기계공학과 대학원**명지대학교 기계공학과
***포항공과대학교 기계공학과
**Dept. of Mechanical Engineering, Myongi University
***Dept. of Mechanical Engineering, POSTECH
Abstract
This paper presents a numerical investigation of the effect of the dihedral stator on the loss in a transonic axial compressor. Four stator geometries with different stacking line variables are tested in the flow simulations over the whole operating range. It is found that a large shroud loss at the rotor outlet and the subsequent shroud corner separation in the stator passage occur at low mass flow rate. The hub dihedral stator and bowed blade generate unexpected hub-corner-separation, thereby causing a large total pressure loss over the entire operating range. However, the corresponding blockage forces the high momentum flow near the hub to divert toward the upper part of the passage suppressing the negative axial velocity region. The dihedral stator increases deflection angle and secondary vorticity near the endwall where the dihedral is applied. As a result, the endwall loss which is related to the endwall relative velocity decreases.
Keywords:
Dihedral, Transonic Axial Compressor, Corner Separation, Blockage, Endwall Loss키워드:
상반각, 천음속 축류 압축기, 코너 박리, 막힘 현상, 끝벽 손실1. 서 론
축류 압축기는 가스 터빈 엔진을 구성하는 중요한 요소 중 하나로 항공 분야 및 산업 전반에 걸쳐 두루 사용되고 있다. 이러한 압축기는 설계 제한조건이 까다롭고 유동장이 매우 복잡하기 때문에 압축기 성능을 향상시키고 작동 영역을 확보하기 위해서는 내부 유동에 대한 자세한 연구가 필요하다.
압축기는 저유량 영역에서 날개 흡입면과 끝벽 사이에서 코너 박리(corner separation)를 발생시키며 이는 유로를 막아 손실을 발생시키고 작동 영역을 축소시키는 요인이 된다.(1~4) 많은 연구진들은 코너 박리를 억제하고 압축기 성능을 향상시키기 위해 스윕(sweep), 상반각(dihedral), 린(lean) 등과 같은 삼차원 날개 형상 제어 방법들을 고안해왔다(5~10). 이 중 상반각은 블레이드 스태킹 라인(stacking line)을 원주방향으로 기울임으로써 벽 근처 손실을 줄여주는 방법으로 알려져 있다. Sasaki 등(5)은 익렬 실험을 통해 상반각이 블레이드 스팬 중심에 손실을 집중시키지만 끝벽 근처 부하를 줄여주어 코너 박리 발생이 지연됨을 보였다. Gümmer 등(6)은 상반각 블레이드가 압력 구배를 변화시킴으로써 내부 유동이 반경 방향으로 재분배되고 이를 통해 이차 유동의 크기가 줄어들었다는 결론을 얻었다. 보우드(bowed) 블레이드는 상반각을 허브와 쉬라우드에 동시에 적용하여 블레이드가 마치 활처럼 휘어진 형상을 의미한다. Weingold 등(7)은 보우드 정익을 통해 저유량 영역에서 내부 막힘 현상 및 손실이 줄어드는 결과를 얻었으며, Fischer 등(8) 또한 고부하 조건에서 코너 박리 감소를 통해 정압력비가 상승하는 결과를 얻었다.
본 연구에서는 이러한 상반각 정익이 천음속 축류 압축기 내부 손실에 미치는 영향을 살펴보기 위해 서로 다른 상반각 정익 형상에 대해 수치해석을 수행하였다. 해석은 실험 결과와의 비교를 통해 타당성을 검증하였으며 압축기 내부의 전압력 손실, 역류 영역 및 이차 유동 등의 비교를 통해 성능 변화를 분석하였다.
2. 압축기 모델 및 수치해석 방법
2.1 Stage 37
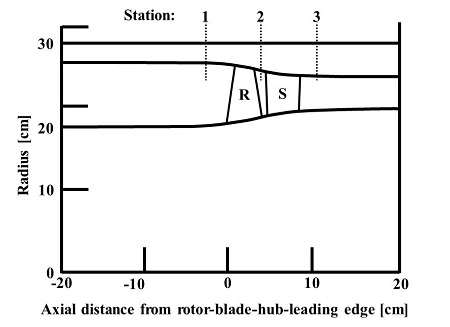
본 연구에서는 1단 천음속 축류 압축기, Stage 37 (Fig. 1)을 사용하여 수치해석을 수행하였다. Stage 37은 NASA에서 항공기용 다단 압축기의 첫 번째 단을 목적으로 설계된 압축기로써 실험을 통해 설계 검증이 수행되었다(11,12).Fig. 2는 Stage 37에 대한 자오면 형상 및 실험 측정점을 나타낸 그림이다. 측정점 1, 2, 3은 각각 동익 입구, 동익 출구(정익 입구), 정익 출구를 나타낸다. 압축기의 동익과 정익은 각각 36개와 46개의 블레이드로 구성 되어 있으며 이 외의 압축기 설계 재원은Table 1과 같다.
2.2 상반각 정익
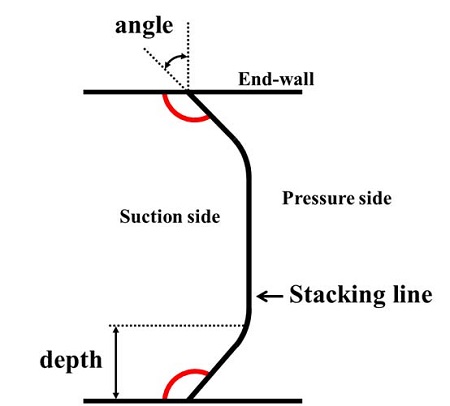
블레이드 스태킹 라인은 각 높이별 블레이드 절단면의 무게 중심점을 잇는 선으로, 일반적으로 각 단면을 수직으로 관통한다. 상반각을 적용하였을 때Fig. 3과 같이 축방향으로 블레이드 스택킹 라인을 바라 보았을 때 블레이드 흡입면이 끝벽과 둔각을 이루고 있는 경우를 양의 상반각이라 하고 반대로 예각을 이룰 때는 음의 상반각이라 한다. 기존의 연구 등을 통해서는 양의 상반각이 음의 상반각보다 압축기 성능에 더 긍정적인 영향을 미친다고 알려져 있다.(5,6) 보우드 블레이드는 양의 상반각을 허브와 쉬라우드 양쪽에 적용하여Fig. 3과 같이 활처럼 휘어진 블레이드를 의미한다. 본 연구에서는Fig. 3에서 정의한 형상 변수(angle, depth)를 이용하여 전체 블레이드 각도 30°, 높이 대비 깊이 20%를 갖는 상반각 정익을 설계하였다. 이들은 각각 상반각 적용 위치에 따라 허브 상반각 정익, 쉬라우드 상반각 정익, 그리고 보우드 블레이드이며 본 연구에서는 기준 형상과 더불어 서로 다른 총 4개의 정익 형상에 대해 수치해석을 수행하였다.
3. 수치해석방법
수치해석에는 상용 소프트웨어인 ANSYS CFX 13.0을 사용하여 압축기 성능 및 내부 유동장을 계산하였다. 3차원 압축성 RANS 방정식을 유한체적법을 이용하여 계산하였으며, 작동 유체는 이상 기체로 가정하였다. 난류 모델로는 SST 모델을 사용하여 역압력 구배에 따른 박리를 더 정확히 예측하도록 하였다.
NASA Stage 37은 동익과 정익이 각각 36개와 46개의 블레이드로 구성되어 있다. 본 연구에서는 정상, 비정상 해석을 효과적으로 수행하기 위해 현절비(solidity)를 유지한 채 정익 블레이드 수를 46개에서 48개로 늘려주었다. 계산 도메인은 최종적으로 동익과 정익 모두 원주 방향으로 30°를 갖도록 동익 블레이드 3개, 정익 블레이드 4개로 구성하였다.
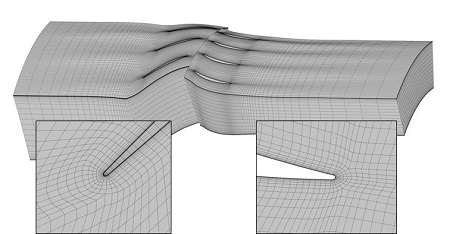
수치해석에 사용한 격자는 ANSYS TurboGrid 13.0을 사용하여Fig. 4와 같이 구성하였다. 블레이드 주위에는 표면 근처의 유동을 효과적으로 예측하기 위해 O-type 격자계를 적용하였으며 모든 벽 표면 근처에서는y+를 5 이하로 맞춰주었다. 이후 격자 의존도 시험을 거쳐 최종적으로 하나의 유로에 해당하는 동익과 정익 격자수를 각각 254,589개와 171,595개로 선정한 후 익렬비 3:4, 총 150만개의 격자에 대해 해석을 수행하였다.
경계조건으로는 실험에서 사용한 조건과 일치하도록 전압력, 전온도 조건을 입구 조건으로 설정해주었으며 출구에서는 스팬 위치에 따른 압력 분포를 고려하기 위해 스팬방향 50% 위치에서 원주방향으로 평균한 정압력 조건을 설정해주었다. 압축기 전체 작동 영역에 대한 성능 결과를 얻기 위해 출구 정압력을 기준 압력에서부터 점차 높여가며 계산을 수행하였고 더 이상 계산이 수렴하지 않는 지점을 스톨이 발생한 지점이라 정의하였다. 벽 조건으로는 단열 조건과 no-slip 조건을 설정해주었으며, 동익과 정익 사이 경계면에는 원주 방향으로 값을 평균하는 혼합면 기법을 사용하였다.
4. 연구 결과
4.1 수치해석 검증
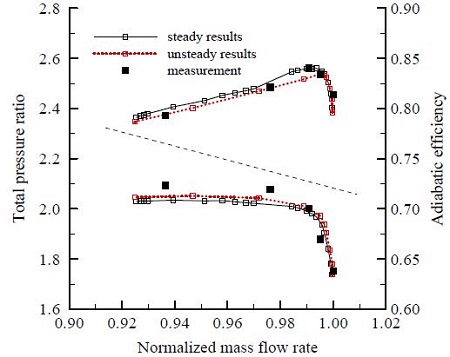
수치해석 결과를 검증하기 위해 기준 형상에 대해 설계 회전속도의 100%에 해당하는 전압력비와 단열효율을 실험 결과(11,12) 와 비교하였다.Fig. 5의 x축은 작동 유량을 초크 유량으로 무차원화한 값을 사용하였으며 y축의 전압력비와 단열효율은 아래의식 (1),(2)와 같이 정의 하였다. 여기서Pt,1,Pt,3,Tt,1,Tt,3는 각각 동익 입구 전압력, 정익 출구 전압력, 동익 입구 전온도, 정익 출구 전온도이며 γ는 이상기체의 비열비를 의미한다.
| (1) |
| (2) |
그림에서 볼 수 있듯이 정상해석과 비정상해석 결과 모두 실험 보다 낮은 전압력비와 스톨 한계점 유량 값을 예측하고 있다. 그러나 전체적인 전압력비 경향과 단열효율이 실험값과 일치하며 최대 효율 지점에 해당하는 유량 값을 정확하게 예측하고 있기 때문에 해석 결과가 일정 수준의 타당성을 확보했다고 판단할 수 있다.
4.2 상반각 정익에 따른 손실 분포
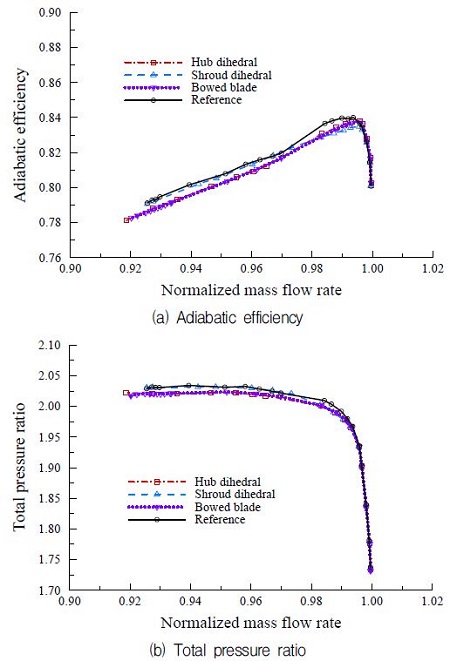
Fig. 6은 정상해석을 통해 얻은 압축기 성능을 정익 형상에 따라 나타낸 그림이다. 허브 상반각과 보우드 정익은 기준 형상 보다 초킹 유량 영역을 제외한 전 작동 영역에서 낮은 단열 효율와 전압력비를 보이지만 기준 형상보다 늘어난 작동영역을 갖는다. 쉬라우드 상반각은 기준형상과 거의 흡사한 압력비를 보이지만 최대 효율점에서는 기준형상보다 낮은 단열 효율을 보인다.
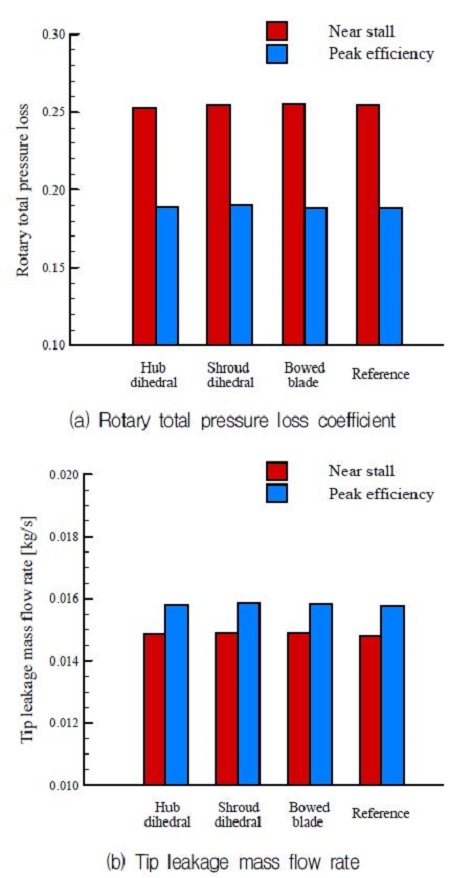
상반각 정익이 압축기 성능에 미치는 영향을 보다 면밀히 분석하기 위해, 정상해석에 따른 동익과 정익 각각의 전압력 손실을 아래와 같이 살펴보았다. 먼저Fig. 7a는 동익 출구면에서 유량 평균한 회전 전압력 손실(ωrot)을 최대효율점(normalized mass flow rate =0.99)과 스톨 근처점(0.93)에서 비교한 그래프이다. 회전 전압력 손실은식 (3),(4)와 같이 동익 입구 전압력과 회전속도성분을 제외한 동익 출구 전압력의 차이를 통해 정의한다. 여기서Ps,2는 동익 출구정압력이며ρ는 작동유체 밀도이다.W2,U2,Um는 동익 출구 상대속도, 동익 출구 회전속도 그리고 미드스팬에서의 압축기 회전속도를 의미한다.
| (3) |
| (4) |
Fig. 7a에서 볼 수 있듯이 동익에서 발생하는 손실은 최대 효율점보다 스톨 근처점에서 더 증가함을 알 수 있다. 이는 익단 간극 및 충격파에 따른 손실이 저유량 조건에서 더 증가하기 때문이며, 유량에 따른 전반적인 동익 손실 경향은Fig. 5의 압축기 전체 단열 효율 그래프와도 일치한다. 그러나 상반각 정익은 정익 형상에 상관없이 각각의 작동 조건에서 모두 일정한 수준의 손실을 보인다. 또한Fig. 7b에서도 마찬가지로 정익 형상에 상관없이 모두 일정한 익단 간극 유량을 보이고 있기 때문에 상반각 정익 형상은 압축기 동익내 유동 특성 및 손실 정도에 있어 거의 영향이 없음을 알 수 있다.
정익 내부 손실은식 (5)와 같이 정의한 정익 전압력 손실을 통해 살펴보았다. 정익은 동익과 달리 회전 좌표계가 아니므로 정익 입구 전압력(Pt,2)과 정익 출구 전압력의 차이를 입구에서의 동압력(Pt,2-Ps,2)으로 나눔으로써 나타낼 수 있다.
| (5) |
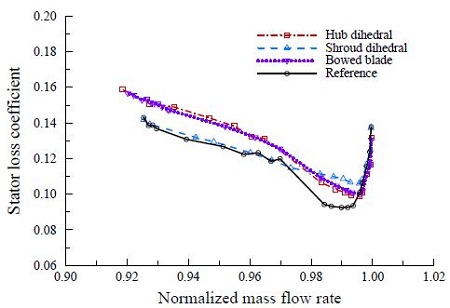
Fig. 8은 위와 같이 정의한 상반각 정익의 손실을 작동 유량에 따라 나타낸 그림이다. 상반각 정익을 적용할 경우 형상에 따라 손실 경향이 서로 다르지만 모든 형상에 대해서 기준 형상보다 손실이 증가하는 결과를 보였다. 먼저 허브 상반각과 보우드 블레이드의 경우 작동 영역은 기준 형상보다 늘어나는 반면 최대 효율점에서 부터 스톨 한계점까지의 손실은 증가하였다. 쉬라우드 상반각만을 적용한 경우에는 작동 영역은 기준 형상과 동일하지만 최대 효율점 근처에서 손실이 증가하였다. 이와 같이 상반각 정익으로 인해 작동영역이 향상되고 전반적인 손실이 증가하는 경향은 Fischer 등(8)의 연구 결과와도 일치한다.
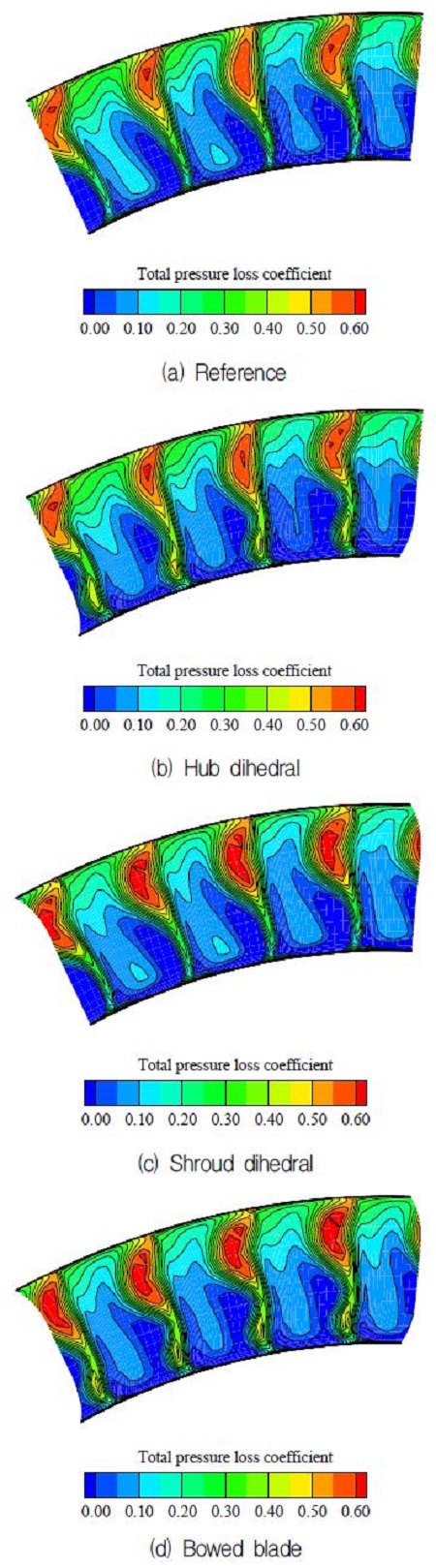
Fig. 9는 스톨 근처점에서 정익 출구 전압력 손실을 기준 형상과 허브 상반각, 쉬라우드 상반각 형상에 대해 서로 비교한 그림이다. 먼저Fig. 9a를 살펴보면 기준 정익 형상일 때 손실이 쉬라우드 근처에 집중되어 있음을 알 수 있다. 이는 동익 익단 간극 유동이 정익 입구 유동각을 증가시킴으로써 정익 내부에 코너 박리를 발생시키기 때문이다. 코너 박리는 유량이 감소할수록 더 악화되며 스톨 한계점에서는 그림에서와 같이 정익 후류와 더불어 스팬 방향 약 70% 높이에서 큰 손실을 일으킨다.
허브 상반각의 경우 기준 정익 형상과 마찬가지로 쉬라우드 근처에 손실이 집중된다(Fig. 9b). 그러나 허브 상반각 정익은 허브 근처에 박리를 추가적으로 발생시킴으로써 기준 형상보다 손실을 증가시킨다. 결과적으로 허브 상반각 정익 뿐만 아니라 보우드 블레이드에서도 전 작동영역에서 기준 형상보다 높은 전압력 손실을 보이게 된다. 보우드 정익은Fig. 8에서와 같이 허브 상반각과 동일한 성능 경향을 보이는데 이는Fig. 9d의 손실 결과와 같이 허브 근처면에서 발생하는 허브 코너 박리에 의한 것으로 보인다.
Fig. 8에서 볼 수 있듯이 쉬라우드 상반각 정익은 저유량 영역에서 기준 형상과 비슷한 수준의 전압력 손실이 발생한다. 그러나Fig. 9c의 쉬라우드 상반각 손실 분포는 기준 형상보다 미세하지만 더 크게 확대되었음을 알 수 있다. 이는 허브 상반각과 마찬가지로 쉬라우드 상반각이 코너 박리의 크기를 증가시켰기 때문이다. 위 사실들을 종합해볼 때 상반각 정익은 적용된 위치에 상관없이 국부적으로 추가적인 박리를 발생시킴으로써 압축기 전체 손실을 증가시킨다는 결론을 얻을 수 있다.
4.3 막힘 현상
블레이드 경계면, 후류, 이차유동 그리고 익단 간극에 의해 발생하는 손실은 유동의 막힘 현상(blockage)과 밀접한 관련이 있다. 천음속 축류 압축기에서는 충격파와 더불어 익단 누설 유동과의 상호작용으로 인한 흡입면 박리가 발생하게 되며 이는 압축기 유로를 막고 운전 영역을 제한하는 원인이 된다.(13,14) 특히 코너 박리는 축 방향 속도 감소와 더불어 역류까지 발생시키기 때문에 유동 막힘 현상은 손실의 주요한 원인이 된다.
정익 출구에서는Fig. 9에서 볼 수 있듯이 손실이 쉬라우드 근처에 집중되어 있다. 따라서 코너 박리에 의해 저속 구간이 발생하거나 또는 박리와 함께 역류가 함께 발생함으로써 축방향 유동이 유로를 따라 흐르지 못하도록 방해하는 막힘 현상이 나타남을 예상할 수 있다.
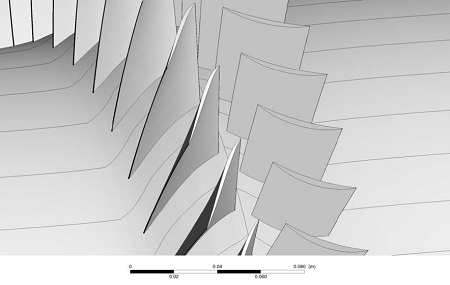
Fig. 10은 스톨 근처점에서 정익 유로 내부에 발생한 축방향 속도 -0.1m/s에 해당하는 등속면을 나타낸 그림으로써, 이를 통해 역류 영역에 따른 막힘 현상을 직관적으로 나타낼 수 있다. 그림에서 볼 수 있듯이 정상해석에 따른 역류 영역은 기준 형상뿐만 아니라 모든 상반각 형상에서 쉬라우드 근처에 크게 발생함을 알 수 있다.
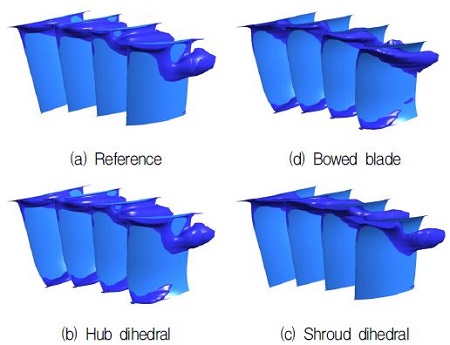
Four different Iso-surfaces of negative axial velocity (-0.1m/s) regions inside stator passage at near stall condition
Table 2는 등속면의 면적을 50% 스팬 방향을 기준으로 허브와 쉬라우드 방향으로 나눈 뒤 각각을 기준 형상의 허브, 쉬라우드 방향 등속면 면적으로 무차원화한 값을 나타낸 표이다.

Normalized areas of iso-surface of negative axial velocity (-0.1m/s) region inside stator passage at near stall condition regarding to the spanwise direction
표를 살펴보면 허브 상반각 정익과 보우드 블레이드 정익은 앞선 손실 분포와 마찬가지로 허브 근처의 역류 영역을 매우 크게 증가시킨다. 그러나 허브 근처와는 반대로 쉬라우드 근처 역류 영역의 크기는 일정 수준 감소하는데 이는 Joslyn 등(1) 의 연구에서 그 원인을 찾을 수 있다. Joslyn 등의 연구에 따르면 작동 유량이 감소하여 정익의 한 쪽 코너 박리의 크기 및 세기가 증가할 경우 반대 쪽 코너 박리는 오히려 영향력이 감소한다고 기술되어 있다. Stage 37의 정익 내부 유동은 쉬라우드 근처에서 손실이 크게 발생하기 때문에 허브 근처에 높은 축방향 유동 모멘텀이 집중된다. 따라서 허브 상반각으로 인해 허브 근처에 손실 영역이 발생할 경우 높은 모멘텀의 유동이 스팬 방향을 따라 미드 스팬으로 이동하기 때문에 쉬라우드 근처 손실은 오히려 일정수준 회복되며, 결과적으로 허브 상반각과 보우드 블레이드에서는Fig. 8에서처럼 기준 형상 보다 더 넓은 작동 영역을 보이게 된다.
4.4 이차 유동과 끝벽 손실
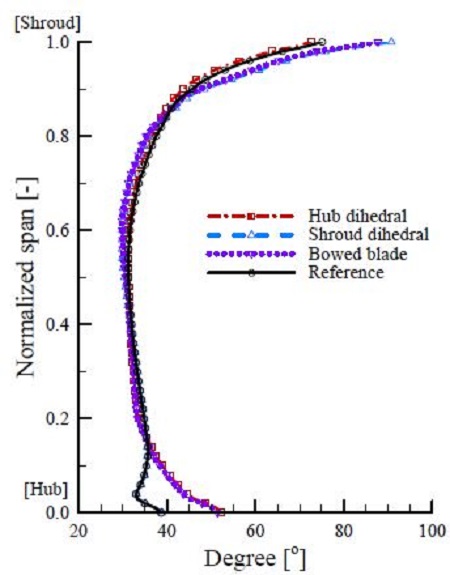
Fig. 11은 정상해석을 통해 정익 형상에 따른 전향각(deflection angle)을 나타낸 그림이다. 여기서 전향각(ϵ)은식 (6)과 같이 정익 입구 유동각(α2)과 정익 출구 유동각(α3)의 차이로 정의된다.
| (6) |
먼저 그림에서 볼 수 있듯이 허브 영역보다는 쉬라우드 근처에서 전향각이 더 큰데 이는 동익 익단 간극으로 인해 쉬라우드 근처 정익 입구 유동각이 허브 영역보다 상대적으로 증가하기 때문이다. 그러나 앞서Fig. 7에서와 같이 상반각 정익은 동익의 유동에 대해 어떠한 영향도 미치지 않기 때문에 정익으로 유입되는 유동은 정익 형상과 상관없이 일정한 입구 유동각을 갖는다.
상반각 정익을 적용할 경우, 그림에서와 같이 허브 상반각 정익과 쉬라우드 상반각 정익은 각각 허브와 쉬라우드 영역에서 전향각을 증가시킨다. Stage 37 정익 특성상 깃출구각(outlet blade angle)은 축 방향과 평행하기 때문에 전향각이 증가할수록 유동의 편차각(deviation angle)은 감소하게 되며, 이는 상반각으로 인해 끝벽 유동의 축방향 속도가 회복됨을 의미한다. 결과적으로 상반각 정익은 끝벽 근처에 코너 박리가 존재함에도 불구하고 깃 뒷전(trailing edge)의 편차각을 줄여줌과 동시에 블레이드를 따라 잘 흐를 수 있도록 유도해주는 역할을 한다.
벽 근처 유동 경계층은 정익 선회에 따른 이차 와도(secondary vorticity)를 발생시킴으로써 정익 내부에 이차 유동(secondary flow)에 따른 손실을 일으킨다. 이차 와도는 미드 스팬을 기준으로 상 · 하부가 각각 서로 다른 방향으로 회전하며 흡입면을 따라 미드 스팬 방향으로 유동을 모이도록 한다. 이 때 이차 와도는 회전 벡터의 선회로 정의 할 수 있으며식 (7)(15)과 같이 전향각과 경계층 와류의 곱으로 그 크기를 나타낼 수 있다. 여기서V와z는 각각 표면 근처 유속과 반경방향 높이 성분을 의미한다.
| (7) |
식 (7)에 따르면 전향각이 증가할수록 이차 와도의 세기가 증가하므로 상반각 정익 끝벽 근처에서는 늘어난 전향각 만큼 반경 방향으로의 유동 혼합이 증가한다. 반경 방향 유동 혼합은 이차 와도의 특성상 흡입면을 따라 끝벽에서부터 미드 스팬 방향으로 유동을 이동시키기 때문에 이 같은 유동 재분배는 결과적으로 끝벽 근처 유동장에 영향을 미침으로써 끝벽 손실에도 변화를 일으킨다.
끝벽 손실은 끝벽 표면 경계층 내부에서 발생하는 익렬 내부 이차 손실(secondary loss)로써, 압축기 내부에는 역압력 구배로 인한 박리가 발생하기 때문에 전체 손실에 있어 끝 벽 손실이 차지하는 비중은 매우 크다. 본 연구에서는 끝벽 손실 분석을 위해식 (8)(16,17)과 같이 끝벽 근처 상대 속도(Vδ)를 이용하여 정의하였다. 이 때 소산 계수(Cd)는 0.002이며Aw는 끝벽의 넓이를 나타낸다.Table 3은 허브와 쉬라우드 각각의 끝벽 손실을 기준 형상에 대해 무차원화하여 나타낸 표이다.
| (8) |
표에서 볼 수 있듯이 허브 상반각 정익과 쉬라우드 상반각 정익은 각각 허브와 쉬라우드의 끝벽 손실을 줄여주며, 상반각을 양쪽 끝벽에 적용한 보우드 블레이드의 경우에서도 마찬가지로 끝벽 손실은 감소하게 된다. 끝벽 손실은식 (8)과 같이 표면 속도의 세제곱으로 정의되기 때문에 표면 속도가 감소할수록 손실은 줄어들게 된다. 앞선 전향각 그래프에서 언급하였듯이 Stage 37 정익의 끝벽 근처에서는 낮은 편차각을 갖기 때문에 축방향과 평행한 유동만이 남게 된다. 즉, 상반각 정익은 늘어난 전향각 만큼 미드 스팬 방향으로 유동을 이동시킴으로써 반경 방향 및 회전 방향 속도 성분으로 인한 끝벽 손실을 감소시킨다.
5. 결 론
본 연구에서는 상반각 정익을 적용한 천음속 축류 압축기에 대해 수치해석을 수행하여 다음과 같은 결론을 얻었다.
- 1) 서로 다른 상반각 정익을 적용한 압축기 유동을 분석한 결과, 동익에서는 정익 형상에 상관없이 동일한 회전 전압력 손실과 익단 간극 유량을 보였다.
- 2) 정익 흡입면과 쉬라우드 끝벽 사이에는 코너 박리가 발생한다. 유량이 감소할수록 코너 박리의 크기와 세기가 증가하여 스톨 근처점에서는 정익 출구의 스팬 방향 70% 지점에서 최대 손실을 보인다.
- 3) 정익 내부 손실은 상반각 형상에 따라 서로 다른 결과를 보인다. 허브 상반각과 보우드 정익의 경우 허브 근처에 추가적인 박리와 함께 역류 영역을 발생시킴으로써 전 작동영역에서 전압력 손실을 증가시킨다. 쉬라우드 상반각 또한 최대 효율점에서 기준 형상보다 높은 전압력 손실을 보인다.
- 4) 허브 상반각으로 인해 발생한 허브 근처 손실은 높은 축방향 모멘텀 유동을 스팬 방향으로 이동시킴으로써 쉬라우드 손실을 억제함과 동시에 전체 압축기 작동 영역을 향상시킨다.
- 5) 상반각 정익은 끝벽 근처의 전향각을 증가시켜 이차 와도의 세기를 증가시키고, 그 결과 반경 방향으로의 유동 혼합을 활발하게 함으로써 끝벽 손실을 감소시킨다.
References
-
Joslyn, H., and Dring, R., (1985), “Axial Compressor Stator Aerodynamics”, Journal of Engineering for Gas Turbines and Power, 107, p485-493.
[https://doi.org/10.1115/1.3239754]

-
Lei, V., Spakovszky, Z., and Greitzer, E., (2008), “A Criterion for Axial Compressor Hub-Corner Stall”, Journal of Turbomachinery, 130, p031006.
[https://doi.org/10.1115/1.2775492]

-
Wei, M., Xavier, O., Lipeng, L., Francis, L., and Feng, G., (2011), “Experimental Study of Corner Stall in a Linear Compressor Cascade”, Chinese Journal of Aeronautics, 24, p235-242.
[https://doi.org/10.1016/S1000-9361(11)60028-9]

-
Choi, M., Baek, J. H., Oh, S. H., and Ki, D. J., (2008), “Role of Hub-Corner-Separation on Rotating Stall in an Axial Compressor”, Trans. Japan Soc. Aero. Space Sci, 51(172), p93-100.
[https://doi.org/10.2322/tjsass.51.93]

-
Sasaki, T., and Breugelmans, F., (1998), “Comparison of Sweep and Dihedral Effects on Compressor Cascade Performance”, Journal of Turbomachinery, 120, p454-464.
[https://doi.org/10.1115/1.2841738]

-
Gümmer, V., Wenger, U., and Kau, H., (2001), “Using Sweep and Dihedral to Control Three-Dimensional Flow in Transonic Stators of Axial Compressors”, Journal of Turbomachinery, 123, p40-48.
[https://doi.org/10.1115/1.1330268]

-
Weingold, H., Neuber, R., Behlk, R., and Potter, G., (1997), “Bowed Stators: An Example of CFD Applied to Improve Multistage Compressor Efficiency”, ASME Journal of Turbomachinery, 119, p161-168.
[https://doi.org/10.1115/1.2841086]

-
Fischer, A., (2004), “Performance of Strongly Bowed Stators in a Four-Stage High-Speed compressor”, ASME Journal of Turbomachinery, 126, p333-338.
[https://doi.org/10.1115/1.1649743]

-
Breugelmans, F., Carels, Y., and Demuth, M., (1984), “Influence of Dihedral on the Secondary Flow in a Two-Dimensional Compressor Cascade”, ASME Journal of Engineering for Gas Turbines and Power, 106, p578-584.
[https://doi.org/10.1115/1.3239609]

-
Gallimore, S., Bolger, J., Cumpsty, N., Taylor, M., Wright, P., and Place, J., (2002), “The Use of Sweep and Dihedral in Multistage Axial Flow Compressor Blading - Part I : University Research and Methods Development”, ASME Journal of Turbomachinery, 124, p521-532.
[https://doi.org/10.1115/1.1507333]

- Reid, L., and Moore, R., (1978), “Design and Overall Performance of Four Highly Loaded, High-Speed Inlet Stages for and Advanced High-Pressure-Ratio Core Compressor”, NASA Report No. TP-1337.
- Moore, R., and Reid, L., (1980), “Performance of Single-Stage Axial-Flow Transonic Compressor with Rotor and Stator Aspect Ratios of 1.19 and 1.26, Respectively, and With Design Pressure Ratio of 2.05”, NASA Report No. TP-1659.
-
S. A. Khali, A. S. Khalsa, I. A. Waitz, C. S. Tan, E. M. greitzer, N. A. Cumpsty, J. J. Adamczyk, and F. E. Marble, (1999), “Endwall Blockage in Axial Compressor”, ASME Journal of Turbomachinery, 121, p499-509.
[https://doi.org/10.1115/1.2841344]

-
K. L. Suder, (1998), “Blockage Development in a Transonic, Axial Compressor Rotor”, ASME Journal of Turbomachinery, 120, p465-476.
[https://doi.org/10.1115/1.2841741]

- S. L. Dixon, and C. A. Hall, (1998), Fluid Mechanics and Thermodynamics of Turbomachinery, 4th ed, Pergamon Press, British.
-
J. D. Denton, (1993), “Loss Mechanisms in Turbomachines”, Journal of Turbomachinery, 115, p621-656.
[https://doi.org/10.1115/1.2929299]

- J. D. Denton, N. A. Cumpsty, (1987), “Loss Mechanisms in Turbomachines”, ImechE Paper No. C260/87.
- ANSYS Inc, (2010), ANSYS CFX 13.0 User’s manual.