소듐냉각고속로 제어봉집합체의 낙하시간 및 충격속도 예측을 위한 CFD 해석

1. 서 론

150MWe 원형소듐냉각고속로(sodium cooled faster reactor, SFR)는 2012년부터 한국원자력연구원(Korea Atomic Energy Research Institute, KAERI)에서 개발되고 있다. 개발되고 있는 내부구조물 중에서 제어봉집합체(control rod assembly)는 원자로의 출력을 제어하는 목적뿐 아니라 원자로의 신속한 정지(scram)를 위하여 사용된다.

원자로의 비상사고 시 원자로를 신속하게 정지하기 위하여 제어봉집합체를 원자로 노심에 신속히 삽입함으로써 원자로를 안전하게 정지시킨다. 현재 상용으로 사용되고 있는 가압경수로(PWR)의 경우 핵연료집합체를 구성하고 있는 안내관(guide tube) 내부로 제어봉(control rod)을 삽입하여 원자로를 긴급하게 정지시키는데 반해 소듐냉각고속로의 경우 핵연료 집합체용 육각덕트(hexagonal duct)와 동일한 외형과 크기의 제어집합체 안내덕트(guide duct) 내부에 제어봉집합체(control rod assembly)를 제어봉 구동장치(control rod drive mechanism)로 체결하고 있다가 비상 시 제어봉집합체를 분리하여 중력에 의해 자유낙하 시킴으로써 원자로를 신속히 정지시키는 구조이다.

제어봉집합체의 낙하시간은 소듐냉각고속로를 안전하게 운영하기 위해 반드시 평가되어야 한다.⁽¹⁾ 또 제어봉집합체의 주요설계변수로는 낙하 시간 외 충격속도가 있는데, 낙하시간은 원자로 안전정지와 관계가 있으며, 충격속도는 제어봉집합체와 안내덕트의 건전성과 관련이 있다. 따라서 적절한 제어봉집합체 낙하시간과 충격속도는 제어봉집합체의 설계에 매우 중요하다.⁽²⁾

가압경수로용 제어봉집합체는 원형의 단순한 형상을 가지고 있어서 이론적인 접근방법^(2∼4)과 FLUENT나 ADINA를 이용한 전산해석방법⁽¹,⁵⁾으로 제어봉 집합체 낙하시간과 유동 현상을 분석하였다. 그러나 소듐냉각고속로용 제어봉집합체는 여러 구조부품으로 이루어진 복잡한 형상을 가지고 있기 때문에 기존 이론 및 전산해석방법을 적용하는데 어려움이 있다. 특히 이전 전산해석에서는 적용한 해석방법에 대한 적합성을 검증하는 절차가 누락되어있을 뿐⁽¹⁾ 아니라 단순한 가압경수로용 제어봉 집합체를 대상으로 해석^(1,5)을 수행하였다.

본 연구에서는 전산유체역학(computational fluid dynamics, CFD)을 이용한 SFR용 제어봉 집합체 낙하시간과 충격속도예측을 위하여 중력에 의한 제어봉집합체의 낙하와 낙하 시 안내덕트 내의 유체항력에 의한 저항을 고려하기 위하여 강체 운동방정식과 유동방정식을 연계한 해석방법을 개발하고, 이를 적용하여 제어봉집합체의 시간에 따른 낙하거리 및 속도변화, 제어봉집합체 내/외부 통과유량 분배비를 예측하였다.

본 해석 이전에 개발된 해석방법의 신뢰성 확보를 위하여 수중 구체 낙하현상에 대하여 해석을 수행하였으며, CFD해석결과와 이론해석결과의 비교를 통하여 전산해석방법의 적합성을 확보하였다.

2. SFR 제어집합체

2.1 구성 및 형상

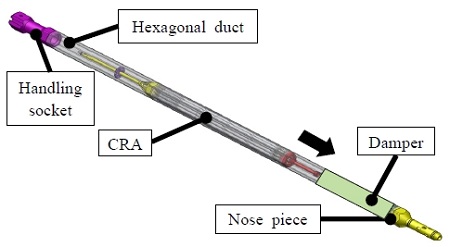
제어봉집합체 낙하해석 시 고려된 형상은 제어봉집합체와 안내덕트로 구성된다. 제어봉 집합체의 외부를 감싸고 있는 안내덕트는 handling socket, hexagonal duct, nose piece 및 damper로 구성되는데, handling socket은 hexagonal duct의 상부 끝단에 장착되며, 안내관으로 유입되는 소듐(sodium)의 배출구 역할을 한다. Hexagonal duct는 제어봉집합체의 낙하경로를 구속하는 역할을 한다. Nose piece 하부에는 9개의 구멍이 위치하고 있으며, 이를 통해 소듐이 hexagonal duct 내부로 유입된다. Nose piece 상부에는 damper가 위치하고 있으며, 제어봉집합체 낙하 시 piston head가 damper 상부의 홈에 안착하게 된다.

제어봉집합체는 19개의 제어봉 및 기타 부속품으로 구성된다. 제어봉은 cladding, top end cap, bottom end cap, wire, spacer, plenum spring, absorber 등으로 구성되며, 개당 무게는 약 1.7kg, 19개 제어봉 무게의 총합은 약 32.3 kg이다. 제어봉집합체를 구성하는 부속품에는 lower adapter, upper adapter, duct, mounting rail, piston head, guide 및 clamping head 등이 있으며, 제어봉 및 부속품을 포함한 제어봉집합체의 무게는 약 48.9kg이다.

정상 운전조건에서는 제어봉집합체의 clamping head 부분이 handling socket의 grapping hole의 높이에 위치하며, 낙하 시 낙하 높이는 약 1m이다. 제어봉집합체 낙하 시 piston head가 damper의 상부 홈에 삽입되며, 낙하 종료 시 lower adapter와 damper가 접촉하게 된다.

안내덕트 및 제어봉집합체의 3차원 형상을 Fig. 1에 나타내었다. 이것은 제어봉집합체가 중력에 의해서 화살표 방향으로 자유낙하 할 때 piston head가 안내덕트 내의 damper에 삽입되기 직전모습을 나타낸다.

Fig. 1

Configuration of a guide duct and control rod assembly

2.2 해석조건

Nose piece의 구멍을 통해 primary sodium pump로부터 안내덕트 내부로 유입되는 소듐의 유량은 약 2.27kg/s이며, 유입되는 소듐의 온도는 430℃이다. Nose piece의 구멍을 통해 유입되는 소듐의 유량은 일정한 것으로 가정하였다. 제어봉 발열에 의한 소듐의 밀도 및 점도 변화가 제어봉집합체의 낙하속도에 미치는 영향은 미미할 것으로 판단됨에 따라 제어봉의 발열은 고려하지 않았으며, 해석영역 내의 소듐 물성치는 일정한 것으로 적용하였다(Table 1). 안내덕트 구성품 중 hexagonal duct 내부에서 육각형 단면의 제어봉집합체가 낙하하기 때문에 낙하 중 제어봉집합체의 회전은 발생하지 않을 것으로 판단하여 제어봉집합체의 낙하 운동을 중력방향의 1차원 병진운동으로 가정하였다. 제어봉집합체는 순수하게 중력에 의해 낙하하며, 해석 시 적용된 중력가속도는 9.81m/s²이다.

Table 1

Material properties of sodium (430 ℃)

2.3 해석방법

SFR용 제어봉집합체 낙하시의 현상을 해석하기 위하여 중력에 의한 제어봉집합체의 낙하와 낙하 시 안내덕트 내의 유체항력에 의한 저항을 고려하기 위하여 강체 운동방정식과 유동방정식을 연계하여 해석을 수행하였다. 안내관 내부 및 제어봉집합체 내/외부를 흐르는 소듐의 유동현상을 계산하기 위해 유한체적법(FVM) 기반의 상용코드인 ANSYS CFX (ver. 15)를 사용하였다.

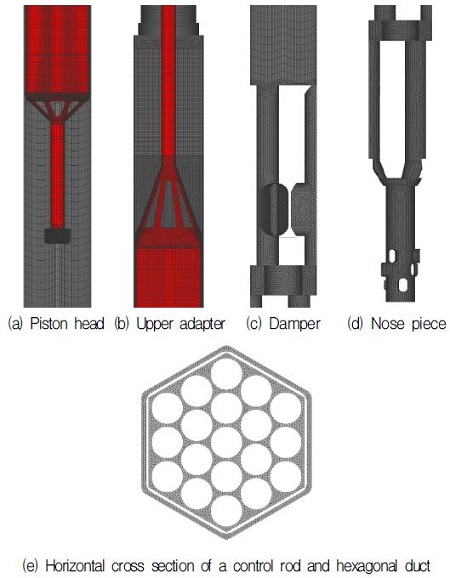
제어봉집합체가 낙하함에 따라 초기 생성된 격자가 꼬이는 격자문제를 해결하기 위하여 sliding mesh 기법과 deforming mesh 기법을 사용하였다.⁽⁶⁾ 제어봉집합체의 낙하에 의한 유동영역 격자의 변형을 처리하기 위해 해석영역 내 격자는 영역에 따라 tetrahedral, hexagonal, prism mesh를 혼합하여 구성하였으며, 압력/속도의 구배가 클 것으로 예상되는 영역에 보다 조밀하게 격자를 구성하여 해석의 정확성을 향상시켰다. 슬라이딩면의 위치와 인터페이스 면에서의 격자의 크기 비율은 기본적으로 해석결과에 영향을 미칠 수 있는데 베어링봉과 가이드 덕트 사이의 거리가 수 mm로 아주 작아서 슬라이딩면의 위치를 이동시키면서 여러 해석 후 결과를 비교하는 작업을 수행하기 불가능하여 슬라이딩하는 두 면의 격자 크기를 동일하게 하고, 시간 간격을 매우 작게 하여, 매 시간단계에서 충분히 해가 수렴하도록 함으로써 슬라이딩면에서 발생하는 오차가 해석결과에 미치는 영향을 최소화시켰다. 해석영역 전체에서 사용된 격자의 수는 약 3,850,000개 이며, Fig. 2에 해석 시 사용된 제어봉집합체의 격자를 나타내었다.

Fig. 2

FVM model for components of a guide duct and control rod assembly

원자로가동 중 제어봉집합체는 원자로 내에 고정되어 있으나 제어봉집합체 유로 내로 일정유속으로 냉각수(coolant)가 상부로 흐르게 된다. 제어봉집합체 유로 내 초기에 형성되는 유동장 초기조건을 확보하기 위해 제어봉집합체의 이동을 구속한 조건에 대한 정상상태(steady state) 해석을 선행하여 비정상상태 해석의 초기조건으로 사용하였다. 운동량 방정식의 점성항에 대한 난류효과를 모사하기 위해 2- equation RANS 난류모델 중 가장 일반적으로 사용되는 standard K-ε 모델을 사용하였다. 비정상 해석의 시간 간격(time step)은 0.001초로 설정하였다. 운동방정식과 운동량 방정식의 discretization scheme은 high resolution advection scheme과 second order backward Euler transient scheme을 사용하였다. 난류 운동에너지 방정식과 소산율 방정식에 대해서는 upwind advection scheme과 first order backward Euler transient scheme을 사용하였다.

3. 수중 구체 낙하에 대한 검증해석

3.1 검증해석 개요 및 해석방법

제어봉집합체 낙하해석 시 적용될 해석방법의 검증을 위해 원통형 수조 내 구체 낙하에 대한 해석을 수행하였다.

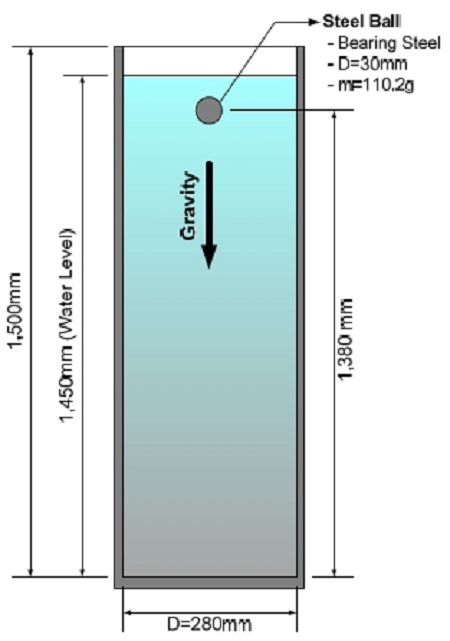
Fig. 3은 구체낙하실험 시 적용된 수조의 개략도인데 해석 시 적용된 수조의 크기는 직경 280mm, 높이 및 수위는 1,450mm이다. 구체는 베어링강(밀도 7,795kg/m³)재질이며, 직경은 30mm이다. 구체의 무게는 약 110.2g이다. 구체의 초기위치는 바닥으로부터 1,380mm이다(Fig. 3).

Fig. 3

Schematic drawing for free falling of a steel ball in water for methodology verification

구체 낙하 시 주변유체의 물성에 따른 영향을 평가하기 위해 수조 내 유체가 공기, 물, 소듐인 3가지 경우에 대하여 해석을 수행하였다.

해석 시에 낙하 중인 구체의 회전은 고려하지 않았으며, 단방향(중력방향) 1자유도 운동방정식을 적용하였다. 해석 시 사용된 격자의 수는 약 1,160,000개이다. 해석방법은 2.3절에 기술된 내용과 동일하다.

3.2 검증해석 결과

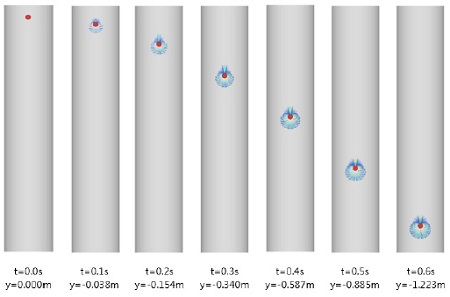
수조 내 유체가 물인 경우의 시간에 따른 구체의 위치변화와 구체 주변의 유동장을 Fig. 4에 나타내었다. 구체의 낙하속도는 중력에 의하여 서서히 증가하는 경향을 보여준다. 하지만, 낙하거리가 충분하지 않아 수조 바닥에 이르는 시점에 서 종단속도(terminal velocity)에는 이르지는 않았다. 구체의 낙하에 따라 구체 하부의 유체는 아래로 밀린 후, 구체의주변을 돌아 상부로 흐르는 유동 패턴을 보여주었다.

Fig. 4

Falling distance of a steel ball in various fluid

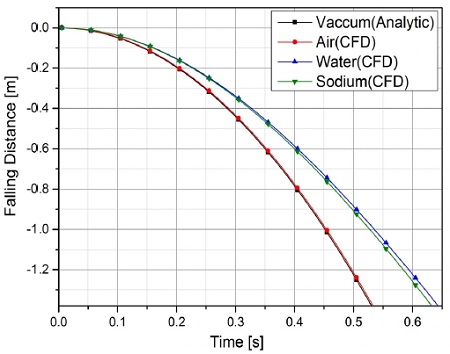
수조 내 유체가 공기, 물, 소듐인 3가지 경우에 대하여 해석된 시간에 따른 구체의 낙하거리를 Fig. 5에 나타내었으며, 추가로 진공상태에서 구체의 낙하거리를 계산하여 함께 나타내었다.

Fig. 5

Falling distance of a steel ball in various fluid

수조 내 유체가 물인 경우, 1.38m의 높이에서 바닥까지 낙하 시에 걸리는 시간은 약 0.63초로 계산되었다. 공기인 경우에는 밀도와 점도가 낮기 때문에 유동저항이 구체의 낙하속도에 미치는 영향이 크지 않아 제일 빨리 낙하하는 것으로 예측되었으며, 이는 유동저항이 없는 진공상태에서의 낙하시간과 비슷하였다.

비등점에서의 소듐의 경우에는 밀도와 점도가 물과 유사하기 때문에 두 매질에서 구체의 시간에 따른 낙하거리가 거의 유사한 경향을 나타내었다.

상기의 해석 결과는 현재의 해석방법이 구체 낙하 시 주변 유체의 물성에 따른 영향을 충분히 반영하고 있음을 보여주는 결과이다.

3.3 이론적 분석

구체의 낙하 시의 운동방정식은 아래와 같다.

$\[ m\frac{\mathit{dV}}{\mathit{dt}}=\mathit{mg}\left(1-\frac{{\rho }_f}{{\rho }_s}\right)-\frac{1}{8}\pi d^2{\rho }_f{V}^2{C}_D \]$

(1)

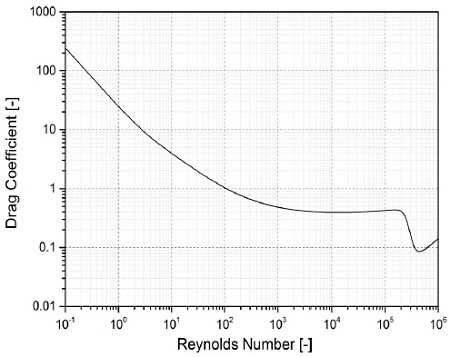
여기서, m은 구체의 질량, V는 낙하속도, t는 시간, g는 중력가속도, ρ는 유체의 밀도, d는 구체의 지름, CD는 구체의 항력계수(drag coefficient)이다. 첨자 f는 유체, s는 구체를 의미한다. Reynolds 수(Re)에 따른 구체(매끈한 표면을 가진 구체)의 항력계수 변화를 Fig. 6에 나타내었고⁽⁷⁾, 이는 아래와 같이 표현할 수 있다.^(8,9)

Fig. 6

Drag coefficient as a function of Reynolds number

$\[ C_D=\frac{24}{\mathit{Re}}+\frac{2.6\left(\frac{\mathit{Re}}{5.0}\right)}{1+\left(\frac{\mathit{Re}}{5.0}\right)}+\frac{0.411{\left(\frac{\mathit{Re}}{\mathrm{263,000}}\right)}^{-7.94}}{1+{\left(\frac{\mathit{Re}}{\mathrm{263,000}}\right)}^{-8.0}}+\left(\frac{R{e}^{0.8}}{\mathrm{461,000}}\right) \]$

(2)

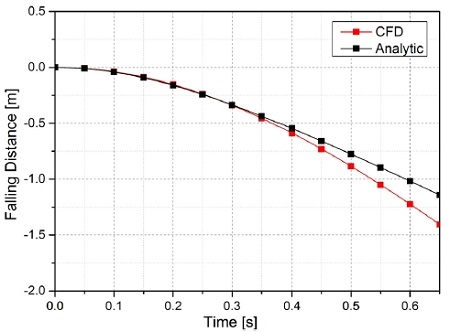
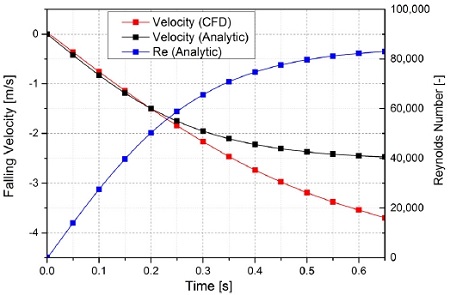
식 (1)과 식 (2)를 사용하여 검증해석과 동일한 조건 하에서 시간에 따른 구체의 낙하거리와 낙하속도에 대한 근사해를 구하여 Fig. 7과 Fig. 8에 나타내었다. CFD해석을 통하여 계산된 낙하속도가 상기 식들을 사용하여 이론적으로 계산된 낙하속도에 비하여 빠른 것을 볼 수 있다. 이러한 낙하속도의 차이가 발생하는 이유를 다음과 같이 분석할 수 있다.

Fig. 7

Falling distance of a steel ball in water

Fig. 6과 식 (2)에 나타낸 항력계수는 Re 수가 일정한 정상상태에서 얻어진 값이지만, 본 연구에서 수행된 CFD해석에서의 물리적 상황은 구체가 낙하함에 따라 Re 수가 연속적으로 변화하는 상황이며(Fig. 8), 이와 같이 Re 수가 연속적으로 변화하는 상황에서 Re 수와 항력계수 간의 관계에 대한 선행연구 자료는 저자들이 아는 범위에서는 존재하지 않는다. 하지만 구체 표면이 거칠거나 구체표면의 유동이 불안정할수록 천이점을 앞당겨 난류경계층(turbulent boundary layer)을 형성시키고 유동박리가 지연되어 얇은 후류(wake)가 형성되어 유동저항이 감소한다는 것은 잘 알려진 사실이다. 구체가 낙하함에 따라 Re 수가 연속적으로 변화하는 상황에서는 Re 수가 일정한 경우에 비해 구체표면의 유동장이 불안정하기 때문에 상대적으로 작은 Re 수에서 유동천이가 발생하고 이에 따라 항력 계수 또한 감소할 것으로 예측된다. 또한 Kikuchi 등⁽¹⁰⁾의 연구결과에서도 비정상상태의 구체낙하 시 정상상태 항력계수를 이용한 correlation과 다른 결과를 나타내는 것을 확인할 수 있다. 정상상태 항력계수를 사용함으로써 발생하는 오차에 대한 상기의 분석의 타당성을 입증하고자 동일 조건하에서 구체낙하실험이 수행할 계획이며 그 결과는 후속논문으로 제출할 계획이다.

Fig. 8

Falling velocity and Reynolds number of a steel ball in water

현재의 CFD 결과는 구체 낙하 중에 발생하는 상기의 물리 현상을 잘 반영하고 있는 것으로 판단되며, 적용된 해석방법을 제어봉 집합체의 낙하 현상 해석에 사용하는 것이 가능하다고 판단된다.

4. 제어봉집합체 낙하 해석결과

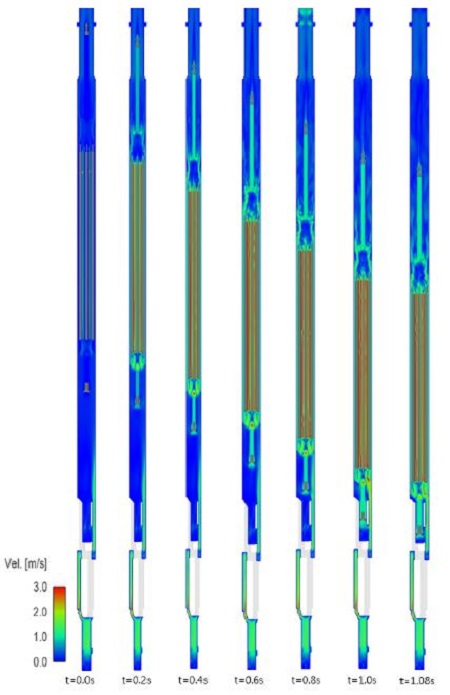
제어봉집합체의 낙하 시의 CFD해석을 수행하였으며, 낙하 동안의 유동장을 Fig. 9에 나타내었다.

Fig. 9

Falling distance of a SFR control rod assembly

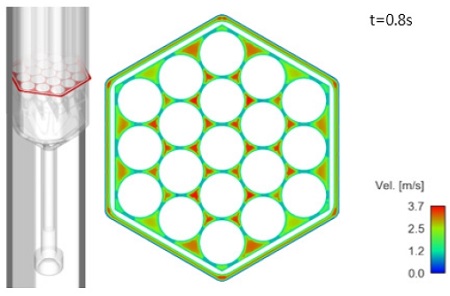
Nose piece 하부의 구멍으로부터 유입된 소듐이 nose piece 및 damper 주변 유로를 통과할 때의 유속이 비교적 빠르게 형성되었다. 하부로부터 유입된 소듐은 대부분 hexagonal duct 측으로 흐르며 piston head 안착 홈 측으로 유입되는 유량은 매우 적은 것을 알 수 있었다. Damper를 통과한 소듐은 hexagonal duct로 유입되면서 유속이 감소하게 되고, 그 이후 hexagonal duct 내부에 위치한 제어봉집합체 내/외부를 통과하는 과정에서 유로 단면적이 급격하게 감소함에 따라 유속이 다시 증가하는 것을 확인할 수 있었다. 제어봉집합체를 통과한 뒤 유로단면적 증가로 유속이 감소하며, 최종적으로 handling socket을 지나 안내관 외부로 유출되었다. 제어봉집합체가 낙하하기 전에는 hexagonal duct 및 제어봉집합체 내부의 유속이 0.5m/s 이하의 낮은 유속으로 형성되지만, 제어봉집합체가 낙하하기 시작함에 따라 제어봉집합체 내부의 유속이 급격하게 증가하였다. 제어봉집합체의 낙하가 제어봉집합체 하부영역의 유동패턴에 미치는 영향은 크지 않았으며, 제어봉집합체의 상부영역에서 와류가 발생 하였다.

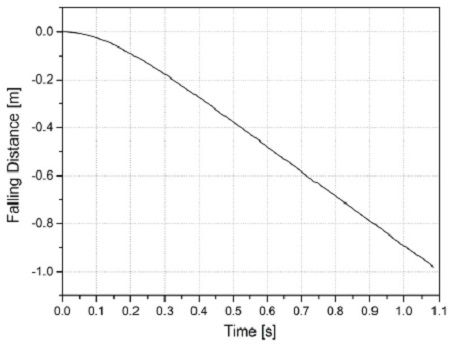
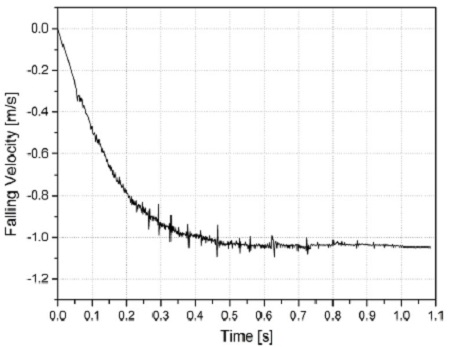
시간에 따른 제어봉집합체의 낙하거리를 Fig. 10에 나타내었으며, 시간에 따른 제어봉집합체의 낙하속도를 Fig. 11에 나타내었다. 낙하 초기에 제어봉집합체의 낙하속도가 급격히 증가하지만, 항력에 의하여 낙하속도의 증가율이 점점 감소하여 약 0.5초 이후에는 낙하속도 가 종단속도(terminal velocity)에 도달하였다.

Fig. 10

Falling distance of a SFR control rod assembly

Fig. 11

Falling velocity of a SFR control rod assembly

제어봉집합체의 piston head가 damper의 안착 홈에 진입하면서 낙하속도가 감소할 것으로 기대하였으나, damper에 의한 낙하속도 감소는 미미하였다. 이는 damper 측면유로를 통과한 소듐이 damper의 piston head 안착 홈 내부로 거의 유입되지 않고, piston head가 damper의 안착 홈에 진입할 때 nose piece 하부 구멍의 단면적이 커서 안착 홈 내부의 압력 증가가 미미하기 때문인 것으로 판단된다. 따라서, 이 부분의 단면적을 보다 줄이면 내부압력증가로 낙하속도의 감쇄가 나타날 것으로 예상된다.

CFD해석을 통해 예측된 제어봉집합체의 수중 1m낙하 시 낙하시간은 약 1.1초이고, 종단속도는 약 1.05m/s 이었다. 제어봉집합체의 충격속도는 종단속도와 동일하게 약 1.05m/s 인 것으로 판단된다.

제어봉집합체의 낙하가 시작되기 전에 제어봉집합체 내/외부 단면을 통과하는 유량은 각각 약 1.68kg/s, 0.61kg/s로 약 2.75:1의 비율이지만 제어봉집합체가 낙하하여 종단속도에 도달한 시간에서 각 단면을 통과하는 유량은 약 10kg/s 및 4.4kg/s로 약 2.3:1이다(Fig. 12). 제어봉집합체의 낙하속도가 증가함에 따라 제어봉집합체 내/외부 단면의 통과유량비가 감소하는 경향을 보이지만 이러한 현상이 제어봉집합체의 낙하속도에 대해 물리적인 의미를 가지지는 않는 것으로 판단되며, 제어봉집합체 내/외부의 유동영역단면의 면적비가 약 2.4:1이기 때문에 이러한 결과가 도출된 것으로 판단된다.

Fig. 12

Falling velocity of a SFR control rod assembly

5. 결론 및 고찰

소듐냉각고속로 제어봉집합체의 낙하시간 및 충격속도를 예측하기 위해 CFD해석을 수행하였다. 이를 위하여 강체의 운동방정식과 유체의 유동방정식을 연계한 해석방법론을 수립하였으며 제어봉집합체의 낙하에 따른 격자변형을 고려하기 위한 격자변형기법을 본 해석에 적용하였다. 제어봉집합체 낙하해석에 적용된 해석방법론의 적합성을 검증하기 위하여, 수중 구체낙하에 대한 검증해석을 수행하였으며 해석결과를 이론적 예측결과와 비교하였다.

검증해석결과, 본 연구에서 적용된 CFD해석방법이 강체의 수중낙하 중에 발생하는 물리현상을 잘 반영하고 있는 것을 이론적 분석을 통하여 확인하였다.

개발/검증된 해석방법론을 적용하여 제어봉집합체 낙하해석을 수행하였으며 본 연구의 결과를 요약하면 다음과 같다.

• 1) 낙하 초기에 제어봉집합체의 낙하속도가 급격히 증가하지만 낙하속도의 증가율이 항력증가로 인하여 점점 감소하여 약 0.5초 이후에는 낙하속도가 종단속도 약 1.05m/s에 도달한다.
• 2) 제어봉집합체의 piston head가 damper의 안착 홈에 진입하면서 낙하속도가 감소할 것으로 기대하였으나, damper에 의한 낙하 종단의 속도감소가 크게 발생하지 않아 제어봉집합체의 충격속도는 종단속도와 동일하게 약 1.05m/s이다.
• 3) CFD해석을 통해 예측된 제어봉 집합체의 수중 1m낙하 시 낙하시간은 약 1.1초이다.
• 4) 제어봉집합체의 낙하 전, 제어봉집합체 내/외부 단면을 통과하는 유량비는 약 2.75:1 이며, 제어봉집합체가 낙하하여 종단속도에 도달한 시간에 각 단면을 통과하는 유량비는 약 2.3:1이다.

향후 본 연구 결과를 바탕으로 수중 1m 낙하 시 낙하시간이 1초 이내 및 충격속도가 종단속도의 약 20% 수준으로 감소되도록 제어봉집합체 및 안내덕트 특히, damper의 주요 설계인자들을 도출, 변경한 후 수중 낙하시험을 통하여 CFD해석결과를 검증할 계획이다.

Acknowledgments

이 논문은 2014년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(사업명, No. 2012M2A8A2025639)

References

• Kim, K. R., Jang, K. J., Park, J. S., and Lee, W. J., (2010), “Drop time evaluation for SMART control rod assembly”, Proceeding of KFMA2010.
• Choi, K. S., and Kim, I. K., (1994), “Development of A computer program for drop time and impact velocity of the rod cluster control assembly”, Nuclear Engineering and Technology, 26(2), p197-204.
• Andriambololona, H., Bosselut, D., and Massin, P., (2007), “Methodology for a numerical simulation of an insertion or a drop of the rod cluster control assembly in a PWR,”, Nuclear Engineering and Design, 237(6), p600-606. [https://doi.org/10.1016/j.nucengdes.2006.09.001]
• Donis, J. M., and Goller, H., (1972), “A mathematical model of a control rod drop”, Nuclear Engineering and Design, 23(1), p107-120. [https://doi.org/10.1016/0029-5493(72)90193-8]
• Yoon, K. H., Kim, J. Y., Lee, K. H., Lee, Y. H., and Kim, H. K., (2009), “Control rod drop analysis by finite element method using fluid-structure interaction for a pressurized water reactor power plant”, Nuclear Engineering and Design, 239(10), p1857-1861. [https://doi.org/10.1016/j.nucengdes.2009.05.023]
• CFX manual, (2014), “ANSYS CFX Ver. 15,”, ANSYS Inc.
• Morrison, F. A., (2013), “Data correlation for drag coefficient for sphere”, Department of Chemical Engineering, Michigan Technological University, Houghton, MI, http://www.chem.mtu.edu/~fmorriso/DataCorrelationForSphereDrag2013.pdf.
• Schlichting, H., (1995), Boundary Layer Theory, McGraw-Hill, New York.
• White, F. M., (2006), Fluid Mechanics, 6th edition, McGraw-Hill, New York.
• Kikuchi, K., Konno, T., Ichikawa, S., Kubota, Y., and Mochizuki, O., (2013), “Unsteady Drag Coefficient of a Falling Sphere in Water”, JSME, 79(798), p151-163. [https://doi.org/10.1299/kikaib.79.151]