[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 19, No. 2, pp.5-10

ISSN: 2287-9706 (Print)

Print publication date Apr 2016

Received 11 Aug 2015 Revised 05 Jan 2016 Accepted 11 Jan 2016

DOI: https://doi.org/10.5293/kfma.2016.19.2.005

다점 피토관을 이용한 기체 유량 측정의 불확도 평가

양인영^*^{, †} ; 이보화^*

*한국항공우주연구원 엔진시스템연구팀

Uncertainty Assessment of Gas Flow Measurement Using Multi-Point Pitot Tubes

Inyoung Yang^*^{, †} ; Bo-Hwa Lee^*

*Engine system research team, Korea Aerospace Research Institute

Correspondence to: ^†E-mail : iyyang@kari.re.kr

Abstract

Gas flow measurement in a closed duct was performed using multi-point Pitot tubes. Measurement uncertainty was assessed for this measurement method. The method was applied for the measurement of air flow into a gas turbine engine in an altitude engine test facility. 46 Pitot tubes, 15 total temperature Kiel probes and 9 static pressure tabs were installed in the engine inlet duct of inner diameter of 264 mm. Five tests were done in an airflow range of 2~10 kg/s. The flow was compressible and the Reynolds numbers were between 450,000 and 2,220,000. The measurement uncertainty was the highest as 6.1% for the lowest flow rate, and lowest as 0.8% for the highest flow rate. This is because the difference between the total and static pressures, which is also related to the flow velocity, becomes almost zero for low flow rate cases. It was found that this measurement method can be used only when the flow velocity is relatively high, e.g., 50 m/s. Static pressure was the most influencing parameter on the flow rate measurement uncertainty. Temperature measurement uncertainty was not very important. Measurement of boundary layer was found to be important for this type of flow rate measurement method. But measurement of flow non-uniformity was not very important provided that the non-uniformity has random behavior in the duct.

Keywords:

Gas Flow Measurement, Multi-point Pitot Tubes, Measurement Uncertainty, Boundary Layer

키워드:

기체 유량 측정, 다점 피토관, 측정 불확도, 경계층

1. 서 론

한국항공우주연구원에서는 가스 터빈 엔진의 고공 환경 성능을 시험적으로 평가하기 위한 엔진고공환경시험설비(altitude engine test facility; AETF)를 운용하고 있다. 가스 터빈 엔진 중 터보젯 및 터보팬 엔진의 경우 엔진의 성능을 평가하기 위해서는 엔진으로 유입되는 공기의 유량을 평가하는 것이 반드시 필요하다. 이에 따라 AETF에는 벤투리 파이프 형식의 유량계를 설치하여 사용하고 있다. 그러나 벤투리 파이프가 대형, 대용량(공기 유량 2~10kg/s)임으로 인해 교정의 어려움 등이 있어 다른 공기 유량 측정 방법을 사용하여 상호 검증하는 것이 필요하였다.

벤투리 파이프 이외의 유량 측정 방법으로는 초음파 유량계, 열선식 유량계 등 다른 유량 측정 방법이 있다. 이 연구에서는 다점 피토관을 이용한 기체 유량 측정 방법을 적용하고자 하였다. 이것은 시험 대상물인 엔진 입구에서의 시험 조건(온도, 압력)을 정확히 정의하기 위해 기왕에 다점 피토관을 설치하여 사용하는 것이 필요하기 때문이었다. 이 연구에서는 이러한 기체 유량 측정 방법을 사용하는 데 있어서 측정 불확도를 평가함으로써 이 방법이 실효성을 가질 수 있는 측정 범위를 파악하고 이 방법의 측정 불확도를 향상시킬 수 있는 방법을 모색하고자 하였다.

다점 피토관을 사용한 기체 유량 측정 및 불확도 평가 방법에 관해서는 ISO 3966 표준⁽¹⁾을 참조할 수 있으나, 기존 연구 사례 중에서는 이를 충실히 따른 것이 많지 않다. 피토관의 가장 대표적인 용례인 유동 속도 측정에 관해서는 최진철⁽²⁾, 오세윤⁽³⁾ 등의 연구가 있으나 관내에서의 유량 측정과 연결시킨 연구는 아니었다. 임재명⁽⁴⁾, Nguyen⁽⁵⁾ 등의 연구는 유량 측정에 관한 연구이기는 하나 압축성을 고려하지 않은 저속 유동을 대상으로 하는 연구였다. 이번 연구에서는 저자 일동이 기존에 수행한 연구⁽⁶⁾의 연장선상에서 이상과 같은 연구 사례에서 다루지 않았던 압축성 기체 유동의 관내 유량 측정에 관한 연구를 수행하고자 하였으며, 앞서 언급한 ISO 표준에 따라 실제 시험 데이터를 적용해 보고자 하였다.

2. 기체 유량 측정 및 불확도 평가 방법

2.1 다점 피토관 배치

엔진고공환경시험설비에서는 엔진 공급 배관 상류에 벤투리 파이프가 설치되어 있다. 이 연구에서는 이에 더하여 엔진 입구 배관에 다점 피토관을 설치하여 공급 공기 유량을 측정하고자 하였다. 엔진 입구 배관은 내경 264mm인 원형 배관이다. 공기 유량 범위는 2~10kg/s이며 이 때 관내 유속은 최대 90m/s로서 압축성이 고려되어야 하는 조건이다.

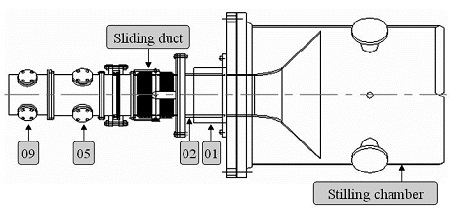
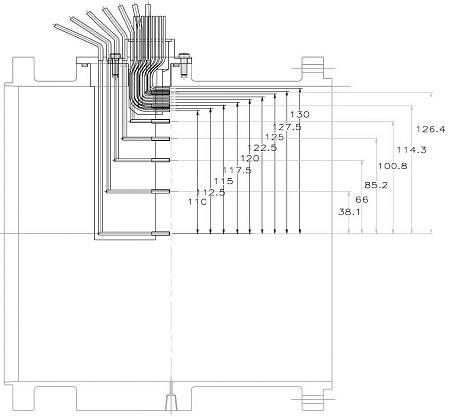
Fig. 1은 엔진 입구 배관의 형상이며 유동 방향은 그림의 오른쪽에서 왼쪽이다. 그림에서 “Stilling chamber”로 표시된 부분의 상류에 벤투리 파이프가 설치되어 있으며 “09”로 표시된 section의 하류에 엔진이 설치되어 있다. 다점 피토관은 “05”로 표시된 section에 장착된다. Fig. 2는 05 section에 설치된 다점 피토관의 배관 내 반경 방향 위치를 나타낸다. 피토관은 레이크의 형태로 설치되어 있는데, Fig. 2와 같이 반경 방향으로 16개의 피토관이 배치된 레이크가 배관 안에 원주 방향으로 120˚ 간격으로 3세트 설치되어 있다. 단, 배관 중심에 위치한 피토관은 그 중 1세트에만 있으며 나머지 2세트에는 없으므로 나머지 2세트에는 15개씩의 피토관이 있다(총 46개 피토관). 이와 별도로 공기 유동의 전온도를 측정하는 Kiel type 프로브 레이크가 있는데, 역시 3세트이며, 원주 방향으로 120˚ 간격으로 설치되어 있고, 각각 반경 방향으로 5개의 프로브에서 전온도를 측정한다(총 15개 프로브). 또한 05 section의 벽면에 40˚ 간격으로 9개의 측정용 hole을 설치하여 각각의 벽면 정압력을 측정한다.

Fig. 1

Layout of the test facility

Fig. 2

Layout of the multi-point Pitot tubes (Numbers are the distance from the duct center line (in mm))

2.2 기체 유량 측정 방법

기체 유량 측정 방법은 이보화 등⁽⁶⁾에 상세히 기술되어 있는데, 여기에서는 논문의 전개를 위하여 간략히 인용하고, 부록에 ISO 3966 표준⁽¹⁾과의 차이를 기술하였다.

공기 유량 W₀₅는 식 (1)로 계산한다. 식 (1)에서 공기 유속 V₀₅는 배관 내 유동의 마하 수 M_D_,05와 유동의 음속 a₀₅를 구하여 식 (2)와 같이 계산한다. 음속은 식 (3)과 같이 계산하며, 여기에서 정온도 T_s_,05는 식 (4)로 계산한다. 식 (1)에서의 밀도 ρ₀₅는 식 (5)로 계산한다.

W 05 = ρ 05 π 4 D 052 V 05

(1)

V 05 = M D, 05 × a 05

(2)

a 05 = γ RT s, 05

(3)

T s, 05 = T t, 05 1 + γ - 1 2 M D, 05 2

(4)

ρ 05 = p s, 05 RT s, 05

(5)

여기에서 p_s_,05는 원주 방향으로 여러 위치에서 측정한 벽면 정압력 M_D_,05,_k의 산술평균값이다. 그런데 M_D_,05나 T_t_,05는 반경 방향으로도 일정하지 않기 때문에 각 지점에서 측정한 압력과 온도를 사용한 평균값을 적용하여야 한다. 위 식 (2) 및 식 (4)에서 M_D_,05와 T_t_,05는 각 프로브가 대표하는 배관 내 면적의 가중 인자를 고려한 면적 평균으로 구한다. 즉,

M D, 05 = ∑ i = 2 17 M D, 05, i + M D, 05, i - 1 2 r p t, i 2 - r p t, i - 1 2 D 052 / 4

(6)

T t, 05 = ∑ j = 2 5 T t, 05, j + T t, 05, j - 1 2 r T t, j 2 - r T t, j - 1 2 D 052 / 4

(7)

여기에서 i, j는 각각 전압력 레이크, 전온도 레이크 상의 프로브의 번호이며 r_pt,i, r_Tt,j는 그 각각의 프로브의 반경 방향 위치이다. 전온도 T_t_,05,_j는 직접적인 측정값이며 M_D_,05,_i는 식 (8)과 같이 구한다.

M D, 05, i = 2 γ - 1 p t, 05, i - p s, 05 p s, 05

(8)

정리하면, 공기 유량은 각 프로브에서 측정한 전온도, 전압력, 정압력과 나머지 인자(덕트 직경, 기체 상수, 기체 비열비, 프로브의 위치)의 함수이다. 이 나머지 인자는 아래와 같이 상수로 가정하였다.

(1) R=287.04, γ=1.4인 상수이다.
(2) D₀₅, r_pt,i, r_Tt,j는 기하학적 측정으로 얻어지는 값이며 상수이다.

2.3 측정 불확도 계산 방법

측정 불확도 계산 방법은 ISO⁽⁷⁾의 방법을 따른다. 측정 불확도 계산에 있어서 R, γ, D₀₅, r_pt,i, r_Tt,j의 측정 불확도는 무시하였다. 결과적으로 기체 유량의 측정 불확도에 기여하는 변수는 p_t_,05,_i, T_t_,05,_j, p_s_,05,_k의 세 변수이다. 이 세 변수 각각의 감도 계수와 표준 측정 불확도를 계산하고 이를 합성하여 기체 유량의 측정 불확도를 계산한다. 식으로 나타내면 식 (9)와 같다.

u 2 W 05 = ∑ i ∂ W 05 ∂ p t, 05, i 2 u 2 p t, 05, i + ∑ j ∂ W 05 ∂ T t, 05, j 2 u 2 T t, 05, j + ∑ k ∂ W 05 ∂ p t, 05, k 2 u 2 p s, 05, k

(9)

여기에서 감도 계수를 계산하기 위한 편미분은 각 측정 인자 1% 변화에 대한 W₀₅의 변화량으로 수치적으로 근사화하여 계산한다. 측정 인자 p_t_,05,_i, T_t_,05,_j, p_s_,05,_k의 표준 측정 불확도는 실제 시험 데이터의 산포 및 각각의 측정 계통 상에서 발생하는 불확도 요인을 A형⁽⁷⁾과 B형⁽⁷⁾ 방법으로 평가한다. 이 연구에서 p_t_,05,_i 및 p_s_,05,_k 측정 센서는 실제로는 대기압과의 차압을 측정하며, 그 측정값에 대기압 측정 센서의 측정값을 더하여 p_t_,05,_i=p_t_,05,_i,g+p_atm, p_s_,05,_k=p_s_,05,_k,g+p_atm과 같이 계산되므로 이를 합성하여야 한다. 또한 p_t_,05,_i,g와 p_s_,05,_k,g는 센서의 불확도 외에 추가 불확도 요인이 없으나 p_atm은 센서 불확도에 아날로그-디지털 변환(ADC) 보드의 불확도를 추가하여야 한다. T_t_,05,_j도 센서 불확도에 ADC 보드의 불확도를 추가하여야 한다. Table 1에 이러한 측정 불확도 요인을 정량화하여 정리하였다.

Table 1

Uncertainty components and their values

3. 측정 불확도 평가 및 분석

3.1 시험 데이터

측정 불확도 평가를 위하여 실제 시험을 수행하였다. 시험은 정해진 배관 및 다점 피토관 형상에 대해 공기 유량 약 2~10kg/s 범위 내의 5개 공기 유량 값에 대해 수행하였다. 시험 데이터 및 그로부터 위 2.2절과 같은 방법으로 계산한 유량 데이터는 Table 2와 같다. 표에서 전압력, 전온도, 정압력 데이터는 편의상 1개 대표 센서의 값만 나타내었다. 파이프 레이놀즈 수는 Re_D=450,000~2,220,000 범위이다.

Table 2

Airflow measurement uncertainty and uncertainty percentage contributions of each measured parameters

W₀₅는 벤투리 유량계로 측정한 W_ven에 비하면 최대 1.73%까지 차이가 난다. 저유량에서는 W_ven보다 W₀₅가 많은 것으로 측정되고 고유량에서는 적은 것으로 측정되는데, 아래에 기술한 것처럼 저유량에서는 W₀₅의 불확도가 다소 높기 때문에 고유량에서의 경향을 받아들이는 것이 옳다고 판단된다. W_ven보다 W₀₅가 적게 측정되는 이유에 대해서는 추가적인 분석이 필요하다.

3.2 측정 불확도 평가

2.3절의 방법으로 평가한 유량의 확장 불확도(extended uncertainty)도 Table 2에 나타내었다. 불확도의 절대값(2×uW₀₅)을 보면 대체로 저유량에서 값이 크고 고유량에서 값이 작음을 알 수 있다. 따라서 상대 측정 불확도도 저유량에서 크다. Case 1(유량 2.015kg/s)에서는 상대 확장 불확도가 6.1%에 이르러 다점 피토관을 이용한 유량 측정을 적용하는 것이 적절하지 못한 영역이라 할 수 있다. 반면 case 2(유량 3.911kg/s) 이상에서는 불확도가 2% 이하이므로 다른 측정 방법과 비교해 나쁘지 않다고 할 수 있다.

Table 3

Air flow calculation result based on various assumptions

불확도의 절대값이 저유량에서 큰 이유는 다음과 같다. 다점 피토관을 이용한 유량 측정 방법에서는 유동의 전압력과 정압력의 차(p_t_,05,_i-p_s_,05)를 이용하여 유량을 계산하는데(식 (8)) 저유량에서는 이 값이 거의 0에 가까워지기 때문에 p_t_,05,_i나 p_s_,05_k의 감도 계수가 커져 측정 불확도가 커진다. 이번 연구에서의 데이터를 보면 case 1에서는 p_t_,05,_i-p_s_,05=0.556kPa이고 case 2에서는 p_t_,05,_i-p_s_,05=7.70kPa이다. 참고문헌 (1)에 따르면 이번 시험에서 p_t_,05,_i-p_s_,05=3Pa 이상이면 피토관을 이용한 유량 측정 방법을 적용할 수 있다고 하였으나(해당 문헌 8.1절의 조건식) 실제로는 불확도 측면에서 만족할 만한 측정을 하기 위해서는 그보다 훨씬 높은 차압 조건이 필요하였다.

또한 Table 2에는 각 측정 인자가 공기 유량의 측정 불확도에 얼마나 기여하는지를 나타내는 불확도 퍼센트 기여도(uncertainty percentage contribution; UPC)를 함께 나타내었는데, 편의상 46개 전압력 측정 인자의 UPC의 합, 15개 전온도 측정 인자의 UPC의 합, 9개 정압력 측정 인자의 UPC의 합으로 나타내었다. 이 연구에서 사용한 데이터의 경우 정압력의 UPC가 나머지 인자에 비해 크게 높았으며, 다음으로 전압력, 전온도의 순이었다. 전온도의 UPC는 고유량에서 늘어나며, 전압력과 정압력의 UPC는 유량에 따라 뚜렷한 경향이 나타나지 않았다.

3.3 경계층 데이터가 유량 계산 결과에 미치는 영향

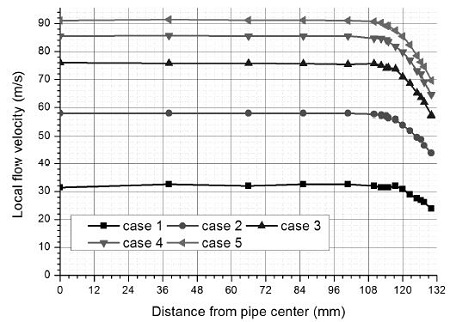
Fig. 3은 피토관 데이터를 이용하여 계산한, 각 시험 조건별 덕트 내 반경 방향 유속 분포를 나타낸다. 그림을 보면 case 1의 경우에는 경계층 두께가 약 12mm 정도이고 나머지 case의 경우에는 20mm 내외이다. 또한 유속이 높을수록 경계층 두께가 두꺼워지는 것도 관찰된다.

Fig. 3

Flow velocity distribution at each radius for various test cases

경계층을 무시하고 배관 중심에 가까운 5개의 피토관에서 측정한 전압력만을 사용하여 유량을 계산한 결과를 Table 3에 나타내었다. 경계층을 고려한 Table 2의 결과에 비해 유량이 5.3~6.4% 높게 계산되었다. 따라서 다점 피토관을 사용한 유량 측정의 경우 경계층을 잘 측정하는 것이 반드시 필요함을 알 수 있다.

3.4 유동 불균일성이 유량 계산 결과에 미치는 영향

이 연구의 경우 원주 방향으로는 3군데에서만 측정했으므로 측정 데이터를 사용하여 유동 불균일성을 논하기는 어렵지만 유동 불균일성의 영향을 일반화하여 논의하는 데에 참고값으로 삼기로 한다. 이 연구에서의 유동은 경계층이 있는 유동인 관계로 반경 방향의 불균일성은 필연적으로 존재하므로 원주 방향의 불균일성만 다루기로 하고 유동 불균일도를 “동일한 반경에 있는 3개의 전압력 측정값의 표준 편차(σ(p_t_,05,_r))”로 정의하였다.

유동 불균일도는 유속에 따라서도 다르고 반경 방향 위치에 따라서도 다른데, 시험 데이터로부터 계산한 각 반경에서의 유동 불균일도의 최대값(max(σ(p_t_,05,_r)))을 Table 3에 나타내었다. 표를 보면 유동 불균일도는 유량 계산의 참조값인 p_t_,05,_i-p_s_,05과 비교하면 7.2~12%에 달하는 큰 값이며, 시험 조건에 따라서는 case 1에서 최소이고 case 5에서 최대이다.

유동 불균일도를 무시하고 측정을 수행하여 이를 바탕으로 유량을 계산하는 경우 유동 불균일도를 고려하는 것에 비해 유량 계산 결과가 얼마나 차이가 나는지를 알아보기 위해 시험 데이터 중 1개 레이크의 측정값만을 사용하여 유량을 계산해 보았다. 그 결과를 Table 3에 나타내었는데, Table 2와 비교하여 최대 0.6% 차이가 났다. 유동 불균일도에 비하여 유량 계산값의 차이가 적은 것은 이번 연구의 시험에서 유동의 불균일도가 어느 한 방향으로 편중되지 않았기 때문이다. 또한 유동 불균일도를 정의하는 데 사용된 p_t_,05,_i의 공기 유량에 대한 UPC가 앞서 3.2절에서 기술한 것처럼 높지 않다는 점도 원인이다.

4. 결 론

이상과 같은 연구 결과로부터 다음 결론을 얻었다.

1) 다점 피토관을 이용한 기체 유량 측정은 일정한 조건 하에서 다른 기체 유량 측정 방법에 비해 경쟁력이 있는 측정 불확도를 확보할 수 있어 충분히 사용 가능한 방법이다.
2) 이 방법은 배관 내 유속에 따라 측정 불확도가 달라지므로 필요한 측정 불확도를 확보하기 위해서는 배관 내 최저 유속을 제한하여 사용할 필요가 있다. 이 방법을 사용할 수 있는 유속은 일반적인 산업 현장에서 사용하는 것보다는 고속이다.
3) 이 방법에서는 배관 내 유동의 정압력을 정확히 측정하는 것이 가장 중요하며 유량 측정의 불확도를 향상시키기 위해서는 가장 먼저 정압력 측정의 불확도를 향상시키는 것이 필요하다.
4) 이 방법에서는 경계층을 반드시 고려하여야 한다.
5) 유동 불균일성이 있는 유동이라 해도 불균일성이 특정 방향으로 편중되지 않는다면 기체 유량 계산 결과에 큰 영향을 미치지 않는다.

Acknowledgments

본 논문은 2015년도 국가과학기술연구회 사업 재원으로 지원을 받아 작성된 논문임(CMPp.-13-5-KARI).

References

ISO, (2008), Measurement of Fluid Flow in Closed Conduits – Velocity Area Method Using Pitot Static Tubes, ISO 3966:2008.
Choi, J. C., Lee, K. G, and Park, C. W, (2001), “Development of the Pitot-Tube to Measure Flight Altitude and Velocity,”, Journal of the Korean Society of Propulsion Engineers, 5(3), p19-2424.
Oh, S. Y, Lee, J. G, Kim, S. C, Kim, S. H, and Ahn, S. K, (2012), “An Experimental Study of Test Section Velocity Calibration for Low-Speed Wind Tunnel,”, Journal of The Korean Society for Aeronautical and Space Sciences, 40(3), p230-236. [https://doi.org/10.5139/JKSAS.2012.40.3.230]
Lim, J. M, (2000), An Experimental Study on the Flow Measurement by Using Multi-point Pitot Tube, Master Thesis, Mokpo National University.
Nguyen, D. T, (2013), Evaluation of Uncertainty for Gas Flow Measurement with S Pitot Tube, Master Thesis, University of Science and Technology.
Lee, B. H, Lee, K. J, and Yang, S. S, (2010), “The Preduction of Air Flow and Pressure Loss at Inlet Duct,”, Journal of the Korean Society of Propulsion Engineers, 14(1), p48-55.
ISO/IEC, (2008), Uncertainty of Measurement – Part 3: Guide to the Expression of Uncertainty in Measurement, ISO/IEC Guide 98-3.

Appendix

이 논문에서 사용한 공기 유량 측정 방법은 ISO 3966 표준(이하 “표준”으로 칭함)과 거의 동일하며, 아래와 같은 점에서만 차이가 있다.

1) 이 논문에서의 유동 마하 수는 표준에서 제시한 상한인 마하 0.25보다 높다. 따라서 표준의 Annex E에 제시된 압축성 유동에 대한 식을 사용하였다.
2) 이 논문에서 사용한 피토관은 표준 피토관과 형상의 차이가 있다. 이 논문에서 사용한 장치는 여러 개의 전압력 프로브를 rake 형태로 동시에 사용하며, 각 프로브는 단면이 flat한 형상이다.
3) 정압력 탭은 프로브 상에 위치하지 않고 덕트 벽면에 위치한다. 정압력 탭의 유동 방향 위치는 전압력 프로브의 tip과 동일한 위치이다. 유동 방향과 수직한 임의의 단면 전체에서 정압력은 일정한 것으로 가정하였다.
4) 표준에서는 속도 적분 시 벽면에서의 유속 분포를 Karman의 법칙으로 고려했으나 이 논문에서는 벽면 non-slip 조건과 power 법칙(7승)으로 고려했다.
5) 표준에 제시된 피토관의 stem에 대한 보상, 반경 방향 속도 분포에 대한 보상, 난류에 대한 보상(표준 12장 참조)은 이 논문에서는 수행하지 않았다.